函数单调性的概念
函数单调性的概念)

目 录
• 函数单调性的定义 • 判断函数单调性的方法 • 函数单调性的性质 • 函数单调性的应用 • 反例与特殊情况
01 函数单调性的定义
单调增函数
01
02
03
总结词
单调增函数是指函数在某 个区间内,随着自变量的 增加,函数值也单调增加 的函数。
详细描述
单调增函数的定义是,对 于任意两个数$x_1$和 $x_2$($x_1 < x_2$), 如果函数$f(x)$满足 $f(x_1) leq f(x_2)$,则称 $f(x)$在区间$[x_1, x_2]$ 上单调增。
单调函数的连续性是其基本性质之一。在单调递增的函数中,如果函数在某一点的左侧 小于该点的值,那么在该点的右侧也必然小于该点的值,即函数值随着自变量的增大而 增大。同样地,在单调递减的函数中,函数值随着自变量的增大而减小。因此,单调函
数在其定义域内是连续的,不存在间断点。
单调函数的可导性
总结词
单调函数的可导性是指函数在单调区间 内是可导的,即函数的导数在单调区间 内存在且不为零。
数学表达
如果对于所有$x_1 < x_2$, 都有$f(x_1) geq f(x_2)$, 则称$f(x)$为减函数。
严格单调函数
总结词
严格单调函数是指函数在某个区间内,对于任意两个不同的自变量,其函数值也不同的函 数。
详细描述
严格单调函数的定义是,对于任意两个不同的数$x_1$和$x_2$($x_1 < x_2$),如果函数 $f(x)$满足$f(x_1) < f(x_2)$或$f(x_1) > f(x_2)$,则称$f(x)$在区间$[x_1, x_2]$上严格单调。
数学表达
数学函数的单调性

05
单调性的扩展知识
单调性与周期性
总结词
函数的单调性与周期性是两个相对独立的概念,但它 们之间也存在一定的联系。
详细描述
单调性是指函数在某一区间内的增减性,而周期性是指 函数按照一定的时间间隔重复出现的现象。虽然单调性 不直接决定函数的周期性,但它们在某些情况下会相互 影响。例如,一些周期函数可能在某些周期内表现出单 调性,而单调函数可能在不同的单调区间内具有不同的 周期。
总结词
单调性与函数值的大小关系是指,在单调递增的函数中 ,自变量x越大,函数值y也越大;在单调递减的函数中 ,自变量x越大,函数值y越小。
详细描述
单调性是描述函数值随自变量变化趋势的一种特性。对 于单调递增的函数,随着自变量x的增大,函数值y也相 应增大。这意味着在函数的整个定义域内,随着x的增加 ,y的值也持续增加。而对于单调递减的函数,随着x的 增大,y的值反而减小。这种单调性可以通过函数的导数 或微分进行判断。
单调性与不等式
总结词
单调性是解决不等式问题的关键因素之一,通过分析函数的单调性可以解决许多不等式问题。
详细描述
不等式是数学中一类重要的方程,通过分析函数的单调性可以解决许多不等式问题。例如,利用函数的单调递增 性质可以证明不等式,通过构造函数并在特定的区间内证明其单调递增,从而证明不等式的正确性。此外,利用 函数的单调性还可以求解一些不等式问题,例如求解一些函数的极值问题等。
要点二
详细描述
单调性的传递性是数学函数的一个重要性质。如果函数f在某 个区间I内单调增加,并且函数g在另一个区间J内也单调增加, 那么复合函数f○g(即f和g的复合函数)在f和g都有定义的区 间I∩J内也将单调增加。同样地,如果f和g都是单调减少的, 则f○g也将是单调减少的。
函数的单调性(定义法)

函数的单调性知识点:1.函数单调性定义(1).定义法,对任意的x1,x2∈D,D⊆I,x1>x2 ,若f(x1)−f(x2)>0则称f(x)在D 内是单增,若f(x1)−f(x2)<0则称f(x)在D内是单减.(2). 对定义在D上的函数f(x),设x1,x2∈D, D⊆I , x1<x2,则有:①f(x1)−f(x2)x1−x2>0⇔f(x)是D上的单调递增函数;②f(x1)−f(x2)x1−x2<0⇔f(x)是D上的单调递减函数.(注意:函数的单调性的局部性(注意:函数的单调性,从定义上来讲,是指函数在定义域的某个子区间上的单调性,是局部的特征,在某个区间上单调,在整个定义域上不一定单调。
求单调区间时,必须先求出函数的定义域;单调区间只能用区间表示,若有多个单调区,应分别写),函数的单调性最值主要涉及初等函数、复合函数、抽象函数、分段函数等情况.)2.复合函数的单调性:3.几种常见函数的单调性:f(x)=ax+bcx+d (abcd≠0,bc≠ad);f(x)=ax +bx(ab≠0)例1.多种方法判断下列函数的单调性:(1).f(x)=x + 1x x∈(0,1)(2).y=x−1xx∈(0,+∞); (3).y=x3x∈R;(4).f(x)=axx²−1,x∈(-1,1)(a≠0)(5).f(x)=x+√1+x2,x∈R例2.(1).已知f(x)=x(x≠a),若a>0且f(x)在(1.+∞)内单调递减,求a的x−a在区间[1,2]上都是减函数,求a的取值取值范围. (2).若f(x)=−x2+2ax,与g(x)=ax+1范围.(3).已知函数f(x)= √3−ax(a≠1)若f(x)在区间(0,1]上是减函数,则a−1实数a的取值范围.(4).已知函数f(x)=√x²+1–ax(a>0)①.证明当a≥1时,函数f(x)在区间[0,+∞)上为单调减函数.②.若函数f(x)在区间[1,+∞)上是增函数,求a的取值范围。
函数的单调性

4.1、函数的单调性函数的单调性就是函数的一种增减性,主要看y 随x 的变化而发生的一种变化情况,简单的说当y 随x 的增大而增大时,就说y 是在相应的x 的取值范围内是增函数,对应的区间为其增区间;而当y 随x 的增大而减小时,我们就说y 是在相应的x 的取值范围内是减函数,对应的区间为其减区间。
A 、定义:一般地,设函数)(x f 的定义域为I 。
如果对于定义域I 内的某个区间D 上的任意两个自变量的值21,x x ,当21x x <时,都有)()(21x f x f <,那么就说函数)(x f 在区间D 上是增函数。
如果对于定义域I 内的某个区间D 上的任意两个自变量的值21,x x ,当21x x <时,都有)()(21x f x f >,那么就说函数)(x f 在区间D 上是减函数。
如果函数)(x f y =在区间D 上是增函数或减函数,那么就说函数)(x f y =在这一区间上具有(严格的)单调性,区间D 叫做)(x f y =的单调区间。
B 、函数单调性的证明对于某区间内的函数的单调性,一般利用定义来证明,其基本步骤如下: (1)取值:设21,x x 为该区间内的任意两个值,并且21x x <;(2)作差变形:作差)()(21x f x f -,并利用因式分解、配方、有理化等方法向有利于判断差值的符号的方向变形;(3)定号:确定差值的符号,当符号不确定时,可考虑分类讨论; (4)下结论:根据函数的单调性的定义得出结论。
C 、函数单调性的判断判断函数单调性的常用方法有:(1)定义法:即“取值——变形——定号——下结论”;(2)图像法:先作出函数的图像,在利用图像的形象直观判断函数的单调性;(但应注意极值点及其拐点) (3)复合法:)(x f y =增 增 减 减(4)导数法:求出函数导数后,在令其导数大于零的x 的连续区间为其单调递增区间,令其导数小于零的x 的连续区间为其单调递减区间;4.1.1、函数单调性的判断与证明A 、函数单调性的证明:1、证明函数12)(+-=x x f 在R 上是减函数。
函数的单调性知识点
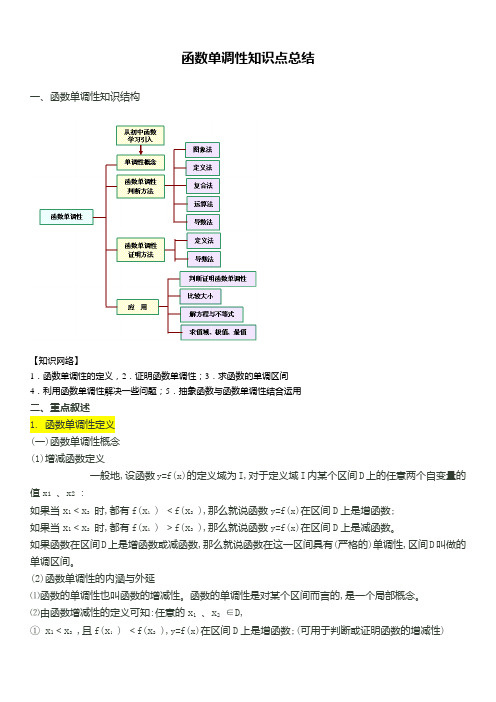
函数单调性知识点总结一、函数单调性知识结构【知识网络】1.函数单调性的定义,2.证明函数单调性;3.求函数的单调区间4.利用函数单调性解决一些问题;5.抽象函数与函数单调性结合运用二、重点叙述1. 函数单调性定义(一)函数单调性概念(1)增减函数定义一般地,设函数y=f(x)的定义域为I,对于定义域I内某个区间D上的任意两个自变量的值x1、x2 :如果当x1<x2时,都有f(x1 ) <f(x2 ),那么就说函数y=f(x)在区间D上是增函数;如果当x1<x2时,都有f(x1 ) >f(x2 ),那么就说函数y=f(x)在区间D上是减函数。
如果函数在区间D上是增函数或减函数,那么就说函数在这一区间具有(严格的)单调性,区间D叫做的单调区间。
(2)函数单调性的内涵与外延⑴函数的单调性也叫函数的增减性。
函数的单调性是对某个区间而言的,是一个局部概念。
⑵由函数增减性的定义可知:任意的x1、x2∈D,① x1<x2 ,且f(x1 ) <f(x2 ),y=f(x)在区间D上是增函数;(可用于判断或证明函数的增减性)② y=f(x)在区间D 上是增函数,且x 1<x 2 , f(x 1) <f(x 2 ) ;(可用于比较函数值的大小) ③ y=f(x)在区间D 上是增函数,且f(x 1) <f(x 2 ), x 1<x 2 。
(可用于比较自变量值的大小) 2. 函数单调性证明方法证明函数单调性的方法有:定义法(即比较法);导数法。
实际上,用导数方法证明一般函数单调性是很便捷的方法,定义法是基本方法,常用来证明解决抽象函数或不易求导的函数的单调性。
(1)定义法:利用增减函数的定义证明。
在证明过程中,把数式的大小比较转化为求差比较(或求商比较)。
⑴转化为求差比较证明程序:①设任意的x 1 、x 2∈D,使x 1<x 2 ; ②求差—变形—判断正负;此为关键步骤,变形大多要“因式分解”。
求差:; 变形:化简、因式分解; 判断:差的符号的正或负。
函数的单调性

二、函数单调性的判断与证明 a 例2判断函数 f(x)=x+ (a>0)在(0,+∞)上的单调性. x 【解析】解法一:定义法略,一般不用此方法. a a 解法二:f′(x)=1- 2,令 f′(x)≥0,则 1- 2≥0, x x ∴x≥ a或 x≤- a(舍). a 令 f′(x)≤0,则 1- 2≤0, x ∴- a≤x≤ a,∵x>0,∴0<x≤ a. ∴f(x)在(0, a]上为减函数,在[ a,+∞)上为增 函数.
三、函数单调性应用 例3 (1) 已知函数 f(x)= x2+ 2(a- 1)x+ 2 在区间 (- ∞,4]上是减函数,求实数 a 的取值范围. (2)已知函数 f(x)在实数集中满足 f(xy)=f(x)+f(y), 且 f(x)在定义域内是减函数. ①求 f(1)的值; ②若 f(2a-3)<0,试确定 a 的取值范围.
【解析】依据函数解析式,通过判断定义域和单调 性,逐项验证. A 项,函数定义域为 R,但在 R 上为减函数,故不 符合要求;B 项,函数定义域为 R,且在 R 上为增函数, 故符合要求;C 项,函数定义域为(0,+∞),不符合要 求;D 项,函数定义域为 R,但在(-∞,0]上单调递减, 在[0,+∞)上单调递增,不符合要求.
a 4.若函数 f(x)=-x +2ax 与 g(x)= 在区间[1, x+1 2]上都是减函数,则 a 的取值范围是( D ) A.(-1,0)∪(0,1) B.(-1,0)∪(0,1] C.(0,1) D.(0,1] 【解析】∵f(x)=-x2+2ax=-(x-a)2+a2,由图 象可知, 当 a≤1 时,f(x)在[1,2]上是减函数. a g(x)= ,当 a>0 时,在[1,2]上是减函数, x+ 1 ∴a 的取值范围是(0,1].
函数单调性的概念

在[0, )上单调增加; f (0) 0,
当x 0时, x ln(1 x ) 0, 即 x ln(1 x ).
利用单调性证明不等式的步骤: ①将要证的不等式作 恒等变形(通常是移项)使 一端为0另一端即为所作的辅助函数f(x);
②求 f ( x ) 验证f(x)在指定区间上的单调性; ③与区间端点处的函数值或极限值作比较即得证.
/
例3.设f (x) = ax3+x恰有三个单调区间,试确定a的 取值范围,并求其单调区间.
解: f x 3ax 2 1,
若a 0, 则f x 在(-, )恒正, f x 只有一个单调区间,与题意不符.
1 1 1 2 若a<0,则f x 3a x x , 3a x 3a 3a 3a 1 1 a 0时, f x 有三个单调区间,(-,],[ , ) -3a -3a 1 1 为它的减区间, , 为它的增区间. -3a -3a
当 x 1时, f ( x ) 0, 在( ,1]上单调增加; 当1 x 2时,
f ( x ) 0, 在[1,2]上单调减少;
当2 x 时, f ( x ) 0, 在[2, )上单调增加;
单调区间为 ( ,1], [1,2], [2, ).
2
x 0, ln( x 1 x ) ln 1 0
2
x 0时, f ( x) f ( x ) f (0) 0
x 0时,1 x ln( x 1 x ) 1 x .
2 2
例8.设f ( x), g ( x)在[a, b]上可导, 且f ( x) g ( x),
函数的单调性奇偶性与周期性

函数的单调性、奇偶性与周期性基础知识一、函数的单调性 1. 单调性概念如果函数y= f (x )对于定义域I 内某个区间上的任意两个自变量的值x 1、、x 2,当x 1、<x 2时, ①都有f (x 1)< f (x 2),则称f (x )在这个区间上是增函数(或单调递增),而这个区间称函数的一个单调递增区间 ;②都有f (x 1)> f (x 2),则称f (x )在这个区间上是减函数(或单调递减),而这个区间称函数的一个单调减区间.注意,若函数f (x )在整个定义域I 内只有唯一的一个单调(递增或递减)区间,则f (x )称单调函数.2. 函数的单调性与其导函数的正负有如下关系:在某个区间(,)a b 内,如果/()0f x >,那么函数()y f x =在这个区间内是单调递增; 如果/()0f x <,那么函数()y f x =在这个区间内是单调递减。
二、函数的奇偶性 3.奇偶性概念如果对于函数f (x )定义域内的任意x ,①都有f (-x )=-f (x ),则称f (x )为奇函数;②都有f (-x )= f (x ),则称f (x )为偶函数;③如果函数f (x )不具有上述性质,则f (x )不具有奇偶性.④如果函数同时具有上述两条性质,则f (x )既是奇函数,又是偶函数。
注意:函数f (x )具有奇偶性的必要条件是其定义域关于原点对称。
4.性质:一个函数是奇函数的充要条件是它的图象关于原点对称;一个函数是偶函数的充要条件是它的图象关于y 轴对称。
5.函数f (x )为奇函数,且在0x =处有定义,则(0)0f =三、函数的周期性 6.周期性概念如果存在一个非零常数T ,使得对于函数定义域内的任意x ,都有f (x+T )= f (x ),则称f (x )为周期函数。
T 是f (x )的一个周期。
若f (x )的周期中,存在一个最小的正数,则称它为f (x )的最小正周期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长郡中学高一第一学期第一次模块检测卷
时量:120分钟 满分:150分
一、选择题:本大题共I5小题,每小题3分.共45分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.A {x |x 410x N }B {x |x 20m m N }++=∈==∈已知集合是与的公倍数,,,, 则A 与B 的关系是( )
2.已知S={X|X 是平行四边形或梯形},A={X|X 是平行四边形},B={X|X 是菱形},C={X|X 是矩形},下列式子不成立的是
A 、
B
C x1x ⋂={是正方形}
B 、∁A B={x|邻边不相等的平行四边形},
C 、∁S A={x|x 是梯形}.
D 、A B C ⋃= 3.2U 3U R A {x |}B {x |x 12x 200}7
x x -==≤=-+<⋃-,已知集合0,,则(A B )= A 、{}x |x 210x ≤>或 B 、{}x |x 210x ≤≥或
C 、{}x |x 27x <≥或
D 、{}x |x 37x ≤>或
4、下列每组函数中f (x )与g (x )相同的是 A.2
x f x 1g x 1x x
=-=-(),() B. 33f x g x ()x x ==()
,() C. 0f x 1g x x ==()
,() D. 361x f x g x x x
==(),()5.已知f(x)=x 2+bx+c,且f(1)=f(3)=0,则f(x)的单调递减区间为( )
6、已知函数f(x)是定义在上的奇函数,当x>0时,()2f x (1)x x =-那么方程f(x)=0的实数跟个数为
A 、1
B 、2
C 、3
D 、4
7、已知集合2{1}A x x ==,{ax 10}B x ==-若A B A =,则实数a 的取值为
A 、1
B 、-1
C 、-1,1
D 、-1,0,1
8、已知13-33,x +x =x x -+=则
A 、85
B 、35
C 、18
D 、35±
9、化简2222(2)()a a a a ---+÷-的结果为
A 、1
B 、-1
C 、2211a a -+
D 、2211
a a +- 10、函数y 3x =与1y 3x
=-的图像关于 A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y =x 对称 11、已知函数,则实数a 的取值范围是
A 、(,1)(2,)-∞-+∞
B 、(1,2)-
C 、(2,1)-
D 、(,2)(1,)-∞-+∞
12、设函数f(x)x ∈(R )
为奇函数,()1f 12=,()()()f x+2f x f 2=+,则()f 5= A 、0 B 、1 C 、52
D 、5 13、若二次函数()2f x 21ax ax =++在[]3,2-上有最大值4,则实数a 的值为
A 、-3
B 、38
C 、
D 、 14、已知集合{y ()0}A x x y x =+=(,),{y 1}B x y ==(,),则A
B =
A 、{(1,1),(1,1)}--
B 、{(1,1)}-
C 、{(1,1),(0,1),(0,1),(1,1)}---
D 、{(1,1),(0,1),(0,1)}--
15、定义在(0,)+∞上的函数f(x)满足()()f 2x 2f x =,且当[)1,2x ∈时,f(x)=2-x ,x 1、x 2是方程f(x)=a (0<a 《1)的两个实根,则x 1-x 2不可能是
A 、30
B 、56
C 、80
D 、112
二、填空题:本大题共5小题,每小题3分,共15分,把答案填写在题中的横线上
16、已知函数()24x f x 1x +-=,则它的定义域为 17、已知集合,当A 为非空集合时a 的取值范围是
18、一种产品的产量原来为a ,在今后m 年内,计划使产量每年比上一年增加p %,则产量y 随年数x 变化的函数解析式为 ,定义域为 。
19、用min {a ,b ,c }表示a ,b ,c 三个数的最小者,设()f x min -2x+210-x x ≥={,,}(0) (1)f (3)=
(2)若0《x 《8,记f (x )的最大值为M ,最小值为m ,则M+m =
20、若13x <<,
(1)方程①有解时a 的最大值为
(2)方程①有两个不同解时a 的取值范围是
三、解答艇:本大题共5小题,每小题8分,共40分,要求写出必要的文字说明、证明过程或演算步骤。
21.(本小题满分8分)
计算:
(1)43333133246339
(2)20.52037103720.12392748
π+++--()()-
22.(本小题满分8分)
设全集U R =,已知集合2M (3)0)x =+≤{x },261N?{2()}2
x x x -== (1)求()U M N ⋂
(2)记集合()U A M N =⋂,已知{}B xla 1x 5a,a R =-≤≤-∈,若A B B ⋂=,求a 的取值范围.
23.(本小题满分8分)
已知函数()2x f x =,1()22x g x =
+ (1)求两数g(x)的值域.
(2)当f(x)=g (x)时,求2x 的值.
24.(本小题满分8分)
设函数()221
x f x a =-+ (1)求函数f(x)为奇函数时a 的值.
(2)探索f(x)的单调性、并使用单调函数定义给出证明.
(3)若关于x 的不等式()2f x kx 10-+>恒成立.求k 的取值范围.
25.(本小题满分8分)
已知某产品关税与市场供应量P的关系式近似地满足()
P x=(其
中,t为关税的税率,且
1
0,
2
t
⎡⎫
∈⎪
⎢⎣⎭,x为市场价格,b、k为常数),当t=
1
8
时的
市场供应量曲线如下:
(1)根据图象求k和b的值;
(2)若市场需求量为Q,它近似满足()
1 11-x
2
Q x2
=,当P=Q时的市场价格称为平衡价格,为使市场平衡价格控制在不低于9元,求税率t的最小值。
