!七大晶系十四种布喇菲格子
1.6 倒格子和布里渊区
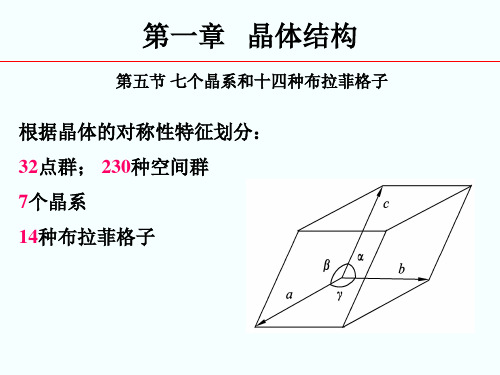
第五节 七个晶系和十四种布拉菲格子
根据晶体的对称性特征划分： 32点群； 230种空间群 7个晶系 14种布拉菲格子
晶系 三斜 单斜 正交 三方 四方
对称性特征 只有1或 i 唯一2或 m 三个2或 m 唯一3 或 唯一4 或
第一章 晶体结构 a b c
C1、 Ci a b c ==90º C2、CS、C2h D2、C2V、D2h C 3 、 S6 、 D 3 C3Ｖ、D3d C4、S4、C4h、D4 C4V、D2d、D4h
晶胞参数
所属点群
Bravais格子 简单三斜 简单单斜 底心单斜 简单、底心、体 心、面心正交 三方 简单四方 体心四方 六方
第五节 七个晶系和十四种布拉菲格子
a b c = ＝= 90º a=b=c = ＝ 90º a=b c = ＝= 90º
六方
唯一6 或
a=b c C6、C3h、C6h、D6、 = ＝ 90º =120º C6V、D3h、D6h
第一章 晶体结构
第六节 倒格子和布里渊区
① ② O
③
二维正方格子的布里渊区
二维正方格子的布里渊区
①
②
二维正方格子的布里渊区
①
②
第一章 晶体结构
第六节 倒格子和布里渊区
二维正方格子的10个布里渊区
பைடு நூலகம்
第一章 晶体结构
第六节 倒格子和布里渊区
二维六方格子的10个布里渊区
第一章 晶体结构
第六节 倒格子和布里渊区
立方
四个3
a=b=c = ＝＝ 90º
T、Th、Td O、 Oh
简单、体心、面 心立方
第一章 晶体结构
第五节 七个晶系和十四种布拉菲格子
布拉维晶格在三维平面上的七大晶系14种晶格
布拉维晶格在三维平面上有七大晶系，14种晶格分别为三斜晶系、单斜晶系、正交晶系、四方晶系、立方晶系、三方晶系、六角晶系。
依照简单、体心、面心及底心一、等轴晶系（立方晶系）等轴晶系的三个轴长度一样，且相互垂直，对称性最强。
这个晶系的晶体通俗地说就是方块状、几何球状，从不同的角度看高低宽窄差不多。
如正方体、八面体、四面体、菱形十二面体等，它们的相对晶面和相邻晶面都相似，这种晶体的横截面和竖截面一样。
此晶系的矿物有黄铁矿、萤石、闪锌矿、石榴石，方铅矿等。
请看这种晶系的几种常见晶体的理论形态：等轴晶系的三个晶轴(x轴y轴z轴)一样长,互相垂直常见的等轴晶系的晶体模型图等轴晶系的各种宝石金刚石晶体翠榴石黄铁矿萤石八面体和立方体的聚形的方铅矿二、四方晶系四方晶系的三个晶轴相互垂直，其中两个水平轴（x轴、y轴）长度一样，但z轴的长度可长可短。
通俗地说，四方晶系的晶体大都是四棱的柱状体，（晶体横截面为正方形，但有时四个角会发育成小柱面，称“复四方”），有的是长柱体，有的是短柱体。
再，四方晶系四个柱面是对称的，即相邻和相对的柱面都一样，但和顶端不对称（不同形）；所有主晶面交角都是九十度交角。
请看模型图：四方晶系的晶体如果z轴发育，它就是长柱状甚至针状；如果两个横轴（x、y）发育大于竖轴z轴，那么该晶体就是四方板状常见的一些四方晶系的晶体模型符山石的晶体锡石的长柱状晶体（顶端另有斜生的小晶体）。
请注意看柱体的棱角发育成窄小晶面，此种晶体又叫“复四方”——四个主柱面，四个小柱面这是短柱状锆石，柱体几乎不发育。
象个四方双锥体或假八面体三、三方晶系和六方晶系三方晶系和六方晶系有许多相似之处，一些矿物专著和科普书刊往往将二者合并在一起，或干脆就称晶体有六大晶系。
与前面讲的五个晶系最大的不同是三方/六方晶系的晶轴有四根，即一根竖直轴（z轴）三根水平横轴（x、y、u轴）。
竖轴与三根横轴的交角皆为90度垂直，三根横轴间的夹角为120度（六方晶系为60度，也可说成三横轴前端交角120度。
布拉菲点阵
关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲（August Bravais，1811—1863），法国物理学家，于1845年推导出了三维晶体原子排列的所有14种点阵结构，首次将群的概念应用到物理学，为固体物理学做出了重大贡献。
这是非常有意义的结论，为了纪念他，后人称这14种点阵为布拉菲点阵。
除此之外，布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中，布拉菲晶格（又译布拉菲点阵）是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲（A.Bravais）于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点，它们分别属于七个晶系。
空间点阵到底有多少种排列形式？按照“每个阵点的周围环境相同”的要求，在这样一个限定条件下，法国晶体学家布拉菲（A. Bravais）曾在1848年首先用数学方法证明，空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形，为了研究方便，可以在空间点阵中取一个具有代表性的基本小单元，这个基本小单元通常是一个平行六面体，整个点阵可以看作是由这样一个平行六面体在空间堆砌而成，我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时，只需选取其中一个单胞来研究即可。
在同一空间点阵中，可以选取多种不同形状和大小的平行六面体作为单胞，如下图所示：其选取方式有，1．固体物理选法：在固体物理学中，一般选取空间点阵中体积最小的平行六面体作为单胞，这样的单胞只能反映其空间点阵的周期性，但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2．晶体学选法：由于固体物理单胞只能反映晶体结构的周期性，不能反映其对称性，所以在晶体学中，规定了选取单胞要满足以下几点原则：①要能充分反映整个空间点阵的周期性和对称性；②在满足①的基础上，单胞要具有尽可能多的直角；③在满足①、②的基础上，所选取单胞的体积要最小。
布拉菲点阵
关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲（August Bravais，1811—1863），法国物理学家，于1845年推导出了三维晶体原子排列的所有14种点阵结构，首次将群的概念应用到物理学，为固体物理学做出了重大贡献。
这是非常有意义的结论，为了纪念他，后人称这14种点阵为布拉菲点阵。
除此之外，布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中，布拉菲晶格（又译布拉菲点阵）是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲（A.Bravais）于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点，它们分别属于七个晶系。
空间点阵到底有多少种排列形式？按照“每个阵点的周围环境相同”的要求，在这样一个限定条件下，法国晶体学家布拉菲（A. Bravais）曾在1848年首先用数学方法证明，空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形，为了研究方便，可以在空间点阵中取一个具有代表性的基本小单元，这个基本小单元通常是一个平行六面体，整个点阵可以看作是由这样一个平行六面体在空间堆砌而成，我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时，只需选取其中一个单胞来研究即可。
在同一空间点阵中，可以选取多种不同形状和大小的平行六面体作为单胞，如下图所示：其选取方式有，1．固体物理选法：在固体物理学中，一般选取空间点阵中体积最小的平行六面体作为单胞，这样的单胞只能反映其空间点阵的周期性，但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2．晶体学选法：由于固体物理单胞只能反映晶体结构的周期性，不能反映其对称性，所以在晶体学中，规定了选取单胞要满足以下几点原则：①要能充分反映整个空间点阵的周期性和对称性；②在满足①的基础上，单胞要具有尽可能多的直角；③在满足①、②的基础上，所选取单胞的体积要最小。
十四种布拉菲格子
就目前所知，晶体多达20000多种以上，它们的几何 就目前所知，晶体多达 多种以上， 多种以上 外形更是多姿多彩、精美绝伦、奥妙无比， 外形更是多姿多彩、精美绝伦、奥妙无比，足以让所有 的能工巧匠叹为观止！然而，种类繁多、 的能工巧匠叹为观止！然而，种类繁多、形状各异的晶 体在微观结构的周期性特征上却是极其简单的， 体在微观结构的周期性特征上却是极其简单的，描述晶 体微观结构周期性特征的Bravais格子总共只有十四种不 格子总共只有十四种不 体微观结构周期性特征的 格子总共只有十四种 同的类型。 同的类型。
Pearson记法 →
hR
7°立方(Cubic) 晶系 立方(Cubic) Bravais格子之惯用元胞的几何特征为： Bravais格子之惯用元胞的几何特征为： 格子之惯用元胞的几何特征为
a = b = c，α = β = γ = 90 0
格点有三种分布方式：其一，分布于惯用元胞的八个顶点上； 格点有三种分布方式：其一，分布于惯用元胞的八个顶点上； 其二，除顶点外，还分布于体心；其三，除顶点外，还分布于六 其二，除顶点外，还分布于体心；其三，除顶点外， Bravais格子 简单立方Bravais格子、 个面心 有 三种Bravais格子，分别称为简单立方Bravais格子、 → 三种Bravais格子，分别称为简单立方Bravais格子 体心立方Bravais格子和面心立方Bravais格子 体心立方Bravais格子和面心立方Bravais格子 Bravais格子 Bravais cP、 cP Pearson记法 → 、
cI和cF，惯用元胞分别如图1.2.6－ 中的（ cI和cF，惯用元胞分别如图1.2.6－1中的（l）图、(m)图和（n） 1.2.6 (m)图 图所示 背景音乐： 背景音乐：
十四种布拉菲格子
a = b ≠ c，α = β = γ = 90 0
格点有两种分布方式：其一，分布于惯用元胞的八个顶点上； 格点有两种分布方式：其一，分布于惯用元胞的八个顶点上；
→ 两种Bravais格子，分别称 其二，除顶点外， 格子， 其二，除顶点外，还分布于体心 有 两种 格子
格子和 为简单四方Bravais格子和体心四方 简单四方 格子 体心四方Bravais格子 Pearson记法 → tP 格子 中的（ ） 和tI，惯用元胞分别如图 ，惯用元胞分别如图1.2.6－1中的（h）图和(i)图所示 － 中的 图
背景音乐： 背景音乐：
图1.2.6－1 －
十四种Bravais格子按点对称性分为七种点对称性类型，分 格子按点对称性分为七种点对称性类型， 十四种 格子按点对称性分为七种点对称性类型 七个晶系。 别对应于七个晶系 下面，将按晶系对这十四种Bravais格子 格子 别对应于七个晶系。下面，将按晶系对这十四种 的主要特征逐一简介
研究晶体表面的对称分布晶体只有三十二种可能的点对称性类型1849年bravaisbravais格子只有七种可能的点对称性类型再考虑到平移对称性格子只有七种可能的点对称性类型再考虑到平移对称性bravais格子只有十四种不同的类型这十四种bravais格子的惯用元胞如图1261所示???发现??指出????进一步指出????首次导出背景音乐
背景音乐： 背景音乐：
19th Cent.初，Weiss ：研究晶体表面的对称分布 初 晶体学坐标系： 晶体学坐标系：晶体分为七个晶系 1830年， Hessel ：研究晶体表面的对称分布 年 三十二种可能的点对称性类型 1849年，Bravais 年
发现→ 七种
指出 晶体只有 →
14种布拉维点阵的结构特征
14种布拉维点阵的结构特征布拉维点阵是描述晶体中原子、离子或分子排列方式的一种数学模型。
有14种布拉维点阵，也被称为14种布拉维格子或14种布拉维空间群。
这些点阵通过特定的对称性元素来定义。
以下是这些14种布拉维点阵的主要结构特征：1三立方格子（Triclinic）：没有垂直平面或轴的对称性。
所有晶胞边长和角度均可不同。
2单斜格子（Monoclinic）：有一个垂直平面。
一个轴有对称性。
3正交格子（Orthorhombic）：三个垂直的平面和三个垂直的轴。
所有晶胞角度均为90度。
4四方格子（Tetragonal）：一个垂直平面和一个垂直轴。
所有晶胞边长相等，两个轴长度相等。
5六方格子（Hexagonal）：六重对称性轴，垂直于平面。
六边形的基本晶胞。
6立方格子（Cubic）：三个垂直平面和三个垂直轴。
所有晶胞边长相等，所有角度均为90度。
7三斜半基心格子（Triclinic P）：没有垂直平面或轴的对称性。
所有晶胞边长和角度均可不同。
8单斜面心格子（Monoclinic P）：有一个垂直平面。
一个轴有对称性。
9正交面心格子（Orthorhombic P）：三个垂直的平面和三个垂直的轴。
所有晶胞角度均为90度。
10四方面心格子（Tetragonal P）：一个垂直平面和一个垂直轴。
所有晶胞边长相等，两个轴长度相等。
11六方面心格子（Hexagonal P）：六重对称性轴，垂直于平面。
六边形的基本晶胞。
12立方面心格子（Cubic P）：三个垂直平面和三个垂直轴。
所有晶胞边长相等，所有角度均为90度。
13三斜体心格子（Triclinic I）：没有垂直平面或轴的对称性。
所有晶胞边长和角度均可不同。
14正交体心格子（Orthorhombic I）：三个垂直的平面和三个垂直的轴。
所有晶胞角度均为90度。
这些布拉维点阵描述了晶体的结构特征，是研究材料科学和晶体学的重要工具。
晶体学基础第二章-晶体的对称分类与布拉菲点阵
2.晶系（crystal system）：7个晶系
三斜晶系：只有 1 或 1
单斜晶系：2 和 m 均不多于一个 正交晶系（斜方晶系）：2 和 m 的总数不少于3个
三方晶系：唯一的一个高次轴是 3 或 3 四方晶系：唯一的一个高次轴是 4 或 4 六方晶系：唯一的一个高次轴是 6 或 6
立方晶系（等轴晶系）：有4个 3
32种点群描述的晶体对称性对应的只有14种布拉菲点阵分为7个晶系沿晶体的对称轴或对称面的法向在一般情况下它们构成斜坐标系三个晶轴之间的夹角二晶体的14种布拉菲点阵布拉菲格子
2.4 晶体的对称分类与布拉菲点阵
一、晶体的对称分类
按晶体的对称性特征晶体分类
1.晶族（crystal category）：3个晶族 低级晶族：无高次轴 中级晶族：只有一个高次轴 高级晶族：高次轴多于一个
3.晶类: 属于同一点群的晶体。32个晶类。
二、晶体的14种布拉菲点阵（布拉菲格子）
—— 32种点群描述的晶体对称性 —— 对应的只有14种布拉菲点阵 —— 分为7个晶系
—— 单胞的三个基矢
沿晶体的对称轴或对称面
的法向，在一般情况下，它们构成斜坐标系
三个晶轴之间的夹角
7大晶系的形成
14种布拉维格子及堆积方式
2.3.4 思考题
• 1. 什么是布拉维格子？试指出14种布拉 维格子的特征。 • 2. 等大球体的紧密堆积有几种形式？并 指出相应的空隙情况。
最紧密堆积的方式有两种，一是六 方最紧密堆积（Cubic closest packing， 缩写为CCP），最紧密排列层平行于 {0001}，可以用ABABAB……顺序来表 示（图2-3-2）。另一种是立方最紧密堆 积（Hexagonal closest packing，缩写为 HCP），最紧密排列层平行于{111}，可 以用ABCABCABC……顺序来表示（图 2-3-3）。自然铜、自然金、自然铂等矿 物的晶体结构属立方最紧密堆积方式， 而锇铱矿以及金属锌等晶体的结构属六 方最紧密堆积方式。
符合对称特点和选择原则的格子共有7 种类型，共计14种不同型式的空间格子， 即通常所称的十四种布拉维格子（the fourteen Bravais space lattices），如图2-31所示。布拉维格子是空间格子的基本组成 单位，只要知道了格子形式和单位平行六 面体参数后，就能够确定整个空间格子的 一切特征。
2.3 14种布拉维格子和球体 紧密堆积
2.3.1 实验目的
• 加深对14种布拉维格子和球体紧密堆积 原理的理解。
2.3.2 基本原理
1. 布拉维格子 只在单位平行六面体的八个角顶上分布有 结点的空间格子，称为原始格子 （Primitive lattice,符号P），在单位平行 六面体的体中心还有一个结点时，则构 成体心格子（Body-centered lattice，符 号I）。
三方菱面体
C:与本晶系 对称不符
I=P F=P
简单四方
C=P
体心四方
F=I
简单立方
14种布拉维格子
14种布拉维格子之八：正交简单（oP)
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之九：正交体心（oI)
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十：正交C心 oC(或 oA, oB）
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十一：正交面心（oF)
请
都是点阵点.黑点
点
与蓝线表示一个
击
正当格子
按
钮
打
开
布拉维格子之七：三方晶系的六方R 心(hR)
请 点 击 按 钮 打 开 晶 格 模 型
三方晶系的六方简单 (hP)
请点击按钮打开晶格模型
六方简单 (hP)格子已用于六方晶系, 现在又可用于三方晶系, 所以只算一种格子. 尽管三方晶系的两种格子------六方简单(hP)和六方R 心(hR)------形状都与六方 晶系的六方简单 (hP)格子相同（即hR是两个晶系共用的）, 但真实的三方晶体中只 有三次对称轴而没有六次对称轴, 六方晶体才有六次对称轴.
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十二：单斜简单（mP)
请点击按钮打开晶格模型
14种布拉维格子之十三：单斜C心（mC)
请点击按钮打开晶格模型
14种布拉维格子之十四：三斜简单 (aP)
请点击按钮打开晶格模型
为什么要考虑带心格子?
立方面心格子，若按左图取素格子只能表现三方对称性；若取右图 所示的复格子就表现出立方对称性(格子选取方式不能改变点阵结构的对 称性,但点阵固有的较高对称性在素格子上可能被掩盖)：
请点击按钮观察动画
请点击按钮打开晶格模型
14种布拉维格子之一：立方简单（cP）
chap结晶学及矿物学 (25)
二十四、十四种空间格子（布拉维格子）
七个晶系---七套晶体常数—七种平行六面体形状。
每种形状有四种类型，那么就有7×4=28种空间格子？
但在这28种中，某些类型的格子彼此重复并可转换，还有一些不符合某晶系的对称特点而不能在该晶系中存
在，因此，只有14种空间格子，也叫14种布拉维格子。
（A.Bravais于1848年最先推导出来的）
例1：四方底心格子＝四方原始格子
所以，在14种布拉维格子中，四方底心格子不需要保留。
例2：立方底心格子不符合等轴晶系对称。
所以，在14种布拉维格子中，立方底心格子不存在。
那么请思考：立方底心格子符合什么晶系的对称？
还应指出的是：对于三、六方晶系的四轴定向也可转换成三轴定向，变为菱面体格子。
现在对于三、六方晶系都用四轴定向。
四轴定向的格子形状为菱形柱。
另外，六方原始格子为六方柱的顶底面加心，不要误认为六方底心格子。
十四种空间格子见表7-1。
四轴定向格
子三轴定向格子两种格子的转换
表7-1。
大连理工大学材料科学基础思考及习题(第二章)
固态结构
7个晶系、14 种布拉菲点阵
7个晶系 立方 四方 菱方 六方 正交
棱边长度及夹角关系
14种布拉菲点阵 简单立方
a=b=c,===90 a=bc,===90 a=b=c,==90 a1=a2=a3c,== 90,=120
体心立方 面心立方
（110）
a h2 k 2 l 2
45o
2
[ 1 10] 方向上的线密度为1（注意最邻近的配位原子）。
（001）
[0 1 0]
（111）面
[u v w] （h k l） 晶带定律
[10 1 ]
（100）
（010）
[ 1 10]
4、渗碳体（Fe3C）是一种间隙化合物，它具有正交点阵结构，其晶格常 数a = 0.4514 nm，b = 0.508 nm，c = 0.6734 nm，其密度 = 7.66 g/cm3， 试求Fe3C每个单位晶胞中含Fe与C原子的数目。（C原子量Ac= 12.011 g/mol，
Fe原子量AFe = 55.85 g/mol）
设定Fe3C晶胞中，C原子个数为x，则Fe原子个数为3x。 根据密度公式：
=
xAC+ 3xAFe Vc NA
计算得到x = 3.968 4
故Fe3C间隙化合物中，每个晶胞内C原子数为4，Fe原子数为12。
c a
b
正交晶系 abc,===90
5、下图为-Fe的X-射线衍射谱，所用X光波长 = 0.1542 nm，试计算每 个峰线所对应的晶面间距，并确定其晶格常数。
以最强衍射峰（110）为例，2 为45o。
根据布拉格定律：n = 2 dhklsin， 则 d110 = n/2sin = 0.1542/[2sin(45/2)] = 0.2015 nm（级数n取1） 又根据立方晶系晶面间距公式 d hkl = 可以计算晶格常数a = 0.2850 nm。
最新布拉菲点阵资料讲解
关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲（August Bravais，1811—1863），法国物理学家，于1845年推导出了三维晶体原子排列的所有14种点阵结构，首次将群的概念应用到物理学，为固体物理学做出了重大贡献。
这是非常有意义的结论，为了纪念他，后人称这14种点阵为布拉菲点阵。
除此之外，布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中，布拉菲晶格（又译布拉菲点阵）是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲（A.Bravais）于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点，它们分别属于七个晶系。
空间点阵到底有多少种排列形式？按照“每个阵点的周围环境相同”的要求，在这样一个限定条件下，法国晶体学家布拉菲（ A. Bravais）曾在1848年首先用数学方法证明，空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形，为了研究方便，可以在空间点阵中取一个具有代表性的基本小单元，这个基本小单元通常是一个平行六面体，整个点阵可以看作是由这样一个平行六面体在空间堆砌而成，我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时，只需选取其中一个单胞来研究即可。
在同一空间点阵中，可以选取多种不同形状和大小的平行六面体作为单胞，如下图所示：其选取方式有，1．固体物理选法：在固体物理学中，一般选取空间点阵中体积最小的平行六面体作为单胞，这样的单胞只能反映其空间点阵的周期性，但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2．晶体学选法：由于固体物理单胞只能反映晶体结构的周期性，不能反映其对称性，所以在晶体学中，规定了选取单胞要满足以下几点原则：①要能充分反映整个空间点阵的周期性和对称性；②在满足①的基础上，单胞要具有尽可能多的直角；③在满足①、②的基础上，所选取单胞的体积要最小。
七大晶系十四种布喇菲格子
四方晶系 六角晶系
a1 a2 a3
900
a1a2 1200
a3 a1, a2 a1 a2 a3
简单四方 体心四方
六角
C4, C4h D4 , C4v D4h , S4 , D2d
C6 , C6h , D6 , C3v D6h , C3h , D2h
立方晶系
a1 a2 a3
900
简单立方 体心立方 面心立方
T , Th , Td O, Oh
底心立方？=简单四方 底心四方=简单四方
体心四方与面心四方等价
a1 a2 a3 a1 a2 a3
05 /13
8) 三角
a1 a2 a3
90 120
9) 简单四方（四角） a1 a2 a3 10) 体心四方（四角） 900
11) 六角
a1 a2 a3
a3 a1, a2
a1a2 1200
12) 简立方 13) 体心立方 14) 面心立方
a1 a2 a3
900
七大晶系的布喇菲格子、晶胞和所属点群
晶系
晶胞基矢的 特性
布喇菲 格子
所属点群
三斜晶系 单斜晶系
a1 a2 a3
a2 a1, a3 a1 a2 a3
简单三斜
C1, Cs
简单单斜
底心单斜 C2 , Cs , C2h
10 /13
正交晶系
a1 a2 a3 a1 a2 a3
简单正交 底心正交 体心正交 面心正交
D2 , C2v , D2h
三角晶系
a1 a2 a3
布拉菲点阵
关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲（August Bravais，1811—1863），法国物理学家，于1845年推导出了三维晶体原子排列的所有14种点阵结构，首次将群的概念应用到物理学，为固体物理学做出了重大贡献。
这是非常有意义的结论，为了纪念他，后人称这14种点阵为布拉菲点阵。
除此之外，布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在以及中，布拉菲晶格（又译布拉菲点阵）是为了纪念在固态物理学的贡献命名的。
法国晶体学家（）于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点，它们分别属于。
空间点阵到底有多少种排列形式？按照“每个阵点的周围环境相同”的要求，在这样一个限定条件下，法国晶体学家布拉菲（A. Bravais）曾在1848年首先用数学方法证明，空间点阵只有14种类型。
这14种空间点阵以后就被称为。
空间点阵是一个三维空间的无限图形，为了研究方便，可以在空间点阵中取一个具有代表性的基本小单元，这个基本小单元通常是一个平行六面体，整个点阵可以看作是由这样一个平行六面体在空间堆砌而成，我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时，只需选取其中一个单胞来研究即可。
在同一空间点阵中，可以选取多种不同形状和大小的平行六面体作为单胞，如下图所示：其选取方式有，1．固体物理选法：在固体物理学中，一般选取空间点阵中体积最小的平行六面体作为单胞，这样的单胞只能反映其空间点阵的周期性，但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2．晶体学选法：由于固体物理单胞只能反映晶体结构的周期性，不能反映其对称性，所以在晶体学中，规定了选取单胞要满足以下几点原则：①要能充分反映整个空间点阵的周期性和对称性；②在满足①的基础上，单胞要具有尽可能多的直角；③在满足①、②的基础上，所选取单胞的体积要最小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
晶系
晶胞基矢的 特性
布喇菲 格子
所属点群
三斜晶系
简单三斜
单斜晶系
简单单斜 底心单斜
01_07_晶格的对称性 —— 晶体结构
正交晶系 三角晶系
简单正交 底心正交 体心正交 面心正交
三角
01_07_晶格的对称性 —— 晶体结构
四方晶系 六角晶系 立方晶系
简单四方 体心四方
六角
简单立方 体心立方 面心立方
01_07_晶格的对称性 —— 晶体结构
9) 简单四方（四角） 10) 体心四方（四角）
01_07_晶格的对称性 —— 晶体结构
11) 六角
01_07_晶格的对称性 —— 晶体结构
12) 简立方 13) 体心立方 14) 面心立方
01_07_晶格的对称性 —— 晶体结构
七大晶系的布喇菲格子、晶胞和所属点群
立方 三角
四方
正交
三斜
按晶胞个点分布特点分为14种布喇菲原胞 1) 简单三斜
01_07_晶格的对称性 —— 晶体结构
2) 简单单斜 3) 底心单斜
01_07_晶格的对称性 —— 晶体结构
4) 简单正交 5) 底心正交 6) 体心正交 7) 面心正交
01_07_晶格的对称性 —— —— 晶体结构
底心立方？=简单四方
底心四方=简单四方
01_07_晶格的对称性 —— 晶体结构
体心四方与面心四方等价
01_07_晶格的对称性 —— 晶体结构
§1.7 晶格的对称性
—— 32种点群描述的晶体对称性 —— 对应的只有14种布喇菲格子 —— 分为7个晶系
—— 晶胞的三个基矢
沿晶体的对称轴或对称面
的法向，在一般情况下，它们构成斜坐标系
三个晶轴之间的夹角
01_07_晶格的对称性 —— 晶体结构
按
晶
胞 六角
基
矢
的
特
征
分 为
单斜
七
大
晶
系
01_07_晶格的对称性 —— 晶体结构