光学信息处理与全息术PPT课件教材讲义
合集下载
《光学信息处理技术》课件
光学信息处理技术在理论和实践 中得到了广泛研究和应用。
光学信息处理技术的发展 趋势
光学信息处理技术将更加智能化、 高效化和便捷化,推动科技进步 和应用创新。
结语
通过本课程,我们总结了光学信息处理技术的基本原理和应用,并展望了未 来光学信息处理技术的发展可能性。
快速傅里叶变换是一种高效计算傅里叶变换的算法,可用于图像频谱分析和滤波。
数字图像处理技术
1 像素图像处理方法
像素图像处理方法以像素为基本处理单元,包括增强、滤波和分割等处理操作。
2 处理方法
数字图像处理方法包括变换、编码和压缩等技术,可用于图像编辑和图像信号分析。
3 区域处理方法
区域处理方法将图像分成不同区域,进行分割、特征提取和对象识别等操作。
光学信息处理技术广泛应用于图像处理、光学光学信息处理技术具有高速、高精度和免疫干扰等优点,但对环境光和噪声敏感。
基本光学信息处理技术
光学显微镜
光学显微镜是一种基于光学原理 的图像放大装置,可观察细小物 体及其结构。
光学干涉仪
光学衍射仪
光学干涉仪是一种利用干涉现象 测量物体形状和表面特性的仪器。
《光学信息处理技术》 PPT课件
本课程介绍了光学信息处理技术的基本原理和应用。通过本课程,你将了解 到光学信息处理技术的概述、基本方法、图像计算方法、数字图像处理技术、 光学识别技术以及其发展前景。
光学信息处理技术概述
定义
光学信息处理技术涉及使用光学原理和技术处理和传输信息的一系列方法和技术。
应用领域
光学衍射仪利用光的衍射现象处 理和分析光的信息,包括干涉、 衍射和散射。
光学信息处理的图像计算方法
1
赫尔曼-默里变换
光学扫描全息ppt课件

光学扫描全息的应用领域
扫描全息显微镜
细胞显微图
三维图像识别
人脸识别Biblioteka 犯罪识别人脸识别系统
三维光学遥感
对地球表面进行拍摄
三维电视
Holoscreen就是把这一 原理应用在了电视上。
看它後面的投影机相当
於光波资讯记录仪,它
的显示器就是用来显示
全息图的。它整个的萤 幕是由 10mm 厚的玻 璃制成。面积为 1.5m x 1.0m 长方形。 外面有一透明的材料覆
激光束技术
是日本Science and Technology公司发明了一种可以用激光束来投射实 体的3D影像,这种技术是利用氮气和氧气在空气中散开时,混合成的 气体变成灼热的浆状物质,并在空气中形成一个短暂的3D图像。这种 方法主要是不断在空气中进行小型爆破来实现的。
广东肇庆
激光技术用于武器制造
盖其上,面积比显示的
屏稍大一点,为 610mm x 814mm。从 图中可以看到 Holoscreen整个占的面 积比较大。它显示的画 面是在半空中。
光学扫描全息涉及两个部分。
1. 光学扫描 2. 光外差法
光学扫描的基本原理
光学扫描的基本原理是光学扫描仪或光学处理器 通过激光束扫描物体信息,光探测器接收所有扫描光 束并输出一个既可以存储又可以显示的电信息,至此, 光信息被转换成电信息。采用传统光学检测器不能 提取物光场的相位信息,然而全息图需要记录相位信 息。
光学扫描全息
主讲人:胡建
首先我们观看一段影片
他为什么可以消失?
他是神仙?
光学扫描全息
光学扫描全息是一种独特的实时全息技术,它使用简单的二维光学扫描 原理来获得一个三维物体的全息图,主要强调全息记录可以通过主动光 学扫描原理完成。
高二物理竞赛光学信息处理PPT(课件)

按处理系统是否满足线性叠加:线性处理和非线性处理。
光
学
第五章 变换光学与全息照相
2、阿贝—波特实验和空间滤波
当a=d/2,即缝宽等 于缝的间隙时,直流分 量为1/2,像场的复振 幅分布仍为光栅结构, 并且周期与物相同,但 强度分布是均匀的,即 实际上看不见条纹。
光
学
第五章 变换光学与全息照相
光学信息处理可从不同角度进行分类:
相衬显微镜的原理是利用位相滤波器将物体的位相变化转换成光的强 弱不同,从而能够被观察到。这对于研究生物细胞组织、金相表面、抛 光表面以及透明材料的不均匀性等的检验很有用途。
光
学
第五章 变换光学与全息照相
3、相衬显微镜的原理 位相物体的透射系数可以写成
t x1,y1 expj x1,y1
对于弱相位物体,可以近似为:
光
学
第五章 变换光学与全息照相
第四节 光学信息处理
1、光学信息处理的概念 Gabor)发明,开始并没有引起人们的注意,只是到了60年代激光的发明使得全息术得到了快速发展,加博才为此获得了诺贝尔奖。
被记录物体反射率或透射率:
光全息主要研究记录携带物体形貌信息的光波的复振幅记录、再现及其应用的技术。
广义来说,若处理的是光学信息、或处理信息的手段是光学手段、或处理以后所得到的结果是光学信息,都可以称为光学信息处理。
被记录物体反射率或透射率: (x, y, z) 物光波(物光): O(x, y)
参考光波(参考光): R(x, y)
再现光: C(x, y) 全息记录介质(全息干板、光电记录器件) 全息图
物光与物体的反射率和透射率及其传播方式有密切的关系
光
学
第五章 变换光学与全息照相
《光学信息处理技术》PPT课件

频谱面上的光场分布与物的结构密切相关,原点附近分布着物的低
频信息;离原点较远处,分布着物的较高的频率分量。
7
§7-1 空间滤波基本原理
二、阿贝—波特(Abbe—Porter)实验(1906)
相干单色平行光照明
实验装置
物平面 细丝网格状物 (正交光栅)
频谱面 放置滤波器
改变物的 频谱结构
像面 观察到各种 不同的像
T ( fx ) = ℱ [ t ( x1 ) ] 它的傅里叶变换—栅状物的夫琅和费衍射图样:
aB d
s
incBfx
sinc
a d
sincB
fx
1 d
sinc
a d
sincB
fx
1 d
......
零级谱
正、负一级谱
高级频谱
强度呈现为一系列亮点,每个
亮点是一个sinc2函数
幅值受单缝衍射限制,包络
带通滤波器:
用于选择某些频谱分量通过,阻挡另一些分量 例:正交光栅上污点的清除
滤波后可在像面 上得到去除了污 点的正交光栅
29
§7-3 空间滤波应用
例: 疵点检查——方向滤波器
印刷电路掩膜的 频谱沿轴分布, 疵点的频谱比较 分散。
此滤波器可提取 出疵点的信息
在输出面上得到 疵点的图像
30
§7-3 空间滤波应用
滤波器:放置在频 谱面中心的孔,仅 让0级谱通过
综合出的像:
仅有边框,不 出现条纹结构
零频分量是一个直流分量,它只代表像的本底
12
原物
通过的频谱 综合出的图像
阻挡零频分量,在一定条件下可使像的衬度发生反转 13
原物
通过的频谱 综合出的图像
信息光学PPT课件第五章光学全息

)
Uc (x,
y, z)
Ae jkr
U
( x,
y,
z)
U( x, y, z) Ae jkr Aexp jk( x cos y cos z cos )
Uc ( x, y, z) Ae jkr U ( x, y, z)
共轭光波的数学表达式为原光波复振幅的共轭复数。
已知 于是
参考波
R
记录介质上的的总光强为 I( x, y) O( x, y) R( x, y) 2
O
物波
记录介质
O( x, y) 2 R( x, y) 2 R( x, y)O( x, y) R( x, y)O( x, y)
O(x, y) 2 R(x, y) 2 2r(x, y)O0(x, y)cos (x, y) (x, y)
参考波
R
O
物波
记录介质
上图为波前记录的示意图,设传播到记录介质上的物光波前复振幅(对于理 想单色光,其空间的复振幅分布是不随时间变化的)为
O( x, y) Oo ( x, y)exp j ( x, y)
传播到记录介质上的参考光波前复振幅
R( x, y) r( x, y)exp j ( x, y)
全息图片
全息图片
当照明光波与参考光波均为正入射的平面波时,入射到 全息上的相位可取为零。这时U3和U4中的系数均为实 数,无附加相位因子,全息图衍射场中的+1级和-1级光 波严格镜像对称。由共轭光波U4所产生的实像,对观察 者而言,该实像的凹凸与原物体正好相反,因而给人以 某种特殊的感觉,这种像称为赝像。
如何得到三维的图像呢?
如果我们能够用某一种方法把物体光波(其中包含振幅和 相位信息)以某种方式记录下来,则当我们想办法把物光波 再现出来的话,就能再现三维的物体。
光学第七章光全息术

U(2 x,
y)
t
(x,
y)U(1 x,
y)
A1
t0
t1
cos k
x2 y2 2z0
A1t0
1 2
ik x2 y2
A1t1e 2z0
1 2
ik x2 y2
A1t1e 2z0
U0 U1
U1
0级为正出射的平面波 1级U1代表发散球面波,发散点为(0,0, z0 ) 1级U1代表汇聚球面波,汇聚点为(0,0,z0 )
Stephen Benton (1941-2003) as well, is amongst the pioneers of modern holography. He is the inventor of Benton holography, also referred to as rainbow holography (1969), a fascinating holographic process that allowed the subsequent realization of holograms that can be illuminated with white light, holograms that display in true colours, and holograms that display true color cinematographic animations
1、 全息术(holography)原理
余弦型环状波带片的衍射
余弦型环状波带片的制备:
平面光和球面光干预,
U1(x, y) A1ei0,
U2 (x,
y)
ik x2 y2 /2 z0
A e2
*
信息光学第七章-光学全息ppt课件
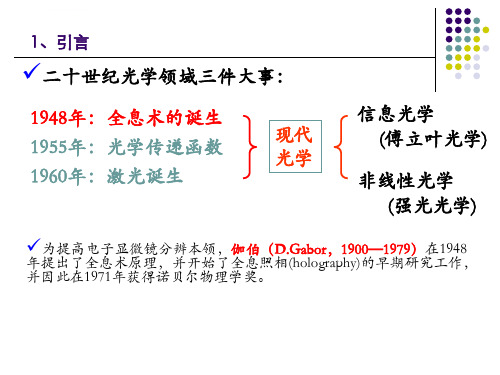
引入一相干参考波,该参考波在H上产生 的复振幅分布为
R x,yr0x,yejrx,y
那么,两波相遇叠加的总光场是
U x ,y O x ,y R x ,y
对应的强度分布为
I x , y U x , y 2 O x , y 2 R x , y 2 O x , y R * x , y O * x , y R x , y
➢用共轭参考波照明
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
2、波前记录与再现
✓用相干光波照射全息图,假定它在全息图平面上的复振幅分布为C(x,y),
全息图的透射光场分布为 U t x , y C t x , y C t b C O 2 C O R * C O * R U 1 U 2 U 3 U 4
4、基元全息图分析
✓全息图可看作是很多基元全息图的线性组合,了解基元全息图的结构和
作用对于深入理解整个全息图的记录和再现机理非常有益。 空域方法是把物体看作一些相干点源的集合,物光波前是所有点源发出的 球面波的线性叠加。每一个点源发出的球面波与参考波干涉,记录的基元 全息图称为基元波带片; 频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加, 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
1、引言
✓全息发展简史
➢ 1948年 Dennis Gabor 提出 “波前重现” 理论
目的:改善电子显微镜的分辨率 光源:汞灯 效果:因光源相干性差,效果很不明显
R x,yr0x,yejrx,y
那么,两波相遇叠加的总光场是
U x ,y O x ,y R x ,y
对应的强度分布为
I x , y U x , y 2 O x , y 2 R x , y 2 O x , y R * x , y O * x , y R x , y
➢用共轭参考波照明
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
2、波前记录与再现
✓用相干光波照射全息图,假定它在全息图平面上的复振幅分布为C(x,y),
全息图的透射光场分布为 U t x , y C t x , y C t b C O 2 C O R * C O * R U 1 U 2 U 3 U 4
4、基元全息图分析
✓全息图可看作是很多基元全息图的线性组合,了解基元全息图的结构和
作用对于深入理解整个全息图的记录和再现机理非常有益。 空域方法是把物体看作一些相干点源的集合,物光波前是所有点源发出的 球面波的线性叠加。每一个点源发出的球面波与参考波干涉,记录的基元 全息图称为基元波带片; 频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加, 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
1、引言
✓全息发展简史
➢ 1948年 Dennis Gabor 提出 “波前重现” 理论
目的:改善电子显微镜的分辨率 光源:汞灯 效果:因光源相干性差,效果很不明显
《光学信息技术原理及应用》(第2版)教学课件 光学信息处理第1讲B

• 函数作为基元函数的情况。根据 函数的筛选性质(A.7,或
《积分变换》P16中1.12式),任何输入函数都可以表达为
fx1,yf,x,ydd
• 积分就是“相加”,筛选性质表明任意函数都可以表示为无穷多的
函数的和,每个 函数的“大小”被输入函数“调制”。
• 函数通过系统后的输出用算符可以表示为
gx2,y L f, x ,y d d
• 对于线性系统的一个重要子类——不变线性系统,分析才变得简单
• 大多数情况下,光学系统都可以看做不变线性系统
19
练习
1、已知函数 U x A ex j2 p f0 x 求下列函数,并作出函 数图形。(1)U x 2(2) UxU*x (3)UxU*x2
2、已知函数
fx re x c 2 r te x 2 c t 求下列函数,
2
近代光学对信息时代发展的重要作用
• 20世纪40年代末提出的全息术
• 50年代产生的光学传递函数
• 60年代发明的激光器
• 70年代发展起来的光纤通信
• 80年代成为微机标准外设的光驱
• 航天航空事业中应用的空间光学,神州五号搭载的相 机拍到美国军用机场照片分辨率一米
3
信息光学的研究方法和用途
17
1.1.2 脉冲响应和叠加积分(2)
• 根据线性系统的叠加性质,算符与加(乘)法的顺序可以交换,算符 与对基元函数积分的顺序也就可以交换
g x2, y f, L x , y d d
• 定义为系统的脉冲响应函数
h x 2 , y ; , L x , y
• 得到系统输出为 “叠加积分”
7
第一章 二维线性系统分析
• 把光学系统看成二维线性系统---信息传输系统,而不 是看成一个物理的成象系统或干涉、衍射系统
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
G( f ) g(x)ei2 fxdx
G( f为) 频率f 附近单位频率间隔的振幅。它表征该成分 对 g贡(献x) 的大小——权重因子
G( f-) f 曲线为振幅随频率的分布 G( f称) 为 g的(x频) 谱函数
g(x)是G(f )的逆傅里叶变换 g(x) F 1{G( f )}
g ( x) 为周期函数等间隔的离散的线状谱 g ( x) 为非周期函数连续频谱
50 x)
表示一个周期为d 的黑白光栅可看成由频率 0 1/ d 及 3 0 , 5 0 许多正弦光栅(强度按正弦分布)组成。
令 / 0 k
k 0
d sin
2
d
2
sin
v sin x 2 f
振幅 1/2
-5ω0 -3ω0 -ω0
-1/5π -1/3π -1/π
1/π 1/3π
T~n
Tnein
1 2 (an
ibn )
傅里叶系数由 积分直接给出
T~n
1 d
d
2 d
T
(
x)
exp(
i2f
n
x)dx
2
Tn 原函数 T (x) 中各种空间频率的成分所占比例
二 维 周 期 函
T (x, y) T0 T~nm exp[2i(nfx x mfy y)] n,m0
T~n,m
总结
傅里叶变换:将函数 g (分x)解成一系列基元函数
的线性组合的方法 线性系统 能够应用叠加原理的物理系统
(许多光学系统都可视为这种系统)
G( f )
一个复杂输入激励引起的输出响应 (1) 激励分解为一系列简单的基元函数的线性组合
(2) 分别计算系统对每个基元输入的响应 (3) 把所有基元响应叠加起来
注意:频谱取一系列分立的值。
二. 任意光栅的屏函数及其傅里叶级数展开 严格空间周期性函数的衍射屏 (透射式或反射式) 光栅
一 周期性 T (x d ) T (x)
正弦光栅 黑白光栅
维 衍 射
尺寸D 有限
x D , or
N
D
其他屏函数
1
2
d
屏
在一定的较大范围内的周期函数—准周期函数
(1) 正弦余弦式
1 dxdy
d
d
2 d
dx
2 d
dyT (x,
y) exp[2i( nfx x
mfy y)]
2
2
数
fx
1 dx
,
fy
1 dy
例:振幅型透射光栅的傅里叶级数展开
光栅常数:d 2b
--空间周期为d 的函数
透射率 T (x) :
--空间位置 x 有确定的函数关系
{ T (x) 1 md x (2m 1)d / 2, m 0,1,2 0 其他
aJ1( 2a f x 2 f y 2 ) fx2 fy2
换 对
1cos(2f0 x ) g( x )
0
L x
2 x L
2
(f)来自1( 2ff0)
1( 2
f
f0)
高斯函数 g(x) exp(ax2 )
exp( 2 f 2 )
a
a
函数 (x)
1
常数 1
( f )
函数 定义:
(x)
光学信息处理 及全息术
6.1 傅里叶变换
一、光学图像的傅里叶频谱分析
1. 空间频率
在光学信息处理中,光学系统所传递和处理的信息是 随空间变化的函数。
一幅图像是一种光的强度和颜色按空间的分布,这种 分布的特征可用空间频率表明。把图象看作是由各种 方向、各种间距的线条组成。
2. 空间频谱(spatial frequency spectrum) 简谐振动是最简单的周期性运动,几个简谐运动可合 成一个较复杂的周期性运动。 傅里叶分析:已知一周期性运动,求组成它的各个简 谐运动频率及相应振幅的方法。 所得的频率及相应振幅的集合为该周期性运动的频谱。
1/5π
振幅频谱
ω0 3ω0 5ω0 ω
功率 1/4
功率频谱
(1/π)2 (1/3π)2 (1/5π)2
(1/π)2 (1/3π)2 (1/5π)2
-5ω0 -3ω0 -ω0
ω0 3ω0 5ω0 ω
以一束单色平行光照射光栅,在其后的透镜焦平面上 得到的光强分布与该光栅本身的透射函数的傅里叶功 率谱相同。
sin
2f n
xdx
2
(2) 余弦相移式
T (x) T0 cn cos(2fn n ) n0
cn
a2n
b2n
,n
tan 1
bn an
cn
bn
n
an
(3) 指数式
屏函数为实函数
Tn
T
n
,
T
n
Tn
T (x) T0
T ei(2fn xn ) n
T0
T~n e i 2f n
n0
n0
在焦面上的亮点代表直流成分,每一对亮点代表光栅 的一个空间频率。
v x
f
非周期函数: g(x)
任意屏函数的傅里叶展开
满足狄利克雷条件并在无穷区间 (, 绝对) 可积
一系列基元函数的线性积分 形式
G(f )是g(x)的傅立叶变换
G( f ) F {g(x)}
g(x) G( f )ei2 fxdf
0
x0 x0
(x) dx 1 单缝函数在缝宽趋于零时的极限
函数---点光源
展开为傅里叶级数
T (x)
1 2
2
sin( 0 x)
2
3
sin( 30 x)
2
5
sin(
50 x)
0 2 / d v0 0 / 2 1/ d
空间频率:单位长度内变化的次数。
注意:时间频率只有一维,为正;空间频率有三维, 可正可负。
T
(x)
1 2
2
sin( 0x)
2
3
sin(
30 x)
2
5
sin(
T (x) T0 an cos 2fn x bn sin 2fn x
n0
n0
f1 1/ d 基频
fn nf1 n / d n次波频率
的一 傅维 里周 叶期 级函 数数
1
T0 d
d
2 d
T
(
x)dx,
2
an
2 d
d
2 d
T
(
x)
cos
2f
n
xdx,
2
bn
2 d
d
2 d
T
(x)
--得到总响应
原函数
频谱函数
缝函数
rect( x ) a
1 0
x x
a 2
a
2
asinc (af )
傅 二维矩形函数
里 叶
rect(
x a
)rect(
y b
)
1 0
xa,y b 22
其它各处
absinc (afx )sinc (bfx )
变
圆函数 circ(
x2
y2
)
1
x2y2 a
a
0 其它各处
