结构力学课件:第五章《静定平面桁架》概论
合集下载
结构力学第5章静定平面桁架共24页PPT资料

此杆内力C与o外py力rFig相h等t 2,01另9一-2杆0为19零A杆s,po如s图e P5-t5y(dL)所td示. 。
(2) T型结点。两杆在同一直线上的三杆结点,当结点不受外 力时,第三杆为零杆,如图5-5(b)所示。若外力F与第三杆共线, 则第三杆内力等于外力F,如图5-5(e)所示。
(a)
Copyright 2019-2019 Aspose Pty Ltd.
(a)
(b )
A
A
B
B
C
图5-1
2.计算简图中引用的基本假定
(1)桁架中的各结点都是光滑的理想铰结点。 (2)各杆轴线都是直线,且在同一平面内并通过铰的中心。 (3)荷载及支座反力都作用在结点上且在桁架平面内。
上述假定,保证了桁架中各结点均为铰结点,各杆内只有
(a)
(b)
(c)
(d)
Ev(ae ) luation only. (f)
eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0
Copyright 2019-2019 Aspose Pty Ltd.
图5-4
§5-2 结点法
桁架计算一般是先求支座反力后计算内力。计算内力时可截 取桁架中的一部分为隔离体,根据隔离体的平衡ห้องสมุดไป่ตู้件求解各杆的 轴力。如果截取的隔离体包含两个及以上的结点,这种方法叫截 面法。如果所取隔离体仅包含一个结点,这种方法叫结点法。
当取某一结点为隔离E体va时lu,a由tio于n结o点nl上y.的外力与杆件内力组 ea成te一d平w面it汇h A交s力p系os,e.则S独lid立e的s f平or衡.方N程ET只3有.5两C个l,ie即ntΣPFxr=o0f,ileFy5=.02。.0
(2) T型结点。两杆在同一直线上的三杆结点,当结点不受外 力时,第三杆为零杆,如图5-5(b)所示。若外力F与第三杆共线, 则第三杆内力等于外力F,如图5-5(e)所示。
(a)
Copyright 2019-2019 Aspose Pty Ltd.
(a)
(b )
A
A
B
B
C
图5-1
2.计算简图中引用的基本假定
(1)桁架中的各结点都是光滑的理想铰结点。 (2)各杆轴线都是直线,且在同一平面内并通过铰的中心。 (3)荷载及支座反力都作用在结点上且在桁架平面内。
上述假定,保证了桁架中各结点均为铰结点,各杆内只有
(a)
(b)
(c)
(d)
Ev(ae ) luation only. (f)
eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0
Copyright 2019-2019 Aspose Pty Ltd.
图5-4
§5-2 结点法
桁架计算一般是先求支座反力后计算内力。计算内力时可截 取桁架中的一部分为隔离体,根据隔离体的平衡ห้องสมุดไป่ตู้件求解各杆的 轴力。如果截取的隔离体包含两个及以上的结点,这种方法叫截 面法。如果所取隔离体仅包含一个结点,这种方法叫结点法。
当取某一结点为隔离E体va时lu,a由tio于n结o点nl上y.的外力与杆件内力组 ea成te一d平w面it汇h A交s力p系os,e.则S独lid立e的s f平or衡.方N程ET只3有.5两C个l,ie即ntΣPFxr=o0f,ileFy5=.02。.0
《静定平面桁架》课件

平面桁架的应用场景
01
桥梁工程
作为桥梁的主要受力结构,承载车辆和人群的重量。
02
建筑工程
用于大型工业厂房、仓库、展览馆等建筑的屋面结构。
03
景观工程
作为景观桥梁、廊道等结构,起到连接和支撑的作用。
平面桁架的基本组成
弦杆
主要承受轴向拉力或压 力,是平面桁架的主要 承载杆件。
腹杆
连接弦杆,主要承受剪 力和扭矩,分为斜腹杆 和竖腹杆两种。
静定平面桁架的研究成果总结
静定平面桁架是一种结构形式简 单、受力性能良好的结构体系, 在桥梁、建筑等领域得到了广泛
应用。
在过去的研究中,静定平面桁架 的静力性能、稳定性、优化设计 等方面得到了深入探讨,取得了
丰硕的成果。
静定平面桁架的承载能力、刚度 和稳定性等方面得到了充分验证 ,为实际工程应用提供了可靠的
静定平面桁架
目录
• 平面桁架概述 • 静定平面桁架的分类 • 静定平面桁架的力学特性 • 静定平面桁架的设计与优化 • 静定平面桁架的实例分析 • 总结与展望
01 平面桁架概述
定义与特点
定义
平面桁架是一种由杆件组成的结 构,其所有杆件都位于同一平面 内。
特点
具有结构简单、受力明确、计算 简便等优点,广泛应用于桥梁、 建筑等领域。
D
静定平面桁架的材料选择
钢材
高强度、轻质、耐腐蚀,广泛用于大型结构 和重载静定平面桁架。
复合材料
铝合金
质轻、耐腐蚀、美观,适用于对视觉要求较 高的场合。
如玻璃纤维和碳纤维,高强度、轻质,适用 于对重量要求极高的场合。
02
01
木质
自然、美观,适用于小型、低负载的静定平 面桁架或装饰性结构。
结构力学课件第五章 桁架

a 为 截 面 单 杆
截 面 单 杆
FP
FP
平行情况
b为截面单杆
所作截面截断三根以上的杆件,如除了杆b外, 其余各杆均互相平行,则由投影方程可求出杆b 轴力。
联合桁架举例一
K
K
用结点法计算出1、2、3结点后,无论向结点 4或结点5均无法继续运算。 作K-K截面:M8=0,求FN5-13;进而可求其它杆内力。
15kN
FB=120kN
B
+60
D
+60 30 40
E G
15kN
20
FAH=120kN 60 A -120 C -20 FAV=45kN 15kN
4m 4m
45
F
-20
15kN 4m
到结点B时,只有一个未知力FNBA, 最后到结点A时,轴力均已求出, 故以此二结点的平衡条件进行校核。
FyDG FxDG
FA
几点结论
(1) 用截面法求内力时,一般截断的 杆件一次不能多于三个(特殊情况例外)。 (2) 对于简单桁架,求全部杆件内力 时, 应用结点法;若只求个别杆件内力, 用截面法。 (3) 对于联合桁架,先用截面法将联 合杆件的内力求出,然后再对各简单桁架 进行分析。
截面法中的特殊情况:
注意
对两未知力交点取矩(称为力矩法) 或沿与两个平行未知力垂直的方向 投影(称为投影法)列平衡方程, 可使一个方程中只含一个未知力。
(1)力矩法 设支座反力已求出。
Ⅰ
FA
Ⅰ
FB
求EF、ED、CD三杆 的内力。 取左部分 作截面Ⅰ-Ⅰ, 为隔离体。
FNCD
0 ME (拉) h
FNEF
FYEF FXEF
《静定平面桁架》课件

直杆
桁架主要由直杆组成,通过节点连接。
节点
节点是直杆的连接点,用于传递力和分散荷载。
平面桁架的应用领域
1 桥梁工程
平面桁架是大跨度桥梁的重要组成部分,如悬索桥和斜拉桥。
2 建筑结构
平面桁架在建筑中用于支撑和分散荷载,如体育场馆和大厦。
3 机械工程
平面桁架被用于构建具有高刚度和轻质化要求的机械结构。
《静定平面桁架》PPT课 件
本课件将介绍《静定平面桁架》的概念、应用领域和基本力学分析要点,使 您能全面了解这一结构,并理解其独特的特点和优势。
什么是平面桁架?
平面桁架是由直杆和节点组成的简化结构,用于支撑和分散荷载。其具有均匀分布应力和高刚度的特点, 广泛应用于桥梁、建筑和机械等领域。
平面桁架在静力平衡条件下,完全确定的节点位置和荷载作用下, 桁架各杆件受力唯一确定的平面桁架。
静定平面桁架的特点及优点
特点
静定平面桁架具有稳定的结构形态和力学性能,能够在荷载作用下保持平衡。
优点
静定平面桁架具有高刚度、轻质化、适应性强的优点,广泛应用于各种工程领域。
静定平面桁架的支座类型
1 均布荷载
均布荷载是指荷载在整个桁架结构上均匀分布的载荷。
2 点荷载
点荷载是指荷载作用在结构的一个或多个点上的载荷。
3 变动荷载
变动荷载是指荷载随时间变化的载荷,如风荷载和地震荷载。
1 铰接支座
2 固定支座
铰接支座能够提供约束水平位移,但允许 承受垂直力。
固定支座能够提供约束水平位移和阻止垂 直力的传递。
静定平面桁架的节点类型
1 钢质节点
2 铝合金节点
钢质节点适用于大跨度和复杂结构,具有 高强度和稳定性。
桁架主要由直杆组成,通过节点连接。
节点
节点是直杆的连接点,用于传递力和分散荷载。
平面桁架的应用领域
1 桥梁工程
平面桁架是大跨度桥梁的重要组成部分,如悬索桥和斜拉桥。
2 建筑结构
平面桁架在建筑中用于支撑和分散荷载,如体育场馆和大厦。
3 机械工程
平面桁架被用于构建具有高刚度和轻质化要求的机械结构。
《静定平面桁架》PPT课 件
本课件将介绍《静定平面桁架》的概念、应用领域和基本力学分析要点,使 您能全面了解这一结构,并理解其独特的特点和优势。
什么是平面桁架?
平面桁架是由直杆和节点组成的简化结构,用于支撑和分散荷载。其具有均匀分布应力和高刚度的特点, 广泛应用于桥梁、建筑和机械等领域。
平面桁架在静力平衡条件下,完全确定的节点位置和荷载作用下, 桁架各杆件受力唯一确定的平面桁架。
静定平面桁架的特点及优点
特点
静定平面桁架具有稳定的结构形态和力学性能,能够在荷载作用下保持平衡。
优点
静定平面桁架具有高刚度、轻质化、适应性强的优点,广泛应用于各种工程领域。
静定平面桁架的支座类型
1 均布荷载
均布荷载是指荷载在整个桁架结构上均匀分布的载荷。
2 点荷载
点荷载是指荷载作用在结构的一个或多个点上的载荷。
3 变动荷载
变动荷载是指荷载随时间变化的载荷,如风荷载和地震荷载。
1 铰接支座
2 固定支座
铰接支座能够提供约束水平位移,但允许 承受垂直力。
固定支座能够提供约束水平位移和阻止垂 直力的传递。
静定平面桁架的节点类型
1 钢质节点
2 铝合金节点
钢质节点适用于大跨度和复杂结构,具有 高强度和稳定性。
第五章静定平面桁架1PPT课件
§5-1平面桁架的计算简图
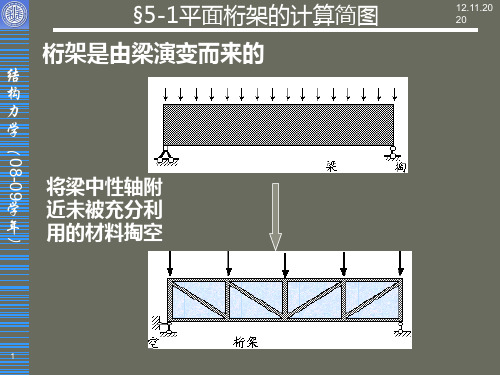
桁架是由梁演变而来的
结 构 力 学 (
08-09
将梁中性轴附
学 近未被充分利
年 )
用的材料掏空
12.11.20 20
1
§5-1平面桁架的计算简图
12.11.20 20
桁架的有关名称
结
构 力
弦杆
上弦杆
学
(
下弦杆
斜杆
腹杆 竖杆
桁高
08-09
学
d
年
结间矩
)
跨度
2
§5-1平面桁架的计算简图
-5
5
10KN
14
§5-2结点法
12.11.20 20
零杆判断举例
结 构
零杆判断小结:
力
学 1.结点仅两杆相连,两杆不共线,且结点无外荷载,
( 则两杆都是零杆
08-09
2.结点仅两杆相连,两杆不共线,若外力与一个杆共
学 年
线,则另一杆是零杆
) 3. 三杆结点,若两杆共线,则第三杆是单杆,若结
点无荷载,则单杆必为零杆,其余两杆轴力大小相等
杆为称为此结点的单杆
08-09
学 结点单杆两种情况
年
) 1.结点只包含两个未知力杆,且 两杆不共线,则每杆都是单杆
单杆
2.结点只包含三个未知力杆,其
中两杆共线,则第三杆是单杆
12
单杆
§5-2结点法
12.11.20 20
结点单杆性质:
结
构 单杆内力由平衡方程直接得出,非单杆须建立
力
联立方程求解;
学
(
对称结构只需计算半边结构,另一半可由 对称性得出
18
§5-2结点法
桁架是由梁演变而来的
结 构 力 学 (
08-09
将梁中性轴附
学 近未被充分利
年 )
用的材料掏空
12.11.20 20
1
§5-1平面桁架的计算简图
12.11.20 20
桁架的有关名称
结
构 力
弦杆
上弦杆
学
(
下弦杆
斜杆
腹杆 竖杆
桁高
08-09
学
d
年
结间矩
)
跨度
2
§5-1平面桁架的计算简图
-5
5
10KN
14
§5-2结点法
12.11.20 20
零杆判断举例
结 构
零杆判断小结:
力
学 1.结点仅两杆相连,两杆不共线,且结点无外荷载,
( 则两杆都是零杆
08-09
2.结点仅两杆相连,两杆不共线,若外力与一个杆共
学 年
线,则另一杆是零杆
) 3. 三杆结点,若两杆共线,则第三杆是单杆,若结
点无荷载,则单杆必为零杆,其余两杆轴力大小相等
杆为称为此结点的单杆
08-09
学 结点单杆两种情况
年
) 1.结点只包含两个未知力杆,且 两杆不共线,则每杆都是单杆
单杆
2.结点只包含三个未知力杆,其
中两杆共线,则第三杆是单杆
12
单杆
§5-2结点法
12.11.20 20
结点单杆性质:
结
构 单杆内力由平衡方程直接得出,非单杆须建立
力
联立方程求解;
学
(
对称结构只需计算半边结构,另一半可由 对称性得出
18
§5-2结点法
教学课件第五章静定平面桁架

60
40
20
-
A
-120 C -20 F -20
15kN 15kN
4m
4m
4m
G
15kN
结点分析时把所有杆内力均画成拉力(含已求得的压力)并代 入方程,然后是拉力的得正值,是压力的得负值。结果为正说 明该杆受拉,结果为负说明该杆受压,这样做不易出错。
§5-2 结点法
小结
• 以结点作为平衡对象,结点承受汇交力 系作用;
2.对称结构受对称荷载作用, 内力和反力均为对称: 受反对称荷载作用, 内力和反力均为反对称。
E 点无荷载,红色杆对不称受轴力处垂的直杆对不称受轴的力杆不受力
FFAAyy
FFBBy y
§5-2 结点法
2.对称结构受对称荷载作用, 内力和反力均为对称: 受反对称荷载作用, 内力和反力均为反对称。 对称结构:几何形状和支座对某轴对称的结构.
FP
§5-2 结点法
关于零杆的判断
桁架中的零杆虽然不受力,但却是保持 结构坚固性所必需的。因为桁架中的载荷往 往是变化的。在一种载荷工况下的零杆,在 另种载荷工况下就有可能承载。如果缺少了 它,就不能保证桁架的坚固性。
分析桁架内力时,如首先确定其中的零杆, 这对后续分析往往有利。
§5-2 结点法
• 按与“组成顺序相反”的原则,逐次建 立各结点的平衡方程,则桁架各结点未 知内力数目一定不超过独立平衡方程数;
• 由结点平衡方程可求得桁架各杆内力。
§5-2 结点法 二、结点法计算简化的途径
1. 对于一些特殊的结点,可以应用平衡条件直 接判断该结点的某些杆件内力为零。 零杆
(1) L型结点:两杆交于一点,若结点无荷载,则两杆 的内力都为零。
第五章静定平面桁架(李廉锟结构力学)全解PPT课件

X0, FN CE FN CH 0
Y0 , 10 2 F k N Cs N Ei n F N C D 0
得
FN CD 1k 0N 215(22.3 61kk 0N N)
F N CH F N CE 2.3 2 6kN
退出
返回
*
§5-2 结点法
5 kN 2m
A 20 kN
10 kN
10 kN 10 kN
通常假定未知的轴力为拉力,计算结果得负值表示轴力 为压力。
退出
返回
*
§5-2 结点法
结构力学
例5-1 试用结点法求三角形桁架各杆轴力。
5 kN 2m
A 20 kN
10 kN
10 kN 10 kN
C
E
F
G
DHBiblioteka 2 m 4=8 m5 kN
B 20 kN
解: (1) 求支座反力。
FxA 0
FyA 20kN(↑)
X0 Y 0
F N AE co sF N AG 0
2k 0 N 5 k N F N Ac E o 0 s
有 所以
FN AE 1k 5N 533.k5N (4压)
F N AG F N AE co s33.2 5 53k 0(N 拉)
退出
返回
*
§5-2 结点法
10 kN
10 kN 10 kN
5 kN
退出
返回
*
§5-1 平面桁架的计算简图
二、按外型分类
1. 平行弦桁架
2. 三角形桁架
3. 抛物线桁架
退出
返回
结构力学
*
§5-1 平面桁架的计算简图
三、按几何组成分类
第05章静定桁架

力学教研室
黑 龙 江 工 程 学 院
22
P
2019/10/14
第五章 静定平面桁架
A
①对称结构在对称荷载作用下,
对称轴上的K 性结点无外力作
用,两斜杆轴力为零。
②由T性结点受力特点,又
黑
可找到四根零杆。
龙
③内接三角形的三顶点不受 力时,内接三角形不受力。
江
又找到六根零杆。
工
00 0
0
0
P
00
程
学
00 0
学 院
ad
RA
2019/10/14
d
YED
力学教研室
力矩法
28
三、投影法
第五章 静定平面桁架
Ⅱ
求DG杆内力
作Ⅱ-Ⅱ截面,
取左部分为隔离体。 由∑Y=0 ,有
RA-P1-P2-P3+YDG=0
YDG=NDGsin=-(RA-P1-P2-P3)
YDG=-V0
此法又称为剪力法。
Ⅱ
黑
龙
江
RA
RB 工
程
DG段V0= (RA-P1-P2-P3)
l/2
拱式结构
特点: 轴压为主,受力较均匀
基础需牢固
B H
黑
龙
VB
江
工
A
C
B
程
学
D 特点: 结构整体来看,受力均匀。
院
横截面弯矩为主,应力分布不均
A
B
梁式结构
为了充分发挥材料的潜力,有 两种处理方案
2019/10/14
力学教研室
4
第五章 静定平面桁架
沿横向将中性轴附近的材料挖去,以节约材料减轻自重。 这样得到的格构式体系称为桁架。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b. 折弦桁架;
(2)按照竖向荷载是否引起水平反力(推力)分为:
a. 梁式桁架(无推力桁架);
b. 拱式桁架(有推力桁架)。
(3)按几何组成方式分为: a. 简单桁架:由一个铰结三角形依次增加二元体
而组成的桁架;
b. 联合桁架:由简单桁架按基本组成规则而联合
组成的桁架;
c.复杂桁架。
返6回
平行弦桁架
返24回
§5-4 截面法和结点法的联合应用 结点法与截面法各有所长,据具体情况选用。有些情
况下,截面法和结点法联合使用,更为方便。举例说明。
例5—1 求桁架中a杆和b杆的内力。
解:(1)求a杆的内力
Ⅰ
b Ya
左作部Ⅰ为S-a隔Ⅰ取离截有K体点面,为,S有a并隔=-离四取S体c
a
K个未知力尚或不能Ya求=-解Y。c
(2)各杆轴都是直线,并在 同一平面内且通过铰的中心;
(3)荷载只作用在结点上 并在桁架平面内。
实际结构与计算简图的差别(主应力、次应力返3)回
铰
返4回
3 .桁架的各部分名称
上弦杆
腹杆
竖杆 斜杆
节间长度d
跨度 L
下弦杆
返5回
4. 桁架的分类
(1)按外形分为:
a. 平行弦桁架; c. 三角形桁架。
1
第五章 静定平面桁架
§5-1 平面桁架的计算简图 §5-2 结点法 §5-3 截面法 §5-4 截面法和结点法的联合运用 §5-5 各式桁架比较 §5-6 组合结构的计算 §5-7 用零载法分析体系的几何组成
2
§5—1 平面桁架的计算简图
1. 桁架:结点均为铰结点的结构。 2. 桁架计算简图的基本假定 (1)各结点都是无摩擦的理想铰;
c
Ⅰ Yc
3P
3P
为体两3P-此,个P2, 求 之S-c 可 出 间P再据-取 其 的由∑P其 一 关 Y+ⅠY=它 或 系a-0-有Ⅰ隔 其 。Y截c离 中=0面
a RA d
YEF
SEF
XEF
SED
SCD d
XED
YED
返21回
(2)投பைடு நூலகம்法
Ⅱ
求DG杆内力 作Ⅱ—Ⅱ截面,
取左部分为隔离体。
Ⅱ
由∑Y=0 有
RA-P1-P2-P3+YDG=0
YDG=SDGsin=-(RA-P1-P2-P3)
YDG
上式括号内之值恰等于相
XDG
应简支梁上DG段的剪力,故
此法又称为剪力法。
则由比例关系可知
Y
X
S X Y
L Ly
L Lx Ly
在S、 X、Y三者中,任知其一
Lx
S
便可求出其余两个,无需使用
三角函数。
返13回
4. 结点法计算举例
(1)首先由桁 架的整体平衡条
HB=12B0kN +60
件求出支反力。
45 30
D
+60
40
(2)截取各结 HA=120AkN 60
点解算杆件内力。
15kN
15kN
+15kN
5. 计算中的技巧
当遇到一个结点上未知力均为斜向时,为简化计算:
(1)改变投影轴的方向 由∑X=0 可首先求出S1
B A
Cd
Y1 X1 B
r
P
S1
A
S2 x
C
(2)改用力矩式平衡方程 将力S1在B点分解为X1、Y1
由∑MC=0
一次求出
X1
Pd h
返15回
6 .几种特殊结点及零杆
(1)L形结点
当结点上无荷载时: S1=0, S2=0
内力为零的杆称为零杆。
(2)T形结点
当结点上无荷载时: S3=0
(3)X形结点
当结点上无荷载时: S1=S2 , S3=S4
(4)K形结点
当结点上无荷载时: S1≠S2 , S3=-S4
返16回
S1
S1
S2
S2
图a L形结点
S1
S3
S3
图b T形结点
S1 S3
S4
S2
图c X形结点
S2 S4
图d K形结点 返17回
7 .零杆的判断 例1
000 0
0
0 0
00
0
8. 几点结论
000
(1)结点法适用于简单桁架,从最后装上的结点 开始计算。
(2)每次所取结点的未知力不能多于两个。
(3)计算前先判断零杆。
返18回
§5-3 截 面 法
1. 截面法的概念: 截面法是作一截面将桁架分成两部 分,任取一部分为隔离体(含两个以上 的结点),用平衡方程计算所截杆件的 内力(一般内力不超过三个)。
2 .截面法据所选方程类型的不同, 又分为力矩法、投影法。
返19回
以例说明
Ⅰ
(1)力矩法
设支反力已求出。
求EF、ED、CD三杆的 内力。
Ⅰ RA
作截面Ⅰ-Ⅰ,取左部分
为隔离体。
RB
SCD
M
0
E(拉)
h
X
EF
M
0
D(压)
H
ad
RA
SEF
YEF XEF
SED
SCD XED
d
YED
载由由作∑RM∑用AR×MDA下=dE2-0=,d0-P下可有1Pd弦以1有-×杆证P22受明d×-拉:0P-力简2dS+,支CXD上桁hEF=H弦架0=杆在0 受竖压向力荷。 得X得E由F ∑SS-CYMCDDERRDOA=ARa0MR+h2A0EPAdd(a有1a拉+PHPP11aPh1d)a2(22adPPd+22d(a)P+02dYdE)D(aM+H20D返d2)0=回0
RA
返22回
3 . 几点结论
(1) 用截面法求内力时,一般截断的
杆件一次不能多于三个(特殊情况例外)。
(2) 对于简单桁架,求全部杆件内力
时, 应用结点法;若只求个别杆件内力,
用截面法。
(3) 对于联合桁架,先用截面法将联
合杆件的内力求出,然后再对各简单桁架
进行分析(见图)。
返23回
ⅠC
A
B
D ⅠE
-120 C -20 VA=45kN 15kN
取结点G隔离体
4m
4m
E 20
F -20
15kN 4m
G
15kN
XSGGE分架次GESG开析,装F 始桁由入计Y架 基 新GG算E的 本 结。几 三 点(何 角 构由由及再S到最故F或组形成C∑比由=结后以由-然A成。2例Y∑0B点到此kA后=F:由N关XC0结结二BS依=此最按系F点时E02可点结次=0桁后二求+k开,1N得点A可取架装5元得k时始只S的N得结为入XS体GY,)有EEE平ED点SC简的=C=规=轴=一G+1-衡F-46单结YXF53则00力0个、=k×GGk条kN点桁NE-依EN53均未EX==件1=、G1E5已2知进E55D=求力k4k3+行-1、NN=25出S2(k校+0(拉CNB02返,k0Ak计核1拉k)N,4N回N算。()(压拉。))
返7回
折弦桁架
返8回
三角形桁架
返9回
梁式桁架
返10回
拱式桁架
返11回
C
A
B
D
E
联合桁架
返12回
§5-2 结点法
1. 求桁架内力的基本方法:结点法和截面法。
2. 结点法:所取隔离体只包含一个结点,称为结点法。
3. 预备知识: 在计算中,经常需要把斜杆的内力S分
解为水平分力X和竖向分力Y。
S
