二三版兼用《运筹学教程》胡运权主编课后习题答案(第五章).ppt
运筹学胡运权 部分课后习题答案
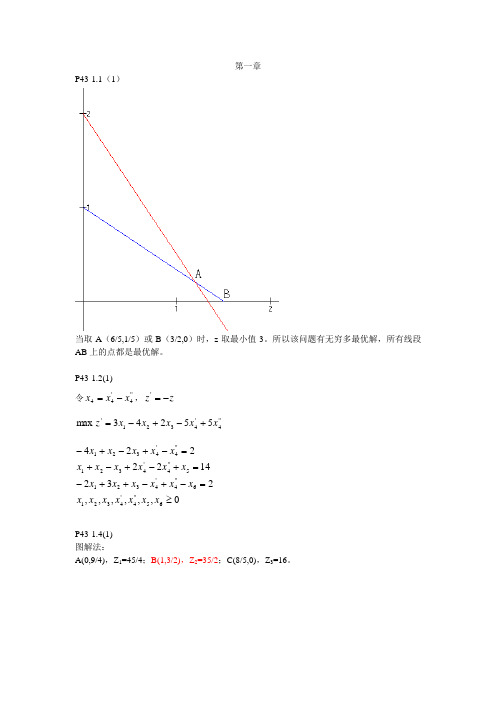
第一章P43-1.1(1)当取A (6/5,1/5)或B (3/2,0)时,z 取最小值3。
所以该问题有无穷多最优解,所有线段AB 上的点都是最优解。
P43-1.2(1)令''4'44x x x -=,z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法:A(0,9/4),Z 1=45/4;B(1,3/2),Z 2=35/2;C(8/5,0),Z 3=16。
单纯形法:10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于:原点;C;B。
P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。
两阶段法:阶段二:P45-1.10证明:CX (0)>=CX*,C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0,即(C*-C)(X*-X (0))>=0。
P45-1.13设饲料i 使用x i (kg ),则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。
运筹学教程(第二版)(胡运权)课后答案(清华大学出版社)

运筹学教程(第⼆版)(胡运权)课后答案(清华⼤学出版社)运筹学教程(第⼆版)习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。
并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。
1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解,1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解, x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。
运筹学清华大学出版社胡运权着课后答案

�12 x1 � 3 x2 � 6 x3 � 3 x4 � 9
(1)
st
��8 ��3
x1 x1
� �
x2 x6
� 4 x3 �0
�
2 x5
� 10
�� x j � 0�, j � 1,� ,6�
min Z � 5 x1 � 2 x2 � 3 x3 � 2 x4
� x1 � 2 x2 � 3 x3 � 4 x4 � 7
运筹学教程�第二版� 习题解答
运筹学教程
1.1 用图解法求解下列线性规划问题。并指出问 题具有惟一最优解、无穷多最优解、无界解还是无可 行解。
min Z � 2 x1 � 3 x2 � 4 x1 � 6 x2 � 6
(1) st .�� 2 x1 � 2 x2 � 4 �� x1 , x2 � 0
Z
0
0.5
2
0
5
0
0
1
1
5
2/5
0
11/5
0
43/5
page 10 6 January 2011
School of Management
运筹学教程
1.4 分别用图解法和单纯形法求解下述线性规划 问题�并对照指出单纯形表中的各基可行解对应图解 法中可行域的哪一顶点。
max Z � 10 x1 � 5 x2 �3 x1 � 4 x2 � 9
max Z � x1 � x2 �6 x1 � 10 x2 � 120 (3) st.�� 5 � x1 � 10 �� 5 � x2 � 8
max Z � 3x1 � 2 x2 �2 x1 � x2 � 2
(2) st.��3x1 � 4 x2 � 12 �� x1, x2 � 0
运筹学教程第三版清华大学出版社出版郭耀煌胡远权编著习题答案习题答案

运筹学教程(第二版)习题解答8.1 证明在9座工厂之间,不可能每座工厂只与其他3座工厂有业务联系,也不可能只有4座工厂与偶数个工厂有业务联系。
解:将有联系的工厂做一条连线。
如果仅有9座工厂只与其他3座工厂有业务联系,说明顶点次数之和为27,矛盾如果只有4座工厂与偶数个工厂有业务联系,其他5个工厂一定与奇数个工厂有业务联系,说明顶点次数之和还是奇数,矛盾。
8.2 有八种化学药品A、B、C、D、E、F、G、H 要放进贮藏室。
从安全角度考虑,下列各组药品不能贮存在同一室内:A—C,A—F,A—H,B—D,B—F,B—H,C—D,C—G,D—E,D—G,E—G,E—F,F—G,G—H,问至少需要几间贮藏室存放这些药品。
解:能贮存在同一室内的两种药品之间作一条连线。
贮存在同一室内的药品应该构成一个完全图。
ABG,CFH ,DE构成完全图。
故,存放这些药品最少需要 3 间储藏室。
8.36个人围成圆圈就座,每个人恰好只与相邻者不相识,是否可以重新就座,使每个人都与邻座认识?解:两个人认识作一条连线。
8.4判定图8-50中的两个图能否一笔画出,若能,则用图形表示其画法。
解:(a)图都是偶点,可以一笔画出。
(b)图只有两个奇点,一个奇点为起点,另一个奇点为终点。
8.5求解如图8-51所示的中国邮路问题,A点是邮局8.6分别用深探法、广探法、破圈法找出图8-52所示图的一个生成树。
8.7设计如图5-53所示的锅炉房到各座楼铺设暖气管道的路线,使管道总长度最(单位:m)。
8.8分别用避圈法和破圈法求图8-54所示各图的最小树8.9 给定权数1,4,9,16,25,36,49,64,81,构造—棵霍夫曼树。
8.10 如图8-55,v0是一仓库,v9是商店,求一条从v0到v9的最短路。
8.11 求图8-56中v1到各点的最短路8.12 求图8-57网络中各顶点间的最短路8.13 某设备今后五年的价格预测分别是(5,5,6,7,8),若该设备连续使用,其第j 年的维修费分别为(1,2,3,5,6),某单位今年购进一台,问如何确定更新方案可使5年里总支出最小(不管设备使用了多少年,其残值为0)解:最优解为:先使用两年,更新后再使用三年。
5.运筹学之运输问题(胡运权版)

第六章运输问题运输问题依然属于线性规划问题的范畴,但是由于其约束方程组的系数矩阵具有特殊的结构,因而可以找到一种比单纯形表更简便的求解方法,正是基于此,运输问题从线性规划中单列出来进行讨论。
本章分为两大部分,前三节介绍求运输问题单纯形方法——表上作业法,第四节重点介绍运用EXCEL电子表格模型解决运输问题。
§1 运输问题的模型与性质1.1运输问题模型运输问题的一般提法是这样的:某种物资有若干个产地和销地,若已知各个产地的产量、各个销地的销量以及各产地到各销地的单位运价(或运输距离)。
问应如何组织调运,才能使总运费(或总的运输量)最省?将此问题更具体化,假定有m个产地,n个销地,a——第i产地的供应量,i=1,2,…,m。
ib——第j销地的需求量,j=1,2,…,n。
jc——从产地i到销地j的单位运费,i=1,2,...,m,j=1,2, (i)n。
x——产地i到销地j的调运数量。
ij则该问题为求解最佳调运方案,即求解所有x的值,使总的运输ij费用11m nij iji j c x==∑∑达到最少。
决策变量为ij x 。
该问题的数学模型形式为:min z =11mnij ij i j c x ==∑∑..s t1miji x=∑≥j b , j =1,2,…,n 。
1nij j x =∑≤ i a , i =1,2,…,m 。
ij x ≥0 ,对所有的i ,j 。
根据该问题中总需求量1m i i a =∑与总供应量1nj j b =∑的关系,可将运输问题分为两类: 1、当1mi i a =∑ =1njj b=∑时,为平衡型运输问题;2、当1m i i a =∑ ≠ 1nj j b =∑ 时,为不平衡型运输问题。
实际上不平衡型运输问题可以转换为平衡型运输问题,我们首先讨论平衡型运输问题,在§3中介绍不平衡型向平衡型的转换。
平衡型运输问题的数学模型形式可表示为: min z =11mnij ij i j c x ==∑∑..s t1miji x=∑ = j b , j =1,2,…,n 。
运筹学 胡运权 课后答案课件

m
a ij y i c j
i1
yi 0
y
无
i
约
束
( j 1,..., n1 )
( j n1 1,..., n ) (i 1,...m 1 ) (i m 1 1,...m )
运筹学 胡运权 课后答案
2.4
运筹学 胡运权 课后答案
运筹学 胡运权 课后答案
2.9
运筹学 胡运权 课后答案
(d)
对偶问题:
max w 2y1 3 y2 5 y3
y1 2y2 y3 2
3 y1
y2 4 y3 2
4 y1 3 y2 3 y3 4
y1 0, y2 0, y3取 值 无 约 束
对偶问题:
m
m i n w b i y i i1
m
a ij y i c j
i1
(1,2章)
运筹学 胡运权 课后答案
图解法:
当 x2 2 x 11 5z经 过 运筹点 学 胡( 运1 权, 课3 2 后) 答案时 , z最 大 。
单纯形法:添加松弛变量化为标准形式,
max z 10x1 5x2 0x3 0x4
3x1 5 x1
4x2 2x2
x3
x4
9 8
x
j
0
( j 1, 2, 3, 4)
运筹学 胡运权 课后答案
1.6(a)
运筹学 胡运权 课后答案
运筹学 胡运权 课后答案
1.7
运筹学 胡运权 课后答案
1.8
(P36公式)表1-24中,x1,x5为基变量,g=1, h=0,l=0。
运筹学 胡运权 课后答案
1.11
运筹学 胡运权 课后答案
二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)
城市
电站
1
2
3
Ⅰ
15
18
22
Ⅱ
21
25
16
第三章习题解答
习题3.12的解答
城市 城市
电站
1-1
城市 1-2
城市2
城市 3-1
城市 3-2
产量
Ⅰ
150 15
15 250 18
22
22 400
Ⅱ
140 21
第三章习题解答
表3-35
食品厂
面粉厂
1
2
3
产量
Ⅰ
3 10
2 20
Ⅱ
4 11
8 30
Ⅲ
8 11
4 20
销量
15 25 20
第三章习题解答
习题3.10的解答
食品厂 面粉厂
Ⅰ Ⅱ Ⅲ 销量
1
3 15 4
8 15
2
10 5 11 20 11 25
3
20 2 8 4
20
4
0 10 0
0 10
产量
20 30 20
B3
B4 产量
A1 A2 A3 销量
3
7
6
45
2
4
3
22
4
3
8
56
3
3
2
2
第三章习题解答
习题3.9的解答
销地
产地
B1 B2 B3 B4 B5 产量A1源自33 7 6 24 0 5
A2
2 4 23 2 0 2
A3 销量
4 33 8 5 30 6 33223
第三章习题解答
3.10 某市有三个面粉厂,它们供给三个面食加工 厂所需的面粉。各面粉厂的产量、各面食加工厂加工 面粉的能力、各面食加工厂和各面粉厂之间的单位运 价,均表示于表3-35中。假定在第1,2和3面食加工厂 制作单位面粉食品的利润分别为12元、16元和11元, 试确定使总效益最大的面粉分配计划(假定面粉厂和面 食加工厂都属于同一个主管单位)。
二三版兼用《运筹学教程》胡运权主编课后习题答案(第五章)ppt
xi
,
yi
0, 且都是整数,i
1,2,, n
第五章习题解答
5.4 篮球队需要选择5名队员组成出场阵容参加比 赛。8名队员的身高及擅长位置见表5-10。
表5-10
队员
12345678
身高(m) 1.92 1.90 1.88 1.86 1.85 1.83 1.80 1.78
擅长位置 中锋 中锋 前锋 前锋 前锋 后卫 后卫 后卫
max Z xi i 1
n
di xi D,
i1
xi是整数
xi ai
i 1,2,, n
第五章习题解答
5.2 要在长度为l的一根圆钢上截取不同长度的零 件毛坯,毛坯长度有n种,分别为aj,(j=1,2,…,n)。 问每种毛坯应当各截取多少根,才能使圆钢残料最少, 试建立本问题的数学模型。
第五章习题解答
表5-11-12-13
产品A
成本
产品B
成本
产品C
成本
产量(件)(元/件) 产量(件) (元/件) 产量(件) (元/件)
0~40
10
0~50
6
0~100
5
41~100
9
51~100
4
100以上
4
101~150
8
100以上
3
150以上
7
解:设x1,x2,x3分别表示三个产品的产量。 Y11,y12,y13,y14对应产品A的4个成本的0-1变量; Y21,y22,y23对应产品B的3个成本的0-1变量; Y31,y32对应产品B的3个成本的0-1变量;
解:设xi表示各种毛坯的数量, i 1,2,, n。
清华大学《运筹学教程》胡运权主编课后习题答案
该题是唯一最优解:
29
17
x1 5 , x2 5 , x3 1, x4 0, Z 5
page 21 13 April 2021
21
School of Management
运筹学教程
第一章习题解答
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
(2)
st
x1 x2 x3 4 2x1 x2 x3 6
x1 0, x2 0, x3无约束
page 6 13 April 2021
6
School of Management
运筹学教程
第一章习题解答
min Z 3x1 4x2 2x3 5x4
4x1 x2 2x3 x4 2
17
School of Management
运筹学教程
第一章习题解答
解:下界对应的模型如下( c,b取小,a取大)
max Z x1 4x2
st.43xx1165xx22
8 10
x1, x2 0
最优值(下界)为:6.4
page 18 13 April 2021
18
School of Management
运筹学教程
第一章习题解答
1.2 将下述线性规划问题化成标准形式。
min Z 3x1 4x2 2x3 5x4
4x1 x2 2x3 x4 2
(1)
st
x12x1x23xx23
2x4 x3
14 x4
. 2
x1, x2 , x3 0, x4无约束
min Z 2x1 2x2 3x3
st
8x1 3x1
清华大学《运筹学教程》胡运权主编课后习题答案(第一章)
m ax Z 3 x1 2 x 2 2 x1 x 2 2 ( 2) st . 3 x1 4 x 2 12 x , x 0 1 2 该问题无可行解
2
( 3)
m axZ x1 x 2 6 x1 10x 2 120 st . 5 x1 10 5 x2 8
1
(3)
max Z x1 x2 6 x1 10x2 120 st . 5 x1 10 5 x 8 2
(4)
m i nZ 2 x1 3 x 2 4 x1 6 x 2 6 (1) st . 3 x1 2 x 2 4 x ,x 0 1 2 无穷多最优解 (蓝 色 线 段 上 的 点 都 是 优 最解 ) x1 6 1 , x2 , 是 其 中 一 个 最 优 解 5 5
唯一最优解, x1 10, x 2 6 Z 16
(4)
max Z 5 x1 6 x2 2 x1 x2 2 st. 2 x1 3x2 2 x ,x 0 1 2
3
该问题有无界解
1.2
将下述线性规划问题化成标准形式。
min Z 3x1 4 x2 2 x3 5 x4 4 x1 x2 2 x3 x4 2 x x x 2 x 14 2 3 4 st 1 . 2 x1 3x2 x3 x4 2 x1 , x2 , x3 0, x4无约束
解:令 w Z , x4 x41 x42, 其 中 x41,x42 0, 同时引入松弛变量 x5, 剩 余 变 量 x6, 则 标 准 形 式 为 : m axw 3 x1 4 x 2 2 x 3 5 x41 5 x42 4 x1 x 2 2 x 3 x41 x42 x x x 2x 2x x 1 2 3 41 42 5 st 2 x1 3 x 2 x 3 x41 x42 x6 x1 , x 2 , x 3 , x41 , x42 , x6 2 14 2 3x2 6 x3 3x4 9 8 x x 4 x 2 x 10 1 2 3 5 st 3x1 x6 0 ( , j 1, ,6) x j 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章习题解答
5.12 现有P个约束条件
a
j 1
n
ij ij
x bi
i 1,2,, p
需要从中选择q个约束条件,试借助0-1变量列出 表达式。
解:设yi是0 1变量, i 1,2, , p yi ( aij xij bi ) 0
j 1 n
i 1,2, , p
第五章习题解答
解:设xi 1表示携带第i件物品,i 1,2, , m。 max Z ci xi
i 1 m
m ai xi a i 1 m bi xi b i 1 xi是0 1变量 i 1,2, m
第五章习题解答
5.6 用割平面法解下列整数规划:
i 1 n
n d i xi D, i 1 x 是整数 i
xi ai
i 1,2, , n
第五章习题解答
5.2 要在长度为l的一根圆钢上截取不同长度的零 件毛坯,毛坯长度有n种,分别为aj,(j=1,2,…,n)。 问每种毛坯应当各截取多少根,才能使圆钢残料最少, 试建立本问题的数学模型。
第五章习题解答
5.5 一个旅行者要在其背包里装一些最有用的旅行 物品。背包容积为a,携带物品总重量最多为b。现有 物品m件,第i件物品体积为ai ,重量为bi(i=1,2,…, m)。为了比较物品的有用程度,假设第j件物品的价值 为ci(i=1,2,…,m)。若每件物品只能整件携带,每 件物品都能放人背包中,并且不考虑物品放人背包后 相互的间隙。问旅行者应当携带哪几件物品,才能使 携带物品的总价值最大,要求建立本问题的数学模型。
0.2
0
1.4
1.1
第五章习题解答
解:最大元素是 ,用它减去所有元素, 1.4 0.1 0.6 1.4 0.2 0 得到矩阵: .4 1.4 1.4 0.35 0.4 0.5 1 0 最优解是: 0 0 0 1 .4 1 . 4 0 .1 0 .1 1 .4 0 . 2 1 .4 1 . 2 0 .8 1 . 4 0 .4 1 .4 1.4 , 0 0 .3
第五章习题解答
表5-11-12-13 产品A 成本 产品B 成本 产品C 成本 产量(件)(元/件) 产量(件) (元/件) 产量(件) (元/件) 0~40 41~100 10 9 0~50 51~100 6 4 0~100 100以上 5 4
101~150
150以上
8
7
100以上
3
解:设x1,x2,x3分别表示三个产品的产量。 Y11,y12,y13,y14对应产品A的4个成本的0-1变量; Y21,y22,y23对应产品B的3个成本的0-1变量; Y31,y32对应产品B的3个成本的0-1变量;
第五章习题解答
5.1 某地准备投资D元建民用住宅。可以建住宅的 地点有n处:A1,A2,…,An。在Ai处每幢住宅的造价 为dj;,最多可造aj幢。问应当在哪几处建住宅,分别 建几幢,才能使建造的住宅总数最多,试建立问题的 数学模型。
解:设xi 表示在Ai处所建住宅的数量 i 1,2, , n。 , max Z xi
第五章习题解答
5.10 有五项设计任务可供选择。各项设计任务的 预期完成时间分别为3,8,5,4,10(周),设计报酬分 别为7,17,11,9,21(万元)。设计任务只能一项一项 地进行,总的期限是20周。选择任务时必须满足下面要 求: 1.至少完成3项设计任务; 2.若选择任务1,必须同时选择任务2; 3.任务3和任务4不能同时选择。 应当选择哪些设计任务,才能使总的设计报酬最大?
第五章习题解答
5.9 解下列0-1型整数规划:
max Z 2 x1 x2 x3 min Z 5 x1 7 x2 10x3 3x4 x5 x1 3 x2 x3 2 x1 3x2 5 x3 x4 4 x5 2 4x x 5 2 3 2 x 6 x 3 x 2 x 2 x 0 ( 2) (1) 1 2 3 4 5 st . x1 2 x2 x3 2 st . x 4x x 4 2 x2 2 x3 x4 x5 1 2 3 1 x1 , x2 , x3 , x4 , x5 0或1 x1 , x2 , x3 0或1 解:此题无解。 解:x1 1, x2 x3 x4 0, Z 2
第五章习题解答
5.11 某城市可划分为11个防火区,已设有4个消防 站,见下图所示。
第五章习题解答
上图中,虚线表示该消防站可以在消防允许时间 内到达该地区进行有效的消防灭火。问能否关闭若干 消防站,但仍不影响任何一个防火区的消防救灾工作。 (提示:对每—个消防站建立一个表示是否将关闭的01变量。)
解:设xi 表示各种毛坯使用圆钢 的数量, i 1,2,, n。 yi 表示各种毛坯在一根圆 钢上可得到的数量。 min Z xi
i 1 n
ai yi l , i 1,2,, n yi xi mi , i 1,2,, n x , y 0, 且都是整数, 1,2,, n i i i
第五章习题解答
5.8 某公司生产A,B和C 3种产品,售价分别为12 元、7元和6元。生产每件A产品需要1h技术服务、10h 直接劳动、3kg材料;生产每件B产品需要2h技术服务、 4h直接劳动、2kg材料;生产每件C产品需要1h技术服 务、5h直接劳动、1k8材料。现在最多能提供100h技术 服务、700h直接劳动、400kg材料。生产成本是生产量 的非线性函数,如表5-11、表5-12、表5-13所示。要求 建立一个总利润最大的生产计划的数学模型。提示: 对每种产品不同成本的产量范围各设一个0-1变量。)
(1)
0 1 解: 0 0
1
0 0 1 0
0 0 0 0
0 0 0 1
1 0 , Z 22 0 0
( 2)
0 0 1 解: 0 0 0
0 1 0 0 0 0 0 0 0 0 0
0 0 0 ,Z 8 0 0 1
max Z x1 x2 2 x1 x2 6 st . 4 x1 5 x2 20 x , x 0, 且为整数 1 2
min Z 5 x1 x2 3 x1 x2 9 x x 5 ( 2) 2 st 1 . x1 8 x2 8 x1 , x2 0, 且为整数 解:x1 4, x2 1, Z 5
出场阵容应满足以下条件: (1) 只能有一名中锋上场; (2) 至少有—名后卫; (3) 如1号和4号均—上场,则6号不出场;
第五章习题解答
(4) 2号和8号至少有一个不出场。 问应当选择哪5名队员上场,才能使出场队员 平均身高最高,试建立数学模型。
解:设xi 1表示第i个队员出场, 1,2, , n。 i 1 8 max Z xi 5 i 1 8 xi 5 i 1 x x 1 x x x 1 2 6 7 8 1 x x 1 x x x 2 8 1 4 6 2 xi是0 1变量
第五章习题解答
5.4 篮球队需要选择5名队员组成出场阵容参加比 赛。8名队员的身高及擅长位置见表5-10。
表5-10 队员 身高(m) 擅长位置 1 1.92 2 1.90 3 1.88 4 1.86 5 1.85 6 1.83 7 1.80 8 1.78
中锋 中锋 前锋 前锋 前锋 后卫 后卫 后卫
(1)
解:x1 1, x2 3, Z 4
第五章习题解答
5.7 用分支定界法解下列整数规划:
max Z 2 x1 x2 x1 x2 5 x x 0 (1) 2 st 1 . 6 x1 2 x2 21 x1 , x2 0, 且为整数 解:x1 3, x2 1, Z 7 min Z 5 x1 x2 2 x3 3 x1 10x2 50 7 x 2 x 28 ( 2) 2 st 1 . x1 , x2 0 x2为整数 解:x1 0, x2 5, x3 0, Z 5
解:设xi 1表示第i个消防站保留, 1,2,3, i 4。 max Z x1 x2 x3 x4 x1 x2 1 x1 1 x1 x2 x3 1 x3 1 x1 x4 1 x1 x2 x4 1 x x 1 x 1 4 4 2 xi是0 - 1变量, i 1,2,3,4 显然,可以关闭 号消防站。 2
y
i 1
p
i
q
第五章习题解答
5.13 解下列系数矩阵的最小化问题:
10 11 4 2 8 7 11 10 14 12 5 6 9 12 14 13 15 11 10 7
3 7 3 6 5 5 6 1 8 4 2 7 2 4 5 3 4 6 6 4 8 7 3 2
第五章习题解答
解:设xi 1表示第i项任务被选中, 1,2,,5。 i max Z 7 x1 17x2 11x3 9 x4 21x5 3x1 8 x2 5 x3 4 x4 10x5 20 x1 x2 x3 x4 x5 3 x1 x2 x x 1 4 3 xi是0 - 1变量, i 1,2,3,4,5
第五章习题解答
5.14 需要分派5人去做5项工作,每人做各项工 作的能力评分见表5-14。应如何分派,才能使总的得 分最大?
表5-14 业务 人员 B1 B2 B3 B4 B5
A1
A2 A3
1.3
0 1.0
0.8
1.2 0
0
1.3 0
0
1.3 1.2
