运筹学____胡运权_课后答案
运筹学教程（第二版）（胡运权）课后答案（清华大学出版社）
运筹学教程（第⼆版）（胡运权）课后答案（清华⼤学出版社）运筹学教程（第⼆版）习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。
并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。
1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解，1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解， x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。
运筹学清华大学出版社胡运权着课后答案
�12 x1 � 3 x2 � 6 x3 � 3 x4 � 9
(1)
st
��8 ��3
x1 x1
� �
x2 x6
� 4 x3 �0
�
2 x5
� 10
�� x j � 0�, j � 1,� ,6�
min Z � 5 x1 � 2 x2 � 3 x3 � 2 x4
� x1 � 2 x2 � 3 x3 � 4 x4 � 7
运筹学教程�第二版� 习题解答
运筹学教程
1.1 用图解法求解下列线性规划问题。并指出问 题具有惟一最优解、无穷多最优解、无界解还是无可 行解。
min Z � 2 x1 � 3 x2 � 4 x1 � 6 x2 � 6
(1) st .�� 2 x1 � 2 x2 � 4 �� x1 , x2 � 0
Z
0
0.5
2
0
5
0
0
1
1
5
2/5
0
11/5
0
43/5
page 10 6 January 2011
School of Management
运筹学教程
1.4 分别用图解法和单纯形法求解下述线性规划 问题�并对照指出单纯形表中的各基可行解对应图解 法中可行域的哪一顶点。
max Z � 10 x1 � 5 x2 �3 x1 � 4 x2 � 9
max Z � x1 � x2 �6 x1 � 10 x2 � 120 (3) st.�� 5 � x1 � 10 �� 5 � x2 � 8
max Z � 3x1 � 2 x2 �2 x1 � x2 � 2
(2) st.��3x1 � 4 x2 � 12 �� x1, x2 � 0
清华大学《运筹学教程》胡运权主编课后习题答案
3 x1 x2 x5 3
st
4 x1 3 x2 x3 x6
x1
2 x2
x4
4
6
x j 0（, j 1,,4）
cj
CB
xB
b
-M x5 3
-M
x6
6
0
x4
4
cj zj
-4 x1 1
-M x6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
3
1
0
4
3 -1
1
20
7M-4 4M-1 -M
小于0 ,因此已经得到唯一最优解，最优解为：
X * 2 5 ,9 / 5,1,0T
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
6x2 x2 x3
15x3 5
15
x j 0（, j 1,,3）
39
1.8 已知某线性规划问题的初始单纯形
表和用单纯形法迭代后得到下面表格,试求括
弧中未知数a∼l值。
项目
X1 X2 X3 X4 X5
X4 6 (b) (c) (d) 1 0
X5 1 -1 3 (e) 0 1
Cj－Zj
a -1 2 0 0
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj－Zj
0 -7 (j) (k) (l)
6 4
x1 , x2 0
无穷多最优解
(蓝 色 线 段 上 的 点 都 是 最优 解 ）
x1
6 5
,
x2
《运筹学(胡运权)》第五版课后习题答案
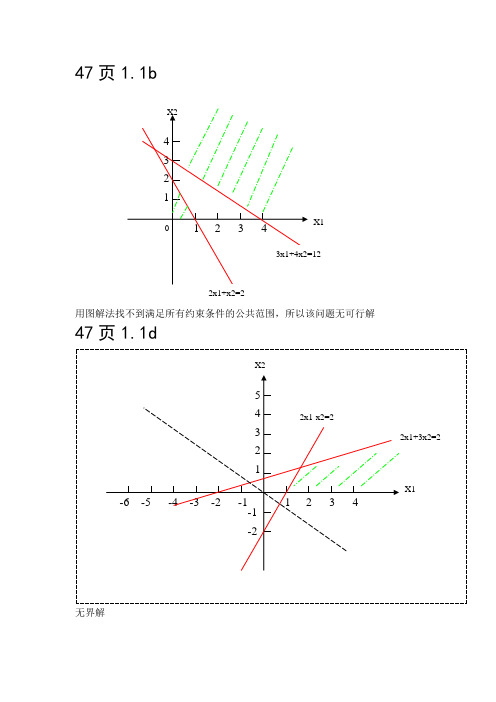
X33.000000 0.000000
X1,X2,X3 0.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.200000
3) 0.000000 0.600000
4) 0.0000000.000000
6) 0.0000000.008571
7) 0.000000 0.110000
8) 0.000000 -1.500000
NO. ITERATIONS= 6
计算lindo截屏
2.1a:
对偶问题为：
maxz=2y1+3y2+5y3
s.t.
y1+2y2+y3≤2
3y3+y2+4y3≤2
4y1+3y2+3y3=4
A1 1200.000000 0.000000
A2 0.000000 9.640000
A3 285.714294 0.000000
B3 10000.0000000.000000
C1 0.000000 15.900000
B1 0.000000 0.230000
A4 342.857147 0.000000
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
运筹学基础及应用第四版胡运权主编课后练习答案
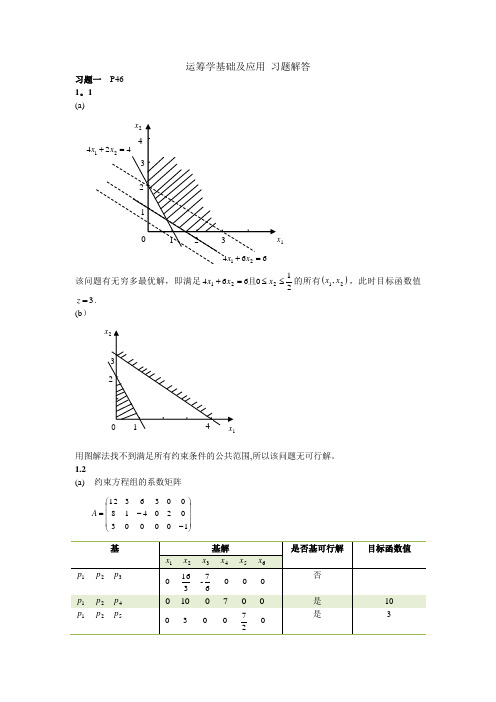
运筹学基础及应用 习题解答习题一 P46 1。
1 (a)该问题有无穷多最优解，即满足210664221≤≤=+x x x 且的所有()21,x x ，此时目标函数值3=z . (b ）用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。
(b) 约束方程组的系数矩阵⎪⎪⎭⎫ ⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。
1。
3(a ）（1） 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ，最大值235=z（2）单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。
令021==x x得基可行解()8,9,0,0=x ，由此列出初始单纯形表 21σσ>。
5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ，2328,1421min =⎪⎭⎫⎝⎛=θ0,21<σσ，表明已找到问题最优解0 , 0 , 23 1,4321====x x x x 。
最大值 235*=z(b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ，最大值217=z（2） 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ，4P ,5P 组成一个基。
令021==x x得基可行解()0,0,15,24,5x =，由此列出初始单纯形表21σσ>。
运筹学（胡运权）第五版课后答案,运筹作业
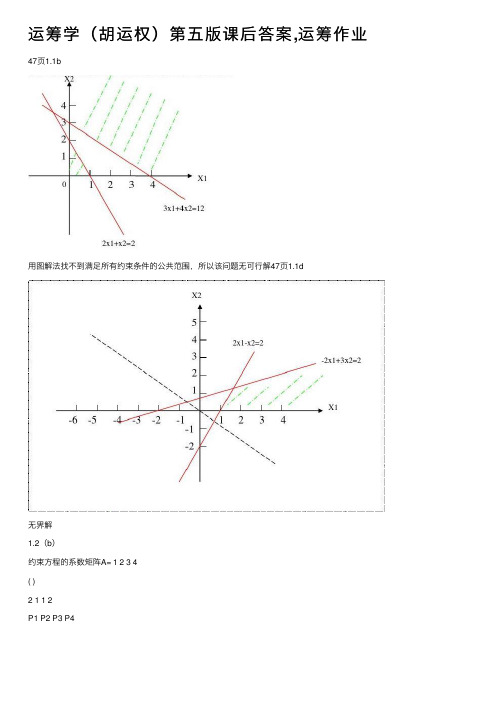
运筹学（胡运权）第五版课后答案,运筹作业47页1.1b⽤图解法找不到满⾜所有约束条件的公共范围，所以该问题⽆可⾏解47页1.1d⽆界解1.2（b）约束⽅程的系数矩阵A= 1 2 3 4( )2 1 1 2P1 P2 P3 P4最优解A=(0 1/2 2 0)T和(0 0 1 1)T49页13题设Xij为第i⽉租j个⽉的⾯积minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13 +6000x23+7300x14s.t.x11+x12+x13+x14≥15x12+x13+x14+x21+x22+x23≥10x13+x14+x22+x23+x31+x32≥20x14+x23+x32+x41≥12Xij≥0⽤excel求解为：⽤LINDO求解：LP OPTIMUM FOUND A T STEP 3OBJECTIVE FUNCTION V ALUE1) 118400.0VARIABLE V ALUE REDUCED COST Z 0.000000 1.000000 X11 3.000000 0.000000X21 0.000000 2800.000000X31 8.000000 0.000000X41 0.000000 1100.000000X12 0.000000 1700.000000X22 0.000000 1700.000000X32 0.000000 0.000000X13 0.000000 400.000000X23 0.000000 1500.000000X14 12.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 -2800.0000003) 2.000000 0.0000004) 0.000000 -2800.0000005) 0.000000 -1700.000000NO. ITERATIONS= 3答若使所费租借费⽤最⼩，需第⼀个⽉租⼀个⽉租期300平⽅⽶，租四个⽉租期1200平⽅⽶，第三个⽉租⼀个⽉租期800平⽅⽶，50页14题设a1，a2，a3, a4, a5分别为在A1, A2, B1, B2, B3加⼯的Ⅰ产品数量，b1，b2，b3分别为在A1, A2, B1加⼯的Ⅱ产品数量，c1为在A2，B2上加⼯的Ⅲ产品数量。
运筹学(胡运权版)第三章运输问题课后习题答案
P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。
其余（非基）变量全等于零。
此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6).总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ij ij x c Z 246685143228116410=⨯+⨯+⨯+⨯+⨯+⨯=2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数）应尽可能地小。
胡运权运筹学教程答案
胡运权运筹学教程答案胡运权运筹学教程答案【篇一运筹学基础及应用第四版胡运权主编课后练习答案】txt 习题一p461.1a23。
b用亂解法找到满足所打约柬条仲的公it范w，所以该问题无可行解。
1.2a约束方程组的系数矩阵r最优解a.o，iao,7，o，ob约束方程组的系数矩阵fi234、4l22i2,最优解1八,0,11,0八v551.3a1图解法⑵单纯形法首先在各约朿条件上添加松弛变铽，将问题转化为标准形式maxz10a-,5a20x30a4[3a-.4义2a39si.[5a-j2x2a48则a,p4组成个猫令a;c20得-站可行解a_0.0.9,8，山此列出初始单纯形表cr20，0-minj2a新的单纯形农为a,xoxax21414mtq.qco，表明已找到问题垴优解._5__25xi，a-30,a4（b）（1）图解法17最优解即为严aixy52x224的解x卩，2v最大值zii22/单纯形法（2）苘先在外约朿条件.h添加松弛变m，将问题转化为标准形式maxz2.v,x2ox30.v4oa55a2156.y,2x2.v424【篇二运筹学（第五版）习题答案】章（39页）1.1用图解法求解下列线性规划问题，并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
（1）maxzx1x25x110x250x1x21x24x1，x20x13x23x1x22x1，x20（3）maxz2x12x2x1-x2-1-0.5x1x22x1，x20（4）maxzx1x2x1-x203x1-x2-3x1，x20解（1）（图略）有唯一可行解，maxz14（2）（图略）有唯一可行解，minz9/4（3）（图略）无界解（4）（图略）无可行解1.2将下列线性规划问题变换成标准型，并列出初始单纯形表。
（1）minz-3x14x2-2x35x44x1-x22x3-x4-2x1x23x3-x414-2x13x2-x32x42 x1，x2，x30，x4无约束（2）maxszkpkzkaikxiki1k1xk1mik1i1,...,nxikOi1n;k1,,m1解设z-z,x4x5-x6,x5,x60标准型maxz3x1-4x22x3-5x5-x60x70x8-mx9-mx10s.t.-4x1x2-2x3x5-x6x10 2x1x23x3-x5x6x714-2x13x2-x32x5-2x6-x8x92x1,x2,x3,x5,x6,x7,x8 ,x9,x100⑵解加入人工变量x1,x2,x3,xn，得maxs1/pki1nk1mikxik-mx1-mx2-..-mxns.t.xixik1i1,2,3,nk1mxik0,xi 0,i1,2,3n;k1,2.,m是任意正整数1.3在下面的线性规划问题中找出满足约束条件的所有基解。
(完整word版)运筹学(胡运权)第五版课后答案,运筹作业
47页1.1b羅蕿用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解薅47页1。
1d蒂无界解（b）衿1.2蕿约束方程的系数矩阵A=1234莇2112蚄P1P2P3P4,运筹作业肀最优解A=（01/220）T和(0011）T页13题肆49膃设Xij为第i月租j个月的面积羄minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x 14螁s.t.聿x11+x12+x13+x14≥15膃x12+x13+x14+x21+x22+x23≥10膀x13+x14+x22+x23+x31+x32≥20艿x14+x23+x32+x41≥12袇Xij≥0芃用excel求解为：薁用LINDO求解：羁LPOPTIMUMFOUNDATSTEP3薆OBJECTIVEFUNCTIONVALUE 蚇1)118400.0羂VARIABLEVALUEREDUCEDCOST 荿Z0.0000001。
000000虿X113.0000000。
000000螇X210。
0000002800。
000000莃X318。
0000000.000000肁X410.0000001100。
000000莈X120.0000001700.000000袆X220.0000001700。
000000螄X320.0000000。
000000蕿X130.000000400.000000膇X230。
0000001500。
000000袆X1412.0000000.000000袁ROWSLACKORSURPLUSDUALPRICES芁2)0。
000000—2800。
000000羆3）2.0000000.000000羆4)0。
000000—2800.000000节5）0。
000000-1700.000000蝿NO。
ITERATIONS=3罿答若使所费租借费用最小，需第一个月租一个月租期300平方米，租四个月租期1200平方米，第三个月租一个月租期800平方米,页14题肆50蚃设a1，a2，a3,a4,a5分别为在A1，A2，B1，B2，B3加工的Ⅰ产品数量，b1，b2，b3分别为在A1，A2，B1加工的Ⅱ产品数量,c1为在A2，B2上加工的Ⅲ产品数量。
《运筹学(胡运权)》第五版课后习题答案
用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解
47页1.1d
无界解
1.2（b）
约束方程的系数矩阵A= 1 2 3 4
2 1 1 2
P1 P2 P3 P4
基
基解
是否可行解
目标函数值
X1 X2 X3 X4
P1 P2
-4 11/2 0 0
否
P1 P3
2/5 0 11/5 0
是
43/5
程序法
6.4a
破圈法
避圈法
最小部分树16
6.4b
最小部分树32
172页6.11
红色曲线为使用一年卖出
蓝色曲线为使用两年卖出
绿色曲线为使用三年卖出
紫色曲线为使用四年卖出
最短路程为3.7万元，路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4
三种方案分别为：第一年年初买新车，年末卖掉再买新车，一直用到第四年年末卖掉；
x2≤4+(1-y2)M
y1+y2=1
y1,y2=0或1
e)设yi= 1第i组条件起作用
0第i组条件不起作用i=1,2则
x1+x2≤5-(1-y1)M
x1≤2-(1-y2)M
x3≥2+(1-y3)M
x3+x4≥6+(1-y4)M
y1+y2+y3+y4≥2
y1,y2,y3,y4=1或0
4.2
minz=
d)
maxz=3x1+x2+4x3-0.4y
s.t.
6x1+3x2+5x3≤45
3x1+4x2+5x3-y≤30
《运筹学(胡运权)》第五版课后习题答案
B2 10000.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.168000
3) 0.000000 1.500000
4) 0.000000 0.075000
5) 5628.571289 0.000000
5.3c
因为使mind1-,故在x1+x2=40的右侧，若使mind4+,则在x1+x2=50的左侧，即阴影区域，因为在阴影部分无法使2d2-+d3-最小，故比较E（20，30）,F（24，26）,E点:d2-=4,d3-=0 min2d2-+d3-=8,F点:d2-=0,d3-=4, min2d2-+d3-=4,故选F点
X2 0.000000 2.000000
X33.000000 0.000000
X1,X2,X3 0.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.200000
3) 0.000000 0.600000
4) 0.0000000.000000
设a1，a2，a3, a4,a5分别为在A1,A2,B1,B2,B3加工的Ⅰ产品数量，b1，b2，b3分别为在A1,A2,B1加工的Ⅱ产品数量，c1为在A2，B2上加工的Ⅲ产品数量。则目标函数为‘
maxz= (1.25-0.25)( a1+a2+a3)+(2-0.35) b3+(2.8-0.5)c1 -0.05(a1+b1)-
程序法
6.4a
破圈法
避圈法
运筹学清华大学出版社 胡运权着 课后答案
�
x 32
�
x4
�
6
�� x1 , x 2 , x31 , x32 , x 4 � 0
page 7 6 January 2011
School of Management
运筹学教程
1.3 对下述线性规划问题找出所有基解�指出哪 些是基可行解�并确定最优解。
max Z � 3 x1 � x2 � 2 x3
�� x1 � 0 , x 2 � 0 , x3无约束
page 5 6 January 2011
School of Management
运筹学教程
minZ � �3x1 � 4x2 �2x3 �5x4
�4x1 � x2 � 2x3 � x4 � �2
(1)
st�����x12�x1x�2 �3xx23
� � x1 � x2 � x3 � 4
(2)
st
� �
� 2 x1 � x2 � x3 � 6
�� x1 � 0, x2 � 0, x3无约束
max Z � 2 x1 � 2 x2 � 3 x31 � 3 x32
� � x1 � x 2 � x31 � x32 � 4
st
� �
2
x1
�
x2
�
x 31
page 14 6 January 2011
School of Management
运筹学教程
l.6 考虑下述线性规划问题�
max Z � c1 x1 � c2 x2 � a11 x1 � a12 x2 � b1
st .��a21 x1 � a22 x2 � b2 �� x1, x2 � 0
式中�1≤c1≤3, 4≤c2≤6, -1≤a11≤3, 2≤a12≤5, 8≤b1≤12, 2≤a21≤5, 4≤a22≤6, 10≤b2≤14,试确定 目标函数最优值的下界和上界。
《运筹学(胡运权)》第五版课后习题答案
X2 0.000000 2.000000
X3 3.000000 0.000000
X1,X2,X30.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.200000
3) 0.000000 0.600000
P1 P4
-1/3 0 0 11/6
否
P2 P3
0 1/2 2 0
是
5
P2 P4
0 -1/2 0 2
否
P3 P4
0 0 1 1
是
5
最优解A=(0 1/2 2 0)T和(0 0 1 1)T
49页13题
设Xij为第i月租j个月的面积
minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x14
x41+x42+x43+x44+x45=1
x11+x21+x22+x23=1
x12+x22+x32+x42=1
x13+x23+x33+x43=1
x14+x24+x34+x44=1
x15+x25+x35+x45=1
xij=1或0（i=1,2,3,4 j=1,2,3,4,5）
由excel计算得出；张游仰泳，王游蛙泳，赵游自由泳，预期总成绩为126.2s.
6x1+3x2+5x3+8x4≤45
《运筹学(胡运权)》第五版课后习题答案
x11+x12+x13+x14#43;x23≥10
x13+x14+x22+x23+x31+x32≥20
x14+x23+x32+x41≥12
Xij≥0
用excel求解为：
用LINDO求解：
LP OPTIMUM FOUND AT STEP 3
OBJECTIVE FUNCTION VALUE
程序法
6.4a
破圈法
避圈法
最小部分树16
6.4b
最小部分树32
172页6.11
红色曲线为使用一年卖出
蓝色曲线为使用两年卖出
绿色曲线为使用三年卖出
紫色曲线为使用四年卖出
最短路程为3.7万元，路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4
三种方案分别为：第一年年初买新车，年末卖掉再买新车，一直用到第四年年末卖掉；
0.03(a2+b2+c1)-0.06(a3+b3)-0.11(a4+c1)-0.05a5
=0.95a1+0.97a2+0.94a3+1.5b3+2.1c1-0.05b1-0.11a4-0.05a5
s.t.
5a1+10b1≤6000
7a2+b2+12c1≤10000
6a3+8a3≤4000
4a4+11c1≤7000
NO. ITERATIONS= 0
可知购进原材料15个单位为宜。
4.1
a）设yi= 1第i组条件起作用
0第i组条件不起作用
x1+x2≤2-(1-y1)M M—充分大正数
清华大学《运筹学教程》胡运权主编课后习题答案(第一章)
2)c=0
3)c>0
d<0 d=0 d>0
0
c 3 d 4
A1点 A1点 A3点
A2A3线段
3 c 5 4 d 2
c 5 d 2 c 5 d 2
c 3 d 4
A2点
A1A2线段 A1点
l.6 考虑下述线性规划问题：
max Z c1 x1 c2 x2 a11 x1 a12 x2 b1 st .a21 x1 a22 x2 b2 x1 , x2 0
-1
x2
0
x3
0
x4
-M
x5
-M
x6
CB
xB
x5
x6
x4
i
-M -M 0
3 6 4
[3] 4 1
1 3 2
0 -1 0
0 0 1
1 0 0
0 1 0 0
1 3/2 4 3 6/5 9/5
cj zj
7M-4
1 2 3 1 0 0 0
4M-1
1/3 [5/3] 5/3
5M/3+1/3
-M
0 -1 0 -M
0
0 0 1 0
0
1/3 -4/3 -1/3
-7M/3+4/3
-4 -M 0
x1
0
1 0 0
x6
x4
cj zj
cj
x6
是否基 可行解
Z
(x1,x2,x3)
(x1,x2,x4) (x1,x2,x5) (x1,x2,x6)
0
0 0 7/4
61/3
10 3 -4
-7/6
0 0 0
《运筹学(胡运权)》第五版课后习题答案
VARIABLE VALUE REDUCED COST
Z 0.000000 1.000000
X11 3.000000 0.000000
X21 0.000000 2800.000000
X31 8.000000 0.000000
X41 0.000000 1100.000000
X12 0.000000 1700.000000
程序法
6.4a
破圈法
避圈法
最小部分树16
6.4b
最小部分树32
172页6.11
红色曲线为使用一年卖出
蓝色曲线为使用两年卖出
绿色曲线为使用三年卖出
紫色曲线为使用四年卖出
最短路程为3.7万元，路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4
三种方案分别为：第一年年初买新车，年末卖掉再买新车，一直用到第四年年末卖掉；
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
d)
maxz=3x1+x2+4x3-0.4y
s.t.
6x1+3x2+5x3≤45
3x1+4x2+5x3-y≤30
x1,x2,x3,y≥0
用lomdo求解为
LP OPTIMUM FOUND AT STEP 0
OBJECTIVE FUNCTION VALUE
运筹学基础及应用第四版胡运权主编课后练习答案
运筹学基础及丨、V:用习题解答习题一 P461.1(a)2 = 3。
(b)用亂解法找+到满足所打约柬条仲的公：it•范W，所以该问题无可行解。
1.2(a)约束方程组的系数矩阵最优解A.=(o，i a o,7，o，o)r(b)约束方程组的系数矩阵 f I 2 3 4、4 = l2 2 I 2,最优解1 = (^,0，11，0^ V55 )"1.3(a)(1)图解法⑵单纯形法首先在各约朿条件上添加松弛变铽，将问题转化为标准形式max z = 10a-, +5a'2 +0x3 +0a4[3a-. +4 义2 + A3 = 9 si.<[5a-j + 2X2 + a'4 = 8则A，P4组成个猫《=令 A = ;c2 = 0得-站可行解a_ = (0.0.9,8)，山此列出初始单纯形表cr 2 >0， 0 - minj 2Ax2xi =~，a-3 =0, a 4最优解即为严+2X2=24的解x =卩，2V 最大值z : IA"i + X y =5I 2 2 /新的单纯形农为A', Xo X A14 14_5_ _25M ~T?q.qcO ，表明已找到问题垴优解.(b)(1)图解法17(2)单纯形法苘先在外约朿条件.h 添加松弛变M ，将问题转化为标准形式 max z = 2.v, + x 2 + Ox 3 + 0.v 4 + Oa 5 5a'2 + = 15 6.y, + 2x 2 + .v 4 = 240 00 --2 *^4o A :5、Q 0 一4(7,^2 <0,表明已找到问题最优解^ =1，X 2=- , A-32L估• 17Hi Z =——21.6(a)在约朿条件中添加松弛变量或剩余变量，且令k = jc 2 -a :； (a*2 > 0,.v ； > o)Xx = ~X->该问题转化为max z' = -3a, - x 2 + .v 2 - 2a 3 + 0.v 4 + (Xv 5 2x | + 3a -2 - 3a 2+ 4a 3 +a 4 =12攀 M I4a'| +x 2 -A*2 -2a*3 —^5 =8 3a*, -X 2 +X 2 — 3a*3 = 6A*,, A '2，X 2, x 3，A-4 , A 3 ^ 0-K 约朿系数矩陴为23 -34 I 0 4 丨-1-20-13 -丨丨一3 0 0在A 屮人为地添加两列单位向虽/>7，2 3 -3 4 1 0 0 0 4 丨-1 -2 t) -1 丨 0 3-1 I -3 0 0 0 1令 max z'= -3a -i - x 2 +x 2- 2.v 3 + Oa:., + 0.v 5 - Mx 6 - Mx 7 得初始单纯形表15最大a 4 = 0，x 5SS ^ Xi x 2x 4 x 5 x 6-2 0 0M -M4 10 -I 0 00 0 0-3 + 7M -J 1 -2-5M 0 -M 0 0-I-5(b)在约朿条件中添加松弛变M 或剩余变M ，.R 令a:3 (jc 3>0,.x ；>0)该问题转化为max z • = 一3^ - 5.v 2 + x ?- x ? + 0,v 4 + Ox 5 x, + 2X 2 + x^- x^-x 4 =6 2.v, + x 2- 3jc 3 - 3^：3 + a*5 = 16 x 2+ 5 a*3 一 5a*3= 10 •v p A ：2，“x 4，A 5^0艽约柬系数矩阵为213-30-1 115-50 0v/ft A 屮人为地添加两列单位向觉p 7, 121-1-1010、2 13-30 100 115 -5 0 0 01、 /令 max z , = -3a*, 一 5,v 2 + .v 3 一 x 3 + 0x 4 + 0x s 一 Mx b - Mx 1衍初始单纯形表0 0 -M - M X. X, X,X, X, X, X, x n-A/ x 616-M x 7 10-3 + 2A/ 5 + 3M 1+6M -1-6M -M 0 0 0(a)解1:大\1法在上述线性规划问题中分别减去剩余变萤x 4，x 6,〜再加上人工变蛩15，17，'，得max z = 2x t - x2 + 2x3 + 0,v4 - Mx s + 0,v6 - Mx7 + 0a8- Mx^-3 + 7M -J 1 -2-5M 0 -M 0 0A', + X 2 + A ：3 - + JC 5 = 6 -2x l + jc 3 — a*6 + x 1 —2 2x z — j c 3 - a *8+ j c 9 =0a-,,.v 2,a*3,j:4,a:5,^6,x 7,x 8,a-9 >0，r,其中MS 个任意人的正数-据此可列出单纯形表22MMMjc, x 2x 4X5 X6 A-M x s 6 -M x 7一2 —Ma 、00 0 0[2]0 M 02-M 3A/-1 2 + A/ -M 1/2 -1/2 0 0-1/2 -1/2x s-M x,—Ix\ [1]1/2^ 5M 3 … ^… A/ I 1 3A/ 2-M0 ----- + — - M0 -M 0 ------------------ 一十 ---2 2 2 2 2 2-M jr 5 3 2 .v 3 2 -I x 2 I 3/2 -3/2 1/2 -1/2 -11-1/2 1/2 -1/2 1/20 0 0 1 1 03/40 0?>M +3 -5M -3 M-3M4Af+5 0 ■M22 2x, 3/4 A 3 7/2 7/40 00 1 0| 43/8 - 8 8-5/4 -M8山单纯形表计算结果可以ft 出，ct 4 >0且％<0(/ =丨，2，3),所以该线性规划问题有无界解 解2:两阶段法。