Eviews数据统计与分析教程6章 基本回归模型的OLS估计-加权最小二乘法
EVIEWS面板数据分析操作教程及实例解析
模型选择对分析结果影响
模型适用性
根据研究目的和数据特征选择合 适的面板数据模型，如固定效应 模型、随机效应模型等。
模型假设
确保所选模型满足基本假设，如 线性关系、误差项独立同分布等 ，否则可能导致结果不准确。
模型比较与选择
通过比较不同模型的拟合优度、 参数显著性等指标，选择最优模 型进行分析。
操作规范性与结果可靠性保障措施
操作步骤规范
结果验证与解读
对分析结果进行验证，确保结果的合理性和准确性 ；同时，正确解读分析结果，避免误导读者。
严格按照EVIEWS软件的操作步骤进行分析 ，避免操作失误或遗漏关键步骤。
数据分析报告
编写详细的数据分析报告，包括数据来源、 处理方法、模型选择、分析结果及解读等， 以便读者全面了解分析过程。
方和来估计模型参数。
广义最小二乘法（GLS）
02
当存在异方差性或自相关性时，采用广义最小二乘法进行参数
估计，以提高估计效率。
最大似然法（ML）
03
适用于随机效应模型等复杂面板数据模型，通过最大化似然函
数来估计模型参数。
模型诊断与检验
残差分析
检查残差是否满足独立同分布等假设条件， 以评估模型的拟合效果。
07 EVIEWS面板数 据分析操作注意 事项
数据质量对分析结果影响
数据来源
确保数据来自可靠、权威的来源，避免使用不准确或存在偏见的数 据。
数据完整性
检查数据是否存在缺失值、异常值或重复值，这些问题可能导致分 析结果失真。
数据处理
对数据进行适当的预处理，如清洗、转换和标准化，以提高数据质量 和一致性。
增强了解决实际问题的能力
通过实例解析和操作演示，学员们学会了如何运用所学知识解决实际问题，提高了分析 问题和解决问题的能力。
OLS估计和预测
• 在命令栏里输入最小二乘估计的命令：ls + 因变量＋c（常数项）＋自变量 • 在这个例子中是：ls ed c fi
对于这个估计结果我们一定要予以充分的关注，在以后的 许多其他检验中，我们都会涉及到对它的分析和应用。
第四步：参数分析：
• 下面会出现一个对话 框(如下页图) ：
▲点击确定之后，会建立一个workfile，或者说 我们已经有了张桌子，下面就是具体操作了。 ▲值得注意的是在随后出现的小的workfile对话 框也有一个标题栏，它也有自己的诸多用处，这 在以后会具体讲解。
二、 一元线性回归模型的ols估计
• 例：ＯＬＳ估计一元线性回归模型
R2
SSR SST
2 ˆ ( y y ) i 2 ( y y ) i i 1 i 1 n
n
•
•
n 1 R 1 (1 R 2 ) nk
2
SE
2 ˆ ( y y )
nK
参数说明2
• 第四个指标为残差平方和，这个值 也是越小越好。
2 ˆ SSE ( yi yi )
（如果关系存在且不为虚假关系的话）
• 其次它说明了各个自变量对因变量影响的 力度是不同的 • 再次它为我们对未来经济运行状况提供了 预测分析的可能。
三、一元线性回归模型的预测
• 模型经过估计后如果通过检验，则意味着 它可以被付诸于应用，这里我们介绍它的 一种最常见的应用——预测。； • 要对一元线性模型进行预测，需要在已知 解释变量值的条件下进行。 • 本例中我们有1998年度的fi值为10000.00亿 元。
DW
参数说明3
加权最小二乘法的基本思想即大残差
加权最小二乘法(WLS) 是一种统计学方法，它用于解决带有误差的线性回归问题。
它的基本思想是在最小二乘法的基础上，通过给每个样本点赋予不同的权重，来解决样本点的误差不同的问题。
基本思想就是，通过给不同的样本点赋予不同的权重，来解决样本点的误差不同的问题。
在WLS中，每个观测值都有一个相应的权重。
权重是与观测值相关的标量值，可以用来衡量观测值的置信度或相对重要性。
权重越大，观测值对结果的影响就越大。
大残差的定义是指比较大的样本误差。
在WLS中，我们通过减小大残差对结果的影响来提高结果的精确度。
加权最小二乘法
obs 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
Y 1578 1654 1400 1829 2200 2017 2105 1600 2250 2420 2570 1720 1900 2100 2300
X 24127 25604 26500 27670 28300 27430 29560 28150 32100 32500 35250 33500 36000 36200 38200
6
2。模型变换法
（1）模型变换法的定义 （2）模型变换法的关键 （3）模型变换法的变换过程 （4）实际处理异方差时，f(xi)的常用形式 （5）常用变换举例 （6）利用EViews作模型变换
8
3。加权最小二乘法
（1）加权最小二乘法的思路 （2）加权最小二乘法的机理 （3）加权最小二乘法的定义 （4）OLS是加权最小二乘法的特例 （5）加权最小二乘法与模型变换法所得结 果是一致 （6）在EViews中实现加权最小二乘法
30
obs 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Y 264 105 90 131 122 107 406 503 431 588 898 950 779 819 1222 1072
X 8777 9210 9954 10508 10979 11912 12747 13499 14269 15522 16730 17663 18575 19535 21163 22880
43
（2）G-Q检验
1。求两个子样回归方程残差平方和 加载(lx4下)yfch.wf工作文件到内存 SORT X 按居民收入排序 SMPL 1 12 LS Y C X 得ESS1 SMPL 20 31 LS Y C X 得ESS2
加权最小二乘回归系数的估计计算过程
加权最小二乘回归系数的估计计算过程1. 概述加权最小二乘回归是一种对数据进行线性建模的方法，在现实应用中经常被使用。
通过加权最小二乘回归，我们可以得到对数据的线性关系进行建模的最佳拟合直线，并估计出各个自变量的系数。
本文将详细介绍加权最小二乘回归系数的估计计算过程，以便读者能够深入了解这一方法的原理和实现。
2. 加权最小二乘回归的基本原理加权最小二乘回归方法是最小化因变量的观测值与回归函数预测值之间的加权残差平方和来确定回归系数的方法。
其数学表达式为：（1）min∑wi(yi - β0 - β1xi1 - ... - βpxip)^2其中wi是观测值的权重，yi表示因变量的观测值，β0是截距项，β1到βp为自变量系数，xi1到xip为自变量观测值。
3. 加权最小二乘回归系数的估计计算步骤加权最小二乘回归系数的估计计算过程可以分为以下几个步骤：（1）计算加权变量根据给定的权重，对自变量和因变量进行加权变换，得到加权后的自变量和因变量。
（2）构建加权矩阵根据加权后的自变量和因变量，构建加权矩阵。
加权矩阵是一个n×(p+1)的矩阵，其中n为样本量，p为自变量的个数。
（3）计算加权矩阵的转置矩阵对加权矩阵进行转置，得到加权矩阵的转置矩阵。
（4）计算加权矩阵的乘积将加权矩阵和其转置矩阵相乘，得到乘积矩阵。
（5）计算乘积矩阵的逆矩阵对乘积矩阵进行求逆运算，得到逆矩阵。
（6）计算加权矩阵和因变量的乘积将加权矩阵和因变量相乘，得到乘积向量。
（7）计算回归系数利用逆矩阵和乘积向量，通过线性代数方法计算得到回归系数的估计值。
4. 加权最小二乘回归的优势加权最小二乘回归相对于普通最小二乘回归的优势在于，它能够更好地处理数据的异方差性。
在普通最小二乘回归中，对所有观测值一视同仁，忽略了不同观测值的方差可能不同的情况。
而通过加权最小二乘回归，我们可以根据数据的特点赋予不同观测值不同的权重，从而更准确地估计回归系数。
Eviews数据统计与分析教程章基本回归模型的OLS估计普通最小二乘法
EViews统计分析基础教程
三、 多元线性回归模型
通常情况下，把多元线性回归方程中的常数项看作虚拟 变量的系数，在参数估计过程中该常数项始终取值为1。 因而模型的解释变量个数为k+1.多元回归模型的矩阵形 式为
Y = X + u 其中，Y是因变量观测值的T维列向量；X是所有自变量 （包括虚拟变量）的T个样本点观测值组成的T×（k+1） 的矩阵；是k+1维系数向量；u是T维扰动项向量。
EViews统计分析基础教程
五、 线性回归模型的检验
3.异方差性检验
（1）图示检验法
图示检验法通过散点图来判断用OLS方法估计的模 型异方差性，这种方法较为直观。通常是先将回归 模型的残差序列和因变量一起绘制一个散点图，进 而判断是否存在相关性，如果两个序列的相关性存 在，则该模型存在异方差性。
EViews统计分析基础教程
EViews统计分析基础教程
五、 线性回归模型的检验
4.序列相关检验
（1）杜宾（D .W .—Durbin-Watson）检验法
如果，
0 < D .W . < dt ，存在一阶正自相关 dt < D .W . < du ，不能确定是否存在自相关 du < D .W . < 4－du ，不存在自相关 4－du < D .W . < 4－dt 不能确定是否存在自相关 4－dt < D .W . < 4 ，存在一阶负自相关
EViews统计分析基础教程
五、 线性回归模型的检验
1.拟合优度检验
拟合优度检验用来验证回归模型对样本观测值（实
际值）的拟合程度，可通过R2统计量来检验。
EViews统计分析基础教程
经验分享,使用eviews做回归分析
[经验分享] 使用eviews做线性回归分析Glossary:ls(least squares)最小二乘法R-sequared样本决定系数（R2）：值为0-1，越接近1表示拟合越好，>0.8认为可以接受，但是R2随因变量的增多而增大，解决这个问题使用来调整Adjust R-seqaured()S.E of regression回归标准误差Log likelihood对数似然比：残差越小，L值越大，越大说明模型越正确Durbin-Watson stat：DW统计量，0-4之间Mean dependent var因变量的均值S.D. dependent var因变量的标准差Akaike info criterion赤池信息量(AIC)（越小说明模型越精确）Schwarz ctiterion:施瓦兹信息量（SC）（越小说明模型越精确）Prob(F-statistic)相伴概率fitted(拟合值)线性回归的基本假设：1.自变量之间不相关2.随机误差相互独立，且服从期望为0，标准差为σ的正态分布3.样本个数多于参数个数建模方法:ls y c x1 x2 x3 ...x1 x2 x3的选择先做各序列之间的简单相关系数计算，选择同因变量相关系数大而自变量相关系数小的一些变量。
模型的实际业务含义也有指导意义，比如m1同gdp肯定是相关的。
模型的建立是简单的，复杂的是模型的检验、评价和之后的调整、择优。
模型检验：1）方程显著性检验（F检验）：模型拟合样本的效果，即选择的所有自变量对因变量的解释力度F大于临界值则说明拒绝0假设。
Eviews给出了拒绝0假设(所有系统为0的假设)犯错误(第一类错误或α错误)的概率(收尾概率或相伴概率)p 值，若p小于置信度(如0.05)则可以拒绝0假设，即认为方程显著性明显。
2）回归系数显著性检验（t检验）：检验每一个自变量的合理性|t|大于临界值表示可拒绝系数为0的假设，即系数合理。
Eviews基本操作 (2)
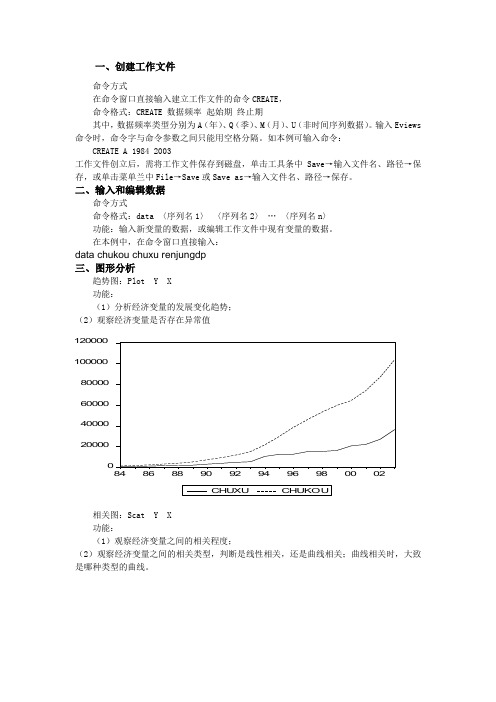
一、创建工作文件命令方式在命令窗口直接输入建立工作文件的命令CREATE ， 命令格式：CREATE 数据频率 起始期 终止期 其中，数据频率类型分别为A （年）、Q （季）、M （月）、U （非时间序列数据）。
输入Eviews 命令时，命令字与命令参数之间只能用空格分隔。
如本例可输入命令：CREATE A 1984 2003工作文件创立后，需将工作文件保存到磁盘，单击工具条中Save →输入文件名、路径→保存，或单击菜单兰中File →Save 或Save as →输入文件名、路径→保存。
二、输入和编辑数据命令方式命令格式：data 〈序列名1〉 〈序列名2〉 … 〈序列名n 〉 功能：输入新变量的数据，或编辑工作文件中现有变量的数据。
在本例中，在命令窗口直接输入：data chukou chuxu renjungdp 三、图形分析趋势图：Plot Y X 功能：（1）分析经济变量的发展变化趋势； （2）观察经济变量是否存在异常值02000040000600008000010000012000084868890929496980002相关图：Scat Y X 功能：（1）观察经济变量之间的相关程度；（2）观察经济变量之间的相关类型，判断是线性相关，还是曲线相关；曲线相关时，大致是哪种类型的曲线。
20000400006000080000100000120000010000200003000040000CHUXUC H U K O U四、OLS 估计参数在主菜单命令行键入 LS Y C X单击Equation 窗口中的Resid 按钮，将显示模型的拟合图和残差图-10000-50000500010000-2000002000040000600008000010000012000084868890929496980002单击Equation 窗口中的View → Actual, Fitted, Resid → Table 按钮，可以得到拟合直线和残差的有关结果五、预测在Equation 框中选Forecast 项后，弹出Forecast 对话框，Eviews 自动计算出样本估计期内的被解释变量的拟合值，拟合变量记为chukouF ，其拟合值与实际值的对比图如下-2000002000040000600008000010000012000084868890929496980002scalar CHUKOU1 = -5719.991597 + 2.116770043*0 + 3.773129627*0区间估计coef(2) confintconfint(1)=1243-@qtdist(.975,20)*eq01.@sddep confint(2)=1243+@qtdist(.975,20)*eq01.@sddep coef(4) confint1confint1(1)=eq01.@coefs(2)-@qtdist(.975,20)*eq01.*@stderrs(2) confint1(2)=eq01.@coefs(2)+@qtdist(.975,20)*eq01.*@stderrs(2) confint1(3)=eq01.@coefs(3)-@qtdist(.975,20)*eq01.*@stderrs(3) confint1(4)=eq01.@coefs(3)+@qtdist(.975,20)*eq01.*@stderrs(3)六、非线性回归模型的估计1．倒数模型：μββ++=XY 110 在命令窗口直接依次键入GENR X1=1/X LS Y C X12．多项式模型：μβββ+++=2210X X Y 在命令窗口直接依次键入GENR X1=X GENR X2=X^2 LS Y C X1 X23．准对数模型：μββ+++=X Y ln 10 在命令窗口直接依次键入GENR lnX=LOG(X)LS Y C lnX4．双对数模型：μββ+++=X Y ln ln 10 在命令窗口直接依次键入GENR lnX=LOG(X) GENR lnY=LOG(Y)LS lnY C lnX七、异方差检验与解决办法1．X e -2相关图检验法LS Y C X 对模型进行参数估计 GENR E=RESID 求出残差序列GENR E2=E^2 求出残差的平方序列 SORT X 对解释变量X 排序SCAT X E2 画出残差平方与解释变量X 的相关图2．戈德菲尔德——匡特检验已知样本容量n=26，去掉中间6个样本点（即约n/4），形成两个样本容量均为10的子样本。
eviews基本回归模型
2019/1/15 21
7. 因变量均值和标准差（Mean/S.D. dependent var） y 的均值和标准差由下面标准公式算出：
y yi T
i 1
T
sy
y
T t 1
i
y
2
T 1
作为一个规则，如果 DW 值接近 2 ，证明不存在序列相关。 在例 1 的结果中， DW 值很小，表明残差中存在序列相关。关 于 Durbin-Watson 统计量和残差序列相关更详细的内容参见 “序列相关理论”。 对于序列相关还有更好的检验方法。在 “序列相关的检
验”中，我们讨论Q统计量和 LM检验，这些都是比DW统计
2019/1/15
3
§ 6.2 在EViews中对方程进行说明 当创建一个方程对象时，会出现如下对话框：
在这个对话框中需要说明三件事：方程说明，估计方法，估 计使用的样本。在最上面的编辑框中，可以说明方程：因变量 （左边）和自变量（右边）以及函数形式。 有两种说明方程的基本方法：列表法和公式法。列表法简单 但是只能用于不严格的线性说明；公式法更为一般，可用于说明 非线性模型或带有参数约束的模型。
2019/1/15 16
6.4.2 方程统计量
1. R2 统计量(R-squared)
R2 统计量衡量在样本内预测因变量值的回归是否成功。R2
是自变量所解释的因变量的方差。如果回归完全符合，统计值 会等于 1。如果结果不比因变量的均值好，统计值会等于 0。 R2 可能会由于一些原因成为负值。例如，回归没有截距或常数， 或回归包含系数约束，或估计方法采用二阶段最小二乘法或
ARCH方法。
EViews计算R2 的公式为： ˆ u ˆ u 2 R 1 ( y y )( y y ) ，
计量经济学案例eviews
案例分析1.问题的提出和模型的设定根据我国1978—1997年的财政收入Y 和国民生产总值X 的数据资料，分析财政收入和国民生产总值的关系建立财政收入和国民生产总值的回归模型。
假定财政收入和国民收入总值之间满足线性约束，则理论模型设定为i i i u X Y ++=21ββ其中i Y 表示财政收入，i X 表示国民生产总值。
表1我国1978—1997年财政收入和国民生产总值2.参数估计进入EViews 软件包，确定时间范围；编辑输入数据；选择估计方程菜单，估计样本回归函数如下表 2obsX Y 19783624.100 1132.260 19794038.200 1146.380 19804517.800 1159.930 19814860.300 1175.790 19825301.800 1212.330 19835957.400 1366.950 19847206.700 1624.860 19858989.100 2004.820 198610201.40 2122.010 198711954.50 2199.350 198814922.30 2357.240 198916917.80 2664.900 199018598.40 2937.100 199121662.50 3149.480 199226651.90 3483.370 199334560.50 4348.950 199446670.00 5218.100 199557494.90 6242.200 199666850.50 7407.990 1997 73452.50 8651.140估计结果为Y=858.3108 + 0.100031X(12.78768) (46.04788)R^2=0.991583 S.E.=208.508 F=2120.408括号内为t统计量值。
3.检验模型的异方差（一）图形法1、EViews软件操作。
Eviews数据统计与分析教程6章 基本回归模型的OLS估计-加权最小二乘法
EViews统计分析基础教程
Байду номын сангаас
四、非线性最小二乘法（NLS）
基本原理： 设定非线性回归模型的一般式为 yi = f(xi, ,β) + μi i=1，2,…，n 则其残差平方和为
（1）
2 n ˆ S ( ) = y f x , （2） ˆ i i i 1 能使(2)达到最小的为参数β的非线性最小二乘估计。要 得到β的估计值，首先对式（1）中的β求偏导，然后令 该式等于0。 还可以通过迭代法求的近似值，先给出参数估计的初始 值，然后通过迭代法得到一个新的估计值，重复迭代直 到估计值收敛为止。
EViews统计分析基础教程
五、广义矩估计（GMM）
基本原理： 广义矩估计是设定参数满足的一种理论关系。其原理是 选择参数估计尽可能接近理论上关系，把理论关系用样 本近似值代替；并且估计量的选择就是要最小化理论值 和实际值之间的加权距离。参数要满足的理论关系通常 是参数函数f(θ)与工具变量Zt之间的正则条件，即 E[f(θ)′Z]=0，θ是被估计参数 广义矩估计法（GMM）中估计量选择的标准是，使工 具变量与函数f(θ)之间的样本相关性越接近于0越好。
EViews统计分析基础教程
五、广义矩估计（GMM）
EViews基本操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，在 “Method”中选择“GMM”后弹出如下图所示的方程设 定对话框。
基本思路： 赋予每个观测值残差不同的权数，从而使得回归模型的随 机误差项具有同方差性。
EViews统计分析基础教程
一、加权最小二乘法（WLS）
Eviews估计方法汇总
Eviews估计方法汇总来源：计量经济学01最小二乘法（1）普通最小二乘估计（OLS）：这是使用的最为普遍的模型，基本原理就是估计残差平方和最小化，不予赘述。
（2）加权最小二乘估计（WLS）Eviews路径：LS模型设定对话框-----optionsOLS的假设条件最为严格，其他的估计方法往往是在OLS的某些条件无法满足的前提下进行修正处理的。
WLS就是用来修正异方差问题的。
在解释变量的每一个水平上存在一系列的被解释变量值，每一个被解释变量值都有自己的分布和方差。
在同方差性假设下，OLS对每个残差平方ei^2都同等看待，即采取等权重1。
但是，当存在异方差性时，方差δi^2越小，其样本值偏离均值的程度越小，其观测值越应受到重视，即方差越小，在确定回归线时的作用应当越大；反之方差δi^2越大，其样本值偏离均值的程度越大，其在确定回归线时的作用应当越小。
WLS的一个思路就是在拟合存在异方差的模型的回归线时，对不同的δi^2区别对待。
在利用样本估计系数时依旧是使得总体残差最小化，但是WLS会给每个残差平方和一个权重wi=1/δi。
这样，当δi^2越小，wi越大；反之，δi^2越大，wi越小。
Eviews的WLS没有要求权重因子必须是1/δi。
一般纠正异方差性的方法还包括模型变换法，这种方法假定已知Var（ui）=δi^2=δ^2*f(Xi)，令权重wi=f(Xi)^（1/2），用f(Xi)^（1/2）去除原模型，可知随机干扰项转换为ui/f(Xi)^（1/2），这时Var（ui）=δi^2=δ^2，即实现了同方差。
由上面的分析可知，WLS核心就是找到一个等式：Var（ui）=δi^2=δ^2*f(Xi)。
这个等式经过调整更容易理解：δ^2=δi^2/f(Xi)或δ=δi/f(Xi)^（1/2）。
δ为某一常数，权重wi=1/f(Xi)^（1/2），经过wi的加权便实现了同方差。
前面提到的特殊权重wi=1/δi，即f(Xi)=1/δi^2,这时δ=δi/f(Xi)^（1/2）=1。
eviews基本操作介绍
31
4 对象类型
除了序列对象和方程对象外还有许多其他类型的对象; 每种对象在对象集合中都有一个特定的图标表示 对象集合 虽然也是对象但对象集合没有图标;因此工作文件和数据库 不能放在其他的工作文件或数据库中
32
基本对象操作
30
3 对象过程PROC
许多EViews对象还包括过程Procedure 与视图一样的是;过 程通常以图表或坐标的形式显示在对象窗口中；与视图不同的 是;过程改变数据;无论对象本身中的还是其他对象中的
很多过程还创建新的对象 比如说序列对象含有进行平滑与 季节调整的过程;该过程可以创建一个新的含有平滑以及调整 后的数据的序列 方程对象的过程可以建立新的序列来包含残差 拟合值 以及预测
Eviews 统计分析 从入门到精通
第一章 Eviews简介
Eviews简介 Eviews的主窗口 工作文件的建立与工作文件窗口 对象的建立和对象窗口
Eviews简介
EViews的用途：统计 计量分析和预测 除菜单操作外;EViews还提供命令语言;矩阵语言和程序 设计 Eviews软件基础 —— 介绍EViews的基本用法 解释如何使 用EViews来管理数据 第一部分：数据分析基础 —— 描述使用EViews来完成数 据的基本分析
Eviews 全称 Econometrics Views ; 是美 国 QMS 公司 推 出 的 基于 Windows平台的专门从事数据分析 回归分析和预测的 计算机软件;Eviews是当今世界上最优秀的计量经济软件之一 ;其具有操作简便 界面友好 功能强大等特点;在科学数据分析 与评价 金融分析 经济预测 销售预测和成本分析等领域具有 广泛的影响 虽然EViews是由经济学家开发的并大多在经济 领域应用;但它的适用范围不应只局限于经济领域
Eviews统计第六章
自相关检验及修正的EViews操作
1.绘图检验自相关问题的EViews操作 进行了OLS回归后，选择EViews主窗口的Quick|Graph命令，输入残差序列名 （Resid），选择图形类型，最后单击确定键即得到残差图。绘制残差序列图也可以通 过Equation对象窗口的Resids按钮或View|Acutal,Fitted,Residual命令实现。 2.DW检验操作 通常OLS回归估计输出结果中包含着对模型的D.W.检验结果，无需单独进行操作。通 过查询DW临界值表可以判断模型自相关问题。DW统计量值越接近2，表明自相关程 度越弱。
异方差与加权最小二乘法 3.异方差的常用检验方法
观表现出变量之间的关系。利用时间序列 图、散点图以及残差序列对解释变量的散点图可以直观的 对模型否存在异方差进行初步判断。 （2）怀特检验 怀特检验通过OLS估计求得残差的估计值，然后利用残差 估计值的平方与解释变量及其交叉项辅助回归式，得到拟 合优度 ，从而构建统计量进行检验。 怀特检验的原假设为原回归模型不存在异方差，被择假设 为原回归模型存在异方差。
应用普通最小二乘法时要求模型的随机误差项必须满足：
（1）无偏性假定。即所有随机误差项的期望为0 （2）同方差性假定。即所有随机误差项的方差相等 （3）无序列相关性假定。即随机误差项之间无序列相关性 （4）解释变量与随机误差项相互独立。即解释变量X为非随机变量 （5）正态性假定。即随机误差项服从均值为0的正态分布。
5.异方差形式未知时的模型处理方法-White异方差一致协方差估计 当异方差形式未知时，无法使用加权最小二乘法（Weighted Least Square，WLS）消除异方差，此时需要采用White异方差一致协方差 估计。
利用Eviews软件进行最小二乘法回归实例
例题中国居民人均消费支出与人均GDP（1978-2000），数据（例题1-2），预测，2001年人均GDP为4033.1元，求点预测、区间预测。
（李子奈，p50）解答：一、打开Eviews软件，点击主界面File按钮，从下拉菜单中选择Workfile。
在弹出的对话框中，先在工作文件结构类型栏（Workfile structure type）选择固定频率标注日期（Dated – regular frequency），然后在日期标注说明栏中（Date specification）将频率（Frequency）选为年度（Annual），再依次填入起止日期，如果希望给文件命名（可选项），可以在命名栏（Names - optional）的WF项填入自己选择的名称，然后点击确定。
此时建立好的工作文件如下图所示：在主界面点击快捷方式（Quick）按钮，从下拉菜单中选空白数据组（Empty Group）选项。
此时空白数据组出现，可以在其中通过键盘输入数据或者将数据粘贴过来。
在Excel文件（例题1-2）中选定要粘贴的数据，然后在主界面中点击编辑（Edit）按钮，从下拉菜单中选择粘贴（Paste），数据将被导入Eviews软件。
将右侧的滚动条拖至最上方，可以在最上方的单元格中给变量命名。
二、估计参数在主界面中点击快捷方式（Quick）按钮，从下拉菜单中选择估计方程（Estimate Equation）在弹出的对话框中设定回归方程的形式。
在方程表示式栏中（Equation specification ），按照被解释变量（Consp ）、常数项（c ）、解释变量（Gdpp ）的顺序填入变量名，在估计设置（Estimation settings ）栏中选择估计方法（Method ）为最小二乘法（LS – Least Squares ），样本（Sample ）栏中选择全部样本（本例中即为1978－2000），然后点击确定，即可得到回归结果。
计量经济学EVIEWS教程
计量经济学EVIEWS教程计量经济学软件包Eviews教程二、创建工作文件如果不对工作文件进行保存，工作文件中的任何东西，关闭机器时将被丢失。
建立工作文件的方法：点击File/New/Workfile。
选择数据类型和起止日期，并在出现的对话框中提供必要的信息：适当的时间频率（年、季度、月度、周、日）；确定起止日期或最大处理个数下面的图片说明了具体操作过程。
1、打开新建对象类型对话框，选择工作文件Workfile，见图二。
（图二）2、打开工作文件新建对话框，要求在Workfile Structure Type 对话框中选择数据结构类型：（1）Dated—regular frequency（默认），见（图三）a；（图三）a（2）Unstructed/Undated，见（图三）b；（图三）b （3）Balanced Panel，见（图三）c。
（图三）c 3、点击OK确认，得新建工作文件窗口，见图四。
（图四）工作文件窗口：它有标题栏、控制按钮和工具条。
标题栏指明窗口的类型workfile、工作文件名。
工具条按钮:Views观察按钮，Procs 过程按钮，Object对象按钮，Print打印选项按钮，Save（保存）工作文件，Details+/-显示/不显示对象的相关信息，Show用来生成对象的一个显示窗口，Fetch（从磁盘上读取数据），Store（将数据存储到磁盘），Delete（删除）对象，Gener（利用已有的序列生成新的序列），Sample（设置观察值的样本区间）。
4、保存工作成果：将工作成果保存到磁盘，点击工具条中save\输入文件名、路径\保存，或点击菜单栏中File\Save或Save as \输入文件名、路径\保存。
5、打开工作文件：我们可以打开一个已有的工作文件继续以前的工作，点击主菜单中的File\Open\Workfile\选定文件\打开。
三、输入和编辑数据输入数据有两种基本方法：data命令方式和鼠标图形界面方式1、data命令方式：命令格式为：data <序列名1> <序列名2>......<序列名n>，序列名之间用空格隔开，输入全部序列后回车就进入数据编辑窗口，如图五所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
EViews统计分析基础教程
二、广义最小二乘法（GLS）
基本原理： 再求模型(3)的滞后1期即(t-1)期的回归模型，并在两侧 同乘 yt-1= 0 + 1x1t-1 +2x2t-1 +…+kxkt-1+ ut-1 (4) 用（2）式与(4)相减，得 ut- yt-1 = 0 (1-)+1(x1t-x1t-1)+ …+k(xk-1- xkt-1) + vt (5) 令 yt* = yt - yt -1 xjt* = xjt -xjt -1, j = 1 , 2 , … k (6) 0* = 0 (1 - ) 则yt* = 0*+ 1 x1 t* + 2 x2 t* +… + k xk t* + vt 如果模型不存在异方差和序列相关，则使用广义最小二 乘法等于普通最小二乘法。
EViews统计分析基础教程
三、两阶段最小二乘法（TSLS）
EViews操作：
选择主菜单栏中的“Object”| “New Object” | “Equation” 选项，或者选择“Quick”| “Estimate Equation” 选项，在 打开的方程对话框的“Method”种选择“TSLS”法，会得 到如下对话框。
f
i i i
1
f x i
1
μt
x μt) = E(
1
μt)2
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
消除方法（EViews操作） （1）用最小二乘法（OLS）估计方程，得到残差序列； （2）根据残差序列计算出加权序列； （3）选择EViews主菜单栏中的“Quick”| “Estimate Equation”选项，弹出下图所示的对话框。 包括两个选项卡： （1）“Specification”选项 卡 （2）“Options”选项卡
ቤተ መጻሕፍቲ ባይዱ
EViews统计分析基础教程
五、广义矩估计（GMM）
EViews基本操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，在 “Method”中选择“GMM”后弹出如下图所示的方程设 定对话框。
EViews统计分析基础教程
三、两阶段最小二乘法（TSLS）
基本原理：
两阶段最小二乘法分两个阶段： 第一阶段:找到工具变量，用最小二乘估计法（OLS）对 模型中的每一解释变量与工具变量做回归； 第二阶段:用第一阶段的拟合值代替内生变量，对原方 程进行第二次回归，这次回归得到的系数就是用两阶段 最小二乘法得到的新估计值。
EViews统计分析基础教程
五、广义矩估计（GMM）
EViews基本操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，在 “Method”中选择“GMM”后弹出如下图所示的方程设 定对话框。
基本思路： 赋予每个观测值残差不同的权数，从而使得回归模型的随 机误差项具有同方差性。
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
基本原理： 设一元线性方程为
yt =β0 +β1xt +μt 如果随机误t差项的方差Var(μt)与解释变量成比例关系，
即
Var(μt) = σt2 = f(xt)×σ2 说明随机误差项的方差与解释变量xt之间存在相关性，即存
EViews统计分析基础教程
第6章 基本回归模型的OLS估计
重点内容：
• 加权最小二乘法（消除异方差）
• 广义最小二乘法（消除序列相关和异方差）
• 广义矩估计
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
当线性回归模型出现异方差时，所得到的估计量是非有效 的。用加权最小二乘法（WLS）可以解决异方差问题。
EViews统计分析基础教程
本章小结：
• 了解WLS、GLS、NLS、TSLS、GMM五种估计方 法的基本原理 • 掌握这五种估计法的EViews相关操作
在“Equation specification”（方程设定）中列出方程的被 解释变量和所有解释变量（包括常数项），在 “Instrument list”（工具变量列表）中，列出工具变量名。
注意：工具变量的个数不能比被估计参数的个数少，否则广义矩估 计法（GMM）的估计量不可识别。同样，在这里常数项会被自动 加入工具变量列表中。
EViews统计分析基础教程
五、广义矩估计（GMM）
基本原理： 广义矩估计是设定参数满足的一种理论关系。其原理是 选择参数估计尽可能接近理论上关系，把理论关系用样 本近似值代替；并且估计量的选择就是要最小化理论值 和实际值之间的加权距离。参数要满足的理论关系通常 是参数函数f(θ)与工具变量Zt之间的正则条件，即 E[f(θ)′Z]=0，θ是被估计参数 广义矩估计法（GMM）中估计量选择的标准是，使工 具变量与函数f(θ)之间的样本相关性越接近于0越好。
EViews统计分析基础教程
四、非线性最小二乘法（NLS）
EViews操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，打开方程 设定对话框，在“Equation specification”中输入非线性模 型的表达式，如“y c 1/x”，即为双曲线的回归模型。 EViews软件会自动用非线性最小二乘法（NLS）进行估 计，因而建立方程时，只输入非线性表达式即可。例如 y =axb ，只需输入“y= c(1)*x^c(2)”即可。
基本原理：
通过变换原回归模型，使随机误差项消除自相关，进而 利用普通最小二乘法估计回归参数 。 设原回归模型是 yt = 0 + 1x1t + 2 x2t+…+ kxkt +ut (t = 1, 2, …, n )（1） 其中，ut具有一阶自回归形式 ut = ut-1 + vt （2） vt 满足线性回归模型的基本假定条件，把（2）式代入 （1）式中，得 yt = 0+1x1t+2x2t+…+0xkt+ut- 1 + vt （3）
EViews统计分析基础教程
四、非线性最小二乘法（NLS）
基本原理： 设定非线性回归模型的一般式为 yi = f(xi, ,β) + μi i=1，2,…，n 则其残差平方和为
（1）
2 n ˆ S ( ) = y f x , （2） ˆ i i i 1 能使(2)达到最小的为参数β的非线性最小二乘估计。要 得到β的估计值，首先对式（1）中的β求偏导，然后令 该式等于0。 还可以通过迭代法求的近似值，先给出参数估计的初始 值，然后通过迭代法得到一个新的估计值，重复迭代直 到估计值收敛为止。
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
消除方法（EViews操作） 在“Specification”选项卡的“Equation specification”文 本框中输入用OLS（普通最小二乘法）估计的方程。 在“Options”选项卡中，选中“Weighted LS/TSLS”复 选框，并在“Weighted”的文本框中输入加权序列的名 称，例如输入“w”。 加权序列“w ”用OLS估计模型 时得到的残差序列的绝对值的 倒数序列。填好后再单击 “确定”按钮
EViews统计分析基础教程
四、非线性最小二乘法（NLS）
非线性模型包括可线性化的非线性模型和不可线性化的 非线性模型。可线性化的模型是指该模型可以通过线性 化的处理变为线性模型，如一元二次方程，幂函数等。 例如： y =axb lny =lna+blnx 即 y﹡=a﹡+bx﹡ 并非所有的函数均可被线性化，能被线性化的可以继续 用OLS等线性回归模型适用的方法进行估计，不能被线 性化的模型就可以用非线性最小二乘法（Nonlinear Least Square，NLS）进行估计。
EViews统计分析基础教程
五、广义矩估计（GMM）
广义矩估计法（Generalized Method of Moments，GMM） 则可以不受模型假定的限制，它不要求随机扰动项一定 非序列相关，不存在异方差等，并且所得到的参数估计 值比用其他估计方法得到的参数估计值更与实际接近。 广义矩估计法（GMM）是一个大样本估计，其估计量 在大样本下有效，在小样本下无效。
EViews统计分析基础教程
二、广义最小二乘法（GLS）
广义最小二乘法（Generalized Least Squared，GLS） 常用来对存在序列相关和异方差的模型进行估计。普通 最小二乘法（OLS）和加权最小二乘法（WLS）是广义 最小二乘法（GLS）的特例。
EViews统计分析基础教程
二、广义最小二乘法（GLS）
EViews统计分析基础教程
三、两阶段最小二乘法（TSLS）
EViews操作：
在上图的方程设定（Equation specification）的文本框中 列出解释变量和被解释变量， 在工具变量列表（Instrument list）的文本框中输入工具 变量。 在进行两阶段最小二乘估计时，方程中的工具变量数至 少要与估计系数相等。常数项常常用来做工具变量。
在异方差问题。
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
消除方法： 用
1 f