【精编】2019年北京市高考数学模拟考试理科试卷及解析
2019北京卷理科数学解析版
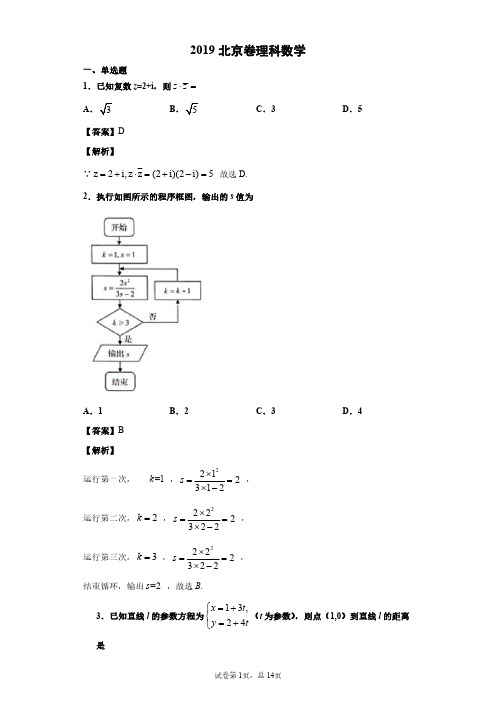
2019北京卷理科数学一、单选题1.已知复数z =2+i ,则z z ⋅=A B C .3D .5【答案】D 【解析】∵z 2i,z z (2i)(2i)5=+⋅=+-=故选D.2.执行如图所示的程序框图,输出的s 值为A .1B .2C .3D .4【答案】B 【解析】运行第一次,=1k ,2212312s ⨯==⨯-,运行第二次,2k =,2222322s ⨯==⨯-,运行第三次,3k =,2222322s ⨯==⨯-,结束循环,输出=2s ,故选B .3.已知直线l 的参数方程为13,24x t y t =+⎧⎨=+⎩(t 为参数),则点(1,0)到直线l 的距离是A .15B .25C .45D .65【答案】D 【解析】直线l 的普通方程为()()41320x y ---=,即4320x y -+=,点()1,0到直线l 的距离65d ==,故选D.4.已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则A .a 2=2b 2B .3a 2=4b 2C .a =2bD .3a =4b【答案】B 【解析】椭圆的离心率2221,2c e c a b a ===-,化简得2234a b =,故选B.【点睛】本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识、基本运算能力的考查.5.若x ,y 满足|1|x y ≤-,且y ≥−1,则3x+y 的最大值为A .−7B .1C .5D .7【答案】C 【解析】由题意1,11yy x y -≤⎧⎨-≤≤-⎩作出可行域如图阴影部分所示.设3,3z x y y z x =+=-,当直线0:3l y z x =-经过点()2,1-时,z 取最大值5.故选C.6.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg E m m E =,其中星等为m 1的星的亮度为E 2(k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为A .1010.1B .10.1C .lg10.1D .10–10.1【答案】D 【解析】两颗星的星等与亮度满足12125lg 2E m m E -=,令2 1.45m =-,126.7m =-,()1212221g(1.4526.7)10.155E m m E =-=-+=,10.110.112211010E EE E -=⋅=,故选D.7.设点A ,B ,C 不共线,则“AB 与AC的夹角为锐角”是“||||AB AC BC +>”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【解析】∵A 、B 、C 三点不共线,∴|AB +AC|>|BC|⇔|AB +AC |>|AB -AC|⇔|AB +AC |2>|AB -AC |2AB ⇔•AC >0AB ⇔与AC的夹角为锐角.故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC|”的充分必要条件,故选C.8.数学中有许多形状优美、寓意美好的曲线,曲线C :221||x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C ;③曲线C 所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是A .①B .②C .①②D .①②③【答案】C 【解析】由221x y x y +=+得,221y x y x -=-,2222||3341,10,2443x x x y x ⎛⎫-=-- ⎪⎝⎭,所以x 可为的整数有0,-1,1,从而曲线22:1C x y x y +=+恰好经过(0,1),(0,-1),(1,0),(1,1),(-1,0),(-1,1)六个整点,结论①正确.由221x y x y +=+得,222212x y x y+++,解得222x y +≤,所以曲线C 上任意一点.结论②正确.如图所示,易知()()()()0,1,1,0,1,1,,0,1A B C D -,四边形ABCD 的面积13111122ABCD S =⨯⨯+⨯=,很明显“心形”区域的面积大于2ABCD S ,即“心形”区域的面积大于3,说法③错误.故选C.二、填空题9.函数f (x )=sin 22x 的最小正周期是__________.【答案】 2π.【解析】函数()2sin 2f x x ==142cos x -,周期为2π【点睛】本题主要考查二倍角的三角函数公式、三角函数的最小正周期公式,属于基础题.10.设等差数列{a n }的前n 项和为S n ,若a 2=−3,S 5=−10,则a 5=__________,S n 的最小值为__________.【答案】0.-10.【解析】等差数列{}n a 中,53510S a ==-,得322,3a a =-=-,公差321d a a =-=,5320a a d =+=,由等差数列{}n a 的性质得5n ≤时,0n a ≤,6n ≥时,n a 大于0,所以n S 的最小值为4S 或5S ,即为10-.11.某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.【答案】40.【解析】在正方体中还原该几何体,如图所示几何体的体积V=43-12(2+4)×2×4=4012.已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.【答案】如果l⊥α,m∥α,则l⊥m.【解析】将所给论断,分别作为条件、结论,得到如下三个命题:(1)如果l⊥α,m∥α,则l⊥m.正确;(2)如果l⊥α,l⊥m,则m∥α.不正确,有可能m在平面α内;(3)如果l⊥m,m∥α,则l⊥α.不正确,有可能l与α斜交、l∥α.13.设函数f(x)=e x+a e−x(a为常数).若f(x)为奇函数,则a=________;若f(x)是R 上的增函数,则a 的取值范围是___________.【答案】-1;(],0-∞.【解析】若函数()xxf x e ae -=+为奇函数,则()()(),xx x x f x f x eae e ae ---=-+=-+,()()1 0x x a e e -++=对任意的x 恒成立.若函数()xxf x e ae -=+是R 上的增函数,则()' 0xxf x e ae-=-≥恒成立,2,0x a e a ≤≤.即实数a 的取值范围是(],0-∞14.李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x 元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.①当x =10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x 的最大值为__________.【答案】130.15.【解析】(1)x =10,顾客一次购买草莓和西瓜各一盒,需要支付(60+80)-10=130元.(2)设顾客一次购买水果的促销前总价为y 元,120y <元时,李明得到的金额为y ×80%,符合要求.120y ≥元时,有(y -x )×80%≥y ×70%成立,即8(y -x )≥7y ,x ≤8y ,即x ≤(8y)min =15元.所以x 的最大值为15.三、解答题15.在△ABC 中,a =3,b −c =2,cos B =12-.(Ⅰ)求b ,c 的值;(Ⅱ)求sin (B –C )的值.【答案】(Ⅰ)375a b c =⎧⎪=⎨⎪=⎩;(Ⅱ).【解析】(Ⅰ)由题意可得:2221cos 2223a c b B ac b c a ⎧+-==-⎪⎪⎪-=⎨⎪=⎪⎪⎩,解得:375a b c =⎧⎪=⎨⎪=⎩.(Ⅱ)由同角三角函数基本关系可得:3sin 2B ==,结合正弦定理sin sin b c B C =可得:sin 53sin 14c B C b ==,很明显角C为锐角,故11cos 14C ==,故()sin sin cos cos sin B C B C B C -=-=16.如图,在四棱锥P –ABCD 中,PA ⊥平面ABCD ,AD ⊥CD ,AD ∥BC ,PA =AD =CD =2,BC =3.E 为PD 的中点,点F 在PC 上,且13PF PC =.(Ⅰ)求证:CD ⊥平面PAD ;(Ⅱ)求二面角F–AE–P 的余弦值;(Ⅲ)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF内,说明理由.【解析】(Ⅰ)由于PA ⊥平面ABCD ,CD ⊂平面ABCD ,则PA ⊥CD ,由题意可知AD ⊥CD ,且PA ∩AD =A ,由线面垂直的判定定理可得CD ⊥平面PAD .(Ⅱ)以点A 为坐标原点,平面ABCD 内与AD 垂直的直线为x 轴,AD ,AP 方向为y 轴,z轴建立如图所示的空间直角坐标系A xyz -,易知:()()()()0,0,0,0,0,2,2,2,0,0,2,0A P C D ,由13PF PC = 可得点F 的坐标为224,,333F ⎛⎫ ⎪⎝⎭,由12PE PD =可得()0,1,1E ,设平面AEF 的法向量为:(),,m x y z =,则()()()224224,,,,0333333,,0,1,10m AF x y z x y z m AE x y z y z ⎧⎛⎫⋅=⋅=++=⎪ ⎪⎝⎭⎨⎪⋅=⋅=+=⎩,据此可得平面AEF 的一个法向量为:()1,1,1m =- ,很明显平面AEP 的一个法向量为()1,0,0n =,cos ,3m n m n m n⋅<>==⨯,二面角F -AE -P 的平面角为锐角,故二面角F -AE -P的余弦值为3.(Ⅲ)易知()()0,0,2,2,1,0P B -,由23PG PB = 可得422,,333G ⎛⎫- ⎪⎝⎭,则422,,333AG ⎛⎫=- ⎪⎝⎭,注意到平面AEF 的一个法向量为:()1,1,1m =-,其0m AG ⋅=且点A 在平面AEF 内,故直线AG 在平面AEF 内.17.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A ,B 两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A ,B 两种支付方式都不使用的有5人,样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下:交付金额(元)支付方式(0,1000](1000,2000]大于2000仅使用A 18人9人3人仅使用B10人14人1人(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A ,B 两种支付方式都使用的概率;(Ⅱ)从样本仅使用A 和仅使用B 的学生中各随机抽取1人,以X 表示这2人中上个月支付金额大于1000元的人数,求X 的分布列和数学期望;(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A 的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A 的学生中本月支付金额大于2000元的人数有变化?说明理由.【解析】(Ⅰ)由题意可知,两种支付方式都是用的人数为:1003025540---=人,则:该学生上个月A ,B 两种支付方式都使用的概率4021005p ==.(Ⅱ)由题意可知,仅使用A 支付方法的学生中,金额不大于1000的人数占35,金额大于1000的人数占25,仅使用B 支付方法的学生中,金额不大于1000的人数占25,金额大于1000的人数占35,且X 可能的取值为0,1,2.()32605525p X ==⨯=,()22321315525p X ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭,()32625525p X ==⨯=,X 的分布列为:X12()p X 6251325625其数学期望:()61360121252525E X =⨯+⨯+⨯=.(Ⅲ)我们不认为样本仅使用A 的学生中本月支付金额大于2000元的人数有变化.理由如下:随机事件在一次随机实验中是否发生是随机的,是不能预知的,随着试验次数的增多,频率越来越稳定于概率。
2019年高考理科数学北京卷理数(附参考答案和详解)

绝密★启用前 6月7日15:00-17:002019年普通高等学校招生全国统一考试(北京卷)数学(理工农医类)总分:150分考试时间:120分钟★祝考试顺利★注意事项:1、本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证条形码粘贴在答题卡的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:选出每小题答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸、答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内,写在试题卷、草稿纸、答题卡上的非答题区域均无效。
4、考试结束后,将本试卷和答题卡一并上交。
第I卷一、选择题:本题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2019北京卷·理)已知复数2iz=+,则z z⋅=()A.3B.5C.3D.5【解析】因为2iz z⋅=+⋅-=.故选D.z=+,所以2iz=-,所以(2i)(2i)5【答案】D2.(2019北京卷·理)执行如图所示的程序框图,输出的s值为()A.1B.2C.3D.4【解析】1,1k s ==;第一次循环:2s =,判断3,2k k <=;第二次循环:2s =,判断3,3k k <=;第三次循环:2s =,判断3k =.故输出2,故选B. 【答案】B3.(2019北京卷·理)已知直线l 的参数方程为13,24x t y t=+⎧⎨=+⎩(t 为参数),则点(1,0)到直线l 的距离是( )A.15B.25C.45D.65【解析】由题意可知直线l 的普通方程为4320x y -+=,由点到直线的距离公式可得点(1,0)到直线l的距离65d ==.故选D. 【答案】D4.(2019北京卷·理)已知椭圆22221(0)x y a b a b+=>>的离心率为12,则( )A.222a b =B.2234a b =C.2a b =D.34a b =【解析】因为椭圆的离心率为12c e a ==,所以224a c =.又222a b c =+,所以2234a b =.故选B. 【答案】B5.(2019北京卷·理)若x ,y 满足||1x y ≤-,且1y ≥-,则3x y +的最大值为( )A.7-B.1C.5D.7【解析】由||1x y ≤-,且1y ≥-,得10,10,1.x y x y y -+≥⎧⎪+-≤⎨⎪≥-⎩作出可行域如图阴影部分所示.设3z x y =+,则3y x z =-+,作直线0:3l y x =-,并进行平移.显然当0l 经过点(2,1)A -时,z 取得最大值,max 3215z =⨯-=.故选C. 【答案】C6.(2019北京卷·理)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足12125lg2E m m E -=,其中星等为k m 的星的亮度为(1,2)k E k =.已知太阳的星等是26.7-,天狼星的星等是 1.45-,则太阳与天狼星的亮度的比值为( )A.10.110B.10.1C.lg10.1D.10.110-【解析】由题意知,126.7m =-,2 1.45m =-,代入所给公式得1251.45(26.7)lg 2EE ---=,所以12lg10.1E E =,所以10.11210EE =.故选A. 【答案】A7.(2019北京卷·理)设点A ,B ,C 不共线,则“AB 与AC 的夹角为锐角”是“AB AC BC +>”的( ) A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解析】因为设点A ,B ,C 不共线,由向量加法的三角形法则,可知BC AC AB =-,所以||||AB AC BC +>等价于||||AB AC AC AB +>-,因模为正,故不等号两边平方得22222||||cos 2||||cos AB AC AB AC AC AB AC AB θθ++⋅⋅>+-⋅⋅(θ为AB 与AC 的夹角),整理得4||||cos 0AB AC θ⋅⋅>,故cos 0θ>,即θ为锐角.又以上推理过程可逆,所以“AB 与AC 的夹角为锐角”是“AB AC BC +>”的充分必要条件.故选C. 【答案】C8.(2019北京卷·理)数学中有许多形状优美、寓意美好的曲线,曲线22:1||C x y x y +=+就是其中之一(如图).给出下列三个结论: ①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C③曲线C 所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是( )A.①B.②C.①②D.①②③【解析】由221||x y x y +=+,当0x =时,1y =±;当0y =时,1x =±;当1y =时,01x =±,.故曲线C 恰好经过6个整点:(0,1)A ,(0,1)B -,(1,0)C ,(1,1)D ,(1,0)E -,(1,1)F -,所以①正确.由基本不等式,当0y >时,22221||1||12x y x y x y xy ++=+=+≤+,所以222x y +≤222x y +≤②正确.如图,由①知矩形CDFE 的面积为2,△BCE 的面积为1,所以曲线C 所围成的“心形”区域的面积大于3,故③错误.故选C. 【答案】C第Ⅱ卷二、填空题:本题共6小题,每小题5分。
2019年高考数学(理)模拟试题(三)含答案及解析

2019年高考数学(理)模拟试题(三)含答案及解析2019年高考数学(理)模拟试题(三)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数z满足(1-i)z=2+i,则z的共轭复数在复平面内对应的点在()A。
第一象限B。
第二象限C。
第三象限D。
第四象限2.设集合M={x|x<36},N={2,4,6,8},则M∩N=()A。
{2,4}B。
{2,4,6}C。
{2,6}D。
{2,4,6,8}3.下图中的图案是我国古代建筑中的一种装饰图案,形若铜钱,寓意富贵吉祥.在圆内随机取一点,则该点取自阴影区域内(阴影部分由四条四分之一圆弧围成)的概率是()A。
1/4B。
1/3C。
1/2D。
2/34.将5个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A。
42种B。
48种C。
54种D。
60种5.如图所示是一个几何体的三视图,则这个几何体外接球的体积为()A。
32π/3B。
64π/3C。
32πD。
64π/26.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后入称之为三角形的欧拉线.已知△ABC的顶点A(2,0),B(0,4),AC=BC,则△ABC的欧拉线方程为()A。
2x+y-3=0B。
2x-y+3=0C。
x-2y-3=0D。
x-2y+3=07.执行如图所示的程序框图,则输出S的值为()A。
2019年北京卷理科数学高考真题及答案解析(word精编)

2019年普通高等学校招生全国统一考试数 学(理)(北京卷)第一部分(选择题 共40分)一、 选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)(A(B(C )3(D )5 (2)执行如图所示的程序框图,输出的s 值为(A )1(B )2(C )3(D )4(3)已知直线l 的参数方程为x =1+3t y =2+4tìíî (t 为参数),则点(1,0) 到直线l 的距离是(A )15(B)2 5(C)4 5(D)6 5(4)已知椭圆2x2a +2y2b=1(a>b>0)的离心率为12,则(A)a2=2b2.(B)3a2=4b2.(C)a=2b(D)3a=4b(5)若x,y满足的最大值为(A)-7 (B)1(C)5 (D)7(6)在天文学中,天体的明暗程度可以用星等或亮度来描述。
两颗星的星等与亮度满足m2-m1=52lgE1E2,其中星等为m k的星的亮度为E k(k=1,2)。
已知太阳的星等为-26.7,天狼星的星等为-1.45,则太阳与天狼星的亮度的比值为(A)1010.1(B)10.1(C)lg10.1(D)10-10.1(7)设点A,B,C不共线,则“与的夹角是锐角”是“的(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(8)数学中有许多形状优美、寓意美好的曲线,曲线C:x2+y2=1+x y就是其中之一(如图)。
给出下列三个结论:①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C上任意一点到原点的距离都不超过2;③曲线C所围城的“心形”区域的面积小于3.其中,所有正确结论的序号是(A)①(B)②(C)①②(D)①②③第二部分(非选择题共10分)二、填空题共6小题,每小题5分,共30分。
(9) 函数f(x)=sin22x的最小正周期是________。
2019年最新北京市高考一模考试数学试题(理)有答案解析

北京市一模统一考试高三数学(理科)本试卷共6页,满分150分,考试时间120分钟第Ⅰ卷(选择题)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合2{|02},{|1}A x x B x x =≤≤=>,则AB = ( )A.{|01}x x ≤≤B.{|0x x >或1}x <-C. {|12}x x <≤D.{|02}x x <≤2.复数21i i =+( ) A.1i + B .1i - C. 1i -+D .1i --3.已知两条直线,a b 和平面α,若,a b b α⊥⊄,则“a α⊥”是“//b α”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件4.某三棱锥的三视图如图所示,则该三棱锥的最长棱的长为 ( ) AC.25.执行如图所示的程序框图,若输出的a 的值为15,则判断框应填写 ( ) A .2 B .3 C .4 D .5(4题图)2013201420151季度 2季度 3季度 4季度 1季度 2季度 3季度 4季度 1季度2013年 2014年 2015年年份增长率/%6.已知等比数列{}n a 的公比1q ≠,则下面说法中不正确...的是 ( ) A.2{}n n a a ++是等比数列 B.对于k *∈N ,1k >,112k k k a a a -++≠C .对于n *∈N ,都有20n n a a +>D .若21a a >,则对于任意n *∈N ,都有1n n a a +> 7.如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全市生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是 ( ) A .近三年该市生产总值为负增长 B. 近三年该市生产总值为正增长 C .该市生产总值2013年到2014年 为负增长,2014年到2015年为正增长 D.以上A 、B 、C 的判断都不正确8.已知偶函数()f x ,奇函数()g x 的图像分别如图(1)、图(2)所示,方程(())0f g x =,(())0g f x =的实根的个数分别为,a b ,则a b += ( )A .3B .7C .10D .14)二、填空题:本大题共6小题,每小题5分,共30分.9. 某校高一学雷锋志愿小组共有8人,其中一班、二班、三班、四班各2人,现在从中任选3人,要求每班至多选1人,不同的选取方法的种数为 .(图2)x10. 2022年冬奥会高山滑雪项目将在延庆小海坨山举行。
2019年北京市首师大附中高考数学一模试卷(理科) 解析版

2019年北京市首师大附中高考数学一模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若(1﹣2i)z=5i(i是虚数单位),则|z|的值为()A.3B.5C.D.2.(5分)在各项均为正数的等比数列{a n}中,a6=3,则a4+a8=()A.有最小值6B.有最大值6C.有最大值9D.有最小值3 3.(5分)秦九韶是我国南宋时期的数学家,他在《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图是实现该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为()A.5B.12C.25D.504.(5分)已知正六棱柱的底面边长和侧棱长相等,体积为.其三视图中的俯视图如图所示,则其左视图的面积是()A.B.C.8cm2D.4cm25.(5分)已知平面区域,夹在两条斜率为的平行直线之间,且这两条平行直线间的最短距离为m.若点P(x,y)∈Ω,则z=mx﹣y的最小值为()A.B.3C.D.66.(5分)如图,平面四边形ABCD中,∠ABC=∠ADC=90°,BC=CD=2,点E在对角线AC上,AC=4,AE=1,则的值为()A.17B.13C.5D.17.(5分)某校校庆期间,大会秘书团计划从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,根据工作特点要求甲、乙两人中至少有1人参加,则甲、乙都被选中且列队服务时不相邻的概率为()A.B.C.D.8.(5分)某公司有4家直营店a,b,c,d,现需将6箱货物运送至直营店进行销售,各直营店出售该货物以往所得利润统计如下表所示.根据此表,该公司获得最大总利润的运送方式有()A.1种B.2种C.3种D.4种二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.9.(5分)若展开式中的二项式系数和为64,则n等于,该展开式中的常数项为.10.(5分)椭圆的左、右焦点分别为F1,F2,P为椭圆M上任一点,且|PF1|•|PF2|的最大值的取值范围是[2c2,3c2],其中,则椭圆m的离心率e的取值范围是.11.(5分)在极坐标系中,过点且平行于极轴的直线的极坐标方程是.12.(5分)如图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2,…,17)建立模型=﹣30.4+13.5t;根据2010年至2016年的数据(时间变量t的值依次为1,2,…,7)建立模型②=99+17.5t.利用这两个模型,该地区2018年的环境基础设施投资额的预测值分别为,;并且可以判断利用模型得到的预测值更可靠.13.(5分)对于函数y=f(x),若存在区间[a,b],当x∈[a,b]时,f(x)的值域为[ka,kb](k>0),则称y=f(x)为k倍值函数.若f(x)=lnx+x是k倍值函数,则实数k 的取值范围是.14.(5分)定义:对于数列{x n},如果存在常数p,使对任意正整数n,总有(x n+1﹣p)(x n﹣p)<0成立,那么我们称数列{x n}为“p﹣摆动数列”①若a n=2n﹣1,b n=q n(﹣1<q<0),n∈N*,则数列{a n}“p﹣摆动数列”,{b n}“p﹣摆动数列”(回答是或不是);②已知“p﹣摆动数列”{c n}满足c n+1=,c1=1.则常数p的值为;三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)已知函数f(x)=sin(﹣2x)﹣2sin(x﹣)cos(x+).(Ⅰ)求函数f(x)的最小正周期和单调递增区间;(Ⅱ)已知x1,x2是函数y=f(x)﹣的两个零点,求|x1﹣x2|的最小值.16.(14分)空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.现统计邵阳市市区2016年10月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.(1)求这60天中属轻度污染的天数;(2)求这60天空气质量指数的平均值;(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.17.(13分)在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE=,A1F=,CE⊥EF.(Ⅰ)证明:平面ABB1A1⊥平面ABC;(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.18.(13分)圆x2+y2=2与x轴交于F1、F2两点,P为圆上一点.椭圆=1(a>b >0)以F1、F2为焦点且过点P.(Ⅰ)当P点坐标为(x0,)(x0>0)时,求x0的值及椭圆方程;(Ⅱ)若直线1与(Ⅰ)中所求的椭圆交于A、B不同的两点,且点C(0,﹣1),||=||,求直线l在y轴上截距b的取值范围.19.(14分)已知函数f(x)=e x[x3﹣2x2+(a+4)x﹣2a﹣4],其中a∈R,e为自然对数的底数.(1)若函数f(x)的图象在x=0处的切线与直线x+y=0垂直,求a的值;(2)关于x的不等式f(x)<﹣e x在(﹣∞,2)上恒成立,求a的取值范围;(3)讨论函数f(x)极值点的个数.20.(13分)已知集合A1,A2,…,A n为集合U的n个非空子集,这n个集合满足:①从中任取m个集合都有≠U成立;②从中任取m+1个集合都有=U成立.(Ⅰ)若U={1,2,3},n=3,m=1,写出满足题意的一组集合A1,A2,A3;(Ⅱ)若n=4,m=2,写出满足题意的一组集合A1,A2,A3,A4以及集合U;(Ⅲ)若n=10,m=3,求集合U中的元素个数的最小值.2019年北京市首师大附中高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若(1﹣2i)z=5i(i是虚数单位),则|z|的值为()A.3B.5C.D.【分析】直接利用复数的模的求法的运算法则求解即可.【解答】解:(1﹣2i)z=5i(i是虚数单位),可得|(1﹣2i)||z|=|5i|,解得|z|=.故选:D.【点评】本题考查复数的模的运算法则的应用,复数的模的求法,考查计算能力.2.(5分)在各项均为正数的等比数列{a n}中,a6=3,则a4+a8=()A.有最小值6B.有最大值6C.有最大值9D.有最小值3【分析】由题意设出等比数列的公比,把a4、a8用a6和公比表示,然后利用基本不等式求得答案.【解答】解:设等比数列{a n}的公比为q(q>0),∵a6=3,∴,∴a4+a8=.当且仅当q=1时上式等号成立.故选:A.【点评】本题考查等比数列的通项公式,考查了利用不等式求最值,是基础题.3.(5分)秦九韶是我国南宋时期的数学家,他在《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图是实现该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为()A.5B.12C.25D.50【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量v的值,模拟程序的运行过程,可得答案.【解答】解:模拟程序的运行,可得x=2,n=4,v=1,i=3,满足进行循环的条件i>0,v=5,i=2,满足进行循环的条件i>0,v=12,i=1,满足进行循环的条件i>0,v=25,i=0不满足进行循环的条件i>0,退出循环,输出v的值为:25故选:C.【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答,属于基础题.4.(5分)已知正六棱柱的底面边长和侧棱长相等,体积为.其三视图中的俯视图如图所示,则其左视图的面积是()A.B.C.8cm2D.4cm2【分析】由已知可求出正六棱柱的底面边长和侧棱长均为2cm,故左视图是长方形,长为,宽为2,由此能求出左视图的面积.【解答】解:设正六棱柱的底面边长和侧棱长均为a,则体积V=Sh=6×=,解得a=2,故左视图是长方形,长为,宽为2,面积为×2=故选:A.【点评】本题考查三视图与直观图的关系,正确判断几何体的形状是解题的关键.5.(5分)已知平面区域,夹在两条斜率为的平行直线之间,且这两条平行直线间的最短距离为m.若点P(x,y)∈Ω,则z=mx﹣y的最小值为()A.B.3C.D.6【分析】由约束条件作出可行域,结合题意求出m,利用目标函数的几何意义,求解即可.【解答】解:由约束条件作出可行域如图,∵平面区域Ω夹在两条斜率为﹣的平行直线之间,且两条平行直线间的最短距离为m,则m==.令z=mx﹣y=x﹣y,则y=x﹣z,由图可知,当直线y=x﹣z过B(2,3)时,直线在y轴上的截距最大,z有最小值为:=.故选:A.【点评】本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.6.(5分)如图,平面四边形ABCD中,∠ABC=∠ADC=90°,BC=CD=2,点E在对角线AC上,AC=4,AE=1,则的值为()A.17B.13C.5D.1【分析】利用余弦定理求出BE,cos∠BEC,再根据二倍角公式得出cos∠BED,从而可计算出结论.【解答】解:由题意可知CE=3,∠BCE=60°,∴EB=,∴cos∠BEC=,∴cos∠BED=2cos2∠BEC﹣1=.∴.故选:D.【点评】本题考查了平面向量的数量积运算,考查余弦定理的应用,属于中档题.7.(5分)某校校庆期间,大会秘书团计划从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,根据工作特点要求甲、乙两人中至少有1人参加,则甲、乙都被选中且列队服务时不相邻的概率为()A.B.C.D.【分析】先求出基本事件总数n=(+)=720,再求出甲、乙都被选中且列队服务时不相邻包含的基本事件个数m==120,由此能求出甲、乙都被选中且列队服务时不相邻的概率.【解答】解:从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,根据工作特点要求甲、乙两人中至少有1人参加,且列队服务,基本事件总数n=(+)=720,甲、乙都被选中且列队服务时不相邻包含的基本事件个数m==120,甲、乙都被选中且列队服务时不相邻的概率p==.故选:C.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.8.(5分)某公司有4家直营店a,b,c,d,现需将6箱货物运送至直营店进行销售,各直营店出售该货物以往所得利润统计如下表所示.根据此表,该公司获得最大总利润的运送方式有()A.1种B.2种C.3种D.4种【分析】结合获利表格,通过6箱货物的分配方法,求解最大获利,推出结果.【解答】解:6箱货物的分配方法有:6,0,0,0;5,1,0,0;4,2,0,0;3,3,0,0;4,1,1,0;2,2,2,0;3,2,1,0;1,1,2,2;1,1,1,3类型.而6,0,0,0;5,1,0,0;4,2,0,0;3,3,0,0;4,1,1,0;2,2,2,0;类型中获利的最大值不超过:16.a,b,c,d;总获利分配货物:1 2 2 1 4+4+5+4=17.1 3 1 1 4+7+2+4=17.2 3 0 1 6+7+0+4=17.该公司获得最大总利润的运送方式有:3种.故选:C.【点评】本题考查排列组合的实际应用,分析表格与题意是解题的关键,难度比较大.二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.9.(5分)若展开式中的二项式系数和为64,则n等于6,该展开式中的常数项为15.【分析】由题意可得得2n=64,求得n=6.在展开式的通项公式中,令x的幂指数等于零,求得r的值,即可求得展开式中的常数项.【解答】解:由展开式中的二项式系数和为64,可得2n=64,∴n=6.由于=,展开式的通项公式为T r+1=•x12﹣2r•x﹣r=•x12﹣3r,令12﹣3r=0,r=4,故该展开式中的常数项为==15,故答案为6,15.【点评】本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.10.(5分)椭圆的左、右焦点分别为F1,F2,P为椭圆M上任一点,且|PF1|•|PF2|的最大值的取值范围是[2c2,3c2],其中,则椭圆m的离心率e的取值范围是.【分析】根据题意,|PF1|•|PF2|的最大值为a2,则由题意知2c2≤a2≤3c2,由此能够导出椭圆m的离心率e的取值范围.【解答】解:∵|PF1|•|PF2|=(a+ex)(a﹣ex)=a2﹣e2x2≤a2,∴|PF1|•|PF2|的最大值为a2,∴由题意知2c2≤a2≤3c2,∴,∴.故椭圆m的离心率e的取值范围.答案:【点评】|PF1|•|PF2|的最大值=a2是正确解题的关键.11.(5分)在极坐标系中,过点且平行于极轴的直线的极坐标方程是ρsinθ=﹣2.【分析】如图所示,在Rt△OPQ中,利用直角三角形的边角关系及诱导公式化简求解即可.【解答】解:如图所示在Rt△OPQ中,ρ==,可化为ρsinθ=﹣2.过点且平行于极轴的直线的极坐标方程是ρsinθ=﹣2.故答案为:ρsinθ=﹣2.【点评】本题考查极坐标系的应用,熟练掌握直角三角形的边角关系及诱导公式是解题的关键.12.(5分)如图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2,…,17)建立模型=﹣30.4+13.5t;根据2010年至2016年的数据(时间变量t的值依次为1,2,…,7)建立模型②=99+17.5t.利用这两个模型,该地区2018年的环境基础设施投资额的预测值分别为226.1(亿元),256.5 (亿元);并且可以判断利用模型②得到的预测值更可靠.【分析】根据两个模型分别求出2018年的预测值,然后对比2016年的预测值,进行比较即可确定两个模型的预测值的可靠性.【解答】解(1)①y=﹣3.04+13.5×19=226.1(亿元).②y=99+17.5×9=256.5 (亿元).(2)当年份为2016,对于模型①:t=17,y=﹣3.04+13.5×17=199.1 (亿元),对于模型②:t=7,y=99+17.5×7=221.5 (亿元),所以②的准确度较高,①偏差较大,所以选择②得到的预测值更可靠.故答案为:226.1(亿元);256.5 (亿元).【点评】本题主要考查线性回归方程的应用,结合条件求出对应的预测值是解决本题的关键.13.(5分)对于函数y=f(x),若存在区间[a,b],当x∈[a,b]时,f(x)的值域为[ka,kb](k>0),则称y=f(x)为k倍值函数.若f(x)=lnx+x是k倍值函数,则实数k的取值范围是(1,1+).【分析】由于f(x)在定义域{x|x>0} 内为单调增函数,利用导数求得g(x)的极大值为:g(e)=1+,当x趋于0时,g(x)趋于﹣∞,当x趋于∞时,g(x)趋于1,因此当1<k<1+时,直线y=k与曲线y=g(x)的图象有两个交点,满足条件,从而求得k的取值范围.【解答】解:∵f(x)=lnx+x,定义域为{x|x>0},f(x)在定义域为单调增函数,因此有:f(a)=ka,f(b)=kb,即:lna+a=ka,lnb+b=kb,即a,b为方程lnx+x=kx的两个不同根.∴k=1+,令1+=g(x),令g'(x)==0,可得极大值点x=e,故g(x)的极大值为:g(e)=1+,当x趋于0时,g(x)趋于﹣∞,当x趋于∞时,g(x)趋于1,因此当1<k<1+时,直线y=k与曲线y=g(x)的图象有两个交点,方程k=1+有两个解.故所求的k的取值范围为(1,1+),故答案为(1,1+).【点评】本题主要考查利用导数求函数的值的方法,体现了转化的数学思想,属于基础题.14.(5分)定义:对于数列{x n},如果存在常数p,使对任意正整数n,总有(x n+1﹣p)(x n﹣p)<0成立,那么我们称数列{x n}为“p﹣摆动数列”①若a n=2n﹣1,b n=q n(﹣1<q<0),n∈N*,则数列{a n}不是“p﹣摆动数列”,{b n}是“p﹣摆动数列”(回答是或不是);②已知“p﹣摆动数列”{c n}满足c n+1=,c1=1.则常数p的值为;【分析】(1)由{a n}是关于n的递增数列,可知不满足定义,由b n=q n(﹣1<q<0)可知正负交替出现,易求出p的值;(2)先对n取特殊值确定p的取值范围,再根据对任意的正整数n都成立,求出p的值.【解答】(1)由a n=2n﹣1知道{a n}是递增数列,故不存在满足定义的p,又因为b n=q n(﹣1<q<0)可知b n正负数值交替出现,故p=0时满足定义.(2)因为数列{c n}是“p﹣摆动数列”,故n=1时有(x2﹣p)(x1﹣p)<0,可求得,又因为使对任意正整数n,总有(c n+1﹣p)(c n﹣p)<0成立,即有(c n+2﹣p)(c n+1﹣p)<0成立,则(c n+2﹣p)(c n﹣p)>0,>p,所以c1>p,c3>p,…,c2n﹣1同理c2<p,c4<p,…,c2n<p,,即,解得,即,所以c2n<p<c2n﹣1同理,解得,即,综上,.故答案为:不是;是;.【点评】本题属于新定义型问题,综合考查数列、不等式的知识,难度较大.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)已知函数f(x)=sin(﹣2x)﹣2sin(x﹣)cos(x+).(Ⅰ)求函数f(x)的最小正周期和单调递增区间;(Ⅱ)已知x1,x2是函数y=f(x)﹣的两个零点,求|x1﹣x2|的最小值.【分析】(Ⅰ)利用两角和差的正弦公式以及三角函数的倍角公式,辅助角公式进行化简,结合周期公式,以及函数的单调性进行求解即可.(Ⅱ)根据零点求出sin(2x﹣)=的根,利用作差法进行求解即可,【解答】解:(Ⅰ)f(x)=sin(﹣2x)=sin cos2x﹣cos sin2x﹣2sin(x﹣)cos(x+π﹣)=cos2x+sin2x+2sin(x﹣)cos(x﹣)=cos2x+sin2x+sin(2x﹣)=cos2x+sin2x﹣cos2x=sin2x﹣cos2x=sin(2x﹣),则函数f(x)的最小正周期T==π,由2kπ﹣≤2x﹣≤2kπ+,k∈Z,得kπ﹣≤x≤kπ+,k∈Z,即函数的单调递增区间为[kπ﹣,kπ+],k∈Z.(Ⅱ)x1,x2是函数y=f(x)﹣的两个零点,∴由y=f(x)﹣=0得f(x)=,则由sin(2x﹣)=得2x1﹣=2k1π+①,2x2﹣=2k2π+,②,则②﹣①得2(x2﹣x1)=2(k2﹣k1)π+,即(x2﹣x1)=(k2﹣k1)π+,则|x1﹣x2|=|(k2﹣k1)π+|,k1,k2∈Z,则当k1=k2时,|x1﹣x2|取得最小值,最小值为|x1﹣x2|=.【点评】本题主要考查三角函数的图象和性质,利用两角和差的正弦公式以及辅助角公式进行化简,以及利用三角函数值的关系是解决本题的关键.16.(14分)空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.现统计邵阳市市区2016年10月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.(1)求这60天中属轻度污染的天数;(2)求这60天空气质量指数的平均值;(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.【分析】(1)(2)根据频率分布直方图,计算即可;(3)求出空气质量为轻度污染或轻度污染以上的概率P1,得到出现雾霾概率,从而求出邵阳市恰有1天出现雾霾天气的概率.【解答】解:(1)依题意知,轻度污染即空气质量指数在151﹣200之间,共有0.003×50×60=9天.(2)由直方图知60天空气质量指数的平均值为.(3)空气质量为轻度污染或轻度污染以上的概率P1=0.15+0.05=0.2,∴出现雾霾概率为,∴未来2天里,恰有1天为雾霾天气的概率.【点评】本题考查了频率分布直方图的应用问题,也考查了相互独立事件的概率的计算问题,是中档题.17.(13分)在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE=,A1F=,CE⊥EF.(Ⅰ)证明:平面ABB1A1⊥平面ABC;(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.【分析】(I)取AB的中点D,连结CD,DF,DE.计算DE,EF,DF,利用勾股定理的逆定理得出DE⊥EF,由三线合一得CD⊥AB,故而CD⊥平面ABB1A1,从而平面ABB1A1⊥平面ABC;(II)以C为原点建立空间直角坐标系,求出和平面CEF的法向量,则直线AC1与平面CEF所成角的正弦值等于|cos<>|.【解答】证明:(I)取AB的中点D,连结CD,DF,DE.∵AC=BC,D是AB的中点,∴CD⊥AB.∵侧面ABB1A1是边长为2的正方形,AE=,A1F=.∴A1E=,EF==,DE==,DF==,∴EF2+DE2=DF2,∴DE⊥EF,又CE⊥EF,CE∩DE=E,CE⊂平面CDE,DE⊂平面CDE,∴EF⊥平面CDE,又CD⊂平面CDE,∴CD⊥EF,又CD⊥AB,AB⊂平面ABB1A1,EF⊂平面ABB1A1,AB,EF为相交直线,∴CD⊥平面ABB1A1,又CD⊂平面ABC,∴平面ABB1A1⊥平面ABC.(II)∵平面ABB1A1⊥平面ABC,∴三棱柱ABC﹣A1B1C1是直三棱柱,∴CC1⊥平面ABC.∵CA⊥CB,AB=2,∴AC=BC=.以C为原点,以CA,CB,CC1为坐标轴建立空间直角坐标系,如图所示:则A(,0,0),C(0,0,0),C1(0,0,2),E(,0,),F(,,2).∴=(﹣,0,2),=(,0,),=(,,2).设平面CEF的法向量为=(x,y,z),则,∴,令z=4,得=(﹣,﹣9,4).∴=10,||=6,||=.∴sin<>==.∴直线AC1与平面CEF所成角的正弦值为.【点评】本题考查了面面垂直的判定,线面角的计算,空间向量的应用,属于中档题.18.(13分)圆x2+y2=2与x轴交于F1、F2两点,P为圆上一点.椭圆=1(a>b >0)以F1、F2为焦点且过点P.(Ⅰ)当P点坐标为(x0,)(x0>0)时,求x0的值及椭圆方程;(Ⅱ)若直线1与(Ⅰ)中所求的椭圆交于A、B不同的两点,且点C(0,﹣1),||=||,求直线l在y轴上截距b的取值范围.【分析】(Ⅰ)由圆与x轴的交点为(,0)得椭圆的焦距2c=2,从而椭圆方程化为+=1,①将P()代入圆,能求出,从而P(,),由此能求出b2=1,进而能求出椭圆方程.(Ⅱ)由||=||,得点C在线段AB的中垂线上,当k=0时,l与椭圆交于两点都满足题意,从而b∈(﹣1,1),当k≠0时,设A(x1,y1),B(x2,y2),中点M(x′,y′),由,得()x2+2kbx+b2﹣1=0,由,得3k2﹣b2+1>0,再利用点差法能求出结果.【解答】解:(Ⅰ)由圆与x轴的交点为(,0)得椭圆的焦距2c=2,∴a2﹣b2=2,∴a2=2+b2,∴椭圆方程化为+=1,①将P()代入圆,得,∴,∴P(,)代入①式,得+=1,解得b2=1,∴椭圆方程为.(Ⅱ)由||=||,得点C应该在线段AB的中垂线上,当k=0时,l与椭圆交于两点都满足题意,∴b∈(﹣1,1),当k≠0时,设A(x1,y1),B(x2,y2),中点M(x′,y′),由,消y得()x2+2kbx+b2﹣1=0,由,得3k2﹣b2+1>0,②由,作差,得(x1+x2)(x1﹣x2)+(y1+y2)(y1﹣y2)=0,由,及=k,得x′+3ky′=0,③∵MC⊥AB,∴x′+k(y′+1)=0,④由③④得,代入y′=kx′+b中,得k2=,⑤将⑤式代入②式,得0<b<2,由⑤得2b﹣1>0,∴b>,∴b的取值范围是().综上,当k=0时,直线l在y轴上的截距的取值范围是(﹣1,1),当k≠0时,直线l在y轴上的截距的取值范围是().【点评】本题考查实数值、椭圆方程、纵截距的取值范围的求法,考查椭圆、直线方程、点差法等基础知识,考查运算求解能力,考查化归与转化思想,是中档题.19.(14分)已知函数f(x)=e x[x3﹣2x2+(a+4)x﹣2a﹣4],其中a∈R,e为自然对数的底数.(1)若函数f(x)的图象在x=0处的切线与直线x+y=0垂直,求a的值;(2)关于x的不等式f(x)<﹣e x在(﹣∞,2)上恒成立,求a的取值范围;(3)讨论函数f(x)极值点的个数.【分析】(1)求出函数的导数,求得切线的斜率,由两直线垂直的条件:斜率之积为﹣1,解方程可得a的值;(2)由题意可得x3﹣2x2+4x﹣<a(x﹣2),令x﹣2=t(t<0),运用参数分离和构造g(t),求得单调性,可得a的范围;(3)求出函数的导数,令h(x)=x3﹣x2+ax﹣a,由h(x)=0,即为a(x﹣1)=x2﹣x3,运用参数分离,求得令m=x﹣1,可得h(m)=,求得h (m)的单调区间,可得a的范围,即有f(x)的极值点的个数.【解答】解:(1)函数f(x)=e x[x3﹣2x2+(a+4)x﹣2a﹣4]的导数为f′(x)=e x•(x3﹣x2+ax﹣a),图象在x=0处的切线斜率为﹣a,切线与直线x+y=0垂直,可得﹣a=1,解得a=﹣1;(2)关于x的不等式f(x)<﹣e x在(﹣∞,2)上恒成立,即为x3﹣2x2+(a+4)x﹣2a﹣<0在x<2恒成立.即有x3﹣2x2+4x﹣<a(2﹣x),令x﹣2=t(t<0),可得﹣a<,令g(t)=,t<0,g′(t)==<0,即g(t)在t<0递减,可得g(t)>0,可得﹣a≤0,即a的取值范围是[0,+∞);(3)由f(x)的导数为f′(x)=e x•(x3﹣x2+ax﹣a),令h(x)=x3﹣x2+ax﹣a,由h(x)=0,即为a(x﹣1)=x2﹣x3,若x=1时,方程不成立;若x≠1时,a=,令m=x﹣1,可得h(m)===,h′(m)=,当m>0即x>1时,h(m)递减,m<﹣1时,h(m)递增,﹣1<m<0时,h(m)递减.则当a=0时,f′(x)=x2(x﹣1),显然x>3,f(x)递增,x<0或0<x<3时,f(x)递减,即有x=3为极值点;当a>0时,a=h(m)有一个解,f(x)有一个极值点;当a<0时,a=h(m)有三个解,f(x)有三个极值点.综上可得,a=0时,f(x)有一个极值点;a>0时,f(x)有一个极值点;a<0时,f(x)有三个极值点.【点评】本题考查导数的运用:求切线的斜率,注意运用导数的几何意义和两直线垂直的条件,考查不等式恒成立问题的解法,注意运用参数分离和构造函数法,考查函数的极值点的个数,注意运用分类讨论的思想方法,属于难题.20.(13分)已知集合A1,A2,…,A n为集合U的n个非空子集,这n个集合满足:①从中任取m个集合都有≠U成立;②从中任取m+1个集合都有=U成立.(Ⅰ)若U={1,2,3},n=3,m=1,写出满足题意的一组集合A1,A2,A3;(Ⅱ)若n=4,m=2,写出满足题意的一组集合A1,A2,A3,A4以及集合U;(Ⅲ)若n=10,m=3,求集合U中的元素个数的最小值.【分析】(Ⅰ)由U={1,2,3},n=3,m=1,能求出满足题意的一组集合A1,A2,A3.(Ⅱ)由n=4,m=2,能出满足题意的一组集合A1,A2,A3,A4和集合U.(Ⅲ)由n=10,m=3,得集合U中的元素个数的最小值为120个.先证明若{i1,i2,i3}≠{j1,j2,j3},则,,B j≠B i,则A1,A2,…,A10的3个集合的并集共计有=120个.把集合U中120个元素与A1,A2,…,A10的3个集合的并集B i=建立一一对应关系,从而集合U中元素个数大于等于120.【解答】解:(Ⅰ)∵集合A1,A2,…,A n为集合U的n个非空子集,这n个集合满足:①从中任取m个集合都有A i1∪A i2∪…∪A im≠U成立,②从中任取m+1个集合都有=U成立.U={1,2,3},n=3,m=1,∴满足题意的一组集合A1={2,3},A2={2,3,6},A3={1,3,5}.(Ⅱ)∵n=4,m=2,∴满足题意的一组集合A1={4,5,6},A2={2,3,6},A3={1,3,5},A4={1,2,4},集合U={1,2,3,4,5,6}.(Ⅲ)∵n=10,m=3,∴集合U中的元素个数的最小值为120个.下面先证明若{i1,i2,i3}≠{j1,j2,j3},则,,B j≠B i,反证法:假设B j=B i,设i1∉{j1,j2,j3},由假设B i=B j≠∪,设D j=∁U B j,设x∈D j,则x是,,中都没有的元素,x∉B j,∵,,,四个子集的并集为U,∴⊂B i=B j与x∉B j矛盾,∴假设不正确,若{i1,i2,i3}≠{j1,j2,j3},且,,B j≠B i成立,则A1,A2,…,A10的3个集合的并集共计有=120个.把集合U中120个元素与A1,A2,…,A10的3个集合的并集B i=建立一一对应关系,∴集合U中元素个数大于等于120,下面我们构造一个有120个元素的集合U:把与B i=(i=1,2,…,120)对应的元素放在异于,的集合中,∴对于任意一个3个集合的并集,它们都不含与B i对应的元素,∴B i≠U,同时,对于任意的4个集合设为的并集,则由上面的原则与,,对应的元素在集合中,即对于任意的4个集合的并集为全集U .【点评】本题考查集合的求法,考查集合中最少的元素个数的判断与证明,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.。
北京专家2019届高考模拟试卷(三)理科数学参考答案

北京专家2019届高考模拟试卷(三)理科数学参考答案1.A 【解析】12(12)(34)5101234252555i i i i z i i -----====--+,||z ∴==. 2.B 【解析】集合{}12A x R x x =∈≤>或,{}12B x R x x =∈<>或,{}12U B x R x =∈≤≤ð,所以(){}1U A B =I ð,故选B.3.A 【解析】若1sin 2α=,由(0,)απ∈,故6πα=或56πα=,故“1sin 2α= ”是“6απ= ”的必要不充分条件,故选A.4.D 【解析】设等比数列{}n a 的公比是q ,因为51a =,则41a q =,6a q =,依题意,得1524q q +=?,即22520q q -+=,解得2q =或12q =,因为{}n a 递增,所以2q =,则2754a a q =?,故选D.5.C 【解析】如图所示,抛物线C 的焦点(0,1)F ,过F 作直线l 的垂线,垂足为H ,线段FH 与C 的交点,即为点P ,由抛物线的定义,点P 到准线m 的距离即为PF ,所以最小值为点F 到直线l 的距离FH =,故选C. 6.C 【解析】由22+3AP BP CP 0uu u r uu r uu r +=得2(2)30DP CP +=uu u r uu r,其中,点D 是AB 边的中点,所以点P 是在CD 上,且43CP DP uu r uu u r =,△APC 与△APD 共高,于是△APD 的面积是34S ,故△APB 的面积是32S ,故选C. 7.D 【解析】令sin cos ()x x xf x x-=,由()()f x f x -=-,则()f x 的图象关于原点成中心对称,排斥选项A,当0x +®时,()f x ??,排斥B,C,由sin cos 0x x x -=,知存在1(,)42x p p Î,使得1()0f x =,还存在25(,)4x p p Î,使得2()0f x =,符合上述条件是选项D.8.B 【解析】设事件A:函数()b f x ax x =+在区间轾上不单调的事件,样本空间01(,)01a a b b 禳ì<?镲?W =眄?<?镲?î铪,因为函数()f x在纟çç棼上递减,在÷+?÷上递增,所以(,)A a b 禳镲=蜽<睚镲铪11(,)32b a b a 禳ì镲?=蜽<<眄?ï镲î铪,因此,11111223()112A P A 骣琪??琪桫===W ,故选B. 9.A 【解析】易知2A =,2sin 1j =,由“五点法”知2p j p <<,则56p j =,且332p pw j ?=,得2w =,所以5()2sin 26f x x p骣琪=+琪桫,5()2sin 226g x x 骣骣p p 琪琪=-+琪琪桫桫2sin 26x p 骣琪=-琪桫, 因为5612x pp -#,则22263x p p p -??,递减满足22263x p p p ??,即5312xpp#,故选A. 10.C 【解析】因为()2201F A F B λλ=<<uuu r uuu r,所以点A 在2F B 之间,由2F A 垂直于1l ,得2,,==F A b OA a 又||||3||+=OA OB AB ,222||||||-=OB OA AB ,得3||4=AB a ,设2,∠=AOF α则2∠=π-AOB α,()22tan 3tan 2tan 21tan 4π-=-=-=--αααα,带入tan =b a α得3=ba, 所以224354F A b F B b a λ===+uuu r uuu r .故选C. 11.B 【解析】取AB 的中点为M ,设1O 是△ABC 的外心,过点1O 作平面ABC 的垂线1OO,13CO =因为O 为CD 中点,则三棱锥D ABC -的高12DH OO =,又2133D ABC V DH三棱锥-=?得2DH =,所以11OO =,故Q 球O 的半径2R OC ==,表面积为2416R p p =故选B.12.A 【解析】由函数ln 1()e x x x f x x +=+,得21l n ()e xx xf x x-'=-,当(0,1)x ∈时,10,ln 0x x ->->,所以()0f x '>,当(1,)x ∈+∞时,10,ln 0x x -<-<,所以()0f x '<,故()f x 在(0,1)单调递增,在(1,)+∞单调递减,又因为222221122211ln 1111()0,(1)101e ee e e ef e f e e e ++=+=-<=+>,当0x >时,()0f x >,所以,方程()()22()2()1[()1][()1]0f x mf x m f x m f x m -+-=---+=恰好有3个不相等的实根,需要满足:101110m e m ⎧<+<+⎪⎨⎪-<⎩,解得1(1,)e m ∈-,故选A.二、填空题(共4小题,每小题5分,共20分)13.1或3【解析】由题意,221:()8C x y a +-=圆心为1(0,)C a ,半径为,222:()2C x a y -+=圆心为2(,0)C a ,圆心距d ==,由两圆只有一个公共点,故12d r r =+或121d r r a =-⇒=或3a =. 14.72ln 212-【解析】联立22,,4y x x y ì=ïïíï=ïî得2x =,2223112172ln 2ln 241212ABC x S dx x x x 骣骣琪琪=-=-=-琪琪桫桫ò曲边△.F 到平面ECM 的距离为h ,由图知点F 到平面ECM 的距离等于点B 到平面ECM 的距离,作BH 垂直于CM 于H ,在三角形BCM中,解得BH,所以h =.由cos cos cos cos A B C B C +和诱导公式,得()cos cos cos cos B C B C B C -++,得sin sin cos B C B C ,又sin 0B >,所以tan C ,0C p <<,得3C p=,由三角形面积公式,得)()2123sin 232242428ABCa bS ab C a b 骣+琪==W=琪桫△,此时236,23,a b a b ì+=ïí=ïî 得32a =,1b =, 由余弦定理,得2229371424c a b ab =+-=+-=, 又因为CD 是边AB 上中线,由平行四边形的性质,得 ()()2222913222142CD c a b 骣琪+=+=+=琪桫,所以21944CD =,所以CD =. 三、解答题(共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.【解析】(I)当1n =时,1116a S ==;若2n ³(*n N Î)时,22710n S n n =-+-,21(1)27(1)10n S n n -=--+--,1228n n n a S S n -=-=-+,显然,当1n =时,12128a ??,故数列{}n a 的通项公式是16,1228,2n n a n n ì=ï=í-+?ïî……6分(II)**,114(),15()n n na n n N a a n n N ì#?ï=íï-澄î, ……8分 若114n #(*n N Î)时,12n T a a =++…n a +12a a =++…n a +22710n S n n ==-+-;….9分 若15n ³(*n N Î)时,21414271410172T =-+?=,于是201214151620()T a a a a a a =+++-+++1214121415202()()a a a a a a a a =+++-++++++214=. …………12分18.【解析】(I )由题意,甲公司平均月薪的估计值=0.25+0.47+0.39+0.111=7.6()x ⨯⨯⨯⨯甲千元 甲公司平均月薪的估计值=0.13+0.25+0.37+0.29+0.1511+0.0513=7.5()x ⨯⨯⨯⨯⨯⨯乙千元 因为x x <乙甲,故从平均月薪收入更高的角度,应选择甲公司. ………………4分(注:本题也可以从其它统计数据特征进行分析,只要利用统计思想分析合理,都视为正确.) (II )设甲公司有1n 人,则113000.31000n n =⇒=(人) 设乙公司有2n 人,则224000.22000n n =⇒=(人) 两公司月薪不低于10000元的总人数为10000.120000.2500⨯+⨯=(人) 故月薪不低于1000元频率为500130006=.………………8分 (Ⅲ)分 6.734 6.635k =>,故有99%的把握认为就业意愿与年龄结构有关. ………………12分19.【解析】(I)∵E 是BC 的中点,∴ 12BE BC =,∵ 12AD BC =,∴ AD BE = ,又 ∵AD ∥BC (即AD ∥BE ),∴ 四边形ABED 是平行四边形, ∴ ED ∥BA ,又 ∵ ED Ë平面PBA ,BA Ì平面PBA ,∴ ED ∥平面PBA ,又 ∵点E ,F 分别是棱BC ,PC 的中点,∴EF ∥BP ,又 ∵EF Ë平面PBA ,BP Ì平面PBA ,∴EF ∥平面PBA ,∵ED ,EF 是平面FED 内两相交直线, ∴平面PAB ∥平面FED .………6分(II)∵点P 在平面ABCD 内的射影H 是AB 的中点,∴PH ^平面ABCD ,即得PH AB ^ ,由12AD CD BC ==,E 是BC 的中点,90BCD??,易得2AB =,1HE BH AH ===,HE AB ^,建立如图空间直角坐标系H xyz -,则()0,0,0H ,()1,0,0B ,()0,1,0E ,()1,0,0A -,()1,2,0C -,()2,1,0D -,()0,0,1P ,11(,1,)22F -,……7分因为平面CEF 与坐标轴既不平行又不垂直,所以平面CEF 的一个法向量可设(),,1x y =n ,因为11(,0,)22EF uu u r =-,(1,1,0)EC =-uu ur ,于是0,0EF EC n n uu u ruu u r ì?ïíï?î,即100x x y ì-+=ïí-+=ïî,得11x y ì=ïí=ïî,即(1,1,1)n =,因为平面EFD ^y 轴,所以平面EFD 的一个法向量(0,1,0)m =,………10分 设二面角C EF D --的平面角为q (02pq <<), cos q ×=n m n m分),故二面角C EF D --………12分 20.【解析】(Ι)由题意得122226c b c a ⎧⋅⋅=⎪⎨⎪+=⎩,又由222a b c =+,解得2243a b ⎧=⎪⎨=⎪⎩,故椭圆E 的方程为22143x y +=;………….5分 (Ⅱ)由题意直线AB 的斜率存在且不为0,设直线AB 的方程为1x my =+,1122(,),(,)A x y B x y ,则22(,)D x y -,直线AD 与直线BC 的交点记为T ,由对称性可知T 点必在x 轴上,设(0,)T t ,联立221143x my x y=+⎧⎪⎨+=⎪⎩,得22(34)690m y my ++-=,122122634934m y y m y y m -⎧+=⎪⎪+⎨⎪⋅=-⎪+⎩,(*) ………….8分 直线AD 的方程为121112()y y y y x x x x +-=--,令0y =得()112112y x x x x y y --=++,………….10分 ()()112112211221122112121212(1)(1)21y x x x y y x y x y my y my y my y x y y y y y y y y --++++++∴====+++++,带入(*)式得2292341434m m m ⎛⎫⋅- ⎪+⎝⎭+=+,故直线AD 与直线BC 的交点过定点,定点坐标为(4,0).…12分 21.【解析】(I) 当32a =时,2()3ln f x x x x =-+,其定义域为(0,)+?, 1(21)(1)()23x x f x x x x--¢=-+=,当10,(1,)2x 骣琪??琪桫时,()0f x ¢>,所以()f x 的递增区间是10,2骣琪琪桫和()1,+?;当1,12x 骣琪Î琪桫时,()0f x ¢<,所以()f x 在1,12骣琪琪桫上递减, 因此,()f x 的极大值点是12x =,极小值点是1x =.………4分(II)2221()x ax f x x-+¢=,依题意, 设m ,n (m n <)是方程22210x ax -+=不同的两正根,依根与系数关系,得m n a +=,12mn =,又m n <,于是12m ?1n <?,当112x 轹êÎê滕时,11max ()()()f x f x f m ?;当2x úÎú棼时,22min()()()f x f x f n ?,………6分所以()()()G a f m f n =-2()()2()ln m m n m n a m n nm=-+-++ 2()()2()()ln(2)m n m n m n m n m =-+--++2()()ln(2)m n m n m =--++2221ln(2)4m m m =-+,令22m t =(112t ?),………8分 于是1()()ln 22t G a g t t t ==-+,()()22211110222t g t t t t -¢=--+=-<,所以()g t ()g t 在1,02轹÷ê÷ê滕上递减,1(1)()()2g g t g <?,即30()ln 24g t <?, 故()G a 的取值范围是30,ln 24纟ç-úçú棼.………12分22.【解析】(I)由2cos ,12sin x y q q ìïíï=+î分别得2cos x q -……①,12sin y q -=,……②由①、②得曲线C的普通方程为22((1)4x y -+-=,………2分由2cos 203pr q 骣琪++=琪桫得,cos sin 20r q q -+=(3分),由极直互化公式cos ,sin x yr q r q ì=ïí=ïî, 得曲线l的直角坐标方程为20x -+=;………5分(II)设圆心C ,设l 与C 相交于点A ,B ,当PC l ^,且点P 在¼AmB 上时,点P 到l 的距离最大, 此时,射线CP 对应的最小正角为300q =?(8分),2cos3001P x ?,12sin3001P y =+?-故点点P的直角坐标为(1-.………10分23.【解析】(I )令()()4h x f x =+,于是2,1,1()34,1,216,2x x h x x xx x ìï+<-ïïï=+-#íïïï->ïî(1分)不等式()40f x +?等价于 1,20x x ì<-ïí+?ïî或11,2340x x ì-#ïíï+?î或1,260x x ì>ïíï-?î,………2分 即得,21x -?-或112x -#或162x <?, 亦即,26x-#,故原不等式()40f x +?的解集为{}26x R x ∈-≤≤.………5分 (II )2,1,1()3,1,212,2x x f x x x x x ìï-<-ïïï=-#íïïï->ïî(6分),所以()f x 在1,2纟ç-?úçú棼上递增,在1,2轹÷+?ê÷ê滕上递减,所以max 13()22f x f 骣琪==琪桫, 存在0x R Î,使得()2052m m f x +?成立,所以2max53()22m m f x +?, 所以22530m m +-?,解得132m -#, 故m 的取值范围是13,2轾-犏犏臌. ………10分。
2019年高考理科数学北京卷(附参考答案和详解)

4!数学中 有 许 多 形 状 优 美/寓 意 美 好 的 曲 线# 曲线 .,#$0&$'!0"#"& 就是 其 中 之 一$如 图 %!给 出 下 列 三 个 结 论 ,
曲线 . 恰 好 经 过 & 个 整 点 $即 横/纵 坐 标
均 为 整 数 的 点 %-
第4题图
曲线 . 上任意一点到原点的距离都不超过槡$-
三 解 答 题解答应写出文字说明证明过程或演算步骤
!"!$本小题满 分 !+ 分%在 '+0. 中#''+#(()'$#5290'
(
! $
!
$!%求(#) 的 值 -
$$%求9/: $0(.%的值!
.!( .
!&!$本小题满分!)分%如图#在 四 棱 锥 12+0.5 中#1+& 平
面 +0.5#+5&.5#+5,0.#1+'+5'.5'$#0.'+!
曲线 . 所围成的&心形'区域的面积小于+! 其 中 #所 有 正 确 结 论 的 序 号 是
*% -%
! ! !,% ! ! !.%
$! ! %
第二部分
二 填 空 题本大题共&小题每 小 题 " 分共 +# 分!把 答 案
填在题中横线上
8!函数 *$#%'9/:$$# 的最小正周期是!!!!! !#!设 等 差 数 列!'-"的 前- 项 和 为,-#若'$ ' (+#," ' (!##
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学(理科)试题2019.3㊀㊀本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1-2页,第Ⅱ卷3-4页,共150分,测试时间120分钟.注意事项:㊀㊀选择题为四选一题目,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上.第Ⅰ卷(共60分)一㊁选择题:本大题共12小题,每小题5分,共60分.把正确答案涂在答题卡上.1.若复数z=21+i,其中i为虚数单位,则z=A.1+i B.1-i C.-1+i D.-1-i2.已知集合A={x|l o g3x<1},B={x|x+1x-2<0},则A.AɘB={x|-1<x<3}B.AɘB={x|0<x<2}C.AɣB={x|-1<x<2}D.AɣB={x|0<x<3}3.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的焦距为10,点P(1,2)在C的渐近线上,则C的方程是A.x280-y220=1B.x220-y280=1C.x25-y220=1D.x220-y25=14.在等比数列{a n}中,a1=1,a5+a7a2+a4=8,则a6的值为A.4B.8C.16D.325.如图,әA B C中,A D=23A B,B E=12B C,则D Eң=A.13A Cң-12A BңB.13A Cң-16A BңC.12A Cң-13A BңD.12A Cң-16A Bң6.设有下列四个命题:p1:若a<b,则a2<b2;p2:若x>0,则s i n x<x;p3: f(x)f(-x)=-1 是 y=f(x)为奇函数 的充要条件;p4: 等比数列{a n}中,a1>a2>a3 是 等比数列{a n}是递减数列 的充要条件.其中,真命题的是A.p1,p3B.p2,p3C.p2,p4D.p3,p4数学(理科)试题㊀第1页(共4页)7.正整数N除以正整数m后的余数为n,记为Nʉn(M O D m),例如25ʉ1(M O D6).如图所示的程序框图的算法源于 中国剩余定理 ,若执行该程序框图,当输入N=25时,则输出N=A.31B.33C.35D.37(第7题图)㊀㊀㊀㊀㊀(第8题图)8.已知某几何体的三视图如图所示,则该几何体外接球的表面积为A.143πB.7πC.11πD.14π9.设f(x)是定义在R上周期为2的函数,且f(x)=c o s2πx,0ɤxɤ11-l o g2x,1<x<2{,记g(x)=f(x)-a.若12<a<1,则函数g(x)在区间[-2,3]上零点的个数是A.5B.6C.7D.810.为推广羽毛球运动的发展,某羽毛球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员4名,其中种子选手2名.从这7名运动员中随机抽取4人参加比赛,设事件A为 选出的4人中恰有2名种子选手且这2名种子选手来自同一个协会 ,则P(A)=A.435B.635C.935D.183511.已知抛物线C:y2=4x的焦点为F,直线y=3(x-1)与C交于A㊁B(A在x轴上方)两点,若A Fң=mF Bң,则实数m的值为A.32B.3C.2D.312.在四面体A B C D中,若A D=D B=A C=C B=1,则四面体A B C D体积的最大值是A.2327B.13C.239D.33数学(理科)试题㊀第2页(共4页)第Ⅱ卷(共90分)二㊁填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.某单位200名职工的年龄分布情况如图所示.现要从中抽取50名职工作样本,若采用分层抽样方法,则40~50岁年龄段应抽取㊀㊀㊀㊀人.14.某超市中秋节期间举行有奖销售活动,凡消费金额满200元的顾客均获得一次抽奖的机会,中奖一次即可获得5元红包,没有中奖不得红包.现有4名顾客均获得一次抽奖机会,且每名顾客每次中奖的概率均为0.4,记X 为4名顾客获得的红包金额总和,则P (10ɤX ɤ15)=㊀㊀㊀㊀.15.数列{a n }的前n 项和为S n ,若a 1=1,a n ʂ0,3S n =a n a n +1+1,则a 2019=㊀㊀㊀㊀.16.已知函数f (x )=x 2+2a x ,g (x )=4a 2l n x +b ,设两曲线y =f (x ),y =g (x )有公共点P ,且在P 点处的切线相同,当a ɪ(0,+ɕ)时,实数b 的最大值是㊀㊀㊀㊀.三㊁解答题:本大题共6小题,共70分.解答应写出文字说明㊁证明过程或演算步骤.17.(本小题满分12分)已知函数f (x )=4s i n x c o s (x -π6).(1)求f (x )的单调递增区间;(2)在әA B C 中,角A ,B ,C 的对边分别为a ,b ,c .若f (A 2)=1,a =2,求әA B C 面积的最大值.18.(本小题满分12分)如图,在等腰梯形A B C D 中,A B ʊC D ,A B >C D ,E ,F 为A B 的三等分点,且E F =C D .将әA E D 和әB F C 分别沿D E ㊁C F 折起到A ㊁B 两点重合,记为点P .(1)证明:平面P C F ʅ平面P E F ;(2)若P F =F C ,求P D 与平面P F C 所成角的正弦值.19.(本小题满分12分)已知椭圆T :x 2a 2+y 2b2=1(a >b >0)的左㊁右焦点分别为F 1㊁F 2,离心率为32,过F 2且与x 轴不重合的直线l 交椭圆T 于A ㊁B 两点,әA B F 1的周长为8.(1)求椭圆T 的标准方程;(2)已知直线l 1:y =k x +m ,直线l 2:y =2(k x +m )(0<m <1).设l 1与椭圆T 交于M ㊁N 两点,l 2与圆C :x 2+y 2=a 2交于P ㊁Q 两点,求S әM O N S әP O Q的值.数学(理科)试题㊀第3页(共4页)20.(本小题满分12分)改革开放以来,我国经济持续高速增长.如图给出了我国2003年至2012年第二产业增加值与第一产业增加值的差值(以下简称为:产业差值)的折线图,记产业差值为y (单位:万亿元).(1)求出y 关于年份代码t 的线性回归方程;(2)利用(1)中的回归方程,分析2003年至2012年我国产业差值的变化情况,并预测我国产业差值在哪一年约为34万亿元;(3)结合折线图,试求出除去2007年产业差值后剩余的9年产业差值的平均值及方差(结果精确到0.1).附:回归直线的斜率和截距的最小二乘法估计公式分别为:^b =ðni =1(t i-t )(y i-y )ðni =1(t i-t )2,^a =y -^b t .样本方差公式:s 2=1n ðni =1(yi -y )2.参考数据:y =110ð10i =1y i =10.8,ð10i =1(t i -t )(y i -y )=132,ð10i =1(y i -y )2=211.6.21.(本小题满分12分)已知函数f (x )=e 2x -3-(2x -3)2.(1)证明:当x ȡ32时,f (x )ȡ1;(2)设g (x )=14+l n x 2,若存在实数x 1,x 2,使得f (x 1)+(2x 1-3)2=g (x 2),求x 2-x 1的最小值.请考生在第22~23题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)在直角坐标系x O y 中,直线l 1的参数方程为x =2+ty =34k t {(t 为参数),直线l 2的参数方程为x =-2+my =-mk{(m 为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρs i n (θ+π4)=22,l 3与C 的交点为A ㊁B ,M 为线段A B 的中点,求M 的极径.23.(本小题满分10分)已知函数f (x )=|2x +1|+|x -a |.(1)当a =1时,求不等式f (x )<3的解集;(2)若不等式|x -2|+|x -a |ɤf (x )+m 2+32m 恒成立,求实数m 的取值范围.数学(理科)试题㊀第4页(共4页)数学(理科)试题参考答案2019.3一㊁选择题:本大题共12小题,每小题5分,共60分.把正确答案涂在答题卡上.1.A㊀2.B ㊀3.C ㊀4.D㊀5.D㊀6.C ㊀7.A㊀8.C ㊀9.D㊀10.B ㊀11.D㊀12.A二㊁填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.15㊀14.312625㊀15.3028㊀16.2e三㊁解答题:本大题共6小题,共70分.解答应写出文字说明㊁证明过程或演算步骤.17.解:(1)f (x )=4s i n x c o s (x -π6)=4s i n x (c o s x c o s π6+s i n x s i n π6)=4s i n x (32c o s x +12s i n x )=23s i n x c o s x +2s i n 2x 2分…………………………………=3s i n 2x +(1-c o s 2x )=3s i n 2x -c o s 2x +1=2s i n (2x -π6)+14分……………………………………………………………………令-π2+2k πɤ2x -π6ɤπ2+2k π,k ɪZ ,得-π6+k πɤx ɤπ3+k π,k ɪZ所以f (x )的单调递增区间为[-π6+k π,π3+k π](k ɪZ ).6分…………………………(2)因为f (A 2)=2s i n (A -π6)+1=1,且A ɪ(0,π),所以A =π68分…………………由a 2=b 2+c 2-2b c c o s A ,得4=b 2+c 2-3b c ȡ(2-3)b c所以b c ɤ42-3=4(2+3),当且仅当b =c =2+6时,等号成立10分…………………………………………………所以S әA B C =12b c s i n A ɤ12ˑ4(2+3)ˑ12=2+3.即әA B C 面积的最大值为2+312分……………………………………………………数学(理科)试题答案㊀第1页(共5页)18.(1)证明:因为A B ʊC D ,E F =C D ,所以四边形C D E F 为平行四边形.所以øA E D =øA F C ,又因为әA E D ɸәB F C ,所以øA E D =øB F C ,从而øA F C =øB F C =90ʎ所以P E ʅE D ,P F ʅF C ,2分………………………………………………………………因为C F ʊD E ,所以P E ʅF C ,又因为P E ɘP F =P ,P E ,P F ⊂平面P E F ,4分…………………………………………所以F C ʅ平面P E F ,又因为F C ⊂平面P F C ,所以平面P E F ʅ平面P F C .5分……………………………………………………………(2)在平面P E F 内作P O ʅE F ,垂足为O ,取C D 的中点为M .由(1)可知,F C ʅ平面P E F ,故F C ʅP O ,可得P O ʅ平面C D E F ,所以P O ʅO M ,P O ʅO F又因为P F =P E ,所以O E =O F ,所以O M ʊF C ,所以O F ʅO M ,所以O P ,O F ,O M 两两垂直,7分…………………………………………………………以O 为坐标原点,建立如图所示的空间直角坐标系,设P F =F C =2,而әP E F 为等边三角形所以P (0,0,3),F (1,0,0),C (1,2,0),D (-1,2,0)所以P F ң=(1,0,-3),P C ң=(1,2,-3),P D ң=(-1,2,-3),9分……………………………………………………………设n =(x ,y ,z )为平面P F C 的法向量,由n P F ң=0n P C ң=0{,即x -3z =0x +2y -3z =0{可取n =(3,0,1)11分……………………………………………………………………设P D 与平面P F C 所成角为θ,则s i n θ=n P D ң|n | |P D ң|=64所以P D 与平面P F C 所成角的正弦值为64.12分………………………………………19.解:(1)由题意可知,4a =8,e =c a =322分…………………………………………………所以,a =2,c 2=3,b 2=1所以椭圆T 的标准方程为:x 24+y 2=14分………………………………………………数学(理科)试题答案㊀第2页(共5页)(2)原点O (0,0)到直线l 1的距离为d 1=m 1+k2,由x 24+y 2=1y =k x +m ìîíïïï,得(1+4k 2)x 2+8k m x +4m 2-4=0Δ=(8k m )2-4(1+4k 2)(4m 2-4)=16(4k 2-m 2+1)>0x 1+x 2=-8k m 1+4k 2,x 1 x 2=4m 2-41+4k 26分…………………………………………………|MN |=1+k 2|x 1-x 2|=1+k 21+4k244k 2-m 2+1,所以әM O N 的面积为S әM O N =12|MN | d 1=2m 4k 2-m 2+11+4k 28分………………圆C 的方程为x 2+y 2=4圆C 的圆心O (0,0)到直线l 2的距离为d 2=2m1+4k2所以|P Q |=24-d 22=44k 2-m 2+11+4k2所以әP O Q 的面积为S әP O Q =12|P Q | d 2=4m 4k 2-m 2+11+4k211分………………所以SәM O N S әP O Q =12.12分………………………………………………………………………20.解:(1)t =110(1+2+3+ +9+10)=5.51分……………………………………………ð10i =1(t i-t )2=(t 1-t )2+ +(t 10-t )2=(1-5.5)2+(2-5.5)2+ +(10-5.5)2=2ˑ(4.52+3.52+2.52+1.52+0.52)=82.52分……………………………………………………………………^b =ð10i =1(t i-t )(y i-y )ð10i =1(t i-t )2=13282.5=1.63分………………………………………………^a =y -b t =10.8-1.6ˑ5.5=2所以回归方程^y =1.6t +24分……………………………………………………………数学(理科)试题答案㊀第3页(共5页)(2)由(1)知^b =1.6>0故2003年至2012年我国产业差值逐年增加,平均每年增加1.6万亿元6分…………令1.6t +2=34解得t =20故预测在2022年我国产业差值为34万亿元.8分………………………………………(3)结合折线图,2007年产业差值为10.8万亿元,除去2007年(t =5时)产业差值外的9年的产业差值平均值为19ˑ(10ˑ10.8-10.8)=10.810分……………………………………………………又因为ð10i =1(yi -y )2=211.6所以除去2007年(t =5时)产业差值外的9年的产业差值的方差为19ˑ[211.6-(10.8-10.8)2]ʈ23.512分……………………………………………21.解:(1)令t =2x -3,当x ȡ32时,f (x )ȡ1等价于:当t ȡ0时,e t -t 2-1ȡ0.设函数u (t )=e t -t 2-1,则u ᶄ(t )=e t-2t .2分……………………………………………[u ᶄ(t )]ᶄ=e t-2.当t ɪ[0,l n 2)时,u ᶄ(t)为减函数,当t ɪ(l n 2,+ɕ)时,u ᶄ(t)为增函数.3分…………………………………………………所以u ᶄ(t )ȡu ᶄ(l n 2)=2-2l n 2>0.所以u (t )在[0,+ɕ)上为增函数,所以u (t )ȡu (0)=0.即当x ȡ32时,f (x )ȡ1.5分………………………………………………………………(2)设f (x 1)+(2x 1-3)2=g (x 2)=m ,则e 2x 1-3=14+l n x 22=m 因为x 1ɪR ,所以e 2x 1-3>0,即m >0所以2x 1-3=l n m ,l n x 22=m -14所以x 1=l n m +32,x 2=2e m -14,x 2-x 1=2e m -14-l n m +32(m >0)7分……………………令h (x )=2e x -14-l n x +32(x >0),则h ᶄ(x )=2e x -14-12x ,所以[h ᶄ(x )]ᶄ=2e x -14+12x2>09分……………………………………………………………………………………………所以h ᶄ(x )在(0,+ɕ)上为增函数,且h ᶄ(14)=010分…………………………………当x >14时,h ᶄ(x )>0;当0<x <14时,h ᶄ(x )<0.所以,h (x )在(0,14)上为减函数,在(14,+ɕ)上为增函数,数学(理科)试题答案㊀第4页(共5页)所以,当x =14时,h (x )取得最小值,此时h (14)=12+l n2,即x 2-x 1的最小值为12+l n212分………………………………………………………22.解:(1)直线l 1的普通方程为y =34k (x -2)2分…………………………………………直线l 2的普通方程为y =-x +2k4分………………………………………………………消去k 得x 24+y 23=1,即C 的普通方程为x 24+y 23=1.5分…………………………………………………………(2)设A (x 1,y 1),B (x 2,y2)l 3化为普通方程为x +y =1,联立x +y =1x 24+y23=1{得7x 2-8x -8=07分…………………………………………………所以x 1+x 2=87,y 1+y 2=2-(x 1+x 2)=67所以M (47,37)9分…………………………………………………………………………ρ2=(47)2+(37)2=(57)2所以M 的极径为57.10分…………………………………………………………………23.解:(1)当a =1时,不等式f (x )=|2x +1|+|x -1|<3,当x ɤ-12时,-2x -1+1-x <3即x >-1,解得-1<x ɤ-12;1分…………………当-12<x <1时,2x +1+1-x <3即x <1,解得-12<x <1;2分……………………当x ȡ1时,2x +1+x -1<3,无解3分……………………………………………………所以不等式f (x )=|2x +1|+|x -a |<3的解集为(-1,1)4分………………………(2)|x -2|+|x -a |ɤf (x )+m 2+32m 整理为|x -2|-|2x +1|ɤm 2+32m 令g (x )=|x -2|-|2x +1|,需g (x )m a x ɤm 2+32m 5分………………………………由g (x )=x +3,x <-12-3x +1,-12ɤx ɤ2-x -3,x >2ìîíïïïïïï,所以g (x )m a x =g (-12)=528分……………………所以52ɤm 2+32m ,即2m 2+3m -5ȡ0,解得m ȡ1或m ɤ-52,所以实数m 的取值范围是m ȡ1或m ɤ-52.10分………………………………………数学(理科)试题答案㊀第5页(共5页)。
