组合图形面积计算练习
小学五年级数学《组合图形的面积》试题及答案

五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
小学五年级组合图形面积练习题
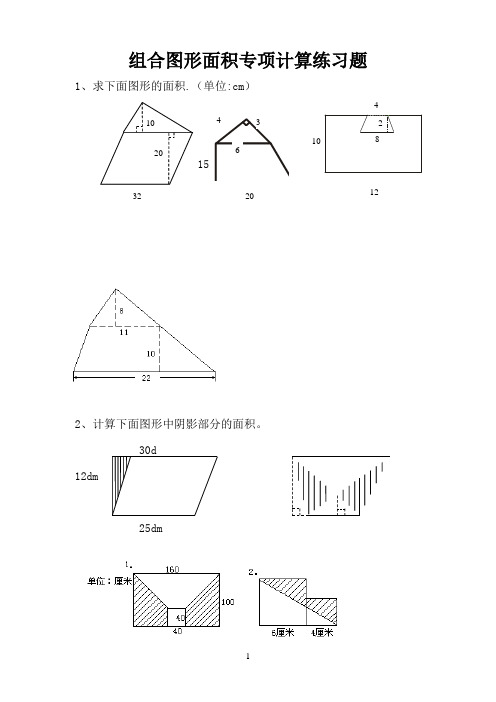
组合图形面积专项计算练习题1、求下面图形的面积.(单位:cm )152、计算下面图形中阴影部分的面积。
30d12dm25dm2010643482 1032 20123、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴.③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
4、求下面各图形的面积。
(单位:分米)13cm16cm12cm 7cm8dm8dm3dm5、“实践操作"显身手:6、如右图所示,平行四边形的面积是48平方厘米,求阴影部分的面积。
7、如右图所示,梯形中阴影部分的面积是150平方厘米,求梯形的面积16cm2、求下面图形的面积。
25组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合.由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4.采用割、补、分解、代换等方法,可将复杂问题变得简单。
一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?1.求四边形ABCD的面积.(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积.3.有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米.求原来梯形的面积.正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍.求中间长方形的面积。
1.(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积.2.正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3.求下图长方形ABCD的面积(单位:厘米).四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
五年级组合图形练习题

五年级组合图形练习题练习题一:组合图形的面积计算1. 问题描述下图中的图形由若干个矩形组成,每个矩形的长和宽分别如下:•矩形A:长5cm,宽4cm•矩形B:长8cm,宽3cm•矩形C:长6cm,宽2cm•矩形D:长3cm,宽5cm请计算以下问题:1.整个图形的面积是多少平方厘米?2.图形中矩形A所占比例是多少?2. 解题思路问题1中要求求出整个图形的面积,而这个图形由四个矩形组成。
我们可以分别计算每个矩形的面积,然后将它们相加得到整个图形的面积。
问题2中要求求出矩形A在整个图形中所占的比例。
我们可以先计算出整个图形的面积,再计算矩形A的面积,最后用矩形A的面积除以整个图形的面积即可得到所占比例。
我们可以使用以下公式来计算矩形的面积:$$ \\text{面积} = \\text{长} \\times \\text{宽} $$3. 解题步骤3.1 计算每个矩形的面积根据给定的长和宽,我们可以得到每个矩形的面积:•矩形A的面积为 $5 \\text{ cm} \\times 4 \\text{ cm} = 20 \\text{ cm}^2$•矩形B的面积为 $8 \\text{ cm} \\times 3 \\text{ cm} = 24 \\text{ cm}^2$•矩形C的面积为 $6 \\text{ cm} \\times 2 \\text{ cm} = 12 \\text{ cm}^2$•矩形D的面积为 $3 \\text{ cm} \\times 5 \\text{ cm} = 15 \\text{ cm}^2$3.2 计算整个图形的面积将每个矩形的面积相加即可得到整个图形的面积:$$ \\text{整个图形的面积} = 20 \\text{ cm}^2 + 24\\text{ cm}^2 + 12 \\text{ cm}^2 + 15 \\text{ cm}^2 = 71\\text{ cm}^2 $$3.3 计算矩形A所占比例将矩形A的面积除以整个图形的面积即可得到所占比例:$$ \\text{矩形A所占比例} = \\frac{20 \\text{ cm}^2}{71 \\text{ cm}^2} $$通过计算得知,矩形A所占比例约为 0.2817,即约为28.17%。
最新苏教版五年级数学上册组合图形的面积专项练习

组合图形的面积专项练习[基础巩固]1.平行四边形的面积公式是(),用字母表示为()。
2.三角形的面积公式是(),用字母表示为()。
3.梯形的面积公式是(),用字母表示为()。
[学以致用]一、选一选。
1.两个()的三角形一定能拼成一个平行四边形。
A.底相等B.面积相等C.等底等高D.完全相同2.一个三角形的高扩大到原来的2倍,底扩大到原来的4倍,面积扩大到原来的( )倍。
A.2B.4C.6D.83.将一些练习本擦成一个长方体,再将它均匀地斜放,如图,这时从正面看到的图形是一个近似的平行四边形,比较两图从正面看到的图形,( )。
A.周长相等,面积不等B.周长不等,面积相等C.周长、面积都相等D.周长、面积都不相等4.李大爷用同样长的篱笆靠墙围了两个养鸡场,这两个养鸡场的面积相比( )。
A.①号大B.②号大C.同样大D.无法确定二、填一填。
1.在括号里填合适的单位。
(1)无锡太湖广场的面积约是67( )。
(2)地球面积约5.1亿()。
(3)港珠澳大桥沉管隧道长度约为5664( )。
(4)中央大厅的面积约3600( )。
2.39公顷=( )平方米 4800公顷=( )平方千米540000平方米=( )公顷 36平方千米=( )平方米3.一个三角形底是16厘米,面积是40平方厘米,这条底边上的高是( )厘米。
4.在一个底是8厘米,高是4厘米的平行四边形中画一个最大的三角形,这个三角形的面积是( )平方厘米。
5.一个平行四边形与一个三角形等底等高,三角形的面积是32平方厘米,平行四边形的面积是( )平方厘米。
6.一个三角形和一个平行四边形的高和面积均相等,如果平行四边形的底是8米,那么三角形的底是( )米;如果三角形的底是4米,那么平行四边形的底是( )米。
7.一个梯形和一个三角形的高相等,面积也相等。
已知梯形的上、下底分别是5分米和7分米,这个三角形的底是( )分米。
8.一个直角梯形的周长是64分米,它的两条腰分别长13分米、15分米,这个直角梯形的面积是( )平方分米。
组合图形的面积练习题5道

组合图形的面积练习题5道2、求下面图形的面积。
你能想出几种方法。
、求下面图形的面积。
2、计算下面图形中阴影部分的面积。
30dm25dmm七、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
8dm16cm8dm②已知S平=48dm2,求S阴。
④求S阴。
312cm三、“实践操作”显身手:10分16cm2、求下面图形的面积。
组合图形面积计算练习姓名:1、计算下列组合图形的面积2、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
12cm②已知S平=48dm2,求S阴。
dm ④求S阴。
dm组合图形面积计算练习姓名:1、求下面各图形的面积。
3、求下面图形的面积。
16cm4、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
5、计算右边图形的面积。
发展题:如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
组合图形的面积如图,ABCD是直角梯形,求阴影部分的面积和。
下图1的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
下图2中,边长为10和15的两个正方体并放在一起,求三角形ABC的面积。
下图3中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
下图1中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
下图2中三角形ABC面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影的面积。
下图3中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
下图1求四边形ABCD的面积。
下图2已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
下图3图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
下图4中两个完全一样的三角形重叠在一起,求阴影部分的面积。
下图1中,甲三角形的面积比乙三角形的面积大多少平方厘米?下图2中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?如下图3,正方形ABCD 中,AB=4厘米,EC=10厘米,求阴影部分的面积。
常见组合图形面积计算实例
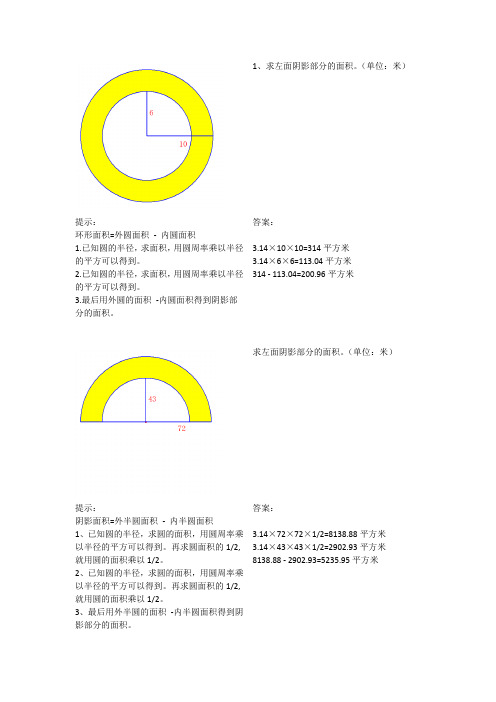
1、求左面阴影部分的面积。
(单位:米)提示:环形面积=外圆面积-内圆面积1.已知圆的半径,求面积,用圆周率乘以半径的平方可以得到。
2.已知圆的半径,求面积,用圆周率乘以半径的平方可以得到。
3.最后用外圆的面积-内圆面积得到阴影部分的面积。
答案:3.14×10×10=314平方米3.14×6×6=113.04平方米314 - 113.04=200.96平方米求左面阴影部分的面积。
(单位:米)提示:阴影面积=外半圆面积-内半圆面积1、已知圆的半径,求圆的面积,用圆周率乘以半径的平方可以得到。
再求圆面积的1/2,就用圆的面积乘以1/2。
2、已知圆的半径,求圆的面积,用圆周率乘以半径的平方可以得到。
再求圆面积的1/2,就用圆的面积乘以1/2。
3、最后用外半圆的面积-内半圆面积得到阴影部分的面积。
答案:3.14×72×72×1/2=8138.88平方米3.14×43×43×1/2=2902.93平方米8138.88 - 2902.93=5235.95平方米求左面阴影部分的面积。
(单位:米)提示:阴影部分面积可以用正方形的面积减去圆形的面积。
1、求正方形面积已知正方形的边长,求面积,用边长乘以边长可以得到。
2、求圆面积已知圆的直径,求面积,先用直径除以2得到半径,再用圆周率乘以半径的平方可以得到。
3、求阴影面积,用正方形面积减去圆的面积答案:1、正方形面积32×32=1024平方米2、圆面积32÷2=16米3.14×16×16=803.84平方米3、阴影面积1024- 803.84=220.16平方米求左面阴影部分的面积。
(单位:米)提示:阴影部分面积可以三角形面积减去右空白面积。
三角形面积是长方形面积的一半,右空白面积是长方形面积与半圆面积差的一半。
长方形的长就是圆的直径,宽是圆的半径。
五年级组合图形面积练习题
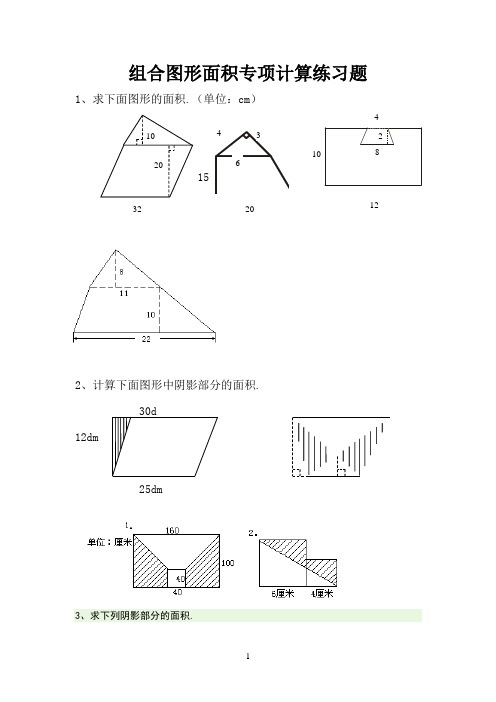
组合图形面积专项计算练习题1、求下面图形的面积.(单位:cm)152、计算下面图形中阴影部分的面积.30d12dm25dm3、求下列阴影部分的面积.201064 34821032 20 12①②已知S平=48dm2.求S阴.③已知:阴影部分的面积为24 ④求S阴.平方厘米.求梯形的面积.4、求下面各图形的面积.(单位:分米)13cm16cm12cm7cm 8dm8dm3dm5、“实践操作”显身手:6、如右图所示.平行四边形的面积是48平方厘米.求阴影部分的面积.7、如右图所示.梯形中阴影部分的面积是150平方厘米.求梯形的面积16cm12cm14cm 24m10m8m1、求下面图形中阴影部分的面积.2、求下面图形的面积.5625组合图形是由两个或两个以上的简单的几何图形组合而成的.组合的形式分为两种:一是拼合组合.二是重叠组合.由于组合图形具有条件相等的特点.往往使得问题的解决无从下手.要正确解答组合图形的面积.应该注意以下几点:1.切实掌握有关简单图形的概念、公式.牢固建立空间观念;2.仔细观察.认真思考.看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4.采用割、补、分解、代换等方法.可将复杂问题变得简单.一个等腰直角三角形.最长的边是12厘米.这个三角形的面积是多少平方厘米?1.求四边形ABCD的面积.(单位:厘米)2.已知正方形ABCD的边长是7厘米.求正方形EFGH的面积.3.有一个梯形.它的上底是5厘米.下底7厘米.如果只把上底增加3厘米.那么面积就增加4.5平方厘米.求原来梯形的面积.正图正方形中套着一个长方形.正方形的边长是12厘米.长方形的四个角的顶点把正方形的四条边各分成两段.其中长的一段是短的2倍.求中间长方形的面积.1.(如下图)已知大正方形的边长是12厘米.求中间最小正方形的面积.2.正图长方形ABCD的面积是16平方厘米.E、F都是所在边的中点.求三角形AEF 的面积.3.求下图长方形ABCD的面积(单位:厘米).四边形ABCD和四边形DEFG都是正方形.已知三角形AFH的面积是7平方厘米.三角形CDH的面积是多少平方厘米?1.图中两个正方形的边长分别是6厘米和4厘米.求阴影部分的面积.2.下图中两个完全一样的三角形重叠在一起.求阴影部分的面积.(单位:厘米)3.下图中.甲三角形的面积比乙三角形的面积大多少平方厘米?下图中正方形的边长为8厘米.CE为20厘米.梯形BCDF的面积是多少平方厘米?1.如下图.正方形ABCD中.AB=4厘米.EC=10厘米.求阴影部分的面积.2.在一个直角三角形铁皮上剪下一块正方形.并使正方形面积尽可能大.正方形的面积是多少?(单位:厘米)3.图中BC=10厘米.EC=8厘米.且阴影部分面积比三角形EFG的面积大10平方厘米.求平行四边形的面积.图中ABCD是长方形.三角形EFD的面积比三角形ABF的面积大6平方厘米.求ED的长.1.如图.平行四边形BCEF中.BC=8厘米.直角三角形中.AC=10厘米.阴影部分面积比三角形ADH的面积大8平方厘米.求AH长多少厘米?2.图中三个正方形的边长是1厘米、2厘米和3厘米.求图中阴影部分的面积. 3.正方形的边长是2(a+b).已知图中阴影部分B的面积是7平方厘米.求阴影部分A和C的和是多少平方厘米?。
五年级组合图形的面积典型例题(供参考)

五年级上册组合图形面积计算题求以下图形的面积:(单位:cm )435254367886101:一个等腰直角三角形,最长的边是10厘米,那个三角形的面积是多少平方厘米?【巩固练习1】:如图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的极点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
2: 求右面平行四边形的周长。
8612【巩固练习2】:求右面三角形的AB 上的高。
典型例题3:求右图等腰直角三角形中阴影部份的面积。
(单位:厘米)【巩固练习3】:求四边形ABCD 的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积别离是多少?【巩固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积别离是多少?典型例题5:图中两个正方形的边长别离是10厘米和6厘米,求阴影部份的面积。
【巩固练习5】:410CBA543图中两个正方形的边长别离是6厘米和4厘米,求阴影部份的面积。
【巩固练习6】求右图等腰直角三角形中阴影部份的面积。
(单位:厘米)典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=3cm ,DB=4cm ,两个三角形面积和是多少?二、已知正方形ABCD 的边长是7厘米,求正方形EFGH 的面积。
3、求以下图长方形ABCD 的面积(单位:厘米)。
4、如图,用48m 长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?五、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=4cm ,DB=6cm ,两个三角形面积和是多少?【典型例题】DBA610DBA20m 墙【例1】 已知平行四边表的面积是28平方厘米,求阴影部分的面积。
【练一练】如果用铁丝围成如下图一样的 平行四边形,需要用多少厘米铁丝? (单位:厘米)【例2】下图中甲和乙都是正方形,求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形的面积计算练习课
潘昶小学吴宝华
一、教学目的:
1、使学生明确知道组合图形就是几个基本图形组合而成的。
2、会正确的分解图形,并能正确的求组合图形的面积。
3、在探索的过程中,培养学生的分析能力和空间观念。
4、在探索多种解法的同时,培养学生的创新意识。
二、准备剪好的五种基本图形。
三、教学重难点:
重点:利用正方形、长方形、平行四边形、三角形、梯形这些平面图形面积来求组合图形的面积。
难点:根据图形特征采用什么方法来分解组合图形,达到分解的图形既明确而又准确求出它的面积。
四、教学过程
(一)、引入: 请看屏幕:出示谜语(草地上来了一群羊《打一水果》;又来了一群羊《打一水果》)请学生猜谜语,激发学生的学习热情。
(二)复习
1、电脑显示已学过的长方形、正方形、平行四边形、三角形、梯形,让学生分别说出图形名称和面积计算字母公式。
电脑闪烁补上面积计算字母公式。
(这里通过实物感知,了解各平面图形的特征,说出面积公式,加深对旧知识的复习,沟通新旧知识的联系,为巩固
加深新知识做好铺垫。
)
2、提问:什么是组合图形?(由几个简单图形组成的图形。
)计算组合图形的面积一般有几种方法?(分割法、添补法、平移法)(三)指导练习
1、求下列图形的面积,认真观察仔细想。
(单位;cm)
(电脑显示图形)
先让学生独立解决问题,再组织学生交流算法。
(1)分割法:把它分割成一个平行四边形和一个三角形,求这两个图形的面积和。
(12×45)+(25×8)÷2
(2)添补法:把它填补成一个大的平行四边形和一个小的平行四边形,用大平行四边形面积减去小的平行四边形面积。
15×8﹣3×2
(3)添补法:把它填补成一个大正方形和一个小平行四边形,用大正方形面积减去小平行四边形面积。
12×12﹣8×4
2、学校开运动会要制作一些锦旗,试样如图所示。
一面锦旗需要多少平方厘米的布料?(电脑显示图形)
先让学生独立解决问题,再组织学生交流算法。
(1)分割法:把它分割成两个梯形,求这两个图形的面积和。
[(60+45)×(30÷2)÷2]×2
把它分割成一个长方形和两个三角形,求这三个图形的面积和。
30×45+[30÷2×(60-45)÷2]×2
(2)添补法:添上一个三角形,求长方形和三角形的面积差。
(30×60)-[30×(60-45)÷2]
3、电脑出示题目
先让学生独立解决问题,再组织学生交流算法。
[(40+70)×30÷2] -30×15
4、电脑出示题目
先让学生独立解决问题,再组织学生交流算法。
(1)分割法。
把它分割成两个小长方形和一个大长方形,求这三个图形的面积和。
[(20-4×2)×4] ×2+(26-4×2)×20
[(26-4×2)×4] ×2+(20-4×2)×26
(2)添补法
添上四个小正方形,求长方形和四个小正方形的面积差。
26×20-4×4×4
5、电脑出示题目
先让学生独立解决问题,再组织学生交流算法。
本题解题思路是:(1)菜地实际占地面积=长方形面积+梯形面积
(2)菜地面积×0.25kg=菜地施肥量
6、电脑出示题目
先让学生独立解决问题,再组织学生交流算法。
本题解题思路是:墙的面积×185=需要砖的块数
7、电脑出示题目
先让学生独立解决问题,尤其是要指导学生看图,提醒学生过直角顶点做一条高,注意观察空白三角形的底和长方形长,空白三角形的高和长方形的宽是什么关系,再组织学生交流算法。
4×2.2÷2
(四)、拓展练习
电脑出示题目
先指导学生理解题意,让学生明确要求各部分的面积应先求出总面积(即图中长方形的面积),然后,根据各部分与总面积之间的关系分别求出相应的面积。
接着,让学生独立解决问题,再组织学生进行全班交流。
五、全课小结
通过这节课的练习,你们有什么体会?
在我们生活中,还有许多比这更复杂的图形。
但无论多复杂的图形,我们都可以通过割、补的方法,将复杂图形转化成基本图形来计算。
