江苏省溧阳市戴埠高级中学高中数学6空间两直线的位置关系(1)学案(无答案)苏教版必修2
空间点、直线、平面之间的位置关系 (教师版)
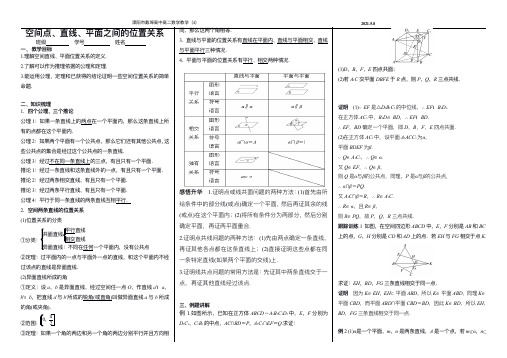
A.A,M,O 三点共线
B.A,M,O,A1 共面
C.A,M,C,O 共面
溧阳市戴埠高中高二数学教学(4)
D.B,B1,O,M 共面
②直线 AM 与 BN 是平行直线;
答案 ABC
③直线 BN 与 MB1 是异面直线;
解析 ∵ M∈ A1C,A1C㱬平面 A1ACC1,
④直线 AM 与 DD1 是异面直线.
与⻓方形 BCC1B1 的中心,则下列说法正确的是( )
A.直线 MN 与直线 A1B 是异面直线 B.直线 MN 与直线 DD1 相交 C.直线 MN 与直线 AC1 是异面直线
4.(多选题)如图是正方体或四面体,P,Q,R,S 分别是所在 棱的中点,则这四个点共面的图是( )
D.直线 MN 与直线 A1C 平行
得 cos∠
55
12+ 2 2- 2 MOD= 2×1× 5
2
= 5, 5
2
即异面直线 AD1 与 DB1 所成⻆的余弦值为 5. 5
学案作业
班级
学号
姓名
1.已知平面α,β,γ两两垂直,直线 a,b,c 满足:a㱬α,b㱬β,c㱬γ,
则直线 a,b,c 不可能满足以下哪种关系( )
A.两两垂直
B.两两平行
所以平面 ABC∩平面β=CD.
7.在三棱锥 A-BCD 的边 AB,BC,CD,DA 上分别取 E,F,
G,H 四点,如果 EF∩HG=P,则点 P( )
A.一定在直线 BD 上
B.一定在直线 AC 上
C.在直线 AC 或 BD 上
D.不在直线 AC 上,也不在直线 BD 上
答案 B
解析 如图所示,
溧阳市戴埠高中高二数学教学(4)
江苏省溧阳市戴埠高级中学高中数学9直线与平面位置关系学案2(无答案)苏教版必修2

直线与平面的位置关系(2)学案班级学号姓名一、学习目标1.掌握直线和平面垂直的定义:2.掌握直线和平面垂直的判定定理和性质定理:3.掌握判定直线平面垂直的方法:二、课堂学习重点:直线与平面垂直的定义,判定定理和性质定理.难点:线面垂直的判定定理和性质定理的应用.三、知识建构1、直线a与平面α互相垂直.2、叫平面α的垂线直线a的垂面垂足.3、思考:在平面中,过一点有且只有一条直线与已知直线垂直,那么,在空间:(1)过一点有几条直线与已知平面垂直?(2)过一点有几个平面与已知直线垂直?4、叫做这个点到这个平面的距离.5、直线与平面垂直的判定定理图形:符号:6、直线与平面垂直的性质定理.图形:符号:证明:7、叫做这条直线和这个平面的距离.四、数学运用:例1、求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.例2、已知://l α.求证:直线l 上各点到平面α的距离相等.例3、如图, 已知PA α⊥,PB β⊥, 垂足分别为A 、B , 且l αβ=,求证:AB l ⊥.例4、Rt ABC ∆所在平面外一点S ,且SA SB SC ==.(1) 求证:点S 在斜边中点D 的连线SD ⊥面ABC ;(2) 若直角边BA BC =,求证:BD ⊥面SAC .五、课后复习1. 已知直线,,l m n 与平面α,指出下列命题是否正确,并说明理由.(1) 若l α⊥,则l 与α相交.(2) 若,,,m n l m l n αα⊂⊂⊥⊥则l α⊥.(3) 若//,,l m m n αα⊥⊥,则.l n ⊥2.给出下列四个结论:A BP α β l(1)若直线垂直于平面内的两条直线,则这条直线与平面垂直.(2)若直线与平面内的任意一条直线都垂直,则这条直线与平面垂直.(3)若直线垂直于梯形的两腰所在的直线,则这条直线垂直于两底所在的直线.(4)若直线垂直于梯形的两底所在的直线,则这条直线垂直于两腰所在的直线,其中正确的结论的序号为 .3.判断下列命题的真假:(1) 平行于同一直线的两条直线平行;(2) 平行于同一平面的两条直线平行;(3) 垂直于同一直线的两条直线平行;(4) 垂直于同一平面的两条直线平行.4.共点的三条线段,.OA OB OC 两两垂直,则OA BC ⊥5.在四面体ABCD 中,面是直角三角形的至多有 个..6.证明在正方体1111ABCD A BC D -中,AC ⊥平面11BDB D .7.已知,,PA PB αβ⊥⊥垂足分别为,,A B 且l αβ=求证;l ⊥平面APB8.在正方体''''ABCD A B C D -中,求证;'AC BD ⊥。
江苏省溧阳市戴埠高级中学高中数学 18平面上两点间的距离学案(无答案)苏教版必修2

平面上两点间的距离 学案班级 学号 姓名学习目标:1. 经历两点间的距离和中点坐标公式的推导,并熟记公式;2. 会求两点间的距离和求中点的坐标;3. 运用数形结合的思想方法分析和解决问题,培养数形结合的意识.重点难点:重点:两点的距离公式和中点坐标公式的理解和应用.难点:两点的距离公式和中点坐标公式的推导.课堂学习:一、问题探索:1. 已知()1,3A -,()3,2B -,()6,1C -,()2,4D ,四边形ABCD 是否为平行四边形?2. 已知()15,2P --,()23,4P ,求它们之间的距离.3. 已知()2,4P -,()3,7Q ,则PQ 的中点M 的坐标为 .二、知识建构(1)平面上两点间的距离已知()111,P x y ,()222,P x y ,则它们之间的距离12PP= . 当12x x =时,12PP = ;当12y y =时,12PP = ;原点()0,0O 与任一点(),P x y 的距离OP = .(2)中点坐标公式对于平面上的两点()111,P x y ,()222,P x y ,线段12PP 的中点是()00,M x y ,则 .三、典型例题例1:(1)求)3,1(-A ,)5,2(B 两点之间的距离;(2)已知)10,0(A ,)5,(-a B 两点之间的距离为17,求实数a 的值.变式:已知两点()2,3A ,()1,4B -,点(),P x y 到点,A B 的距离相等,求实数,x y 满足的条件.例2:已知ABC ∆的顶点坐标为(1,5),A -(2,1),(4,7)B C --,求BC 边上的中线AM 的长和AM 所在的直线方程.例3:已知ABC ∆是直角三角形,斜边BC 的中点为M ,建立恰当的直角坐标系,证明:BC AM 21=.四、课后复习1. 已知()8,10A ,()4,4B -,则AB = ,线段AB 中点的坐标为 .2. 已知ABC ∆的顶点坐标为()3,2A ,()1,0B ,(2C ,求AB 边上的中线CM 的长为 .3. 已知两点()1,4P -,()3,2A ,则点A 关于点P 的对称点B 的坐标为 .4. 已知点()1,2P -,则点P 关于原点对称点的坐标为 ,关于x 轴对称点的坐标为 ,关于y 轴对称点的坐标为 .5. 已知,A B 两点都在直线1y x =--,且,A B ,则AB = .6. 设点A 在x 轴上,点B 在y 轴上,线段AB 的中点M 的坐标是()2,1-,则AB = .7. 已知点()1,2A -,()0,4B ,点C 在x 轴上,且AC BC =,则点C 的坐标为 .8. 已知点()1,3M -,()5,1N ,点(),P x y 到点,M N 的距离相等,则点(),P x y 所满足的方程是 .9. 已知ABC ∆的顶点坐标是()2,1A ,()2,3B -,()0,1C -,求ABC ∆三条中线所在的直线方程和三条中线的长度.10. 在ABC ∆中,已知点()5,2A -,()7,3B ,且边AC 的中点M 在y 轴上,边BC 的中点N 在x 轴上,求:(1)顶点C 的坐标;(2)直线MN 的方程.11. 已知平行四边形ABCD 的三个顶点()3,0A -,()2,2B -,()5,2C ,求顶点D 的坐标.12. 已知ABC ∆的三个顶点分别为()1,1A -,()1,3B -,()3,0C .(1)求证:ABC ∆是直角三角形;(2)求ABC ∆的面积.。
江苏省溧阳市戴埠高级中学高中数学苏教版必修2学案:8直线与平面位置关系1 [ 高考]
![江苏省溧阳市戴埠高级中学高中数学苏教版必修2学案:8直线与平面位置关系1 [ 高考]](https://img.taocdn.com/s3/m/13c8a06f336c1eb91a375ded.png)
FE A 直线与平面的位置关系(1) 学案班级 学号 姓名一、学习目标1.了解空间直线与平面的位置关系:2.了解直线与平面平行的判定定理和性质定理:3.培养学生的空间想象能力二、课堂学习重点:1、空间直线与平面的位置关系,2、直线与平面的平行性质及判定。
难点:1、用图形表示直线与平面的位置关系,2、定理的证明及应用。
三、知识建构通过观察, 得出如下结论:1、 直线a 与平面α平行。
2、 直线a 与平面α相交。
3、 直线a 在平面α内。
5、直线与平面平行:(1)直线与平面平行的判定定理文字叙述:符号表示:(2)直线与平面平行的性质定理文字叙述:符号表示:证明四、数学运用:例1、 如图已知E 、F 分别是三棱锥A BCD -的侧棱AB ,AD 的中点,求证://EF 平面BCDm l n γβα例2、 一个长方体木块如图所示,要经过平面1A 1C 内一点P 和棱BC 将木块锯开,应该怎样画线?例3、 求证:如果三个平面两两相交于三条直线,并且其中两条直线平行,那么第三条直线也和它们平行,例4、 已知//AB α,//AC BD ,C α∈,D α∈求证:AC BD =五、课后复习:1、若直线过平面外一点时,则此直线与该平面的位置关系为 。
2、对于a A α=和//a α两种情形,可以统一用符号 来表示3、过两条异面直线中的一条可作 个平面与另一条直线平行。
4、给出下列命题:⑴若直线l 上有无数个点不在平面α内,则//l α⑵如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行。
⑶若直线l 与平面α平行,则l 与平面α内的任意一条直线平行其中正确的命题有 个。
5、一条线段的两个端点到一平面的距离相等,这条线段所在直线与这个平面的位置关系是 。
6、一条直线若同时平行于两个相交平面,则这条直线与这两个平面的交线的位置关系是7、如图,在长方体1AC 的侧面和底面所在的平面中:(1)与直线AB 平行的平面是 。
江苏省溧阳市戴埠高级中学高中数学20直线的方程(2)学

直线的方程(2) 学案 班级 学号 姓名学习目标1. 掌握直线方程的两点式、截距式,了解直线方程的两点式、截距式之间的联系与区别;2. 能根据条件熟练地求出满足已知条件的直线方程;3. 明确直线方程的两点式、截距式适用的条件.课堂学习一、重点难点重点:直线方程的两点式、截距式;难点:直线方程的两点式和截距式适用的条件.二、知识建构 1.求出符合下列条件的直线方程:(1)直线经过点(1,2),1(1,)2-; (2)直线经过点(1,2),(1,2)-;(3)直线经过点(0,2),(1,0); (4)直线经过点(1,2),(1,2)--.2.问题:我们知道已知直线的斜率及其上的一个点,或已知直线的斜率及其在y 轴上的截距能求出直线方程;如果已知直线经过两个点,或已知直线的在x 轴上的截距和在y 轴上的截距如何求直线方程?已知直线l 经过两点111(,)P x y ,222(,)P x y 12()x x ≠,求直线l 的方程.小结:⑴经过两点111(,)P x y ,222(,)P x y 12()x x ≠的直线方程的两点式为 ;适用范围是 .⑵已知直线l 与x 轴的相交于点(,0),a 则称a 直线在 ,与y 轴相交于(0,),b 则称b 为直线l 在 ,当0,0,a b ≠≠则直线l 的方程1x y a b+=叫做直线的 方程三、典型例题例1.分别写出经过下列两点的直线方程(1))2,1(),3,1(- (2))0,2(),3,0(-例2.已知直线l 与x 轴 的交点(,0)a ,与y 轴 的交点(0,)b ,其中0,0a b ≠≠,求直线l 的方程.例3.三角形的顶点是(5,0)A -、(3,3)B -、(0,2)C ,求这个三角形三边所在直线方程.例4.求经过点(4,3)-且在两坐标轴上的截距相等的直线方程.变式1:上题中改为求绝对值相等的直线方程,结果如何?变式2:求过点(4,3)M -,并且在x 轴上的截距是在y 轴上的截距2倍的直线的方程;变式3:求过点(4,3)M -,且与两坐标轴围成等腰直角三角形,求此直线的方程.课后复习1.在x 轴,y 轴上的截距分别为2,3-的直线方程的截距式为 .2.将两点式323212---=--x y 转化为截距式为 . 3.过点()4,3-且在两坐标轴上的截距的绝对值相等的直线方程有 个.4.直线230x y a --=在坐标轴上的截距之和为 .5.如果直线043=+-k y x 在两坐标轴上的截距之和为2,那么实数k 的值为 .6.过点()0,2P -,()3,0Q 的直线的截距式方程为 .7.直线)3(03212---=---x y 的倾斜角为 . (以下各题选做在作业本上)8.已知两点)12,8(),2,3(B A(1)求出直线AB 方程;(2)若点),2(a C -在直线AB 上,求实数a 的值.9.已知菱形的两条对角线长分别为8和6,以菱形的中心为坐标原点,较长对角线所在的直线为x 轴,建立直角坐标系,求出菱形各边所在的直线方程.10.直线l 经过点()3,1-,且与两坐标轴围成一个等腰直角三角形,求直线l 的方程.11.求过点)1,3(-P ,且在两坐标轴上的截距的绝对值相等的直线l 方程.12.已知直线l 过点(2,1)P ,且与x 轴的正半轴交于点A ,与y 轴的正半轴交于点B . 当ABO ∆面积为92个平方单位时,求直线l 的方程.。
江苏省溧阳市戴埠高级中学高中数学 7空间两直线的位置关系(2)学案(无答案)苏教版必修2

空间两条直线的位置关系(2) 学案 班级 学号 姓名学习目标(1)理解并掌握异面直线定义,并能正确表示异面直线,增强学生的画图能力和空间想象能力;(2)理解并掌握异面直线所成角的定义、范围及应用,进一步培养学生将空间问题转化为平面问题的能力.课堂学习一、重点难点重点:异面直线的概念及判断;异面直线所成的角.难点:异面直线的判断.二、建构数学问题一:长方体1111ABCD A B C D 中,棱AB 与1A C 的位置关系是基本图形表示:推理过程:定理: 符号语言:异面直线,a b 所有的角: 异面直线所有的角的范围:异面直线的垂直:三、数学应用例1.指出下列命题是否正确:(1)过直线外一点可作无数条直线与已知直线成异面直线;(2) 过直线外一点只有一条直线与已知直线垂直.例2.已知1111ABCD A B C D -是棱长为a 的正方体.(1) 正方体的哪些棱所在的直线与直线1BC 是异面直线?(2) 求异面直线1AA 与BC 所成的角;(3) 求异面直线1BC 与AC 所成的角.变式:如图正方体1111ABCD A B C D -中,与1BC 所成角为60o 的异面直线有 ; 与1BC 所成角为90o 的异面直线有 ;与1BC 所成角为45o 的异面直线有 .例3.已知A 是BCD ∆所在平面外一点,AB AC AD BC CD DB =====,E 是BC 的中点.(1)求证:直线AE 与BD 是异面直线.(2)求直线AE 与BD 所成角的余弦值.课后复习1. 下列说法能表示,a b 是异面直线的是 . ① a b =∅I 且a 不平行于b ;②a α⊂,b β⊂且a b =∅I ;③a α⊂,b β⊂;④不存在任何平面α,使a α⊂,且b α⊂;⑤a α⊂,b α⊄.2. 空间四边形ABCD 中,,,,E F G H 分别是,,,AB BC CD DA 的中点.若AC BD a ==,且AC 与BD 所成的角为60o ,则四边形EFGH 的面积为 .3. 如果,a b 是异面直线,直线c 与,a b 都相交,那么由这三条直线中的任意两条所确定的平面共有 个.4. 如果直线,a b 分别是长方体的相邻两个面的对角线所在的直线,那么a 与b 的位置关系是 .5. 如图,在正方体1111ABCD A B C D -中,1AA a =,,E F 分别是,BC DC 的中点,则异面直线1AD 和EF 所成角的大小为 .6. 如图所示,已知P 为ABC ∆所在平面外一点,PC AB ⊥,2PC AB ==.,E F 分别为PA 和BC 的中点.(1)求证:EF 和PC 是异面直线;(2)求EF 和PC 所成的角.7. 如图,在三棱锥A BCD -中,,,,E F G H 分别是,,,AB BC CD DA 的中点.(1) 求证:四边形EFGH 是平行四边形;(2) 若AC BD =,求证:四边形EFGH 是菱形;(3) 当AC 与BD 满足什么条件时,四边形EFGH 是正方形.。
江苏省溧阳市戴埠高级中学高中数学11平面与平面位置关系教学案(无答案)苏教版必修2
A DBC A'D'B'C'平面与平面的位置关系--平行 教学案一、教学目标1.理解两个平面的位置关系;2.理解并掌握两个平面平行的判定定理;3.理解并掌握两个平面平行的性质定理. 二、课堂学习重点:两平面平行的判定定理和性质定理. 难点:两平面平行的判定定理和性质定理. 三、知识建构1、 两平面互相平行. 23、两平面平行的判定定理是 符号表示: .4、 公垂线5、 公垂线段6、 两平行平面间的距离,7、两平面平行的性质定理:图形表示: 符号表示:定理的证明:四、典型例题:例1、 在长方体ABCD A B C D ''''-中,求证: 平面//C DB '平面AB D ''例2、 求证:如果一条直线垂直于两个平行平面中的一个平面,那么这边垂直于另一个平面.例3、 在三棱柱ABC A B C '''-中,点D ,E 分别是BC 与B C ''的中点,求证:平面A EB '//平面ADC '例4. 如图,在正三棱柱111ABC A B C -中,点在边BC 上,1AD C D ⊥,且E 是11B C 的中点.求证:1//A E 平面1ADC五、课后复习:判断下列命题是否正确,并证明理由.(1) 若平面a 内的两条直线分别与平面b 平行,则a 与b 平行 ( ) (2) 若平面a 内有无数条直线与平面b 平行,则a 与b 平行 ( ) (3) 平行于同一条直线的两个平面平行( )A A'1A A(4) 过已知平面外一点有且只有一个平面与已知平面平行 ( ) (5) 过已经平面外一条直线,必能作出与已经平面平行的平面 ( ) (6) 两个平面分别经过两条平行直线,则这两个平面互相平行 ( ) 2、两个平面的位置关系有 3、在如下命题(1)平行于同一条直线的两个平面平行 (2)垂直于同一条直线的两个平面平行 (3)平行于同一个平面的两个平面平行 (4)垂直于同一个平面的两条直线平行 正确的是 . 4、(1)已知一个平面外的一条直线上的两点到平面的距离相等,则这条直线与这个平面位置关系是 .(2)已知平面内有三点到另一平面的距离相等,则这两个平面的们位置关系是 .5、设E ,F ,11,E F 分别是长方体1111ABCD A BC D -的棱AB ,CD ,1111,A B C D 的中点,求证:平面1//ED 平面1BF6、求证:夹在两个平行平面间的平行线段相等.(需要作出图形,写出已知,求证)7、已知平面a 、b 、直线l 、且//a b ,l b ⊄,//l a 求证://l b1A A8、在正方体1111ABCD A BC D -中,E ,F ,G 分别是BC ,11B C ,AD 的中点. (1)求证:平面//BFG 平面1EC D ;(2)求证:1D ∈平面BFG .。
江苏省溧阳市戴埠高级中学高中数学24空间直角坐标系及空间两点间距离学案(无答案)苏教版必修2
空间直角坐标系及空间两点间距离学案班级_________ 学号_____________ 姓名______________ 学习目标1.经历运用空间直角坐标系来描述空间图形的过程,初步建立数感和空间感;2.通过类比的思想让学生得出空间直角坐标系的定义、建立方法以及空间点的坐标确定方法;3.通过类比思想掌握空间两点间的距离公式,并理解公式使用的条件;4.会用空间两点间的距离公式计算和证明,通过综合运用公式提高分析和解决问题的能力。
课前准备1.复习平面直角坐标系中表示点的方法 ____________________________2.复习平面直角坐标系中两点间距离公式_3.复习平面直角坐标系中中点坐标公式 _______________________________课堂学习一、重点难点重点:空间直角坐标系的建立;通过表示特殊长方体顶点的坐标,探索空间两点间的距离公式•难点:根据点的位置表示出点的坐标;空间两点间的距离公式的推导及其应用二、知识建构新知1:空间直角坐标系的含义从空间某一个定点0引三条________________________________ 数轴,这样就建立了空间直角坐标系O xyz .点0叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为_____________________________ 新知2:右手直角坐标系的含义在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向, 若中指指向z轴的正方向,则称这个坐标系为右手直角坐标系新知3:空间直角坐标系的画法1.x轴与y轴、x轴与z轴均成_—而z轴______________ y轴.2.y轴与z轴的单位长度 ______ , x轴上的单位长度______新知4:空间任意一点的坐标的含义对于空间任意一点A作点A在三条坐标轴上的, 即经过点A作三个平面分别______ 于x轴、y轴和z轴,它们与x轴、y轴和z轴分别交于P,Q, R点,点P,Q, R在相应数轴上的坐标依次为x,y,z,我们把有序实数组(x, y,z)叫做点____________ ,记为新知5:空间任意两点A(x-|, y1,z1), B(x2, y2, z2)间的距离 _____________________________ 新知6:已知点A(x1, y1, z!), B(x2, y2,z2),则线段AB中点C的坐标是 _______________三、典型例题例1.在空间直角坐标系中,作出点 5,4,6例2.如图,已知长方体 ABCD ABCD 的边长为AB 12, AD 8, AA 5.以这个长方学习反思1:在空间直角坐标系中,x 轴上的点、xOy 坐标平面内的点的坐标各有什么特点?例3 .( 1)在空间直角坐标系 O xyz 中,画出不共线的3个点 P,Q, R ,使得这3个点的坐 标都满足z 3,并画出图形。
江苏省溧阳市戴埠高级中学高中数学12平面与平面位置关
D B'C'D'A'ACB 平面与平面的位置关系--垂直 学案班级 学号 姓名一、教学目标1.了解二面角、二面角的平面角等相关概念;2.会在正方体、长方体中直接求出一些二面角的大小;3.理解和掌握面面的垂直的判定和性质定理.二、课堂学习1.二面角: .2.二面角的平面角: . 3.直二面角: .4.平面与平面垂直: .三、知识建构1、平面与平面垂直的判定定理.图形: 符号:2、平面与平面垂直的性质定理.图形: 符号:证明:四、典型例题 例1、 在正方体ABCD A B CD '''-中.(1) 求二面角D AB D '--的大小; (2) 求二面角A AB D '--的大小.D B 1C 1D 1A 1A CB 例2、 在正方体ABCD A BCD ''''-中,求证:平面A C CA ''⊥平面B D DB ''.例3、 求证:如果两个平面互相垂直,那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内.例4、 在正方体1111ABCD A BC D -中,求二面角1C BD C --的正切值.五、课后复习1、 判断下列命题是否正确,并说明理由A 1(1) 若αγ⊥,βγ⊥,则//αβ. (2) 若αβ⊥,βγ⊥,则αγ⊥.(3) 若1//αα,1//ββ,αβ⊥,则11αβ⊥.(4) 若平面α内的两条相交直线分别平行平面β内的两条相交直线,则//αβ. (5) 若两个平面分别经过两条平行直线,则这两个平面互相平行. (6) 已知平面外的一条直线上有两个点到这个平面距离相等,则这条直线与该平面平行. (7) 已知平面α内有三个点到另一个平面的距离相等则两个平面平行.2、 如图、,αβ,γ平面,l αβ=,a αγ= , b βγ=,l γ⊥,指出图中哪个角是二面角l αβ--的平面角 .3、如果一个二面角的两个半平面与另一个二面角的两个半平面互相垂直,则有关这个二面角的大小关系,下列说明正确的是 . ①相等 ② 互补 ③相等或互补 ④无法确定4、α,β是两个不同的平面,m ,n 是平面α及β之外的两条不同的直线,给出四个论断① m n ⊥ ② αβ⊥ ③ n β⊥ ④ m α⊥,以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确一个命题 .5、已知正方形1111ABCD A BC D -,求证:平面1B AC ⊥平面11B BDD .6、在四棱锥P ABCD -中,若PA ⊥平面ABCD ,且四边形ABCD 是菱形. 求证:平面PAC ⊥平面PBD .A 17、如图:已知AB 是平面α的垂线,AC 是平面α的斜线.CD α⊂,CD AC ⊥. 求证:平面ABC ⊥平面ACD .8、在正方体1111ABCD A BC D -中E 为1DD 的中点,求证:平面EAC ⊥平面1ABC .1。
江苏省溧水县第二高级中学高中数学 第07课时空间两直线的位置关系1教学案 苏教版必修2
总 课 题 点、线、面之间的位置关系总课时 第7课时 分 课 题空间两条直线的位置关系分课时第1课时教学目标 了解空间中两条直线的位置关系;理解并掌握公理4;理解并掌握等角定理. 重点难点 公理4及等角定理. 引入新课1.问题1:在平面几何中,两直线的位置关系如何?问题2:没有公共点的直线一定平行吗?问题3:没有公共点的两直线一定在同一平面内吗?2.异面直线的概念:________________________________________________________________________. 3.空间两直线的位置关系有哪几种?位置关系共面情况公共点个数4.公理4:(文字语言)____________________________________________________.(符号语言)____________________________________________________.5.等角定理:____________________________________________________________.例题剖析例1 如图,在长方体1111D C B A ABCD -中,已知F E 、分别是BC AB 、的中点.求证:11//C A EF .例2 已知:BAC ∠和111C A B ∠的边11//B A AB ,11//C A AC ,并且方向相同.求证:111C A B BAC ∠=∠.B FD A 1B 1例3 如图:已知1E E 、分别为正方体1111D C B A ABCD -的棱11D A AD 、的中点.求证:111B E C CEB ∠=∠.巩固练习1.设1AA 是正方体的一条棱,这个正方体中与1AA 平行的棱共有( )条.A .1B .2C .3D .42.A 是BCD ∆所在平面外一点,N M ,分别是ABC ∆和ACD ∆的重心,若a BD =, 则MN =____________________.3.如果OA ∥11A O ,OB ∥11B O ,那么∠AOB 与∠111B O A 之间具有什么关系?4.已知111CC BB AA ,,不共面,且11//BB AA ,11BB AA =,11//CC BB ,11CC BB =. 求证:ABC ∆≌111C B A ∆.课堂小结了解空间中两条直线的位置关系;理解并掌握公理4;理解并掌握等角定理. 课后训练班级:高一()班某某:____________一 基础题1.若把两条平行直线称为一对,则在正方体12条棱中,相互平行的直线共有_______对.BC ED A 1E 1B 1B1ABCC 12.已知AB ∥PQ ,BC ∥QR ,∠︒=30ABC ,则∠PQR 等于_________________. 3.空间三条直线c b a 、、,若c b b a ////,,则由直线c b a 、、确定________个平面. 二 提高题4.三棱锥BCD A -中,H G F E ,,,分别是DA CD BC AB ,,,的中点. (1)求证:四边形EFGH 是平行四边形;(2)若BD AC =,求证:四边形EFGH 是菱形;(3)当AC 与BD 满足什么条件时,四边形EFGH 是正方形.5.在正方体1AC 中,CF F A CE E A ==1111,,求证:11F E ∥EF .三 能力题6.已知H G F E 、、、分别是空间四边形四条边DA CD BC AB 、、、上的点. 且2==HDAHEB AE ,G F 、分别为CD BC 、的中点,求证:四边形EFGH 是梯形.A 1 D 1 C 1BFCG DH EA7.已知三棱锥BCD A -中,H G F E ,,,是DA CD BC AB ,,,的中点,43==FH EG ,,求22BD AC +.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间两条直线的位置关系(1)学案
班级 __________ 学号 ______________ 姓名_______________ 学习目标
(1)了解空间中两条直线的位置关系,培养学生的作图能力和空间想象能力;
(2)理解并掌握公理4及等角定理,培养学生将空间问题转化为平面问题的能力和逻辑思维能力.
课堂学习
一、重点难点
重点:异面直线的概念;公理4及等角定理.
难点:公理4及等角定理的应用.
二、建构数学
问题一:长方体ABCD A, B1C1D1的棱AA i ,与棱AB和
BB i所在直线的位置关系;棱AA与棱CD所在的直线位
护¥方
异面直线的概念:______________________________________________________
注意:不要把异面直线误解为:分别在不同平面内的两条直线为异面直线
位置关系
共面关系公共点个数
问题二:观察长方体ABCD A1B1C1D1, AA1 _________________ BB1 , BB1 CC1,贝U AA
CC1.
公理4 : ____________________________________________
符号表示:
公理4即______________________ ,这个性质在平面、空间都适用•
公理4作用:_______________________________________________
观察例1中的BEF和B1^C1的两边____________________ ,大小关系是
猜想:__________________________________________________________________________________
推导证—
A —
-<7
A _
B 思考:若定理中将“方向相同”这一条件去掉,会有什么样的结论?
三、数学应用
例1.如图,在长方体ABCD A1B1C1D1中,已知E,F分别是AB,AC的中点.求证: EF //AC1
变式训练:已知空间四边形ABCD,E,F,G,H分别是边AB, BC,CD,DA的中点,求证: 四边形EFGH是平行四边形
例2.如图.已知E,E1分别为正方体ABCD A1B1C1D1的棱AD,A1D1的中点,求证:
C1 E-i B-i CEB .
课后复习
1.设AA i是正方体的一条棱,这个正方体中与AAi 平行的棱有条.
2.①对于不重合的三条直线a,b,c,若a//b, b//c,则a,c可确定一个平面;②空间中,
过直线外一点可作多条直线与这条直线平行;③垂直于同一条直线的两条直线平行;④四条
边均相等的四边形是平面图形.上述命题正确的序号有
3.①没有公共点的两条直线是平行直线;②两条直线不相交就平行;③两条直线有既不相
交又不平行的情况;④一条直线和两条相交直线中的一条平行,它也可能和另一条平行.期中正确的是
4.如果角和角的两边分别平行,50°,贝U .
5.如图在一个长方体木块的AC i面上有一点P,过P点画一
直线和棱CD平行,应怎样画?____________ . ________ 若要求过P
点画一直线和BD平行,应怎样画?
6.已知:棱长为a的正方体ABCD A i B i C i D i中,M,N分别为GD i,A,D i的中点,求证:四边形MNAC 是梯形.
D
A B
0) M
8
7.如图,在正方体 ABCD A 1B 1C 1D 1中,E,F,G 分别为棱CC i , BB i , DD i 的中点,
证明: BFC GD 1E .
R
1
邑
■。
