四格表卡方计算表
卡方检验含四格表x平方检验[优质内容]
![卡方检验含四格表x平方检验[优质内容]](https://img.taocdn.com/s3/m/bfb3930984868762cbaed549.png)
10.8
高级培训
11
用基本公式计算卡方值:
2
(20
25.8)2
(24 18.2)2
(2115.2)2
(5
10.8)2
25.8
18.2
15.2
10.8
8.40
高级培训
12
四格表卡方检验的专用公式:
2
(ad bc)2n
1
(a b)(a c)(b d )(c d )
高级培训
13
3、查界值表,确定P值,做出推断结论 自由度=1,Χ20.05(1)=3.84, Χ2> Χ20.05(1), 所以 , P<0.05,在α=0.05的检验水准下,拒绝H0, 差异有统计 学意义,也就是试验组与对照组的总体有效率不等.
3.查χ2界值表,确定P值,做出推断结论
υ=2, χ20.05(2)=5.99, χ2 > χ20.05(2),则P<0.05,在α=0.05的水 准下,拒绝H0,可以认为三种治疗方案的有效率有差别。
高级培训
34
例8.6 某研究人员收集了亚洲、欧洲和北美洲人的A、B、 AB、O血型资料,结果见下表,其目的是研究不同地区 的人群血型分类构成比是否一样。
若H0成立,两种属性不一致的两个格子理论频数都应该是 (b+c)/2
高级培训
24
配对检验公式推导:
bc
(+,)和(,+)两个格子中的理论频数均为
2
b c 40 时
2
(AT)2
(b b c )2 2
(c b c)2 2
T
bc
bc
2
2
(b c)2
~ 2 分布
四格表资料的卡方检验excell计算模板(2011.11.8 赵建军)
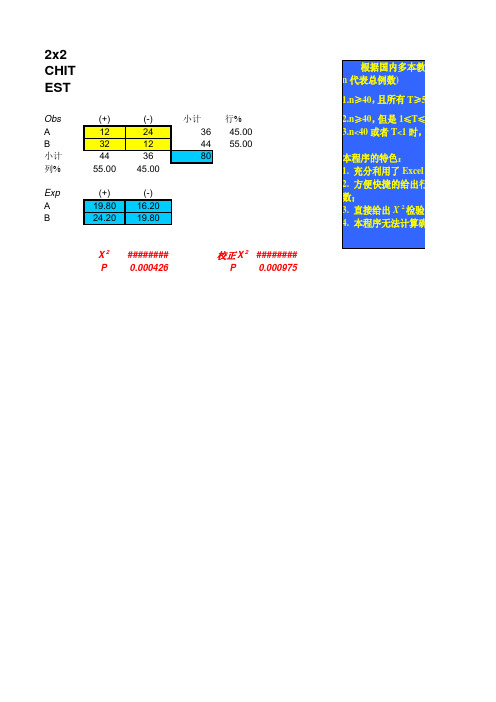
的特色: 利用了 Excel 的特点,只需在四格表内填入数字即可完成所有操作; 快捷的给出行、列小计,行与列的率或构成比,总例数及理论频数等各项参
给出 X 2 检验(包括校正)的统计量和 P 值; 序无法计算确切概率。
1.n≥40, 且所有 T≥5 时用 X 2 检验的
2.n≥40, 但是 1≤T≤5 时, 用连续性 3.n<40 或者 T<1 时,不能用 X 2 检验6
校正 X 2 ########
P 0.000975
本程序的特色: 1. 充分利用了 Excel 的特点,只需在 2. 方便快捷的给出行、列小计,行 数; 3. 直接给出 X 2 检验(包括校正)的 4. 本程序无法计算确切概率。
2x2 CHITEST
Obs A B 小计 列% Exp A B (+) 12 32 44 55.00 (+) 19.80 24.20 (-) 24 12 36 45.00 (-) 16.20 19.80 小计 36 44 80 行% 45.00 55.00
根据国内多本教科书介绍,四格 n 代表总例数)
据国内多本教科书介绍,四格表分类资料统计方法的选择:(T 代表理论频数, 例数)
, 且所有 T≥5 时用 X 2 检验的基本公式, 若 P ≈α时改用 Fisher 确切概率法;
, 但是 1≤T≤5 时, 用连续性校正的 X 2 检验(Yates’ correction for continuity); 或者 T<1 时,不能用 X 2 检验,改用 Fisher 确切概率法。
卡方检验

a. 0 cells (.0%) have expected count less than 5. T he minimum expected count is 37.88.
AREA * BL OOD Crosstabulation BLOOD A AREA 亚洲 Count Expected Count % within AREA Count Expected Count % within AREA Count Expected Count % within AREA 321 379.4 29.7% 408 349.6 41.0% 729 729.0 35.1% B 369 247.2 34.2% 106 227.8 10.7% 475 475.0 22.9% AB 95 68.7 8.8% 37 63.3 3.7% 132 132.0 6.4% O 295 384.6 27.3% 444 354.4 44.6% 739 739.0 35.6% Total 1080 1080.0 100.0% 995 995.0 100.0% 2075 2075.0 100.0%
合计
11
36
15
27
26
53
11+2<40,使用校正公式计算卡方统计量
建立数据库
设立三个变量:jia、yi、weight jia代表甲法:+赋值为1,-赋值为0 yi代表乙法:+赋值为1,-赋值为0 Weight代表例数
对数据加权
配对卡方检验
Case Processing Summary Cases Missing N Percent 0 .0%
204(a+b)
64(c+d)
12.75
3.13
四格表卡方检验

四格表确切概率法的基本思想
在四格表周边合计固定不变的条件下,改 变某一格子的实际频数,列出a、b、c、d各种 组合的四格表,按公式8-9计算每个四格表的概 率,然后计算单侧或双侧累积概率,并与检验 水准α比较,作出是否拒绝H0的结论。
P (a b)!(c d )!(a c)!(b d )! a! b! c! d ! n!
第13页/共42页
例8-1 用专用公式 计算 2 值:
2 (271 26 5 74)2 376 56.77 , df 1
276100 345 31
查
2界
值
表
,
2 0.05,1
3.84
下结论:
2
2 0.05,1
3.84;
P 0.05,按 0.05水准,
拒
绝H
,
0
接
受H
,
1
可
以
认
为
疗
效
四格表确切概率法系英国统计学家fisher于1934年提出又称fisher精切概率法fiserexacttest在四格表周边合计固定不变的条件下改变某一格子的实际频数列出abcd各种组合的四格表按公式89计算每个四格表的概率然后计算单侧或双侧累积概率并与检验水准比较作出是否拒绝h组别改善无效合计红花散1520安慰剂1417181937例83研究中药制剂红花散改善周围血管闭塞性病变患者的皮肤微循环状况以安慰剂作对照将37个病例随机分到两组结果如表85分析红花散的疗效
第6页/共42页
一、卡方检验的基本思想
例8-1 对表8-1资料推断两药的疗效有无差别
H0:
1
,即两药总体有效率相等
2
由于总体有效率未知,将两组数据合并,计算合并
x2检验或卡方检验和校正卡方检验的计算

x2检验或卡方检验和校正卡方检验的计算x2检验(chi-square test)或称卡方检验x2检验(chi-square test)或称卡方检验,是一种用途较广的假设检验方法。
可以分为成组比较(不配对资料)和个别比较(配对,或同一对象两种处理的比较)两类。
一、四格表资料的x2检验例20.7某医院分别用化学疗法和化疗结合放射治疗卵巢癌肿患者,结果如表20-11,问两种疗法有无差别?表20-11 两种疗法治疗卵巢癌的疗效比较组别有效无效合计有效率(%)化疗组19 24 43 44.2 化疗加放疗组34 10 44 77.3合计53 34 87 60.9表内用虚线隔开的这四个数据是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2行2列表(2×2 contingency table)从该资料算出的两种疗法有效率分别为44.2%和77.3%,两者的差别可能是抽样误差所致,亦可能是两种治疗有效率(总体率)确有所不同。
这里可通过x2检验来区别其差异有无统计学意义,检验的基本公式为:式中A为实际数,以上四格表的四个数据就是实际数。
T为理论数,是根据检验假设推断出来的;即假设这两种卵巢癌治疗的有效率本无不同,差别仅是由抽样误差所致。
这里可将两种疗法合计有效率作为理论上的有效率,即53/87=60.9%,以此为依据便可推算出四格表中相应的四格的理论数。
兹以表20-11资料为例检验如下。
检验步骤:1.建立检验假设:H0:π1=π2H1:π1≠π2α=0.052.计算理论数(TRC),计算公式为:TRC=nR.nc/n 公式(20.13)式中TRC是表示第R行C列格子的理论数,nR为理论数同行的合计数,nC为与理论数同列的合计数,n为总例数。
第1行1列: 43×53/87=26.2第1行2列: 43×34/87=16.8第2行1列: 44×53/87=26.8第2行2列: 4×34/87=17.2以推算结果,可与原四项实际数并列成表20-12:表20-12 两种疗法治疗卵巢癌的疗效比较因为上表每行和每列合计数都是固定的,所以只要用TRC式求得其中一项理论数(例如T1.1=26.2),则其余三项理论数都可用同行或同列合计数相减,直接求出,示范如下:T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算x2值按公式20.12代入4.查x2值表求P值在查表之前应知本题自由度。
x2检验或卡方检验和校正卡方检验的计算

x2检验或卡方检验和校正卡方检验的计算x2检验(chi-square test)或称卡方检验x2检验(chi-square test)或称卡方检验,是一种用途较广的假设检验方法。
可以分为成组比较(不配对资料)和个别比较(配对,或同一对象两种处理的比较)两类。
一、四格表资料的x2检验例20.7某医院分别用化学疗法和化疗结合放射治疗卵巢癌肿患者,结果如表20-11,问两种疗法有无差别?表20-11 两种疗法治疗卵巢癌的疗效比较表用虚线隔开的这四个数据是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2行2列表(2×2 contingency table)从该资料算出的两种疗法有效率分别为44.2%和77.3%,两者的差别可能是抽样误差所致,亦可能是两种治疗有效率(总体率)确有所不同。
这里可通过x2检验来区别其差异有无统计学意义,检验的基本公式为:式中A为实际数,以上四格表的四个数据就是实际数。
T为理论数,是根据检验假设推断出来的;即假设这两种卵巢癌治疗的有效率本无不同,差别仅是由抽样误差所致。
这里可将两种疗法合计有效率作为理论上的有效率,即53/87=60.9%,以此为依据便可推算出四格表中相应的四格的理论数。
兹以表20-11资料为例检验如下。
检验步骤:1.建立检验假设:H0:π1=π2H1:π1≠π2α=0.052.计算理论数(TRC),计算公式为:TRC=nR.nc/n 公式(20.13)式中TRC是表示第R行C列格子的理论数,nR为理论数同行的合计数,nC为与理论数同列的合计数,n为总例数。
第1行1列: 43×53/87=26.2第1行2列: 43×34/87=16.8第2行1列: 44×53/87=26.8第2行2列: 4×34/87=17.2以推算结果,可与原四项实际数并列成表20-12:表20-12 两种疗法治疗卵巢癌的疗效比较因为上表每行和每列合计数都是固定的,所以只要用TRC式求得其中一项理论数(例如T1.1=26.2),则其余三项理论数都可用同行或同列合计数相减,直接求出,示如下:T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算x2值按公式20.12代入4.查x2值表求P值在查表之前应知本题自由度。
卡方检验

2
3.03 ,
=1
2<3.84=2
按 =0.05 水 准 , 不 拒 绝 H0, …
配对四格表资料的 检验
2
也称McNemar检验(McNemar's test)
例 6-8 表 6-9
甲 法
两种血清学检验结果比较
乙 法 + - 10 (b) 11 (d) 21 90 42 132 合计
n2 n2 n
一般地,
理论频数
n n (行合计)(列合计) = R C 总计 n
例题:计算以下四格表的各理论频数: (1) (2) 35 27 25 8 16 33 15 22
2 检验的基本思想可通过其基本公式来解释:
2
观察值 理论值
理论值
2
A T 2
2
1
2
( / 21)
e
2 / 2
Ý ß ×·
×Ó ¶ £ 1 Ô É È ½
0.2 0.1 0.0 0 3
3.84
×Ó ¶ £ 2 Ô É È ½ ×Ó ¶ £ 3 Ô É È ½ ×Ó ¶ £ 6 Ô É È ½
P=0.05的临界值
7.81 12.59
6
9 12 ¿ ·Ö ¨½ µ
* 图形:单峰,正偏峰; 自由度 很大时, 近似地服从正态分布.有 2 ( ) 2 Z , ( )服从均数为 ,方差为2 的正态分布 2
2 ( )
χ2分布(chi-square distribution)
0.5 0.4 0.3
f ( ) 2( / 2) 2
2
2 =2.734<3.84,P>0.05,不拒绝无效假设H0
统计方法卡方检验

卡方检验用途:可以对两个率或构成比以及多个率或构成比间的差异做统计学检验第一节. 四格表资料的χ2检验例8.1 为了解铅中毒病人是否有尿棕色素增加现象,分别对病人组和对照组的尿液作尿棕色素定性检查,结果见表8.1,问铅中毒病人和对照人群的尿棕色素阳性率有无差别?表8.1 两组人群尿棕色素阳性率比较组别阳性数阴性数合计阳性率%病人29(18.74) 7(17.26) 36 80.56对照9(19.26)28(17.74) 37 24.32合计38 35 73 52.05卡方检验的基本思想表1中29、7、9、28是构成四格表资料的四个基本格子的数字,其余行合计和列合计以及总的合计都可以根据该四个数字推算出来,故该类资料被称为四格表资料四格表卡方检验的步骤以例8.1为例1.建立假设:H0:π1 = π2H1:π1≠π2α=0.05四格表的四格子里的数字是实际数,在表1中四个数字旁边括号中的四个数字为理论数,其含义是当无效假设成立的时候,理论上两组人群各有多少阳性和阴性的人数。
若H0:π1=π2成立→p1=p2=p即假设两组间阳性率无差别,阳性率都是等于合计的52.05%,那么铅中毒病人36人,则理论上有36 ╳52.05%=18.74人为阳性;对照组37人,则理论上有37 ╳52.05%=19.26人为阳性。
故每个实际数所对应的理论数算法是,该实际数对应的行和乘列和再除以总的N样本含量。
即TRC=nR nC / n2.计算理论数第1行1列: T11=36×38/73= 18.74依次类推T12 = 17.26T21 = 19.26T22 = 17.74四格表中理论数的两大特征:(1)理论频数表的构成相同,即不但各行构成比相同,而且各列构成比也相同;(2)各个基本格子实际数与理论数的差别(绝对值)相同。
一、卡方检验基本公式A: 实际数 T: 理论数卡方检验的基本思想是看理论数与实际数的吻合程度上述公式中卡方统计量的大小取决于实际数和理论数的相差大小情况,如果无效假设成立的话,那么实际数和理论数不应该相差过大,所以卡方统计量应该较小,而如果卡方统计量越大,则越有可能推翻无效假设而得出有统计差异的结论。
