第五章 递归函数论
5 函数(递归部分)

递归深度 0(主程序) 1 2 3 4 5 6
f(n) f(6) f(6)=6×f(5) f(5)=5×f(4) f(4)=4×f(3) f(3)=3×f(2) f(2)=2×f(1) f(1)=1×f(0) f(0)=1 (返回) [递推阶段]
2.递归过程 递归过程
6×120=720 5×24=120 4×6=24 3×2=6 2×1=2 1×1=1
当n>=3 >
long fib(long n) 请分析该问题是否可以用递归算法解决? 请分析该问题是否可以用递归算法解决? { 若可以,请写出该递归算法。 若可以,请写出该递归算法。 if(n==1 || n==2) return n; else return fib(n-2)+fib(n-1); }
15
三、递归问题举例
一、汉诺塔问题 传说印度布拉马圣殿( 传说印度布拉马圣殿(Temple of Brahma)的教 ) 士们有一黄铜烧铸的平台, 士们有一黄铜烧铸的平台,上立三根金刚石柱 柱上堆放了64个金盘子 子。A柱上堆放了 个金盘子,每个盘子都比 柱上堆放了 个金盘子, 其下面的盘子略小一些。 其下面的盘子略小一些。当教士们将盘子全部 柱移到C柱以后 从A柱移到 柱以后,世界就到了末日。当然, 柱移到 柱以后,世界就到了末日。当然, 这个问题还有一些特定的条件, 这个问题还有一些特定的条件,那就是在柱子 之间只能移动一个盘子并且任何时候大盘子都 只能移动一个盘子并且 之间只能移动一个盘子并且任何时候大盘子都 不能放到小盘子上。教士们当然还在忙碌着, 不能放到小盘子上。教士们当然还在忙碌着, 因为这需要2 次移动。 因为这需要 64-1次移动。如果一次移动需要一 次移动 秒钟,那么全部操作需要5000亿年以上时间。 亿年以上时间。 秒钟,那么全部操作需要 亿年以上时间
大一c语言章节知识点

大一c语言章节知识点第一章:基本概念和数据类型C语言的历史背景C语言的特点和优势关键字和标识符数据类型及其表示范围变量的定义和声明常量的定义和分类运算符的分类和优先级第二章:运算符和表达式算术运算符和表达式逻辑运算符和表达式位运算符和表达式赋值运算符和表达式关系运算符和表达式条件运算符和表达式运算符的优先级和结合性第三章:控制语句顺序结构选择结构(if语句、switch语句)循环结构(for循环、while循环、do-while循环)循环控制语句(break、continue、goto)嵌套控制语句第四章:数组和字符串数组的定义和初始化数组的访问和操作多维数组字符数组和字符串的处理字符串的输入和输出第五章:函数和递归函数的调用和返回函数的参数传递(值传递、地址传递)递归函数的原理与应用递归和迭代的比较第六章:指针指针的定义和声明指针与数组的关系指针的运算(指针的加减、指针的比较)指针与字符串的处理函数指针和指针数组第七章:结构体和共用体结构体的定义和初始化结构体中成员的访问和操作结构体的嵌套和对齐枚举类型的定义和应用第八章:文件操作文件的打开和关闭文件的读写操作(字符型文件、二进制文件)文件指针的位置控制文件的随机访问和更新第九章:动态内存管理内存分配与释放的概念malloc函数和free函数的使用calloc函数和realloc函数的使用动态分配二维数组的操作第十章:预处理指令宏定义的使用条件编译指令的应用文件包含指令的作用错误指示和行控制指令无论是在学习C语言的过程中,还是在实际应用中,以上这些章节知识点都是非常重要的。
掌握这些知识点,将帮助你深入了解C语言的基本原理和常用功能,为编写高效、健壮的程序奠定扎实基础。
在学习过程中,请务必理解并实践每个章节的知识点,并结合实际案例进行练习和应用,以加深对C语言的理解和应用能力。
祝你在学习C语言的道路上取得优异的成绩!。
数理逻辑中的递归论研究

数理逻辑中的递归论研究数理逻辑是研究符号形式系统的一门学科,而递归论则是其中重要的分支之一。
递归论研究的是递归函数和可计算性理论,它在计算机科学以及数学领域具有重要的地位。
本文将从递归论的基本概念、递归函数以及可计算性理论等方面进行论述,以展示数理逻辑中的递归论研究的重要性和深远影响。
一、递归论的基本概念递归论是数理逻辑中研究递归函数和可计算性理论的分支。
递归函数是一种可以通过有限步骤计算得到结果的函数。
而可计算性理论则探讨的是哪些函数是可计算的,也即存在一种算法可以计算出该函数的值。
递归论的基本概念包括递归函数、图灵机以及可计算函数等。
在递归论中,递归函数是一种可以通过无限步骤的重复计算得到结果的函数。
递归函数的定义采用了递归的方式,即函数的定义中包含对函数自身的引用。
而图灵机是递归论中的重要概念之一,它是一种抽象的计算模型,可以对递归函数的计算过程进行模拟和描述。
可计算函数则是指可以通过图灵机模拟计算的函数,也即存在一种算法可以计算出该函数的值。
二、递归函数的性质和应用递归函数在递归论中具有重要的性质和广泛的应用。
首先,递归函数具有封闭性,即如果一个函数在其定义中引用了自身,则称其为递归函数。
递归函数在数理逻辑和计算机科学中有着广泛的应用,例如在数学中的斐波那契数列、计算机编程中的递归调用等。
此外,递归函数还具有可计算性和不可计算性的性质。
在递归论中,可计算函数指的是可以通过图灵机计算的函数,它们可以由递归函数表示并进行计算。
而不可计算函数则是指无法通过图灵机计算的函数,例如停机问题。
递归论对于可计算函数和不可计算函数的研究,为计算机科学中的可计算性理论奠定了基础。
三、可计算性理论的研究可计算性理论是递归论中的重要内容之一,它研究的是可计算函数的性质和计算复杂性。
在可计算性理论中,人们提出了许多重要的概念和理论,如图灵机、可计算复杂性以及不可判定性等。
图灵机是可计算性理论中的重要工具,它是一种抽象的计算模型,可以模拟和描述递归函数的计算过程。
Python语言程序设计基础(第2版)第五章答案

第5章函数和代码复用5.1 函数的基本使用[5.1]: A[5.2]: D[5.3]: 错误。
[5.4]: 合法,因为Python语言是解释执行,即只要在真正调用函数之前定义函数,都可以进行合法调用。
5.2 函数的参数传递[5.5]: 在函数定义时,直接为可选参数指定默认值。
可选参数必须定义在非可选参数后面,可选参数可以有多个。
[5.6]: 在函数定义时,可变参数通过在参数前增加星号(*)实现。
可变数量参数只能在参数列表最后,即它只能有一个。
[5.7]: 返回值是元组类型。
[5.8]: 位置传递:支持可变数量参数,但容易忘记实参的含义;名称传递:不易忘记实参的含义,但不支持可变数量参数。
[5.9]: 如果函数里没有创建同名变量,则可以直接使用,不需global声明。
5.3 模块3:datetime库的使用[5.10]:print( "现在是{0:%Y}年{0:%m}月{0:%d}日{0:%I}:{0:%M}".format(datetime.now()))[5.11]: 答案不限。
举一个例子,输出美式日期格式:print("{0:%I}:{0:%M} {0:%b} {0:%d} {0:%Y}".format(datetime.now()))[5.12]: datetime对象可以直接做加减运算,所以可以用这样的方式给程序计时:1 2 Start = datetime.now() ... # 要计时的代码4 5 6 End = datetime.now() Cost = End – Start Print(Cost)5.4 实例7:七段数码管绘制[5.13]: 相当于C语言中的三目运算符。
[5.14]: 隐藏画笔的turtle形状。
[5.15]: 对应相应的年月日文字输出。
5.5 代码复用和模块化设计[5.16]: 错误,因为”使用函数“是“模块化设计“的必要条件。
第5章递归第1讲-什么是递归

python——递归函数
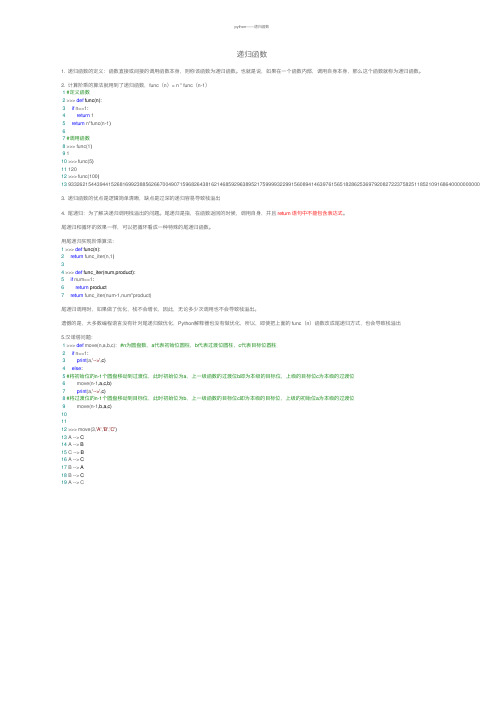
python——递归函数递归函数1. 递归函数的定义:函数直接或间接的调⽤函数本⾝,则称该函数为递归函数。
也就是说,如果在⼀个函数内部,调⽤⾃⾝本⾝,那么这个函数就称为递归函数。
2. 计算阶乘的算法就⽤到了递归函数,func(n)= n * func(n-1)1#定义函数2 >>> def func(n):3if n==1:4return 15return n*func(n-1)67#调⽤函数8 >>> func(1)9 110 >>> func(5)11 12012 >>> func(100)13 9332621544394415268169923885626670049071596826438162146859296389521759999322991560894146397615651828625369792082722375825118521091686400000000000000000003. 递归函数的优点是逻辑简单清晰,缺点是过深的递归容易导致栈溢出4. 尾递归:为了解决递归调⽤栈溢出的问题。
尾递归是指,在函数返回的时候,调⽤⾃⾝,并且 return 语句中不能包含表达式。
尾递归和循环的效果⼀样,可以把循环看成⼀种特殊的尾递归函数。
⽤尾递归实现阶乘算法:1 >>> def func(n):2return func_iter(n,1)34 >>> def func_iter(num,product):5if num==1:6return product7return func_iter(num-1,num*product)尾递归调⽤时,如果做了优化,栈不会增长,因此,⽆论多少次调⽤也不会导致栈溢出。
遗憾的是,⼤多数编程语⾔没有针对尾递归做优化,Python解释器也没有做优化,所以,即使把上⾯的 func(n)函数改成尾递归⽅式,也会导致栈溢出5.汉诺塔问题:1 >>> def move(n,a,b,c): #n为圆盘数,a代表初始位圆柱,b代表过渡位圆柱,c代表⽬标位圆柱2if n==1:3print(a,'-->',c)4else:5#将初始位的n-1个圆盘移动到过渡位,此时初始位为a,上⼀级函数的过渡位b即为本级的⽬标位,上级的⽬标位c为本级的过渡位6 move(n-1,a,c,b)7print(a,'-->',c)8#将过渡位的n-1个圆盘移动到⽬标位,此时初始位为b,上⼀级函数的⽬标位c即为本级的⽬标位,上级的初始位a为本级的过渡位9 move(n-1,b,a,c)101112 >>> move(3,'A','B','C')13 A --> C14 A --> B15 C --> B16 A --> C17 B --> A18 B --> C19 A --> C。
数据结构课件第5章递归

return fact; }
递归调用执行情况如下:
int fact (int w) {1if ( w==0) 2 fact= 1; 3else 4fact=w* fact( w-1); }
递归思路
实际上, 递归思路是把一个不能或不好直接求解 的“大问题”转化成一个或几个“小问题”来解决, 再把这些“小问题”进一步分解成更小的“小问题” 来解决,如此分解,直至每个“小问题”都可以直接解 决(此时分解到递归出口)。
但递归分解不是随意的分解,递归分解要保证“大 问题”与“小问题”相似,即求解过程与环境都相似。 并且有一个分解的终点。从而使问题可解。
假 设 f(A,i-1) 已 求 出 , 则 f(A,i)=MIN(f(A,i1),A[i]),其中MIN()为求两个值较小值函数。因 此得到如下递归模型:
A[0] 当i=0时 f(A,i)=
MIN(f(A,i-1),A[i]) 其他情况
由此得到如下递归求解算法:
float f(float A[],int i) { float m;
n!
n
1, (n 1)!,
当n 0时 当n 1时
该问题的算法为: int Fact ( int n )
{ int m; if (n= =0) return(1); else { m=n*Fact(n-1); return(m); } }
例如: 试编一个递归函数,求第n项Fibonacci级数的
} } // delete
5.3 递归算法到非递归算法的转换
递归算法有两个基本特性:一是递 归算法是一种分而治之的、把复杂问 题分解为简单问题的求解问题方法,对 求解某些复杂问题,递归算法分析问题 的方法是十分有效的;二是递归算法 的时间/空间效率通常比较差。
C语言的递归函数原理和应用场景

C语言的递归函数原理和应用场景递归是编程中一种强大而常用的技巧,尤其在C语言中,递归函数被广泛应用。
递归函数是指在函数体内调用函数本身的一种函数形式。
通过不断调用自身,递归函数能够解决一些需要重复执行的任务,使得代码更加简洁、易读、易于理解。
一、递归函数的原理递归函数的原理可以通过以下步骤来理解:1. 基本条件:递归函数中需要有一个基本条件,当满足这个条件时,递归函数将不再调用自身,结束递归。
2. 自调用:在递归函数体中,通过函数自身的调用来实现重复执行的效果。
3. 函数参数:递归函数在每次调用自身时,往往会传入不同的参数,这些参数可以决定递归的结束条件或下一次递归的运算逻辑。
4. 递归调用:递归函数在函数体内部通过调用自身来实现循环执行的效果。
二、递归函数的应用场景递归函数在编程中有许多实际应用场景,下面列举了一些常见的应用场景来说明递归函数的实用性。
1. 阶乘计算:递归函数可以非常方便地求解阶乘。
例如,对于n的阶乘可以表示为n! = n * (n-1)!,其中(n-1)!可以通过递归函数来计算。
2. 斐波那契数列:斐波那契数列是一个经典的递归问题。
数列中的每个数都是前两个数的和,即fib(n) = fib(n-1) + fib(n-2)。
通过递归函数可以很容易地计算出斐波那契数列的值。
3. 文件系统遍历:递归函数可以用来遍历文件系统中的目录结构。
通过递归调用函数来进入子目录,逐层遍历文件和文件夹,实现对整个文件系统的扫描。
4. 数据结构操作:递归函数也可以用于对各种数据结构的操作。
比如,针对树形结构的遍历、查找等操作,递归函数能够更加简洁地实现。
5. 图算法:在图算法中,递归函数常用于深度优先搜索(DFS)的实现。
通过递归调用函数,可以遍历图的各个节点,查找目标节点,或者找到所有可能的路径。
总结:递归函数是一种基于函数自身调用的编程技巧,通过重复调用自身,递归函数能够解决一些需要重复执行的任务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
迭乘算子:取A为乘法,将An+1记为
x n
f ( x) f (0) f (1) f (n)
xn
二、原始递归式
标准形式: (1) 不含参数的原始递归式的标准形式 (2) 含参数的原始递归式的标准形式
例(递归式) 阶乘函数
1 n! n(n 1)!
当n 0 当n 1
(1) 不含参数的原始递归式
g (0) a g (n 1) B(n, g (n))
其中,a为一常数,B(x,y)为已知函数。
阶乘函数n!
1 n! n(n 1)!
不含参数的原始递归式表示:
g (0) 1 g (n 1) (n 1)n! (n 1) g (n) SI21 (n, g (n)) I 22 (n, g (n)) B(n, g (n))
✘
y
其中, a为常数。
迭置法
定义:设新函数在某一变元处的值与诸旧函数的 n个值有关,如果n不随新函数的变元组的 变化而变化,则称该新函数是由旧函数利 用迭置而得。
一、(m,n)标准迭置
定义:设有一个m元函数f(y1,…,ym),有m个n元函数
g1(x1,…,xn)、 … … 、gm(x1,…,xn), 令:
a 4
二、凑合定义法
假设数论语句A1、A2、…、Ak, 对任何一个变元组
(X1,X2,…,Xn),有且仅有一个语句Ai成立。
令:
f1 ( x1 , x n ) f 2 ( x1 , x n ) h( x 1 , x n ) f ( x , x ) n k 1 当A1 (x1 , x n )为真 当A 2 (x1 , x n )为真 当A k (x1 , x n )为真
h2(x1,x2)=S2OI22(x1,x2)
h3(x1,x2)=g (I22(x1,x2))
故函数h(x1,x2)是由函数h1、h2、h3对f作 (3,2)迭置而得。
例
下面的迭置化为(m,n)标准迭置:
h(x1,x2,x3)=f(3,g1(x1,2),g2(x1,x2),x3)
解:h(x1,x2,x3)=f(h1,h2,h3,h4)
h(x1,…,xn)=f(g1,…,gm)
称之为(m,n)标准迭置。
并称函数h是由m个g对f作(m,n)迭置而得, 简记为:
h= f(g1,…,gm)
例
下面的迭置化为(m,n)标准迭置:
h(x1,x2)=f(x1,2,g(x2))
解:h(x1,x2)=f(h1,h2,h3)
其中,
h1(x1,x2)=I21(x1,x2)
若把A(x,y)固定,而把函数f(x)看作为被改造函数, 则称g(n)是由旧函数f(x)利用迭函算子A而得。
迭函算子
g(0)=f(0) g(n+1)= A g(n)f(n+1)
g(n)
A
g(n+1)
f(n+1)
迭加算子、迭乘算子
迭加算子:取A为加法,将An+1记为
xn
x n
f ( x) f (0) f (1) f (n)
当n 0 当n 1
其中,函数B(x,y)为 ×(SI21,I22),是已知函数。 书上少S,这里假定乘法×已定义
(2)含参数的原始递归式
g (u1 , u 2 ,, u k ,0) A(u1 , u 2 ,, u k ) g (u1 , u 2 ,, u k , n 1) B(u1 , u 2 ,, u k , n, g (u1 , u 2 ,, u k , n))
二、原始递归函数的构造过程
原始递归函数的例子:
f(x,y)=x+y
f(x,y)=xy f(x,y)= min(x,y) f(x,y)= max(x,y) f(x, y)= x y
f(x)=Nx
f(x)=rs(x,2)
f(x)=D(x)
f(x,y)=x y
例 (p58)试用凑合定义法定义函数lm(x,3),并 把它化为迭置。
解:
x lm( x,3) 3x
当x为3的倍数 当x不为3的倍数
根据凑合定义法知: lm(x,3)= xNct(x为3的倍数)+3xNct(x不为3的倍数) = xN(N2 rs(x,3))+3x N (N rs(x,3)) = xN3rs(x,3)+3x N2 rs(x,3) = xNrs(x,3)+3x N2 rs(x,3) = xNrs(x,3)+xN2 rs(x,3)+2 x N2rs(x,3) = x+2 x N2 rs(x,3)
2
第五章 递归函数论
5.1 数论函数和数论谓词 5.2 函数的构造 5.2.1 迭置法 5.2.2 算子法 5.2.3 原始递归函数
5.2.2 算子法
定义:设新函数在某一变元组处的值与诸旧函
数的n 个值有关,如果n 随新函数的变元
组的变化而变化,则称该新函数是由旧
函数利用算子而得。
一、迭函算子
其中, A(u1,u2, …,uk)、B(u1,u2,…,uk,x,y)为已知函数。
第五章 递归函数论
5.1 数论函数和数论谓词 5.2 函数的构造 5.2.1 迭置法 5.2.2 算子法 5.2.3 原始递归函数
一、原始递归函数的构造方法
(1) 本原函数为原始递归函数;
(2) 对已建立的原始递归函数使用迭置而得的 函数仍为原始递归函数; (3) 对已建立的原始递归函数使用原始递归式 而得的函数仍为原始递归函数。 原始递归函数——由本原函数出发,利用迭置和 原始递归式而得的函数。
例 将下列凑合定义化为迭置
f ( x1 ), h ( x1 , x 2 ) g( x 2 ), 当x1 x 2时, 当x1 x 2时。
h ( x1 , x 2 ) f(x1 )Nct(x 1 x 2 ) g (x 2 )Nct(x 1 x2) f(x1 )Nct(x2 x1 0) g(x 2 )Nct(x x 2 0) 1 1 f(x1 )NN (x 2 x1 ) g (x 2 )NN (x1 1 x2 ) f(x1 )N(x2 x1 ) g (x 2 )N(x1 1 x2 )
其中,
h1(x1,x2,x3)=S3OI31(x1,x2,x3) h2(x1,x2,x3)=g1(I31(x1,x2,x3),S2OI32(x1,x2,x3)) h3(x1,x2,x3)=g2(I31(x1,x2,x3),I32(x1,x2,x3)) h4(x1,x2,x3)=I33(x1,x2,x3)
g(f(x))
f(g(x)) h(f(x), g(x)) h(f1(x),f2(x)) ……
——函数的迭置(合成)
迭置与非迭置的例子
设有函数S(x), S2(x)=S(S(x)), S3(x)=S(S(S(x))), …… 考察:
a
✔ S (x)=S(S(… (S(x)) … )
a
考察:
Sy(x)=S(S(… (S(x)) … )
2 2
例 将下列凑合定义化为迭置
f ( x1 ), h ( x1 , x 2 ) g( x 2 ), 当x1 x 2时, 当x1 x 2时。
h ( x1 , x 2 ) f(x1 )Nct(x 1 x 2 ) g (x 2 )Nct(x 1 x2 ) f(x1 )Nct(x x 2 0) g(x 2 )Nct(x x 2 0) 1 1 f(x1 )NN2 (x1 x 2 ) g(x 2 )NN(x1 x2 ) f(x1 )N(x1 x 2 ) g(x 2 )N (x1 x2 )
例 (p60) f(x,y)=x+y
f(x,y) 可用含参数x的原始递归表示如下:
f ( x,0) x f ( x, y 1) x y 1 f ( x, y) 1 SI33 ( x, y, f ( x, y )) B( x, y, f ( x, y))
其中,B=SI33为函数的迭置。
例
f(x,y)=xy
可用原始递归表示如下:
f ( x,0) 0 f ( x, y 1) xy x f ( x, y) x B( x, y, f ( x, y))
其中,B为+(I33,I31),它为函数的迭置。
例(p60)
f (n) g ( x)
故函数h(x1,x2,x3)是由函数h1、h2、h3、h4
对f作(4,3)迭置而得。
例
下面的迭置化为(m,n)标准迭置:
h(x1,x2,x3)=f(3,g1(x1,2),g2(x1,x2),x3)
解:h(x1,x2,x3)=f(h1,h2,h3,h4)
其中,
h1(x1,x2,x3)=S3OI31(x1,x2,x3) h2(x1,x2,x3)=g1(I31(x1,x2,x3),S2OI32(x1,x2,x3)) h3(x1,x2,x3)=g2(I31(x1,x2,x3),I32(x1,x2,x3)) h4(x1,x2,x3)=I33(x1,x2,x3)
f ( x) rs( x,2)
可用原始递归表示如下:
f (0) rs(0,2) 0 f ( x 1) rs( x 1,2) Nrs ( x,2) Nf ( x) B( x, f ( x))
书上错 f(x+1,2)
其中,B=N I22。
例
f(x)=Nx
故函数h(x1,x2,x3)是由函数h1、h2、h3、h4
对f作(4,3)迭置而得。
