计量型统计过程控制
什么是SPC?怎么用SPC?

什么是SPC?怎么⽤SPC?1- What:什么是SPCSPC:统计过程控制SPC说到底,就是⼀个图表,把⽣产过程中的数据,收集起来⽤图表的形式展现出来。
它的作⽤可以⼤致总结为:⽅便⼤家从图表中,找出有异常的数据。
跟进数据趋势,预见异常发⽣的可能。
数据异常后,做出相应的改善对策SPC中有8种图表,根据不同的场景,使⽤不同的图表。
但是需要说明的是,这些图⽚都长的⼀样:是的,都长成上⾯这个样⼦。
当我花了两个星期,跟吃屎⼀样,把SPC⼿册啃完,画出那8个图之后,也发出了同样的感叹:卧草,都TM⼀样的,不就是个趋势图嘛!当然,趋势图也是数据统计,所以也可以看做是SPC的⼀种实现⽅法。
SPC本质上就是⼀种特殊的趋势图,不过SPC给他们起来⼀个更有⽓质的名字:控制图。
当然了,控制图还要和普通的趋势图有差异的,具体表现为以下⼏点:1. 控制图都有上下控制线和中⼼线,UCL和LCL(具体会在6-How⾥⾯说明)2. 控制图的数据收集规则、数据分析的规则,更加的繁琐,更加的严格3. 控制图⼀定要有相应的改善输出恩,SPC就是这么⼀个玩意⼉。
需要说明的是,SPC和标准值没有关系,没有标准值也是可以做SPC控制图的。
2- Why:为什么要⽤SPC说实话:都TM是客户要求的,是⽼板要求。
(当我们是⼯程师的时候,都是这么想的)说假话:为了及时发现⽣产过程中,由特殊原因导致的异常,及时改善。
为了深⼊分析系统中的普通原因,进⼀步提⾼产品品质,为客户提供更好的产品。
(当成为⼀个⼯⼚的品质副总时,如何将⼀线数据浮上来,你会⾃然⽽然的想到SPC)在思考为什么要⽤SPC时,我们的观点和认知,是随着职位不断成长的。
不要硬逼着⾃⼰去理解SPC⼿册⾥,那⼗⼏页鸡汤式的SPC概述。
格局到了,⾃然就理解了。
但是SPC的作⽤是不会发⽣变化的,做就对了。
3- When:在什么时候⽤SPCSPC⼿册⾥⾯说,SPC只有在过程受控状态下,才能使⽤。
但是实际上,SPC就是⼀个图表,任何情况,任何产品,只要有数据就可以⽤SPC控制图。
SPC控制图类型

SPC控制图选择的技巧SPC介绍:SPC统计过程控制(Statistical Process Control),简称SPC,是一种借助数理统计方法的过程控制工具。
在企业的质量控制中,可应用SPC对质量数据进行统计、分析从而区分出生产过程中产品质量的正常波动与异常波动,以便对过程的异常及时提出预警,提醒管理人员采取措施消除异常,恢复过程的稳定性,从而提高产品的质量。
SPC目的:SPC目的是建立并保持过程处于可接受的并且稳定的水平,以确保产品和服务符合规定的要求。
而要实现SPC的目的主要用到的工具手段就是控制图。
控制图主要是一个统计管理工具。
既然是统计那么就离不开数据,数据是统计技术的基础。
在SPC统计过程的,为不同的数据应用不同的控制图来统计。
那么SPC统计过程中的数据分为哪几种呢?首先数据主要分为两大类,一个是计量型数据,另一个是计数型数据。
计量型数据是指连续测量所得的质量特性值,如长度、重量、强度、化学成分、时间、电阻等。
计数型数据是指按个数数得的非连续性取值的质量特性值,如铸件的疵点数,统计抽样中的不合格判定数、审核中的不合格项数等可以用0、1、2、3、、、等阿拉伯数字数下去的数据。
其中计数型数据又可分为计件值与计点值,其中计件值是指是按件、按个、按项计数的数据。
例如:不合格品件数、温控器个数、质量检验项目等;计点值是指是指按缺陷点计数,例如:铸件的沙眼数、布匹上的疵点数、电路板上的焊接不良数等离散性数据。
控制图在众多现代化工厂中得到了普遍应用,并凭借其强大的分析功能,为工厂带来丰厚的实时收益。
最初的控制图分为计量型与计数型两大类,包含七种基本图表。
计量型控制图包括:∙IX-MR(单值移动极差图)∙Xbar-R(均值极差图)∙Xbar-s(均值标准差图)计数型控制图包括:∙P(用于可变样本量的不合格品率)∙Np(用于固定样本量的不合格品数)∙u(用于可变样本量的单位缺陷数)∙c(用于固定样本量的缺陷数)控制图的介绍:虽然最初被引入企业的只有7种基本控制图,但很多企业仍从这7种图表的有效运用中获得显著收益。
统计过程控制(4)
SPC(Statistical Process Control)统计过程控制一、统计过程控制的基本概念 ⒈ 统计的概念统计(Statistical ,简称S ):有目的地收集数据、整理数据、并使用相应的方法制图,列表与分析数据的过程。
⒉ 过程(Process ,简称P):在ISO9000:2000版中,过程的定义是一组将输入转化为输出的相互关联和相互作用的活动。
⒊ 控制(Control ,简称C ):所谓控制就是通过对图表与数据的分析研究,对过程的异常采取相应的措施进行监控的一种持续改进的活动。
⒋ 统计过程控制(SPC )的涵义:统计过程控制(Statistical Process Control ,简称SPC )是为了贯彻预防原则,应用统计技术对过程中的各个阶段进行评估与监察,建立并保持过程处于可接受的并稳定的水平,从而保证产品和服务符合规定的要求的一种技术。
统计技术涉及数理统计的许多分支,但SPC 中的主要工具是控制图。
因此,要想推行SPC 必须对控制图有一定深入的了解,否则就不可能通过SPC 取得真正的实效。
⒌ SPC 的特点:① 强调全员参与,而不是只依靠少数质量管理人员;② 强调应用统计方法来保证预防原则的实现;③ SPC 不是用来解决个别工序采用什么控制图的问题,SPC 强调从整个过程、整个体系出发来解决问题。
SPC 的重点就在于P (Process ,过程)。
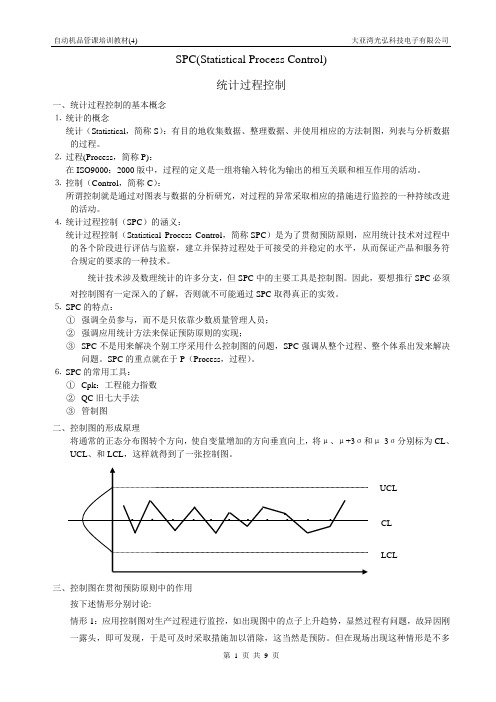
⒍ SPC 的常用工具:① Cpk :工程能力指数 ② QC 旧七大手法③ 管制图二、控制图的形成原理将通常的正态分布图转个方向,使自变量增加的方向垂直向上,将μ、μ+3σ和μ-3σ分别标为CL 、UCL 、和LCL ,这样就得到了一张控制图。
三、控制图在贯彻预防原则中的作用按下述情形分别讨论:情形1:应用控制图对生产过程进行监控,如出现图中的点子上升趋势,显然过程有问题,故异因刚一露头,即可发现,于是可及时采取措施加以消除,这当然是预防。
计量型统计过程控制

PPT文档演模板
2020/12/8
计量型统计过程控制
学习目的
完成对本模块的学习后,学员将能够:
建立下列控制图: 计量型 I-MR:Individuals and Moving Range(个体与移动极差图) Xbar&R:Xbr and Range(均值与极差图) Xbar&S:Xbar and Standard deviation(均值与标准差图)
够估计中心趋势和稳定性变化
•X,R
PPT文档演模板
X,R
06-9
计量型统计过程控制
X bar图
计量型控制图涉及连续性变量,其中所关 注的统计量是中心趋势和变异(散布)。
X bar图随时测量变量的中心趋势。它使用 来自大小为N的样本的平均值,或X-bar。
图的中心线由平均值的长期平均水平或Xdouble bar描绘出来。
如果找不到可归因原因,则该过程是处于 失控(统计上)状况
✓ 如果连续证据显示过程稳定的,则失控状况是一个假警报 ✓ 除非图形样式是由某一批产品所导致的,否则该过程是不稳定的,
并且必须采取措施来找出不稳定的根本原因
PPT文档演模板
06-12
计量型统计过程控制
•Xbar&R控制图界限
PPT文档演模板
UCL=12.95
(X图的系数通常为2.66)
对于MR图:
UCL=D4R n=2)
UCL=3.267*1.37)
UCL=4.48
LCL=X-E2R LCL=9.31-(2.66*1.37) LCL=5.67
LCL=D4R(D3.D4是基于 LCL=0*1.37) LCL=0
PPT文档演模板
SPC基础培训

的统计量(例如:均值,极
差,标准差) 必须正确分析图表
所采取的纠正措施必须适当
6σ——我们的工作方式
五、统计过程控制:SPC控制图
控制线与规格线 注意:控制图中的控制限与规格限是不一样的!每个过 程可按是否满足过程或产品规格和是否受控分成4类。 过程 过程受控吗
受控
产品规格 符合 第一类
不受控
6σ——我们的工作方式
五、统计过程控制:认识SPC
普通原因与特殊原因 可指出的原因: 在过程中不时常发生的变化原因 当发生时,会将整个过程分布改变 除非对所有的变化特殊要因找出和处理,它们会持续 以不可预测的方式影响过程输出
特殊 原因
明天的质量不稳定
如果存在特殊原因,过程输出是随时间不稳定的
第三类
不符合
第二类
第四类
6σ——我们的工作方式
五、统计过程控制:与过程能力的关系
过程控制与过程能力的关系 • 最理想的是第一类,过程受控,过程或产品符合要求。 • 第二类虽然受控,但普通原因的变化大。
• 第三类过程或产品符合要求,但不受控,必须找出特殊 原因。
• 第四类不受控,过程或产品也不符合要求,普通原因和 特殊原因都存在。
备注:E2=A2 n½
6σ——我们的工作方式
一、计量型统计过程控制:IM-R图
极差或标准差
历史背景:
当施华德在1920年开发这些控制图时,没有简 单的方法来计算出标准差。因此,极差方法就 成为SPC应用中根深蒂固的方法。
6σ——我们的工作方式
一、计量型统计过程控制:IM-R图
创建I-MR图
5.计算控制限 I图:UCL=X+E2R=9.31+2.66x1.4=13.034 UCL=X-E2R=9.31-2.66x1.4=5.586 MR图: UCL=D4R=3.267x1.4=4.574 LCL=D3R=0x1.4=0
SPC-计量型数据模块10

SPC-计量型数据模块10SPC(统计过程控制)是一种质量管理工具,旨在监控和控制过程的稳定性和可靠性。
计量型数据模块10是SPC中的一个重要组成部分,用于收集、分析和监控计量型数据,以帮助企业实现质量的持续改进。
本文档将详细介绍SPC-计量型数据模块10的功能和使用方法。
1. 功能介绍SPC-计量型数据模块10提供了以下主要功能:1.1 数据收集该模块可以从多种来源收集计量型数据,包括传感器、测量仪器和记录表等。
用户可以手动输入数据,或通过数据接口自动导入数据。
收集的数据可以是连续或离散的,并且可以包含多个测量指标。
1.2 数据分析SPC-计量型数据模块10能够对收集的数据进行各种分析,以获取统计特征和趋势。
这些分析包括:•均值和标准差的计算•直方图和箱线图的绘制•数据分布分析•数据关联和相关性分析用户可以根据自己的需要选择特定的分析方法,以便更好地理解数据的状态和性质,并采取相应的措施。
1.3 监控和控制SPC-计量型数据模块10可以监控数据的稳定性和可靠性,通过检测异常值、偏离控制限的数据和趋势变化等情况,及时发现潜在的问题。
用户可以设置上下控制限,并根据控制图上的警告信号进行相应的调整和改进。
2. 使用方法下面是使用SPC-计量型数据模块10的步骤:2.1 数据收集首先,需要收集计量型数据。
可以通过传感器、测量仪器或手动记录表等方式获取数据。
确保数据的准确性和完整性,并将其保存在电脑或服务器中。
2.2 数据导入如果数据已经保存在电脑或服务器中,可以通过数据接口将其导入到SPC-计量型数据模块10中。
选择相应的数据导入选项,并按照提示完成导入过程。
确保导入的数据格式正确,以便后续的分析和控制。
2.3 数据分析在导入数据后,可以开始进行数据分析。
选择要分析的数据集、测量指标和分析方法,然后点击开始分析按钮。
系统将根据选择的方法计算统计特征和绘制相应的图表。
查看分析结果,并对数据的分布、趋势和异常进行评估。
统计过程控制(SPC)及反应计划

深圳亚翔塑胶五金厂ATLAS PLASTICS&METAL PRODUCT FACTORY SZ文件/指引名称统计过程控制(SPC)及反应计划文件/指引编号TS-QW-EG-04页数1/8文件/指引版本 A 生效日期2006-06-01编写人吴永东部门主管审批李承俊管理者代表确认金东奎生效日期版本修改履历2006-06-01 A 首次发行受控编号1A 2A 3A 4A 5A 6A 7A 8A 接收部门总经办营业部采购部工程部成型部品质部装配部仓务部接收人/受控编号9A 10A 11A接收部门行政部财务部信息技术部接收人/文件控制印章如印章之颜色不是红色﹐则是非受控副本﹐文件/指引名称统计过程控制(SPC)及反应计划文件/指引编号TS-QW-EG-04页数2/8文件/指引版本 A 生效日期2006-06-011. 目的通过应用控制图方法,对产品制造过程关键工序的主要质量特性/重要特性进行控制,及时发现异常因素并加以消除,确保工序处于稳定的受控的状态。
2. 范围适用于公司生产过程各关键工序主要质量特性/重要特性的控制。
3. 术语及定义3.1术语σ标准偏差 CL 中心线LCL 控制下限 LSL 规格下限UCL 控制上限 USL 规格上限SPC 统计过程控制 PP 过程实绩CP 能力指数 CPk 稳定过程的能力指数3.2定义计量型数据:可以连续不间断取值的数据。
计数型数据:不可以连续不间断取值的数据。
稳定性:不存在变差的特殊原因处于统计控制的状态。
规格限:本公司或由供应商或客户对相关过程或产品特性所定的控制界限。
变差:过程的单个输出之间不可避免的差别,原因可分成两类:普通和特殊原因。
4.职责4.1技术部4.1.1 在制定控制计划中确定关键的工序参数或控制特性;4.1.2 选取合适的控制图类型(如: X-R,np图),确定取样数量及测试频率;4.1.3 计算持续的中心线和控制界限,包括对控制界限进行修订;4.1.4 检查完成的控制图,分析其趋势/异常情形;4.1.5 工序能力的研究。
统计过程控制(SPC)

1.分析过程阶段 通过PFMEA、小组会议、与主管专家、操作人员 的商讨,对控制图的分析,变差特殊原因与 普通原因的识别等技术,达到对过程现有状况的 了解。并回答下列问题: 本过程应做什么? 会出现什么问题? 本过程正在做什么?是否在生产废品和需返工产品? 本过程是否处于统计控制状态? 本过程是否有能力?是否可靠?
4.两种过程能力研究:长期研究和短期研究 短期过程能力研究是从一个操作循环中获取的测量 为基础,在判定该过程没有发现特殊原因,可以计 算短期能力指数。其用途: ①验证首批产品; ②机器能力研究; ③验证一个新的或经修改的过程的实际性能是否符 合工程参数。 长期过程能力研究是通过长时间进行测量所收 集的数据为基础,其用途是用来描述过程在很长时 间内的变差原因出现后能否满足顾客要求的能力。
八、控制图的益处
1.便于操作者在现场使用; 2.有助于过程在质量上和成本上持续地、可预测地 保持; 3.当过程处于统计控制状态,可以通过减少普通原 因和调整过程中心线,提高质量和降低成本; 4.提供有关过程特性能信息交流的共同语言。 5.通过区分变差的普通原因和特殊原因,为确定采 取局部措施还是系统措施提供依据。减少问题的混 淆、时间和资源的浪费。
二、收集数据
1.选择子组容量、频率、子组数
①在X—R控制图中,子组的容量是恒定的。
②每隔一定的周期(如15min或每班两次)抽取子组。 ③足够的子组数可以确保发现变差的主要原因。一般情 况下,至少应满足:25个子组,100个数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11
Appendix: Control Chart Constants : X-MR 附录:控制图表常数 X-MR
Subgroup Size n
2 3 4 5 6 7 8 9 10
E2 2.660 1.772 1.457 1.290 1.184 1.109 1.054 1.010 0.975
D3 * * * * * 0.076 0.136 0.184 0.223
1.2
1.8
0.7
1. Record the individual measurements for each subgroup 为每个子 群记录个体的测量值
2. Compute the Moving Range for each subgroup starting with subgroup 2. MR equals the Range for the subgroup and the previous subgroup's value. 从subgroup 2 开始为每个子群计算变动范围 MR 等于子群和当前子群值的变动范围。
Variable Statistical Process Control
计量型统计过程控制
1
Learning Objectives 学习目的
Upon completion of this module, the participants will be able to: 完成对本模块的学习后,学员将能够:
? Construct the following Control Charts :
建立下列控制图:
? Variables: ? I-MR: Individuals and Moving Range
(个体与移动极差图)
? Xbar & R: Xbar and Range
(均值与极差图)
? Xbar & S: Xbar and Standard deviation
the MR chart
1 R = 6 ( .5 +.9 + 3.1 + 1.2 +1.8 + .7) = 1.37
计算R,所有MR ‘S的平均值,R将会给出MR图的中心线
10
Formula For I-MR Chart Calculation I-MR Chart控制限计算公式:
MR Chart MR 图
? Plot I-MR Chart 画出:I-MR图
7
Creating I –图
14
Value Individual
13 12 11 10
9 8 7 6
5
Subgroup
1
5
Range
4 3
oving
2 1
M
0
I and MR Chart for C1
Subgroup 2 : MR = 8.5 - 8.0 = .5
Subgroup 3 : MR = 8.5 - 7.4 = 1.1
Subgroup 4 : MR = 10.5 - 7.4 = 3.1
9
Creating the I-MR Control Charts 创建 I-MR 控制图
Sample X MR
(8.0 + 8.5 + 7.4 + 10.5 + 9.3 + 11.1 + 10.4) = 9.31
7 计算X,所有个体值的平均值, X将会给出 X图的中心线
4. Compute R, the average of all of the MR's. R will give the center line on
12
D4 3.267 2.575 2.282 2.115 2.004 1.924 1.864 1.816 1.777
d2 1.128 1.693 2.059 2.326 2.534 2.704 2.847 2.970 3.078
Creating the I-MR Control Charts 创建 I-MR 控制图
1
2
3
4
8
8.5
7.4
10.5
0.5
0.9
3.1
5
6
7
9.3
11.1
10.4
1.2
1.8
0.7
3. Compute X, the average of all of the individual values. X will give the center line on the X chart.
1 X =
2
3
4
5
6
UCL=13.04 Mean=9.314 LCL=5.591 7 UCL=4.574
R=1.4 LCL=0
8
Creating the I-MR Control Charts 创建 I-MR 控制图
Samp le
X
MR
1
2
3
4
5
6
7
8
8.5
7.4
10.5
9.3
11.1
10.4
0.5
1.1
3.1
XBar-R 图: 均值和极差图
3 XBar-S Chart: Xbar and Standard Deviation Chart
XBar-S 图:均值和标准差图
3
Creating I – MR Chart with Minitab 用Minitab 创建I-MR 图
? I – MR Chart: Individuals and moving Range Chart. Each subgroup is made up by a single sample. I-MR: 个体与移动极差图,也叫X-MR图,子群由单一的测量值组成
(均值与标准差图)
2
Control Chart Types 控制图类型
Variable Control Charts: 计量型控制图:
1 I-MR Chart: Individual and Moving Range Chart
I-MR 图: 个体和移动极差图
2 XBar-R Chart: Xbar and Range Chart
5. Calculate the Control Limits : 计算控制限:
UCL MR=D4R LCL MR=D3R
X Chart X图
UCL X=X+E2R LCL X=X-E2R
In I-MR Charts, E 2=2.66. Other constants refer
to the follow table. 在I- MR 图中,E2=2.66, 公式中其它常数见下表 或本节后附录.
