ARCGIS多边形重心 方法一
识别多边形中心点的方法

识别多边形中心点的方法全文共四篇示例,供读者参考第一篇示例:多边形是一个平面图形,由若干个线段组成,每个线段都相邻接且不相交,而且首尾相连,形成一个封闭图形。
多边形的中心点是指多边形的质心,也是多边形的重心。
识别多边形中心点是在计算机视觉和图像处理中一个重要的问题,可以帮助我们进行图像分析、目标定位等相关任务。
本文将介绍几种常用的方法来识别多边形的中心点。
方法一:几何中心法在数学几何中,多边形中心点通常是指多边形的“几何中心”,也称几何质心。
几何中心法是最简单直观的方法,通过计算多边形的顶点坐标的平均值来得到多边形的中心点。
具体步骤如下:1. 对多边形的所有顶点坐标进行求和,并除以顶点的个数,得到一个平均坐标作为中心点的坐标。
2. 将得到的中心点坐标绘制在多边形的内部,即可得到多边形的中心点。
这种方法简单易行,适用于正规的凸多边形。
但对于不规则的凸多边形或凹多边形,可能会得到与我们期望不同的结果。
重心法也是一种常用的计算多边形中心点的方法。
重心是一个物理学和工程学概念,是指一个图形的“平均质量点”。
在数学上,一个多边形的重心定义为其所有小面积的中点的平均。
计算多边形的重心的方法是将多边形分解成多个三角形,计算每个三角形的重心,最后取所有三角形重心的平均值作为多边形的重心。
具体步骤如下:1. 将多边形分解成若干个三角形,可以采用三角剖分算法进行分解。
2. 计算每个三角形的重心,即三个顶点坐标的平均值。
通过重心法计算多边形中心点,可以更准确地反映多边形的形状和结构。
但对于复杂的多边形,计算过程可能比较复杂。
方法三:最小外接矩形法最小外接矩形法是另一种计算多边形中心点的方法。
这种方法不需要对多边形进行三角剖分,而是根据多边形的外包矩形来确定多边形的中心点。
计算多边形的最小外接矩形的步骤如下:1. 找到多边形的外包矩形,即包含多边形的最小矩阵。
最小外接矩形法适用于不规则多边形的中心点计算,并且计算效率高,较为简单。
基于ArcGIS和Excel制作“地理重心”图——以中国人口重心图为例

2018年 第 14期
多媒体辅助教学
基 于 A r c G I S 和 E x c e l 制 作 “地 理 重 心 绍兴市高级中学,浙江绍兴312000;2.华中师范大学城市与环境科学学院,湖 北 武 汉 430079)
摘 要 :GIS软件可以开发多样的地理学习资源,培养学生的地理学习兴趣,在地理教学中的应用越来越广。本文 利用ArcGIS和Excel两 种 工 具 ,对 地 理 重 心 图 制 作 步 骤 作 简 单 探 讨 ,以 期 帮 助 学 生 突 破 此 类 图 表 的 阅 读 障 碍 ,提 升 课 堂教学效果。
Mi• M4參
m2參 ■ •
M3• Mi•
图1 重心计算区域示意图
在实际分析中,子 区 域 重 心 坐 标 (Xl,yi) 的确定 有 两 种 方 法 :① 子 区 域 政 府 驻 地 坐 标 ,如计算中国人口 重 心 时 ,可以用省会坐标替代子区域的重心坐etpointIndex.hteml)。 ②用ArcGIS软 件 “要 素 转 点 ”工具生成区域的重心坐 标 ,具 体 方 法 将 在 下 文 进 行 介 绍 。接 下 来 ,文章以中 国 人 口 重 心 图 制 作 为 例 介 绍 具 体 步 骤 ,制 作 流 程 如 图 2 所示。
字 段 ,操作过程如图4所 示 。
框 选 择 “点的x坐 标 ” ,选 择 “地理坐标系” ,单位选 择 “十进制度” ,点击确定。按 照 同 样 的 方 法 生 成 “点 的y坐标” ,操作过程见图5 。
这 样 ,各 省 的 地 理 重 心 坐 标 已 经 计 算 完 毕 。现在 需要将生成的各省重心经纬度导出。右 击 “各省重心” 图 层 ,依次点击一 “打开属性表”一 “表属性”一 “导 出” ,选择保存路径 并 修 改 名 称 ,保 存 类 型 为 “dbase 表” ,操作过程如图6所 示 。
计算几何-多边形重心公式
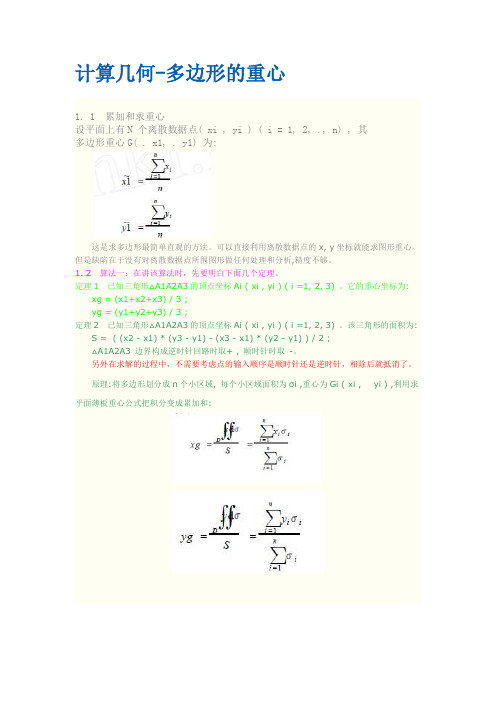
计算几何-多边形的重心1. 1 累加和求重心设平面上有N 个离散数据点( xi , yi ) ( i = 1, 2, ., n) , 其多边形重心G( . x1, . y1) 为:这是求多边形最简单直观的方法。
可以直接利用离散数据点的x, y坐标就能求图形重心。
但是缺陷在于没有对离散数据点所围图形做任何处理和分析,精度不够。
1. 2算法一:在讲该算法时,先要明白下面几个定理。
定理1已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。
它的重心坐标为: xg = (x1+x2+x3) / 3 ;yg = (y1+y2+y3) / 3 ;定理2已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。
该三角形的面积为: S = ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2 ;△A1A2A3 边界构成逆时针回路时取+ , 顺时针时取-。
另外在求解的过程中,不需要考虑点的输入顺序是顺时针还是逆时针,相除后就抵消了。
原理:将多边形划分成n个小区域, 每个小区域面积为σi ,重心为Gi ( xi , yi ) ,利用求平面薄板重心公式把积分变成累加和:由前面所提出的原理和数学定理可以得出求离散数据点所围多边形的一般重心公式:以Ai ( xi , yi ) ( i = 1, 2, ., n) 为顶点的任意N边形A1A2 .An ,将它划分成N - 2个三角形(如图1) 。
每个三角形的重心为Gi (xi , . yi ) ,面积为σi。
那么多边形的重心坐标G( x2, .y2) 为:图1 多边形分解例题:HDU 1115 Lifting the Stone代码:如下。
1 #include<stdio.h>2 #include<math.h>3 #include<stdlib.h>4struct centre5 {6double x , y ;7 };8int cas , n ;9double Area( centre p0 , centre p1 , centre p2 )10 {11double area = 0 ;12 area = p0.x * p1.y + p1.x * p2.y + p2.x * p0.y - p1.x * p0.y - p2.x * p1.y - p0.x * p2.y;13return area / 2 ; // 另外在求解的过程中,不需要考虑点的输入顺序是顺时针还是逆时针,相除后就抵消了。
多边形的重心

台北市立敦化國民中學資源丙班
多邊形的重心
218吳昀昕 218吳昀昕 222許晉婕 222許晉婕 223游凱婷 223游凱婷 指導老師:桂雪萍老師、 指導老師:桂雪萍老師、蔡芸蘭老師
※方法二─三角形的重心 方法二─
做法〉任兩中線( 〈做法〉任兩中線(連三角形任一邊的中點至對 頂點的線段)的交點,即為此三角形之重心。 頂點的線段)的交點,即為此三角形之重心。 分析〉一中線可以平分此三角形的面積( 〈分析〉一中線可以平分此三角形的面積(等底 同高) 若此三角形是一張紙,厚度忽略不計, 同高),若此三角形是一張紙,厚度忽略不計, 則中線也可平分重量。因此, 則中線也可平分重量。因此,兩中線的交點便 是重量的平衡點─重心。 是重量的平衡點─重心。 課內教材, p.s 課內教材,不再多說
※方法三─正多邊形及圓形的重心 方法三─
做法〉 〈做法〉正多邊形─取兩條線對稱軸的交點(奇數 邊形之對稱軸為點與對邊中點的連線;偶數邊形 的對稱軸為點與對點的連線),即為重心。圓形─ 圓心即為重心。 〈分析〉正多邊形的線對稱軸便是面積平分線, 分析〉 也就是質量平分線;圓形亦同。(同上) →感覺上,似乎在平面圖形上找出兩條可平分面 積(質量)的線,在找出其交點即可找到重心。
A
所以,綜合上面的比例,我們不難了解:兩三角 形重心的連線─也就是整支槓桿─,必須以b: a(a:b的反比)的比例來分,配合上兩端質量a:b, 才可以符合槓桿原理:重量1X臂長1=重量2X臂長2。 ﹝例二﹞以圖二中之四邊形 例二﹞ ABCD:1.連AC得∆BAC、∆DAC G 2.作∆ACD、∆ABC之重心g1、g2 3.作DF⊥AC於F,BE⊥AC於E 4.在g1g2上運用「平行線裁等比 例線段」的性質(取g2D’=DF, 圖二 D’B’=BE,連g1B’再過D’做一直 線平行於g1B’交g1g2於G,則 g2G:Gg1=DF:BE),畫出G點 即為四邊形ABCD之重心
ARCGIS多边形重心
3.用excel打开polygon_feat.dbf文件,将x、y坐标选出来,并将其复制到记事本
4.选择tools----add xy data,将上述记事本文件打开,并相应确定x、y
方法二:
1.选择Hawthstools----》vector editing tools----》generate polygon centroid points,打开多边形重心文件即可看到各多边形的重心
打开上述新图层的属性表新增x坐标和y坐标的属性列右击选择calculate??geometry重新获取点状地物其相应的xy坐arctoolbox----data management tools---features----feature to point:转换后出现的点并不是重心所在的位置,其点所有的属性与该多边形的属性表完全一致(polygon-feat)
arcgis 计算中心线算法

arcgis 计算中心线算法ArcGIS计算中心线算法是一种用于生成地理数据中线性特征的中心线(也称为中轴线)的方法。
该算法基于栅格数据模型,通过计算每个像素的质心来确定中心线的位置。
下面将详细介绍ArcGIS计算中心线算法的实现过程。
1. 导入数据首先,需要将要处理的地理数据导入ArcGIS中。
可以是矢量数据或栅格数据,但栅格数据更为常见。
中心线算法主要针对线性特征,如道路、河流等,因此需要选择包含这些特征的数据集。
2. 栅格化处理对于矢量数据,需要进行栅格化处理,将矢量数据转换为栅格数据。
在ArcGIS中,可以使用“栅格化”工具来完成这一步骤。
栅格大小可以根据需要进行设置,通常情况下,较小的栅格大小可以更好地保留数据的细节,但也会增加计算量。
3. 计算质心对于每个栅格单元,ArcGIS计算中心线算法会计算其质心。
质心是指一个平面图形的几何中心,对于矩形或正方形等规则形状,质心可以通过公式计算得出。
但是,对于不规则形状,如多边形或曲线等,计算质心的方法较为复杂。
对于规则形状,可以通过以下公式计算质心:质心(x,y) = (x1 + x2 + x3 + x4) / 4, (y1 + y2 + y3 + y4) / 4其中,(x1,y1),(x2,y2),(x3,y3)和(x4,y4)是四个顶点的坐标。
对于不规则形状,可以使用扫描线算法来计算质心。
该算法的基本思想是沿着一条条扫描线,计算每个扫描线上与形状相交的点的数量和位置,然后根据这些信息来确定形状的质心。
具体实现过程较为复杂,但ArcGIS已经实现了这一算法,可以直接使用。
4. 确定中心线位置在计算出每个栅格单元的质心后,ArcGIS计算中心线算法会根据这些质心来确定中心线的位置。
通常情况下,中心线会位于栅格单元的几何中心或质心之间。
具体来说,如果一个栅格单元包含一条线性特征的一部分,那么中心线就会位于该栅格单元的质心之间。
如果一个栅格单元不包含线性特征,则中心线不会经过该栅格单元。
求任意多边形的重心

求任意多边形的重心线垂法,具体方法是:用细线提起该物体,在该物体上画细线的延长线,再移位用细线提起该物体,在该物体上画细线的延长线,两线的交叉点就是这一物体在这平面上的重心,其它面同理.平面多边形,不管多复杂,理论上都可以用尺规作图,作出它的重心三角形的重心作法很容易,我就不多说了,对于任意多边形,甚至是几个彼此分开的多边形组成的复杂图案,重心作图法就比较复杂,需要用到一些复杂的定理首先来看下面的几个定理(它们的证明比较复杂,你可以自己尝试证明)定理1:由两个图形A,B合并而成的一个图形C,则C的重心必在A的重心与B的重心连接的线段上。
(注意,此定理也适用于A B彼此分开,没有公共点的情形)定理2:由两个A,B合并而成的一个图形C,A的重心为点a, B的重心为点b, C的重心为点c, A的面积为Sa, B的面积为Sb,则下面条件成立:(1)点c 必在线段ab 上(2) ac * Sa = bc * Sb根据以上定理,特别是定理1,我们就可以从理论上用尺规作图作出作任意多边形的重心.1.四边形的重心作法:连接出四边形的一条对角线,这样四边形就变成两个三角形的组合体,分别作出两个三角形的重心,并连接两个重心成一条线段AB,同样,连接出四边形的另一条对角线,四边形就变成另外两个三角形的组合体,分别作出这两个三角形的重心,并连接两个重心成一条线段CD,则线段AB,CD的交点就是四边形的重心。
(根据定理1)2.五边形的重心作法:连接出五边形的任一条对角线,将五边形分为1个三角形与一个四边形组合体,分别作出三角形的重心,和四边形的重心,并连成线段AB;连接五边形的另外一条对角形,将五边形分为另1个三角形与四边形的组合体,分别作出三角形与四边形的重心,并连接成线段CD;则AB、CD的交点就是五边形的重心。
3、用数学归纳法,对于六边形、七边形,N边形,都可以用上述方法,先连接出一条对角线,将N边形化为一个三角形与(N-1)边形,或四边形与(N-2)边形,然后分别作出重心,并连接成线段,然后再连接另外一条对象线,分别作出两个组合体的重心并连接成线段,两条线段的交点就是N边形的重心。
第008篇:ArcGIS中点对落入多边形的位置关系(相邻相离)的判定

第008篇:ArcGIS中点对落入多边形的位置关系(相邻相
离)的判定
场景:我最近做了一件事情,首先我有一个点矢量文件(Point),其中所有的点都是成对编号的,字段名为“编号”,内容依次为1 1 2 2 3 3 4 4 5 5……这样所有的点对都做好了“配对”。
另外,我还有一个多边形矢量文件(Polygon),内部包含了N多个多边形。
理论上来说,所有的点对都应该落入相邻多边形中才满足我的应用需求,然鹅如何实现的这样的判定呢?我目前只有下面这个方法:
方法原理:将所有的点对连成线,用线穿过的面个数来判断点落入的多边形是相邻还是相离。
如果两点之间的连线与两个多边形相交(Intersect),则说明两点分别落入了两多边形内。
如果两点之间的连线与多个多边形或单个多边形相交,则说明这两点落入了相离多边形或同一个多边形内部。
操作方法:
(1)Point to Line
Data MManagment下找Point to Line工具,按“编号”字段生成线。
(2)Spatial join
选中线文件和面文件,空间关系选Intersect,生成空间连接结果。
在生成的结果文件里会有一个字段写着Join_*,字段值里就写着每条线与几个多边形Intersect了。
