2018年浙江省杭州市【滨江区中考数学二模试卷】含答案
2018年浙江省杭州市中考数学试卷含答案解析(Word版)
浙江省杭州市2018年中考数学试题一、选择题1.=（）A. 3B. -3C.D.2.数据1800000用科学计数法表示为（）A. 1.86B. 1.8×106C. 18×105D. 18×1063.下列计算正确的是（）A. B. C. D.4.测试五位学生“一分钟跳绳”成绩，得到五个各不相同的数据，统计时，出现了一处错误：将最高成绩写得更高了。
计算结果不受影响的是（）A. 方差B. 标准差C. 中位数D. 平均数5.若线段AM，AN分别是△ABC边上的高线和中线，则（）A. B. C. D.6.某次知识竞赛共有20道题，规定：每答对一题得+5分，每答错一题得-2分，不答的题得0分。
已知圆圆这次竞赛得了60分，设圆圆答对了道题，答错了道题，则（）A. B. C. D.7.一个两位数，它的十位数字是3，个位数字是抛掷一枚质地均匀的骰子（六个面分别有数字1—6）朝上一面的数字。
任意抛掷这枚骰子一次，得到的两位数是3的倍数的概率等于（）A. B. C. D.8.如图，已知点P矩形ABCD内一点（不含边界），设，，，，若，，则（）A. B.C. D.9.四位同学在研究函数（b，c是常数）时，甲发现当时，函数有最小值；乙发现是方程的一个根；丙发现函数的最小值为3；丁发现当时，．已知这四位同学中只有一位发现的结论是错误的，则该同学是（）A. 甲B. 乙C. 丙D. 丁10.如图，在△ABC中，点D在AB边上，DE∥BC，与边AC交于点E，连结BE，记△ADE，△BCE的面积分别为S1，S2，（）A. 若，则B. 若，则C. 若，则D. 若，则二、填空题11.计算：a-3a=________。
12.如图，直线a∥b，直线c与直线a，b分别交于A，B，若∠1=45°，则∠2=________。
13.因式分解：________14.如图，AB是⊙的直径，点C是半径OA的中点，过点C作DE⊥AB，交O于点D，E 两点，过点D作直径DF，连结AF，则∠DEA=________。
杭州市二模数学答案2018年
2018年杭州市各类高中招生文化考试全真模拟（二模）数学答案选择：DCDDA DBCCD填空：11.1，；12.40˚；13.4；14.或;15.或16.;17.解：（1）由题意c==50，a=50×0.2=10，b==0.28，c=50；故答案为10，0.28，50；（2）将频数分布表直方图补充完整，如图所示：（3）所有被调查学生课外阅读的平均本数为：（5×10+6×18+7×14+8×8）÷50=320÷50=6.4（本）．（4）该校七年级学生课外阅读7本及以上的人数为：（0.28+0.16）×1200=528（人）．18.解：（1）∵一次函数y=（3﹣m）x+2m﹣9的图象与y轴的负半轴相交，y随x 的增大而减小，∴，解得3＜m＜4.5，∵m为整数，∴m=4．（2）由（1）知，m=4，则该一次函数解析式为：y=﹣x﹣1．∵﹣1≤x≤2，∴﹣3≤﹣x﹣1≤0，即y的取值范围是﹣3≤y≤0．19. (1)证明：∵四边形ABCD是矩形∴∠A=∠D=∠C=90°，∵△BCE沿BE折叠为△BFE，∴∠BFE=∠C=90°，∴∠AFB+∠DFE=180°﹣∠BFE=90°，又∵∠AFB+∠ABF=90°，∴∠ABF=∠DFE，∴△ABF∽△DFE；(2) tan∠EBC=20. （1）证明：连接OE．∵OE=OB，∴∠OBE=∠OEB，∵BE平分∠ABC，∴∠OBE=∠EBC，∴∠EBC=∠OEB，∴OE∥BC，∴∠OEA=∠C，∵∠ACB=90°，∴∠OEA=90°∴AC是⊙O的切线；（2）解：连接OE、OF，过点O作OH⊥BF交BF于H，由题意可知四边形OECH为矩形，∴OH=CE，∵BF=6，∴BH=3，在Rt△BHO中，OB=5，∴OH==4，∴CE=4．21. 解：（1）当1≤x＜50时，y=（200﹣2x）（x+40﹣30）=﹣2x2+180x+2000；（2）当1≤x＜50时，y=﹣2x2+180x+2000，y=﹣2（x﹣45）2+6050．∴a=﹣2＜0，∴二次函数开口下，二次函数对称轴为x=45，当x=45时，y最大=6050，当50≤x≤90时，y=（200﹣2x）（70﹣30）=﹣80x+8000，∵y随x的增大而减小，∴当x=50时，y最大=4000，综上所述，该商品第45天时，当天销售利润最大，最大利润是6050元22. 解：（1）∵函数图象与x轴有两个交点，∴m≠0且[﹣（2m﹣5）]2﹣4m（m﹣2）＞0，解得：m＜且m≠0．∵m为符合条件的最大整数，∴m=2．∴函数的解析式为y=2x2+x．（2）①抛物线的对称轴为x=﹣=﹣．∵n≤x≤﹣1＜﹣，a=2＞0，∴当n≤x≤﹣1时，y随x的增大而减小．∴当x=n时，y=﹣3n．∴2n2+n=﹣3n，解得n=﹣2或n=0（舍去）．∴n的值为﹣2．②∵y=2x2+x=2（x+）2﹣，∴M（﹣，﹣）．如图所示：当点P在OM与⊙O的交点处时，PM有最大值．设直线OM的解析式为y=kx，将点M的坐标代入得：﹣k=﹣，解得：k=．∴OM的解析式为y=x．设点P的坐标为（x，x）．由两点间的距离公式可知：OP==，解得：x=2或x=﹣2（舍去）．∴点P的坐标为（2，1）．∴当点P与点M距离最大时函数C2的解析式为y=2（x﹣2）2+1．23.(1); (2)(3)。
2018滨江二模卷(有答案)
2018年杭州市各类高中招生模拟试卷（二）第一部分听力略第二部分阅读理解（共两节，满分40分）第一节（共15小题，每小题2分，满分30分）AI was telling my boy Sonny the story of the hare and the tortoise. At the end I said, " Son, remember: Be slow and steady ( 坚定的), and that will win the race. Don't you think there's something to learn from the tortoise?"Sonny opened his eyes wide, “Do you mean next time when I'm entering for the 60-metre race I should wish that Billy, Tony and Sandy would all fall asleep halfway?”I was shocked, “But the tortoise didn't wish that the hare would fall asleep!”“He must have wished that,” Sonny said, “Otherwise how could he be so foolish as to race with the hare? He knew very well the hare ran a hundred times faster than he himself did.”“He didn't have such a wish,” I kept on. “He won the race by perseverance ( 毅力), by pushing on steadily.”Sonny thought a while. “That's a lie,” he said. “He won it because he was lucky. If the hare hadn't happened to fall asleep, the tortoise would never have won the race. He could be as steady as you like, or a hundred times steadier, but he'd never have won the race. That's for sure.”I gave up. Today's children are not like what we used to be. They're just hopeless.16.The writer argued with his son because ______.A. he liked tortoises while his son liked haresB. they disagreed about whether the tortoise was foolishC. he tried to teach his son a moral lesson but the son had totally different opinionD. he liked the story of the hare and the tortoise while his son didn't.17. Sonny believed that the tortoise ________.A. won the race by his own hard workingB. took a risk by agreeing to run a raceC. was not given a fair chance in the raceD. in fact did win the race luckily18. Billy, Tony and Sandy must be________.A. boys who were unknown to Sonny's fatherB. boys who Sonny has run races with beforeC. boys who Sonny has never raced with beforeD. boys who Sonny did not expect to race with again19. According to the passage, who do you think learnt a lesson?A. The tortoiseB. SonnyC. The hareD. Sonny's fatherCDBDBCan you imagine that several hundred years ago, tomatoes were seen as toxic food in Europe? What made Europeans believe this was John Gerard’s publication of Herbal in 1597. Gerard wrote: “The leaves and stalks of the tomato plant are toxic.” Undoubtedly, Gerard’s opinion was based on a misunderstanding of tomatoes. But his opinion was widely spread in Britain and North America for over two hundred years.In the late 1700s, a lot of Europeans held more fears for tomatoes. A nick name for the fruit was “poison apple” because it was believed that aristocrats(贵族) got sick and died after eating them. But the actual reason was the pewter plates they used. Since tomatoes are high in acidity, when placed on the plates, the lead(铅) in the plates would dissolve. This caused many deaths. This is unluckily, no one knew this at that time. So the innocent tomatoes were picked as the killer. Today, more than one and a half billion tons of tomatoes are produced every year around the world. Tomatoes are cooked in various ways. This healthy and tasty food finally wins its innocence(清白) back.20. What does the underlined word “toxic” in paragraph 1 mean?A. deliciousB. nutritious(营养)C. poisonousD. safe21. What do we know about the book Herbal?A. It was written by an American writer.B. It was published about 400 years ago.C. Tomatoes were described as good food.D. Chinese herbal medicine was included.22. What’s the passage mainly about?A. Europeans’ fears for tomatoesB. History of tomato plantingC. Why do people eat so many tomatoesD. How did the tomato prove its valueCBACEvery spring, the cherry trees in Washington, DC take bloom(花), beginning one of the country’s loveliest celebrations, the National Cherry Blossom Festival (March 17-April 15). Book your trip now to see this lively display of pink and white in this city full of history! Washington, DC Cherry Blossom In-Depth tourPrice: $45Available: Mar 25- Apr 15Period: 1DayHighlights: Visit Washington, DC; experience the peak(高峰) period of cherry blossom (April 8-12)Route: Guests would start to celebrate the National Cherry Blossom Festival and discover the beauty of cherry blossoms. Next, we will begin our sightseeing city tour including Lincoln Memorial, White House, US Capitol, Madam Tussauds Wax Museum, Washington Monument and International Spy Museum. Then visit the Jefferson Memorial, the best location to view the cherry blossoms. Finally, guests may board a Potomac River cruise to see the city from the water. Then tour ends.Price Include: Ground TransportationService fee for the tour guide: $10/personAdmission Fees(入场费):Note: if you would like to join in the optional(可选择的) activities, please pay the fee incash(现金) to the tour guide. You cannot buy the tickets on your own or use City Passes. The tour guide will arrange the tickets for the group.23. On March 25, tourists can enjoy ______.A. the cherry blossoms in full bloomB. the anniversary celebration of the gift of treesC. a discounted tour of a city foil of historyD. the National Cherry Blossom Festival24. The tour covers ______ tourist spots without admission fees.A. fourB. fiveC. sevenD. eight25. Tourists are supposed to ______.A. pay the service fee for the tour guideB. take care of the ground transportationC. show the City Pass at the ticket officeD. choose at least one optional destination26. It costs ______ for you and your grandpa (aged 67) to go on the tour, with the wax museum included.A. $156B. $143C. $153D. $108DBACDWe desire to believe that we can get fit without effort. We invent chocolate-chip cookie diets to make us thin while eating fat. We wish to get fit from doing nothing. We wish to lie in bed, think about going to the gym and then, get the body of a Greek god.A new study from Brian Clark at Ohio University shows that sitting still, while just thinking about exercise, might make us stronger. Clark and his colleagues asked 29 volunteers and wrapped their wrists in surgical casts for a whole month. During this month, half of the volunteers thought about exercising their immobilized (使不动)wrists. For 11 minutes a day, 5 days a week, they sat completely still and focused their entire mental effort on pretending to flex their muscles. When the casts were removed, the volunteers that did mental exercises had wrist muscles that were two times stronger than those who had done nothing at all.The idea behind the research is not a new concept-just a concept that’s often neglected in the field of neuroscience(神经科学): our bodies and our brains develop together. Even though we treat our mind and bodies as two separate things(brain vs brawn; mind vs matter), they are finally andclosely connected.Indeed, even before Brian Clark published his study, other researchers had explained links between the brain and the muscles. Ten years ago, Guang Yue at the Cleveland Clinic reported that imaginary exercise increases the strength of finger muscles by up to 35%. Just five years ago, Kai Miller at the University of Washington, showed that imaginary exercise activates the same brain areas that are activated during real exercise. Brain Clark's research adds to this body of knowledge and provides believable facts about the role of neuromuscular(神经肌肉的) pathways in strength training.27. What's the purpose of chocolate-chip cookie diets?A. To keep strong.B. To grow thinner.C. To keep fat. D To have muscles28. The experiment proves that .A. wrapping their wrists may be quickB. showing their muscles needs effortsC. sitting still might make us strongerD. thinking about exercise is so useful29. Which of the following concepts is often neglected according to the passage?A. Our mind and bodies are two separate thingsB. Our bodies and brains develop togetherC. Our mind has a close relation to bodiesD. Our mind has little effect on our brains30. what's the best title for the passage?A. How to Grow Stronger Without Lifting Weights.B. H0w to Carry out a Muscle Exercise Program.C How to Prevent Muscle From Growing Thinner.D. How to Provide Pathways in Strength Training,Keys: B C B A第二节（共5小题，每题2分，满分10分）请仔细阅读下面短文，从A到F的六个选项中选出符合各段主题的句子，完成31-35题。
2018年浙江省杭州市中考数学试卷含答案
2018年浙江省杭州市中考数学试卷一、选择题：本大题有10个小题，每小题3分，共30分。
在每小题给出的四个选项中，只有一项是符合题日要求的。
1．（3.00分）|﹣3|=（）A．3 B．﹣3 C．D．﹣2．（3.00分）数据1800000用科学记数法表示为（）A．1.86B．1.8×106C．18×105D．18×1063．（3.00分）下列计算正确的是（）A．=2 B．=±2 C．=2 D．=±24．（3.00分）测试五位学生的“一分钟跳绳”成绩，得到五个各不相同的数据，在统计时，出现了一处错误：将最高成绩写得更高了，计算结果不受影响的是（）A．方差 B．标准差C．中位数D．平均数5．（3.00分）若线段AM，AN分别是△ABC的BC边上的高线和中线，则（）A．AM＞AN B．AM≥AN C．AM＜AN D．AM≤AN6．（3.00分）某次知识竞赛共有20道题，规定：每答对一道题得+5分，每答错一道题得﹣2分，不答的题得0分，已知圆圆这次竞赛得了60分，设圆圆答对了x道题，答错了y道题，则（）A．x﹣y=20 B．x+y=20 C．5x﹣2y=60 D．5x+2y=607．（3.00分）一个两位数，它的十位数字是3，个位数字是抛掷一枚质地均匀的骰子（六个面分别标有数字1﹣6）朝上一面的数字，任意抛掷这枚骰子一次，得到的两位数是3的倍数的概率等于（）A．B．C．D．8．（3.00分）如图，已知点P是矩形ABCD内一点（不含边界），设∠PAD=θ1，∠PBA=θ2，∠PCB=θ3，∠PDC=θ4，若∠APB=80°，∠CPD=50°，则（）A．（θ1+θ4）﹣（θ2+θ3）=30°B．（θ2+θ4）﹣（θ1+θ3）=40°C．（θ1+θ2）﹣（θ3+θ4）=70°D．（θ1+θ2）+（θ3+θ4）=180°9．（3.00分）四位同学在研究函数y=x2+bx+c（b，c是常数）时，甲发现当x=1时，函数有最小值；乙发现﹣1是方程x2+bx+c=0的一个根；丙发现函数的最小值为3；丁发现当x=2时，y=4，已知这四位同学中只有一位发现的结论是错误的，则该同学是（）A．甲B．乙C．丙D．丁10．（3.00分）如图，在△ABC中，点D在AB边上，DE∥BC，与边AC交于点E，连结BE．记△ADE，△BCE的面积分别为S1，S2（）A．若2AD＞AB，则3S1＞2S2B．若2AD＞AB，则3S1＜2S2C．若2AD＜AB，则3S1＞2S2D．若2AD＜AB，则3S1＜2S2二、填空题：本大题有6个小题，每小题4分，共24分。
2018年杭州市中考模拟数学试卷(附参考答案)
2018年杭州市中考数学模拟试卷考生须知：1.本试卷分试题卷和答题卷两部分，满分120分，考试时间100分钟.2.答题时，应该在答题卷指定位置内写明校名、姓名和准考证号.3.所有答案都必须做在答题卷指定位置上，请务必注意试题序号和答题序号相对应.4.考试结束后，上交试题卷和答题卷.一. 选择题（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中, 只有一个是正确的. 注意可以用多种不同的方法来选取正确答案.1、下列各数中，比1小的数是( ▲ )A ．-1+2B ．C ．π-D ．0(3)-2、把y y x -2分解因式是（ ▲ ）A ．2(1)y x -B ．(1)y x +C ．(1)y x -D ．(1)(1)y x x +-3、如图，在△ABC 中，DE∥BC，AD=6，DB=3，则的值为( ▲ )A ．B ．C ．D ．4、一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是( ▲ )A ．至少有1个球是黑球B ．至少有1个球是白球C ．至少有2个球是黑球D ．至少有2个球是白球5、若一个直六棱柱的三视图如图所示，则这个直六棱柱的体积为（ ▲ ）A ． 4B ．5.4C ．5D ．5.5 6、已知方程012=-+x x，下列说法中正确的是（▲ ）A ．该方程有两个相等的实数根B ．该方程有两个不相等的实数根，且它们互为相反数C ．该方程有一根为251+D. 该方程有一根为黄金分割比7、下列各式计算正确的有（ ▲ ）A.323452)2()q (q p q p p =÷B. 25)5)(5(2--=--+-a a a C. 2322(5)210x x y x x y --=-- D.2121422+=---a a a a8、已知点A （﹣1，m ），B （1，m ），C （2，m +1）在同一个函数图象上，这个函数图象可以是（ ▲ ）A ．B ．C ．D ．9、已知⊙O 的半径为3，△ABC 内接于⊙O ，AB=32，AC=33，D 是⊙O 上一点，且AD=3，则CD 的长应是（ ▲ ） (西湖区试题改编) A ．3 B ．3或6 C ．3 D ．3或610、如图，在菱形ABCD 中，AB CF AD CE BC AG CD AH ⊥⊥⊥⊥,,,，垂足分别为点H ，G ，E ，F.若图中四边形APCQ 的面积为菱形ABCD 的四分之一，则sinB 的值（ ▲ ） （课本改编） A.23 B.43 C.55 D.54二. 填空题(本题有6个小题, 每小题4分, 共24分) )要注意认真看清题目的条件和要填写的内容, 尽量完整地填写答案.11、用科学记数方法表示=0000907.0 .12、已知ab b a =+，则=--)1(1b a ）（ . 13、如图，直线AB ∥CD ，BC 平分∠ABD ，∠1=67°，则∠2＝ 度．14、为了喜迎2022年杭州承办第19届亚运会，某校举行文艺演出，组建46人的合唱队和30人的舞蹈队，现根据演出需要，从舞蹈队中抽调部分同学参加合唱队，使合唱队的人数恰好是舞蹈队人数的3倍．设从舞蹈队中抽调x 人参加合唱队，可列方程为 .（杭州市中考试题改编） 15、若关于x,y 方程组⎩⎨⎧+=--=+4633232k y x k y x 的解为⎩⎨⎧==by ax ，且3<k ，则t=a-3b 的取值范围是 .（杭州市中考试题改编） 16、如图，在平行四边形ABCD 中，AB=10，AD=15，tanA=34，点P 为AD 边上任意一点，连接PB ，将PB 绕着P 点逆时针旋转90得到线段PQ ，若点Q 恰好落在平行四边形ABCD 的边所在的直线上，则PB= . （杭州市中考试题改编）三. 解答题 (本题有7个小题, 共66分)解答应写出文字说明,证明过程或推演步骤.如果觉得有些题目有点困难,那么把自己能写出的解答写出一部分也可以. 17、（本题6分）“你记得父母的生日吗？”这是某校在九年级学生中开展主题为“感恩”教育时设置的一个问题，有以下四个选项：A ．父母生日都记得；B ．只记得母亲生日；C ．只记得父亲生日；D ．父母生日都不记得．在随机调查了（1）班和（2）班各50名学生后，根据相关数据绘出如图所示的统计图． （1）补全频数分布直方图；（2）据此推算，九年级共900名学生中，“父母生日都不记得”的学生共多少名？（3）若两个班中“只记得母亲生日”的学生占22%，则（2）班“只记得母亲生日”的学生所占百分比是多少？18、（本题8分）已知111222---++=x xx x x A （1）化简A ； （2）当x 满足不等式组，且x 为整数时，求A 的值．19、（本题8分）如图，△ABC 中，AB=AC ，D 是BC 中点，BE⊥AC 于E ， （1）求证：△ACD∽△BCE；（2）若AB=5，BC=6，求CE 的长．（课本改编）20、（本题10分）如图，正比例函数x y 21-=的图象与反比例函数1k y x-=的图象分别交于M ，N 两点，已知点M （﹣2，m ）． （1）求N 的坐标；（2）若1122(,),(,)A x y B x y 是反比例函数1k y x-=图像上的两点，当12y y >时，比较12,x x 的大小．（课本改编）21、（本题10分）如图，在△ABC 中，BA=BC ，以AB 为直径的⊙O 分别交AC ，BC 于点D ，E ，BC 的延长线与⊙O 的切线AF 交于点F ． （1）求证：∠ABC=2∠CAF；（2）若AC=102，CE ：EB=1：4，求CE ，AF 的长． （课本改编）22、（本题12分）设抛物线C 的解析式为k k kx x y )3(22++-=，k 为实数.（1）①求出该抛物线的顶点坐标（用k 表示）；②说明当k 变化时，该抛物线的顶点在一条定直线上；（2）已知一直线与该抛物线中任意一条都相截，且截得的线段长都为6，求这条直线的解析式.（全国数学竞赛试题改编） 23、（本题12分）如图1，在△ABC 中，BC=4，以线段AB 为边作△ABD，使得AD=BD ，连接DC ，再以DC 为边作△CDE，使得DC=DE ，∠CDE=∠ADB=α．（1）如图2，当∠ABC=45°且α=90°时，用等式表示线段AD ，DE 之间的数量关系； （2）将线段CB 沿着射线CE 的方向平移，得到线段EF ，连接BF ，AF ． ①若α=90°，依题意补全图3，求线段AF 的长； ②求出线段AF 的长（用含α的式子表示）．数学参考答案及评分标准一、选择题（每小题3分，共30分）二、填空题（每小题4分，共24分）11．51007.9-⨯ 12. 1 13． 46 14．)30(346x x -=+ 15. -14<t<14 16. 28,54,8 三、解答题 (本题有7个小题， 共66分)17、解：（1）一班中A 类的人数是：50﹣9﹣3﹣20=18（人）． 1分 如图所示．1分（2）（名）； 2分（3）设（2）班“只记得母亲生日”的学生有x 名，依题意得：，解得x=13，∴，即（2）班“只记得母亲生日”的学生所占百分比是26%． 2分 ﹣）∵19、（1）证明：∵AB=AC，D 是BC 中点， ∴AD⊥BC，∴∠ADC=90°， 1分 ∵BE⊥AC， ∴∠BEC=90°，∴∠ADC=∠BEC， 1分 而∠ACD=∠BCE，∴△ACD∽△BCE． 2分 （2）∵△ACD∽△BCE∴AC CDBC CE = 2分 ∴536=CE ∴518=CE 2分20、解：（1）∵点M （﹣2，m ）在正比例函数y=﹣21x 的图象上， ∴m=﹣21×（﹣2）=1， ∴M（﹣2，1）， 2分∴根据中心对称性得到N(2，-1) 2分（2）∵反比例函数y=1k x-的图象经过点M （﹣2，1）， ∴反比例函数的解析式为y=﹣x2． 1分因为A,B 是反比例函数y=2x -图像上的两点，所以有121222,y y x x --==， 1分 ∵12y y >∴1222x x ->- ∴21122()0x x x x -> 2分①当12,x x 同号时，21x x >； ②当12,x x 异号时，有12x x <. 2分 （图像法分情况讨论也好，给分）21.（1）证明：如图，连接BD ． ∵AB 为⊙O 的直径， ∴∠ADB=90°，∴∠DAB+∠ABD=90°． 2分 ∵AF 是⊙O 的切线， ∴∠FAB=90°， 1分 即∠DAB+∠CAF=90°． ∴∠CAF=∠ABD． ∵BA=BC，∠ADB=90°， ∴∠ABC=2∠ABD． ∴∠ABC=2∠CAF． 2分 （2）解：如图，连接AE ． ∴∠AEB=90°． 设CE=x ， ∵CE：EB=1：4，∴EB=4x，BA=BC=5x ，AE=3x ． 在Rt△ACE 中，AC 2=CE 2+AE 2． 即（210）2=x 2+（3x ）2． ∴x=2．∴CE=2， 3分∴EB=8，BA=BC=10，AE=6． ∵tan∠ABF BAAFEB AE ==∴1086AF =． ∴AF=7.5 2分22、(1)①配方得，()k k x y 32+-=，顶点坐标为()k k 3,； 3分②设顶点坐标为（x,y ），则x=k,y=k 3,消去k 得到直线x y 3=，该抛物线的顶点在定直线x y 3=上； 3分（2）要使该直线与抛物线中任意一条相截且截得线段长都是6，则该直线必须平行于x y 3=， 2分设其为b x y +=3，考虑其与2x y =相交于点A,B ，分别过点A 作x 轴的垂线，过点B 作y 轴的垂线，交于点C ，则⎩⎨⎧+==bx y x y 32，即有032=--b x x ，解出2433,bx C B +±=， 2分所以BC=321=AB ,即有3=-C B x x ,所以有4b+3=9，解之23=b ，所以这条直线的解析式为233+=x y . 2分23、解：（1）AD+DE=4，理由是：如图1，∵∠ADB=∠EDC=∠α=90°，AD=BD ，DC=DE ， ∴AD+DE=BC=4； 2分（2）①补全图形，如图2， 2分 设DE 与BC 相交于点H ，连接AE ， 交BC 于点G ，∵∠ADB=∠CDE=90°， ∴∠ADE=∠BDC， 1分 在△ADE 与△BDC 中，，∴△ADE≌△BDC，∴AE=BC，∠AED=∠BCD． 2分 ∵DE 与BC 相交于点H ， ∴∠GHE=∠DHC，∴∠EGH=∠EDC=90°，∵线段CB 沿着射线CE 的方向平移，得到线段EF ， ∴EF=CB=4，EF∥CB， ∴AE=EF，∵CB∥EF，∴∠AEF=∠EGH=90°，∵AE=EF，∠AEF=90°，∴∠AFE=45°，∴AF==4； 2分②如图2，过E作EM⊥AF于M，∵由①知，AE=EF=BC，∴∠AEM=∠FME=，AM=FM，∴AF=2FM=EF×sin=8sin． 3分。
2018浙教版杭州下城中考数学二模真题卷答案
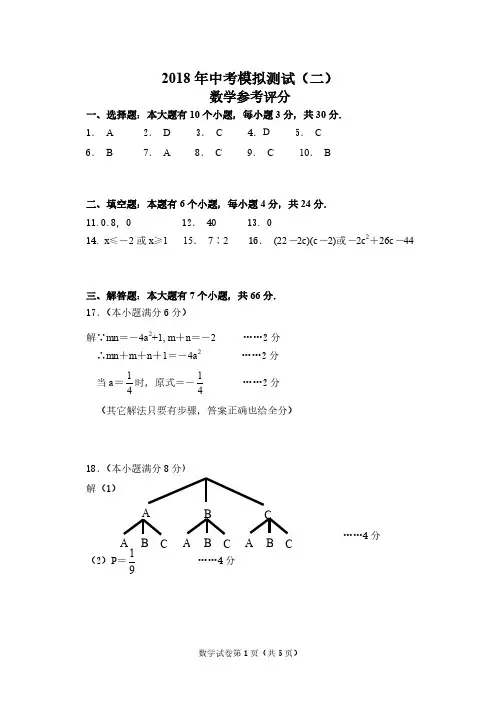
2018年中考模拟测试（二）数学参考评分一、选择题：本大题有10个小题，每小题3分，共30分. 1． A 2． D 3． C 4．D 5． C 6． B 7． A 8． C 9． C 10． B二、填空题：本题有6个小题，每小题4分，共24分. 11.0.8, 0 12． 40 13. 014. x ≤－2或x ≥1 15． 7∶2 16． (22－2c )(c －2)或－2c 2＋26c －44三、解答题：本大题有7个小题，共66分. 17．（本小题满分6分）解∵mn ＝－4a 2+1, m ＋n ＝－2 ……2分 ∴mn ＋m ＋n ＋1＝－4a 2 ……2分 当a ＝14时，原式＝－14……2分 （其它解法只要有步骤，答案正确也给全分）18．（本小题满分8分) 解（1） (4)分 （2）P ＝19……4分B AC B A C A B C CBA19．（本小题满分8分)证明：∵AB ＝AC ，D ，E 分别为两腰AB ，AC 的中点 ∴DB ＝EC ，∠B ＝∠C ……2分 又∵BF ＝CG ∴BG ＝CF∴△BDG ≌△CEF ……3分 ∴∠DGB ＝∠EFC∴HF ＝GH ……3分20．（本小题满分10分）解（1）由题意可知：221410k k k k ≠⎧⎨--+>⎩（）（）……3分∴k ＜18，且k ≠0. ……2分 （缺k ≠0，共扣1分）（2）把x ＝1代数二次函数表达式得a ＝2， ∴点A （1，2），又∵y ＝x ＋b ＋2的图象过点A （1，2） ……3分∴2＝1＋b ＋2∴b ＝－1 ……2分21.（本小题满分10分） 解（1）连结BC ∵AB 为直径∴∠ACB =90° ……1分 又∵AB =6cm , ∠CAB ＝60°BADC E GF H （第19题）ABPCQ∴AC ＝AB ▪ cos ∠CAB ＝3cm ……3分（2）①过O 作OD ⊥PQ 于D ，连结OQ ∵PQ ∥AC ，AP =1cm ，OA =3cm∴PD ＝OP cos 60°＝1cm ，OD……2分 ∴DQcm∴PQ =(1)cm ……2分 ② t =3……2分22．（本小题满分12分） 解（1）由题意可知4211a b a b +=⎧⎨+=⎩或4211a b a b +=⎧⎨+=-⎩∴1232a b ⎧=-⎪⎪⎨⎪=⎪⎩或3252a b ⎧=⎪⎪⎨⎪=-⎪⎩ ∴y ＝12-x 2＋32x 或y ＝32x 2－52x ……4分 （2）由题意可知A （m ,m ）或（m ，－m ）∴m ＝32m 2－52m 或－m ＝32m 2－52m ∴m =73或1 ……4分（3）当x ≥56时，对于y ＝32x 2－52x 有“y 随x 的增大而增大”当x ≤32时，对于y ＝12-x 2＋32x 有“y 随x 的增大而增大”∴56≤x ≤32∴t1的最小值为56，t2的最大值为32……4分23.（本小题满分12分）解（1）连结BD在菱形ABCD中∠C＝60°，∴△BCD为正三角形……2分∵∠C＝60°，AB＝4，BE＝EC∴DE⊥BC∴DE＝……2分（2）∵∠DAG＝∠FEG，∠DGA＝∠FGE ∴△AGD∽△EGF……2分∴AG GE DG GF=又∵∠AGE＝∠DGF∴△AGE∽△DGF ……2分（3）过A作AM⊥CD于M∵△AGE∽△DGF∴∠AED＝∠GFD又∵BC∥AD，DE⊥BC∴AD⊥DE∴△ADE∽△AFM ……2分∴AD AM DE MF=∴MF＝3∴DF＝MF－MD＝1 ……2分（其它解法请酌情给分）（第23题）AGFEDBC。
2018年中考数学二模试卷含答案
2018年中考数学二模试卷一、选择题（本大题共20小题，每小题3分，共60分）1．（﹣）﹣1的倒数是（）A．B．C．﹣ D．﹣2．下列计算正确的是（）A．（﹣3a）2+4a2=a2B．3a2﹣（﹣2a）2=﹣a2C．3a•4a2=12a2D．（3a2）2÷4a2=a23．已知点M（1﹣2m，m﹣1）关于原点的对称点在第一象限，则m的取值范围在数轴上表示正确的是（）A．B．C．D．4．下列图形是几家电信公司的标志，其中既是轴对称图形又是中心对称图形的是（）A．B．C．D．5．化简÷（1+）的结果是（）A．B．C．D．6．长方体的主视图、俯视图如图所示（单位：m），则其左视图面积是（）A．4m2B．12m2C．1m2D．3m27．某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）A．50（1+x2）=196 B．50+50（1+x2）=196C．50+50（1+x）+50（1+x）2=196 D．50+50（1+x）+50（1+2x）=1968．2017年“端午节”期间，小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩，小明与小亮通过抽签方式确定景点，则两家都抽到东营港的概率是（）A．B．C．D．9．已知空气的单位体积质量为1.24×10﹣3克/厘米3，1.24×10﹣3用小数表示为（）A．0.000124 B．0.0124 C．﹣0.00124 D．0.0012410．某班七个合作学习小组人数如下：4、5、5、x、6、7、8，已知这组数据的平均数是6，则这组数据的中位数是（）A．5 B．5.5 C．6 D．711．把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长为（）A．B．5 C．4 D．12．如图，直线y=与双曲线y=（k＞0，x＞0）交于点A，将直线y=向上平移4个单位长度后，与y轴交于点C，与双曲线y=（k＞0，x＞0）交于点B，若OA=3BC，则k 的值为（）A．3 B．6 C．D．13．如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为（）A． cm B． cm C． cm D．4cm14．如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，则sin∠CBD的值等于（）A．OM的长B．2OM的长C．CD的长D．2CD的长15．若正比例函数y=mx（m≠0），y随x的增大而减小，则它和二次函数y=mx2+m的图象大致是（）A．B．C．D．16．如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD；其中正确结论的是（）A．①②③B．①②④C．①③④D．②③④17．如图，点E是矩形ABCD的边CD上一点，把△ADE沿AE对折，点D的对称点F恰好落在BC上，已知折痕AE=10cm，且tan∠EFC=，那么该矩形的周长为（）A．72cm B．36cm C．20cm D．16cm18．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF 于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF=2S△ABE，其中正确结论有（）A．2个B．3个C．4个D．5个19．二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（）A．2个B．3个C．4个D．5个20．如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（）A．B．C．D．二、填空题（本小题共4小题，每小题3分，共12分）21．因式分解2x4﹣2= ．22．方程=的解为．23．如图，正三角形ABC的边长是2，分别以点B，C为圆心，以r为半径作两条弧，设两弧与边BC围成的阴影部分面积为S，当r=时，S为．24．如图，在平面直角坐标系中，直线l经过原点，且与y轴正半轴所夹的锐角为60°，过点A（0，1）作y轴的垂线l于点B，过点B1作直线l的垂线交y轴于点A1，以A1B、BA 为邻边作▱ABA1C1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2，以A2B1、B1A1为邻边作▱A1B1A2C2；…；按此作法继续下去，则C2017的坐标是．三、解答题（本题共5小题，48分）25．（8分）甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天，且甲队单独施工45天和乙队单独施工30天的工作量相同．（1）甲、乙两队单独完成此项任务需要多少天？（2）若甲、乙两队共同工作了3天后，乙队因设备检修停止施工，由甲队继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？26．（8分）如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直与x轴，垂足为点B，反比例函数y=（x＞0）的图象经过AO的中点C，且与AB相交于点D，OB=4，AD=3，（1）求反比例函数y=的解析式；（2）求cos∠OAB的值；（3）求经过C、D两点的一次函数解析式．27．（10分）已知∠ACD=90°，MN是过点A的直线，AC=DC，DB⊥MN于点B，如图（1），易证BD+AB=CB，过程如下：过点C 作CE ⊥CB 于点C ，与MN 交于点E ∵∠ACB+∠BCD=90°，∠ACB+∠ACE=90°，∴∠BCD=∠ACE ．∵四边形ACDB 内角和为360°，∴∠BDC+∠CAB=180°． ∵∠EAC+∠CAB=180°，∴BD+AB=CB ．∴∠EAC=∠BDC 又∵AC=DC ， ∴△ACE ≌△DCB ， ∴AE=DB ，CE=CB ， ∴△ECB 为等腰直角三角形，∴BE=CB ．又∵BE=AE+AB ， ∴BE=BD+AB ．（1）当MN 绕A 旋转到如图（2）和图（3）两个位置时，BD 、AB 、CB 满足什么样关系式，请写出你的猜想，并对图（3）给予证明． （2）MN 在绕点A 旋转过程中，当∠BCD=30°，BD=时，则CD= ，CB= ．28．（10分）如图1，在Rt △ABC 中，∠BAC=90°，AD ⊥BC 于点D ，点O 是AC 边上一点，连接BO 交AD 于F ，OE ⊥OB 交BC 边于点E ． （1）求证：△ABF ∽△COE ； （2）当O 为AC 的中点，时，如图2，求的值； （3）当O 为AC 边中点，时，请直接写出的值．29．（12分）如图，已知抛物线y=x 2+bx+c 经过△ABC 的三个顶点，其中点A （0，1），点B （﹣9，10），AC ∥x 轴，点P 是直线AC 下方抛物线上的动点． （1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．2018年中考数学二模试卷参考答案与试题解析一、选择题（本大题共20小题，每小题3分，共60分）1．（﹣）﹣1的倒数是（）A．B．C．﹣ D．﹣【考点】6F：负整数指数幂；17：倒数．【分析】先计算负整数指数幂，再依据倒数的定义可得．【解答】解：∵（﹣）﹣1=﹣，∴（﹣）﹣1的倒数为﹣，故选：C．【点评】本题主要考查负整数指数幂和倒数的定义，熟练掌握负整数指数幂是解题的关键．2．下列计算正确的是（）A．（﹣3a）2+4a2=a2B．3a2﹣（﹣2a）2=﹣a2C．3a•4a2=12a2D．（3a2）2÷4a2=a2【考点】4I：整式的混合运算．【分析】各项计算得到结果，即可作出判断．【解答】解：A、原式=9a2+4a2=13a2，不符合题意；B、原式=3a2﹣4a2=﹣a2，符合题意；C、原式=12a3，不符合题意；D、原式=9a4÷4a2=a2，不符合题意，故选B【点评】此题考查了整式的混合运算，熟练掌握公式及法则是解本题的关键．3．已知点M（1﹣2m，m﹣1）关于原点的对称点在第一象限，则m的取值范围在数轴上表示正确的是（）A．B．C．D．【考点】R6：关于原点对称的点的坐标；C4：在数轴上表示不等式的解集；CB：解一元一次不等式组．【分析】先确定出点M在第三象限，然后根据第三象限内点的横坐标与纵坐标都是负数列出不等式组，然后求解得到m的取值范围，从而得解．【解答】解：∵点M（1﹣2m，m﹣1）关于原点的对称点在第一象限，∴点M（1﹣2m，m﹣1）在第三象限，∴，解不等式①得，m＞，解不等式②得，m＜1，所以，m的取值范围是＜m＜1，在数轴上表示如下：．故选C．【点评】本题主要考查了平面直角坐标系中，各象限内点的坐标的符号的确定方法，以及关于原点对称的两点坐标之间的关系以及一元一次不等式组的解法．4．下列图形是几家电信公司的标志，其中既是轴对称图形又是中心对称图形的是（）A．B．C．D．【考点】P3：轴对称图形；R5：中心对称图形．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、不是轴对称图形，也不是中心对称图形．故错误；B、不是轴对称图形，也不是中心对称图形．故错误；C、是轴对称图形，也是中心对称图形．故正确；D、不是轴对称图形，是中心对称图形．故错误．故选C．【点评】掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180°后与原图重合．5．化简÷（1+）的结果是（）A．B．C．D．【考点】6C：分式的混合运算．【分析】首先对括号内的式子通分相加，然后把除法转化成乘法，进行约分即可．【解答】解：原式=÷=•=．故选A．【点评】本题主要考查分式的混合运算，通分、因式分解和约分是解答的关键．6．长方体的主视图、俯视图如图所示（单位：m），则其左视图面积是（）A．4m2B．12m2C．1m2D．3m2【考点】U3：由三视图判断几何体．【分析】左视图面积=宽×高．【解答】解：由主视图易得高为1，由俯视图易得宽为3．∴左视图面积=1×3=3（m2）．故选D．【点评】主视图确定物体的长与高；俯视图确定物体的长与宽．7．某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）A．50（1+x2）=196 B．50+50（1+x2）=196C．50+50（1+x）+50（1+x）2=196 D．50+50（1+x）+50（1+2x）=196【考点】AC：由实际问题抽象出一元二次方程．【分析】主要考查增长率问题，一般增长后的量=增长前的量×（1+增长率），如果该厂八、九月份平均每月的增长率为x，那么可以用x分别表示八、九月份的产量，然后根据题意可得出方程．【解答】解：依题意得八、九月份的产量为50（1+x）、50（1+x）2，∴50+50（1+x）+50（1+x）2=196．故选C．【点评】本题考查了由实际问题抽象出一元二次方程，增长率问题，一般形式为a（1+x）2=b，a为起始时间的有关数量，b为终止时间的有关数量．8．2017年“端午节”期间，小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩，小明与小亮通过抽签方式确定景点，则两家都抽到东营港的概率是（）A．B．C．D．【考点】X6：列表法与树状图法．【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两家抽到东营港的情况，再利用概率公式求解即可求得答案．【解答】解：用A、B、C表示：东营港、黄河入海口、龙悦湖；画树状图得：∵共有9种等可能的结果，则两家都抽到东营港的有3种情况，∴则两家都抽到东营港的概率是=；故选D．【点评】本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．9．已知空气的单位体积质量为1.24×10﹣3克/厘米3，1.24×10﹣3用小数表示为（）A．0.000124 B．0.0124 C．﹣0.00124 D．0.00124【考点】1K：科学记数法—原数．【分析】科学记数法的标准形式为a×10n（1≤|a|＜10，n为整数）．本题把数据“1.24×10﹣3中1.24的小数点向左移动3位就可以得到．【解答】解：把数据“1.24×10﹣3中1.24的小数点向左移动3位就可以得到为0.001 24．故选D．【点评】本题考查写出用科学记数法表示的原数．将科学记数法a×10﹣n表示的数，“还原”成通常表示的数，就是把a的小数点向左移动n 位所得到的数．把一个数表示成科学记数法的形式及把科学记数法还原是两个互逆的过程，这也可以作为检查用科学记数法表示一个数是否正确的方法．10．某班七个合作学习小组人数如下：4、5、5、x、6、7、8，已知这组数据的平均数是6，则这组数据的中位数是（）A．5 B．5.5 C．6 D．7【考点】W4：中位数；W1：算术平均数．【分析】根据平均数的定义先求出这组数据x，再将这组数据从小到大排列，然后找出最中间的数即可．【解答】解：∵4、5、5、x、6、7、8的平均数是6，∴（4+5+5+x+6+7+8）÷7=6，解得：x=7，将这组数据从小到大排列为4、5、5、6、7、7、8，最中间的数是6；则这组数据的中位数是6；故选：C．【点评】此题考查了中位数，掌握中位数的概念是解题的关键，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）．11．把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长为（）A．B．5 C．4 D．【考点】R2：旋转的性质．【分析】先求出∠ACD=30°，再根据旋转角求出∠ACD1=45°，然后判断出△ACO是等腰直角三角形，再根据等腰直角三角形的性质求出AO、CO，AB⊥CO，再求出OD1然后利用勾股定理列式计算即可得解．【解答】解：∵∠ACB=∠DEC=90°，∠D=30°，∴∠DCE=90°﹣30°=60°，∴∠ACD=90°﹣60°=30°，∵旋转角为15°，∴∠ACD1=30°+15°=45°，又∵∠A=45°，∴△ACO是等腰直角三角形，∴AO=CO=AB=×6=3，AB⊥CO，∵DC=7，∴D1C=DC=7，∴D1O=7﹣3=4，在Rt△AOD1中，AD1===5．故选B．【点评】本题考查了旋转的性质，等腰直角三角形的判定与性质，勾股定理的应用，根据等腰直角三角形的性质判断出AB⊥CO是解题的关键，也是本题的难点．12．如图，直线y=与双曲线y=（k＞0，x＞0）交于点A，将直线y=向上平移4个单位长度后，与y轴交于点C，与双曲线y=（k＞0，x＞0）交于点B，若OA=3BC，则k 的值为（）A．3 B．6 C．D．【考点】GB：反比例函数综合题．【分析】先根据一次函数平移的性质求出平移后函数的解析式，再分别过点A、B作AD⊥x 轴，BE⊥x轴，CF⊥BE于点F，再设A（3x， x），由于OA=3BC，故可得出B（x， x+4），再根据反比例函数中k=xy为定值求出x【解答】解：∵将直线y=向上平移4个单位长度后，与y轴交于点C，∴平移后直线的解析式为y=x+4，分别过点A、B作AD⊥x轴，BE⊥x轴，CF⊥BE于点F，设A（3x， x），∵OA=3BC，BC∥OA，CF∥x轴，∴△BCF∽△AOD，∴CF=OD，∵点B在直线y=x+4上，∴B（x， x+4），∵点A、B在双曲线y=上，∴3x•x=x•（x+4），解得x=1，∴k=3×1××1=．故选：D．【点评】本题考查的是反比例函数综合题，根据题意作出辅助线，设出A、B两点的坐标，再根据k=xy的特点求出k的值即可．13．如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为（）A． cm B． cm C． cm D．4cm【考点】M4：圆心角、弧、弦的关系；KD：全等三角形的判定与性质；KQ：勾股定理．【分析】连接OD，OC，作DE⊥AB于E，OF⊥AC于F，运用圆周角定理，可证得∠DOB=∠OAC，即证△AOF≌△OED，所以OE=AF=3cm，根据勾股定理，得DE=4cm，在直角三角形ADE中，根据勾股定理，可求AD的长．【解答】解：连接OD，OC，作DE⊥AB于E，OF⊥AC于F，∵∠CAD=∠BAD（角平分线的性质），∴=，∴∠DOB=∠OAC=2∠BAD，∴△AOF≌△ODE，∴OE=AF=AC=3（cm），在Rt△DOE中，DE==4（cm），在Rt△ADE中，AD==4（cm）．故选：A．【点评】本题考查了翻折变换及圆的有关计算，涉及圆的题目作弦的弦心距是常见的辅助线之一，注意熟练运用垂径定理、圆周角定理和勾股定理．14．如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，则sin∠CBD的值等于（）A．OM的长B．2OM的长C．CD的长D．2CD的长【考点】M5：圆周角定理；T1：锐角三角函数的定义．【分析】作直径AE，连接BE．得直角三角形ABE．根据圆周角定理可证∠CBD=∠MAO，运用三角函数定义求解．【解答】解：连接AO并延长交圆于点E，连接BE．则∠C=∠E，由AE为直径，且BD⊥AC，得到∠BDC=∠ABE=90°，所以△ABE和△BCD都是直角三角形，所以∠CBD=∠EAB．又△OAM是直角三角形，∵AO=1，∴sin∠CBD=sin∠EAB==OM，即sin∠CBD的值等于OM的长．故选：A．【点评】考查了圆周角定理和三角函数定义．此题首先要观察题目涉及的线段，然后根据已知条件结合定理进行角的转换．15．若正比例函数y=mx（m≠0），y随x的增大而减小，则它和二次函数y=mx2+m的图象大致是（）A．B．C．D．【考点】H2：二次函数的图象；F4：正比例函数的图象．【分析】由y=mx（m≠0），y随x的增大而减小，推出m＜0，可知二次函数y=mx2+m的图象的开口向下，与y则交于负半轴上，由此即可判断．【解答】解：∵y=mx（m≠0），y随x的增大而减小，∴m＜0，∴二次函数y=mx2+m的图象的开口向下，与y则交于负半轴上，故选A．【点评】本题参考二次函数的性质、正比例函数的性质等知识，解题的关键是熟练掌握正比例函数以及二次函数的性质，属于中考常考题型．16．如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD；其中正确结论的是（）A．①②③B．①②④C．①③④D．②③④【考点】L9：菱形的判定；KK：等边三角形的性质；KO：含30度角的直角三角形．【分析】根据已知先判断△ABC≌△EFA，则∠AEF=∠BAC，得出EF⊥AC，由等边三角形的性质得出∠BDF=30°，从而证得△DBF≌△EFA，则AE=DF，再由FE=AB，得出四边形ADFE为平行四边形而不是菱形，根据平行四边形的性质得出AD=4AG，从而得到答案．【解答】解：∵△ACE是等边三角形，∴∠EAC=60°，AE=AC，∵∠BAC=30°，∴∠FAE=∠ACB=90°，AB=2BC，∵F为AB的中点，∴AB=2AF，∴BC=AF，∴△ABC≌△EFA，∴FE=AB，∴∠AEF=∠BAC=30°，∴EF⊥AC，故①正确，∵EF⊥AC，∠ACB=90°，∴HF∥BC，∵F是AB的中点，∴HF=BC，∵BC=AB，AB=BD，∴HF=BD，故④说法正确；∵AD=BD，BF=AF，∴∠DFB=90°，∠BDF=30°，∵∠FAE=∠BAC+∠CAE=90°，∴∠DFB=∠EAF，∵EF⊥AC，∴∠AEF=30°，∴∠BDF=∠AEF，∴△DBF≌△EFA（AAS），∴AE=DF，∵FE=AB，∴四边形ADFE为平行四边形，∵AE≠EF，∴四边形ADFE不是菱形；故②说法不正确；∴AG=AF，∴AG=AB，∵AD=AB，则AD=4AG，故③说法正确，故选：C．【点评】本题考查了菱形的判定和性质，以及全等三角形的判定和性质，解决本题需先根据已知条件先判断出一对全等三角形，然后按排除法来进行选择．17．如图，点E是矩形ABCD的边CD上一点，把△ADE沿AE对折，点D的对称点F恰好落在BC上，已知折痕AE=10cm，且tan∠EFC=，那么该矩形的周长为（）A．72cm B．36cm C．20cm D．16cm【考点】LB：矩形的性质；PB：翻折变换（折叠问题）．【分析】根据矩形的性质可得AB=CD，AD=BC，∠B=∠D=90°，再根据翻折变换的性质可得∠AFE=∠D=90°，AD=AF，然后根据同角的余角相等求出∠BAF=∠EFC，然后根据tan∠EFC=，设BF=3x、AB=4x，利用勾股定理列式求出AF=5x，再求出CF，根据tan∠EFC=表示出CE并求出DE，最后在Rt△ADE中，利用勾股定理列式求出x，即可得解．【解答】解：在矩形ABCD中，AB=CD，AD=BC，∠B=∠D=90°，∵△ADE沿AE对折，点D的对称点F恰好落在BC上，∴∠AFE=∠D=90°，AD=AF，∵∠EFC+∠AFB=180°﹣90°=90°，∠BAF+∠AFB=90°，∴∠BAF=∠EFC，∵tan∠EFC=，∴设BF=3x、AB=4x，在Rt△ABF中，AF===5x，∴AD=BC=5x，∴CF=BC﹣BF=5x﹣3x=2x，∵tan∠EFC=，∴CE=CF•tan∠EFC=2x•=x，∴DE=CD﹣CE=4x﹣x=x，在Rt△ADE中，AD2+DE2=AE2，即（5x）2+（x）2=（10）2，整理得，x2=16，解得x=4，∴AB=4×4=16cm，AD=5×4=20cm，矩形的周长=2（16+20）=72cm．故选A．【点评】本题考查了矩形的对边相等，四个角都是直角的性质，锐角三角函数，勾股定理的应用，根据正切值设出未知数并表示出图形中的各线段是解题的关键，也是本题的难点．18．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF 于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF=2S△ABE，其中正确结论有（）A．2个B．3个C．4个D．5个【考点】LE：正方形的性质；KD：全等三角形的判定与性质；KK：等边三角形的性质．【分析】通过条件可以得出△ABE≌△ADF，从而得出∠BAE=∠DAF，BE=DF，由正方形的性质就可以得出EC=FC，就可以得出AC垂直平分EF，设EC=x，BE=y，由勾股定理就可以得出x 与y的关系，表示出BE与EF，利用三角形的面积公式分别表示出S△CEF和2S△ABE，再通过比较大小就可以得出结论．【解答】解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°．∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°．∴∠BAE+∠DAF=30°．在Rt△ABE和Rt△ADF中，，Rt△ABE≌Rt△ADF（HL），∴BE=DF（故①正确）．∠BAE=∠DAF，∴∠DAF+∠DAF=30°，即∠DAF=15°（故②正确），∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∵AE=AF，∴AC垂直平分EF．（故③正确）．设EC=x，由勾股定理，得EF=x，CG=x，AG=AEsin60°=EFsin60°=2×CGsin60°=x，∴AC=，∴AB=，∴BE=﹣x=，∴BE+DF=x﹣x≠x，（故④错误），∵S△CEF=x2，S△ABE=x2，∴2S△ABE=x2=S△CEF，（故⑤正确）．综上所述，正确的有4个，故选：C．【点评】本题考查了正方形的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，等边三角形的性质的运用，三角形的面积公式的运用，解答本题时运用勾股定理的性质解题时关键．19．二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（）A．2个B．3个C．4个D．5个【考点】H4：二次函数图象与系数的关系．【分析】（1）正确．根据对称轴公式计算即可．（2）错误，利用x=﹣3时，y＜0，即可判断．（3）正确．由图象可知抛物线经过（﹣1，0）和（5，0），列出方程组求出a、b即可判断．（4）错误．利用函数图象即可判断．（5）正确．利用二次函数与二次不等式关系即可解决问题．【解答】解：（1）正确．∵﹣ =2，∴4a+b=0．故正确．（2）错误．∵x=﹣3时，y＜0，∴9a﹣3b+c＜0，∴9a+c＜3b，故（2）错误．（3）正确．由图象可知抛物线经过（﹣1，0）和（5，0），∴解得，∴8a+7b+2c=8a﹣28a﹣10a=﹣30a，∵a＜0，∴8a+7b+2c＞0，故（3）正确．（4）错误，∵点A（﹣3，y1）、点B（﹣，y2）、点C（，y3），∵﹣2=，2﹣（﹣）=，∴＜∴点C离对称轴的距离近，∴y3＞y2，∵a＜0，﹣3＜﹣＜2，∴y1＜y2∴y1＜y2＜y3，故（4）错误．（5）正确．∵a＜0，∴（x+1）（x﹣5）=﹣3/a＞0，即（x+1）（x﹣5）＞0，故x＜﹣1或x＞5，故（5）正确．∴正确的有三个，故选B．【点评】本题考查二次函数与系数关系，灵活掌握二次函数的性质是解决问题的关键，学会利用图象信息解决问题，属于中考常考题型．20．如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（）A．B．C．D．【考点】E7：动点问题的函数图象．【分析】由点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，得到BE=CF=t，则CE=8﹣t，再根据正方形的性质得OB=OC，∠OBC=∠OCD=45°，然后根据“SAS”可判断△OBE≌△OCF，所以S△OBE=S△OCF，这样S四边形OECF=S△OBC=16，于是S=S四边形OECF﹣S△CEF=16﹣（8﹣t）•t，然后配方得到S=（t﹣4）2+8（0≤t≤8），最后利用解析式和二次函数的性质对各选项进行判断．【解答】解：根据题意BE=CF=t，CE=8﹣t，∵四边形ABCD为正方形，∴OB=OC，∠OBC=∠OCD=45°，∵在△OBE和△OCF中，∴△OBE≌△OCF（SAS），∴S△OBE=S△OCF，∴S四边形OECF=S△OBC=×82=16，∴S=S四边形OECF﹣S△CEF=16﹣（8﹣t）•t=t2﹣4t+16=（t﹣4）2+8（0≤t≤8），∴s（cm2）与t（s）的函数图象为抛物线一部分，顶点为（4，8），自变量为0≤t≤8．故选：B．【点评】本题考查了动点问题的函数图象：先根据几何性质得到与动点有关的两变量之间的函数关系，然后利用函数解析式和函数性质画出其函数图象，注意自变量的取值范围．二、填空题（本小题共4小题，每小题3分，共12分）21．因式分解2x4﹣2= 2（x2+1）（x+1）（x﹣1）．【考点】55：提公因式法与公式法的综合运用．【分析】首先提公因式2，然后利用平方差公式即可分解．【解答】解：原式=2（x4﹣1）=2（x2+1）（x2﹣1）=2（x2+1）（x+1）（x﹣1）．故答案是：2（x2+1）（x+1）（x﹣1）．【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．22．方程=的解为x=2 ．【考点】B3：解分式方程．【分析】方程两边都乘以最简公分母（x﹣1）（2x+1）把分式方程化为整式方程，求解后进行检验．【解答】解：方程两边都乘以（x﹣1）（2x+1）得，2x+1=5（x﹣1），解得x=2，检验：当x=2时，（x﹣1）（2x+1）=（2﹣1）×（2×2+1）=5≠0，所以，原方程的解是x=2．故答案为：x=2．【点评】本题考查了解分式方程，（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．23．如图，正三角形ABC的边长是2，分别以点B，C为圆心，以r为半径作两条弧，设两弧与边BC围成的阴影部分面积为S，当r=时，S为﹣1 ．【考点】MO：扇形面积的计算．【分析】首先求出S关于r的函数表达式，分析其增减性；然后根据r的取值，求出S的最大值与最小值，从而得到S的取值．【解答】解：如右图所示，过点D作DG⊥BC于点G，易知G为BC的中点，CG=1，在Rt△CDG中，由勾股定理得：DG==，设∠DCG=θ，则由题意可得：S=2（S扇形CDE﹣S△CDG）=2（﹣×1×）=﹣，∴S=﹣．当r增大时，∠DCG=θ随之增大，故S随r的增大而增大．当r=时，DG=1，∵CG=1，故θ=45°，∴S=﹣=﹣1，故答案为：﹣1．【点评】本题考查扇形面积的计算、等边三角形的性质、勾股定理等重要知识点．解题关键是求出S的函数表达式．24．如图，在平面直角坐标系中，直线l经过原点，且与y轴正半轴所夹的锐角为60°，过点A（0，1）作y轴的垂线l于点B，过点B1作直线l的垂线交y轴于点A1，以A1B、BA 为邻边作▱ABA1C1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2，以A2B1、B1A1为邻边作▱A1B1A2C2；…；按此作法继续下去，则C2017的坐标是（﹣×42016，42017）．【考点】F8：一次函数图象上点的坐标特征；D2：规律型：点的坐标；L5：平行四边形的性质．【分析】先求出直线l的解析式为y=x，设B点坐标为（x，1），根据直线l经过点B，求出B点坐标为（，1），解Rt△A1AB，得出AA1=3，OA1=4，由平行四边形的性质得出A1C1=AB=，则C1点的坐标为（﹣，4），即（﹣×40，41）；根据直线l经过点B1，求出B1点坐标为（4，4），解Rt△A2A1B1，得出A1A2=12，OA2=16，由平行四边形的性质得出A2C2=A1B1=4，则C2点的坐标为（﹣4，16），即（﹣×41，42）；同理，可得C3点的坐标为（﹣16，64），即（﹣×42，43）；进而得出规律，求得C n的坐标是（﹣×4n﹣1，4n），即可求得C2017的坐标．【解答】解：∵直线l经过原点，且与y轴正半轴所夹的锐角为60°，∴直线l的解析式为y=x，∵AB⊥y轴，点A（0，1），∴可设B点坐标为（x，1），将B（x，1）代入y=x，得1=x，解得x=，∴B点坐标为（，1），AB=．在Rt△A1AB中，∠AA1B=90°﹣60°=30°，∠A1AB=90°，∴AA1=AB=3，OA1=OA+AA1=1+3=4，∵▱ABA1C1中，A1C1=AB=，∴C1点的坐标为（﹣，4），即（﹣×40，41）；由x=4，解得x=4，∴B1点坐标为（4，4），A1B1=4．在Rt△A2A1B1中，∠A1A2B1=30°，∠A2A1B1=90°，∴A1A2=A1B1=12，OA2=OA1+A1A2=4+12=16，∵▱A1B1A2C2中，A2C2=A1B1=4，∴C2点的坐标为（﹣4，16），即（﹣×41，42）；同理，可得C3点的坐标为（﹣16，64），即（﹣×42，43）；以此类推，则C n的坐标是（﹣×4n﹣1，4n），∴C2017的坐标是（﹣×42016，42017）．故答案为（﹣×42016，42017）．【点评】本题考查了平行四边形的性质，解直角三角形以及一次函数的综合应用，先分别求出C1、C2、C3点的坐标，从而发现规律是解题的关键．三、解答题（本题共5小题，48分）25．甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天，且甲队单独施工45天和乙队单独施工30天的工作量相同．（1）甲、乙两队单独完成此项任务需要多少天？（2）若甲、乙两队共同工作了3天后，乙队因设备检修停止施工，由甲队继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？【考点】B7：分式方程的应用；C9：一元一次不等式的应用．【分析】（1）设乙队单独完成此项任务需要x天，则甲队单独完成此项任务需要（x+10）天，根据甲队单独施工45天和乙队单独施工30天的工作量相同建立方程求出其解即可；（2）设甲队再单独施工a天，根据甲队总的工作量不少于乙队的工作量的2倍建立不等式求出其解即可．【解答】解：（1）设乙队单独完成此项任务需要x天，则甲队单独完成此项任务需要（x+10）天，由题意，得，解得：x=20．经检验，x=20是原方程的解，∴x+10=30（天）答：甲队单独完成此项任务需要30天，乙队单独完成此项任务需要20天；（2）设甲队再单独施工a天，由题意，得，解得：a≥3．答：甲队至少再单独施工3天．【点评】本题是一道工程问题的运用，考查了工作时间×工作效率=工作总量的运用，列分式方程解实际问题的运用，分式方程的解法的运用，解答时验根是学生容易忽略的地方．26．如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直与x轴，垂足为点B，反比例函数y=（x＞0）的图象经过AO的中点C，且与AB相交于点D，OB=4，AD=3，（1）求反比例函数y=的解析式；（2）求cos∠OAB的值；（3）求经过C、D两点的一次函数解析式．【考点】G8：反比例函数与一次函数的交点问题；G6：反比例函数图象上点的坐标特征．【分析】（1）设点D的坐标为（4，m）（m＞0），则点A的坐标为（4，3+m），由点A的坐标表示出点C的坐标，根据C、D点在反比例函数图象上结合反比例函数图象上点的坐标特征即可得出关于k、m的二元一次方程，解方程即可得出结论；。
初三滨江二模数学试卷答案
一、选择题（每题5分，共50分）1. 答案：D解析：由题意可知，等腰三角形的底角相等，故选D。
2. 答案：A解析：根据勾股定理，直角三角形的两条直角边的平方和等于斜边的平方，故选A。
3. 答案：C解析：根据函数的性质，当x增大时，y也增大，故选C。
4. 答案：B解析：由题意可知，一次函数的斜率为负，故选B。
5. 答案：D解析：根据圆的性质，圆心到圆上任意一点的距离都相等，故选D。
6. 答案：A解析：由题意可知，等边三角形的三个角都相等，故选A。
7. 答案：C解析：根据三角函数的定义，正弦值为对边与斜边的比值，故选C。
8. 答案：B解析：由题意可知，平行四边形的对边平行且相等，故选B。
9. 答案：D解析：根据数列的性质，奇数项为正数，偶数项为负数，故选D。
10. 答案：A解析：由题意可知，等腰三角形的底角相等，故选A。
二、填空题（每题5分，共50分）11. 答案：4解析：由题意可知，等腰三角形的底边长为8，高为4，故底边上的中线长为4。
12. 答案：3解析：根据勾股定理，直角三角形的两条直角边的平方和等于斜边的平方，故斜边长为3。
13. 答案：2解析：由题意可知，一次函数的斜率为-1，故截距为2。
14. 答案：-1解析：由题意可知，一次函数的斜率为-1，故y的截距为-1。
15. 答案：2解析：根据圆的性质，圆心到圆上任意一点的距离都相等，故半径为2。
16. 答案：60°解析：由题意可知，等边三角形的每个角为60°，故选60°。
17. 答案：5解析：根据三角函数的定义，正弦值为对边与斜边的比值，故正弦值为5。
18. 答案：3解析：由题意可知，平行四边形的对边平行且相等，故对边长为3。
19. 答案：8解析：由题意可知，数列的公差为2，首项为2，故第n项为8。
20. 答案：90°解析：由题意可知，等腰三角形的底角相等，故顶角为90°。
三、解答题（每题20分，共80分）21. 答案：（1）证明：连接AB、CD，由题意可知，AB=CD，AC=BD，故四边形ABCD为平行四边形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018年浙江省杭州市滨江区中考数学二模试卷一、仔细选一选（本题有10个小题，每小题3分，共30分）每小题给出的四个选项中，只有一个是正确的1．（3分）﹣5的相反数是（）A．5 B．C．﹣5 D．0.52．（3分）长度分别为2，7，x的三条线段能组成一个三角形，x的值可以是（）A．4 B．5 C．7 D．93．（3分）在Rt△ABC中，∠C=90°，AB=5，BC=3，则cosA=（）A．B．C．D．4．（3分）如图，已知在Rt△ABC中，∠C=90°，AC=BC，AB=12，点P是Rt△ABC 的重心，则点P到AB所在直线的距离等于（）A．2 B．2 C．3 D．45．（3分）以下是某手机店1～4月的两张销售情况统计图，根据统计图，四个同学得出了以下四个结论，其中正确的为（）A．4月××手机销售额为60万元B．4月××手机销售额比3月有所上升C．3月××手机销售额比2月有所上升D．3月与4月××手机的销售额无法比较，只能比较该店销售总额6．（3分）课本上有一例题：求方程组的自然数解，是这样解的：因为x，y为自然数，列表尝试如下：x0123456y6543210 300x+150y900105012001350150016501800可见只有x=4，y=2符合这个方程组，所以方程组的解为，从上述过程可以看出，这个求方程组解的思路是（）A．先消元，然后转化为一元一次方程，解这个一元一次方程，即可得方程组的解B．先列出第一个方程组的解，再列出第二个方程的解，然后找出两个方程的公共解，即为所求的解C．先列出第一个方程的解，再将这些解顺次代入第二个方程进行检验，若等式成立，则可得方程组的解D．先任意给出一对自然数，假定是解，然后代入两个方程分别检验，两个都成立，则可得方程组的解7．（3分）若2x+5＜0．则（）A．x+1＜0 B．1﹣x＜0 C．＜﹣1 D．﹣2x＜128．（3分）在平面直角坐标系内P点的坐标是（cos30°，tan45°），则P点关于y 轴对称点P′的坐标为（）A．（﹣，﹣1）B．（﹣1，）C．（，﹣1）D．（﹣，1）9．（3分）如图，矩形ABCD中，AB=4，BC=3，将△ABC沿AC折叠，点B落到E 点，此时AE交CD于F，则AF：EF=（）A．24：7 B．25：7 C．2：1 D．3：110．（3分）对于二次函数y=ax2+（﹣2a）x（a＜0），下列说法正确的个数是（）①对于任何满足条件的a，该二次函数的图象都经过点（2，1）和（0，0）两点；②若该函数图象的对称轴为直线x=x0，则必有1＜x0＜2；③当x≥0时，y随x的增大而增大；④若P（4，y1），Q（4+m，y2）（m＞0）是函数图象上的两点，如果y1＞y2总成立，则a≤﹣．A．1个 B．2个 C．3个 D．4个二、认真填一填（本题有6个小题，每小题4分，共24分）11．（4分）实数4的算术平方根是．12．（4分）分解因式：x2y﹣y= ．13．（4分）一个布袋里装有4个只有颜色不同的球，其中3个红球，1个白球．从布袋摸出1个球，不放回，再摸出1个球，则两次摸到的球都是红球的概率是．14．（4分）在Rt△ABC中，∠ABC=90°，AB=2，BC=1，把△ABC分别绕直线AB 和BC旋转一周，所得几何体的全面积分别记作S1，S2，则S1：S2= ．15．（4分）已知⊙O的半径为7cm，直线l1∥l2，且l1与⊙O相切，圆心O到l2的距高为8cm，则l1与l2的距离为cm．16．（4分）▱ABCD中，CD=2，BC=4，BD=2，对角线AC，BD交于点O，将△CDO绕点O顺时针旋转，使点D落在AD上D′处，点C落在C'处，C′O交AD于点P，则△OPD′的面积是．三、全面答一答（本题有7个小题，共66分）解答应写出文字说明，证明过程或推演步骤17．（6分）甲、乙两人加工同一种直径为100mm的零件，现从它们加工好的零件中随机各抽取6个，量得它们的直径如下（单位：mm）甲：98，102，100，100，101，99乙：100，103，101，97，100，99（1）分别求出上述两组数据的平均数和方差；（2）结合（1）中的统计数据，请你评价两人的加工质量．18．（8分）如图1为一圆柱形零件，其底面为圆，如图2．（1）请用直尺和圆规作出图2圆的圆心（画出图形，不写作法，保留作图痕迹）；（2）已知该底面圆的直径为100mm，要在圆柱上用刀削出宽为28mm的一块平面，如图3，问吃刀深度h为多少？19．（8分）（1）如图1．△ABC中，∠C为直角，AC=6，BC=8，D，E两点分别从B，A开始同时出发，分别沿线段BC，AC向C点匀速运动，到C点后停止，他们的速度都为每秒1个单位，请问D点出发2秒后，△CDE的面积为多少？（2）如图2，将（1）中的条件“∠C为直角”改为∠C为钝角，其他条件不变，请问是否仍然存在某一时刻，使得△CDE的面积为△ABC面积的一半？若存在，请求出这一时刻，若不存在，请说明理由．20．（10分）如图，已知在正方形ABCD中，E，F分别是BC，CD上的点，AE⊥BF于点G．（1）求证：AE=BF；（2）如果E是BC的中点，求△ABG和四边形ADFG的面积的比．21．（10分）（1）如图1是一家唇膏卖家的礼品装，卖家采用了正三梭柱形盒子，里面刚好横放一支圆柱形唇膏，右图是其横载面，△ABC为正三角形．求这个包装盒空间的最大利用率（圆柱体积和纸盒容积的比）；（2）一个长宽高分别为l，b．h的长方体纸箱装满了一层高为h的圆柱形易拉罐如图2．求纸箱空间的利用率（易拉罐总体积和纸箱容积的比）；（3）比较上述两种包装方式的空间利用率哪个大？22．（12分）一次函数y=ax+b（a≠0）和反比例函数y=（k≠0）交于A，B两点，点A的坐标为（x0，y0）（1）若x0+y0=b，求a的值；（2）若A，B关于原点中心对称，且x0=﹣2，y0=2﹣b；①求一次函数和反比例函数的关系式；②取一次函数图象上一点P（﹣2+m，n1）其中m＞0且m≠2，反比例函数图象上一点Q（﹣2+m，n2），请比较n1，n2的大小．23．（12分）2016年12月华为瓦特实验室试验一种新型快充电池，充电时电池的电量y（%）是充电时间x（分）的一次函数，其中y≤100（%）．已知充电前电量为0（%），测得充电10分钟后电量达到100（%），充满电后手机马上开始连续工作，工作阶段电池电盘y是工作时间x的二次函数，如图所示，A是该二次函数顶点，又测得充满电后连续工作了40分钟，这时电量降为20（%），厂商规定手机充电时不能工作，电量小于10（%）时手机部分功能将被限制，不能正常工作．（1）求充电时和充电后使用阶段y关于x的函数表达式（不用写出取值范围）；（2）为获得更多实验数据，实验室计划在首次充满电并使用40分钟后停止工作再次充电，充电6分钟后再次工作，假定所有的实验条件不变请问第二次工作的时间多长（电量到10（%）就停止工作）？2018年浙江省杭州市滨江区中考数学二模试卷参考答案与试题解析一、仔细选一选（本题有10个小题，每小题3分，共30分）每小题给出的四个选项中，只有一个是正确的1．（3分）﹣5的相反数是（）A．5 B．C．﹣5 D．0.5【分析】根据相反数的定义，可得答案．【解答】解：﹣5的相反数是5，故选：A．【点评】本题考查了相反数，在一个数的前面加上负号就是这个数的相反数．2．（3分）长度分别为2，7，x的三条线段能组成一个三角形，x的值可以是（）A．4 B．5 C．7 D．9【分析】根据三角形的三边关系：①两边之和大于第三边，②两边之差小于第三边即可得到答案．【解答】解：7﹣2＜x＜7+2，5＜x＜9，只有选项C符合题意．故选：C．【点评】此题主要考查了三角形的三边关系，解题的关键是熟练掌握三角形的三边关系定理．3．（3分）在Rt△ABC中，∠C=90°，AB=5，BC=3，则cosA=（）A．B．C．D．【分析】首先利用勾股定理求得AC的长，然后利用余弦的定义即可求解．【解答】解：AC===4，则cosA==．故选：C．【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．4．（3分）如图，已知在Rt△ABC中，∠C=90°，AC=BC，AB=12，点P是Rt△ABC 的重心，则点P到AB所在直线的距离等于（）A．2 B．2 C．3 D．4【分析】连接CP并延长，交AB于D，根据重心的性质得到CD是△ABC的中线，PD=CD，根据直角三角形的性质求出CD，计算即可．【解答】解：连接CP并延长，交AB于D，∵P是Rt△ABC的重心，∴CD是△ABC的中线，PD=CD，∵∠C=90°，∴CD=AB=6，∵AC=BC，CD是△ABC的中线，∴CD⊥AB，∴PD=2，即点P到AB所在直线的距离等于2，故选：A．【点评】本题考查的是三角形的重心的概念和性质，三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．5．（3分）以下是某手机店1～4月的两张销售情况统计图，根据统计图，四个同学得出了以下四个结论，其中正确的为（）A．4月××手机销售额为60万元B．4月××手机销售额比3月有所上升C．3月××手机销售额比2月有所上升D．3月与4月××手机的销售额无法比较，只能比较该店销售总额【分析】根据××手机的销售额=当月手机销售总额×对应百分比对各选项逐一判断可得．【解答】解：A、4月××手机销售额为65×17%=11.05万元，此选项错误；B、3月××手机销售额为60×18%=10.8万元，所以4月××手机销售额比3月有所上升，此选项正确；C、2月××手机销售额为80×15%=12万元，3月××手机销售额比2月有所下降，此选项错误；D、3月××手机销售额为10.8万元、4月××手机销售额为11.05万元，此选项错误；故选：B．【点评】本题考查了条形统计图，利用销售总额乘以三星所占的百分比得出三星的销售额是解题关键．6．（3分）课本上有一例题：求方程组的自然数解，是这样解的：因为x，y为自然数，列表尝试如下：x0123456y6543210 300x+150y900105012001350150016501800可见只有x=4，y=2符合这个方程组，所以方程组的解为，从上述过程可以看出，这个求方程组解的思路是（）A．先消元，然后转化为一元一次方程，解这个一元一次方程，即可得方程组的解B．先列出第一个方程组的解，再列出第二个方程的解，然后找出两个方程的公共解，即为所求的解C．先列出第一个方程的解，再将这些解顺次代入第二个方程进行检验，若等式成立，则可得方程组的解D．先任意给出一对自然数，假定是解，然后代入两个方程分别检验，两个都成立，则可得方程组的解【分析】利用二元一次方程组的解的定义判断即可．【解答】解：从上述过程可以看出，这个求方程组解的思路是，先列出第一个方程的解，再将这些解顺次代入第二个方程进行检验，若等式成立，则可得方程组的解．故选：C．【点评】此题考查了二元一次方程组的解，以及一元一次方程的解，方程组的解即为能使方程组中两方程都成立的未知数的值．7．（3分）若2x+5＜0．则（）A．x+1＜0 B．1﹣x＜0 C．＜﹣1 D．﹣2x＜12【分析】利用不等式的基本性质，将两边不等式同时减去5再除以2，不等号的方向不变，即可得到不等式的解集．【解答】解：∵2x+5＜0∴移项，得2x＜﹣5，系数化1，得x＜﹣2.5，∴x+1＜0；故选：A．【点评】本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．8．（3分）在平面直角坐标系内P点的坐标是（cos30°，tan45°），则P点关于y 轴对称点P′的坐标为（）A．（﹣，﹣1）B．（﹣1，）C．（，﹣1）D．（﹣，1）【分析】直接利用特殊角的三角函数值代入，再利用关于y轴对称横坐标互为相反数进而得出答案．【解答】解：∵P点的坐标是（cos30°，tan45°），∴P（，1），∴P点关于y轴对称点P′的坐标为：（﹣，1）．故选：D．【点评】此题主要考查了关于y轴对称点的性质以及特殊角的三角函数值，正确记忆横纵坐标的关系是解题关键．9．（3分）如图，矩形ABCD中，AB=4，BC=3，将△ABC沿AC折叠，点B落到E 点，此时AE交CD于F，则AF：EF=（）A．24：7 B．25：7 C．2：1 D．3：1【分析】根据折叠的性质得到AE=AB，∠BAC=∠EAC，根据平行线的性质、等腰三角形的判定定理得到FD=FE，根据勾股定理计算即可．【解答】解：由折叠的性质可知，AE=AB，∠BAC=∠EAC，∵AB∥CD，∴∠BAC=∠DCA，∴∠EAC=∠DCA，∴FA=FC，∴FD=FE，在Rt△AFD中，AF2=AD2+DF2，即AF2=32+（4﹣AF）2，解得，AF=，∴DF=4﹣=，∴AF：EF=AF：DF=25：7，故选：B．【点评】本题考查的是翻转变换的性质、矩形的性质，翻转变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．10．（3分）对于二次函数y=ax2+（﹣2a）x（a＜0），下列说法正确的个数是（）①对于任何满足条件的a，该二次函数的图象都经过点（2，1）和（0，0）两点；②若该函数图象的对称轴为直线x=x0，则必有1＜x0＜2；③当x≥0时，y随x的增大而增大；④若P（4，y1），Q（4+m，y2）（m＞0）是函数图象上的两点，如果y1＞y2总成立，则a≤﹣．A．1个 B．2个 C．3个 D．4个【分析】根据函数的性质和函数的图形，依次分析①②③④，选出正确的即可．【解答】解：①把（2，1）和（0，0）代入二次函数，等号成立，故对于任何满足条件的a，该二次函数的图象都经过点（2，1）和（0，0）两点符合题意，①正确，②∵该二次函数的图象都经过点（2，1）和（0，0）两点，且a＜0，抛物线开口向下，∴对称轴x0≥2，故若该函数图象的对称轴为直线x=x0，则必有1＜x0＜2不符合题意，②错误，③当x≥0时，根据二次函数的性质，y先随x的增大而增大，到达顶点后，y随着x的增大而减小，故当x≥0时，y随x的增大而增大不符合题意，③错误，④若P（4，y1），Q（4+m，y2）（m＞0）是函数图象上的两点，如果y1＞y2总成立，说明抛物线对称轴x0=1﹣≤4，解得：a，④正确，即正确的为①④，故选：B．【点评】本题考查二次函数的性质和二次函数图象上点的坐标特征，掌握分析图象并结合函数性质解题的能力是解决本题的关键．二、认真填一填（本题有6个小题，每小题4分，共24分）11．（4分）实数4的算术平方根是2 ．【分析】依据算术平方根根的定义求解即可．【解答】解：∵22=4，∴4的算术平方根是2．故答案为：2．【点评】本题主要考查的是算术平方根的定义，掌握算术平方根的定义是解题的关键．12．（4分）分解因式：x2y﹣y= y（x+1）（x﹣1）．【分析】观察原式x2y﹣y，找到公因式y后，提出公因式后发现x2﹣1符合平方差公式，利用平方差公式继续分解可得．【解答】解：x2y﹣y，=y（x2﹣1），=y（x+1）（x﹣1），故答案为：y（x+1）（x﹣1）．【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．13．（4分）一个布袋里装有4个只有颜色不同的球，其中3个红球，1个白球．从布袋摸出1个球，不放回，再摸出1个球，则两次摸到的球都是红球的概率是．【分析】画树状图展示所有12种等可能的结果数，再找出两次都摸到红球的结果数然后根据概率公式求解．【解答】解：画树状图如下：，一共12种可能，两次都摸到红球的有6种情况，所以两次摸到的球都是红球的概率是=，故答案为：．【点评】此题考查的是用列表法或树状图法求概率．解题的关键是要注意是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．14．（4分）在Rt△ABC中，∠ABC=90°，AB=2，BC=1，把△ABC分别绕直线AB 和BC旋转一周，所得几何体的全面积分别记作S1，S2，则S1：S2= ．【分析】先利用勾股定理计算出AC，由于△ABC分别绕直线AB和BC旋转一周，所得几何体为底面半径为1和2的圆锥，所以根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长分别计算出两个圆的侧面积，从而得到S1，S2的值，最后计算它们的比值．【解答】解：∵∠ABC=90°，AB=2，BC=1，∴AC==，∴S1=π×12+×2π×1×=（+1）π，S2=π×22+×2π×2×=（2+4）π，∴S1：S2=（+1）π：（2+4）π=．故答案为．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．15．（4分）已知⊙O的半径为7cm，直线l1∥l2，且l1与⊙O相切，圆心O到l2的距高为8cm，则l1与l2的距离为1或15 cm．【分析】根据直线与圆的位置关系由l1与⊙O相切得到O点到l1的距离为7cm，而圆心O到l2的距离89cm，根据平行线间的距离的定义得到当圆心O在两平行直线之间：l1与l2之间的距离=8cm+7cm；当圆心O在两平行直线的同侧：l1与l2之间的距离为8cm﹣7cm．【解答】解：∵l1与⊙O相切，∴O点到l1的距离为7cm，当圆心O在两平行直线之间：l1与l2之间的距离=8cm+7cm=15cm；当圆心O在两平行直线的同侧：l1与l2之间的距离为8cm﹣7cm=1cm，∴l1到l2的距离为1cm或15cm．故答案为：1或15．【点评】本题考查了直线与圆的位置关系：设⊙O的半径为r，圆心O到直线l 的距离为d，直线l和⊙O相交⇔d＜r；直线l和⊙O相切⇔d=r；当直线l和⊙O 相离⇔d＞r．也考查了平行线间的距离．16．（4分）▱ABCD中，CD=2，BC=4，BD=2，对角线AC，BD交于点O，将△CDO绕点O顺时针旋转，使点D落在AD上D′处，点C落在C'处，C′O交AD于点P，则△OPD′的面积是．【分析】过点O作OE⊥AD，作C'F⊥AD，D'G⊥OC'，E，G，F为垂足，根据CD=2，BC=4，BD=2，可证△BCD是直角三角形，∠DBC=30°，可求△C'D'O各边长，以及GD'的长，由OE∥C'F可求OP的长，即可求△OPD′的面积．【解答】解：过点O作OE⊥AD，作C'F⊥AD，D'G⊥OC'，E，G，F为垂足∵CD=2，BC=4，BD=2∴CD2+BD2=4+12=16BC2=16∴CD2+BD2=BC2．∴∠BDC=90°∵sin∠DBC=，∴∠DBC=30°∵ABCD是平行四边形∴DO==BO，CO=AO，AD∥BC∴∠ADB=∠DCB=30°在Rt△DCO中，CO==∵旋转∴DO=D'O=，C'D'=2，∠C'D'O=90°，C'O=CO=∴∠DD'O=∠D'DO=30°，OE⊥AD∴∠C'D'D=60°，OE=DO=，∵C'F⊥AD，∠C'D'D=60°∴∠D'C'F=30°∴DF==1，C'F=DF=∵S='△C'D'O∴GD'=∵OE⊥AD，C'F⊥AD∴OE∥C'F∴且OP+C'P=OC'=∴OP='=×OP×GD'==∴S△OPD故答案为．【点评】本题考查旋转的性质，平行四边形的性质，勾股定理，平行线分线段成比例，关键是灵活运用这些性质解决问题．三、全面答一答（本题有7个小题，共66分）解答应写出文字说明，证明过程或推演步骤17．（6分）甲、乙两人加工同一种直径为100mm的零件，现从它们加工好的零件中随机各抽取6个，量得它们的直径如下（单位：mm）甲：98，102，100，100，101，99乙：100，103，101，97，100，99（1）分别求出上述两组数据的平均数和方差；（2）结合（1）中的统计数据，请你评价两人的加工质量．【分析】（1）直接利用平均数公式和方差公式计算得出答案；（2）直接利用（1）中所求结合方差的意义得出答案．【解答】解：（1）=（98+102+100+100+101+99）=100，=（100+103+101+97+100+99）=100，=[（98﹣100）2+（102﹣100）2+（100﹣100）2+（100﹣100）2+（101﹣100）2+（99﹣100）2]=；=[（100﹣100）2+（103﹣100）2+（101﹣100）2+（97﹣100）2+（100﹣100）2+（99﹣100）2]=；（2）平均数都等于标准值，但甲的方差比乙的方差小，所以甲的质量更好．【点评】此题主要考查了方差以及算术平方根，正确记忆方差公式是解题关键．18．（8分）如图1为一圆柱形零件，其底面为圆，如图2．（1）请用直尺和圆规作出图2圆的圆心（画出图形，不写作法，保留作图痕迹）；（2）已知该底面圆的直径为100mm，要在圆柱上用刀削出宽为28mm的一块平面，如图3，问吃刀深度h为多少？【分析】（1）在⊙O上任意取A、C、B三点，分别作线段AC、BC的垂直平分线，交点即为圆心O．（2）构造直角三角形解决问题即可；【解答】解：（1）如图2中，⊙O即为所求．（2 ）如图3中，作OH⊥EF于H，交⊙O于G．在Rt△OHF中，OF=50，FH=14，∴OH==48，∴GH=OG﹣OH=50﹣48=2即h=2 （mm））答：吃刀深度应为2mm．【点评】本题考查作图﹣应用与设计，垂径定理等知识，解题的关键是熟练掌握基本知识，学会构造直角三角形解决问题，属于中考常考题型．19．（8分）（1）如图1．△ABC中，∠C为直角，AC=6，BC=8，D，E两点分别从B，A开始同时出发，分别沿线段BC，AC向C点匀速运动，到C点后停止，他们的速度都为每秒1个单位，请问D点出发2秒后，△CDE的面积为多少？（2）如图2，将（1）中的条件“∠C为直角”改为∠C为钝角，其他条件不变，请问是否仍然存在某一时刻，使得△CDE的面积为△ABC面积的一半？若存在，请求出这一时刻，若不存在，请说明理由．【分析】（1）根据三角形的面积公式即可求出答案．（2）过B，D作AC边上的高DH，BG，设D，E运动时间为x秒，根据锐角三角函数可分别求出DH、BG，然后利用三角形面积公式即可求出答案．【解答】解：（1）2秒后（2）如图，过B，D作AC边上的高DH，BG设D，E运动时间为x秒，则（8﹣x）（6﹣x）sin∠BCG=××6×8sin∠BCG解得x=2或x=12（不合），所以D点出发2秒钟时△CDE的面积为△ABC面积的一半，【点评】本题考查一元二次方程的应用，解题的关键是熟练运用三角形的面积公式，本题属于中等题型．20．（10分）如图，已知在正方形ABCD中，E，F分别是BC，CD上的点，AE⊥BF于点G．（1）求证：AE=BF；（2）如果E是BC的中点，求△ABG和四边形ADFG的面积的比．【分析】（1）根据正方形的性质得到AB=BC，∠ABC=∠BCD=90°，得到△ABE≌△BCF，根据全等三角形的性质证明；（2）证明△ABG∽△BCF，根据相似三角形的面积比等于相似比的平方计算．【解答】（1）证明：∵四边形ABCD为正方形，∴AB=BC，∠ABC=∠BCD=90°，∵AE⊥BF，∴∠BAE=∠CBF，在△ABE和△BCF中，，∴△ABE≌△BCF，∴AE=BF；（2）解：∵∠BAE=∠CBF ，∠AGB=∠BCD=90°，∴△ABG ∽△BCF ，∵E 是BC 中点，∴AB ：BF=2：，∴S △ABG ：S △BCF =4：5，∵S △BCF ：S ABCD =5：20，∴S △ABG ：S ADFG =4：11．【点评】本题考查的是正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质，掌握相关的判定定理和性质定理是解题的关键．21．（10分）（1）如图1是一家唇膏卖家的礼品装，卖家采用了正三梭柱形盒子，里面刚好横放一支圆柱形唇膏，右图是其横载面，△ABC 为正三角形．求这个包装盒空间的最大利用率（圆柱体积和纸盒容积的比）；（2）一个长宽高分别为l ，b ．h 的长方体纸箱装满了一层高为h 的圆柱形易拉罐如图2．求纸箱空间的利用率（易拉罐总体积和纸箱容积的比）；（3）比较上述两种包装方式的空间利用率哪个大？【分析】（1）如图1，设⊙O 半径为r ，纸盒长度为h'，则CD=r ，BC=2r ．根据圆柱的体积和棱柱的体积公式分别求得圆柱型唇膏和纸盒的体积，然后求其比值；（2）求得易拉罐总体积和纸箱容积，然后求得比值；（3）利用（1）（2）的数据进行解答．【解答】解：（1）由题意，⊙O 是△ABC 内接圆，D 为切点，如图1，连结OD ，OC ．设⊙O 半径为r ，纸盒长度为h'，则CD=r ，BC=2r则圆柱型唇膏和纸盒的体积之比为：（）（2）易拉罐总体积和纸箱容积的比：=；（3）∵=∴第二种包装的空间利用率大．【点评】考查了勾股定理的应用，圆的有关计算，立体图形的体积公式，综合性较强，需要学生对所学知识的系统掌握．22．（12分）一次函数y=ax+b（a≠0）和反比例函数y=（k≠0）交于A，B两点，点A的坐标为（x0，y0）（1）若x0+y0=b，求a的值；（2）若A，B关于原点中心对称，且x0=﹣2，y0=2﹣b；①求一次函数和反比例函数的关系式；②取一次函数图象上一点P（﹣2+m，n1）其中m＞0且m≠2，反比例函数图象上一点Q（﹣2+m，n2），请比较n1，n2的大小．【分析】（1）利用待定系数法即可解决问题；（2）利用待定系数法把问题转化为方程组解决即可；（3）画出函数图象，利用图象法即可解决问题；【解答】解：（1）由x0+y0=b及把A（x0，y0）代入y=ax+b（a≠0）得，解得x0（a+1）=0，所以a+1=0，a=﹣1．（2）①由题意可知A的坐标为（﹣2，2﹣b），又A，B关于原点中心对称所以点B的坐标为（2，b﹣2）代入y=ax+b（a≠0）得，解得，代入得点A的坐标是（﹣2，2）且y=﹣x，∴．②由图象得当﹣2＜﹣2+m＜0，或﹣2+m＞2，即0＜m＜2，或m＞4使，n1＜n2，当0＜﹣2+m＜2，即2＜m＜4时，n1＞n2，当﹣2+m=2，即m=4时，n1=n2．【点评】本题考查反比例函数与一次函数的交点问题，解题的关键是熟练掌握待定系数法解决问题，学会利用图象法解决问题属于中考常考题型．23．（12分）2016年12月华为瓦特实验室试验一种新型快充电池，充电时电池的电量y（%）是充电时间x（分）的一次函数，其中y≤100（%）．已知充电前电量为0（%），测得充电10分钟后电量达到100（%），充满电后手机马上开始连续工作，工作阶段电池电盘y是工作时间x的二次函数，如图所示，A是该二次函数顶点，又测得充满电后连续工作了40分钟，这时电量降为20（%），厂商规定手机充电时不能工作，电量小于10（%）时手机部分功能将被限制，不能正常工作．（1）求充电时和充电后使用阶段y关于x的函数表达式（不用写出取值范围）；（2）为获得更多实验数据，实验室计划在首次充满电并使用40分钟后停止工作再次充电，充电6分钟后再次工作，假定所有的实验条件不变请问第二次工作的时间多长（电量到10（%）就停止工作）？【分析】（1）设充电时的函数表达式为y=kx+b，把点A的坐标代入即可，设充电后的函数表达式为y=a（x﹣10）2+100，把点（50，20）代入即可，（2）首次充满电并使用40分钟后，电量为20（%），充电6分钟，充电速率与（1）相同，求出此时电量y1，将y1与y=10分别代入二次函数解析式即可得解．【解答】解：（1）设充电时的函数表达式为y=kx+b，将A（10，100）代入y=kx得：k=10，即充电时函数表达式为：y=10x，因为二次函数顶点为A（10，100），且过点B（50，20）设y=a（x﹣10）2+100，再将（50，20）代入得：，所以，（2）开始充电时，电量为20（%），充电速率不变，充电6分钟，此时电量y1=20+10×6=80，当=80时，接的：x=﹣10（舍去）或x=30，把y=10代入二次函数解析式得：﹣（x﹣10）2+100=10解得：x=﹣30+10（舍去）或x=30+10，即：第二次工作的时间为30﹣10﹣30=30﹣20，答：第二次工作的时间为30﹣20（分钟）．【点评】本题考查了二次函数的应用，解题关键（1）利用待定系数法求解析式，（2）观察图象分析题意结合（1）的解析式进行求解．。