系统动力学模型
系统动力学模型在供应链管理中的应用和分析

系统动力学模型在供应链管理中的应用和分析供应链管理是指领导和协调一系列活动,以实现从原材料采购到最终产品交付的整个过程。
在复杂的全球化市场环境中,供应链管理变得越来越复杂,需要项目经理和管理团队不断优化和改进供应链中的各个环节,以提高效率、降低成本并提供更好的客户服务。
系统动力学(system dynamics)是一种用于模拟和理解系统行为的方法。
通过建立动态模型,系统动力学可以帮助我们了解和预测供应链中各个环节之间的相互作用、反馈机制以及如何应对变化。
一、系统动力学模型的构建1. 定义系统的边界和目标:在应用系统动力学模型前,需要明确供应链的边界和目标。
供应链可以被视为一个系统,包括供应商、制造商、分销商和客户等各环节。
边界的明确有助于确定建模的范围和目标。
2. 建立库存-订单循环模型:库存是供应链中重要的变量之一,它直接影响到供应链的效率和成本。
系统动力学模型可以帮助我们分析和优化库存管理策略,以减少库存水平并降低库存成本。
3. 考虑供需关系和反馈机制:供应链中的供需关系和反馈机制经常会导致波动和不稳定性。
建立系统动力学模型时,需要考虑这些相互作用和反馈,以更好地理解系统行为并采取相应的改进措施。
二、系统动力学模型在供应链管理中的应用1. 预测和规划:系统动力学模型能够帮助预测供应链中不同环节的需求,进而帮助企业制定更准确的生产和采购计划。
通过模拟不同的情景和变化,系统动力学模型可以帮助企业制定更灵活的供应链策略,以适应市场需求和变化。
2. 库存管理:库存是供应链中的重要因素,它直接关系到成本和客户服务水平。
通过建立系统动力学模型,企业可以更好地理解库存的变化和波动,从而制定更合理的库存管理策略。
模型可以帮助企业预测库存需求、库存水平和回应时间,并优化相应管理措施。
3. 供应链协同和协作:供应链中的各个环节之间存在相互依赖和协作关系。
系统动力学模型可以帮助企业建立一个集成的供应链网络,并分析供应链中不同环节之间的相互作用和反馈机制。
(完整版)系统动力学模型SD3

(19) rabbit births = Rabbit Population * rabbit birth rate Units: Rabbit/Year
(20) rabbit crowding = Rabbit Population/carrying capacity Units: Dmnl
建立表函数的原则
1. 建立表函数时大致要考虑:曲线的斜率和形状,一个或一个以上的特 殊点和参考曲线。
2. 设置曲线的斜率。使之与其表示的影响的性质吻合,负值斜率代表负 反馈,正值斜率代表正反馈。
3. 选择曲线的形状。小心确定在极端条件下和曲线中部的斜率与曲线的 值。
4. 尽可能在表函数上把x,y的特殊点标出,如:x,y分别取0和1时,极端 条件下的x,y值和某些研究问题所要求的特殊点。
LEVEL.K*CONST
LEVEL.K/LIFE
(GOAL.K-LEVEL.K)/ADJTM
LEVEL.K*AUX.K与LEVEL.K/AUX.K EFFECT.K+NORM.K(某些因素的影响作用+额定速率)
EFFECT.K*NORM.K(额定速率与某个(或几个)因子的乘积)
LEVEL.K*CONST
建立方程的目的:在于使模型能用计算机模拟(或得到解析 解),以研究模型假设中隐含的动力学特性,并确定解决问题 的方法与对策。
状态变量与Level方程 速率(变化率)方程 辅助方程 SD模型举例
5.1.1 状态变量与Level方程
状态变量是随时间而变化的积累量,是物质、能量与信息的储存环节。 如:人口、企业雇员人数、库存、生产能力、银行存款等。
系统动力学模型SD1

系统动力学模型 System Dynamics
系统动力学模型 System Dynamics
1.3 系统动力学理论基本观念
(八)开放复杂系统的其他重要性质
(1)在非平衡状态下运动、发展、进化是开放复杂系统的一个重 要动态行为特征。系统动力学所研究的系统,诸如社会、经济、生 态系统,都具有这一特性。
系统动力学模型 System Dynamics
系统动力学模型 System Dynamics
1.3 系统动力学研究问题的过程
建立数学的规范的模型是第三个步骤。
主要任务:用系统动力学语言表述系统及其结构
1)建立L,R,A,C诸方程; 2)确定与估计参数; 3)给所有N方程,C方程与表函数赋值。
系统动力学模型 System Dynamics
系统动力学模型 System Dynamics
系统动力学模型 System Dynamics
1.1 系统动力学—学科基础
系统动力学的学科基础可划分为三个层次:
(1)方法论——系统方法论。即其基本原则是将所研究 对象置于系统的形式中加以考察。
(2)技术科学和基础理论——主要有反馈理论、控制论、 信息论、非线性系统理论,大系统理论和正在发展中的 系统学。 (3)应用技术——计算机模拟技术。为了使系统动力学 的理论与方法能真正用于分析研究实际系统,使系统动 力学模型成为实际系统的“实验室”,必须借助计算机 模拟技术。如:社会经济动力学:经济理论、决策理论 和组织理论等。
系统动力学模型 System Dynamics
系统动力学模型 System Dynamics
1.2 系统动力学基ห้องสมุดไป่ตู้概念
模型:是客观存在的事物与系统的模仿、代表或替代物。 它描述客观事物与系统的内部结构、关系与法则。 如:脑力模型、物理模型、数学模型、计算机模型或者 前述模型的组合。
系统动力学九种模型

系统动力学九种模型标题:系统动力学九种模型:一种掌握复杂系统行为的有力工具引言:系统动力学是一门研究动态系统行为的学科,旨在通过模型和模拟来分析和预测系统的行为。
在系统动力学中,有九种常用的模型,它们分别从不同角度和层次探索和描述系统的行为。
本文将深入探讨系统动力学中的九种模型,并分享对这些模型的观点和理解。
第一部分:系统动力学简介与基本概念1.1 系统动力学的定义和应用领域1.2 动态系统和反馈环路的基本概念第二部分:系统动力学九种模型的介绍与分析2.1 流量模型:描述物质或信息在系统中的流动2.2 资源积累模型:描述资源的积累和消耗2.3 优先水平与延迟模型:描述不同的优先级和延迟对系统行为的影响2.4 饱和非线性模型:描述系统在达到饱和点后的行为变化2.5 非线性积分模型:描述系统内部非线性交互对整体行为的影响2.6 动态变化和叠加模型:描述系统多个变量之间的相互作用与叠加效应2.7 时滞模型:描述系统行为中存在的时间滞后和延迟2.8 分层模型:描述系统中的层次结构以及不同层次之间的相互作用2.9 非线性交互模型:描述系统中多个元素之间的非线性相互作用第三部分:系统动力学九种模型的应用案例分析3.1 商业经济领域中的应用案例3.2 环境与能源管理中的应用案例3.3 社会系统中的应用案例3.4 健康医疗领域中的应用案例第四部分:总结与回顾性内容4.1 对系统动力学九种模型的综合回顾4.2 对应用案例的总结与反思结论:系统动力学九种模型是一种有力的工具,能够揭示系统行为的本质和规律。
通过对这些模型的研究和应用,我们能够更深入地理解和预测复杂系统的行为。
在不同领域的实践中,系统动力学九种模型已经取得了许多成功的应用案例。
然而,我们也要意识到这些模型只是对现实世界的近似和抽象,对复杂系统行为的完整描述还需要我们的不断深入研究和探索。
(2000字)4.1 对系统动力学九种模型的综合回顾在前面的章节中,我们对系统动力学九种模型进行了详细的介绍。
系统动力学9种模型

系统动力学9种模型
1. 线性模型:描述系统中各个变量之间的线性关系。
2. 非线性模型:描述系统中各个变量之间的非线性关系,如指数、对数等。
3. 离散模型:描述系统中的变量在离散时间点上的演化。
4. 连续模型:描述系统中的变量在连续时间上的演化,通常使用微分方程表示。
5. 离散时间模型:描述系统中的变量在离散时间点上的演化,并考虑时间的影响。
6. 连续时间模型:描述系统中的变量在连续时间上的演化,并考虑时间的影响。
7. 混合模型:结合离散和连续时间的特点,描述系统中的变量的演化。
8. 离散状态模型:描述系统中的变量仅存在有限个离散状态的演化。
9. 连续状态模型:描述系统中的变量存在无穷个连续状态的演化。
系统动力学模型

系统动力学模型系统动力学模型是指它是一种分析和模拟物理系统及其动力学过程的数学技术。
它可以用来研究运动学,控制系统,流体动力学,形式力学,电学,冲击学和弹性动力学等领域的数学模型,并可用于实际的工程问题的解决。
系统动力学模型基于物理系统的动力学处理和控制问题,用来研究物体的运动行为。
例如,系统动力学模型可以用来探讨汽车的运动性,即汽车在不同条件下的行驶特性,以确定汽车行驶性能的最佳状态。
此外,系统动力学模型还可以模拟任意静力学,力学,流体力学或热力学系统的运动模式。
系统动力学模型的建立要求具备完备的物理基础知识,形成一个系统模型的首要任务是了解物理系统的特性和行为,因此必须确定物理系统的运动方程和力学特征,物理量的表达式在构建模型时必须明确。
模式构建完成后,需要求解模型,并将模型运用到实际问题中,用以求解物理过程及其动力学运行状态。
为此,我们可以使用计算机模拟技术来求解模型,用以检验结果的正确性和准确性。
系统动力学模型在很多领域中都发挥着重要的作用,例如机械系统的设计,控制系统的调整,电子电气系统的设计,机器人的控制,航空航天技术,建筑工程设计等。
例如,在机器人技术中,系统动力学模型可以模拟机器人的运动特性,帮助机器人决定如何完成任务。
此外,系统动力学模型在工程设计中也有广泛应用,可用于分析和解决工程设计问题,以便改善工程性能。
例如,系统动力学模型可以帮助分析和解决结构物振动问题,提高结构物的稳定性和耐久性,以及改善系统的可靠性。
此外,系统动力学模型也可以帮助优化控制系统的性能,以提高系统的功率和可靠性。
综上所述,系统动力学模型是一个强大的工具,可以帮助我们研究和分析物理系统及其动力学过程,从而有效地改善工程性能。
它在机械,控制,电子,航空航天等各个领域都有广泛的应用,并被广泛用来分析和解决工程设计问题。
系统动力学模型在物理系统控制中的应用

系统动力学模型在物理系统控制中的应用引言:物理系统的控制一直是科学研究和工程应用的重要领域。
近年来,随着科技的不断进步和计算机技术的快速发展,系统动力学模型在物理系统控制中的应用越来越受到关注。
系统动力学模型是一种描述和分析系统行为的数学工具,它能够帮助研究人员深入理解物理系统的运行机制,并为系统控制提供有效的方法和策略。
本文将探讨系统动力学模型在物理系统控制中的应用,并介绍其优势和挑战。
一、系统动力学模型的基本原理系统动力学模型是一种建立在物理系统动力学原理基础上的数学模型。
它通过描述系统的状态、变量和相互作用关系,来研究系统的行为和演化规律。
系统动力学模型主要包括状态方程、输入输出关系和参数估计等组成部分。
其中,状态方程描述了系统各个状态变量之间的演化关系,输入输出关系则描述了系统输入与输出之间的关系。
通过对系统动力学模型的建立和求解,可以预测系统的未来状态和行为,并制定相应的控制策略。
二、系统动力学模型在物理系统控制中的应用案例1. 汽车动力系统控制汽车动力系统是一个复杂的物理系统,其控制涉及到发动机、传动系统和车辆行驶等多个方面。
系统动力学模型可以帮助研究人员深入理解汽车动力系统的工作原理,并优化控制策略。
例如,通过建立发动机的燃烧过程模型和传动系统的动力学模型,可以实现对汽车动力输出的精确控制,提高燃油利用率和减少尾气排放。
2. 电力系统稳定控制电力系统是一个巨大而复杂的物理系统,其稳定控制涉及到发电、输电和用户负荷等多个环节。
系统动力学模型可以帮助研究人员分析电力系统的稳定性问题,并设计相应的控制策略。
例如,通过建立电力系统的节点电压和功率平衡方程模型,可以实现对电力系统的稳定控制,避免电力系统崩溃和停电。
三、系统动力学模型在物理系统控制中的优势1. 深入理解系统行为:系统动力学模型能够帮助研究人员深入理解物理系统的运行机制和行为规律,从而为系统控制提供更准确的理论基础。
2. 预测系统未来状态:系统动力学模型能够通过对系统的状态方程进行求解,预测系统的未来状态和行为,为系统控制提供预测和决策依据。
(完整版)系统动力学模型案例分析
系统动力学模型介绍1.系统动力学的思想、方法系统动力学对实际系统的构模和模拟是从系统的结构和功能两方面同时进行的。
系统的结构是指系统所包含的各单元以及各单元之间的相互作用与相互关系。
而系统的功能是指系统中各单元本身及各单元之间相互作用的秩序、结构和功能,分别表征了系统的组织和系统的行为,它们是相对独立的,又可以在—定条件下互相转化。
所以在系统模拟时既要考虑到系统结构方面的要素又要考虑到系统功能方面的因素,才能比较准确地反映出实际系统的基本规律。
系统动力学方法从构造系统最基本的微观结构入手构造系统模型。
其中不仅要从功能方面考察模型的行为特性与实际系统中测量到的系统变量的各数据、图表的吻合程度,而且还要从结构方面考察模型中各单元相互联系和相互作用关系与实际系统结构的一致程度。
模拟过程中所需的系统功能方面的信息,可以通过收集,分析系统的历史数据资料来获得,是属定量方面的信息,而所需的系统结构方面的信息则依赖于模型构造者对实际系统运动机制的认识和理解程度,其中也包含着大量的实际工作经验,是属定性方面的信息。
因此,系统动力学对系统的结构和功能同时模拟的方法,实质上就是充分利用了实际系统定性和定量两方面的信息,并将它们有机地融合在一起,合理有效地构造出能较好地反映实际系统的模型。
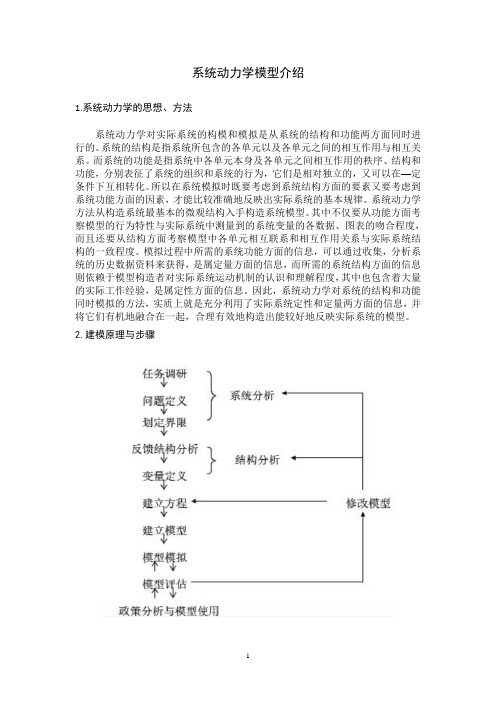
2.建模原理与步骤(1)建模原理用系统动力学方法进行建模最根本的指导思想就是系统动力学的系统观和方法论。
系统动力学认为系统具有整体性、相关性、等级性和相似性。
系统内部的反馈结构和机制决定了系统的行为特性,任何复杂的大系统都可以由多个系统最基本的信息反馈回路按某种方式联结而成。
系统动力学模型的系统目标就是针对实际应用情况,从变化和发展的角度去解决系统问题。
系统动力学构模和模拟的一个最主要的特点,就是实现结构和功能的双模拟,因此系统分解与系统综合原则的正确贯彻必须贯穿于系统构模、模拟与测试的整个过程中。
与其它模型一样,系统动力学模型也只是实际系统某些本质特征的简化和代表,而不是原原本本地翻译或复制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10章系统动力学模型系统动力学模型(System Dynamic)就是社会、经济、规划、军事等许多领域进行战略研究的重要工具,如同物理实验室、化学实验室一样,也被称之为战略研究实验室,自从问世以来,可以说就是硕果累累。
1 系统动力学概述2 系统动力学的基础知识3 系统动力学模型第1节系统动力学概述1、1 概念系统动力学就是一门分析研究复杂反馈系统动态行为的系统科学方法,它就是系统科学的一个分支,也就是一门沟通自然科学与社会科学领域的横向学科,实质上就就是分析研究复杂反馈大系统的计算仿真方法。
系统动力学模型就是指以系统动力学的理论与方法为指导,建立用以研究复杂地理系统动态行为的计算机仿真模型体系,其主要含义如下:1 系统动力学模型的理论基础就是系统动力学的理论与方法;2 系统动力学模型的研究对象就是复杂反馈大系统;3 系统动力学模型的研究内容就是社会经济系统发展的战略与决策问题,故称之为计算机仿真法的“战略与策略实验室”;4 系统动力学模型的研究方法就是计算机仿真实验法,但要有计算机仿真语言DYNAMIC的支持,如:PD PLUS,VENSIM等的支持;5 系统动力学模型的关键任务就是建立系统动力学模型体系;6 系统动力学模型的最终目的就是社会经济系统中的战略与策略决策问题计算机仿真实验结果,即坐标图象与二维报表;系统动力学模型建立的一般步骤就是:明确问题,绘制因果关系图,绘制系统动力学模型流图,建立系统动力学模型,仿真实验,检验或修改模型或参数,战略分析与决策。
地理系统也就是一个复杂的动态系统,因此,许多地理学者认为应用系统动力学进行地理研究将有极大潜力,并积极开展了区域发展,城市发展,环境规划等方面的推广应用工作,因此,各类地理系统动力学模型即应运而生。
1、2 发展概况系统动力学就是在20世纪50年代末由美国麻省理工学院史隆管理学院教授福雷斯特(JAY、W、FORRESTER)提出来的。
目前,风靡全世界,成为社会科学重要实验手段,它已广泛应用于社会经济管理科技与生态灯各个领域。
福雷斯特教授及其助手运用系统动力学方法对全球问题,城市发展,企业管理等领域进行了卓有成效的研究,接连发表了《工业动力学》,《城市动力学》,《世界动力学》,《增长的极限》等著作,引起了世界各国政府与科学家的普遍关注。
在我国关于系统动力学方面的研究始于1980年,后来,陆续做了大量的工作,主要表现如下:1)人才培养自从1980年以来,我国非常重视系统动力学人才的培养,主要采用“走出去,请进来”的办法。
请进来就就是请国外系统动力学专家来华讲学,走出去就就是派留学生,如:首批派出去的复旦大学管理学院的王其藩教授等,另外,还多次举办了全国性的讲习班。
2)编译编写专著组织专家编译了《工业动力学》,《城市动力学》等。
编写专著有:王其藩著《系统动力学》,《高级系统动力学》;胡玉奎著《系统动力学》,王洪斌著《系统动力学教程》,贾仁安著《系统动力学教程》等。
3)引进专业软件引进的软件有:MICRO-DYNAMO,DYNAMAP2,DYNAMO I∏∏,STELLA,PD PLUS等,近几⋅年又引进的最先进实用的VENSIM专业软件。
并自行研制了一些专用软件。
4)新设课程新开设了系统动力学专业课程。
在几十所大学的管理系或管理学院以及科研单位的研究生开设了系统动力学课程。
5)组织机构与学术会议于19 年成立了全国系统动力学委员会。
组建了一些专门研究机构与教学机构。
开展了许多专项研究工作。
建立了国家总体系统动力学模型,省与地区的发展战略研究系统动力学模型,省级能源,环境预测系统动力学模型及科技,工业,农业林业等行业发展战略研究系统动力学模型等。
1986年8月,在上海召开的“全国系统动力学学术研讨会“上,140多名代表提交了95篇有关系统动力学理论与应用研究方面的论文。
1987年6月,在上海召开的国际学术会议上我国代表交流了29篇论文,占会议论文数的45%。
1988年7月,美国圣迭戈召开了国际学术年会,我国有十名代表参加,交流论文十多篇。
1989年7月,在西德斯图加特召开的国际学术年会上,我国学者交流论文14篇,有4人参加会议。
目前,在我国系统动力学已经发展成熟,并正向深入与全面应用延伸,形成了一支强大的研究力量,发展趋势瞧好,有理由相信,系统动力学必将在我国社会,经济,科技,管理与生态等领域的研究中发挥更大作用。
第2节系统动力学的基础知识系统动力学模型建立的基本知识,基本原理主要有:因果关系图,模型流图及模型的组成等。
现分别介绍。
2、1 因果关系1 因果关系因果关系就是指由原因产生某结果的相互关系。
从哲学角度讲,原因与结果就是揭示客观事物的因果联系的重要哲学概念,它们就是客观事物普遍联系与相互作用的表现形式之一。
原因就是某种事物或现象,就是造成某种结果的条件;结果就是原因所造成的事物或现象,就是在一定阶段上事物发展所达到的目标状态。
通常用箭头线来表示,它有正因果关系与负因果关系两种,如图9—1。
P169原因结果+ 就业机会E 迁入人口数I- 死亡率R 总人口数P 正因果关系:两个变量呈同方向变化趋势,如:E增加,I增加;E减少,I减少。
负因果关系:两个变量呈异方向变化趋势,如:R增加,P减少;R减少,P增加。
2)因果关系环图因果关系环图就是指由两个或两个以上的因果关系连接而成的闭合回路图示。
它定性描述了系统中变量之间的因果关系。
它有正负因果关系环图两种,如图9—3,图9--4所示:P169正因果关系环图:它会引起系统内部活动加强。
准则:若各因果关系均为正,则该环为正因果关系环;若各因果关系为负的个数就是偶数时,则该环也为正因果关系环。
负因果关系环图:它会引起系统内部活动减弱。
准则:若各因果关系均为负,则该环为负因果关系环;若因果关系为负的个数就是奇数,则该环为负因果关系环。
再如:生态学人口增长因果关系环图,如图9—5,图9--6 所示:P1702、2 系统动力学模型流图系统动力学模型流图简称SD流图,就是指由专用符号组成用以表示因果关系环中各个变量之间相互关系的图示。
它能表示出更多系统结构与系统行为的信息,就是建立SD模型必不可少的环节,对建立SD模型起着重要作用。
其专用符号主要有八个:1)水平变量水平变量符号就是表示水平变量的积累状态的符号,它就是SD 模型中最主要的变量。
它由五部分组成,即:输入速率,输出速率,流线,变量名称及方程代码(L),如图所示。
2)速率变量速率变量符号就是表示水平变量变化速率的变量。
它能控制水平变量的变化速度,就是可控变量。
它由三部分组成,即:输入信息变量,变量名称及方程代码(R)。
如图所示。
3)辅助变量辅助变量符号就是辅助水平变量等的变量。
如图所示。
4)外生变量外生变量符号如图所示。
5)表函数表函数符号如图所示。
常数符号如图所示。
7)流线流线符号又有物质流线,信息流线,资金流线,及订货流线四种: 物质流线符号就是表示系统中流动着的实体,如图所示。
信息流线符号就是表示联接积累与流速的信息通道,如图所示。
资金流线符号就是表示资金,存款及货币的流向,如图所示。
订货流线符号就是表示订货量与需求量的流向,如图所示。
8)源与沟源符号与沟符号如图所示。
2、3 系统动力学模型系统动力学模型就是由六种基本方程与专门的输出语句组成。
其六种方程的标志符号分别为:L:水平变量方程; R:速率变量方程;A:辅助变量方程; N:计算初始值方程;C:赋值予常数方程; T:赋值予表函数中Y坐标值。
L方程就是积累方程;R,A方程就是代数运算方程;C,T,N方程就是提供参数值方程,并在同一次模拟中其值保持不变。
L 方程就是计算水平变量积累值的方程,其一般表示形式为:L K J JK JK POP POP DT (BR DR )其中,L:水平变量方程代码,表示方程性质。
DT:时间间隔,即时间增量。
、J:表示前一刻。
、K:现在时刻。
、L:未来一时刻。
J POP ⋅:过去一时刻人口数。
K POP ⋅:现在时刻人口数。
L POP ⋅:未来一时刻人口数。
JK BR ⋅:过去至现在该段时刻的人口出生率。
JK DR ⋅:过去至现在该时刻段的人口死亡率。
积累就是系统内部流的堆积量,它等于过去一时刻的积累加上积累变动量,即变动增量。
积累变动量就是时间间隔与输入流速与输出流速之差的乘积。
2)R 方程R 方程就是计算单位时间流量的方程,即流速或速率。
其一般表示形式为:R J JK POP BRF BR ⋅⋅⨯= R J JK POP DRF DR ⋅⋅⨯=R K KL POP BRF BR ⋅⋅⨯= R K KL POP DRF DR ⋅⋅⨯=其中,JK BR ⋅:过去至现在时刻的出生率,单位(人/年);JK DR ⋅:过去至现在时刻的死亡率,单位(人/年);KL BR ⋅:现在至未来时刻的出生率;单位(人/年);KL DR ⋅:现在至未来时刻的死亡率,单位(人/年);BRF : 出生系数,单位(人/年.人);DRF : 死亡系数,单位(人/年.人);J POP ⋅:过去时刻人口总数;K POP ⋅:现在时刻人口总数。
3)A 方程A 方程就是辅助变量方程,用于对辅助变量赋值,其一般表示形式为:A ),22(k K pop sum TPOP ⋅⋅=其中,K TPOP ⋅:表示现在人口总数。
),22(k pop SUM ⋅:求与函数,表示求算现在22个年龄组的总与。
4)N 方程N 方程就是变量初始值方程,表示对变量赋初始值,起一般表示形式为:N )1()1(AGE IPOP AGE POP =其中,)1(AGE POP :表示各年龄组人口初始值。
)1(AGE IPOP :就是表函数,表示存储22个年龄组的初始值。
5)T方程T方程就是表函数方程,表示对相应的纵坐标Y赋值。
6)C方程C方程就是常数方程,表示对常数变量赋值。
第3节系统动力学模型系统动力学模型应用分析的一般步骤为:1 明确问题明确的问题就是:系统的范围:空间范围,如安徽省区域;时间范围,如1961年 --- 2050年;时间间隔,DT=1年,等等。
解决途径: 计算机仿真实验。
数据资料: 人口总数,出生率,死亡率,自然增长率等。
2 明确目标人口总数变化趋势;自然增长率控制目标;出生率控制目标;死亡率控制目标等。
3 绘制系统流图1)因果关系环图主要变量清单,即列出主要变量的清单,以利于因果关系环流图的绘制。
如:总人口数,出生率,死亡率,出生系数,死亡系数。
很容易绘制出下图:2)SD 模型流图在因果关系环图的基础上可得SD 模型流图如图 所示。
4 SD 模型的建立根据上述介绍知识与分析步骤,可得简单的安徽省人口SD 模型如下:* POPULAYION SD MODEL OF ANHUIL )(K J K J J K DR BR DT POP POP ⋅⋅⋅⋅-*+=R K L K POP BRF BR ⋅⋅*=R )K L K POP DRF DR ⋅⋅*=N 60000000=POPC 005.0=BRFC 003.0=DRFSPEC DT=1/PRINT 1)POP,2)BR,3)DR,PLOT POP,BR,DRPLOT POP说明:1)人口数分22个年龄组,即:1岁,2 — 4,5 — 9,10 — 14,。
