理想气体温标
新概念物理教程热学答案第一章温度

新概念物理教程热学答案第一章温度1-1在什么温度下,下列一对温标给出相同的读数:(1)华氏温标和摄氏温标;(2)华氏温标和热力学温标;(3)摄氏温标和热力学温标?解:(1)当时,即可由时,解得故在(2)又当时则即解得:故在(3)若则有时,显而易见此方程无解,因此不存在的情况。
1-2定容气体温度计的测温泡浸在水的三相点槽内时,其中气体的压强为50mmHg。
(1)用温度计测量300K的温度时,气体的压强是多少?(2)当气体的压强为68mmHg时,待测温度是多少?解:对于定容气体温度计可知:(2)1-3用定容气体温度计测得冰点的理想气体温度为273.15K,试求温度计内的气体在冰点时的压强与水的三相点时压强之比的极限值。
解:根据已知冰点。
1-4用定容气体温度计测量某种物质的沸点。
原来测温泡在水的三相点时,其中气体的压强;当测温泡浸入待测物质中时,测得的压强值为减为200mmHg时,重新测得,当从,当再抽出一些测温泡中抽出一些气体,使气体使减为100mmHg时,测得.试确定待测沸点的理想气体温度.解:根据从理想气体温标的定义:时,T约为400.5K亦即沸点为400.5K.依以上两次所测数据,作T-P图看趋势得出题1-4图1-5铂电阻温度计的测量泡浸在水的三相点槽内时,铂电阻的阻值为90.35欧姆。
当温度计的测温泡与待测物体接触时,铂电阻的阻值为90.28欧姆。
试求待测物体的温度,假设温度与铂电阻的阻值成正比,并规定水的三相点为273.16K。
解:依题给条件可得则故,1-6在历史上,对摄氏温标是这样规定的:假设测温属性某随温度t 做线性变化即,并规定冰点为设解:和,汽化点为分别表示在冰点和汽化点时某的值,试求上式中的常数a和b。
由题给条件可知由(2)-(1)得将(3)代入(1)式得1-7水银温度计浸在冰水中时,水银柱的长度为4.0cm;温度计浸在沸水中时,水银柱的长度为24.0cm。
(1)在室温时,水银柱的长度为多少?(2)温度计浸在某种沸腾的化学溶液中时,水银柱的长度为25.4cm,试求溶液的温度。
温标9

温标2014190102004 航空航天学院王云川1、经验温标经验温标的建立三要素:为了定量地进行温度的测量,必须确定温度的数值表示方法,即温标(1)选择测温物质和测温参量。
即选择某一特定物质的某一随温度变化的属性(表示这种属性的物理量,叫测温参量)来标记温度。
当温度改变时,不仅液体体积会随之变化,物质的其他物理属性,如一定容积气体的压强、一定压强气体的体积、导体的电阻、灯丝颜色、热电偶电动势等都会发生变化。
原则上讲,任一物质的任一物理属性,只要它随温度的改变而单调地变化,都可以被选用来标记温度。
(2)规定测温参量随温度的变化关系。
即要将所选择的测温参量的变化与温度变化联系起来,对测温参量随温度的变化关系作出某种规定,然后根据这个规定来确定温度的数值。
为了简单起见,一般规定测温参量与温度之间呈线性关系。
(3)选择参考点,并规定其数值。
选择便于复现的某个温度点为参考点,并给予它们一定的数值,这样其他各点的温度数值才可以再根据测温参量随温度的变化关系而确定出来。
建立温标必须具备的三个要素当中,前两个为测温依据,后一个为标度方法。
不难看出,这样建立的温标所测温度依赖于测温物质和测温参量的选择。
这种利用特定测温物质的特定测温参量建立的温标统称为经验温标。
经验温标具有相对性,即当我们规定某一测温参量随温度作线性变化而建立起某种经验温标后,再利用这种温标制成的温度计去测量其他测温参量随温度的变化关系时,它就不再是线性的了。
这就是说,根据每种经验温标所进行的温度测量,只是相对于该种温度所赖以建立的测温依据来说才是正确的。
2 、理想气体温标由于经验温标具有相对性,就需要选定某一特定种类的温度计作为标准,来调整其他各种温度计的标度,同时在恒温点的规定与分度不同的温标间建立起某种对应关系,这在建立标准温标之后是很容易进行的。
19 世纪中叶,对气体性质的研究已经很成熟了,建立起了一些气体定律,能够较正确地反映气体膨胀的规律。
理想气体温标

广西物理第20卷响到整个理想气体温标的准确性。
由于水的三相点温度Ttr在实验装置中其值可以长期保持在万分之一度内不变
,不受其它
条件影响,并且易于复现。所以1954年第十届国际计量大会决定采用水的三相点温度作为定
标点,并严格规定它的数值。使得在此规定下建立起来的理想气体温标既能满足热力学的理
点为定标点后,新的理想气体温标定义为:
T=TtrlimPtr
0P
Ptr=273
.16KlimPtr0P
Ptr
(V不变)(8)
此外,值得注意的是,水的三相点温度为00098,这是以冰点为0测到的。这表明,实
际上冰点约低于三相点00098度。现在规定水的三相点为001,则此摄氏0低于三相点
失。下面用实验结果来具体说明这一点。
设想用一定容气体温度计测量水的沸点的温度。假设最初温度计测温泡内贮有较多的气
体,它在冰点温度时的压强Pi为
1000mmHg。用Ps1000表示这时测得的气体在水的沸点时的压
强值。根据(6)式可确定沸点的温度为T(Ps)
=273.15
Ps
为是规定的,而应是在绝对温标中的测量值。由(4)式知冰点的绝对温度为
Ti=
100PiPs-
Pi(V不变)(5)
所以只要测得Pi和
Ps的值,则冰点的绝对温度便可得出。历史上所测冰点温度如下表:
表1历年所测冰点的温度(绝对温标)摘要
实验室时间Ti(
)
5J.A.BeattieThethermodynamictemperatureoftheicepointTemperature(Reinhold,NewYork1941)74~8819
大学物理学第7章气体动理论(Temperature)

4
研究对象:大量无规则热运动气体分子构成的系统 研究内容:物质与冷热有关的性质及这些性质的变化
对象特点:单个分子 无序性、偶然性、遵循力学规律 整体(大量分子):服从统计规律
mvx
l2
立直角坐标系。
a
O
-mvx
X
(2)选任意一个分子a作为研
究对象,求其对A1面的压力 Z
l1
分子“a” 的速度:
分子“ a”碰撞器壁A1面一次所受的冲量:
由牛顿第三定律可知,器壁A1面受分子碰撞一次所受的冲量:
23
分子“ a”相继碰撞器壁A1面两次所用的时间为: 单位时间内,分子“ a”与器壁A1面碰撞的次数为: 单位时间内,分子“ a”对器壁A1面的冲量即冲力为:
如压强 p、体积 V、温度 T等 .
平衡态:一定量的气体,在不受外界的影响下, 经过一 定的时间, 系统达到一个稳定的, 宏观性质不随时间变 化的状态称为平衡态 .(理想状态)
平衡态的特点
( p,V ,T )
p
*( p,V ,T )
o
V
1)单一性(
处处相等);
2)物态的稳定性---与时间无关;
3)自发过程的终点;
(2)在平衡态下,分子按位置的分布是均匀的 n dN N
则各处分子数密度是相同的。
dV V
(3) 分子速度指向任何方向的机会是一样, 或分子速度按方向的分布是均匀的。
vx2 vy2 vz2
各个方向的速度分量的平均值相等。
vx 2
v1 x 2
物理学20-理想气体的状态方程

h
8
平衡态与稳定态的区别
平衡态(equilibrium state):
在不受外界影响的条件下(与外界无任何
形式的物质与能量交换),系统的宏观性质
稳定态可以划分成一系列近似的平衡态。
平衡态判据:系统内部温度均匀、压强均匀。
h
10
平衡态系统 系统分类(按系统所处状态):
非平衡态系统 热平衡态: 在无外界的影响下,不论系统初始状态如 何,经过足够长的时间后,系统的宏观性质不随时间 改变的稳定状态。
平衡条件: (1) 系统与外界在宏观上无能量和物质的交换, (2) 系统的宏观性质不随时间改变。
h
热力学系统的平衡态
• 热力学系统(thermodynamic system), 简称系统(system), 它是指在给定的范围内, 由大量的微观粒子所组成的宏观
物体.
例如: 气缸
外界 系统
外界
• 对所研究的热力学系统能够发生相互作用的其它物体, 称 为外界或环境.
• 与外界没有任何相互作用的热力学系统, 称为孤立系统 (isolated system). 它只是一个理想的概念.
• 与外界有能量交换, 但没有物质交换的热力学系统, 称为 封闭系统(closed system).
• 与外界既有能量交换, 又有物质交换的热力学系统, 称为 开放系统(open system).
h
7
我们主要讨论系统宏观状态的一种特殊情况即所谓的平衡态.
• 平衡态(equilibrium state)是指热力学系统内部 没有宏观的粒子流动和能量流动的状态, 这时系 统的各种宏观性质不随时间变化.
引力场中热力学的基本原理

引力场中热力学的基本原理罗凌霄(大理大学工程学院,云南大理,671003)摘要:建立了引力场中的理想气体温标,导出引力场中的理想气体的物态方程,重申了玻耳兹曼常量与引力势的函数关系,并给出引力场中温度的微观解释。
给出引力势不随时间改变的情况下,引力势随位置的改变可以忽略的不太大的空间内的热力学第一定律的表述,以及热力学第二定律的表述。
最后,清楚地导出了引力场中的熵概念以及熵增加原理,并且阐明了熵增加原理的适用条件是周围相关环境的引力场不随时间改变。
关键词:引力场;热力学;玻耳兹曼常量;质根动量;热诱变在文献[1]中,我们已经弄清楚,超氢相对基准中玻耳兹曼常量是引力势的函数,超氢绝对基准中玻耳兹曼常量与引力势无关,并且,我们建立了引力场中的黑体辐射理论与恒星辐射理论。
以此为基础,本文要构建引力场中热力学的基本原理。
1、引力场中的平衡态在不受外界拂扰的条件下,宏观性质不随时间变化的状态叫做平衡态。
这里所说的不受外界拂扰,是指外界对系统既不作功,也不传热,并且外界在系统所在处激发的引力势不随时间改变。
2、引力场中的热平衡如果两个各自处于平衡态的热力学系统用导热丝作热接触而不改变状态,那么就说这两个热力学系统处于热平衡。
导热丝由芯线和外壳构成,芯线是良导体,外壳是绝热材料,外壳的内壁是热辐射的全反射膜,在两端芯线稍微突出。
用导热丝对各自处于热平衡的系统A和B作热接触是这样进行的:让导热丝a的一端与系统A接触,另一端伸向系统B,直到稍微超过两个系统间的中界位置。
如果系统A的状态因此发生改变,那么采取措施让它恢复原态。
让导热丝b的一端与系统B接触,另一端伸向系统A,直到稍微超过两个系统间的中界位置。
如果系统B的状态因此发生改变,那么采取措施让它恢复原态。
然后让两根导热丝彼此相邻的两个裸露端接触。
作者简介:罗凌霄(1964—),男,白族,云南剑川人,大理大学教授,主要从事电磁场理论、数学场论、量子理论和引力理论的研究工作.如果系统A 和B 的状态并不因此而改变,我们就说当初的系统A 和B 处于热平衡。
高二物理竞赛课件理想气体的压强温度公式

a.温度是分子平均平动动能的量度,反映无规则 热运动的剧烈程度;
b.温度是大量分子集体表现,对个别分子温度没 有意义。
【问题】温度所反映的运动是否包括气体系统 的整体运动?
理想气体的温度公式
【解释现象】大气组成
w 3 kT 2
w 1 mv2 2
v2 3kT m
vrms
v2
3kT m
vrms,H2 1.93km / s vrms,He 1.37km / s
居室温度保持在 20℃~25℃; 穿衣保持最佳舒适感时,则皮肤的平均温度为 33℃; 饭菜的温度为 46℃~58℃; 饮水时的温度为 44℃~59℃; 泡茶的温度为 70℃~80℃; 洗澡水的温度为 34℃~39℃; 洗脚水的温度为 50℃~60℃; 冷水浴的温度为 19℃~21℃;
理想气体的温度公式
vrms,N2 0.516km / s vrms,O2 0.483km / s
理想气体的内能
一.理想气体模型的改进
放 大
推导压强公式: 理想气体分子 讨论能量问题:理想气体分子
质点
单原子分子 双原子分子 多原子分子
质点 质点+刚性线 质点+刚性线
理想气体的内能
二.自由度 degree of freedom
轴线方位 ()
角度方位 φ
z
x
C(x, y, z)
y
3个平动自由度(t) 3个转动自由度(r)
自由度i t r 6
理想气体的内能
③气体分子自由度: a.单原子分子 自由度 i = t = 3
b. 双原子分子 自由度 i = t+r = 3+2=5
c. 三原子分子 自由度 i = t+r = 3+3=6
热学公式
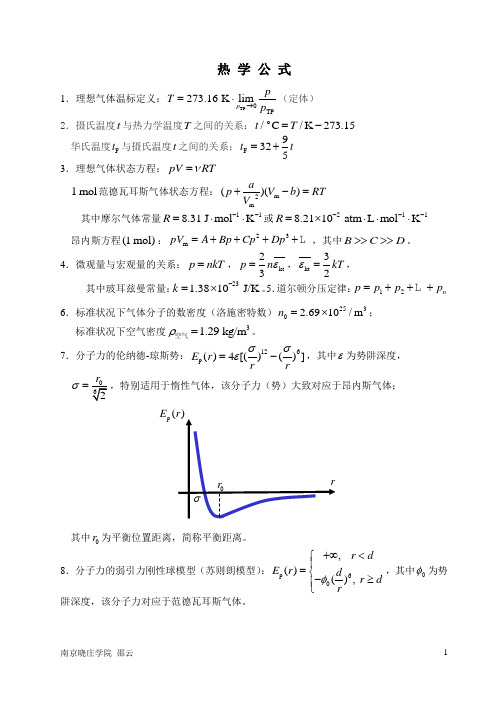
热 学 公 式1.理想气体温标定义:TP 0TP273.16 K limp pT p →=⋅(定体) 2.摄氏温度t 与热力学温度T 之间的关系:o/C /K 273.15t T =- 华氏温度F t 与摄氏温度t 之间的关系:F 9325t t =+ 3.理想气体状态方程:pV RT ν=1 mol 范德瓦耳斯气体状态方程:m 2m()()ap V b RT V +-= 其中摩尔气体常量118.31 J mol K R --=⋅⋅或2118.2110 atm L mol K R ---=⨯⋅⋅⋅ 昂内斯方程(1 mol):23m pV A Bp Cp Dp =++++,其中B C D >>>>。
4.微观量与宏观量的关系:p nkT =,kt 23p n ε=,kt 32kT ε=, 其中玻耳兹曼常量:231.3810 J/K k -=⨯。
5.道尔顿分压定律:12n p p p p =+++6.标准状况下气体分子的数密度(洛施密特数)2530 2.6910/m n =⨯; 标准状况下空气密度31.29 kg/m ρ=空气。
7.分子力的伦纳德-琼斯势:126p ()4[()()]E r rrσσε=-,其中ε为势阱深度,σ=,特别适用于惰性气体,该分子力(势)大致对应于昂内斯气体;其中0r 为平衡位置距离,简称平衡距离。
8.分子力的弱引力刚性球模型(苏则朗模型):p 60, ()(), r d E r d r d rφ+∞<⎧⎪=⎨-≥⎪⎩,其中0φ为势阱深度,该分子力对应于范德瓦耳斯气体。
9.麦克斯韦速率分布函数(概率密度):23/222d ()4π()e d 2πmv kTN m f v v N v kT-==,其简便形式:22()d e d u f v v u -=,其中约化速率p v u v =。
10.三个分子速率的统计平均值:最概然速率:p v ==v ==方均根速率:rms v ===11.麦克斯韦速度分布律:22232()/2d e d d d 2πx y z m v v v kTx y z N m v v v N kT -++⎛⎫= ⎪⎝⎭,其中 x 方向速度分布律:21/2/2d ed 2πxx v mv kTx N m v N kT -⎛⎫= ⎪⎝⎭, 引入约化速度分量px vv ξ=后,上式可简化为2d ()d d x v x x N f v v N ξξ-==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.24 105
m3
所以,分子本身的体积占气体 总体积的10-1, 当然就必须考虑了。
范德瓦耳斯认为, 考虑了分子的体积,分子可以自由活动的空间减 小了,1mol的理想气体方程应该修改为
Pv b RT 或 P RT vb b-----与分子的体积有关的修正常数。
2.考虑分子之间的相互作用力
从物质的微观结构出发,用统计平均的方 法,研究热现象及规律的微观本质。
·两种方法相辅相成。
三.几个概念
1.宏观量与微观量
(1)宏观量 (macroscopic quantity) ·表征系统整体性质的物理量 ·可直接测量(如体积、压强)
广延量:有累加性(如质量、能量) 强度量:无累加性(如温度、压强)
容积为10 l 的瓶内贮有氢气,因开关 损坏而漏气,在温度为 7 。 C ,气压 计的读数为 50atm。过了些时候,温度 上升为 17 。 C ,气压计的读数未变, 问漏去了多少质量的氢。
一氧气瓶的容积是32 l ,其中氧气的压强 是 130atm,规定瓶内氧气压强降到 10atm 时就得充气,以免混入其他气体而需洗瓶, 今有一玻璃室,每天需用 1.0atm氧气400 l ,问一瓶氧气能用几天。
温度固定点:冰点为0 0C,沸点为100 0C 测温物质:水银 测温属性:水银的高度,高度与温度成正比
1.理想气体温标 (> 0.5K范围适用(低压3He气))
定义水的三相点
T3 273.16 K
T PV T3 P3V3
只要测定了某状态的P,V 值,即可得该状态下 理想气体温标有效范围内,两种温标一致。
平衡态下状态参量不随时间变化
在 P—V 图上一个点表示一个平衡态。
4.状态方程(equation of state) 状态参量之间的函数关系 f (P,V,T) = 0
理想气体状态方程: PV NkT 或 P nkT PV M RT νRT μ
摩尔气体常数 R 8.31J mol -1 K1 阿伏加德罗常数 N A 6.021023mol -1 波尔兹曼常数 k R 1.381023 J K 1
引言
一.热学研究对象及内容
1.对象:热力学系统
▲由大量分子或原子组成 ▲系统外的物体称外界
2.内容:与热现象有关的性质和规律
热现象:物质中大量分子热 运动的集体表现。
二.热学的研究方法 1.宏观描述方法—热力学方法
由实验确定的基本规律,研究 热现象的宏观特性和规律。
对系统进行整体描述。
2.微观描述方法—统计物理方法
M
理想气体温标定义得到
★通常,我们说温度不太低、压强不太高的气体 近似看成理想气体,我们也常说理想气体很稀薄
求氧气在压强为1.0atm ,温度为27 。 C 时 的密度和分子数密度。
一端封闭的玻璃管长70.0cm ,贮有空气,气体 上面有一段长为20.0cm 的水银柱,将气柱封住, 水银面与管口对齐,今将玻璃管的开口端用玻璃 片盖住,轻轻倒转后再除去玻璃片,因而使一部 分水银漏出。当大气压为75.0cmhg 时,六在管 内的水银柱有多长?
T:K (kelvin) T3 = 273.16K
3.摄氏温标
t = (T - 273.15) ℃ t3 = 0.01℃
4.华氏温标
tF = [32 + (9/5)t] F ·水 冰点:tF = 32 F
沸点:tF = 212 F
理想气体: 严格遵守
PV
m RT
的气体
M
m PV RT
是由玻马定律、阿伏加德罗定律、
NA
理想气体的物态方程
P nkT
PV M RT RT
μ 实际气体的物态方程(1mol)
范德瓦耳斯方程 (半经验)
p
a v2
v
b
RT
昂尼斯方程 (经验)
pv A Bp Cp2 Dp3 .....
(A、B、C、D----维里系数,与温度T有关)
第1章 温度 (自学) (Temperature)
考虑气体分子本身的体积 考虑分子之间的相互作用力
范德瓦尔斯 (1837-1923) 荷兰人
1910年获诺贝尔奖
1. 考虑气体分子本身的体积
标准状态下,1 mol气体的体积为 22.4升=2.2410-2m3
因为分子的半径 r 10-10 m 分子的体积 (4/3) r 3 4.210-30 m3,
(2)微观量(microscopic quantity) ●描写单个微观粒子运动状态的物理量 ●一般不能直接测量(如分子质量、能量)
宏观量是微观量的统计平均值
2.平衡态(equilibrium state)
在不受外界影响的条件下,系统宏观 性质不随时间改变的状态(热动平衡)。
3.状态参量
描述系统平衡态的宏观参量常用:P,V,T
理想气体的物态方程
P nkT
PV M RT RT
μ 实际气体的物态方程(1mol)
范德瓦耳斯方程 (半经验)
p
a v2
v
b
RT
昂尼斯方程 (经验)
pv A Bp Cp2 Dp3 .....
(A、B、C、D----维里系数,与温度T有关)
范德瓦耳斯方程
对理想气体模型作了两方面的修正:
1 mol气体中分子的总体积为 610234.210-30 = 2.5210-6 m3
分子本身的体积约占气体总体积的10-4,可以忽略。
分子本身的体积2.5210-6 m3。
但是在1000大气压下,1mol气体的体积就小了。
设
P1V1 P2V2 ,
T1
T2
并且T1 T2
有
V2
P1V1 P2
1 2.24102 1000
当气体的压强比较大时,分子的 数密度大,分子之间的距离小, 分子之间的作用力不能忽略了。
范氏微观简化模型:
f
斥力
合力
r0
O
sr
10 -9m
d
引力
分子力
f
有引力的 分子刚球模型
sr
O d
范氏气体模型
设容器内部某个分子a, 在它的分子作用球球面内的 其他分子对 a 分子的作用力 相互抵消。
一.热平衡态
两系统热接触下,相当长时间后达到的共同平衡态。
二.温度
1.热平衡定律(热力学第零定律) 实验表明:若A与C热平衡,B与C热平衡 则A与B热平衡
2.温度:处于热平衡的系统所具有 的共同的宏观性质称温度。
三.温标(temperature scales)
温标建立三要素:温度固定点、测温物质、测温属性 水银温度计(摄氏温标)
