小学部编道德与法治二年级上册高效课堂资料《三角形三边关系的探究》_练习题
人教部编版四年级数学下册 5.2 三角形三边关系-课时练.doc

5.2 三角形三边关系1、在能拼成三角形的各组小棒下面画答案:第1、2、3个都能组成一个三角形,第4个不能。
2、宁宁要去书店,有几种走法?哪种走法最近?为什么?答案:一共有4条路,其中从宁宁家经过明明家到达书店的路线最近,因为宁宁家学校和书店形成了一个三角形形状,根据三角形三边关系,两边之和总大于第三条边,所以这条路是最近的。
3、用长分别是4厘米、6厘米和10厘米的三根小棒,能摆出一个三角形吗? 答案:不能。
4、判断:下组中的三根小棒能围成一个三角形吗?(×)3厘米 4厘米 12厘米______因为3+4<12,所以给出三根小棒不能围成一个三角形;故答案为:×.1、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seenthe Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn'thave known my way about.The weather was splendid on that day, which I thought was rare. I still remember some peopletold me that in Britain there was weather and no climate. During the same day, it might snow in the morning, rain at noon, shine in the afternoon and be windy before the night falls. So I think I was lucky 。
《三角形的三边关系》同步练习题

4.1.2 三角形的三边关系基础训练1.一个等腰三角形的两边长分别为4,8,则它的周长为( )A.12B.16C.20D.16或202.△ABC的三边长a,b,c满足关系式(a-b)(b-c)(c-a)=0,则这个三角形一定是( )A.等腰三角形B.等边三角形C.等腰直角三角形D.无法确定3.已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )A.6条B.7条C.8条D.9条4.三角形的三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是( )A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形5.三角形按边可分为( )A.等腰三角形、直角三角形、锐角三角形B.直角三角形、不等边三角形C.等腰三角形、不等边三角形D.等腰三角形、等边三角形6.下列说法:①等边三角形是等腰三角形;②等腰三角形也可能是直角三角形;③三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.其中正确的有( )A.1个B.2个C.3个D.4个7.若一个三角形的两边长分别为3和7,则第三边长可能是( )A.6B.3C.2D.118.下列长度的三根小木棒能构成三角形的是( )A.2 cm,3 cm,5 cmB.7 cm,4 cm,2 cmC.3 cm,4 cm,8 cmD.3 cm,3 cm,4cm9.下列长度的三条线段能组成三角形的是( )A.5,6,10B.5,6,11C.3,4,8D.4a,4a,8a(a>0)10.长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )A.1种B.2种C.3种D.4种11.已知三角形的三边长分别为4,5,x,则x不可能是( )A.3B.5C.7D.912.已知三角形的三边长为连续整数,且周长为12 cm,则它的最短边长为( )A.2 cmB.3 cmC.4 cmD.5 cm13.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边的取值范围是( )A.1 cm<AB<4 cmB.5 cm<AB<10 cmC.4 cm<AB<8 cmD.4 cm<AB<10 cm14.一个等腰三角形的两边长分别是3和7,则它的周长为( )A.17B.15C.13D.13或17提升训练15.已知△ABC的两边长分别为3和7,第三边的长是关于x的方程错误!未找到引用源。
三角形三边关系(带答案)

三角形三边关系(带答案)1.某同学手里拿着长为3和2的两个木棍,想要找一个木棍,用它们围成一个三角形,那么他所找的这根木棍长满足条件的整数解是()选项:A.1,3,5.B.1,2,3.C.2,3,4.D.3,4,52.以下列各组线段为边,能组成三角形的是()选项:A.1cm,2cm,4cm。
B.4cm,6cm,8cm。
C.5cm,6cm,12cm。
D.2cm,3cm,5cm3.一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是()选项:A.3cm。
B.4cm。
C.7cm。
D.11cm4.现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是()选项:A.1个。
B.2个。
C.3个。
D.4个5.下列长度的三条线段能组成三角形的是()选项:A.1,2,3.B.3,4,5.C.3,1,1.D.3,4,76.已知等腰三角形三边中有两边的长分别为4、9,则这个等腰三角形的周长为()选项:A.13.B.17.C.22.D.不能确定7.若三角形的两边长分别为6cm,9cm,则其第三边的长可能为()选项:A.2cm。
B.3cm。
C.7cm。
D.16cm8.下列长度的三条线段,不能组成三角形的是()选项:A.3,8,4.B.4,9,6.C.15,20,8.D.9,15,89.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()选项:A.5.B.6.C.11.D.1610.等腰三角形的两条边长分别为3,6,那么它的周长为()选项:A.12.B.15.C.12或15.D.不能确定11.如果等腰三角形的两边长分别为4和7,则三角形的周长为11.12.已知三角形其中两边a=3,b=5,则第三边c的取值范围为2<c<8.13.如果三角形的两条边长分别为23cm和10cm,第三边与其中一边的长相等,那么第三边的长为23cm。
28.在四边形ABCD中寻找一个点O,使得OA+OB+OC+OD之和最小。
三角形的三边关系练习题
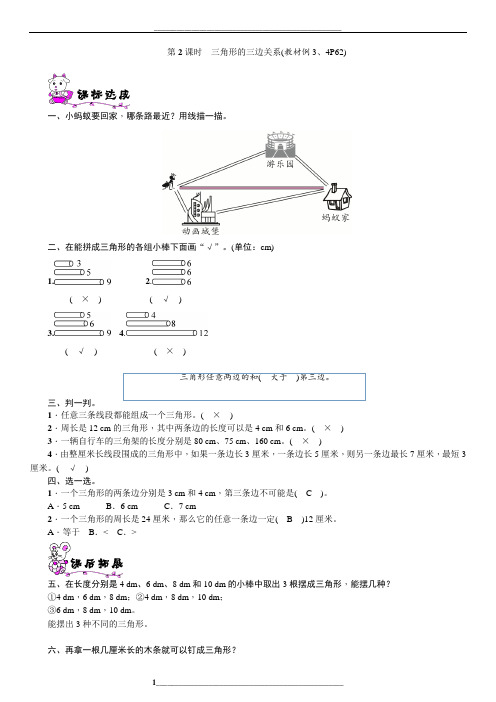
第2课时三角形的三边关系(教材例3、4P62)一、小蚂蚁要回家,哪条路最近?用线描一描。
二、在能拼成三角形的各组小棒下面画“√”。
(单位:cm)1.2.(×) (√)3.4.(√) (×)三角形任意两边的和(大于)第三边。
三、判一判。
1.任意三条线段都能组成一个三角形。
(×)2.周长是12 cm的三角形,其中两条边的长度可以是4 cm和6 cm。
(×)3.一辆自行车的三角架的长度分别是80 cm、75 cm、160 cm。
(×)4.由整厘米长线段围成的三角形中,如果一条边长3厘米,一条边长5厘米,则另一条边最长7厘米,最短3厘米。
(√)四、选一选。
1.一个三角形的两条边分别是3 cm和4 cm,第三条边不可能是(C)。
A.5 cm B.6 cm C.7 cm2.一个三角形的周长是24厘米,那么它的任意一条边一定(B)12厘米。
A.等于B.< C.>五、在长度分别是4 dm、6 dm、8 dm和10 dm的小棒中取出3根摆成三角形,能摆几种?①4 dm,6 dm,8 dm;②4 dm,8 dm,10 dm;③6 dm,8 dm,10 dm。
能摆出3种不同的三角形。
六、再拿一根几厘米长的木条就可以钉成三角形?9-6<第三边<9+6,3<第三边<15,即第三根木条长度大于3厘米,小于15厘米就可以。
七、一个巨人的腿长1.28 m,他一步能走3 m吗?为什么?1.28+1.28=2.56(m) 3 m>2.56 m答:不能。
根据“三角形任意两边的和大于第三边”可知,一个人所走的步长必须小于两条腿长的和,所以他一步不能走3 m。
口算25+35=6072-18=5477+35+23=13524×25=600338-54-46=238125-25=100 36+24=60 55×20=1100 72×125=9000 225+34+775=1034。
三角形的三边关系练习题

三角形的三边关系练习题
一、选择题
1.下列长度的三条线段能组成三角形的是()
A.1,2,3 B.2,2,4 C.3,4,5 D.3,4,8
2.一个三角形的两边长分别为3cm和7cm,则此三角形第三边长可能是() A.3cm B.4 cm C. 7 cm D.11cm
3、等腰三角形的周长为16,且边长为整数,则腰与底边分别为()
A、5,6
B、6,4
C、7,2
D、以上三种情况都有可能
4.一个三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是() A.2 B.3 C.4 D.5
二、填空题
5.若等腰三角形两边长分别为3和5,则它的周长是_______________.
6、三角形三边为3,5, a,则a的范围是 ______________ 。
7、三角形两边长分别为25cm和10cm,第三条边与其中一边的长相等,则第三边长为______ 。
8、等腰三角形两边为5cm和12cm,则周长为_______
9、等腰三角形的周长为14,其中一边长为3,则腰长为_____ 。
10、已知:等腰三角形的底边长为6cm,那么其腰长的范围是 __________
11.已知等腰三角形的两边长分别为11cm和5cm,求它的周长。
12、已知等腰三角形一边长为24cm,腰长是底边的2倍。
求这个三角形的周长。
13.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
14.有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!。
八年级三角形的边角关系练习题(含解析答案)

三角形的边角关系练习题回顾:1、三角形的概念定义:由_______直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、三角形的分类按角分:⎧⎪⎨⎪⎩锐角三角形三角形直角三角形钝角三角形按边分:⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形三角形底边和腰不相等的等腰三角形等腰三角形等边三角形3、三角形的重要线段在三角形中,最重要的三种线段是三角形的中线、三角形的角平分线、三角形的高。
说明:(1)三角形的三条中线的交点在三角形的____部。
(2)三角形的三条角平分线的交点在三角形的______部。
(3)_______三角形的三条高的交点在三角形的内部;______三角形的三条高的交点是直角顶点;_____三角形的三条高所在直线的交点在三角形的外部。
4、三角形三边的关系定理:三角形任意两边的和____第三边;推论:三角形任意两边的差____第三边;说明:运用“三角形中任意两边的和大于第三边"可以判断三条线段能否组成三角形,也可以检验较小的两边的和是否大于第三边。
5、三角形各角的关系定理:三角形的内角和是______度;推论:(1)当有一个角是90°时,其余的两个角的和为90°;(2)三角形的任意一个外角______和它不相邻的两个内角的和。
(3)三角形的任意一个外角______任意一个和它不相邻的内角。
说明:任一三角形中,最多有三个锐角,最少有两个锐角;最多有一个钝角;最多有一个直角。
三角形的计数例1 如图,平面上有A、B、C、D、E五个点,其中B、C、D及A、E、C分别在同一条直线上,那么以这五个点中的三个点为顶点的三角形有( )A、4个B、6个C、8个D、10个解析:连接AB、AD、BE、DE。
课件出示答案: C。
小结:分类讨论是三角形的计数中常见的思路方法.举一反三:1、已知△ABC是直角三角形,且∠BAC=30°,直线EF与△ABC的两边AC,AB分别交于点M,N,那么∠CME+∠BNF=()A、150°B、180°C、135°D、不能确定解析:因为∠A=30°,所以∠NMA+∠MNA=180°—30°=150°,所以∠CME+∠BNF=∠NMA+∠MNA=150°。
(完整版)三角形三边关系(带答案)

(1)用含a的代数式表示第四条边.
(2)当a=7时,还能得到四边形吗?说说理由.
28.如图,在四边形ABCD内找一点O,使OA+OB+OC+OD之和最小,并说出你的理由.
29.若三角形三边长分别为2x,3x,10,其中x为正整数,且周长不超过30,求x的取值范围.写出这个三角形的三边长.
∴x=2,3,4,
故选:C.
点评:
此题主要考查了三角形三边关系,掌握三角形三边关系定理是解题的关键.
2.(2012•郴州)以下列各组线段为边,能组成三角形的是( )
A.
1cm,2cm,4cm
B.
4cm,6cm,8cm
C.
5cm,6cm,12cm
D.
2cm,3cm,5cm
考点:
三角形三边关系.
分析:
根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
30.已知△ABC的三边长a,b,c均为整数,且a和b满足|a﹣4|+(b﹣1)2=0,求△ABC中c边的长.
【考点训练】择题(共10小题)
1.(2011•青海)某同学手里拿着长为3和2的两个木棍,想要找一个木棍,用它们围成一个三角形,那么他所找的这根木棍长满足条件的整数解是( )
A.
2cm
B.
3cm
C.
7cm
D.
16cm
8.(2011•南通)下列长度的三条线段,不能组成三角形的是( )
A.
3,8,4
B.
4,9,6
C.
15,20,8
人教版2022-2023学年数学八年级上学期三角形的三边关系练习题含答案

人教版2022-2023学年数学八年级上学期三角形的三边关系练习题学校:___________姓名:___________班级:___________一、单选题1.如图所示,工人师傅在砌门时,通常用木条BD固定长方形门框ABCD,使其不变形,这样做的数学根据是()A.两点确定一条直线B.两点之间,线段最短C.同角的余角相等D.三角形具有稳定性2.下图所示的五角星是用螺栓将两端打有孔的5根木条连接构成的图形,它的形状不稳定,如果在木条交叉点打孔加装螺栓的办法使其形状稳定,那么至少需要添加()个螺栓A.1B.2C.3D.43.已知三角形的两边长分别为5cm和8cm,则第三边的长可以是()A.2cm B.3cm C.6cm D.13cm4.平行四边形的一边长为10,那么它的两条对角线的长可以是()A.4和6B.6和8C.8和12D.20和30 5.如果三角形的两边长分别为4和7,则周长L的取值范围是()A.3<L<11B.6<L<16C.14<L<22D.10<L<216.一个等腰三角形的底边长是6,腰长是一元二次方程x2−7x+12=0的一根,则此三角形的周长是()A.12B.13C.14D.12或14二、填空题7.若长度分别为3,5,a的三条线段能组成一个三角形,则整数a的最大值为________.8.已知a,b,c是ABC的三边长,则b c a a b c a b c--+-+---=______.9.安排学生住宿,若每间住3人,则还有13人无房可住;若每间住6人,则还有一间不空也不满,则宿舍的房间数量可能为_____.三、解答题10的小数部分为a,8b,求a+b的平方根.11.(1)计算:232cos45°;(2)解不等式组:() 31225233x xx x⎧+>-⎪⎨+≤-⎪⎩.12.请补全证明过程及推理依据.已知:如图,BC//ED,BD平分∠ABC,EF平分∠AED.求证:BD∠EF.证明:∠BD平分∠ABC,EF平分∠AED,∠∠1=12∠AED,∠2=12∠ABC(______________)∠BC∠ED(________)∠∠AED=________(________________)∠12∠AED=12∠ABC∠∠1=________∠BD∠EF(________________).参考答案:1.D【分析】根据三角形具有稳定性解答即可.【详解】解:常用木条固定长方形门框ABCD,使其不变形,这种做法的根据是三角形具有稳定性.故选:D.【点睛】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,通常会把图形变成分成三角形,熟记三角形具有稳定性是解题的关键.2.A【分析】用木条交叉点打孔加装螺栓的办法去达到使其形状稳定的目的,可用三角形的稳定性解释.【详解】如图,A点加上螺栓后,根据三角形的稳定性,原不稳定的五角星中具有了稳定的各边故答案为:A.【点睛】本题考查了三角形的稳定性的问题,掌握三角形的稳定性是解题的关键.3.C【分析】先确定第三边的取值范围,后根据选项计算选择.【详解】设第三边的长为x,∠ 角形的两边长分别为5cm和8cm,∠3cm<x<13cm,故选C.【点睛】本题考查了三角形三边关系定理,熟练确定第三边的范围是解题的关键.4.D【分析】根据平行四边形对角线互相平分和三角形两边之和大于第三边逐项判断即可.【详解】解:如图,设AB=10,对角线相交于点E,它的两条对角线的长为4和6时,465102AE BE++==<,不符合题意;它的两条对角线的长为6和8时,687102AE BE++==<,不符合题意;它的两条对角线的长为8和12时,812102AE BE++==,不符合题意;它的两条对角线的长为20和30时,设AE=15,BE=10,AB BE AE+>,符合题意;故选:D.【点睛】本题考查了平行四边形的性质和三角形的三边关系,解题关键是明确两条较短边的和大于最长边可构成三角形.5.C【分析】根据三角形的三边关系,可得3<第三边<11,即可求解.【详解】解:∠4+7=11,7﹣4=3,∠3<第三边<11,∠4+7+3<L<11+4+7,即14<L<22.故选:C.【点睛】本题主要考查了三角形的三边关系,熟练掌握三角形的两边之和大于第三边,两边之差小于第三边是解题的关键.6.C【分析】通过解一元二次方程x2-7x+12=0求得等腰三角形的两个腰长,然后求该等腰三角形的周长.【详解】解:由一元二次方程x2-7x+12=0,得(x-3)(x-4)=0,∠x-3=0或x-4=0,解得x=3,或x=4;∠等腰三角形的两腰长是3或4;∠当等腰三角形的腰长是3时,3+3=6,构不成三角形,所以不合题意,舍去;∠当等腰三角形的腰长是4时,0<6<8,所以能构成三角形,所以该等腰三角形的周长=6+4+4=14;故选:C .【点睛】本题综合考查了一元二次方程-因式分解法、三角形的三边关系、等腰三角形的性质.解答该题时,采用了“分类讨论”的数学思想.7.7【分析】根据三角形三边关系定理得出5-3<a <5+3,求出即可.【详解】解:由三角形三边关系定理得:5-3<a <5+3,即2<a <8,即符合的最大整数a 的值是7,故答案为:7.【点睛】本题考查了三角形三边关系定理,能根据定理得出2<a <8是解此题的关键,注意:三角形的两边之和大于第三边,三角形的两边之差小于第三边.8.33a b c -+【分析】根据三角形三边关系定理,确定绝对值中式子的符号后化简即可.【详解】∠a ,b ,c 是ABC 的三边长,∠a +c >b ,b +c >a , ∠b c a a b c a b c --+-+---=a c b a b c a b c +-+-++--=33a b c -+,故答案为:33a b c -+.【点睛】本题考查了三角形三边关系定理,绝对值的化简,熟练掌握三角形三边关系定理是解题的关键.9.5或6【分析】设共有x 间宿舍,则共有(313)x +个学生,然后根据每间住6人,则还有一间不空也不满,列出不等式组进行求解即可.【详解】解:设共有x 间宿舍,则共有(313)x +个学生,依题意得:3136(1)3136x x x x +>-⎧⎨+<⎩,解得:1319 33x<<.又x为正整数,5x∴=或6.故答案为:5或6.【点睛】本题主要考查了一元一次不等式组的应用,解题的关键在于能够准确根据题意列出不等式组进行求解.10.a+b的平方根为±1;34<,43-<-,由不等式的性质求得a、b 的值,再计算求值即可;【详解】解:∠34<,∠526<<,∠43-<-,∠485<<,∠253a=-=,844b==∠a+b=1,∠a+b的平方根为±1;【点睛】本题考查了无理数的估算,不等式的性质,平方根的计算;掌握无理数的估算方法是解题关键.11.(1)82;(2)﹣5<x≤﹣1【分析】(1)根据有理数乘方,最简二次根式,特殊角的三角函数值,二次根式的加减法计算求解;(2)根据一元一次不等式组的解法,先分别求出两个不等式的解集,再确定不等式组的解集.【详解】解:(1)232cos45°=2==82;(2)() 31225233x xx x⎧+>-⎪⎨+≤-⎪⎩①②,不等式∠的解集是:x>﹣5,不等式∠的解集是:x≤﹣1,∠原不等式组的解集是:﹣5<x≤﹣1.【点睛】本主要考查了实数的运算,一元一次不等式组的解法,理解有理数乘方,最简二次根式,特殊角的三角函数值,二次根式的加减法,一元一次不等式组的解法是解答关键.12.角平分线的定义;已知;∠ABC;两直线平行,同位角相等;∠2;同位角相等,两直线平行【分析】根据角平分线的定义得出∠1=12∠AED,∠2=12∠ABC,根据平行线的性质定理得出∠AED=∠ABC,求出∠1=∠2,再根据平行线的判定定理推出即可.【详解】证明:∠BD平分∠ABC,EF平分∠AED,∠∠1=12∠AED,∠2=12∠ABC(角平分线的定义)∠BC∠ED(已知)∠∠AED=∠ABC(两直线平行,同位角相等)∠12∠AED=12∠ABC∠∠1=∠2∠BD∠EF(同位角相等,两直线平行).故答案为:角平分线的定义;已知;∠ABC;两直线平行,同位角相等;∠2;同位角相等,两直线平行.【点睛】本题考查了角平分线的定义,平行线的性质定理和判定定理等知识点,能熟记平行线的性质定理和判定定理是解此题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学部编道德与法治二年级上册高效课堂资料
“三角形三边关系的探究”练习题
一、填一填
由三条()围成的图形叫做三角形。
一个三角形有( )个顶点,()个角,()条边。
二、判断
下面三根小棒可以围成一个三角形吗?你是怎么判断的?(能的在下面画“√”)
三、试一试
现有长度为2cm,3cm,4cm,5cm的木棒,从中任取三根围成一个三角形,可以怎样选?
四、选一选
1、下面各组中的三条线段,可以围成一个三角形的()
A、2、4、6
B、2、5、5
C、2、2、5
D、3、4、7
2、已知一个三角形的两条边是7厘米和8厘米,则第三条边不可能是()
A、2厘米
B、3厘米
C、14厘米
D、1厘米
五、先想一想,再小组内说一说
(1)3根同样长的小棒,能否首尾相连地摆成一个三角形?
(2)4根同样长的小棒,能否首尾相连地摆成一个三角形?
六、解决问题
1、小明要做一个三角形的支架,他的手中有两根长度分别是4分米、8分米的木条,他还需
要一根几分米长的木条就能完成他的心愿?
2、已知一个三角形的两条边分别是7cm 、3cm,第三条边可能是多少厘米?
“三角形三边关系的探究”当堂测评
班级:________ 姓名:__________ 成绩:_________
1.判断(能的在下面画“√”)
2. 一个三角形的两边分别是5和6,另一条边可能是()
A、小于11
B、大于11
C、小于11大于1
3.两根小棒分别是5cm、10cm,再有一根()㎝的小棒就能围成一个三角形。
A、5cm
B、6cm
C、4cm
D、15cm
4. 写出三角形第三边的长度
6厘米和6厘米,第三边可能长_______________厘米
3厘米和4厘米,第三边可能长_______________厘米
5. 如果三角形的两条边的长分别是5cm和8cm,那么第三条边的长最短是()厘米,最
长是()厘米。
(填整厘米数)
6. 一个三角形的各边长都是整厘米数,其中两条边分别是7cm,8cm,那么这个三角形的周长最长是()厘米,最少是()厘米。
