[K12学习]山西省平遥县高中数学 第二章 基本初等函数(Ⅰ)2.1.1 指数与指数幂的运算(1)教
高中数学 第二章 基本初等函数(Ⅰ)2.1 指数函数 2.1.1 第2课时 指数幂及运算讲义教案

学习资料第2课时指数幂及运算学习目标核心素养1.理解分数指数幂的含义,掌握根式与分数指数幂的互化.(重点、难点)2.掌握实数指数幂的运算性质,并能对代数式进行化简或求值.(重点)1.通过分数指数幂、运算性质的推导,培养逻辑推理素养.2.借助指数幂的运算性质对代数式化简或求值,提升数学运算素养.1.分数指数幂的意义分数指数幂正分数指数幂规定:a错误!=错误!(a〉0,m,n∈N*,且n〉1)负分数指数幂规定:a错误!=错误!=错误!(a〉0,m,n∈N*,且n>1) 0的分数指数幂0的正分数指数幂等于0,0的负分数指数幂没有意义提示:①若a=0,0的正分数指数幂恒等于0,即错误!=a错误!=0,无研究价值.②若a<0,a错误!=错误!不一定成立,如(-2)错误!=错误!无意义,故为了避免上述情况规定了a>0。
2.有理数指数幂的运算性质,(1)a r a s=a r+s(a>0,r,s∈Q).(2)(a r)s=a rs(a〉0,r,s∈Q).(3)(ab)r=a r b r(a〉0,b>0,r∈Q).3.无理数指数幂一般地,无理数指数幂aα(a〉0,α是无理数)是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.1.下列运算结果中,正确的是()A.a2a3=a5B.(-a2)3=(-a3)2C.(错误!-1)0=1 D.(-a2)3=a6A[a2a3=a2+3=a5;(-a2)3=-a6≠(-a3)2=a6;(a-1)0=1,若成立,需要满足a≠1,故选A.]2.4错误!等于()A.25 B.错误!C。
错误!D。
错误!B[4错误!=错误!=错误!,故选B。
]3.已知a〉0,则a错误!等于()A.错误!B。
错误!C.错误!D.-错误!B[a错误!=错误!=错误!。
]4.(m错误!)4+(-1)0=________.m2+1[(m错误!)4+(-1)0=m2+1。
高中数学必修一第二章 基本初等函数(Ⅰ) 第二章 2

答案
(2)a的n次方根的表示 n 的奇偶性 a 的 n 次方根的表示符号 a 的取值范围
n 为奇数
na
n 为偶数
±n a
a∈R [0,+∞)
(3)根式 式子 n a 叫做根式,这里n叫做 根指,数a叫做被开方数.
答案
知识点二 根式的性质 思考 我们已经知道若 x2=3,则 x=± 3,那么( 3)2 等于什么? 32呢?
为奇数时,x=n a,n 为偶数时,x=±n a(a>0);负数没有偶次方根,0 的任何次方根都是 0.
2.掌握两个公式:(1)(n a)n=a;(2)n 为奇数,n an=a,n 为偶数,n an=
|a|=a-,a,
a≥0, a<0.
3.一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还 是负数,还要分清n为奇数和偶数这两种情况.
解析答案
(3)( a-1)2+ 1-a2+3 1-a3. 解 由题意知a-1≥0, 即a≥1. 原式=a-1+|1-a|+1-a=a-1+a-1+1-a=a-1.
反思与感悟
解析答案
跟踪训练2 求下列各式的值:来自7 (1)-27;
解 7 -27=-2.
4 (2)
3a-34(a≤1);
解 4 3a-34=|3a-3|=3|a-1|=3-3a.
►Living without an aim is like sailing without a compass. 生活没有目标,犹如航海没有罗盘。
►A man is not old as long as he is seeking something. A man is not old until regrets take the place of dreams. 只要一个人还有追求,他就没有老。直到后悔取代了梦想,一个人才算老。
高中数学 第二章 基本初等函数(Ⅰ)2.1.1 函数的概念和图象(二)课件 苏教版必修1.pptx

3.若函数y=f(x)的图象经过点(0,1),则函数y=f(x-1)的图象必经过点 __(1_,_1_)__.
12345
26 答案
4.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余 下的路程,建立坐标系,其中纵轴表示离学校的距离,横轴表示出发后的 时间,则下图中较符合此学生走法的是____④____.(填序号)
6
知识点二 函数图象的初步应用
思考
如图是一个函数f(x)的图象,那么函数f(x)的定义域、值域是 什么?f 12和 f 13谁大?
7 答案
梳理
如果已知函数图象,可以从中知道函数的定义域、值域、上升、下降趋 势、某些特殊点的坐标等性质.
9
题型探究
10
类型一 画函数的图象
例1 画出下列函数的图象.
12 解答
(3)y=x2+x,x∈[-1,1). 解 y=x2+x,x∈[-1,1)的图象是y=x2+x,x∈R的图象上x∈[-1,1) 的一段,其中点(-1,0)在图象上,用实心点表示;点(1,2)不在图象上, 用空心点表示:
解答
反思与感悟
函数图象受对应法则和定义域的双重影响,故画图时要关注定义域, 另外画图时要标明关键点坐标,如最高点、最低点、与x轴、y轴交点, 点的虚实要分清.
5 答案
梳理
将自变量的一个值x0作为横坐标,相应的函数值f(x0)作为纵坐标,就 得到坐标平面上的一个点(x0,f(x0)).当自变量取遍函数定义域A中的 每一个值时,就得到一系列这样的点.所有这些点组成的集合(点集) 为{(x,f(x))|x∈A},即{(x,y)|y=f(x),x∈A},所有这些点组成的图 形就是函数y=f(x)的图象.
值域:[1,10).
【配套K12】山西省平遥县高中数学第二章基本初等函数Ⅰ2.2.1对数与对数运算1教案新人教A版必修1

对数与对数运算【教学目标】对数的运算性质【重点难点】准确应用对数的运算性质及对数恒等式.【教学过程】一、情景设置问题:①我们知道,对数运算可看作指数运算的逆运算,你能从指数与对数的关系以及指数运算性质,得出相应的对数运算性质吗?②如我们知道a m=M, a n=N, a m⋅a n= a m+n,那m+n如何表示,能用对数式运算吗?③在上述②的条件下,类比指数运算性质能得出其他对数运算性质吗?二、探索研究(1)推导:①设a m=M, a n=N,由于a m⋅a n= a m+n,由对数的定义得到:loga M=m, logaN=n, loga(M⋅N)=logaM+logaN仿照上述过程,由a m÷a n= a m-n和(a m)n=a mn得出对数其他运算性质②③得出对数的运算性质:如果a>0,a≠1,M>0,N>0, 那么①loga (M⋅N)=logaM+logaN ②logaMN=logaM –logaN ③logaM n=nlogaM(2)你能否用最简练的语言描述上述运算性质?①②③(3) 上述运算性质中的字母的取值有什么限制吗?三、教学精讲例1.用loga x,logay, logaz表示下列各式:①loga xyz②logax2y3z③loga3xy2z④loga(x4z3y2)例2.求下列各式的值:①2log 510+log 50.25 ②log 2(47⨯25) ③12lg 3249- 43lg 8+lg 245四、课堂练习1.求下列各式的值:①5110log 25- ②2log 32-log 3329+log 38 -53log 252.求解下列各题:①若lgm=b-lgn,则m 用n,b 表示为____________.②已知log 29=a,log 25=b.用a,b 表示log 275.五、本节小结熟练掌握对数的运算性质及初步应用【教学后记】。
山西省平遥县高中数学第二章基本初等函数Ⅰ2.2.2对数函数及其性质1教案

对数函数及其性质【教学目标】1.进一步理解对数函数的图象和性质;2.熟练应用对数函数的图象和性质,解决一些综合问题。
【重点难点】教学重点:对数函数的图象和性质. 教学难点:对数函数的性质的综合运用. 【教学过程】 一、情景设置1.画出函数x y x y x y lg ,log ,log 52===的图象。
回答下列问题.(1)函数x y a log =与x y a1log =,0(>a 且)0≠a 有什么关系?图象之间又有什么特殊的关系?(2)以x y x y x y lg ,log ,log 52===的图象为基础,在同一坐标系中画出x y x y x y 1015121log ,log ,log ===的图象.(3)已知函数x y x y x y x y a a a a 4321log ,log ,log ,log ==== 的图象,则底数之间的关系:_______________________________.y=log a 1xy=log a 2x y=log a 3xy=log a 4x2.根据对数函数的图象和性质填空.(1)已知函数x y 2log =,则当0>x 时,∈y ;当1>x 时,∈y ; 当10<<x 时,∈y ;当4>x 时,∈y .(2)已知函数x y 31log =,则当10<<x 时,∈y ;当1>x 时,∈y ;当5>x 时,∈y ;当20<<x 时,∈y ;当2>y 时,∈x . 二、教学精讲例1.溶液酸碱度的测量。
溶液酸碱度是通过PH 刻画的。
PH 的计算公式为PH=-lg[H],其中[H]表示溶液中氢离子的浓度,单位是摩尔/升。
(1)根据对数函数性质及上述PH 的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;(2)已知纯净水中氢离子的浓度为[H]=10摩尔/升,计算纯净水的PH 。
高中数学 2.1.1.1 基本初等函数(Ⅰ)课件 新人教A版必修1

4 (1)
-24;
5 (2)
2-π5;
4 (3)
x+14;
3 (4)
x-63.
由题目可获取以下主要信息:
①所给形式均为n an的形式;
②n an形式中 n 分为奇数和偶数两种. 解答本题可依据根式的性质
n an=|aa|
n为大于1的偶数 n为大于1的奇数
,完成化简.
[解题过程]
4 (1)
-24=2;
5 (2)
2-π5=2-π;
4 (3)
x+14=|x+1|=x-+x1-1
x≥-1 x<-1 ;
3 (4)
x-63=x-6.
[题后感悟] 解决根式的化简问题,首先要分 清根式为奇次根式还是偶次根式,然后运用根 式的性质进行解答.
1.下列各式总能成立的是( )
A.(4 a-4 b)4=a-b
B.(4 a+b)4=a+b
【错因】 4 1- 24≠1- 2,而是4 1- 24
=|1- 2|= 2-出错原因是n an=a(a∈ R)成立的条件是 n 为正奇数,如果 n 为正偶数,
那么n an=|a|. 【正解】 3 1+ 23+4 1- 24=(1+ 2) +|1- 2| =1+ 2+ 2-1=2 2.
(3)当 n 为大于 1 的偶数时,n a只有当 a≥0 时 有意义,当 a<0 时无意义.n a(a≥0)表示 a 在实 数范围内的一个 n 次方根,另一个是-n a, ±n an=a. (4)式子n an对任意 a∈R 都成立.
◎计算:3 1+ 23+4 1- 24.
【错解】 3 1+ 23+4 1- 24=(1+ 2) +(1- 2)=2.
a叫 a 的算术平方根. 2.开立方与立方根,若 x3=a,则求 x 的运算
高一数学必修一第二章基本初等函数知识点总结
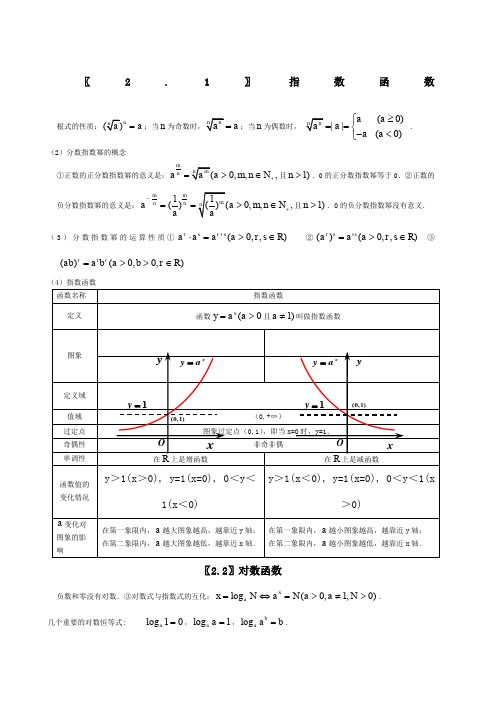
〖2.1〗指数函数根式的性质:n a =;当na =;当n 为偶数时,(0)|| (0) a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m naa m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,mm nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.(3)分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈(4)指数函数〖2.2〗对数函数负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>.几个重要的对数恒等式: log 10a =,log 1aa =,logb a a b =.常用对数与自然对数:常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…).对数的运算性质 如果0,1,0,0aa M N >≠>>,那么①加法:log log log ()aa a M N MN += ②减法:log log log a a aMM N N-=③数乘:log log ()na a n M Mn R =∈ ④log a N a N = ⑤log log (0,)b n a a nM M b n R b=≠∈⑥换底公式:log log (0,1)log b a b NN b b a=>≠且换底公式的推论: (5)对数函数〖2.3〗幂函数(1)幂函数的定义 一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数.(2)幂函数的图象(3)幂函数的性质 ①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限. ②过定点:所有的幂函数在(0,)+∞都有定义,并且(1,1). 图象都通过点0α>,③单调性:如果则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当qpα=(其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则q py x =是奇函数,若p 为奇数q 为偶数时,则q py x=是偶函数,若p 为偶数q 为奇数时,则qpy x=是非奇非偶函数.⑤图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x =上方,若1x >,其图象在直线y x=下方.。
高中数学 第二章 基本初等函数(Ⅰ)2.1 指数函数 2.1.2 第1课时 指数函数的图象及性质讲

学习资料2.1。
2 指数函数及其性质第1课时指数函数的图象及性质学习目标核心素养1.理解指数函数的概念与意义,掌握指数函数的定义域、值域的求法.(重点、难点) 2.能画出具体指数函数的图象,并能根据指数函数的图象说明指数函数的性质.(重点)1.通过学习指数函数的图象,培养直观想象的数学素养.2.借助指数函数的定义域、值域的求法,提升逻辑推理素养.1.指数函数的概念一般地,函数y=a x(a〉0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
2.指数函数的图象和性质,a的范围a>10<a<1图象性质定义域R值域(0,+∞)过定点(0,1),即当x=0时,y=1单调性在R上是增函数在R上是减函数奇偶性非奇非偶函数对称性函数y=a x与y=a-x的图象关于y轴对称(2)指数函数值随自变量有怎样的变化规律?提示:(1)指数函数y=a x(a〉0且a≠1)的图象“升”“降”主要取决于字母a.当a>1时,图象具有上升趋势;当0〈a<1时,图象具有下降趋势.(2)指数函数值随自变量的变化规律1.下列函数一定是指数函数的是()A.y=2x+1B.y=x3C.y=3·2x D.y=3-xD[由指数函数的定义可知D正确.]2.函数y=3-x的图象是()A B C DB[∵y=3-x=错误!错误!,∴B选项正确.]3.若指数函数f(x)的图象过点(3,8),则f(x)的解析式为()A.f(x)=x3B.f(x)=2xC.f(x)=错误!错误!D.f(x)=x错误!B[设f(x)=a x(a>0且a≠1),则由f(3)=8得a3=8,∴a=2,∴f(x)=2x,故选B。
]4.函数y=a x(a〉0且a≠1)在R上是增函数,则a的取值范围是________.(1,+∞)[结合指数函数的性质可知,若y=a x(a>0且a≠1)在R上是增函数,则a〉1.]指数函数的概念①y=(-8)x;②y=2x2-1;③y=a x;④y=2·3x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数与指数幂的运算
【教学目标】
理解根式的概念
【重点难点】
根式的概念
【教学过程】
一、情景设置
课题引入:以课本P48页问题1、问题2引入。
讨论:
①什么是平方根?什么是立方根?一个数的平方根有几个, 立方根呢?
②如x4=a,x5=a, x6=a,根据上面的结论我们又能得到什么呢?
③根据上面的结论我们能得到一般性的结论?
④可否用一个式子表达呢?
二、探索研究
1.整数指数幂的运算法则
①②③
2.n次方根的定义:
说明:①n次方根的定义是和的推广。
②在实数范围内,正数的奇次方根是一个,负数的奇次方根是一个.
零的奇次方根是.设a∈R,n是大于1的奇数,则a的n次方根记作.
③在实数范围内,正数的偶次方根有个,它们互为,零的偶次方根是,负数的
偶次方根.设a≥0,n是大于1的偶数,则a的n次方根是.
三、教学精讲
①式子n a 叫做,n叫做,a叫做.
②(n a )n= ;
当n 为奇数时, n a n = .当n 为偶数时,n a n = =⎩⎨⎧
例1、求下列各式的值 ① 3(-8)3 ②(-10)2 ③4(3-π)4 ④(a-b)2 (a>b)
例2、计算:5-26+5+2 6
四、课堂练习
1.下列运算正确的是( )
(A)(-a 2)3=(-a 3)2
(B)(-a 2)3=-a 2+3 (C)(-a 2)3=(-a)6
(D)(-a 2)3=(-1)3a 2×3=-a 6 2.若a =(2+3)-1,b =(2-3)-1,则(a +1)-2-( b +1)-2的值是( )
3.下列有四个命题
①正数的偶次方根是一个正数;②正数的奇次方根是一个正数;
③负数的偶次方根是一个负数;④负数的奇次方根是一个负数.
其中正确命题的个数是( )
(A)0个
(B)1个 (C)2个 (D)3个 4.a∈R,n∈N *,下列四个运算恒成立的是( )
(A) (n a )n =a
(B) (n |a| )n =|a| (C)(n a )n =|a| (D) n a n =|a| 5.已知3a =2,3b =5,则3
2a -b =____________ 答案:DDCB 45
五、本节小结 ①如果x n =a ,那么x 叫做 ,其中n>1,且n ∈N *
.当n 是奇数时,正数的n 次方根 ,负数的n 次方根是 .a 的n 次方根用符号 表示.
式子n a 叫做根式,这里n 叫做根指数,a 叫做被开方数.
②当n 是偶数时,正数的n 次方根 .此时,正数a 的正的n 次方根用符号 表示,负的n 次方根用符号 表示.正的n 次方根与负的n 次方根可以合并成±n a (a>0).由此可得:负数没有偶次方根;0的任何次方根都是0,记作n 0=0.
③(n a )n = ; 当n 为奇数时,n a n = .当n 为偶数时,n a n =⎩⎨⎧
【教学后记】。
