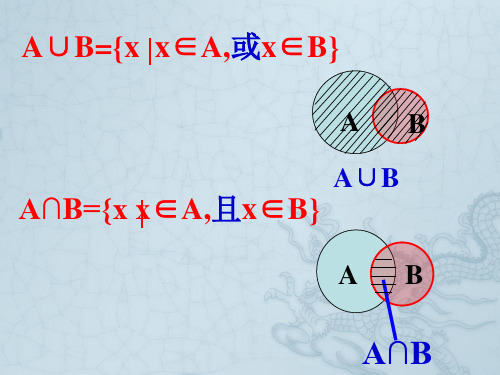
集合的基本运算(全集与补集)

1.2.2集合的基本运算（二） ---补集
温故知新
（1）集合与集合之间的关系有几种？分别是什么？ （2）交集与并集的定义分别是什么？
交集：给定两个集合 A，B，由既属于 A 又属 于B 的所有公共元素构 成的集合，叫做 A，B 的交集．记作：AnB
并集：给定两个集合 A ，B ，由属于 A 或属 于B 的所有元素构成的 集合，叫做 A，B 的并集． 记作：AUB
作业
1、教材19页A组2、3，B组1 2、练习册：题组一、题组二、题组三
冬瓜、虾、毛豆
一.全集
新知全解
全集U
冬瓜、 虾、毛豆、
黄瓜、 鲫鱼、 茄子 猪肉、 芹菜、 土豆
全集的定义
一般地，如果一个集合含有我们所研究问题中所涉及的所有元素，
那么就称这个集合为全集，
通常记作U.
二.补集
冬瓜、虾、毛豆
A 在全集 U 中的补集
1、定义 如果 集合 A 是全集 U 的一个子集 ，由 U 中的所有不属于 A 的
U
．
补集的性质：
补集的性质
（1）A ∪ CU A＝ （2）A ∩ CU A = （3） CU(CUA)＝
U； ； A．
U A
CUA
互动探究（交并补的混合运算）
例1:设全集为R,A={x|x<5},B={x|x>3}.求值：
(1)A∩B;
(2)A∪B;
(4)(CRA) ∩ (CRB);
(3) CRA, CRB; (5) CR(A ∪ B);
补集的综合应用（多维训练）
例2：已知集合A={x|x<a},B={x|1<x<3}，若AUCRB=R,求实数a的取值范围； 解：CRB={x|x≤1或x≥3}，结合数轴分析可得a≥3
变式（1）：上例中若改为B={x|1≤x≤3}其余条件不变，求实数a的取值范围； （2）：上例中若改为A={x|x≤a},B={x|1≤x≤3}其余条件不变，求实数
情境导入
我校食堂计划前两天买菜的品种构 成了集合U
第一天买进的品种构成了 集合 A
冬瓜、 虾、
毛豆
黄瓜、鲫鱼、茄子 猪肉、芹菜、土豆
黄瓜ቤተ መጻሕፍቲ ባይዱ鲫鱼、茄子 猪肉、芹菜、土豆
问1 集合 A 与集合 U 是什么关系 ？ 问2 在计划买进的品种中，如果将还没买进的品种构成的集合记为 B，则集合 B 中的元素是什么？
元素构成的集合，叫做 A 在U 中的补集．
记作 : CU A
读作 : A 在 U 中的补集
2．用 Venn 图表示出 “ CU A ”
U A
CUA
问题导引
例1 已知：全集U ＝ { 1，2，3，4，5，6 }，
集合 A＝ { 1，3，5 }，
则 CU A＝
{ 2，4，6 }
；
A ∩ CU A＝
；
A∪CU A ＝
a的取值范围。 解：（1）CRB={x|x<1或x>3}，结合数轴分析可得a>3 （2）CRB={x|x<1或x>3}，结合数轴分析可得a≥3
课堂小结
回顾本节课你有什么收获？ 1.全集和补集的概念. 2.补集的性质. 3.用数轴法和图示法求交集、并集、补集.
合作探究
设全集U＝{2,3，a2＋2a－3}，A＝{|2a－1|,2}，CUA＝{5}，求实数a的值 【解】因为CUA＝{5}，所以5∈U且5∉A，所以a2＋2a－3＝5，且|2a－ 1|≠5，解得a＝2或a＝－4，即实数a的值是2或－4. 【错因】本题解答错误在于忽略了集合A的元素|2a－1|是由a确立的，事 实上，当a＝2时，|2a－1|＝3，A＝{2,3}，符合题意，而当a＝－4时，A＝ {9,2}，不是U的子集． 【正解】 因为CUA＝{5}，则5∈U且|2a－1|＝3.解得：a＝2，即a的取值 是2. (也可以采用错解中的步骤，最后加上错因分析中的验证一步)．