量子力学第2章 周世勋
量子力学第二版(周世勋)

2µ
2µ
= qBnη = nB ⋅ qη
2µ
2µ
= nBNB ,
其中, M B
=
qη 2µ
是玻尔磁子,这样,发现量子化的能量也是等间隔的,而且
具体到本题,有
∆E = BM B
根据动能与温度的关系式
∆E = 10 × 9 × 10−24 J = 9 × 10−23 J
E = 3 kT 2
以及
1k ⋅ K = 10−3 eV = 1.6 × 10−22 J
∂ ∂r
(1 eikr ) − r
1 eikr r
∂ ∂r
(1 r
e
−ikr
ρ )]r0
=
iη [1 (− 2m r
1 r2
+ ik 1) − 1 (− rr
1 r2
−
ik
1 r
)]ρr0
可见,
ρ J2
=
−
ηk mr 2
ρr0
=
−
ηk mr 3
ρr
与rρ反向。表示向内(即向原点) 传播的球面波。
补充:设ψ (x) = eikx ,粒子的位置几率分布如何?这个波函数能否归一化?
1.3 氦原子的动能是 E = 3 kT (k 为玻耳兹曼常数),求 T=1K 时,氦原子的德布罗意波 2
长。
解 根据
2
PDF 文件使用 "pdfFactory Pro" 试用版本创建
知本题的氦原子的动能为
1k ⋅ K = 10−3 eV ,
E = 3 kT = 3 k ⋅ K = 1.5 ×10−3 eV , 22
解 关于两个光子转化为正负电子对的动力学过程,如两个光子以怎样的概率转化为正 负电子对的问题,严格来说,需要用到相对性量子场论的知识去计算,修正当涉及到这个过 程的运动学方面,如能量守恒,动量守恒等,我们不需要用那么高深的知识去计算,具休到 本题,两个光子能量相等,因此当对心碰撞时,转化为正风电子对反需的能量最小,因而所 对应的波长也就最长,而且,有
量子力学教程(周世勋)课后习题详细解答

量子力学课后习题详细解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv echv d kThv v v 11833-⋅=πρ, (1) 以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dvλλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThc e kT hc ehcλλλλλπρ ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
周世勋《量子力学教程》配套题库章节题库波函数和薛定谔方程【圣才出品】
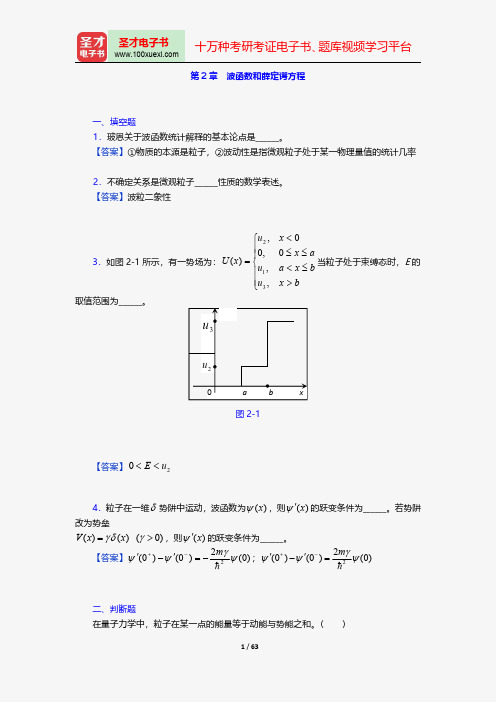
如果题目中没有给定 为能量本征态,则也可判定它所对应的能量高,因为它可能是 基态、第一激发态和第二激发态的组合(依赖于 b 和 c 的大小)。因此在此态中的能量平均
值也要高于 描写的状态的能量平均值。
3.写出动量表象中的不含时 S.eq。 答:经典能量方程
在动量表象中,算符化规则为
(1)
(2) 将此规则运用于式(1),并将式(1)两边分别作用于动量空间波函数φ(p)上,即得动 量表象中的不含时 S.eq
4.质量为 m 的粒子处于能量为 E 的本征态,波函数为
ቤተ መጻሕፍቲ ባይዱ问粒
子在什么样的位势中运动?
答:这也是直接应用 S.eq 解题的例子,S.eq 联系了 m,ħ,V,E 和 (x),知道
了其中一部分,就可以求出其他部分。
本题中要求解位势,从 S.eq
出发,只要把已知的
能量本征函数 (x)代入运算,即可得解
3 / 63
圣才电子书 十万种考研考证电子书、题库视频学习平台
5.简述波函数和它所描写的粒子之间的关系。
答:微观粒子的状态可用一个波函数完全描述,从这个波函数可以得出体系的所有性质。
波函数一般应满足连续性、有限性和单值性三个条件。
微观粒子的状态波函数 用算符 Fˆ 的本征函数 展开( Fˆn nn ,Fˆ ):
三、名词解释题 1.基本量子条件。
答:[xˆ , xˆ ] 0 ,[ pˆ , pˆ ] 0 ,[xˆ , pˆ ] i 。
2.能级简并、简并度。 答:量子力学中,把处于不同状态、具有相同能量、对应同一能级的现象称为能级简并; 把对应于同一能级的不同状态数称为简并度。
四、简答题 1.分别说明什么样的状态是束缚态、简并态与负宇称态? 答:当粒子的坐标趋向无穷远时,波函数趋向零,称之为粒子处于束缚态。若一个本征 值对应一个以上的本征态,则称该本征值是简并的,所对应的本征态即为简并态,本征态的 个数就是相应的简并度。将波函数中的坐标变量改变一个负号,若新波函数与原波函数相差 一个负号,则称其为负宇称态。
量子力学教程-周世勋-第二章波函数

在上式中令 a=0,然后再将 x 改为 x − a 得:
δ [( x − a) 2 ] =
δ ( x − a)
x−a
(2.2-20)
(8) ln x 的微商
m iπ ⎧ ⎪ln x e = ln x m iπ x < 0 ln x = ⎨ x>0 ⎪ ⎩ln x
所以得:
d ln x 1 = ± iπδ ( x) dx x
ε → 0+
lim
1 1 = ± iπδ ( x) ,或 x m iε x 1 1 1 lim ( − ) 者说 iπ ε →0+ x m iε x
⎧0 x < 0 ⎪ ⎪1 x x=0 ∫ −∞ δ ( x ')dx ' = h( x) = ⎨ ⎪2 ⎪1 x > 0 ⎩
H(x)称为亥维赛(heaviside)单元函数。显然有:
(2.2-14)
dh( x) = δ ( x) dx
(6)根据(2.2-6)式可得:
(2.2-15)
f ( x) = ∫ ∞ −∞ f ( a )δ ( x − a ) da f (a) = ∫ ∞ −∞ f ( x )δ ( x − a ) dx
+ε = ∫a a −ε f ( a )δ [( x − a )( a − b)]dx + ∫
b +ε
b −ε
f (b)δ [(b − a)( x − b)]dx
=
∞ f ( x) f (a) f (b) + =∫ [δ ( x − a ) + δ ( x − b)]dx −∞ a − b a −b a −b
值得注意的是,不同体系的态的叠加是没有意义的。例如,在双狭缝衍射中,如果封闭其中的 一个狭缝,则可得到两个单狭缝体系,这两个单狭缝体系以及双狭缝体系都是不同的体系,所以双 狭缝衍射中的可能态不能视为两个单狭缝衍射可能态的叠加。
周世勋量子力学课件第二章

单个粒子在该处出现 (微粒观点) 的概率大 粒子在某处出现的概率和该处波函数振幅的平方成正比
物质波的 强度大
假设衍射波波幅用 Ψ(r) 描述,与光学相 似,衍射花样的强度则用 |Ψ(r)|2 描述,但意义 与经典波不同。
|Ψ(r)|2 的意义是代表粒子出现在r点附近概率的 大小,确切地说,|Ψ(r)|2ΔxΔyΔz 表示 在r点处,体积元ΔxΔyΔz中找到粒子的概率。 据此,描写粒子的物质波是概率波,反映微观客 体运动的一种统计规律性,波函数Ψ(r)有时也称为概 率波幅(概率幅)。波函数在空间某点的强度(振幅 绝对值的平方)和在这点找到粒子的概率成比例,由 波函数还可以得到体系的各种性质。这就是首先由 Born 提出的波函数的统计解释。 量子力学的第一条基本假定(或公设)
…………
同时粒子N出现在( rN , rN drN )中的几率
?
思考题1 设粒子波函数为 ( x, y, z) ,求在(x, x+dx)范围中找到粒子的几率。
思考题2 N粒子系的波函数为(r1, r2 ,...rN , t ) , 求在( r1 , r1 dr1 )中找到粒子1的几率(其他粒子 的位置不限)。
屏上出现的 电子说明电 子的粒子性。
7个电子在观察 屏上的图像 100个电子在 屏上的图像
单个电子的去向是概率性的,但随着电子数目的增多 显示出统计规律性。
结论:衍射实验所揭示的电子的波动性是: 许多电子在同一个实验中的统计结果,或者是一 个电子在许多次相同实验中的统计结果。 波函数正是为了描述粒子的这种行为而引进的,在 此基础上,Born 提出了波函数意义的统计解释。
(2) 粒子由波组成
电子是波包。把电子波看成是电子的某种实际 结构,是三维空间中连续分布的某种物质波包, 因此呈现出干涉和衍射等波动现象,并且认为 波包的大小即电子的大小,波包的群速度即电 子的运动速度。 什么是波包?波包是各种波数(波长)平面波 的迭加,强度只在空间有限区域中不为零。
周世勋量子力学第二章知识题

第二章 波函数和薛定谔方程2.1. 证明在定态中,几率流密度与时间无关. 解: 几率流密度公式为()**2J iψψψψμ=∇-∇ 而定态波函数的一般形式为()(),iEtt eψψ-=r r将上式代入前式中得:()()()()**2J r r r r i ψψψψμ⎡⎤=∇-∇⎣⎦ 显然是这个J 与时间无关.2.2. 由下列两定态波函数计算几率流密度;(1) ,e r ikr 11=ψ (2) ikr e r-=12ψ 从所得结果说明1ψ表示向外传播的球面波,2ψ表示向内(即向原点)传播的球面波.解: 在球坐标中,梯度算符为1ψ和2ψ只是r 的函数,与ϕθ,无关,所以,()**11211e e e ikr r r r e r ik ik r r r r ψψψ-∂⎛⎫⎛⎫∇==-+=-+ ⎪ ⎪∂⎝⎭⎝⎭()*222111e e e ikr r r r e r ik ik r r r r ψψψψ-∂⎛⎫⎛⎫∇==-+=-+=∇ ⎪ ⎪∂⎝⎭⎝⎭()()**221111ikr r r r e r ik ik r r r r r ψψψψ∂⎛⎫⎛⎫∇==-=-=∇ ⎪ ⎪∂⎝⎭⎝⎭e e e将以上四式代入 ()()()()**2J r r r r i ψψψψμ⎡⎤=∇-∇⎣⎦ (1) 对于ikre r11=ψ12222111122r r r i k p ik r r r r μμμμ⎡⎤=-===⎢⎥⎣⎦p J e e e (2) 对于ikre r-=12ψ212222111122r r r i k p ik r r r r μμμμ⎡⎤==-=-=-=-⎢⎥⎣⎦p J e e e J 计算的结果已经很清楚ikre r11=ψ这样的球面波,是沿r e 方向传播的波, 121p J e rr μ=.而球面 波ikre r-=12ψ传播方向与1ψ相反,即21J J =- 2.3. 一粒子在一维势场()⎪⎩⎪⎨⎧>∞≤≤<∞=ax a x x x U 00中运动,求粒子的能级和对应的波函数.解: 从定态薛定谔方程 02222=+ψμψE dx d 即 02=+''ψψk ()20k E =>可知,其解为ikx ikx Be Ae -+=ψ在0≤x 和a x ≥处,波函数为 0)(=x ψ,在a x ≤≤0处, 波函数为 ikxikx Be Ae -+=ψ 从()00=ψ得 0=+B A 即 B A -=因此有 ()2sin sin ikx ikx A e e iA kx C kx ψ-=-== 从()0=a ψ得 sin 0ka = 即要求 321,,n n ka ==π所以 sin1,2,3n n C x n aπψ==22222an E n μπ = 归一化条件1*=⎰dx ψψ可得aC 2=()()222211sin 1cos 2,cos 1cos 222αααα⎡⎤=-=+⎢⎥⎣⎦ 所以 1,2,30n nx n x a aπψ==≤≤ 综合得: 000n n x x a ax x aπψ≤≤=<>⎩或2.4. 证明()sin20n n A x a x a ax aπψ⎧'+<⎪=⎨⎪≥⎩式中的归一化常数是a A 1='解: 这是宽度为a 2,将坐标原点选在势阱中心而表示的一维无限深势阱的波函数,利用归一化条件得()222220222201sin sin 2222sin 2a aa n n n A x a dx A ydya a a a n A zdz A A a n n ππππππ+-''=+='''==⋅⋅=⎰⎰⎰所以 aeA i 1δ=' 取 0=δ 得2.5. 求一维谐振子处在第一激发态时几率最大的位置. 解: 一维谐振子第一激发态的波函数为 ()()x xex *x 1212112222ψαπαψα=⋅=- 其中几率密度()()22223323222210x x dw x x e x x e dx ααααππ--=-=-= 极值点有 00,,x x =±±∞ 使:()2223224421520x d w x x e dx αααπ-=-+< 只有μω±=±=0x x两个值,所以和μω-=x 处第一激发态粒子出现的几率最大.2.6. 在一维势场中运动的粒子,势能对原点对称:()()x U x U =-,证明粒子定态的波函数具有确定的宇称.解: 定态的波函数满足的薛定谔方程为()()()x E x x H ˆψψ=哈密顿算符 ()()x U dxd x H ˆ+-=222μ 于是当x x -→时,而拉普拉斯算符 ()222222222222dxd x d d dx d μμμ -=--→- 题2.5图 图中取1μω=即在坐标反射下,哈密顿算符不变,即()()x H ˆx Hˆ=- 写出坐标反射后的薛定谔方程()()()x E x x H ˆ-=--ψψ考虑到()()x H ˆx Hˆ=-有 ()()()x E x x H ˆ-=-ψψ 比较 ()()()()()()ˆˆH x x E x H x x E x ψψψψ⎧=⎪⎨-=-⎪⎩ 如果属于能量E 的本征值是非简併的,反射变换前后,状态函数有如下关系()()x x λψψ=-,()()()x x x ψλλψψ2=-=,1±=λ.即()()x x ψψ±=-可见,粒子的定态波函数具有确定的宇称,奇宇称或偶宇称. 当()()x x ψψ-=时,称该波函数为偶宇称. 当时,称该波函数为奇宇称.但是如果属于能量E 的本征值是简併的,特别是()()x x ψλψ-≠这时可以构造两个与之相关的波函数()()()()()(),.f x x xg x x x ψψψψ-=+--=--据此,可知()(),f x f x -=因而具有偶宇称;()().g x g x -=-因而具有奇宇称.以上结果本质上是根据哈密顿的对称性去推知它的本征函数的对称性.一般地,如果属于某一能量的本征态是非简併的, 那么, 能量本征态会携带哈密顿算符的对称性.但是, 如果属于某一能量的本征态是简併的,那么并不是其中的每一个本征态都会携带哈密顿算符的对称性.但总可以通过它们的某种组合使之携带哈密顿算符的对称性.2.7. 一粒子在一维势阱()⎩⎨⎧<>>=ax ax U x U 000 中运动,求束缚态()00U E <<的能级所满足的方程.解: 粒子所满足的方程()()222222d x E x a x a dx ψψμ-=-<<()()()a x x E x U x dxd >=+-33032222ψψψμ令 22 Eμα= ()202 E U -=μβ方程变为()()()()()()⎪⎩⎪⎨⎧>=-''<<-=+''-<=-''ax x x a x a x x ax x x 000323222121ψβψψαψψβψ它们的解分别是:()112212312sin cos sin x xx xA e A e x aB x B x B x a x aC e C e x aββββψψαααδψ--=+<-=+=+-<<=+> 由波函数的有限性条件限制,必须要求120A C ==()12231sin xxA e x aB x a x aC e x aββψψαδψ-=<-=+-<<=> (1)根据波函数在边界上连续及导数连续的条件, 确定常数.(1) 波函数ψ连续1232x a x ax a x a x a x a ψψψψ=-=-==⎧=-=⎪⎨==⎪⎩得 ()()21sin sin aaA eB aC eB a ββαδαδ--⎧=-+⎪⎨=+⎪⎩ (2) (2) 波函数导数ψ'连续[][][][]⎩⎨⎧'='='='-===-=-=a x a x a x a x a x a x 22332211ψψψψψψψψ 得 ()()ctg ctg a a βααδβααδ=-+⎧⎪⎨-=+⎪⎩ (3) 由此明显看出:由(2)可以用消去两个待定系数2A 和1C ;由(3)可以确定δ和能量E .由(3)得 ()()()ctg ctg ctg a a a αδαδαδ+=--+=-所以 ()();0,1,2a k a k αδπαδ+=+-=±±,由此得πδk 21=,由于余切以π为周期, 故只有两个独立解:20πδ,=,把0=δ和2π分别代入(3)式得到确定能量的方程为:0ctg 2tg a a δααβδπααβ==-==将上面的式子同乘以势垒宽度a0ctg 2tg a a aa a aδααβδπααβ==-==再考虑到:()20202222()U E U a a a a μμβα-==-令 22022U a n μ=z a α=22ctg z z n z =--令 221()ctg f z z z n z =+- 同理由第二组解得: 222()tg f z z z n z =--当1,2,3,4n =, 由1()f z 和2()f z 做出图2.7-1, 图2.7-2, 图2.7-3, 图2.7-4.由图2.7-1可以看出:当1n =时()01z <<只有一虚线通过横轴,也就说只存在一个解.对应的是第二组的解.由数值计算可知,此时0.7391z =,由此可算出对应的能级. 由图2.7-2可以看出:当2n =时()02z <<存在两个解.分别对应的是第一组和第二组的解.由数值计算可知,此时对应第一组的解为 1.8955z =,对应第二组的解为,由此可算出对应的能级. 由图2.7-3可以看出:当3n =时()03z <<存在两个解.分别对应的是第一组和第二组的解.由数值计算可知,此时对应第一组的解为 2.2789z =,对应第二组的解为 1.1701z =,由此可算出对应的能级. 由图2.7-4可以看出:当4n =(实际上只要 3.5n >即存在三个解)时()04z <<存在三个解.其中第一组一个解和第二组的两个解.由数值计算可知,此时对应第一组的解为,对应第二组的两个解为别为1.2524,3.5953z =,由此可算出对应的能级.第一组解0δ=由()()21sin sin aaA eB aC e B a ββαδαδ--⎧=-+⎪⎨=+⎪⎩得:()()()123sin sin sin a x a xe B a e x a B x a x a e B a e x aββββψαψαψα-=-<-=-<<=>图2.7-1 图2.7-2图2.7-3 图2.7-4由归一化条件得1sin a xe a e a x ββαψ=-<2sin x a x a αψ=-<<3sin a xe a e x a ββαψ-=>对于第一组解的第一个能级,有:1.8955a α=,20.626019a aβ===取1a =得 1.8955α=,0.626019β=0.6260190.626019120.6260190.6260193sin 1.8955sin 1.8955sin 1.8955x xe e x ax a x a e e ψψψ-=<-=-<<=x a>由上述波函数可绘出图2.7-5第二组解2πδ=由21sin 2sin 2a a A e B a C e B a ββπαπα--⎧⎛⎫=-+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪=+ ⎪⎪⎝⎭⎩得()()()123cos cos cos a x a xe B a e a x B x a x a e B a e x aββββψαψαψα-=-<=-<<=> 由归一化条件得()()()()()(){}()22211122222222222221cos sin cos cos sin cos cos sin 22aaaaaa a x a x aaaaaxax aadx dx dxe B a e dx B x dx e B a e dxBea edx x dx ea e dxa a B a ββββββββψψψααααααααβα∞-∞-∞--∞-∞--∞-=++=++=++⎧⎫⎪⎪=+-⎨⎬⎪⎪⎩⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰123cos cos cos a xa xe a e a xx a x a e a e x aββββαψαψαψ-=-<=-<<=>对于第二组解的第一个能级,有:0.7391a α=20.673596a a β===令1a =得0.7391α=,0.673596β=0.6735960.673596120.6735960.6735963cos 0.7391cos 0.7391cos 0.7391x x e e x ax a x a e e ψψψ-=<-=-<<=x a>由上述波函数可绘出图2.7-6. 照此方法可绘出其它能级对应的波函数.2.8. 分子间的范德瓦尔斯力所产生的势能可以近似地表示为()⎪⎩⎪⎨⎧>≤≤-<≤<∞=bx bx a U ax Ux x U 00010求束缚态的能级所满足的方程.解: 束缚态,即要求01<<-E U .分区域写出薛定谔方程:()()()()()()()()1220222231332244200222x d x U x E x x a dx d x U x E x a x bdxd x E x x bdx ψψψψμψψψμψψμ=<-+=≤≤--=≤≤-=>其中()0222U E k μ-= 则 ()()22220x k x ψψ''-= 其中()1322E U k μ+= 则 ()()23330x k x ψψ''+=其中 422Ek μ-= 则 ()()24440x k x ψψ''-=以上三方程的解分别为:()()()()22442334sin k x kxkxk xx Ae A e x B k x x Ce C e ψψδψ--'=+=+'=+在0x =处, ()200ψ=,得0A A '+=.令A A '=-;对于()4x ψ,当∞→x 应有限,故0C '=, 则波函数可写为图2.7-6图2.7-5()()()()()2242334sin k x kxkxx A e e x B k x x Ce ψψδψ--=-=+= 由波函数导数的连续性得[][]()()[][]()322333223334434tan th tan x a x a x b x b k x a k a k a k k x b k b k ψψψψδψψψψδ====⎧''==+=⎪⎪⎨⎪''==+=-⎪⎩即()113332324tan th ,tan k k k a k a k b k k δδ--⎡⎤⎛⎫+=+=- ⎪⎢⎥⎣⎦⎝⎭由上两式消去δ,得()()11333224tan th tan k k k a b k a k k --⎡⎤⎛⎫-=-- ⎪⎢⎥⎣⎦⎝⎭用到公式111tan tan tan 1x yx y xy---±±= 上式成为 ()()()()()332342232433324332242th th tan th 1th k k k a k k k a k k k k k a b k k k k k k k a k a k k ++-==⎡⎤⎣⎦--。
量子力学(周世勋)第2章课件-10

E ix i t
i E1 t
v( x)e
u( x)e
u( x)e
i ix Et
i E2 t
(2) 2 ( x) u( x)e
(3) 3 ( x) u( x)e
E i t
E i t
4.应用实例
x x
补 充 练 习 题
1. 下列一组波函数共描写粒子的几个不同状态? 并指出每 个状态由哪几个波函数描写。
1 ei 2 x / , 4 ei 3 x / ,
2 ei 2 x / , 5 ei 2 x / ,
| x | a | x | a | x | a | x | a
扫描隧道显微镜就是利用穿透势垒的电流对于金属探针尖端同待测物体表面的距离很敏感的关系可以探测到量级高低起伏的样品表面的地形图10m11?例1
P
电子源
P
O Q
感 光 屏
Q
已知一维粒子状态波函数为 1 2 2 i (r , t ) A exp a x t 2 2 求归一化的波函数,粒子的几率分布,粒子在何处 出现的几率最大。 Ex.1 Solve:
3 3e i (2 x ) / , 6 (4 2i )ei 2 x / .
2.已知下列两个波函数
试判断: (1)波函数 1 ( x) 和 2 ( x) 是否描述同一状态? (2)对 1 ( x) 取 n 2 两种情况,得到的两个波函 数是否等价?
例1: 入射粒子为电子。
设 E=1eV, U0 = 2eV, a = 2× 10-8 cm = 2Å , 算得 D ≈ 0.51。
例2: 入射粒子为质子。
量子力学第2章-周世勋

必须注意
(1)“微观粒子的运动状态用波函数描述,描写粒 子的波是几率波”,这是量子力学的一个基本假设 (基本原理)。
知道了描述微观粒子状态的波函数,就可知道粒 子在空间各点处出现的几率,以后的讨论进一步知道, 波函数给出体系的一切性质,因此说波函数描写体系 的量子状态(简称状态或态) (2)波函数一般用复函数表示。
这就要求在描述微观粒子的运动时,要有创新 的概念和思想来统一波和粒子这样两个在经典物理 中截然不同的物理图像。
德布罗意指出:微观粒子的运动状态可用一个复 函数 (r,t)来描述,函数 (r,t) — 称为波函数。
★ 描述自由粒子的波是具有确定能量和动量的平面波
i(PrEt)
P(r,t)Ae
de Broglie 波
p (r ) r ,td r cp ,tp p d p cp ,t
因此
C (P ,t) 1 (r,t)eiP ,rd3r
(2 )3/2
(r ,t) C (P )P (r ,t)d 3 P
即
(r,t)(21)3/2
C (P ,t)eiP rd3P
显然,二式互为Fourer变换式,所以
做替换:
E i t
即得Schrödinger方程
p i
i (tr ,t) 2 2 2 U (r ,t) (r ,t)
(6)
i (tr ,t) 2 2 2 U (r ,t) (r ,t)
一(、1微)观含粒有波子函运数动对方时程间应的具一阶有导的数特点(r,t)
t
(2)方程必为线性的
(3)质量为 的非相对性粒子(即低速运动的粒
子), 其总能为
EP2
U(r,t)
2
二、自由粒子的运动方程 P (r,t)(21 )3/2e i(P ,rE)t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( r ) p ( r ' ) d p ( r r ') p
p
c p , t ( r ) r , t dr c p, t p pdp
因此
C ( P, t )
r , t 和 C r , t 所描写状态的相对几率是相同的。
粒子在空间各点出现的几率只取决于波函数在空间 各点强度的相对比例,而不取决于强度的绝对大小。
可见, r , t 和 r , t 描述的是同一几率波,所 以波函数有一常数因子不定性。
r , t 和 C r , t 描述同一状态
(1) 是怎样描述粒子的状态呢? (2) 如何体现波粒二象性的? (3) 描写的是什么样的波呢?
二、波函数的统计解释
P
电子源
电子小孔衍射实验
P
O Q
X
感 光 屏
Q
v
a
P
1
0
I
电子单缝衍射实验
电子究竟是什么东西呢?是粒子?还是波?
经典概念 中粒子意 味着 经典概 念中波 意味着
1.有一定质量、电荷等“颗粒性”的属性; 2.有确定的运动轨道,每一时刻有一定 位置和速度。 1.实在的物理量的空间分布作周期性的 变化; 2.干涉、衍射现象,即相干叠加性。
1 2
物 理 意 义 当两个缝都开着时,电子既可能处在 态,也可 1 能处在 态,也可处在 和 的线性迭加态 2 2 1 1 2 。可见, 若 1 和 2 是电子的可能状态, 则 也是电子的可能状态。 反言之,电子经双缝衍射后处于 1 2态,则 电子部分地既可处于 1 态,也可部分地处在 2 态。
电子从晶体表面出射后,既可能处在 (r , t )态,也 P (r , t ), 等状态,按态迭加原 可能处在 P (r , t ) 、
P
理,在晶体表面反射后,电子的状态 可表示成 P 取各种可能值的平面波的线性叠加,即
( r ,t ) ( r ,t ) C ( P ) P
一.电子双缝衍射实验
1
2
P2 P1
实 验 事 实
开1闭2,衍射花样(兰曲线)
1 D
P
1 1
2
S
开2闭1,衍射花样(紫红曲线)
2
2 2
2
2
同时开1,2,衍射花样(黑曲线)
1 2
显然 1 2
2 2
2
1 2
表明几率不遵守迭加原则,而波函数(几率幅)遵 守迭加原则:
则微观粒子在t 时刻出现在 r 处体积元dτ内的 几率 2 dW (r , t ) C (r , t ) d 这表明描写粒子的波是几率波(概率波),反映微 观客体运动的一种统计规律性,波函数 r , t 也称 为几率幅。
按Born提出的波函数的统计解释,粒子在空间中 某一点 r 处出现的概率与粒子的波函数在该点模的 平方成比例
The linear harmonic oscillator
2.8 势垒贯穿
The transmission of potential barrier
§2.1 波函数的统计解释 一、微观粒子状态的描述
微观粒子因具有波粒二象性,其运动状态的描 述必有别于经典力学对粒子运动状态的描述,即微 观粒子的运动状态不能用坐标、速度、加速度等物 理量来描述。
归一化条件消除了波函数常数因子的一种不确定性。
2.单值条件——任意时刻概率密度是唯一的。
3.连续性条件—— 任一点处波函数及其一 阶导数连续
有限、连续和单值称为波函数的标准化条件。
必 须 注 意
( 1 )“微观粒子的运动状态用波函数描述,描写粒 子的波是几率波”,这是量子力学的一个基本假设 (基本原理)。 知道了描述微观粒子状态的波函数,就可知道粒 子在空间各点处出现的几率,以后的讨论进一步知道, 波函数给出体系的一切性质,因此说波函数描写体系 的量子状态(简称状态或态) (2)波函数一般用复函数表示。 (3)波函数一般满足连续性、有限性、单值性。
电子既不是经典的粒子也不是经典的波。
电子究竟是什么东西呢?是粒子?还是波?
粒子性:只是经典粒子概念中的“原子性”或“颗粒性” 即:具有一定质量、电荷等属性的客体。 波动性:波动性中最本质的东西,即:波的相干叠 加性。
电子既是粒子也是波,它是粒子和波动二重性矛盾的统一
▲ 玻恩的解释: 电子的衍射实验
2
可见,波函数模的平方 r , t 与粒子 t时刻在 r 处附近出现的概率成正比。
1926年,玻恩(M.Born)首先提出了波函数的统计解释:
波函数在空间中某一点的强度(波函数模的平方) 与粒子在该点出现的概率成比例。
设粒子状态由波函数
2
(r , t ) 描述,波的强度是
*
(r , t ) (r , t ) (r , t )
P
(r ) p
衍射图样正是这些平 面波叠加干涉的结果
1 i exp[ p r] 3/ 2 ( 2)
Байду номын сангаас考虑到电子的动量可以连续变化
3 (r , t )d P (r , t ) C( P) P
p
p r dr dp ( r ) r , t dr c p, t p ' r 1 i / h p p c p, t e dr dp 3 2
(2 )3/ 2
1
(r , t )e
i P ,r
d 3r
3 (r , t )d P (r , t ) C( P) P
即
(r , t )
(2 )3/ 2
1
i
C ( P, t )e
Pr
d 3P
显然,二式互为Fourer变换式,所以 (r , t ) 与 C ( P, t ) 一 一对应,是同一量子态的两种不同描述方式。
这与经典波截然不同。对于经典波,当波幅增大 一倍(原来的 2 倍)时,则相应的波动能量将为原 来的 4 倍,因而代表完全不同的波动状态。
为消除波函数有任一常数因子的这种不确定性,利 用粒子在全空间出现的几率等于一的特性,提出波函 数的归一化条件:
1.波函数的归一化条件
非相对论量子力学仅研究低能粒子,实物粒子不会 产生与湮灭。这样,对一个粒子而言,它在全空间 出现的几率等于一。
2.1 波函数的统计解释 The Wave function and its statistic explanation
2.2 态叠加原理
The principle of superposition
2.3 薛定谔方程
The Schrödinger equation
2.4 粒子流密度和粒子数守恒定律
The current density of particles and conservation laws
2.5 定态薛定谔方程
Time independent Schrödinger equation
2.6 一维无限深势阱
The infinite potential well
2.7 线性谐振子
这就要求在描述微观粒子的运动时,要有创新 的概念和思想来统一波和粒子这样两个在经典物理 中截然不同的物理图像。
德布罗意指出:微观粒子的运动状态可用一个复 函数 (r , t ) 来描述,函数 (r , t ) — 称为波函数。
★ 描述自由粒子的波是具有确定能量和动量的平面波
P (r , t ) Ae
迭加态的概率:
干涉项
2
1 2
电子穿过狭缝1出现 在P点的几率密度
2
* 1 2 1* 2 1 2
2
2
电子穿过狭缝2出现 在P点的几率密度
当两个缝的几何参数或电子束相对位置不完全对 称时,迭加态 c1 1 c2 2 ,其概率为
c1 1 c2 2 c1c2 1 2 c1 c2 1 2 2 2 2 2 2
P O Q
感 光 屏
P
电子源
Q
衍射实验事实:
(1)入射电子流强度小,开始显示电子的微粒 性,长时间亦显示衍射图样;
(2) 入射电子流强度大,很快显示衍射图样.
波 动 观 点 明纹处: (x,y,z,t)2大
粒 子 观 点 电子出现的概率大
暗纹处: (x,y,z,t)2小
电子出现的概率小
dW (r , t ) 2 (r , t ) C (r , t ) d
称为几率密度(概率密度)
令
(r , t ) C (r , t )
这里的 C 是常数
t 时刻,在空间任意两点 r1 和 r2 处找到粒子的 2 2 相对几率是: C (r1 , t ) (r1 , t ) C (r2 , t ) (r2 , t )
态的迭加原理是量子力学的一个基本假设,它的 正确性也依赖于实验的证实。
Ex: 电子在晶体表面的衍射,动量空间的波函数 电子沿垂直方向射到 单晶表面,出射后将以各 种不同的动量运动,出射 后的电子为自由电子,其 状态波函数为平面波。
P
d
P (r , t )
1 (2 )
3/ 2
i
e
( Pr Et )
i
( Pr Et )
de
Broglie 波
