量子力学教程(第二版)
教学课件 《量子力学教程(第二版)》周世勋

1926 —1927年 戴维孙(Davisson)电子衍射实验
1925年 海森伯(Heisenberg) 矩阵力学
1926年 薛定谔(SchrÖedinger) 波动方程
1928年 狄拉克(Dirac)
RETURN
相对论波动方程
34
三 量子力学的应用简介
1.量子力学是现代物理学和其他自然学科的基础 量子光学、量子电动力学、量子统计 物理学、量子化学、量子生物学、量 子信息学等。
(二)经典物理学的困难与量子物理学的诞生
1. 黑体辐射问题 一个能全部吸收投射在其上面的辐射而 无反射的物体称为绝对黑体,简称黑体。
热平衡时,只与黑体
能
的绝对温度 T 有关而
量
与黑体的形状和材料
密
无关。
度
0
5
10
/10-4 cm
14
(1)维恩(Wien)经验公式
d c1 e3 c2 T d
33
• 量子力学发展简史 A 旧量子论的形成(冲破经典——量子假说)
1900年 普朗克(Planck) 振子能量量子化 1905年 爱因斯坦(Einstein)电磁辐射能量量子化
1913年 玻尔(N.Bohr) 原子能量量子化 B 量子力学的建立(崭新概念)
1923年 德布罗意(de Broglie)电子具有波动性
意义: ①光是由光子组成,能量是量子化的;
RETURN ②微观碰撞事件中能量、动量守恒 。
24
4. 原子结构及其光谱问题
实验:(1)原子是稳定的; (2)氢原子光谱是分立谱线:1911年卢瑟
福 粒子散射实验,原子是有核结构。
经验公式:(巴耳末公式)
RH
1 n2
周世勋《量子力学教程》(第2版)-态和力学量的表象笔记和课后习题(含考研真题)详解(圣才出品)

圣才电子书 十万种考研考证电子书、题库视频学习平台
变换矩阵的物理意义:通过变换矩阵,可将 A 表象的基矢 n 变换为 B 表象的基矢 。
2.幺正算符
在量子力学中,状态随时间的变化可写为 (t) U (t) (0) ,U (t) eiHt/ 是幺正算符。
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 4 章 态和力学量的表象
4.1 复习笔记
一、态的表象及量子力学中的矩阵表示 1.表象 在量子力学中,称态和力学量的具体表示方式为表象。
2.态函数在 Q 表象中的矩阵表示
选定表象后,算符和量子态可以用矩阵表示。在矩阵力学中,Q 表象是以 Q 的本征函
p ] , a
2
[x
1 i 2
p ]
它 们 满 足 有 下 列 关 系 : [a, a ] 1,
x 1 (a a ), 2
H
(a a
1)
(N;
2
2
| n 1 (a)n | 0 。 n!
p i (a a ) , 2
3.其他常用关系式
(1)粒子数算符本征方程 N | n n | n ;
a
* 2
(t
),...,
an*
(t))
。
说明:上述表达只针对分立谱情况。当具有连续谱时,任意波函数 (x, t) 可表示为:
(x,t) an (t)un (x) aq (t)uq (x)dq , n
其中 an (t)
(
x,
t
)u
* n
(
x)dx
,
aq
(t)
(
x,
t
)u
* q
《量子力学教程》第二版答案周世勋原著

《量子力学教程》第二版答案周世勋原著量子力学,作为现代物理学的重要支柱之一,其深奥的理论和复杂的数学推导常常让学习者感到困惑。
而周世勋先生的《量子力学教程》则是众多学习者的重要参考书籍。
然而,在学习过程中,课后习题的答案对于理解和掌握知识起着至关重要的作用。
接下来,让我们一起深入探讨《量子力学教程》第二版的答案。
首先,我们需要明确周世勋先生这本教程的重要地位和价值。
它以清晰的逻辑和严谨的体系,为初学者构建了一个逐步深入量子力学世界的桥梁。
书中涵盖了量子力学的基本概念、原理和重要理论,从波粒二象性到薛定谔方程,从态叠加原理到量子纠缠,无一不是量子力学的核心内容。
在面对课后习题时,答案的作用不仅仅是检验我们对知识的掌握程度,更重要的是帮助我们理清思路,发现自己在理解和应用知识方面的不足。
周世勋原著的答案具有以下几个显著特点。
其一,答案的准确性是毋庸置疑的。
每一个解答都经过了精心的推导和论证,确保与量子力学的基本原理和数学方法相一致。
这对于学习者建立正确的物理观念和数学思维非常重要。
例如,在处理涉及薛定谔方程的问题时,答案中会详细展示如何根据给定的初始条件和边界条件求解方程,以及如何对解进行物理意义的解释。
其二,答案具有很好的逻辑性和条理性。
它们通常会按照一定的步骤和思路进行推导,让学习者能够清晰地看到问题的解决过程。
这种清晰的逻辑结构有助于我们培养良好的解题习惯和思维方式。
比如,在解决关于量子态演化的问题时,答案会先分析问题所涉及的物理概念和原理,然后逐步引入相关的数学工具和计算方法,最后得出结论。
其三,答案注重对知识点的拓展和深化。
除了给出基本的解题方法和结果外,还会对一些相关的概念和理论进行进一步的阐述和讨论。
这使得我们在完成习题的同时,能够对量子力学的知识有更全面和深入的理解。
例如,在解答关于量子测量的问题时,答案可能会涉及到测量的不确定性原理以及它与量子态塌缩之间的关系,从而引导我们思考量子力学中一些更深层次的哲学问题。
周世勋《量子力学教程》(第2版)-量子力学若干进展笔记和课后习题(含考研真题)详解(圣才出品)

第8章量子力学若干进展8.1复习笔记一、朗道能级1.能级推导电子在均匀外磁场B(沿z 方向)中,取朗道规范后,得定态薛定谔方程:ψψψE p p y B e p m H z y x =⎥⎥⎦⎤⎢⎢⎣⎡++⎪⎪⎭⎫ ⎝⎛-=22221 鉴于力学量(,,)x z H p p 互相对易,得相应本征态为:)(),,(/)(y e z y x z p x p i zx χψ +=其中,()y χ满足谐振子能量本征值方程(平衡位置在0y ):)()2()()()(2)(22202222y mp E y y y mc eB m y dy d m z χχχ-=-+- 其中,0||x cp y e B =。
由此可得出朗道能级:2,1()22z z p n c p E n m ω=++ 。
2.结果讨论(1)从经典观点出发:电子沿磁场方向做螺旋运动。
从量子观点出发:电子沿磁场方向做自由运动,在垂直磁场方向绕z 轴旋转。
(2)磁场对能量贡献1||(2z e n B B mcμ+=- ,0z μ<称为朗道抗磁性,与电荷正负无关,是自由带电粒子在磁场中的一种量子效应。
(3)二维电子气的朗道能级简并度是外磁场ϕ中含元磁通量子(0||hc e ϕ=)数目。
二、阿哈罗诺夫-玻姆效应在经典电动力学中,场的基本物理量是电场强度E 和电磁感应强度B,势ψ和A 是为了方便引入的,并不是真实的物理量。
但在量子力学中,势ψ和A 具有可观测意义。
图8-11.实验及其现象如图8-1,从电子枪S 出射的电子束流经双缝和两条路径21,P P 到达屏上,在两条路径中放置一个很长的电流螺线管,垂直纸面,管内磁场强度B 垂直纸面向外(取为z 轴)。
当螺线管通以电流时,屏上出现的干涉条纹产生了移动。
2.现象讨论(1)因螺线管的外部并不存在磁场,所以经典电动力学中,磁场的物理效应不能完全用B 来进行描述。
(2)当螺线管内有磁通ϕ时,电子经过的外部空间B=0,但0≠A 时,因为对包围螺线管的任一闭合回路路径积分有⎰=⋅φl d A ,矢势A 可以对电子发生相互作用。
量子力学教程(第二版)周世勋习题解答
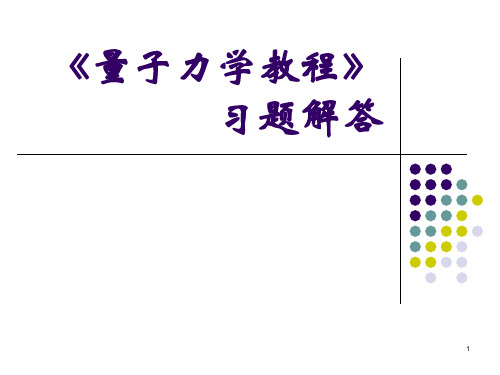
(10) (11) (12) (13)
ek1a B sin k 2aC cosk 2aD 0 0
k1ek1a B k 2 cosk 2aC k 2 sin k 2a D 0 0
0 sin k 2aC cosk 2aD ek1a F 0
(x) c (x)
⑤
④乘 ⑤,得 (x) (x) c2 (x) (x) , 可见,c 2 1 ,所以 c 1
当 c 1时, (x) (x) , (x) 具有偶宇称,
当 c 1时, (x) (x) , (x) 具有奇宇称,
18
当势场满足 U (x) U (x) 时,粒子的定态波函数具有确定的宇称。
3
第一章 绪论
1.1.由黑体辐射公式导出维恩位移定律: mT b, b 2.9 10 3 m0C 。
证明:由普朗克黑体辐射公式:
d
8h c33Βιβλιοθήκη 1hd ,
ekT 1
及 c 、 d c d 得
2
8hc 5
1,
hc
ekT 1
令 x hc ,再由 d 0 ,得 .所满足的超越方程为
kT
d
2
(x)
E
2
(x)
②
12
Ⅲ: x a
2 2m
d2 dx2
3
(x)
U
(x)
3
(x)
E
3
(x)
③
由于(1)、(3)方程中,由于U (x) ,要等式成立,必须
1(x) 0 2 (x) 0
即粒子不能运动到势阱以外的地方去。
方程(2)可变为
d
2 2 ( dx2
量子力学教程(第二版)周世勋习题解答

0 0 e k1a
0
k 2 sin k 2 a k 1 Be k1a
k 2 cos k 2 a k 2 sin k 2 a 0 e k1a sin k 2 a k 2 cos k 2 a sin k 2 a k 1e k1a sin k 2 a
d 21 ( x) dx2
#
x
1 2
4 3 1 1 2 0 , 可见 x 是所求几率最大的位置。 e
9
2.6
在一维势场中运动的粒子,势能对原点对称:U ( x) U ( x) ,证明粒子的定态波函数具有确定的
宇称。 证:在一维势场中运动的粒子的定态 S-方程为
10
2.7 一粒子在一维势阱中
U 0 0, U ( x) 0,
x a x a
运动,求束缚态( 0 E U 0 )的能级所满足的方程。 解:粒子所满足的 S-方程为
2 d 2 ( x) U ( x) ( x) E ( x) 2 dx2
按势能U ( x) 的形式分区域的具体形式为
在各区域的具体形式为 Ⅰ: x 0 Ⅱ: 0 x a
2 d 2 1 ( x) U ( x) 1 ( x) E 1 ( x) 2m dx2 2 d 2 2 ( x) E 2 ( x) 2m dx2
①
②
4
Ⅲ: x a
2 d 2 3 ( x) U ( x) 3 ( x) E 3 ( x) 2m dx2
由③再经 x x 反演,可得①,反演步骤与上完全相同,即是完全等价的。 ④
( x) c ( x)
④乘 ⑤,得
⑤
(x) (x) c 2 (x) (x) , 可见, c 2 1 ,所以 c 1
量子力学教程量子力学教程

归一化条件表示为
d3 r (r, sz ) 2
sz /2
d3
r(
(r,
/
2),
(r
,
/
2))
(r, / (r,
2) / 2)
d3 r[ r, / 2 2 r, / 2 2 ]
(2)
d3 r 1
(12)
并且
2 x
2 y
2 z
I
(单位算符)
(13)
可以证明 的三个分量反对易
x y y x 0 y z z y 0 z x x z 0
(14)
8.1 电子自旋态与自旋算符
量量子子力力学学教程教程(第二版)
式(11)和(14)联立得
)
1
(6)
a 与β构成电子自选态空间的一组正交完备基.一
般自旋态可以展开为
sz
a b
aa
b
波函数表示为
(7)
(r, sz ) r, / 2a r, / 2 (8)
8.1 电子自旋态与自旋算符
量量子子力力学学教程教程(第二版)
பைடு நூலகம்
x
y
y x
i z
y z z y i x
z x x z i y
式(15)与(13)归纳为
(15)
a a i a
(16)
上式与 概括了Pauli 算符的全部代数性质.
量子力学教程(第二版)(精)

ˆ , A ˆ i A ˆ , B ˆ B ˆ i B ˆ , A ˆ , B ˆ 2 A
2 2
ˆ i , A ˆ , B ˆ , A ˆ, B
ˆ A ˆ, B ˆ ˆ /i C C
3.3
共同本征函数
量子力学教程(第二版)
在上面的式子中,
l 和 l z 的本征值都是量子化的.
轨道角动量量子数 磁量子数
2
l
m
对于给定
m l , l 1,
l
,
l
2
的本征函数是不确定的,
因为
, l 1, l , 共有 2l 1 个简并态.
Ylm 就
是用 l z
的本征值来确定这些简并态.
Ylm 为球谐函数, 它们满足
l 2Ylm l l 1 2Ylm ,
lz Ylm m Ylm ,
l 0,1, 2,
,
m l , l 1,
, l 1, l
2
0
* d sin d Ylm , Ylm , δllδmm, 0
3.3
共同本征函数
量子力学教程(第二版) 3.3.3 对易力学量完全集(CSCO)
ˆ(A ˆ ,A ˆ , ), 设有一组彼此独立而且互相对易的厄米算符 A 1 2
它们的共同本征态记为 , 设给定一组量子数
表示一组完备的量子数.
之后, 就能够完全确定体系的唯一
ˆ ,A ˆ , ) 构成体系的一组对易可 一个可能状态, 则我们称 ( A 1 2
1 im m e , 2
m 0, 1, 2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
量子力学教程(第二版)
按Born-Oppenheimer 近似, H2+ 的Hamilton 量为
H
He
1 R
,
He
1 2 2
1 ra
1 rb
(11)
He 是电子的Hamilton 量,其本征方程为
H e
( 1 2 2
1 ra
1 )
rb
(E
1 )
R
(12)
采用变分法求H2+ 的基态波函数.
H2+ 中的电子的波函数可表示为
(5)
其中 Vee 是电子之间Coulomb排斥能, VNN 是原子核 之间Coulomb排斥能, VeN 是电子与原子核之间 Coulomb吸引能,
Te
i
pi2 2m
(对所有电子求和)
(6)
是电子的动能.原子核动能为
12.3 分子结构
量子力学教程(第二版)
TN
a
pa2 2M a
(对所有原子核求和)
12.3 分子结构
(31) (32) (33)
量子力学教程(第二版)
则径向方程为
[
2
2
d2 d R2
L(L 1)2
2R 2
V (R)] (R)
E (R)
径向波函数满足
(34)
(0) 0, () 0 (束缚态) (35)
令分子转动产生的离心势能为
W
(R)
V
(R)
L(L 1)2
2R 2
(36)
下面先粗略地分析分子中的电子激发能、振动 能和转动能的相对大小.
12.3 分子结构
量子力学教程(第二版)
1)设分子大小 a ,一部分电子在整个分子中运 动: x a,
电子的特征动量 电子的特征能量
pe / a Ee 2 / 2ma2
2)假设分子振动的角频率为 ,原子核偏离平
衡位置的距离为 ,
量 子力学教 程 x*t$qZnVkShPdMaI7F4C0z)w&s!pXmUjRfOcL9H6E2B+y(u%r#oWlThQeNbJ8G5D1A-x*t$qYnVkSgPdMaI7F3C0z)v&s!pXmUiRfOcK9H6E2B+x(u%rZoWlThQeMbJ8G4D1A- w*t!qYnVjSgPdLaI6F3C0y)v&s#pXmUiRfNcK9H5E2B+ x(u$rZoWkThQeMbJ7G4D1z- w*t!qYmVjSgOdLaI6F3B0y)v% s#pXlUiQfNcK8H5E2A+ x*u$rZnWkThPeMbJ7G4C1z-
(39)
量子力学教程(第二版)
令
1W 2
(R0 )
1 2
02
R R0
则
2
2
d2
d 2
1 2
02
2
E
( R0 ) 0, () 0
E
E
V
(R0
)
L(L 1)
2 R2
2
0
方程满足边条件的解为
( ) e 2 2 / 2 H ( ) 0 /
12.3 分子结构
(40) (41) (42) (43)
2)
(18)
3 de(ra rb ) (1 R 1 2R2 )eR
π
3
(19)
H
d
2
a
/
rb
d 2 b
/ ra
3
π
d e2ra 1 [1 (1 R)e2R ](20)
rb R
a b d
ab
d
3
d e(ra rb ) (1 R) eR
ra
rb
π
rb
(21)
12.3 分子结构
12.3 分子结构
量子力学教程(第二版)
12.3.3 双原子分子的转动与振动
对于双原子分子,两原子核组成的体系的能量本 征方程为
[
2 2M a
2
1
2 2M b
2 2
V (R)]
Et
引进相对坐标与质心坐标
(28)
R Ra Rb
Rc
M a Ra Ma
M b Rb Mb
令
f (Rc )Φ(R)
R (R) 是振动波函数,0 和 1 分别是两个质子的自旋
12.3 分子结构
量子力学教程(第二版)
单态(s=0)和三重态(s=1)波函数. H2分子中两个原子核 之间的作用力通常认为与核自旋无关,所以两个原子核
自旋之和s=s1+s2是守衡量,即s为好量子数.处于s=0态 的称为仲氢,处于s=1态的称为正氢.
ca a cb b ,
a
3/ 2
π
era ,
b
3/ 2
π
erb
(13)
12.3 分子结构
量子力学教程(第二版)
由于电子感受到的势场对于两个全同核的连线的 中点M具有反射不变性,因此电子状态可以按反
射对称性分类.对于偶宇称ca cb ,对于奇宇
称 ca cb .单电子的试探波函数为
c ( a b ) c ( a b )
1 R
He
(
1 2
2 1
1 ra1
1 ) rb1
(
1 2
2 2
1 ra 2
1 rb 2
)
1 r12
采用变分法求H2 的基态波函数. H2 中的单电子波函数可表示为
(r) 3/2 er
π
12.3 分子结构
(23) (24)
量子力学教程(第二版)
考虑到H2 两个电子波函数的交换反对称性,基态 试探波函数取为
个质子空间坐标交换时,质心运动与振动波函数不改变,但转动 部分波函数改变如下:
YLM (θ,) YLM ( θ, ) (1)LYLM ( ,)
考虑到Fermi子体系波函数的交换反对称性, H2分子 的原子核部分的波函数有下列两种形式:
L 偶,R (R)YLM ( ,)0 (s1z , s2z ), L 奇,R (R)YLM ( ,)1(s1z , s2z ).
E
E L
V (R0 )
(
1) 2
0
L(L 1) 2J
2
其中
J R02
(48)
表示双原子分子的转动惯量.式(48)右边第一项为常数 项,与能谱无关.第二项为振动能,第三项为转动能.通常 2 2J 0 ,能谱将出现转动带结构.即给定的振动态, 不同的L的诸能级构成一个转动带,能量遵守L(L+1)
12.3 分子结构
量子力学教程(第二版)
W(R) 的极小点由下式确定
dW d R R0 0
即
dV dR
R0
L(L 1)
R03
2
0
在R≈ R0 邻域展开W(R)
W
(R)
W
(
R0
)
1 2
W
(
R0
)(R
R0
)
2
V (R0 )
L(L 1)2
2R02
1 2
W
(R0
)(R
R0 )2
12.3 分子结构
(37) (38)
(29) (30)
12.3 分子结构
量子力学教程(第二版)
能量本征方程可以分离为
2
2M
2R
f
(Rc )
Ec
f
(Rc )
2
[
2
2R
V
(R)]Φ(R)
EΦ(R)
式中
M Ma Mb,
MaMb
Ma Mb
采用球坐标,则
Φ(R)
(R)
R
YLM
( ,)
L 0,1, 2, M L, L 1,, L
释放能量
H2 e H2 354 kcal/mol
H2+ 的存在是从它的光谱得以证实.H2+ 也可以吸收 能量而离解
吸收能量
H2 61 kcal/mol H H
12.3 分子结构
量子力学教程(第二版)
下面对比讨论H2+与H2:
图1 (a)氢分子离子,(b)氢分子
1)讨论氢分子离子H2+:
12.3 分子结构
(7)
由于m M ,所以 TN Te, TN 项可以忽略,即讨论电子
运动时,可以忽略 TN ,把原子核看成不动,此即 Born-Oppenheimer 近似.而在研究分子振动和转动
时,电子的组态近似地视为不变,并相应地提供原子核
之间的一种有效势.把电子运动与原子核振动分离
处理的近似性可用无量纲参数 m M 来表征.因为
(44)
量子力学教程(第二版)
Hν为Hermite 函数
H
( )
1
2(
)
l 0
()l l!
(l
2
)(2 )l
(45)
由边条件确定
H (R0 ) 0
(46)
若 L不太大,R0 很小, 接近于正整数,方程的
本征值为
E
(
1 2
)0
(47)
12.3 分子结构
量子力学教程(第二版)
可求出双原子分子的相对运动能为
(14)
由归一化条件得
取 其中
c 2 (2 2) 1, a | b c (2 2 )1/ 2
a b
(15) (16)
12.3 分子结构
量子力学教程(第二版)
由试探波函数,可求出点子的能量平均值
E
1 R
He
a He a b He a 1
(17)
