量子力学教程第二版答案及补充练习
苏汝铿量子力学(第二版)课后习题(含答案)---第四章4.1-4.4#13(延边大学)三年级

4.1.求在动量表象中角动量x L 的矩阵元和2x L 的矩阵元。
解:(1)对于x L 333()31()()()21()()21()()()21()()()2x pp z y z y z y y z y y iip rp ri i p rp r i i p r p r i p p r L ey p z p ed e yp zp e d e i p p e d p pz i p p e d p pz τπτπτππ'-'-'-'--'=-=-∂∂=--∂∂∂∂=--∂∂⎰⎰⎰⎰()()()zy y i p p p p p pzτδ∂∂'=---∂∂(2)对于2x L23232331()()21()()21()()()21)()()()2pp x x z y z y z y z y z y y i ip rp ri i p r p r i i p rp r i i p r p L e L e d e y p z p e d e y p z p y p z p e d e y p z p i p p e p pzτπτπτππ'-'-'-'-'==-=--∂∂=---∂∂⎰⎰⎰⎰3()223221()())()21()()2()()z y z y y z y y zy y r i ip rp r i p p rd i p pe y p z p e d p pz p p e d p pz p p p p p pzττπτπδ-'--'∂∂=---∂∂∂∂=--∂∂∂∂'=---∂∂⎰⎰4.2设厄米算符ˆA ,B 满足22ˆˆ1A B ==,ˆˆˆˆ0AB BA +=,求:(1)在ˆA 表象中,算符ˆA 和ˆB的矩阵表示; (2)在ˆB表象中,算符ˆA 和ˆB 的矩阵表示; (3)在ˆA 表象中,算符ˆB的本征值和本征函数;(4)在ˆB表象中,算符ˆA 的本征值和本征函数; (5)由A 表象到B 的幺正变换矩阵S 。
(完整word版)《量子力学教程》第二版答案及补充练习

1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长 m 与温度
T 成反比,即 m T=b(常量);
并近似计算 b 的数值,准确到二位有效数字。 解 根据普朗克的黑体辐射公式
vdv
8hv 3
c3
1
hv
dv ,
e kT 1
以及
v c ,
v dv v d ,
有
(1)
J2
i 2m
(
2
* 2
2* )
i [1 eikr 2m r
(1 eikr ) 1 eikr
r r
r
r
(1 r
e ikr
)]r0
i [1 ( 2m r
1 r2
ik
1) r
1 ( r
1 r2
ik
1 r
)]r0
k mr2
r0
k mr3
r
可见, J2与r 反向。表示向内(即向原点) 传播的球面波。
Asin
n a
x
Asin ka 0
10
由归一化条件
(x) 2 dx 1
得
A2
a
sin 2
n
xdx
1
0
a
由
a
sin
b
m a
x sin
n a
xdx
a 2
mn
A 2 a
2 (x)
2 sin n x aa
k2
2mE 2
En
22 2ma 2
n2
(n 1,2,3,) 可见 E 是量子化的。
J1
i 2m
(
1
* 1
1* 1)
苏汝铿量子力学(第二版)课后习题(含答案)---第四章4.5-4.7#14(延边大学)三年级

14QM-4.5设粒子处于宽度为的无限深势阱中,求在能量表象中粒子的坐标和动量的矩阵表示。
解:设粒子所处的势场的表达式为(0)()0(0)()x U x x a x a ∞<⎧⎪=≤≤⎨⎪∞>⎩在0x <,x a >两个区域,粒子的波函数均为0.设在0x a ≤≤区域中粒子的波函数为ψ 则它满足薛定谔方程20;2E x a mψψ-''=≤≤ 当 相应的边界条件为:(0)0()0a ψψ=⎧⎨=⎩解得波函数的本征函数为:()sinn n x A x a πψ= 由归一化条件得:n A aπ= 在能量表象中的本征函数为()sin n n n x x a a ππψ=在能量表象中粒子的坐标的矩阵分量为:()()2002222ˆ()()sin sin 114[],,2a a mn n m m n n m x x x x dx mn x x x dx a a a a mn m n m n a m n πππψψπ*-⎛⎫⎛⎫⎛⎫== ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎧--≠⎪⎪-=⎨⎪=⎪⎩⎰⎰ 在能量表象中粒子的动量的矩阵分量为()20022ˆ()()sin sin 211[],0,a amn n m m n h n d m p x p x dx i mn x x dx a a dx a ih mn m n a m n m n πππψψππ*-⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎧--⎪≠=⎨-⎪=⎩⎰⎰ 14QM-4.6证明两个厄米矩阵能用同一个幺正变换对角化的充要条件是它们彼此对易。
证明:我们知道任何一个厄米矩阵能被一个幺正矩阵对角化。
设,A B 两个矩阵是对易的,并且能被幺正矩阵L 对角化证明如下:已知0AB BA -=1()LAL A αβαααβδ-'= 则11LABL LBAL --= 1111LAL LBL LBL LAL ----=1111()()()()LAL LBL LBL LAL αααβαβββαβ----''''''=∑∑11()()A LBL LBL A αααβαβββ--''= 1()()0LBL A A αβααββ-''-= 若要1()0LBL αβ-≠则 A A ααββ''=即αβ= 所以1()LBL B αβαααβδ-'=即B 能被同一幺正矩阵L 对角化。
量子力学(二)习题参考答案

2µ (U1 − E ) h2 2µ E h2
ψ 2 '' ( x) + k 2ψ 2 ( x ) = 0, k =
西华师大物理与电子信息学院
4
四川省精品课程——量子力学补充习题参考答案
ψ 3'' ( x) − β 2ψ 3 ( x) = 0, β =
其解分别为:
2µ (U 2 − E ) h2
ψ 1 ( x) = A1eα x + B1e −α x ψ 2 ( x) = C sin(kx + δ ) ψ 3 ( x ) = A2e β x + B2 e− β x
2
2
⑤
而透射系数
⑥
2) 、当 E<U0 时,有ψ 2 '' ( x ) − k3 2ψ 2 ( x ) = 0 , k3 = 其解为:ψ 2 ( x ) = Ce
− k3 x
+ De k3 x = Ce − k3 x (ψ 2 有限条件)
⑦
以下可以重复前面的求解过程。 不过, 为了简单我们亦可以在前面得到的结果⑤中做代 换 k2 =i k3 ,得到
由(18)式, (16) 、 (17)变成 或由 (19) 式, (16) 、 (17) 变成
(20)或(21)式就是讲义上习题 2.7 的结果。 a) 将 δ = 0 代入ψ 2 ( x) 中有:ψ 2 ( x) = C sin kx 由连续性条件:ψ 2 ( a) = ψ 3 ( a ) → C sin( ka ) = B2 e − β a
ψ m (ϕ ) =
除了 m=0 的态之外, E m 圴是二重简并的。 5、梯形式——— U ( x ) =
0, x < 0 U 0 , x > 0
苏汝铿量子力学(第二版)课后习题(含答案)--第六章6.16-6.18#8(延边大学)三年级

6.16带电粒子在均匀磁场和三维谐振子势场2201()2e U r m r 中运动,求粒子的能谱. 解:该带电粒子的哈密顿量222011()22e e H p A m r m c ,且1()2A B r ,不妨设磁场沿+y 轴方向,则有12A (-By,Bx,0)2222222220012111()()()222x y Lz L zL zHp p m x y p m zlmm H H l1+2 =22222210222201()()()21122()2x y Lz LH p p m x y m H p m z m eBmc1其中+2 拉磨频率易知1H ,2H ,z l 相互对易,所以有共同的本征函数,所以可得到能谱为:221200121(1)();2LLEN N m N N 2 (=,0)6.17自旋为12的粒子,在均匀磁场中运动,磁场的绝对值不变,但各个分量随时间变化如下: sin cos ,sin sin ,cos X yzB B t B B t B B设t=0时自旋在磁场方向上的分量等于12,求在t 时刻粒子跃迁到自旋在磁场方向上的分量等于-12的态中的概率? 解:0000(),(sin cos ,sin sin ,cos )cos sin cos sin sin sin cos sin sin cos cos sin sin cosxy yxyyi titHBBt t t itBt i t e Be 设该粒子磁矩为 = =代入薛定鄂方程:iHt,设()()()a t tb t =,则有00()cos ()sin () (1)()cos ()sin () (2)i ti t i d a t a t eb t B dt id b t b te a t B dt化简得: '112'211i t i tc i ec c i e c其中:1cos ,sin ,BB2212()()i t i ta t c eb tc e解得:222212'''c i c c(*)由初始条件:(0)1(0)0(0)a tb tt2 即c所以设解2sin c t ,代入*式可得:1222tan it(超越方程)若可求得,则可得到()b t ,则所求概率为220(())()1t b t6.18电子和正电子靠库仑吸引力束缚在一起构成一个类氢的系统.在外磁场中它的哈密顿量(l=0)近似为01212()z z eBHH AS S S S mc,A,e,m,c,是正实数,BBz ,12,S S 分别是电子和正电子的自旋算符,0H 包含电子动能,正电子动能及正负电子间的库仑能.对自旋相互作用0HH 用一级微扰计算0H 的四度简并基态的能量分裂.解:01212222012()()()z z x y z z z eB HH AS S S S mc eB H A s s s S S mc =由两自旋为12的粒子系统具有对称三重态和反对称单态,写出其波函数为:12112212123121241()21()()2 波函数正交归一易得:22221122222122223122241()41()41()4()x y z x y z x y z x y z A s s s A A s s s A A s s s A A s s s12112241233124()0()()2()2z z zz z z zz S S S S S S S S所以得到:22210042104'1024202eB Amc A H eB eB A mc mc eB mc解久期方程得:222(1)2222111()444e B EA AA c2二重,-+m。
苏汝铿量子力学(第二版)课后习题(含答案)---第一章1.7-1.8#04(延边大学)三年级

1.7 一个德布罗意波在k空间的表示220()4()a k k C k --=求:(ⅰ)(,)x t ψ和2(,)x t ψ,在时刻t 这是否是个高斯波包? (ⅱ)波包的宽度()x t ∆; (ⅲ)2(,)x t dx ψ∞-∞⎰是否依赖于t ?解:(ⅰ) 由于已知德布罗意波在k 空间的表示220()4()a k k C k --=因此对该一维波包有 ()121(,)()(2)i kx t x t C k e dk ωψπ-=⎰(1)将()k ω在0k 附近展开并略去高阶项有 20001()()()()2g k k v k k k k ωωβ≈+-+- (2) 其中 0()g k d v dk ω= ,022()k d dkωβ= 将(2)式代入(1)式有 20001()[()()]212(,)()()g i k t i kx v k k k k e x t C k edk ωβψαπ-∞-----∞=⎰(3)当220()414()(2)a k k C k eπ--=代入(3)式可得:22200001()()[()()]4212(,)()g a i k t k k i kx v k k k k e x t e dk ωβψαπ-∞------=⎰积分上式可得0022()2()(,)]2(1)g i k tik x x v t x t e e i t ωαψβα--=+则222242()(,)]1g x v t x t tαψβα-=+故在时刻t 这是个高斯波包 (ⅱ) 波包宽度()x t ∆≈(ⅲ) 由222242()(,)]1g x v t x t t αψβα-=+易知2(,)x t dx ψ∞-∞⎰依赖于t1.8将平面波和波包的讨论推广到三维情况,求群速度。
解:对于三维平面波和波包,也可将波包视为由若干个平面波叠家而来,则有 ()321(,)()(2)i k r t r t C k e dk ωψπ⋅-=⎰由于()()i C k C k e α= 令 k r t ϕωα=⋅-+()C k 在点0k k = 周围宽度为k ∆的一个小区域内有一个明显的峰值,只有当相位ϕ在小区域内基本上保持不变时,ψ才有最大值。
苏汝铿量子力学(第二版)课后习题(含答案)---第三章3.14-3.16#10(延边大学)三年级

3.14在0t =时氢原子的波函数为()100210211211,02r ψψψ-⎡⎤=+⎣⎦ ()i 求体系能量的平均值;()ii 求在t 时刻体系处在1,1l m ==态的概率;()iii 求在0t =时,电子处在1010d cm -=范围内的概率;()iv 假定作一次测量后发现222,x L L ==,求测量后的瞬间体系的波函数。
解: ()i E E ψψ=2222122211120nlmnlm nlm nlm nlm E E E E E E ψψψψψψψ=⎛⎫⎛⎫=+++=∑ ()ii ()()()(),11,r t l m r t ωψδδψ=-- ()()()()()()()()222,0exp 11exp ,0,011,015n n iHt iHt r l m r r l m r ψδδψψδδψδδ⎛⎫⎛⎫=⋅--⋅- ⎪ ⎪⎝⎭⎝⎭=--⎛⎫==()iii ()2,0nlm r dr ωψ=⎰()2202221021033222000000,023********exp exp 5523d d d R r r drR R r dr r r r r dr a a a a a =⎡⎤=+⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥=-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎰⎰⎰因为0r d a ≤33222000000345600006812111154081111153240563.510dnlm r r r r dr a a a a a d d d d a a a a ω-⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥≈-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥⎢⎥=-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦=⨯⎰()iv 1,1,0,1l m ==-()210211211,0r ψψ-⎤'=+⎦3.15质量为m 的自由粒子作一维运动,在0t =时的归一化波函数是高斯波包,满足 ()()14222211,0,exp 42x x x x x ψπ⎡⎤⎢⎥=-⎢⎥⎣⎦ ()i 求()122p ∆=()ii 证明在0t >时,粒子的概率密度满足())()222222,,0,x t x x p t m ψψ=+∆ ()iii 用不确定性原理解释()i 和()ii 的结果。
苏汝铿量子力学(第二版)课后习题(含答案)---第二章2.19-2.21#15(延边大学)三年级
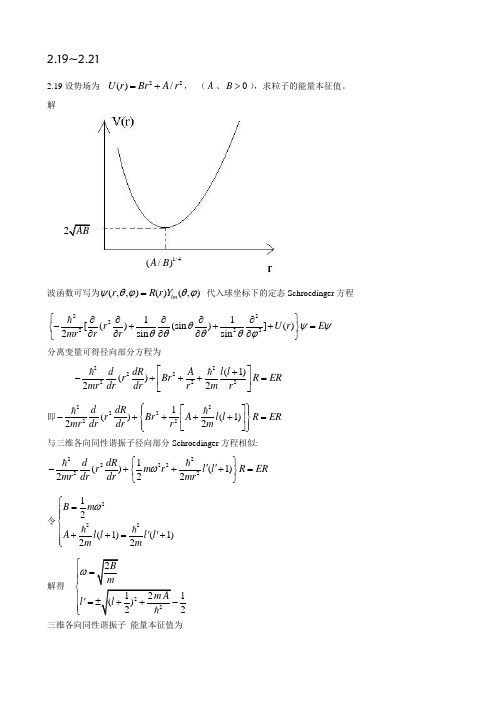
2.19~2.212.19设势场为22()/U r Br A r =+, (A 、0B >),求粒子的能量本征值。
解波函数可写为(,,)()(,)lm r R r Y ψθϕθϕ= 代入球坐标下的定态Schroedinger 方程22222211[()(sin )]()2sin sin r U r E mr r r θψψθθθθϕ⎧⎫∂∂∂∂∂-+++=⎨⎬∂∂∂∂∂⎩⎭分离变量可得径向部分方程为2222222(1)()22d dR A l l r Br R ER mr dr dr r m r ⎡⎤+-+++=⎢⎥⎣⎦ 即2222221()(1)22d dR r Br A l l R ER mr dr dr r m ⎧⎫⎡⎤⎪⎪-++++=⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭与三维各向同性谐振子径向部分Schroedinger 方程相似:22222221()(1)222d dR r m r l l R ER mr dr dr mr ω⎧⎫''-+++=⎨⎬⎩⎭ 令22212(1)(1)22B m A l l l l m m ω⎧=⎪⎪⎨⎪''++=+⎪⎩解得 222121()22B m m A l l ω⎧=⎪⎪⎨⎪'=±++-⎪⎩三维各向同性谐振子 能量本征值为2AB 1/4(/)A B3()2E N ω=+ 其中2r N n l '=+,,0,1,2,r n l '=(……) 故本题所求能量本征值为223(2)221322228422r n r r r r E n l m A B n m B m A n m ω'=++⎡⎤=-+⎢⎥⎣⎦⎡⎤=++⎢⎥⎣⎦,0,1,2,r n l =(……)2.20 一个质量为m 的粒子被限制在半径为r a =和r b =的两个不可穿透的同心球面之间运动,不存在其他势场。
求粒子的基态能量和基态波函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv echv d kThv v v 11833-⋅=πρ, (1) 以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThc e kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThcλλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
1.3 氦原子的动能是kT E 23=(k 为玻耳兹曼常数),求T=1K 时,氦原子的德布罗意波长。
解 根据eV K k 3101-=⋅,知本题的氦原子的动能为,105.123233eV K k kT E -⨯=⋅==显然远远小于2c 核μ这样,便有Ec hc 22核μλ=nmm m37.01037.0105.1107.321024.19396=⨯=⨯⨯⨯⨯⨯=---这里,利用了eV eV c 962107.3109314⨯=⨯⨯=核μ最后,再对德布罗意波长与温度的关系作一点讨论,由某种粒子构成的温度为T 的体系,其中粒子的平均动能的数量级为kT ,这样,其相庆的德布罗意波长就为Tkc hc Ec hc 2222μμλ==据此可知,当体系的温度越低,相应的德布罗意波长就越长,这时这种粒子的波动性就越明显,特别是当波长长到比粒子间的平均距离还长时,粒子间的相干性就尤为明显,因此这时就能用经典的描述粒子统计分布的玻耳兹曼分布,而必须用量子的描述粒子的统计分布——玻色分布或费米公布。
1.4 利用玻尔——索末菲的量子化条件,求:(1)一维谐振子的能量;(2)在均匀磁场中作圆周运动的电子轨道的可能半径。
已知外磁场H=10T ,玻尔磁子124109--⋅⨯=T J M B ,试计算运能的量子化间隔△E ,并与T=4K 及T=100K 的热运动能量相比较。
解 玻尔——索末菲的量子化条件为⎰=nh pdq其中q 是微观粒子的一个广义坐标,p 是与之相对应的广义动量,回路积分是沿运动轨道积一圈,n 是正整数。
(1)设一维谐振子的劲度常数为k ,谐振子质量为μ,于是有22212kx p E +=μ这样,便有)21(22kx E p -±=μ 这里的正负号分别表示谐振子沿着正方向运动和沿着负方向运动,一正一负正好表示一个来回,运动了一圈。
此外,根据221kx E =可解出 kEx 2±=±这表示谐振子的正负方向的最大位移。
这样,根据玻尔——索末菲的量子化条件,有⎰⎰-++-=--+-x x x x nh dx kx E dx kx E )21(2)()21(222μμ⇒nh dx kx E dx kx E x x x x =-+-⎰⎰+--+)21(2)21(222μμ⇒hn dx kx E x x 2)21(22=-⎰+-μ为了积分上述方程的左边,作以下变量代换;θsin 2kEx =这样,便有h nk E d E 2sin 2cos 2222=⎪⎪⎭⎫ ⎝⎛⎰-θθμππ⇒⎰-=⋅222cos 2cos 2ππθθθμh nd k E E⇒h nd kE 2cos 2222=⋅⎰=ππθθμ这时,令上式左边的积分为A ,此外再构造一个积分⎰-⋅=222sin 2ππθθμd kE B这样,便有⎰⎰--⋅=-⋅=⋅=+22222cos 2,22ππππθθμμπθμd kE B A kE d kE B A (1)⎰⎰--==2222,cos )2(2cos ππππϕϕϖθθμd kEd kE这里ϕ =2θ,这样,就有0sin ==-⎰-ππϕμd kEB A (2)根据式(1)和(2),便有kE A μπ=这样,便有h nkE 2=μπ⇒ kh n E μπ2=,k nhμ=其中π2hh =最后,对此解作一点讨论。
首先,注意到谐振子的能量被量子化了;其次,这量子化的能量是等间隔分布的。
(2)当电子在均匀磁场中作圆周运动时,有 B q Rυυμ=2⇒ qBR p ==μυ 这时,玻尔——索末菲的量子化条件就为⎰=πθ20)(nh R qBRd⇒ nh qBR =⋅π22 ⇒ nh qBR =2又因为动能耐μ22p E =,所以,有μμ22)(2222R B q qBR E ==,22B nBN q nB qBn =⋅==μμηη 其中,μ2ηq M B =是玻尔磁子,这样,发现量子化的能量也是等间隔的,而且B BM E =∆具体到本题,有J J E 232410910910--⨯=⨯⨯=∆根据动能与温度的关系式kT E 23=以及J eV K k 223106.1101--⨯==⋅可知,当温度T=4K 时,J J E 2222106.9106.145.1--⨯=⨯⨯⨯=当温度T=100K 时,J J E 2022104.2106.11005.1--⨯=⨯⨯⨯=显然,两种情况下的热运动所对应的能量要大于前面的量子化的能量的间隔。
1.5 两个光子在一定条件下可以转化为正负电子对,如果两光子的能量相等,问要实现实种转化,光子的波长最大是多少?解 关于两个光子转化为正负电子对的动力学过程,如两个光子以怎样的概率转化为正负电子对的问题,严格来说,需要用到相对性量子场论的知识去计算,修正当涉及到这个过程的运动学方面,如能量守恒,动量守恒等,我们不需要用那么高深的知识去计算,具休到本题,两个光子能量相等,因此当对心碰撞时,转化为正风电子对反需的能量最小,因而所对应的波长也就最长,而且,有2c hv E e μ==此外,还有λhcpc E ==于是,有2c hce μλ=⇒2c hc e μλ=nmm m 31266104.2104.21051.01024.1---⨯=⨯=⨯⨯= 尽管这是光子转化为电子的最大波长,但从数值上看,也是相当小的,我们知道,电子是自然界中最轻的有质量的粒子,如果是光子转化为像正反质子对之类的更大质量的粒子,那么所对应的光子的最大波长将会更小,这从某种意义上告诉我们,当涉及到粒子的衰变,产生,转化等问题,一般所需的能量是很大的。
能量越大,粒子间的转化等现象就越丰富,这样,也许就能发现新粒子,这便是世界上在造越来越高能的加速器的原因:期待发现新现象,新粒子,新物理。
第二章波 函数和薛定谔方程2.1证明在定态中,几率流与时间无关。
证:对于定态,可令)]r ()r ()r ()r ([m2i ]e )r (e )r (e )r (e )r ([m2i )(m 2i J e)r ( )t (f )r ()t r (**Et iEt i **Et i Et i **Etiρρρρηρρρρηηρρρρηηηηηψψψψψψψψψψψψψψψ∇-∇=∇-∇=∇-∇===-----)()(,可见t J 与ρ无关。
2.2 由下列定态波函数计算几率流密度:ikr ikr e re r -==1)2( 1)1(21ψψ从所得结果说明1ψ表示向外传播的球面波,2ψ表示向内(即向原点) 传播的球面波。
解:分量只有和r J J 21ρρ在球坐标中 ϕθθϕθ∂∂+∂∂+∂∂=∇sin r 1e r 1e r r 0ρρρr mrk r mr k r r ik r r r ik r r m i r e rr e r e r r e r m i mi J ikr ikr ikr ikr ρηρηρηρηηρ30202201*1*111 )]11(1)11(1[2 )]1(1)1(1[2 )(2 )1(==+----=∂∂-∂∂=∇-∇=--ψψψψ r J 1ρρ与同向。
表示向外传播的球面波。
rmrk r mr k r )]r 1ik r 1(r 1)r 1ik r 1(r 1[m 2i r )]e r 1(r e r 1)e r 1(r e r 1[m 2i )(m2i J )2(3020220ik r ik r ik r ik r *2*222ρηρηρηρηηρ-=-=---+-=∂∂-∂∂=∇-∇=--ψψψψ可见,r J ρρ与2反向。
表示向内(即向原点) 传播的球面波。
补充:设ikx e x =)(ψ,粒子的位置几率分布如何?这个波函数能否归一化?∞==⎰⎰∞∞dx dx ψψ*Θ∴波函数不能按1)(2=⎰∞dx x ψ方式归一化。
