热力学温度公式
工程热力学公式大全

工程热力学公式大全1.热力学第一定律:ΔU=Q-W其中,ΔU表示系统内能的变化,Q表示系统吸收的热量,W表示系统对外所做的功。
2.热力学第二定律(卡诺循环):η=1-Tc/Th其中,η表示热机的热效率,Tc表示冷源温度,Th表示热源温度。
3.单级涡轮放大循环功率:W=h_1-h_2其中,h_1表示压缩机入口焓,h_2表示涡轮出口焓。
4.热力学性质之一:比热容C=Q/(m*ΔT)其中,C表示比热容,Q表示系统吸收的热量,m表示系统的质量,ΔT表示温度变化。
5.热力学性质之二:比焓变ΔH=m*C*ΔT其中,ΔH表示焓变,m表示系统的质量,C表示比热容,ΔT表示温度变化。
6.理想气体状态方程:PV=nRT其中,P表示气体的压力,V表示气体的体积,n表示气体的物质量,R表示气体常数,T表示气体的温度。
7.热机制冷效率:ε=(Qh-Qc)/Qh其中,ε表示热机的制冷效率,Qh表示热机吸收的热量,Qc表示热机传递给冷源的热量。
8.熵变表达式:ΔS=Q/T其中,ΔS表示熵变,Q表示系统吸收的热量,T表示温度。
9.热力学性质之三:比容变β=-(1/V)*(∂V/∂T)_P其中,β表示比容变,V表示体积,T表示温度,P表示压力。
10.工作物质循环效率η_cyc = W_net / Qin其中,η_cyc表示工作物质的循环效率,W_net表示净功,Qin表示输入热量。
这只是一小部分工程热力学公式的示例,实际上工程热力学涉及面较广,还有许多其他常用公式。
与热力学相关的公式使工程师能够更好地理解和解决与能量转换和热力学有关的问题,在工程设计和应用中起到重要的作用。
热学公式整理

热学公式整理
以下是一些常用的热学公式整理:
1. 热传导公式:Q = k * A * ΔT / L
其中,Q表示传热量,k表示热传导系数,A表示传热面积,ΔT表示温度差,L表示传热距离。
2. 热辐射公式:Q = σ * A * ε * T^4
其中,Q表示辐射热能,σ表示斯特藩-玻尔兹曼常数,A表
示辐射面积,ε表示表面发射率,T表示绝对温度。
3. 热膨胀公式:ΔL = α * L * ΔT
其中,ΔL表示长度变化,α表示线膨胀系数,L表示原长度,ΔT表示温度变化。
4. 热容公式:Q = mcΔT
其中,Q表示吸热量或放热量,m表示物体质量,c表示比
热容,ΔT表示温度变化。
5. 热力学第一定律:ΔU = Q - W
其中,ΔU表示内能变化,Q表示吸热量,W表示功。
6. 熵变公式:ΔS = Q / T
其中,ΔS表示熵变,Q表示吸热量或放热量,T表示温度。
物理高中热学公式

物理高中热学公式1. 热力学第一定律:ΔU = Q + W,其中ΔU为内能变化,Q为系统与外界交换的热量,W为系统所做的功。
2. 热力学第二定律:ΔS = Q/T,其中ΔS为系统熵的变化,Q为热量,T为温度。
3. 热容:C = Q/ΔT,其中C为热容,Q为系统吸收或释放的热量,ΔT为温度变化量。
4. 比热容:c = C/m,其中m为物体的质量。
5. 热传导定律:Q = kAΔT/x,其中Q为热量,k为热导率,A为面积,ΔT为温度差,x为导热距离。
6. 热辐射定律:P = σA(T^4 – T0^4),其中P为单位时间内辐射的能量,σ为斯蒂芬—玻尔兹曼常数,A为发射体参考面积,T为发射体温度,T0为参考温度。
7. 热力学循环效率:η = (W净 / Q热) × 100%,其中W净为系统净工作量,Q热为系统吸收的热量。
8. 热力学效率公式:η = (T1 – T2) / T1,其中T1为热源温度,T2为冷源温度。
9. 热平衡方程:m1c1ΔT1 = m2c2ΔT2,其中m为物体的质量,c为比热容,ΔT为温差。
10. 热力学势公式:G = H – TS,其中G为吉布斯自由能,H为焓,T为温度,S为熵。
11. 熵变公式:ΔS = Qrev / T,其中ΔS为系统的熵变,Qrev为可逆过程吸放热量,T为温度。
12. 等温过程:Q = W,即等温过程中外界对系统所做的功等于系统吸收的热量。
13. 等体过程:W = 0,即等体过程中系统不做功,热量全部转化为内能。
14. 等压过程:W = PΔV,即等压过程中外界对系统所做的功等于压力乘以体积的变化量。
15. 等焓过程:Q = ΔH,即等焓过程中外界与系统的热交换量等于系统焓的变化量。
工程热力学的公式大全

工程热力学的公式大全1.热力学第一定律:ΔU=Q-W其中,ΔU表示系统内能的变化,Q表示系统所吸收的热量,W表示系统所做的功。
2.理想气体状态方程:PV=nRT其中,P表示气体的压力,V表示气体的体积,n表示气体的物质的分子数,R表示气体常数,T表示气体的温度。
3.等温过程:Q=W在等温过程中,系统所吸收的热量等于所做的功。
4.绝热过程:P1V1^γ=P2V2^γ在绝热过程中,气体的压强与体积之积的γ次方是一个常数,γ为气体的绝热指数。
5.等容过程:ΔU=Qv在等容过程中,系统内能的变化等于吸收的热量。
6.等压过程:Q=ΔH在等压过程中,系统所吸收的热量等于焓的变化。
7.等焓过程:ΔH=Qp在等焓过程中,焓的变化等于吸收的热量。
8.热机效率:η=1-,Qc,/,Qh热机效率表示热机从高温热源吸收的热量减去放出的低温热量占高温热量的比例。
9.士温定理:η=1-(Tc/Th)士温定理是热力学第二定律的一种表述,表示热机效率与高温热源温度和低温热源温度的比值有关。
10.开尔文恒等式:η=1-(Tc/Th)=1-(,Qc,/,Qh,)开尔文恒等式是士温定理的另一种形式,表示任何热机的效率都不可能达到100%。
11.准静态过程:ΔS=∫(dQ/T)准静态过程中,系统的熵变等于系统吸收的微小热量除以系统的温度积分得到。
12.绝热可逆过程:ΔS=0在绝热可逆过程中,系统的熵不发生变化。
13.熵的增加原理:ΔS总=ΔS系统+ΔS环境≥0根据熵的增加原理,系统与环境的熵的变化之和大于等于0。
14.卡诺循环效率:η=1-(Tc/Th)卡诺循环是理想热机,其效率由高温热源温度和低温热源温度决定。
15.等温膨胀系数:β=(1/V)*(∂V/∂T)p等温膨胀系数表示单位温度升高时体积的变化与体积的比值。
16.等压热容量:Cp=(∂Q/∂T)p等压热容量表示在等压条件下单位温度升高吸收的热量与温度的比值。
17.等容热容量:Cv=(∂Q/∂T)v等容热容量表示在等容条件下单位温度升高吸收的热量与温度的比值。
06-2温度公式、能量按自由度均分原理

v 处在最概然速率 v p 附近
的分子数占总分子数的百分比最大。
20
vp
2kT
m0
f
(v
p
)
8m0 π kT
1/
2
e1
当分子质量 m0
f(v) T1 m0 一定
一定时,T 左图表明:
f
vp (v p )
温度越高,
T2 >T1 速率大的分子数比例越大,
f1(x, y, z,) f2 (x, y, z)
0 0
i 1
4
2.刚体: 刚体不仅有平动,还有转动
(1).确定刚体质心需要三个独立坐标(x,y,z); (2).确定任一条通过质心的轴需要两
个独立坐标 (, )(与x轴、y轴的
夹角);
(3)刚体绕该轴转动需要一个独立坐标 。
0 vp1 vp2
v 气体分子的热运动越激烈。
思考 T 一 定,m2 > m 1,速率分布曲线如何?
21
2.平均速率(average speed)
分立: 平均速率 v Nivi Ni
连续:vi v,Ni dNv=N f (v)dv,
v
0N v d Nv
N
0
d
Nv
0N
M
vp :v :
v2
2:
8 :
π
3 1.41 : 1.60 : 1.73
v 2 —— 讨论分子平均平动动能时用
v —— 讨论分子碰撞问题时用
v p —— 讨论分子的速率分布时用 25
麦克斯韦速率分布的实验验证
热学公式

热学公式一 .平衡态二 .气体状态参量 1.体积V 2.压强p 3.温度T (温标) 三.理想气体状态方程1.理想气体 形式1:molMPV =RT =νRT M 2.理想气体状态方程 形式2: P nkT = 四、理想气体压强公式2213212()323p nmv p n mv n ω=== 122ω=mv 分子平均平动动能四、温度公式 13222ω=mv =kT1.温度的微观本质:理想气体的温度是分子平均平动动能的量度2.温度的实质:分子热运动剧烈程度的宏观表现。
3.方均根速率:⇒==五、气体分子自由度 1.单原子分子i = 3 2.刚性双原子分子i = 5 3.刚性多原子分子i = 6 六. 能量按自由度均分定理一个分子每个自由度上的平均平动动能(平衡态T ): 22211112222x y z mv mv mv kT === 单原子分子 ε=3kT/2 双原子分子 ε=5kT/2 多原子分子 ε=6kT/2=3kT 七. 理想气体的内能22mol M i iE RT RT M ν==(温度 T 的单值函数) 32mol M E RT M =(单原子分子) 52mol M E RT M =(刚性双原子分子) 3molME RT M =(刚性多原子分子)状态从T1→T2,不论经过什么过程,内能变化为2121()2mol M iE E E R T T M ∆=-=- 七.速率分布函数 1)f (v ) 的意义: υdN f(υ)=Nd υ(概率密度) υdN f(υ)d υ=N()Nf dv υdN υ= 2)f (v ) 的归一化条件 0()1f d υυ∞=⎰八、麦克斯韦分子速率分布定律()2322242mv kT m f v ev kT ππ-⎛⎫= ⎪⎝⎭九、分子平均碰撞次数和平均自由程●分子平均碰撞次数2Z d n =v ●平均自由程z λ==v p nkT = λ=一、概念 1.准静态过程 2.内能(1)内能是态函数,其增量仅与始末状态有关,而与过程无关. (2) 对于理想气体来说, 内能是温度的单值函数. 3.准静态过程的功21V V A dA pdV ==⎰⎰规定: 0,0,dV dA >>系统对外作正功;0,0,dV dA <<系统对外作负功;0,0,dV dA ==系统不作功。
热学公式

热学公式一 .平衡态二 .气体状态参量 1.体积V 2.压强p 3.温度T (温标) 三.理想气体状态方程1.理想气体 形式1:molMPV =RT =νRT M 2.理想气体状态方程 形式2: P nkT = 四、理想气体压强公式2213212()323p nmv p n mv n ω=== 122ω=mv 分子平均平动动能四、温度公式13222ω=mv =kT 1.温度的微观本质:理想气体的温度是分子平均平动动能的量度 2.温度的实质:分子热运动剧烈程度的宏观表现。
3.方均根速率:⇒==五、气体分子自由度 1.单原子分子i = 3 2.刚性双原子分子i = 5 3.刚性多原子分子i = 6 六. 能量按自由度均分定理一个分子每个自由度上的平均平动动能(平衡态T ):22211112222x y z mv mv mv kT === 单原子分子 ε=3kT/2 双原子分子 ε=5kT/2 多原子分子 ε=6kT/2=3kT 七. 理想气体的内能22mol M i iE RT RT M ν==(温度 T 的单值函数) 32mol M E RT M =(单原子分子) 52mol M E RT M =(刚性双原子分子) 3molME RT M =(刚性多原子分子) 状态从T1→T2,不论经过什么过程,内能变化为2121()2mol M iE E E R T T M ∆=-=- 七.速率分布函数 1)f (v ) 的意义: υdN f(υ)=Nd υ(概率密度) υdN f(υ)d υ=N()Nf dv υdN υ= 2)f (v ) 的归一化条件()1f d υυ∞=⎰八、麦克斯韦分子速率分布定律()2322242mv kT m f v ev kT ππ-⎛⎫= ⎪⎝⎭九、分子平均碰撞次数和平均自由程●分子平均碰撞次数2Z d n =v●平均自由程z λ==v p nkT =λ=一、概念 1.准静态过程 2.内能(1)内能是态函数,其增量仅与始末状态有关,而与过程无关. (2) 对于理想气体来说, 内能是温度的单值函数. 3.准静态过程的功21V V A dA pdV ==⎰⎰规定: 0,0,dV dA >>系统对外作正功;0,0,dV dA <<系统对外作负功;pVp2V dV+1o2p 1p0,0,dV dA ==系统不作功。
热学公式
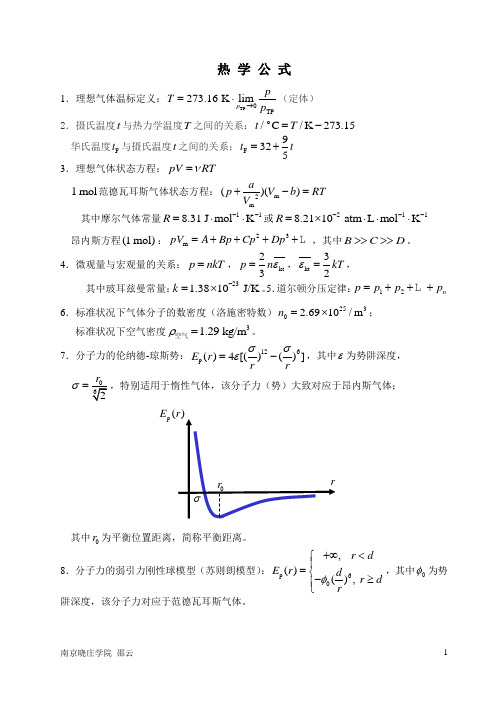
热 学 公 式1.理想气体温标定义:TP 0TP273.16 K limp pT p →=⋅(定体) 2.摄氏温度t 与热力学温度T 之间的关系:o/C /K 273.15t T =- 华氏温度F t 与摄氏温度t 之间的关系:F 9325t t =+ 3.理想气体状态方程:pV RT ν=1 mol 范德瓦耳斯气体状态方程:m 2m()()ap V b RT V +-= 其中摩尔气体常量118.31 J mol K R --=⋅⋅或2118.2110 atm L mol K R ---=⨯⋅⋅⋅ 昂内斯方程(1 mol):23m pV A Bp Cp Dp =++++,其中B C D >>>>。
4.微观量与宏观量的关系:p nkT =,kt 23p n ε=,kt 32kT ε=, 其中玻耳兹曼常量:231.3810 J/K k -=⨯。
5.道尔顿分压定律:12n p p p p =+++6.标准状况下气体分子的数密度(洛施密特数)2530 2.6910/m n =⨯; 标准状况下空气密度31.29 kg/m ρ=空气。
7.分子力的伦纳德-琼斯势:126p ()4[()()]E r rrσσε=-,其中ε为势阱深度,σ=,特别适用于惰性气体,该分子力(势)大致对应于昂内斯气体;其中0r 为平衡位置距离,简称平衡距离。
8.分子力的弱引力刚性球模型(苏则朗模型):p 60, ()(), r d E r d r d rφ+∞<⎧⎪=⎨-≥⎪⎩,其中0φ为势阱深度,该分子力对应于范德瓦耳斯气体。
9.麦克斯韦速率分布函数(概率密度):23/222d ()4π()e d 2πmv kTN m f v v N v kT-==,其简便形式:22()d e d u f v v u -=,其中约化速率p v u v =。
10.三个分子速率的统计平均值:最概然速率:p v ==v ==方均根速率:rms v ===11.麦克斯韦速度分布律:22232()/2d e d d d 2πx y z m v v v kTx y z N m v v v N kT -++⎛⎫= ⎪⎝⎭,其中 x 方向速度分布律:21/2/2d ed 2πxx v mv kTx N m v N kT -⎛⎫= ⎪⎝⎭, 引入约化速度分量px vv ξ=后,上式可简化为2d ()d d x v x x N f v v N ξξ-==。
