第六章-联合概率数据关联算法和多假设滤波器说课讲解
贝叶斯 统计 联合概率

贝叶斯统计联合概率贝叶斯统计是一种基于概率的统计方法,其核心思想是通过利用先验概率和观测数据来更新对事件发生概率的估计。
而联合概率则是贝叶斯统计中重要的概念之一,它描述了两个或多个事件同时发生的概率。
在贝叶斯统计中,联合概率是指两个或多个事件同时发生的概率。
它可以通过乘法规则计算得出,即将各个事件发生的概率相乘。
假设有事件A和事件B,它们的联合概率记作P(A∩B),表示事件A 和事件B同时发生的概率。
联合概率的计算可以通过条件概率和边缘概率来实现。
条件概率是指在已知事件B发生的条件下,事件A发生的概率。
条件概率可以用P(A|B)表示,读作“在B的条件下A发生的概率”。
通过条件概率可以计算出联合概率,即P(A∩B) = P(A|B) × P(B)。
其中,P(B)表示事件B发生的概率,也称为边缘概率。
边缘概率可以通过将事件A和事件B同时发生的概率相加来计算,即P(B) = P(A∩B) + P(A'∩B),其中A'表示事件A的补集。
贝叶斯统计的核心思想是通过观测数据来更新对事件发生概率的估计。
贝叶斯定理是贝叶斯统计的重要工具,它可以用来计算在给定观测数据的条件下,某个事件发生的概率。
根据贝叶斯定理,可以得到后验概率P(A|B) = P(B|A) × P(A) / P(B)。
其中,P(A|B)表示在观测数据B的条件下事件A发生的概率,P(B|A)表示在事件A发生的条件下观测数据B的概率,P(A)表示事件A的先验概率,P(B)表示观测数据B的边缘概率。
贝叶斯统计在实际应用中具有广泛的应用价值。
在机器学习领域,贝叶斯统计可以用于构建分类模型,通过观测数据来估计不同类别的后验概率,从而进行分类预测。
在医学诊断中,贝叶斯统计可以用于估计患病的概率,帮助医生做出准确的诊断。
在金融风险管理中,贝叶斯统计可以用于估计不同投资组合的风险,帮助投资者做出合理的投资决策。
贝叶斯统计中的联合概率是一种描述多个事件同时发生的概率的重要概念。
第六章-联合概率数据关联算法和多假设滤波器演示教学

12
第六章
联合关联事件θi(k)可以表示成矩阵形式:
ˆ (i (k)) ˆijt (i (k)) , j 1,2,...,mk ;i 1,2,...,k
其中,
ˆ ijt
(i
(k
))
1
0
i jt
(k
)
i
(k
)
否则
表示在联合事件中,量测j是否源于目标t。
13
第六章
满足以下两个条件的联合关联事件定义为可行事件:
2
6.1 联合概率数据关联算法
第六章
6.1.1 联合概率数据关联算法的基本思想 联合概率数据关联算法是在仅适用于与单目标跟踪的概率
数据关联算法(PDA)的基础上,提出的适用于多目标跟踪 情形的一种数据关联算法。
3
第六章
1. 模型
假设在杂波环境中已有T个目标,则它们的状态方程 和测量方程分别表示为:
矩阵中其余元素:
jt
1 0
当ωjt=1时,k时刻有效回波Zkj落入确认门Atk; 当ωjt=0时,k时刻有效回波Zkj没落入确认门Atk。 其中,j=1,2,…,mk;t=1,2,…,n。
7
第六章
图1中目标数n=3,有效回波数mk=4,确认矩阵为:
目标3
Zk1 目标1
Zk3 Zk2 目 标 2
Zk4
1,
t (i (k)) 0,
若存在j使t j t 若不存在j使t j t
14
第六章
同样可以定义一个测量关联指示器
j (i (k))
n t0
ˆ ijt (i (k))
1, 0,
ω与22=其1, ω可32能=1,的ω4各3=种1, 其源余目为标0。相关联的概率。
现代信号处理--清华胡广书讲义-第6章滤波器组基础
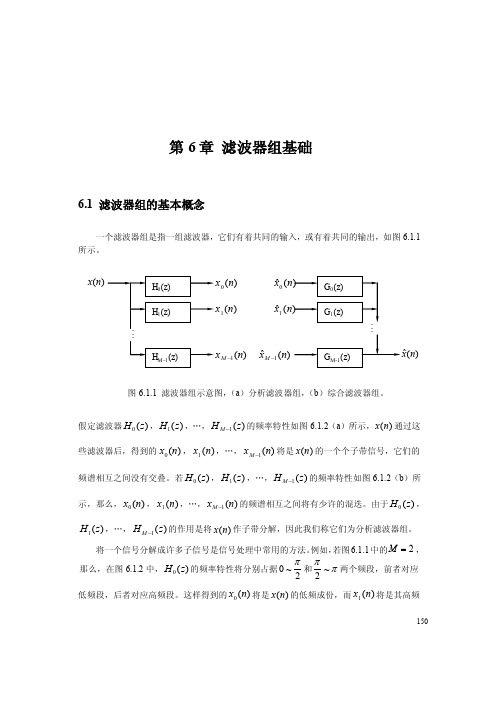
150第6章 滤波器组基础6.1 滤波器组的基本概念一个滤波器组是指一组滤波器,它们有着共同的输入,或有着共同的输出,如图6.1.1所示。
图6.1.1 滤波器组示意图,(a )分析滤波器组,(b )综合滤波器组。
假定滤波器)(0z H ,)(1z H ,…,)(1z H M -的频率特性如图6.1.2(a )所示,)(n x 通过这些滤波器后,得到的)(0n x ,)(1n x ,…,)(1n x M -将是)(n x 的一个个子带信号,它们的频谱相互之间没有交叠。
若)(0z H ,)(1z H ,…,)(1z H M -的频率特性如图6.1.2(b )所示,那么,)(0n x ,)(1n x ,…,)(1n x M -的频谱相互之间将有少许的混迭。
由于)(0z H ,)(1z H ,…,)(1z H M -的作用是将)(n x 作子带分解,因此我们称它们为分析滤波器组。
将一个信号分解成许多子信号是信号处理中常用的方法。
例如,若图6.1.1中的2=M ,那么,在图6.1.2中,)(0z H 的频率特性将分别占据2~0π和ππ~2两个频段,前者对应低频段,后者对应高频段。
这样得到的)(0n x 将是)(n x 的低频成份,而)(1n x 将是其高频)(0n x )(1n x )(1n x M -)(n x(ˆ0x (ˆ1x)(ˆ1n xM -)(ˆn x151成份。
我们可依据实际工作的需要对)(0n x 和)(1n x 作出不同的处理。
例如,若我们希望对)(n x 编码,设)(n x 的抽样频率为20KHz ,若每个数据点用16bit ,那么每秒钟需要的码图6.1.2 分析滤波器组的频率响应,(a )无混迭,(b )稍有混迭流为320Kbit 。
若)(n x 是一低频信号,也即)(n x 的有效成份(或有用成份)大都集中在)(0n x 内,)(1n x 内含有很少的信号能量。
这样,我们可对)(0n x 仍用16bit ,对)(1n x 则用8bit ,甚至是4bit ,由于)(0n x 和)(1n x 的带宽分别比)(n x 减少了一倍,所以,)(0n x 和)(1n x 的抽样频率可降低一倍。
第六章系统辨识与参数估计-数据预处理及相容性检验(精品)

1第六章 数据预处理及相容性检验6.1 前言航行器航行试验数据用于参数辨识之前,需要对试验数据进行预处理和数据相容性检验,目的在于尽可能消除含在数据中的各种噪声和系统误差,以提高辨识结果的准确度。
数据预处理包括:数据野值的识别、剔除与补正;数据加密;数据平滑与微分平滑;滤除高频噪声及以传感器位置校正等。
数据相容性检验的主要功能是将数据中的常值误差,特别是零位漂移误差辨识出来并重新建立没有常值误差的试验数据。
本章还以某型航行器的实测数据预处理为例,给出了具有实际应用意义的数据处理技术及结果。
6.2 数据处理的理论基础6.2.1 信号的分类用数学来描述待辨识系统的某一组输入和某一组输出时间函数间的关系是辨识的基础。
在选择信号的描述方法时,必须考虑信号表示的两个方面:①要表现出信号载有信息的属性;②要给出研究过程信息传递特性的方法。
按时间函数的特点来表达信息,可将信号分为连续信号和采样信号。
在许多情况下,信号的记录可以采用这两种信号中的任一种。
两种信号的记录均有各自的特点,但是利用计算机对记录的信号作处理时,往往需要采样信号,即使采用连续信号,也必须对信号作采样处理。
采样运算是线性运算,即当我们用算子ψ(.)表示这一运算时,对一切α和β,信号u(t)和y(t)均有ψαβαψβψ[()()][()][()]u t y t u t y t +=+(6-2-1)按幅度划分,信号可以分为模拟信号、量化信号和二进制信号。
二进制信号是量化信号的极限情况,量化运算是非线性运算。
因此,在处理量化信号时,这种非线性造成许多数学上的困难。
确定性信号与随机信号也是系统建模和参数辨识中常用的信号分析方式。
由于工程的实际环境,对随机信号的讨论更具有实际意义。
6.2.2 随机信号的描述为了讨论问题的方便,在此我们首先介绍随机信号的一些统计性质。
与确定性信号不一样,对随机信号询问其幅度的瞬时值是没有多少意义的,所以最有用的量是那些关于统计性质的量,如谱密度、数学期望值、方差和相关函数等。
数据融合理论与应用(第二版)课件:联合概率数据关联和多假设滤波器

可行的联合事件的组成,进而可以得到每一个量测与目标关联的事件:
第一个量测与第一个目标关联的事件为
第一个量测不可能与第二个目标关联。
联合概率数据关联和多假设滤波器
第二个量测与第一个目标关联的事件为
第二个量测与第一个目标关联的事件为
联合概率数据关联和多假设滤波器
通过以上例子可以看出,可行矩阵和可行联合事件之间是一一对应的,而
联合概率数据关联和多假设滤波器
设 θ (k ) = { θ i ( k )}θ ki =1 表示在 k 时刻的所有可能的联合事件的集合,θ k 表
示 θ ( k )中元素的个数,其中
表示第 i 个联合事件,它表示 m (k )个量测源的一种可能, θijtj (k )表示量测 j 在
第 i 个联合事件中源于目标 tj ( 0≤ tj ≤ n )的事件, θij 0 表示量测 j 在第 i 个联合事
联合概率数据关联和多假设滤波器
联合概率数据关联和多假设滤波器
这里仍假设不与任何目标关联的量测在体积为V 的确认区域中服从均匀分
布,而与某个目标关联的正确量测服从高斯分布。所不同的只是假设所有的跟
踪门对应整个监督区域,即 P G =1 ,从而有
联合概率数据关联和多假设滤波器
其中与目标 tj 关联的量测服从高斯分布,即
联合概率数据关联和多假设滤波器
将(6-20 )式代入( 6-19 )式立得
联合概率数据关联和多假设滤波器
将(6-32 )式代入( 6-31 )式得
基于( 6-33 )式可以得到第 j 个量测与目标关联的概率为
联合概率数据关联和多假设滤波器
6. 1. 3 协方差计算
基于第 j 个量测对目标 t 的状态估计 ^xtj ( k | k )的协方差为
一种多传感器信息融合的可能性关联方法

通常传感器测 量过程 中存在 多种不确定性 因素 , 不确 定性通常表 现为数据 的不完 整 、 一致及虚假数 据 。这种 不
不确定性破坏 了测量值 和 目标之 间的一一 对应关系 , 导致 测量数据 与 目标对 应关 系 不确 定 , 加 了 目标 关联 的 困 增
tr es q a t aiey t r u h o sb l y d sr u in, h n s o it n p o lm i o v re O mu t tr e a g t u n i t l h o g p s ii t it b t t v i i o t e a s cai rb e o s n e d t a c t l -ag t i d cso su . h i lt n e p r n e f s t e efc ie e s o h rp s d meh d e iin is e T esmu ai x e i o me tv r i h f t n s f e p o o e t o . i e e v t Ke r s tr e s o i t n;p si i t it b t n;u c rany;f z i y wo d : a g t s cai a o o sbl y d s u i i i r o n et it u zy f
第3 1卷
设 A是 论 域 U的 一 个 模 糊 子 集 , 隶 属 度 函 数 为 其
2 2 基 于 目标 特征 的可 能性 分布 .
测量值 Y 与 目标 , k时刻 关于 某特征 的统 计距 离 j 在
D ( J 表 征 二 者 在 该 特 征 上 的 相 关 性 , i ) 大 , 关 i ) D (, 越 相
然 由于 特 征 量 纲 , 同 特 征 对 应 的 a并 不 相 同 ; 可 能 性 不 b为
一种新的概率数据关联滤波算法

一种新的概率数据关联滤波算法
李向阳;嵇成新
【期刊名称】《指挥控制与仿真》
【年(卷),期】2005(027)003
【摘要】在密集多回波条件下对单个机动目标跟踪的情况下,综合利用"最近邻"法和概率数据关联滤波算法,推出了一种基于"最近邻"方法的概率数据关联滤波算法,采用关联区域内总数固定的候选回波来更新被跟踪目标的状态,并进行了计算机仿真.结果表明,新滤波算法的跟踪性能明显要优于概率数据关联滤波算法,而且降低了概率数据关联滤波算法的计算量.因此,可以通过回波的残差协方差矩阵进行衡量,挑选总数固定的"最近邻"回波,取这些回波的加权和作为目标回波用于概率数据关联滤波算法中更新被跟踪目标的状态.
【总页数】4页(P15-17,29)
【作者】李向阳;嵇成新
【作者单位】海军大连舰艇学院,辽宁,大连,116018;海军大连舰艇学院,辽宁,大连,116018
【正文语种】中文
【中图分类】O211.64
【相关文献】
1.一种新的多模型联合概率数据关联方法 [J], 宋春霞;张磊;关锦生
2.一种新的避免航迹合并的联合综合概率数据关联滤波器 [J], 朱昀;王俊;陈刚;郭
帅
3.基于幅值信息的联合概率数据关联粒子滤波算法 [J], 章飞;周杏鹏;陈小惠
4.一种具有关联波门自适应的联合概率数据关联算法 [J], 骆荣剑;唐鉴波;罗凯
5.空地概率数据关联转换量测滤波算法 [J], 罗玉文;柳丹;范雄华;江晶
因版权原因,仅展示原文概要,查看原文内容请购买。
联合概率数据关联算法

联合概率数据关联算法联合概率数据关联算法是一种用于分析和预测多个变量之间关系的方法。
它通过统计学和概率论的原理,利用数据样本中各变量之间的联合概率分布,来揭示它们之间的关联程度和趋势。
这种算法在各个领域都有广泛的应用,例如金融、市场营销、医疗等。
在金融领域,联合概率数据关联算法可以帮助分析师预测股票市场的走势。
通过收集大量的历史股票数据,算法可以分析不同变量之间的关系,如股票价格、交易量、利润等。
通过计算这些变量之间的联合概率分布,可以得出它们之间的相关性。
这样,分析师可以根据这些关联关系来制定投资策略,提高投资收益率。
在市场营销领域,联合概率数据关联算法可以用于分析用户行为和购买决策的关系。
通过收集用户的历史购买数据和行为数据,算法可以分析用户在购买某个产品时的决策因素。
通过计算这些因素之间的联合概率分布,可以得出用户购买某个产品的概率。
这样,市场营销人员可以根据这些关联关系来设计个性化的营销策略,提高销售额和用户忠诚度。
在医疗领域,联合概率数据关联算法可以用于分析疾病的发展和治疗效果的关系。
通过收集患者的病史数据和治疗数据,算法可以分析不同治疗方法对疾病发展的影响。
通过计算这些影响因素之间的联合概率分布,可以得出不同治疗方法的效果。
这样,医生可以根据这些关联关系来选择最有效的治疗方法,提高疾病治愈率。
除了上述领域外,联合概率数据关联算法还可以应用于其他许多领域。
例如,它可以用于天气预测,通过分析气象数据中的各个变量之间的关系,来预测未来的天气情况。
它还可以用于交通流量预测,通过分析交通数据中的各个变量之间的关系,来预测未来的交通状况。
联合概率数据关联算法是一种非常有用的分析方法,它可以帮助我们揭示多个变量之间的关联关系,并用于预测和决策。
通过合理利用这种算法,我们可以在各个领域中提高效率和准确性,为决策者提供更好的决策依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X t (k 1) F t (k) X t (k) W t (k)
Z
(k)
H
(k ) X
t
(k)
V
(k
)
k=0,1,2,…; t=1,2,…,T k=0,1,2,…
其中: Xt(k)——k时刻目标t的状态向量;
初值Xt(0)是均值 为Xˆ t (0 / 0) 、协方差矩阵为 Pˆ t (0 / 0)的随机
9
第六章
首先定义关联事件
θjt≡{有效测量Zj(k)来自目标t} j=1, 2, …, mk; t=1, 2, …, n 当t=0时,θj0表示测量Zj(k)来自杂波或噪声的事件。
记关联事件的后验概率为
jt P{ jt / Z k}
称βjt为关联概率,它是各关联事件出现可能性的度量。 Zk表示全部有效回波的集合。
如果被跟踪的目标的关联门均不相交,或者没有回 波处于相交区域,则多目标跟踪问题就可简化为多目标 环境中的单目标跟踪问题。
5
第六章
2. 确认矩阵的建立
为了表示有效回波和个目标跟踪门的复杂关系,引入了确 认矩阵的概念。
当且仅当回波落入某目标关联区内,它才被认为是有效回 波,否则被拒绝。
实际上,只有落入关联门内的回波,被认为是有效回波。 这样,我们就可以得到包括mk个有效回波,n个目标的有 效矩阵或称确认矩阵。确认矩阵被定义为彼此相交的跟踪 门的最大集合,表示为
效回波mk以相应的关联概率分别对目标t的状态估计的加权和。
11
第六章
现定义联合关联事件
i (k)
mk
i jt
(k
)
j1
表示第i个联合事件,它表示mk个量测源的一种可能。
i jt
(k
)表示量测j在第i个联合事件中源于目标t的事件;
其中0 t n;
i j
0表示量测j在第i个联合事件中源于杂波或虚警。
数据融合
第六章
联合概率数据关联和多假设滤波器
第六章
联合概率数据关联算法和多假设方法被认为是在多目标跟 踪领域最有效的两种关联方法。
多假设跟踪方法考虑回波来源于目标、杂波和新目标等各 种可能的情况。
联合概率数据关联算法是多假设方法的一个特例,避免了 “最邻近”方法“唯一性”可能造成的关联出错,能够较 好的适应密集环境下的多目标跟踪。
矩阵中其余元素:
jt
1 0
当ωjt=1时,k时刻有效回波Zkj落入确认门Atk; 当ωjt=0时,k时刻有效回波Zkj没落入确认门Atk。 其中,j=1,2,…,mk;t=1,2,…,n。
7
第六章
图1中目标数n=3,有效回波数mk=4,确认矩阵为:
目标3
Zk1 目标1
Zk3 Zk2 目 标 2
Zk4
( jt ), j 1,2,..., mk , t 0,1,..., n
(6-1)
6
第六章
其结构如下:
目标t
0 1 2 ··· n
1
11 12
1 21
12
1 mk 1 mk 2
1n
2n
mk
n
其中:ωjt表明第j个有效测量是否位 于 目 标 t 的 跟 踪 门 内 。 t=0 时 , 表 明 “没有目标”,相应的Ω矩阵中t=0对 应的一列元素全部为1,每一个测量 都可能来自于噪声、干扰或杂波相消 剩余。
12
第六章
联合关联事件θi(k)可以表示成矩阵形式:
ˆ (i (k)) ˆijt (i (k)) , j 1,2,...,mk ;i 1,2,...,k
其中,
ˆ ijt
(i
(k
))
1
0
i jtБайду номын сангаас
(k
)
i
(k
)
否则
表示在联合事件中,量测j是否源于目标t。
13
第六章
满足以下两个条件的联合关联事件定义为可行事件:
2
6.1 联合概率数据关联算法
第六章
6.1.1 联合概率数据关联算法的基本思想 联合概率数据关联算法是在仅适用于与单目标跟踪的概率
数据关联算法(PDA)的基础上,提出的适用于多目标跟踪 情形的一种数据关联算法。
3
第六章
1. 模型
假设在杂波环境中已有T个目标,则它们的状态方程 和测量方程分别表示为:
向量,且独立于Wt(k);
Ft(k)——目标t的状态转移矩阵;
4
第六章
Wt(k)——状态噪声,其均值为零的高斯白噪声,有协方差矩阵 E[Wt(k)(Wt(l))T]=Qt(k)δk,l
H(k)——测量矩阵; V(k)——测量噪声,其均值为零的高斯白噪声,有协方差矩阵
E[Vt(k)(Vt(l))T]=Rt(k)δk,l
n=0, 1, 2, 3 mk
1 1 0 0 1
k
1 1
1 1 0 0 1 0
2 3
1 0 0 1 4
对于第量一个测目落标入确跟认踪门内门有相两交个区有域效回的波情Zk形1,,Zk对2;应第某二个些确量认测门可内能也有源两 个于有多效个回波目Z标k2,,Zk联3;合第概三率个确数认据门关有联一的个有目效的回就波是Zk4计,故算ω每11=一1,个ω2量1=1测,
1,
t (i (k)) 0,
若存在j使t j t 若不存在j使t j t
14
第六章
同样可以定义一个测量关联指示器
j (i (k))
n t0
ˆ ijt (i (k))
1, 0,
(1) 每个测量只能源于一个源、 目标或杂波, 即
n
ˆ
i jt
(i
(k
))
1
t0
j=1, 2, …, mk
(2) 每个目标最多只能产生一个回波,即
mk
t (i (k)) ˆijt (i (k)) 1
j1
t=1, 2, …, n
δt(θi(k) )称为目标检测指示器,它表明事件θi(k)中是否 有测量与目标t关联,即目标是否被检测到。
ω与22=其1, ω可32能=1,的ω4各3=种1, 其源余目为标0。相关联的概率。
8
第六章
3.联合关联事件和联合关联概率 为了进行状态估计,首先要解决mk个有效回波与n个目标
配对的问题,即数据关联。 JPDA算法的基本思想在于认为落入目标t的跟踪门内的有
效回波都有可能来自目标t,只是其关联概率不同。
10
第六章
根据全概率公式,有
xˆt (k / k) E[xt (k) | Z k ]
mk
E[xt (k) | jt (k), Z k ]P( jt (k) | Z k )
j0
mk
jt
xˆ
t j
(k
/
k
)
j0
其中,xˆtj (k / k) 表示在时刻k利用卡尔曼滤波对目标t的状态估计。
上式表明,k时刻目标t的状态估计 xˆt (k / k) 是其关联门内各个有
