人教版九年级数学下册28.2 :解直角三角形及其应用 同步练习(含答案)
人教版九年级数学下册28.2《解直角三角形及其应用》同步练习 含答案

2021年人教版九年级下册28.2《解直角三角形及其应用》同步练习一.选择题1.在Rt△ABC中,∠C=90°,∠B=36°,若BC=m,则AB的长为()A.B.m•cos36°C.m•sin36°D.m•tan36°2.如图,△ABC的顶点都在方格纸的格点上,则sin A的值为()A.B.C.3 D.3.如图,已知在4×4的网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则cos∠CAB的值为()A.B.C.D.4.如图,在平面直角坐标系中,P是第一象限内的点,其坐标是(a,3)且OP与x轴的夹角α的正切值是,则sinα的值为()A.B.C.D.5.如图,某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,则滑梯的长AB为()A.100米B.110米C.120米D.130米6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AD与AB的长度之比为()A.B.C.D.7.如图,要测量一条河两岸相对的两点A,B之间的距离,我们可以在岸边取点C和D,使点B,C,D共线且直线BD与AB垂直,测得∠ACB=56.3°,∠ADB=45°,CD=10m,则AB的长约为()(参考数据sin56.3°≈0.8,cos56.3°≈0.6,tan56.3°≈1.5,sin45°≈0.7,cos45°≈0.7,tan45°=1)A.15m B.30m C.35m D.40m8.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为()A.6m B.3m C.9m D.6m9.如图,一艘潜水艇在海面下300米的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960米到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是()A.(480+300)米B.(960+300)米C.780米D.1260米10.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距300m,则图书馆A到公路的距离AB为()A.150m B.150m C.150m D.100m 11.如图,从渔船A处测得灯塔M在北偏东55°方向上,这艘渔船以28km/h的速度向正东方向航行,半小时后到达B处,在B处测得灯塔M在北偏东20°方向上,此时灯塔M与渔船的距离是()A.28km B.14km C.7km D.14km12.如图,两栋大楼相距100米,从甲楼顶部看乙楼的仰角为26°,若甲楼高为36米,则乙楼的高度为()A.(36+100sin26°)米B.(36+100tan26°)米C.(36+100cos26°)米D.(36+)米二.填空题13.在△ABC中,sin B=,tan C=,AB=3,则AC的长为.14.如图,△ABC的顶点都是正方形网格中的格点,则cos A的值为.15.如图,在平面直角坐标系中有一点P(6,8),那么OP与x轴的正半轴的夹角α的余弦值为.16.如图,某商场大厅自动扶梯AB的长为12m,它与水平面AC的夹角∠BAC=30°,则大厅两层之间的高度BC为m.17.如图,大坝横截面的迎水坡AB的坡比为1:2(即BC:AC=1:2),若坡面AB的水平宽度AC为12米,则斜坡AB的长为米.18.再如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为多少km.19.平放在地面上的三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示,量得∠A 为54°,∠B为36°,边AB的长为2.1m,BC边上露出部分BD的长为0.9m,则铁板BC 边被掩埋部分CD的长是m.(结果精确到0.1m.参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38).20.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为.三.解答题21.如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,求sin∠BPC.22.如图,小明为了测量学校旗杆CD的高度,在地面离旗杆底部C处22米的A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°.求旗杆的高度CD.(结果精确到0.1米)【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】23.如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为63°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).[参考数据:sin63°=0.89,cos63°=0.45,tan63°=1.96]24.汝阳某公司举办热气球表演来庆祝开业,如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为37°和45°,A、B两地相距100m.当气球沿与BA平行地飘移100秒后到达D处时,在A处测得气球的仰角为60°.(1)求气球的高度;(2)求气球飘移的平均速度.(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75,≈1.7.)25.如图,某地修建高速公路,要从A地向B地修一座隧道(A、B在同一水平面上),为了测量A、B两地之间的距离,某工程师乘坐热气球从B地出发,垂直上升120米到达C处,在C处观察A地的俯角为42°,求A、B两地之间的距离.(结果精确到1米)[参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90]26.如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台合风中心距离小岛200海里.(1)过点B作BP⊥AC于点P,求∠PBC的度数;(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响?请说明理由.(参考数:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60,≈1.73)参考答案一.选择题1.解:∵∠C=90°,∠B=36°,BC=m,∴cos B=,∴AB==,故选:A.2.解:延长AB到D,连接CD,如右图所示,由题意可得,AC==,CD=1,∴sin∠A==,故选:A.3.解:由题意可得,AC===2,BC==,AB==5,∵(2)2+()2=52,∴AC2+BC2=AB2,∴△ACB是直角三角形,∠ACB=90°,∴cos∠CAB==,故选:B.4.解:过点P作PE⊥x轴于E,如图所示:∵P(a,3),∴OE=a,PE=3,∵tan∠α==,∴a=OE=4,∴OP===5,∴sinα==,故选:A.5.解:∵某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,∴=,则=,解得:AC=120米,故AB===130(米).故选:D.6.解:在Rt△ABC中,∵sin∠ABC=,即sinα=,∴AB=,在Rt△ADC中,∵sin∠ADC=,即sinβ=,∴AD=,∴==,故选:C.7.解:设AB=xm,在Rt△ABD中,∵∠ADB=45°,∴AB=BD=xm,在Rt△ABC中,∵∠ACB=56.3°,且tan∠ACB=,∴BC==≈x,由BC+CD=BD得x+10=x,解得x=30,∴AB的长约为30m,故选:B.8.解:∵迎水坡AB的坡比为1:,∴=,即=,解得,AC=3,由勾股定理得,AB==6(m),故选:A.9.解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.已知AB=960米,∠BAC=30°,∠EBC=60°,∵∠BCA=∠EBC﹣∠BAC=30°,∴∠BAC=∠BCA.∴BC=BA=960(米).在Rt△BEC中,sin∠EBC=,∴CE=BC•sin60°=960×=480(米).∴CF=CE+EF=(480+300)米,故选:A.10.解:由题意得,∠AOB=90°﹣60°=30°,OA=300m,∴AB=OA=150(m),故选:C.11.解:根据题意可知:∠MAB=90°﹣55°=35°,∠ABM=90°+20°=110°,∴∠AMB=180°﹣∠ABM﹣∠MAB=35°,∴∠MAB=∠AMB,∴BM=AB=28×=14(km).所以此时灯塔M与渔船的距离是14km.故选:B.12.解:由题意知:AE=CD=36米,AC=DE=100米,在Rt△ABC中,tan∠BAC=,∴BC=AC tan∠BAC=100tan26°(米),则BD=CD+BC=(36+100tan26°)米,即乙楼的高度为(36+100tan26°)米,故选:B.二.填空题13.解:过A作AD⊥BC,在Rt△ABD中,sin B=,AB=3,∴AD=AB•sin B=1,在Rt△ACD中,tan C=,∴=,即CD=,根据勾股定理得:AC===,故答案为:.14.解:如图,作CH⊥AB于H,设小正方形的边长为1.则AC==,在Rt△ACH中,cos A===,故答案为:.15.解:如图作PH⊥x轴于H.∵P(6,8),∴OH=6,PH=8,∴OP==10,∴cosα===.故答案为:.16.解;在Rt△ABC中,∠BAC=30°,AB=12m,∴BC=m,故答案为:6.17.解:∵大坝横截面的迎水坡AB的坡比为1:2,AC=12米,∴==,∴BC=6(米),∴AB===6(米).故答案为:6.18.解:如图,过B作BE⊥AC于E,过C作CF∥AD,则CF∥AD∥BG,∠AEB=∠CEB=90°,∴∠ACF=∠CAD=20°,∠BCF=∠CBG=40°,∴∠ACB=20°+40°=60°,由题意得,∠CAB=65°﹣20°=45°,AB=30km,在Rt△ABE中,∵∠ABE=45°,∴△ABE是等腰直角三角形,∵AB=30km,∴AE=BE=AB=30(km),在Rt△CBE中,∵∠ACB=60°,tan∠ACB=,∴CE===10(km),∴AC=AE+CE=30+10(km),∴A,C两港之间的距离为(30+10)km,故答案为:(30+10).19.解:在直角三角形中,sin A=,则BC=AB•sin A=2.1sin54°≈2.1×0.81=1.701,则CD=BC﹣BD=1.701﹣0.9,=0.801≈0.8(m),故答案为:0.8.20.解:由题意得:∠BAC=31°,∠CBD=45°,∵∠CBD=∠BAC+∠ACB,∴∠ACB=∠CBD﹣∠BAC=45°﹣31°=14°,故答案为:14°.三.解答题21.解:作AD⊥BC于点D,如右图所示,∵AB=AC=5,BC=8,∴BD=CD=4,∠BAD=∠BAC,∵∠ADB=90°,∴sin∠BAD=,又∵∠BPC=∠BAC,∴∠BPC=∠BAD,∴sin∠BPC=.22.解:由题意得,BE⊥CD于E,BE=AC=22米,∠DBE=32°,在Rt△DBE中,DE=BE•tan∠DBE=22×0.62≈13.64(米),CD=CE+DE=1.5+13.64≈15.1(米),答:旗杆的高CD约为15.1米.23.解:在△ADB中,∠ADB=90°,∠BAD=45°,∴BD=AD=80(米),在△ACD中,∠ADC=90°,∴CD=AD•tan63°=80×1.96≈156.8(米),∴BC=BD+CD=80+156.8=236.8≈237(米),答:该建筑物的高度BC约为237米.24.解:(1)如图,过点C作CE⊥AB于点E,在Rt△ACE中,∵∠CAE=37°,∴CE=AE×tan37°=0.75AE,∴AE=CE,在Rt△BCE中,∵∠CBE=45°,∴BE=CE,∴AB=AE﹣BE=CE﹣CE=CE=100,∴CE=300(米),答:气球的高度为300米;(2)如图,过点D作DF⊥AB于点F,则四边形DFEC是矩形,在Rt△ADF中,∵∠DAF=60°,∴AF=DF=CE=100≈170(米),∴AE=CE=400(米),∴CD=EF=400﹣170=230(米),∴速度为:230÷100=2.3.答:气球飘移的平均速度每分钟为2.3米.25.解:在Rt△ABC中,∵∠ABC=90°,∠A=42°,∴tan42°=,∴AB=≈133(米)答:A、B两地之间的距离约为133米.26.解:(1)∵∠MAC=60°,数学∴∠BAC=30°,又∵BP⊥AC,∴∠APB=90°,∴∠ABP=60°,又∵∠CBN=29°,∠ABN=90°,∴∠ABC=119°,∴∠PBC=∠ABC﹣∠ABP=59°;(2)不会受到影响.理由如下:由(1)可知,∠PBC=59°,∴∠C=90°﹣∠PBC=31°,又∵tan31°=0.60,∴,设BP为x海里,则AP=海里,CP=海里,∴,解得:x≈57,∵57>50,∴沿海城市B不会受到台风影响.。
人教版九年级数学下册28.2 解直角三角形及其应用同步练习附答案【新材料】

28.2 解直角三角形及其应用(一)一、双基整合:1.在下面条件中不能解直角三角形的是()A.已知两条边 B.已知两锐角 C.已知一边一锐角 D.已知三边2.在△ABC中,∠C=90°,a=5,c=13,用科学计算器求∠A约等于()A.24°38′ B.65°22′ C.67°23′ D.22°37′3.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,有下列关系式:•①b=ccosB,②b=atanB,③a=csinA,④a=bcotB,其中正确的有()A.1个 B.2个 C.3个 D.4个4.为测一河两岸相对两电线杆A、B间距离,在距A点15m的C处,(AC⊥AB),测得∠ACB=50°,则A、B间的距离应为( )mA.15sin50° B.15cos50° C.15tan50° D.15cot50°5.在△ABC中,∠C=90°,,三角形面积为52,则斜边c=_____,∠A的度数是____.6.在直角三角形中,三个内角度数的比为1:2:3,若斜边为a,•则两条直角边的和为________.7.四边形ABCD中,∠C=90°,AB=12,BC=4,CD=3,AD=13,•则四边形ABCD•的面积为________.8.如图,小明想测量电线杆AB•的高度,•发展电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度约为_______米.1.41≈1.73)9.如图所示,在Rt△ABC中,a,b分别是∠A,∠B的对边,c为斜边,如果已知两个元素a,∠B,就可以求出其余三个未知元素b,c,∠A.(1)求解的方法有多种,请你按照下列步骤,完成一种求解过程.第一步:已知:a,∠B,用关系式:_______________,求出:_________________;第二步:已知:_____,用关系式:_______________,求出:_________________;第三步:已知:_____,用关系式:_______________,求出:_________________.(2)请你分别给出a,∠B的一个具体数据,然后按照(1)中的思路,求出b,c,∠A的值.bcaA10.在等腰梯形ABCD中,AB∥CD,CD=3cm,AB=7cm,高为,求底角B的度数.11.如图所示,在Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D ,AC=22,AB=23,设∠BCD=α,•求cos α的值.BAC D二、探究创新12.国家电力总公司为了改善农村用电量过高的现状,目前正在全面改造各地农村的运行电网,莲花村六组有四个村庄A ,B ,C ,D 正好位于一个正方形的四个顶点,•现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图所示的实线部分,请你帮助计算一下,哪种架设方案最省电线(以下数据可供参考2=1.414,3=1.732,5=2.236).13.在Rt △ABC 中,∠C=90°,斜边c=5,两直角边的长a ,b 是关于x 的一元二次方程x 2-mx+2m-2=0的两个根,求Rt △ABC 中较小锐角的余弦值。
人教版九年级数学下册第28章锐角三角函数28.2解直角三角形及其应用复习练习及答案

第28章锐角三角函数28.2 解直角三角形及其应用1. 在厶ABC中,/ A=120° AB=4 AC=2 贝卩sinB 的值是()A. 口B .-i C .2 D14 5 7 142. 在Rt△ ABC中,/ C=90 ,若AB=4 sinA=?,则斜边上的高等于()5A. 64 B .兰C . 16 D . 1225 25 5 53. 如图,在Rt△ ABO中,斜边AB= 1,若OC/ BA / AOC= 36°,贝S ()A. 点B到AO的距离为sin 54B. 点B到AO的距离为tan 36 °C. 点A到OC的距离为sin 36 ° sin 54D. 点A到OC的距离为cos 36 sin 544. 如图是教学用直角三角尺,边AC= 30 cm,/ C= 90° tan / BAC=则边BC的长为()A. 30 3 cm B . 20 3 cm C . 10 3 cm D . 5 3 cm\[2 35. 如图,在△ ABC中,cos B= ,sin C= , AC= 5,则厶ABC的面积是()2 5A.fB. 12C. 14D. 21 6•河堤横断面如图所示,堤高BC= 6 m,迎水坡AB的坡比为1 : 3,则AB的长为()A. 12 m B . 4 3 m C . 5 3 m D . 6 3 m7. 如图,在两建筑物之间有一旗杆,高15 m,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角a为60°,又从A点测得D点的俯角B为30°,若旗杆底部G为BC的中点,则矮建筑物的高CD为()A. 20 m B . 10 3 m C . 15 3 m D . 5 6 m8. 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20 n mile,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20 min 后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为()A. 10:3 n mile/h B .30 n mile/h C . 20 ';3 n mile/h D . 30 : 3n mile/h9. 从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是(A. (6+2 .3) 米B (6+3 .3) 米C (6+6 .3 )米D . 12 米10. 如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30° 则B、C两地之间的距离为()3A. 100 3 m B 50 2m C. 50 3m D .咛11. 在Rt△ ABC中,CA= CB AB=込/2,点D在BC边上,连接AD 若tan1/ CAD= 3,贝y BD的长为 _____ .12. 在平面直角坐标系中,点A的坐标为(3 , 0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC= 2,设tan / BOC= m则m的取值范围是________ .13. 在等腰三角形ABC中,/ A= 30°, AB= 8,贝S AB边上的高CD的长是14. 在Rt△ ABC中,/ C=90 , tanA = 4, BC=8 则厶ABC的面积为.315. 等腰三角形的一腰长为6cm,底边长为673cm则其顶角为___________ .16. 在Rt△ ABC中,/ ACB=90 , CDLAB于点D.已知AC=5 , BC=2 那么sin / ACD= _____17. 如图,在Rt△ ABC中,/ C=90°, D为BC上一点,/ DAC=30 , BD=2 AB= 2怎,贝S AC的长是_______ .18. 如图,从地面上点A处测得山顶上铁塔BD的塔顶和塔底的仰角分别为B =60°和a =45°,已知塔高BD=100m那么山高CD= m .(结果保留根号)19. 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C 点处的俯角为45°.则海底C点处距离海面DF的深度为________ 米(结果精确到个位,参考数据:2〜1.414 , . 3〜1.732 , 〜2.236 )…字二…一/产'即~~时•、\I 、20. 如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45° .已知山坡AB垂直于视线AD AB=20米,AE=30米,则这块宣传牌CD的高度为________________ 米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:2〜1.414 , 3〜1.732 ).21. 如图,在△ ABC中,CDLAB 垂足为D.若AB=12 CD=6 tanA=?,求2 sinB+cosB 的值.22. 已知:如图,Rt△ AOB中,/ 0=90,以0A为半径作O Q BC切OO于点C,连接AC交QB于点P.(1) 求证:BP=BC(2) 若sin / PAQ= 1,且PC=7 求OO 的半径.323. 如图,已知某小区的两幢10层住宅楼间的距离为AC= 30 m,由地面向上依次为第1层、第2层,…,第10层,每层高度为3 m假设某一时刻甲楼在乙楼侧面的影长h m.(1)用含a的式子表示h;(不必指出a的取值范围)⑵当a= 30°时,甲楼楼顶B点的影子落在乙楼的第几层?若a每小时增加15°,从此时起几小时后,甲楼的影子刚好不影响乙楼采光?24. 如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、ND 在同一条直线上).求出旗杆MN勺高度.(参考数据:2〜1.4…3〜1.7 , 结果保留整数.)26.如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角a为45° .从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角B为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)[Um答案:1 —10 DBCCA AADCA 11.612.5 m^-2"13.^3^或4 或4 314.2415. 120°16.二3 17. 318. 50 ( 3+1)19. 260020. 5.421. 解:在 Rt △ ACD 中,T/ADC=90,二 tanA 二 CD - 3,二 AD=4 AD AD 2••• BD=AB -AD=12-4=8 在 Rt △BCD 中,BDC=90 , BD=8 CD=6 BC= BD 2 CD 2 =10, • sinB 二 CD 3 , cosB=BD - , • sinB+cosB=3+« =7 . BC 5BC5 5 5 5 22. (1)证明:连接 OC T BC 是O O 切线,•/0(B=90°,「./OCA / BCA=90 , T OA=O , •/ OCA / OAC / BOA=90,•/ OAC+APO=90,T / APO / BPC •/ OAC / BPC=90,•/ BPC / BCA 二 BC=BP(2)解:延长 AO 交O O 于点 E ,连接 CE 在 Rt △ AOP 中, T sin / PAO=,3设 OP=x AP=3x 贝y AO=22x ,T AO=OE 二 OE=22x ,「. AE=^2x , 解得:x=3,・ AO=6 2 .23. 解:(1)如图,过点E 作EF ±AB 于点F.由题意可知,四边形 ACEF 为矩形,• EF = AC= 30, AF = CE= h ,Z BEF= T AB= 3X 10= 30,・ BF = AB- AF = 30- h.T sin / PAO=,3CE = 1 AE 3 AC 2一2 . 3x 7= .・ --------- - AE 3 '3「• h = 30— 30tan a .⑵ 当 a = 30° 时,h = 30 — 30tan 30 ° = 30 — 30^3〜12.7.3T 12.7 — 3~4.2,二当a= 30°时,B 点的影子落在乙楼的第五层.当 h = 0 时,30 — 30ta n a= 0,得 a= 45 °,Ta 每小时增加15°,二从此时起1小时后,甲楼的影子刚好不影响乙楼采光.24. 解:过点A 作AE± MN 于 E ,过点C 作CF 丄MN 于 F ,则 EF=AB-CD=1.7-1.5=0.2 (m ),在 Rt △ AEM 中, v/ AEM=90 , / MAE=45 , • AE=ME 设 AE=ME=xm 贝S MF=(x+0.2 ) m , FC= (28-x ) m在 Rt △ MFC 中, v/ MFC=90,/ MCF=30,二 MF=CF?ta / MCF• x+0.2二乜 (28-x ),解得 9.7,二 MN 二ME+EN=9.7+1.711 米.又•••在 Rt △ BEF 中,tan / BEF = ||, ••• tan a= 30—1,即 30— h = 30tan a, 30答:旗杆MN 的高度约为11米.解:由题意可知/ BAD W ADB=45,二 FD 二EF 二米,在 Rt △ PEH 中, tan B =CG ,二CG=( 5 3+6)?二=5+2 3,:. CD=( 6+2.3 ) 米. PG 326. tan B =EH PHBF ,八 BF =: 5 3,二 PG=BD=BF+FD=35+6, 在 RT A PCG K。
【九年级】九年级数学下28.2解直角三角形及其应用(二)同步练习(人教版附答

【九年级】九年级数学下28.2解直角三角形及其应用(二)同步练习(人教版附答28.2解直角三角形及其应用同步练习(二)一、单选题(本大题共15个子题,每个子题得3分,共计45分)一、一人乘雪撬沿坡度为的斜坡滑下距离(米)与时间(秒)之间的关系为.若滑动时间为秒,则他下降的垂直高度为().a、仪表b.米c、仪表d.米2.如图所示,有人站在楼顶观察对面的直旗杆。
已知观测点到旗杆的距离(长度),测量旗杆顶部的仰角,测量旗杆底部的俯角,则旗杆高度为()a.(b(c.(d(3、如图,在处测得旗杆的顶端的仰角为,向旗杆前进米到达处,在处测得的仰角为,则旗杆的高为()米A.b.Cd.4.在中学升国旗时,同学a站在旗杆底部以引起注意。
当国旗升到旗杆顶端时,同学视线的仰角为。
如果他的眼睛离开地面,旗杆的高度是()a.米b、仪表c.米d、仪表5、如图,一渔船在海岛南偏东方向的处遇险,测得海岛与的距离为海里,渔船将遇险情况报告给位于处的救援船后,沿北偏西方向向海岛靠近,同时,从处出发的救援船沿南偏西方向匀速航行,分钟后,救援船在海岛处恰好追上渔船,那么救援船航行的速度为()海里/小时.A.b.Cd.6.如图所示,为了测量一棵树垂直于地面的高度,在距树底m处测量的树顶仰角为,则树高为()a.米b、仪表c.米d、仪表7、如图,一艘海轮位于灯塔的北偏东方向,距离灯塔海里的点处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离长是()a、大海b.海里c、大海d.海里8.如图所示,该船沿正南方向以每小时海里的匀速航行。
据观察,灯塔位于该地点的西偏南方向。
航行数小时后,它到达了北。
据观察,灯塔的方向是西偏南。
如果船继续向南航行到离灯塔最近的位置,船与灯塔之间的距离约为(通过科学计算器,,)获得)9、小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为米,坡面上的影长为米.已知斜坡的坡角为,同一时刻,一根长为米、垂直于地面放置的标杆在地面上的影长为米,则树的高度为()a、仪表b.米c、仪表d.米10.为了如图所示测量上坡坡道的坡度,小明测量了如图所示的数据,则坡度角的正切值为()a.Bc.D11、如图,长的楼梯的倾斜角为,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角为,则调整后的楼梯的长为()12.如图所示,在,,,中,点是边的中点。
人教版九年级数学下册 28.2 解直角三角形及其应用 同步测试题(有答案)

28.2 解直角三角形及其应用同步测试题(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 在△ABC,∠B=45∘,∠C=30∘,BC边上的高为3,则△ABC的周长是()A.9+3√2B.6+3√2+2√3C.9+3√2+3√3D.3√2+3√32. 如图,点A(1.5, 3)在第一象限,OA与x轴所夹的锐角为α,tanα=()A.1B.1.5C.2D.33. 如图,太阳光线与水平线成70∘角,窗子高AB=2米,要在窗子外面上方0.2米的点D 处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是()A.2tan70∘米 B.2sin70∘米 C. 2.2tan70∘米 D.2.2cos70∘米4. 如图,甲、乙两艘轮船分别在P,M两个港口停靠,港口P在港口M的南偏西22∘方向上.某一天,甲、乙两艘轮船分别从P,M两个港口同时出发,以相同的速度航行,乙轮船向正南方向航行,若干小时后,两轮船在N处相遇,则甲轮船的航行方向是()A.北偏东22∘B.北偏东44∘C.南偏西68∘D.南偏西44∘5. 某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30∘,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60∘,则观光塔AB的高度是()A.50米B.100米C.125米D.150米,则AC是()6. 如图,已知Rt△ABC中,斜边BC上的高AD=4,cos B=45A.5B.4C.3D.45,AC=2√3,则AB=()7. 如图,在△ABC中,∠A=30∘,tan B=√32A.4B.5C.6D.78. 在Rt△ABC中,CD是斜边AB上的高,∠A=30∘,那么下列结论正确的是()A.3AD=7BCB.AB=2ACC.AC=8CDD.16CD2=3AB29. 某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为60∘,已知在钟摆的摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b−a等于()A.1 2B.12−√32C.12+√34D.12−√3410. 如图,淇淇一家驾车从A地出发,沿着北偏东60∘的方向行驶,到达B地后沿着南偏东50∘的方向行驶来到C地,C地恰好位于A地正东方向上,则()①B地在C地的北偏西50∘方向上;②A地在B地的北偏西30∘方向上;③cos∠BAC=√32;④∠ACB=50∘.其中错误的是()A.①②B.②④C.①③D.③④二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 如图,Rt△ABC中,∠C=90∘,D是BC上一点,AD=BD,tan∠ADC=43,AB=4√5,则CD=________.12. 如图,在Rt△ABC中,∠C=90∘,AM是BC边上的中线,cos∠CAM=45,则tan∠B的值为________.13. 从A处测得B处仰角α=18∘36′,那么从B处测得A处的俯角β=________.14. 如图,河坝横断面迎水坡AB的坡比是1:√3,堤高BC=5米,则坝底AC的长度是________米.15. 如图,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,tan∠CPN为________.16. 如图,在△ABC中,∠A=30∘,∠B=45∘,D在AB上,E在AC上,且使AE=EC=DE,那么AD2:BC2等于________.17. 某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45∘,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30∘,则调整后楼梯AD的长为________m.(结果保留根号)18. 在边长为1的正方形网格中,△ABC的位置如图所示,则cos A=________.19. 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60∘,距离为60海里的A处;上午9时到达C处,看到灯塔在它的正北方向.则这艘船航行的速度为________海里/时.三、解答题(本题共计6 小题,共计60分,)20. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A,B两个基地前去拦截,6分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40∘.(1)求甲巡逻艇的航行方向;(2)成功拦截后,甲、乙两艘巡逻艇同时沿原方向返回且速度不变,3分钟后甲、乙两艘巡逻艇相距多少海里?21 小强从自己家的阳台上,看一栋楼顶部的仰角为30∘,看这栋楼底部的俯角为60∘,小强家与这栋楼的水平距离为42m,这栋楼有多高?22 如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点A,再在河这边沿河边取两点B、C,在点B处测得A在北偏东30∘方向上,在点C处测得点A在西北方向上,量得BC长为400米,请你求出该河段的宽度.(结果保留根号)23. 安装在屋顶的太阳能热水器的横截面示意图如图所示.集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O处,⊙O的半径为0.2m,AO与屋面AB的夹角为32∘,BF⊥AB于B,AB=2m,求支架BF的长(精确到0.1m).参考数据:sin32∘=0.32,cos32∘=0.84,tan32∘=0.62.24 随着社会的发展,人们对防洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD,如图所示,根据图中数据计算坝底CD的宽度(结果保留根号).25 北盘江大桥坐落于云南宣威与贵州水城交界处,横跨云贵两省,为目前世界第一高桥.左图是大桥的实物图,右图是从左图中引申出的平面图,测得桥护栏BG=1.8米,拉索AB与护栏的夹角为26∘,拉索ED与护栏的夹角是60∘,两拉索底端距离BD为300m,若两拉索顶端的距离AE为90m,请求出立柱AH的长.(tan26∘≈0.5,sin26∘≈0.4,√3≈1.7)参考答案一、选择题(本题共计10 小题,每题 3 分,共计30分)1.【答案】C【解答】解:作AD⊥BC,∵ AD=3,∠B=45∘,∵ BD=AD=3,AB=√BD2+AD2=3√2,∵ AD=3,∠C=30∘,∵ AC=2AD=6,CD=√AC2−CD2=3√3,∵ △ABC的周长=AB+AC+BC=3√2+6+3√3+3=9+3√2+3√3.故选C.2.【答案】C【解答】解:根据题意得:tanα=31.5=2;故选C.3.【答案】C【解答】解:∵ DA=0.2米,AB=2米,∵ DB=DA+AB=2.2米,∵ 光线与地面成70∘角,∵ ∠BCD=70∘.又∵ tan∠BCD=DBDC,∵ DC=DBtan∠BCD = 2.2tan70m.故选C. 4.【答案】B【解答】解:如图,由题意可知,∠PMN=22∘,PN=MN,所以∠MPN=22∘.所以∠2=∠1=22∘+22∘=44∘.故甲轮船的航行方向是北偏东44∘.故选B.5.【答案】A【解答】解:作EF⊥AC于F,EG⊥DC于G,在Rt△DEG中,EG=12DE=75米,∵ BF=BC−CF=BC−EG=100−75=25米,EF=BFtan∠BEF =BFtan30∘=25√3,∵ ∠AEF=60∘,∵ ∠A=30∘,∵ AF=EFtan A =√3√33=75(米),∵ AB=AF−BF=50(米),故选A.6.【答案】A【解答】解:∵ AD是△ABC的高,∠BAC=90∘,∵ ∠ADB=∠ADC=∠BAC=90∘,∵ ∠B+∠BAD=90∘,∠BAD+∠DAC=90∘,∵ ∠B=∠CAD,∵ cos B=45,AD=4,∵ cos B=cos∠CAD=45=ADAC,即4AC =45,∵ AC=5,故选A.7.【答案】B【解答】解:作CD⊥AB于点D.由题意知,∵ sin A=CDAC,∵ CD=AC sin A=AC sin30∘=2√3×1 =√3,∵ cos A=ADAC,∵ AD=AC cos30∘=2√3×√3 2=3.∵ tan B=CDBD =√32,∵ BD=2.∵ AB=AD+BD=2+3=5.故选B.8.【答案】D【解答】解:∵ 在Rt△ABC中,CD是斜边AB上的高,∠A=30∘,∵ AD=√3CD,CD=√32BC,AC=√32AB,AC=2CD,CD=√32BC,BC=12AB,∵ AD=32BC,AB=2√33AC,CD=√32×12AB=√34AB,∵ 4CD=√3AB,∵ 16CD2=3AB2.故选D.9.【答案】D【解答】解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,所以AD=b,CE=a,CF=b−a,∠AOB=60∘,∵ ∠AOC=30∘.作AF⊥OC与F,则在△AOC中,OF=OA cos30∘=√34,∵ CF=b−a=OC−OF=12−√34,∵ 摆长为0.5米,∵ OA=0.5米,∵ OF=√34,∵ b−a=0.5−√34,∵ b−a=(12−√34)米.故选D.10.【答案】B【解答】如图所示,由题意可知,∠1=60∘,∠4=50∘,∵ ∠5=∠4=50∘,即B在C处的北偏西50∘,故①正确;∵ ∠2=60∘,∵ ∠3+∠7=180∘−60∘=120∘,即A在B处的北偏西120∘,故②错误;∵ ∠1=∠2=60∘,∵ ∠BAC=30∘,∵ cos∠BAC=√32,故③正确;∵ ∠6=90∘−∠5=40∘,即公路AC和BC的夹角是40∘,故④错误.二、填空题(本题共计10 小题,每题 3 分,共计30分)11.【答案】3【解答】解:在Rt△ACD中,tan∠ADC=ACCD =43,设AC=4x,CD=3x,∵ AD=√AC2+CD2=5x,∵ BD=AD=5x,∵ BC=BD+CD=8x,在Rt△ABC中,AC=4x,BC=8x,∵ AB=√AC2+BC2=4√5x,而AB=4√5,∵ 4√5x=4√5,解得x=1,∵ CD=3x=3.故答案为3.12.【答案】23【解答】解:在Rt△ACM中,cos∠CAM=ACAM =45,设AC=4x,则AM=5x,则CM=√AM2−AC2=3x,而AM是BC边上的中线,所以BC=2CM=6x,在Rt△ABC中,tan∠B=ACBC =4x6x=23.故答案为23.13.【答案】18∘36′【解答】解:设A、B两点的水平线分别为AM、BN,依题意,得AM // BN,∠BAM=α=18∘36′,由平行线的性质可知,β=∠ABN=∠BAM=18∘36′.故答案为:18∘36′.14.【答案】5√3【解答】解:∵ 河坝横断面迎水坡AB的坡比是1:√3,∵ BC:AC=1:√3,∵ 堤高BC=5米,∵ 坝底AC=5√3米.故答案为:5√3.15.【答案】2【解答】解:连接格点MN,DM,如图所示:则四边形MNCE是平行四边形,△DAM和△MBN都是等腰直角三角形,∵ EC // MN,∠DMA=∠NMB=45∘,DM=√2AD=2√2,MN=√2BM=√2,∵ ∠CPN=∠DNM,∵ tan∠CPN=tan∠DNM,∵ ∠DMN=180∘−∠DMA−∠NMB=180∘−45∘−45∘=90∘,∵ tan∠CPN=tan∠DNM=DMMN =√2√2=2.故答案为:2.16.【答案】3:2【解答】连接CD,∵ 在△ACD中,AE=EC=DE.∵ ∠CDA=90∘,∵ ∠A=30∘,∵ AC=2CD,AD=√3CD,在Rt△BCD中,∠B=45∘,∵ BD=CD,BC=√2CD,∵ AD2:BC2=(√3CD)2:(√2CD)2=3:2 17.【答案】6√2【解答】解:由题意可得,AB=6m,∠ABC=45∘,∠ACB=90∘,∵ AC=AB⋅sin∠ABC=6×√22=3√2m,又∵ ∠ADC=30∘,∠ACD=90∘,∵ AD=2AC=6√2m.故答案为:6√2m.18.【答案】35【解答】如图,过点C作CD⊥AB于D.∵ AC=√32+42=5,在RtACD中,cos A=ADAC =35,19.【答案】30√3【解答】解:易得∠ABC=30∘,AB=60.∵ BC=AB×cos∠ABC=30√3(海里).∵ 这艘船航行的速度为30√3÷(9−8)=30√3(海里/时).三、解答题(本题共计6 小题,每题10 分,共计60分)20.【答案】解:(1)由已知得,AC=120×660=12(海里),BC=50×660=5(海里),∵ AC2+BC2=AB2,∵ △ABC是直角三角形.∵ ∠CBA=50∘,∵ ∠CAB=40∘∵ 甲的航向为北偏东50∘.(2)甲巡逻船航行3分钟的路程为:120×360=6(海里),乙巡逻船航行3分钟的路程为:50×360=2.5(海里),3分钟后,甲、乙两艘巡逻船相距为:√62+2.52=6.5(海里).【解答】解:(1)由已知得,AC=120×660=12(海里),BC=50×660=5(海里),∵ AC2+BC2=AB2,∵ △ABC是直角三角形.∵ ∠CBA=50∘,∵ ∠CAB=40∘∵ 甲的航向为北偏东50∘.(2)甲巡逻船航行3分钟的路程为:120×360=6(海里),乙巡逻船航行3分钟的路程为:50×360=2.5(海里),3分钟后,甲、乙两艘巡逻船相距为:√62+2.52=6.5(海里).21【答案】这栋楼的高度为56√3m【解答】在Rt△ABD中,∵ ∠BDA=90∘,∠BAD=30∘,AD=42m,∵ BD=AD tan30∘=42×√33=14√3(m).在Rt△ACD中,∠ADC=90∘,∠CAD=60∘,∵ CD=AD tan60∘=42×√3=42√3(m).∵ BC=BD+CD=14√3+42√3=56√3(m).22【答案】解:过A作AH⊥BC于点H,设AH=x,由题意得:∠BAH=30∘,∠ACH=45∘,x,∵ HC=AH=x,BH=√33∵ BC=400米,x+x=400,∵ √33解得:x=600−200√3,即河宽为(600−200√3)米.【解答】解:过A作AH⊥BC于点H,设AH=x,由题意得:∠BAH=30∘,∠ACH=45∘,x,∵ HC=AH=x,BH=√33∵ BC=400米,x+x=400,∵ √33解得:x=600−200√3,即河宽为(600−200√3)米.23【答案】支架BF的长为1.0米.【解答】解:∵ BF⊥AB,∵ 在Rt△OAB中,∵ AB=2米,∠OAB=32∘,∵ OB=AB⋅tan∠OAB,=2⋅tan32∘≈2×0.62=1.24米,∵ BF=OB−OF=1.24−0.2=1.04≈1.0米,24【答案】坝底DC的宽为(19+3√3)m.【解答】.解:在Rt△ADF中,∠D=60∘,cot∠D=DFAF∴DF=AF⋅cot∠D=9×cot60∘=3√3.=9×√33在Rt△BEC中∵∠C=45∘.∴△BEC为等腰三角形.∴EC=BE=9.在矩形AFEB中,FE=AB=10.∴DC=DF+FE+EC=3√3+10+9 =(19+3√3).(m)25【答案】解:设CD=x米,∵ ∠CDE=60∘ , ∠ACB=90∘,在Rt△CED中,CE=DC⋅tan60∘=√3x,∴ AC=AE+CE=90+√3x,∵ ∠ABC=26∘,∴ AC=BC⋅tan26∘=0.5(x+300),90+√3x=0.5(x+300),≈48,解得x=240√3+12011∴ AC=90+48√3≈171.6(m),∴ AH=AC+CH≈171.6+1.8=173.4(m).答:立柱AH的长约为173.4m.【解答】解:设CD=x米,∵ ∠CDE=60∘ , ∠ACB=90∘,在Rt△CED中,CE=DC⋅tan60∘=√3x,∴ AC=AE+CE=90+√3x,∵ ∠ABC=26∘,∴ AC=BC⋅tan26∘=0.5(x+300),90+√3x=0.5(x+300),≈48,解得x=240√3+12011∴ AC=90+48√3≈171.6(m),∴ AH=AC+CH≈171.6+1.8=173.4(m).答:立柱AH的长约为173.4m.。
人教版九年级数学下册28.2: 解直角三角形及其应 用同步练习(附答案)
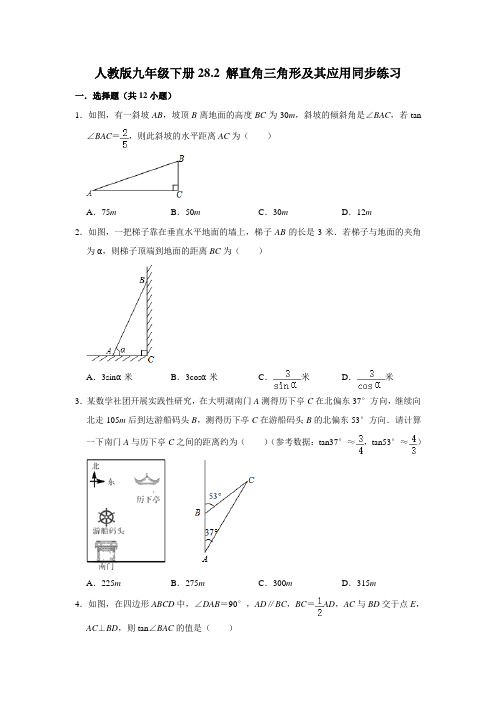
人教版九年级下册28.2 解直角三角形及其应用同步练习一.选择题(共12小题)1.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan ∠BAC=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m2.如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离BC为()A.3sinα米B.3cosα米C.米D.米3.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为()(参考数据:tan37°≈,tan53°≈)A.225m B.275m C.300m D.315m4.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是()A.B.C.D.5.如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为30°,则甲楼高度为()A.11米B.(36﹣15)米C.15米D.(36﹣10)米6.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是()A.10B.8C.4D.27.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为()A.B.C.D.8.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)()A.3.2米B.3.9米C.4.7米D.5.4米9.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是()A.30nmile B.60nmileC.120nmile D.(30+30)nmile10.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为()A.米B.米C.米D.米11.如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为()A.B.C.D.12.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为()(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)A.65.8米B.71.8米C.73.8米D.119.8米二.填空题(共7小题)13.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为米.(结果保留根号)14.如图,河的两岸a,b互相平行,点A,B,C是河岸b上的三点,点P是河岸a上的一个建筑物,某人在河岸b上的A处测得∠P AB=30°,在B处测得∠PBC=75°,若AB =80米,则河两岸之间的距离约为米.(≈1.73,结果精确到0.1米)15.某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车(填“超速”或“没有超速”)(参考数据:≈1.732)16.如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).17.如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为m.(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)18.如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是米(结果保留根号).19.如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为米.(精确到1米,参考数据:≈1.414,≈1.732)三.解答题(共3小题)20.小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:≈1.732)21.如图,学校教学楼上悬挂一块长为3m的标语牌,即CD=3m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2m,小明在E 处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由(图中点A,B,C,D,E,F,H在同一平面内)(参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)22.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上,求旗杆AB的高度.(结果精确到0.1m,参考数据:≈1.41,=1.73)参考答案一.选择题(共12小题)1.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan ∠BAC=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m【解答】解:∵∠BCA=90°,tan∠BAC=,BC=30m,∴tan∠BAC=,解得,AC=75,故选:A.2.如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离BC为()A.3sinα米B.3cosα米C.米D.米【解答】解:由题意可得:sinα==,故BC=3sinα(m).故选:A.3.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为()(参考数据:tan37°≈,tan53°≈)A.225m B.275m C.300m D.315m【解答】解:如图,作CE⊥BA于E.设EC=xm,BE=ym.在Rt△ECB中,tan53°=,即=,在Rt△AEC中,tan37°=,即=,解得x=180,y=135,∴AC===300(m),故选:C.4.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是()A.B.C.D.【解答】解:∵AD∥BC,∠DAB=90°,∴∠ABC=180°﹣∠DAB=90°,∠BAC+∠EAD=90°,∵AC⊥BD,∴∠AED=90°,∴∠ADB+∠EAD=90°,∴∠BAC=∠ADB,∴△ABC∽△DAB,∴=,∵BC=AD,∴AD=2BC,∴AB2=BC×AD=BC×2BC=2BC2,∴AB=BC,在Rt△ABC中,tan∠BAC===;故选:C.5.如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为30°,则甲楼高度为()A.11米B.(36﹣15)米C.15米D.(36﹣10)米【解答】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=10(米),∴AC=ED=BD﹣BE=(36﹣10)(米).∴甲楼高为(36﹣10)米.故选:D.6.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是()A.10B.8C.4D.2【解答】解:∵∠C=90°,cos∠BDC=,设CD=5x,BD=7x,∴BC=2x,∵AB的垂直平分线EF交AC于点D,∴AD=BD=7x,∴AC=12x,∵AC=12,∴x=1,∴BC=2;故选:D.7.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为()A.B.C.D.【解答】解:如图,过C作CD⊥AB于D,则∠ADC=90°,∴AC===5.∴sin∠BAC==.故选:D.8.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)()A.3.2米B.3.9米C.4.7米D.5.4米【解答】解:过点O作OE⊥AC于点F,延长BD交OE于点F,设DF=x,∵tan65°=,∴OF=x tan65°,∴BF=3+x,∵tan35°=,∴OF=(3+x)tan35°,∴2.1x=0.7(3+x),∴x=1.5,∴OF=1.5×2.1=3.15,∴OE=3.15+1.5=4.65,故选:C.9.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是()A.30nmile B.60nmileC.120nmile D.(30+30)nmile【解答】解:过C作CD⊥AB于D点,∴∠ACD=30°,∠BCD=45°,AC=60.在Rt△ACD中,cos∠ACD=,∴CD=AC•cos∠ACD=60×=30.在Rt△DCB中,∵∠BCD=∠B=45°,∴CD=BD=30,∴AB=AD+BD=30+30.答:此时轮船所在的B处与灯塔P的距离是(30+30)nmile.故选:D.10.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为()A.米B.米C.米D.米【解答】解:作AD⊥BC于点D,则BD=0.3=,∵cosα=,∴cosα=,解得,AB=米,故选:B.11.如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为()A.B.C.D.【解答】解:过点A作AD⊥BC,垂足为D,如图所示.在Rt△ACD中,CD=CA•cos C=1,∴AD==;在Rt△ABD中,BD=CB﹣CD=3,AD=,∴AB==2,∴sin B==.故选:D.12.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为()(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)A.65.8米B.71.8米C.73.8米D.119.8米【解答】解:过点E作EM⊥AB与点M,延长ED交BC于G,∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=52米,∴设DG=x,则CG=2.4x.在Rt△CDG中,∵DG2+CG2=DC2,即x2+(2.4x)2=522,解得x=20,∴DG=20米,CG=48米,∴EG=20+0.8=20.8米,BG=52+48=100米.∵EM⊥AB,AB⊥BG,EG⊥BG,∴四边形EGBM是矩形,∴EM=BG=100米,BM=EG=20.8米.在Rt△AEM中,∵∠AEM=27°,∴AM=EM•tan27°≈100×0.51=51米,∴AB=AM+BM=51+20.8=71.8米.故选:B.二.填空题(共7小题)13.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为4﹣4米.(结果保留根号)【解答】解:在Rt△CMB中,∵∠CMB=90°,MB=AM+AB=12米,∠MBC=30°,∴CM=MB•tan30°=12×=4,在Rt△ADM中,∵∠AMD=90°,∠MAD=45°,∴∠MAD=∠MDA=45°,∴MD=AM=4米,∴CD=CM﹣DM=(4﹣4)米,故答案为:4﹣4.14.如图,河的两岸a,b互相平行,点A,B,C是河岸b上的三点,点P是河岸a上的一个建筑物,某人在河岸b上的A处测得∠P AB=30°,在B处测得∠PBC=75°,若AB =80米,则河两岸之间的距离约为54.6米.(≈1.73,结果精确到0.1米)【解答】解:过点A作AE⊥a于点E,过点B作BD⊥P A于点D,∵∠PBC=75°,∠P AB=30°,∴∠DPB=45°,∵AB=80,∴BD=40,AD=40,∴PD=DB=40,∴AP=AD+PD=40+40,∵a∥b,∴∠EP A=∠P AB=30°,∴AE=AP=20+20≈54.6,故答案为:54.615.某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车没有超速(填“超速”或“没有超速”)(参考数据:≈1.732)【解答】解:作AD⊥直线l于D,在Rt△ADB中,∠ABD=45°,∴BD=AD=100,在Rt△ADB中,tan∠ACD=,则CD==100≈173.2,∴BC=173.2﹣100=73.2(米),小汽车的速度为:0.0732÷=52.704(千米/小时),∵52.704千米/小时<速60千米/小时,∴小汽车没有超速,故答案为:没有超速.16.如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为3m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).【解答】解:在Rt△BCD中,tan∠BDC=,则BC=CD•tan∠BDC=10,在Rt△ACD中,tan∠ADC=,则AC=CD•tan∠ADC≈10×1.33=13.3,∴AB=AC﹣BC=3.3≈3(m),故答案为:3.17.如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为262m.(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)【解答】解:作AE⊥BC于E,则四边形ADCE为矩形,∴EC=AD=62,在Rt△AEC中,tan∠EAC=,则AE=≈=200,在Rt△AEB中,∠BAE=45°,∴BE=AE=200,∴BC=200+62=262(m),则该建筑的高度BC为262m,故答案为:262.18.如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是(15+15)米(结果保留根号).【解答】解:过点B作BE⊥AB于点E,在Rt△BEC中,∠CBE=45°,BE=15;可得CE=BE×tan45°=15米.在Rt△ABE中,∠ABE=30°,BE=15,可得AE=BE×tan30°=15米.故教学楼AC的高度是AC=15米.答:教学楼AC的高度是(15)米.19.如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为566米.(精确到1米,参考数据:≈1.414,≈1.732)【解答】解:如图,设线段AB交y轴于C,在直角△OAC中,∠ACO=∠CAO=45°,则AC=OC.∵OA=400米,∴OC=OA•cos45°=400×=200(米).∵在直角△OBC中,∠COB=60°,OC=200米,∴OB===400≈566(米)故答案是:566.三.解答题(共3小题)20.小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:≈1.732)【解答】解:作DC⊥EP交EP的延长线于C,作DF⊥ME于F,作PH⊥DF于H,则DC=PH=FE,DH=CP,HF=PE,设DC=3x,∵tanθ=,∴CP=4x,由勾股定理得,PD2=DC2+CP2,即252=(3x)2+(4x)2,解得,x=5,则DC=3x=15,CP=4x=20,∴DH=CP=20,PH=FE=DC=15,设MF=ym,则ME=(y+15)m,在Rt△MDF中,tan∠MDF=,则DF==y,在Rt△MPE中,tan∠MPE=,则PE==(y+15),∵DH=DF﹣HF,∴y﹣(y+15)=20,解得,y=7.5+10,∴ME=MF+FE=7.5+10+15≈39.8,答:古塔的高度ME约为39.8m.21.如图,学校教学楼上悬挂一块长为3m的标语牌,即CD=3m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2m,小明在E 处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由(图中点A,B,C,D,E,F,H在同一平面内)(参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)【解答】解:能,理由如下:延长EF交CH于N,则∠CNF=90°,∵∠CFN=45°,∴CN=NF,设DN=xm,则NF=CN=(x+3)m,∴EN=5+(x+3)=x+8,在Rt△DEN中,tan∠DEN=,则DN=EN•tan∠DEN,∴x≈0.6(x+8),解得,x=12,则DH=DN+NH=12+1.2=13.2(m),答:点D到地面的距离DH的长约为13.2m.22.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上,求旗杆AB的高度.(结果精确到0.1m,参考数据:≈1.41,=1.73)【解答】解:过点C作CE⊥AB于点E,∵CD=2,tan∠CMD=,∴MD=6,设BM=x,∴BD=x+6,∵∠AMB=60°,∴∠BAM=30°,∴AB=x,已知四边形CDBE是矩形,∴BE=CD=2,CE=BD=x+6,∴AE=x﹣2,在Rt△ACE中,∵tan30°=,∴=,解得:x=3+,∴AB=x=3+3≈8.2m。
人教版初中数学九年级下册 第二十八章《28.2解直角三角形及其应用》同步练习题(含答案)

人教版初中数学九年级下册 第二十八章《28.2解直角三角形及其应用》同步练习题(含答案)1 / 7 《28.2解直角三角形及其应用》同步练习题一、选择题(每小题只有一个正确答案)1.在△ABC 中,∠C=90°,∠BAC=30°,AD 是中线,则tan ∠CDA 的值为( )A. 3B. 2C.D.2.已知在Rt △ABC 中,∠C =90°,sin A = ,AC = ,那么BC 的值为( )A. 2B. 4C.D. 63.3.如图,一个斜坡长130m ,坡顶离水平地面的距离为50m ,那么这个斜坡的坡度为( )A. 512B. 1213C. 513D. 13124.如图,王强同学在甲楼楼顶A 处测得对面乙楼楼顶D 处的仰角为30°,在甲楼楼底B 处测得乙楼楼顶D 处的仰角为45°,已知甲楼高26米,则乙楼的高度为( ≈1.7)( )A. 61.0米B. 61.1米C. 61.2米D. 62.1米5.5.根据所给条件解直角三角形,结果不能确定的是( )①已知一直角边及其对角 ②已知两锐角 ③已知斜边和一锐角 ④已知一直角边和一斜边A. ①②④B. ②③C. ②④D. 只有②6.已知一个等腰三角形腰上的高等于底边的一半,那么腰与底边的比是( )A. 1:B. :1C. 1:D. :1 7.如图,在菱形ABCD 中,DE⊥AB,cosA = ,AE =3,则tan∠DBE 的值是( )A. B. 2 C.D.二、填空题8.在 △ 中, , , ,则 ______ .9.如图,在Rt △ABC 中,∠ACB=90°,AC=8,BC=6,将△ABC 沿BE 折叠,使直角顶点C 落在斜边上的点D 处,则sin ∠CBE 的值为_____.10.一船向东航行,上午8时到达B 处,看到有一灯塔在它的南偏东60°距离为72海里的A 处,上午10时到达C 处,看到灯塔在它的正南方向,则这艘船航行的速度为_____.11.△ABC 中∠A=30°,tanB= ,AC= ,则AB=_______.12.如图,在四边形ABCD 中,对角线AC 、BD 交于点E ,点E 为BD 的中点, 11805tan 2BAC BDC AB CD ACB ∠+∠===∠=,,,则AD = ______ .三、解答题13.如图,在Rt △ABC 中,∠C =90°,∠ABC =75°,点D 在AC上,DC =6,∠DBC =60°,求AD 的长.人教版初中数学九年级下册第二十八章《28.2解直角三角形及其应用》同步练习题(含答案)14.海中有一灯塔C,它的周围12海里有暗礁,渔船跟踪鱼群由西向东航行在A处测得灯塔C在北偏东60°,航行20海里后到达B点,这时测得灯塔C在北偏东30°,如果渔船不改变航向,继续向东航行,有没有触礁的危险?15.如图所示,在四边形ABCD中,∠B=∠D=90°,AB=BC=15千米,CD=3千米.求四边形ABCD的周长和面积(结果保留整数,参考数据:≈1.41,≈1.73,≈2.45).3 / 7人教版初中数学九年级下册 第二十八章《28.2解直角三角形及其应用》同步练习题(含答案)1 / 7参考答案1.B2.A3.A4.B5.D6.A7.B8.60°9.10.18 海里/时11.512.【解析】过B 作BM ⊥CA ,交CA 的延长线于M ,过D 作DN ⊥CA ,垂足为N ,∴∠BME=∠DN90°,∵点E 为BD 的中点,∴BE=DE ,∵∠BEM=∠DEN ,∴△BME ≌△DNE ,∴BM=DN ,∵AB=CD ,∴Rt △ABM ≌Rt △DCN ,∴∠BAM=∠DCN ,∵∠BAC+∠BDC=180°,∠BAC+∠BAM=180°,∴∠BDC=∠BAM ,∴∠BDC=∠DCN ,∴DE=CE ,∴BE=CE=DE ,∴∠DBC=∠ECB ,∴∠DBC+∠BDC=∠ECB+∠DCN ,∴△BCD 是直角三角形,∵tan ∠ACB=12, ∴tan ∠DBC=12, ∵DC=5,∴BC=10,在△BMC 中,设BM=x ,则CM=2x ,由勾股定理得:x 2+(2x )2=102,,∴,由勾股定理得:==∴∴在△ADN中,==.故答案是:.13.解析:在Rt△DBC中,,,,,,∴∠ABD=∠A,14.继续向东航行,没有触礁的危险.解:如图,过C作CD⊥AD于点D.在Rt△CBD中,∠CBD=60°,在Rt△ADC 中,∠CAB=30°,则∠ACB=30°,∴BC=AB=20海里,∠CBD=60°,∴CD=BC•sin∠CBD=BC•sin60°=BC,故CD=(海里).∵>12,∴继续向东航行,没有触礁的危险.15.周长55千米,面积157平方千米.解析:连接AC,人教版初中数学九年级下册第二十八章《28.2解直角三角形及其应用》同步练习题(含答案)∵AB=BC=15千米,∠B=90°,∴∠BAC=∠ACB=45°,AC=15千米.又∵∠D=90°,∴AD===12(千米).∴周长=AB+BC+CD+DA=15+15+3+12≈30+4.23+20.76≈55(千米),面积=S△ABC+S△ACD≈157(平方千米).3 / 7。
2021-2022学年人教版九年级数学下册《28-2解直角三角形及其应用》同步练习题(附答案)

2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》同步练习题(附答案)1.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.(1)求AC的长;(2)求tan∠FBD的值.2.如图,楼顶上有一个广告牌AB,从与楼BC相距15m的D处观测广告牌顶部A的仰角为37°,观测广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留小数点后一位,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)3.如图,一艘货船在灯塔C的正南方向,距离灯塔257海里的A处遇险,发出求救信号.一艘救生船位于灯塔C的南偏东40°方向上,同时位于A处的北偏东60°方向上的B处,救生船接到求救信号后,立即前往救援.求AB的长.(结果取整数)参考数据:tan40°≈0.84,取1.73.4.图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE 平行,踏板CD长为1.5m,CD与地面DE的夹角∠CDE=15°,支架AC长为1m,∠ACD=75°,求跑步机手柄AB所在直线与地面DE之间的距离.(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.73)5.一座吊桥的钢索立柱AD两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索AB的长度.他们测得∠ABD为30°,由于B、D两点间的距离不易测得,通过探究和测量,发现∠ACD恰好为45°,点B与点C之间的距离约为16m.已知B、C、D共线,AD⊥BD.求钢索AB的长度.(结果保留根号)6.2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为30°的河床斜坡边,斜坡BC长为48米,在点D处测得桥墩最高点A的仰角为35°,CD平行于水平线BM,CD长为16米,求桥墩AB 的高(结果保留1位小数).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,≈1.73)7.今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为45°,站在同一队列B处的小刚测得国旗C处的仰角为23°,已知小明目高AE=1.4米,距旗杆CG的距离为15.8米,小刚目高BF=1.8米,距小明24.2米,求国旗的宽度CD 是多少米?(最后结果保留一位小数)(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245)8.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.(1)求∠ABC的度数;(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)9.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)10.如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:方案设计:如图2,宝塔CD垂直于地面,在地面上选取A,B两处分别测得∠CAD和∠CBD的度数(A,D,B在同一条直线上).数据收集:通过实地测量:地面上A,B两点的距离为58m,∠CAD=42°,∠CBD=58°.问题解决:求宝塔CD的高度(结果保留一位小数).参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60.根据上述方案及数据,请你完成求解过程.11.“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从A处测得该建筑物顶端C的俯角为24°,继续向该建筑物方向水平飞行20米到达B处,测得顶端C的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:sin24°≈,cos24°≈,tan24°≈)12.我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,且AB=AC,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点D'的位置,且A,B,D′三点共线,AD′=40cm,B为AD′中点.当∠BAC=140°时,伞完全张开.(1)求AB的长.(2)当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)13.拓展小组研制的智能操作机器人,如图1,水平操作台为l,底座AB固定,高AB为50cm,连杆BC长度为70cm,手臂CD长度为60cm.点B,C是转动点,且AB,BC与CD始终在同一平面内.(1)转动连杆BC,手臂CD,使∠ABC=143°,CD∥l,如图2,求手臂端点D离操作台l的高度DE的长(精确到1cm,参考数据:sin53°≈0.8,cos53°≈0.6).(2)物品在操作台l上,距离底座A端110cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.14.资阳市为实现5G网络全覆盖,2020﹣2025年拟建设5G基站七千个.如图,在坡度为i=1:2.4的斜坡CB上有一建成的基站塔AB,基站塔与水平地面垂直,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A、B、C、D均在同一平面内)(参考数据:sin53°≈,cos53°≈,tan53°≈)(1)求D处的竖直高度;(2)求基站塔AB的高.15.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走2米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1:3(点E、C、B在同一水平线上).(1)求王刚同学从点C到点D的过程中上升的高度;(2)求大树AB的高度(结果保留根号).16.越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角∠MBC=33°,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角∠MEC=45°(点A,D与N在一条直线上),求电池板离地面的高度MN的长.(结果精确到1米;参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)17.学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形AEFD为矩形,点B、C分别在EF、DF上,∠ABC=90°,∠BAD=53°,AB=10cm,BC=6cm.求零件的截面面积.参考数据:sin53°≈0.80,cos53°≈0.60.18.我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿AB摆成如图1所示.已知AB=4.8m,鱼竿尾端A离岸边0.4m,即AD=0.4m.海面与地面AD 平行且相距1.2m,即DH=1.2m.(1)如图1,在无鱼上钩时,海面上方的鱼线BC与海面HC的夹角∠BCH=37°,海面下方的鱼线CO与海面HC垂直,鱼竿AB与地面AD的夹角∠BAD=22°.求点O到岸边DH的距离;(2)如图2,在有鱼上钩时,鱼竿与地面的夹角∠BAD=53°,此时鱼线被拉直,鱼线BO=5.46m,点O恰好位于海面.求点O到岸边DH的距离.(参考数据:sin37°=cos53°≈,cos37°=sin53°≈,tan37°≈,sin22°≈,cos22°≈,tan22°≈)19.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.(1)求∠C的度数;(2)求两棵银杏树B、C之间的距离(结果保留根号).20.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D 处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据tan37°≈0.75,tan53°≈1.33,≈1.73)21.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.(1)求观测点B与C点之间的距离;(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.参考答案1.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,∴AB=10,在Rt△ACB中,由勾股定理得,AC===6,即AC的长为6;(2)如图,连接CF,过F点作BD的垂线,垂足E,∵BF为AD边上的中线,即F为AD的中点,∴CF=AD=FD,在Rt△ACD中,由勾股定理得,AD===2,∵三角形CFD为等腰三角形,FE⊥CD,∴CE=CD=2,在Rt△EFC中,EF===3,∴tan∠FBD===.解法二:∵BF为AD边上的中线,∴F是AD中点,∵FE⊥BD,AC⊥BD,∴FE∥AC,∴FE是△ACD的中位线,∴FE=AC=3,CE=CD=2,∴在Rt△BFE中,tan∠FBD===.2.解:在Rt△BCD中,BC=DC•tan30°=15×≈5×1.73=8.65(m),在Rt△ACD中,AC=DC•tan37°≈15×0.75=11.25(m),∴AB=AC﹣BC=11.25﹣8.65=2.6(m).答:广告牌AB的高度为2.6m.3.解:如图,过点B作BH⊥AC,垂足为H,由题意得,∠BAC=60°,∠BCA=40°,AC=257海里,在Rt△ABH中,∵tan∠BAH=,cos∠BAH=,∴BH=AH•tan60°=AH,AB==2AH,在Rt△BCH中,∵tan∠BCH=,∴CH==(海里),又∵CA=CH+AH,∴257=+AH,所以AH=(海里),∴AB=≈=168(海里),答:AB的长约为168海里.4.解:如图,过C点作FG⊥AB于F,交DE于G.∵CD与地面DE的夹角∠CDE为15°,∠ACD为75°,∴∠ACF=∠FCD﹣∠ACD=∠CGD+∠CDE﹣∠ACD=90°+15°﹣75°=30°,∴∠CAF=60°,在Rt△ACF中,CF=AC•sin∠CAF=m,在Rt△CDG中,CG=CD•sin∠CDE=1.5•sin15°m,∴FG=FC+CG=+1.5•sin15°≈1.3m.故跑步机手柄AB所在直线与地面DE之间的距离约为1.3m.5.解:在△ADC中,设AD=xm,∵AD⊥BD,∠ACD=45°,∴CD=AD=xm,在△ADB中,AD⊥BD,∠ABD=30°,∴AD=BD•tan30°,即x=(16+x)m,解得:x=(8+8)m,∴AB=2AD=2×(8)=(16)m,∴钢索AB的长度为(16)m.6.解:过点C作CE⊥BM于点E,过点D作DF⊥BM于点F,延长DC交AB于点G,在Rt△CEB中,∠CBE=30°,BC=48米,∴CE=BC•sin30°=×48=24(米),BE=BC•cos30°=48×≈24×1.73=41.52(米),∴DG=BF=BE+EF=BE+CD=41.52+16≈41.52+27.68=69.2(米),在Rt△ADG中,AG=DG•tan∠ADG=69.2×tan35°≈69.2×0.70=48.44(米),∴AB=AG+BG=AG+CE=48.44+24=72.44≈72.4(米),答:桥墩AB的高约为72.4米.7.解:作EM⊥CG于M,FN⊥CG于N,由题意得GB=AG+AB=15.8+24.2=40(米),则FN=GB=40米,在Rt△EDM中,∠DEM=45°,∴DM=EM=15.8米,∵MG=AE=1.4米,∴DG=DM+MG=15.8+1.4=17.2(米),∵NG=FB=1.8米,∴DN=17.2﹣1.8=15.4(米),在Rt△CNF中,∠CFN=23°,∵tan∠CFN=≈0.4245,∴CN=0.4245×40≈17.0(米),∴CD=CN﹣DN=17.0﹣15.4=1.6(米)故国旗的宽度CD约为1.6米.8.解:(1)过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK ⊥DE,垂足为K,∵MP=25.3cm,BA=HP=8.5cm,∴MH=MP﹣HP=25.3﹣8.5=16.8(cm),在Rt△BMH中,cos∠BMH===0.4,∴∠BMH=66.4°,∵AB∥MP,∴∠BMH+∠ABC=180°,∴∠ABC=180°﹣66.4°=113.6°;(2)∵∠BMN=68.6°,∠BMH=66.4°,∴∠NMI=180°﹣∠BMN﹣∠BMH=180°﹣68.6°﹣66.4°=45°,∵MN=28cm,∴cos45°==,∴MI≈19.80cm,∵KI=50cm,∴PK=KI﹣MI﹣MP=50﹣19.80﹣25.3=4.90≈4.9(cm),∴此时枪身端点A与小红额头的距离是在规定范围内.9.解:∵CM=3m,OC=5m,∴OM==4(m),∵∠CMO=∠BDO=90°,∠COM=∠BOD,∴△COM∽△BOD,∴,即,∴BD==2.25(m),∴tan∠AOD=tan70°=,即≈2.75,解得:AB=6m,∴汽车从A处前行约6米才能发现C处的儿童.10.解:设CD=xm,在Rt△ACD中,AD=,在Rt△BCD中,BD=,∵AD+BD=AB,∴,解得,x≈33.4.答:宝塔的高度约为33.4m.11.解:过C作CF⊥AD于F,如图所示:则AF=CE,由题意得:AB=20米,∠AEC=90°,∠CAE=24°,∠CBE=45°,∴△BCE是等腰直角三角形,∴BE=CE,设BE=CE=x米,则AF=x米,在Rt△ACE中,tan∠CAE==tan24°≈,∴AE=x米,∵AE﹣BE=AB,∴x﹣x=20,解得:x≈16.4,∴AF≈16.4(米),∴DF=AD﹣AF=60﹣16.4=43.6(米),即这栋建筑物的高度为43.6米.12.解:(1)∵B为AD′中点,∴AB=AD′,∵AD′=40cm,∴AB=20cm;(2)如图,过点B作BE⊥AD于点E,∵AB=BD,∴AD=2AE,∵AP平分∠BAC,∠BAC=140°,∴∠BAE=BAC=70°,在Rt△ABE中,AB=20cm∴AE=AB•cos70°≈20×0.34=6.8(cm),∴AD=2AE=13.6(cm),∵AD′=40cm,∴40﹣13.6=26.4(cm).∴伞圈D沿着伞柄向下滑动的距离为26.4cm.13.解:(1)过点C作CP⊥AE于点P,过点B作BQ⊥CP于点Q,如图:∵∠ABC=143°,∴∠CBQ=53°,在Rt△BCQ中,CQ=BC•sin53°≈70×0.8=56cm,∵CD∥l,∴DE=CP=CQ+PQ=56+50=106cm.(2)手臂端点D能碰到点M,理由:由题意得,当B,C,D共线时,手臂端点D能碰到最远距离,如图:BD=60+70=130cm,AB=50cm,在Rt△ABD中,AB²+AD²=BD²,∴AD=120cm>110cm.∴手臂端点D能碰到点M.14.解:(1)如图,延长AB与水平线交于F,过D作DM⊥CF,M为垂足,过D作DE⊥AF,E为垂足,连接AC,AD,∵斜坡CB的坡度为i=1:2.4,∴=,即=,设DM=5k米,则CM=12k米,在Rt△CDM中,CD=13米,由勾股定理得,CM2+DM2=CD2,即(5k)2+(12k)2=132,解得k=1,∴DM=5(米),CM=12(米),答:D处的竖直高度为5米;(2)斜坡CB的坡度为i=1:2.4,设DE=12a米,则BE=5a米,又∵∠ACF=45°,∴AF=CF=(12+12a)米,∴AE=AF﹣EF=12+12a﹣5=(7+12a)米,在Rt△ADE中,DE=12a米,AE=(7+12a)米,∵tan∠ADE=tan53°≈,∴=,解得a=,∴DE=12a=21(米),AE=7+12a=28(米),BE=5a=(米),∴AB=AE﹣BE=28﹣=(米),答:基站塔AB的高为米.15.解:(1)过点D作DH⊥CE于点H,由题意知CD=2米,∵斜坡CF的坡比为i=1:3,∴,设DH=x米,CH=3x米,∵DH2+CH2=DC2,∴,∴x=2,∴DH=2(米),CH=6(米),答:王刚同学从点C到点D的过程中上升的高度为2米;(2)过点D作DG⊥AB于点G,设BC=a米,∵∠DHB=∠DGB=∠ABC=90°,∴四边形DHBG为矩形,∴DH=BG=2米,DG=BH=(a+6)米,∵∠ACB=45°,∴BC=AB=a(米),∴AG=(a﹣2)米,∵∠ADG=30°,∴,∴,∴a=6+4,∴AB=(6+4)(米).答:大树AB的高度是(6+4)米.16.解:延长BC交MN于点H,AD=BE=3.5,设MH=x米,∵∠MEC=45°,∴EH=x米,在Rt△MHB中,tan∠MBH==≈0.65,解得x=6.5,则MN=1.6+6.5=8.1≈8(米),∴电池板离地面的高度MN的长约为8米.17.解:如图,∵四边形AEFD为矩形,∠BAD=53°,∴AD∥EF,∠E=∠F=90°,∴∠BAD=∠EBA=53°,在Rt△ABE中,∠E=90°,AB=10cm,∠EBA=53°,∴sin∠EBA=≈0.80,cos∠EBA=≈0.60,∴AE=8cm,BE=6cm,∵∠ABC=90°,∴∠FBC=90°﹣∠EBA=37°,∴∠BCF=90°﹣∠FBC=53°,在Rt△BCF中,∠F=90°,BC=6cm,∴sin∠BCF=≈0.80,cos∠BCF=≈0.60,∴BF=4.8cm,FC=3.6cm,∴EF=6+4.8=10.8cm,∴S四边形EFDA=AE•EF=8×10.8=86.4(cm2),S△ABE==×8×6=24(cm2),S△BCF=•BF•CF=×4.8×3.6=8.64(cm2),∴截面的面积=S四边形EFDA﹣S△ABE﹣S△BCF=86.4﹣24﹣8.64=53.76(cm2).18.解:(1)过点B作BF⊥CH,垂足为F,延长AD交BF于E,垂足为E,则AE⊥BF,由cos∠BAE=,∴cos22°=,∴,即AE=4.5m,∴DE=AE﹣AD=4.5﹣0.4=4.1(m),由sin∠BAE=,∴,∴,即BE=1.8m,∴BF=BE+EF=1.8+1.2=3(m),又,∴,即CF=4m,∴CH=CF+HF=CF+DE=4+4.1=8.1(m),即点O到岸边DH的距离为8.1m;(2)过点B作BN⊥OH,垂足为N,延长AD交BN于点M,垂足为M,由cos∠BAM=,∴,∴,即AM=2.88m,∴DM=AM﹣AD=2.88﹣0.4=2.48(m),由sin∠BAM=,∴,∴,即BM=3.84m,∴BN=BM+MN=3.84+1.2=5.04(m),∴=(m),∴OH=ON+HN=ON+DM=4.58(m),即点O到岸边的距离为4.58m.19.解:(1)设AD与BC交于点F,由题意得BE∥AD,∵BE∥AD且∠EBF=60°,∴∠BF A=∠EBF=60°,∵∠BF A=∠C+∠CAD且∠CAD=30°,∴∠C=∠BF A﹣∠CAD=30°;(2)过点B作BG⊥AD于G.∵BG⊥AD,∴∠AGB=∠BGD=90°,在Rt△AGB中,AB=20米,∠BAG=45°,AG=BG=20×sin45°=(米),在Rt△BGF中,∠BFG=60°,∴BF===(米),FG===(米),∵∠C=∠CAD=30°,∴CF=AF=AG+FG=(10+)(米),∴BC=BF+CF=(10+10)米,答:两棵银杏树B、C之间的距离为(10+10)米.20.解:由题意可知AB=24米,∠BDA=53°,∴tan∠BDA==≈1.33,∴AD=≈18.05(米).∵tan∠CAD=tan30°===,∴CD=18.05×≈10.4(米).故办公楼的高度约为10.4米.21.解:(1)如图,过点C作CE⊥AB于点E,根据题意可知:∠ACE=∠CAE=45°,AC=25海里,∴AE=CE=25(海里),∵∠CBE=30°,∴BE=25(海里),∴BC=2CE=50(海里).答:观测点B与C点之间的距离为50海里;(2)如图,作CF⊥DB于点F,∵CF⊥DB,FB⊥EB,CE⊥AB,∴四边形CEBF是矩形,∴FB=CE=25(海里),CF=BE=25(海里),∴DF=BD+BF=30+25=55(海里),在Rt△DCF中,根据勾股定理,得CD===70(海里),∴70÷42=(小时).答:救援船到达C点需要的最少时间是小时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形及其应用同步练习
一、选择题
1、如图,在等腰△ABC中,∠C=90°,AC=6,D是AC上一点,若,则AD的长为()
A. B.2 C.1 D.
2、如图,在平地上种植树时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.5的山坡上种植树,也要求株距为4m,那么相邻两树间的坡面距离约为()
A.4.5m B.4.6m C.6m D.8m
3、在Rt△ABC中,∠C=90°,AC=,AB=2,则∠A等于( )
A.30° B.45° C.60° D.90°
4、在Rt△ABC中,∠C=90°,∠A=45°,点D在AC上,∠BDC=60°,若AD=1,则BD等于( )
A. B. C. D.
5、已知△ABC中,AD是高,AD=2,DB=2,CD=,则∠BAC=( )
A.105° B.15° C.105°或15°D.60°
6、在Rt△ABC中,∠C=90°,,则的值为()
A.2 B.C. D.
7、如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度()
A.增大1.5米B.减小1.5米
C.增大3.5米D.减小3.5米
8、如图,为了测量小河的宽度,小明先在河岸边任意取一点A,再在河岸另一边取两点B、C,测得∠ABC=45°,∠ACB=30°,量得BC为20米,根据以上数据,请帮小明算出河的宽度为结果保留根号()
A 10
B 20
C D
9、如图,P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO等于()
A. B. C. D.
10、如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60度500m处,那么水塔所在的位置到公路的距离AB是()
A.250mB.mC.mD.m
11、如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜, 光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD, 且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是()
A. 6米
B. 8米
C. 18米
D.24米
12、直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则
的值是()
A. B. C. D.
二、填空题
13、一个人沿坡度比为1:2的斜坡向上走了10m,那么它的垂直高度上升了m.
14、在Rt△ABC中,∠C=90°,3a=,则sinA= .
15、如下图,在△ABD中,∠D=90°,AC是角平分线,CD=2cm,则△ABC的AB边上的高等于 cm。
16、如图,张华同学在学校某建筑物的点处测得旗杆顶部点的仰角为,旗杆底部点的俯角为.若旗杆底部点到建筑物的水平距离米,旗杆台阶高1米,则旗杆顶点离地面的高度为米(结果保留根号).
17、如图,两根高分别为4米和7米的竹竿相距6米一根绳子拉直系在两根竹竿的顶端。
则这根绳子长为米.
18、如图,小明在楼顶处测得对面大楼楼顶点处的仰角为52°,楼底点处的俯角为13°.若两座楼与
相距60米,则楼的高度约为米.(结果保留三个有效数字)(,,,,,)
三、简答题
19、在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都
为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:.)
20、如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°°和60°,且A、B、E三点在一条直线上,若BE=15米,求这块广告牌的高度.(取≈1.73,计算结果保留整数)
21、如下图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C 处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(结果精确到1米).
22、如图,一游人由山脚沿坡角为的山坡行走600m,到达一个景点,再由沿山坡行走200m到达山顶,若在山顶处观测到景点的俯角为,求山高。
23、如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60º,沿山坡向上走到P处再测得点C的仰角为45º,已知PA=100m,山坡的坡度为l∶2且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点 P的铅直高度(结果保留根号形式)。
24、如图,已知反比例函数的图象经过点A(),过点A作AB⊥轴于点B,且△AOB的面积为
.
(1)求的值;
(2)若一次函数的图象经过点A,且与轴相交于点C,求∠AC0的度数.
参考答案
一、选择题
1、B;
2、A;
3、A;
4、A;
5、C;
6、C;
7、D;
8、D;
9、B;10、A;11、B;12、C;
二、填空题
13、2
14、
15、2
16、
17、
18、90.6
三、简答题
19、解:在Rt△BCD中,,∴.
在Rt△ACD中,,
∴.
∴.∴.
∴(米)
∴条幅顶端D点距离地面的高度为(米).20、解:∵AB=8,BE=15,∴AE=23,在Rt△AED中,∠DAE=45°∴DE=AE=23.
在Rt△BEC中,∠CBE=60°
∴CE=BE・tan60°=,
∴CD=CE-DE=-23≈2.95≈3
即这块广告牌的高度约为3米。
21、约138米
22、解:过点C作CE∥AD,过点B作BF⊥CD于F,BG⊥AD于G
由题意可知,∠1=45°,∠3=30°
∵BF⊥CD,CD⊥AD,∴BF∥AD
又∵CE∥AD,∴CE∥BF ∴∠2=∠1=45°
在Rt△CBF中,
在Rt△ABG中,
∵BG⊥AD,CD⊥AD,BF⊥CD,∴四边形BFDG是矩形,∴FD=BG=300m ∴CD=CF+FD=()m
答:山高CD为()m。
23、解:如图,过P作PE⊥AB于E, PD⊥OC于D,过A作AF⊥DP于F
∵山坡的坡度为1∶2
∴PE∶AE=1∶2 设PE=K,则 AE=2K
在Rt△APE中,PE2+AE2=AP2
∴
∴
∴OD=AF=PE=
AE=PF=
在Rt△CPD中,∵∠CPD=45º,∴CD=DP
设OA=DF=∴
∴
在Rt△AOC中,
∴,解得
∴
24、解:(1)∵ k<0,∴点A()在第二象限,
∴∵
即∴∴.
把代入中,得.
(2) 把代入中,
得,∴,∴.
令,∴.∴.
∴在
∴∠ACO=30°
11。
