高中化学 阿伏加德罗定律及5个推论
阿伏伽德罗定律及其推论ppt课件.ppt
1．下列说法中正确的是 [
]
A．相同状况下，
气体的摩尔体积约等于22.4L/mol
B．标准状况下，22.4L的任何气体中都
约含有6.02×1023个分子
C．0℃，101kPa条件下，5.6LNH3中约 含有6.02×1023个原子
D．100℃、101kPa条件下，
22.4L水蒸气的质量等于18g
2．同温同压下，物质的量为0.2mol的 N2O（气）和NO2（气），它们的 [ CD ] A．质量相同，体积不同 B．体积相同，分子数不同 C．分子数相同，质量不同 D．体积相同，原子数相同
m
M
n X NA
N
XM
NA
ρ Vm X
ρX
Vm
V
1．利用气体摩尔体积，进行质量与体积 间的相互计算
【例题1】8.5g氨在标准状况时体积是多少升？ 解:氨的式量是17，氨的摩尔质量是17g／mol
n(NH3)=
m(NH3) M(NH3) =
8.5g 17g/mol = 0.5mol
V(NH3)=22.4L／mol×0.5mol=11.2L
等于摩尔质量比。
练习：
ρ1∶ρ2=M 1∶M 2
在标准状况下，空气的平均式量为29，
相同条件下的下列气体密度比空气密度大的是（①③④ ）
①CO2②H2③Cl2④HCl⑤N2
推论5
恒温恒容下，
气体的压强比等于它们的物质的量之比。
即：p1∶p2=n1∶n2
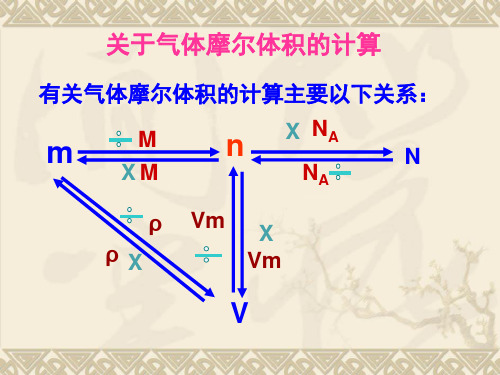
三、关于气体摩尔体积的计算
有关气体摩尔体积的计算主要以下关系：
解得：x=8g m（CO2）=30g-8g=22g
V（CO2）=17.6L-6.4L=11.2L
答：CO的质量为8g，CO2的质量为22g； CO的体积为6.4L，CO2的体积为11.2L。
阿伏加德罗定律及其推论(修改版)2015修改版
第十讲 阿伏加德罗定律及其推论一、阿伏加德罗定律及其推论同温、同压下相同体积的任何气体都含有相同的分子数。
推论：1 同温同压下：111222V n N ==V n N 推论：2 同温同体积下：1122P n =P n 推论：3 同温同压下：1122M ==D M ρρ（相对密度） 二、混合气体平均摩尔质量的求算方法①已知混合物的总质量[m （混）]和总物质的量[n （混）]，则：(混)=)()(混混n m 。
②已知标准状况下混合气体的密度[ρ(混)]，则：(混)=(22.4L/mol)×ρ(混)。
③已知同温、同压下混合气体的密度[ρ(混)]是一种简单气体A 的密度[ρ(A)]的d 倍（也常叫相对密度），则：d=)A ()()A ()(M M 混混=ρρ，即M (混)=d ×M(A)。
④已知混合物各成分的摩尔质量和在混合体系内的物质的量的分数或体积分数(对气体)，则：(混)=M(A)×a%+M(B)×b%+M(C)×c%例题精析【例题1】标准状况下,m g 气体P 和n g 气体R 所含分子数目相同，下列说法中不正确的（ ）A.气体P 和气体R 的相对分子质量之比为n ∶mB.同温同压下,气体P 和R 的密度之比为 m ∶nC.同质量的气体P 和R 的分子个数之比为 n ∶mD.同温同压同体积的气体P 和R 的质量之比为 m ∶n【例题2】有一真空瓶的质量为m 1，该瓶充入空气后总质量为m 2，在相同状况下，若充入某气体A 后，总质量是m 3，求A 的式量。
【例题3】已知空气中氮气和氧气的体积之比大约为4:1；估算空气的平均相对分子质量。
【变式1】某混合气体由H2、O2按物质的量之比比1：8构成，计算该混合气体的平均相对分子量。
该气体对H2的相对密度是多少？【变式2】某混合气体由H2、O2按质量比1：8构成，计算该混合气体的平均相对分子量。
该气体对H2的相对密度是多少？【例题4】标准状况下CO和CO２的混和气体5g 所占体积为 3. 36L。
阿伏伽德罗定律及其推论
A.3∶2
B.1∶3
C.2∶3
D.1∶2
【规范解答】选A。1 mol H2含氢原子2 mol，1 mol NH3含 氢原子3 mol，若H2和NH3所含氢原子数相等，则H2和NH3 的物质的量之比为3∶2，同温同压下气体的体积比等于
其物质的量之比，两个容器的体积比是3∶2。
精品课件
【互动探究】(1)若改为A容器中H2与B容器中 NH3所含原子数相等，则两个容器的体积之比为 ________。
气体摩尔体积（二）
阿伏加德罗定律及其推论
精品课件
气体摩尔体积 定义：单位物质的量的 气体所占的体积 Vm=V/n 单位：L/mol
精品课件
[注意]
★ 气体摩尔体积的数值不是固定不变的，它与 温度和压强有关
★ 气体摩尔体积只适用于气态物质，对于固态 物质和液态物质来讲，都是不适用的。
★ 标准状况下气体摩尔体积约为22.4L/mol （标准状况：T=0 ℃，P=101KPa）
物质的量分数)
精品课件
例题讲析
已知氮气和氨气的混合气体在标准状况 下的密度为1g/L,求混合气体的平均相 对分子质量。
解析：混合气体的平均摩尔质量为： 1g/L×22.4L/mol=22.4g/mol
故混合气体的平均相对分子质量为22.
精品课件
【练习4】
标准状况下
CO和CO２的混和气体 5g 所占体积为 3. 36L。 求CO的质量、CO2的体积及混和气体的平均式量。
精品课件
5. 气体的相对分子质量(M)的计算
(1)已知标准状M=况ρ下标气体. 2密2度.4ρ标
(2)已知两种气体的相对密度D
M(A)=D . M(B)
(3)混合气体的平均相对分子质量(M)
阿伏伽德罗定律及其推论
N
n
×NA
V（气体）
×ρ ÷ρ
m
分子数目
〖阅读材料〗
阿伏加德罗定律
1805年盖·吕萨克在定量研究气体反应体积间的关系时，发 现了气体定律：当温度和压强不变时，参加反应的气体与生成 的气体体积间成简单的整数比。
这一定律的发现，引起了当时许多科学家的注意。贝采利
乌斯首先提出了一个假设：在同温同压时，同体积的任何气体 都含有相同数目的原子。
思考：该假设能否解释如下事实——1体积的氢气和1体积的 氯气反应生成2体积的氯化氢？
为解决矛盾，1811年阿伏加德罗在化学中引入了分子的概念， 提出了阿伏加德罗假说：在同温同压下，同体积的任何气体都 含有相同数目的分子。
一、阿伏加德罗定律
1、含义 同温、同压下，相同体积的任何气体都含有相同
数目的分子数。
2、适用范围：
适用于气态物质（既适用于单一气体，又适用 于混合气体）
二、阿伏加德罗定律推论
推论1：同温同压下，
，M=22.4 ρ气 （ 单位：g/L）
推论3：同温同体积，
阿伏伽德罗定律推论及应用
阿伏伽德罗定律应用
• • 1. 下列叙述正确的是 ( ) A．同温同压下，相同体积的物质，其物质的量必 然相等 • B．任何条件下，等物质的量的乙烯 (C2H4) 和一氧 化碳所含的分子数必然相等 • C．1 L一氧化碳气体一定比1 L氧气的质量小 • D．同温同压下，等体积的物质所含的分子数一定 相等
结论 语言表达 同温、同压下，气体的密度与其 相对分子质量成正比 同温、同压、相同体积的气体， 其质量与相对分子质量成正比
相同条件 公式
结论 语言表达
T、p、m V1 M2 同温、同压下，等质量的气体，其 ＝ V M1 体积与相对分子质量成反比 2 相同 T、V、m p1 M2 同温、同体积下，等质量的气体， ＝ p M1 其压强与相对分子质量成反比 2 相同
阿伏伽德罗定律及其推论
学习目标
• • • • • 【知识目标】 1. 进一步巩固物质的量的概念及其与质量、摩 尔质量、物质的量、物质的粒子数之间的相互 关系 2．知道阿伏伽德罗定律及其推论的概念，学 会有关阿伏伽德罗定律及其推论的应用的简单 计算 【能力目标】 初步学会分析处理数据、推. 相同条件下，同质量的X、Y两种气体， 相对分子质量分别为A、B；则： • (1)X与Y的体积比为________，分子个 数比为________，密度比为________； • (2)相同条件下的X、Y两种气体体积相 同，则X与Y的质量比为________，物质的 量比为________。
阿伏加德罗定律：
同温同压下，相同体积的任何气体都 具有相同的分子数
阿伏加德罗定律：
同温同压下，相同体积的任何气体都 具有相同的分子数
• 例：同温、同压下，CO2与CO的体积分别 为12 mL 、6 mL ,则CO2与CO 物质的量之 比为 2:1
8阿伏伽德罗定律以及推论
阿伏伽德罗定律以及推论【知识整合】一、阿伏加德罗定律在相同温度和压强下，相同体积．．．．．．．．．．．．．的任何气体都含有相同数目的分子数。
注意：在该定律中有“四同”：同温、同压、同体积、同分子数目，有“三同”就可定“一同”。
二、阿伏加德罗定律的推论根据阿伏加德罗定律及气态方程（pV ＝nRT ）限定不同的条件，便可得到阿伏加德罗定律的多种形式， ○1T 、p 相同21N N ＝21V V 同温同压下，气体的分子数与其体积成正比○2T 、V 相同21p p ＝21N N 温度、体积相同的气体，压强与其分子数成正比○3n 、p 相同21V V ＝21T T 分子数相等、压强相同的气体，体积与其温度成正比○4n 、T 相同21p p ＝12V V 分子数相等、温度相同的气体，压强与其体积成反比○5○6○7T 、p 、m 相同21MM ＝12V V 同温同压下，等质量的气体相对分子质量与其体积成反比【典例分析】例1、 同温同压下，质量相等的O 2与CO 2，密度比为_______，体积比为_______；同温同压下，体积相等的O 2与CO 2，密度之比为_______，质量之比为_________。
例2、 同温同压下，某瓶充满O 2，质量为116g ，充满CO 2质量为122g ，充满气体X ，质量为114g ，则X 的相对分子质量为（ ）A ．28B ．60C ．32D ．44例3、体积相同的容器，一个盛有一氧化氮，另一个盛有氮气和氧气，在同温同压下两容器内的气体一定具有相同的（ ） A. 原子总数 B. 质子总数 C. 分子总数 D. 质量例4、某非金属单质A 和氧气发生化合反应生成B 。
B 为气体，其体积是反应掉氧气体积的两倍（同温同压）。
以下对B 分子组成的推测一定正确的是（）A. 有1个氧原子B. 有2个氧原子C. 有1个A 原子D. 有2个A 原子例5、在150℃时，(NH 4)2CO 3分解的方程式为：(NH 4)2CO 3=====△2NH 3↑＋H 2O↑＋CO 2↑，若完全分解，产生的气态混合物的密度是相同条件下氢气密度的( ) A ．96倍 B ．48倍 C ．12倍 D ．10倍【测评反馈】1．同温、同压下，下列有关比较等质量的二氧化硫气体和二氧化碳气体的叙述中正确的是（ ）A ．密度比为16：11B ．密度比为11：16C ．体积比为1：1D ．体积比为11：162．下列各组中，两种气体的分子数一定相等是（ ）A ．温度相同、体积相同的O 2和2NB ．质量相等、密度不等的2N 和42HC C ．体积相等、密度相等的CO 和42H CD ．压强相同、体积相同的2N 和2O3．在一定条件下，气体A 可发生如下反应：，若知所得混合气体对氢气的相对密度为4.25，则A 的相对分子质量可能为（ ） A ．34 B ．8.5C ．17 D ．16 4．在一定温度和压强下，1体积2X （气）和3体积2Y （气）化合生成2体积Z （气），则Z 的分子式是（ ）A ．3XYB ．XYC ．Y X 3D ．32Y X5．在标准状况下，如果25.0LO 含有m 个2O 分子，则阿伏加德罗常数可表示为（ ） A ．m/22.4 B ．44.8mC ．22.4m D ．m/326．在同温、同压下，有同质量的气体X 和Y 。
阿伏伽德罗定律的推论
阿伏伽德罗定律的推论
阿伏伽德罗定律，也被称为物质守恒定律，是化学领域中一个重
要的基本原则。
它表明，在任何化学反应中，所有参与反应的物质的
总质量保持不变。
换句话说，化学反应发生时，物质的总质量既不会
减少也不会增加。
根据阿伏伽德罗定律，可以得出以下推论：
1. 反应物质的质量与生成物质的质量的关系：在一个化学反应中，反应物质的总质量等于生成物质的总质量。
无论是化学反应中发
生的任何变化，总质量都必须保持恒定。
2. 化学计量关系的确定：通过阿伏伽德罗定律，可以确定化学
反应中不同物质的质量之间的化学计量关系。
化学计量关系是化学方
程式中反应物质与生成物质之间的质量比。
通过实验测量出反应物质
和生成物质的质量，可以确定它们之间的化学计量关系，并进一步研
究反应机理和反应速率。
3. 原子守恒定律的推论：阿伏伽德罗定律是原子守恒定律的基础。
原子守恒定律表明，在化学反应中，每种元素的原子数目保持不变。
由于原子不会被创建或消灭，所以反应前后每个元素的原子数目
必须保持一致。
阿伏伽德罗定律的推论为化学研究提供了重要的理论指导。
通过
理解和应用这些推论，化学家能够更好地探索和解释化学反应的本质，并在实际应用中进行合成化学、分析化学、物理化学等领域的研究。
在工业生产中，也可以基于阿伏伽德罗定律来设计和控制化学反应过程，以实现高效、安全和可持续的化学生产。
阿伏加德罗定律及其推论
状态1：P1M1＝ρ1RT1 状态2：P2M2＝ρ2RT2
① ②
① PM RT T —： 1 1 1 1 1 1 ② P2 M 2 2 RT2 2T2
3
第二部分 经典例题赏析 第二部分：经典例题 德 律 其推 考查 1．(1999年上海)由CO2、H2和CO组成的混合气在同温 同压下与氮气的密度相同 则该混合气体中CO2、 同压下与氮气的密度相同。则该混合气体中 H2和CO的体积比为( ) A．29∶8∶13 B．22∶1∶14 C．13∶8∶29 D．26∶16∶57
知识点回顾 阿伏加德罗定律及其推论的内容 4．阿伏伽德罗定律的推论3： 同温、同压、同体积时： 气体质量之比等于构成气体物质分子的摩尔质量之比。 5．阿伏伽德罗定律的推论4： 同温、同体积、同质量时： 气体的压强之比等于构成气体物质分子的摩尔质量的反比。 气体的压强之比等于构成气体物质分子的摩尔质量的反比 6．阿伏伽德罗定律的推论5： 同温、同压时： 气体的密度之比等于构成气体物质分子的摩尔质量之比。
4
m1 M 1 m2 M 2
知识点精讲 ① P1V1 m1M2RT1 m1M2T1 —— ： —— ＝ ———— ＝ ———— ② P2V2 m2M1RT2 m2M1T2 5．阿伏伽德罗定律的推论4： 同温、同体积、同质量时： 体 质量时 (T1 ＝ T2，V1 ＝ V2，m1 ＝ m2 )
P1 M 2 P2 M 1
知识点精讲 克拉伯龙方程的变形形式 m PV RT M m1 状态1：PV RT 1 1 M1 1 状态2： P2V2
m2 RT2 M2
知识点精讲 ① P1V1 m1M2RT1 m1M2T1 —— ： —— ＝ ———— ＝ ———— ② P2V2 m2M1RT2 m2M1T2 3．阿伏伽德罗定律的推论2： 同温 同压 同质量时：(T1 ＝ T2，P1 ＝ P2，m1 ＝ m2 ) 同温、同压、同质量时：
阿伏伽德罗定律及其推论
一、理想气体状态方程：PV=nRT 2、已知两种气体在等温、等容时： 根据 PV=nRT P与n成正比， 即推论1 P1/P2=n1/n2 3、已知两种气体在等温、等压时： V＝m/ ρ ，n＝m/ M， PV=nRT可以改成PM= ρRT，M与ρ成正比 即推论2 M1/M2=ρ1/ρ2
练习1. 依照阿伏加德罗定律，下列叙述中正 确的是( ) A．同温同压下，两种气体的体积之比等于摩 尔质量之比 B．同温同压下，两种气体的物质的量之比等 于密度之比 C．同温同压下，两种气体的摩尔质量之比等 于密度之比 D．同温同体积下，两种气体的物质的量之比 等于压强之比
练ห้องสมุดไป่ตู้2 下列条件下，两瓶气体所含原子数一
定相等的是 （
）
A.同温度、同体积的H2和N2 B.同压强、同体积的N2O和CO2 C.同体积、同密度的C2H4和C3H6 D.同质量、不同密度的N2和CO
理想气体状态方程的应用
——阿伏伽德罗定律及推论
一、理想气体状态方程：PV=nRT P: 气体的压强； V：气体的体积； n：气体的物质的量； T：气体的温度，单位是开尔文。 R：常数。
一、理想气体状态方程：PV=nRT 五个量中有四个是变量，已知两个量相等 能推出另两个的关系，这就是阿伏伽德罗 定律及其推论的由来。 1、已知两种气体在等温、等压时： 根据 PV=nRT V与n成正比， 即阿伏伽德罗定律：V1/V2=n1/n2
阿伏伽德罗定律5个推论
阿伏伽德罗定律5个推论阿伏伽德罗定律是化学中一条非常重要的定律，它描述了电解质溶液中的电离现象。
根据阿伏伽德罗定律，我们可以推导出以下五个推论。
推论一：电离的程度与浓度成正比阿伏伽德罗定律告诉我们，电解质溶液中的电离程度与溶液的浓度成正比。
也就是说，溶液中溶质的浓度越高，溶质的电离程度就越大。
这个推论可以解释为什么浓度较高的电解质溶液具有较好的导电性。
推论二：电离的程度与温度成反比根据阿伏伽德罗定律，电离的程度与温度成反比。
也就是说，随着溶液温度的升高，电解质的电离程度会降低。
这个推论可以帮助我们理解为什么低温下的电解质溶液比高温下的电解质溶液具有更好的导电性。
推论三：弱电解质的电离程度较低根据阿伏伽德罗定律，强电解质的电离程度较高，而弱电解质的电离程度较低。
这是因为强电解质在溶液中能够完全电离，而弱电解质只能部分电离。
这个推论可以帮助我们区分强电解质和弱电解质，并理解它们在溶液中的行为差异。
推论四：电离度与溶液中的电解质种类有关根据阿伏伽德罗定律，溶液中的电离度与电解质的种类有关。
不同的电解质具有不同的电离度，这是由于它们的离子化能力不同。
这个推论可以帮助我们理解为什么不同的电解质在溶液中具有不同的导电性。
推论五：电离度与溶液中的离子价数有关根据阿伏伽德罗定律，溶液中的电离度与电解质的离子价数有关。
离子价数越高的电解质通常具有较高的电离度。
这个推论可以帮助我们理解为什么具有多价阳离子或多价阴离子的电解质在溶液中通常具有较好的导电性。
总结：阿伏伽德罗定律是描述电解质溶液中电离现象的重要定律之一。
根据这个定律，我们可以推导出五个重要的推论。
这些推论帮助我们理解了电解质溶液中电离的规律，以及影响电离程度的因素。
通过学习和应用这些推论，我们可以更好地理解和解释电解质溶液的行为，为化学实验和工业生产提供指导。
阿伏伽德罗定律
（3个数比=物质的量之比=化学
方程式中各物质的系数比；（2）写出化学反应方 程式；（3）由质量守恒定律确定生成物的分子式。
（1）已知标准状况下气体的密度（ρ）求解： M= 22 .4 ρ
V2
n2
[练习1]
同温同压下，同物质的量的乙炔 气体（C2H2）与苯蒸气（C6H6）体积 比是（B） （A）3：1 （B）1：1 （C）1：3 （D）2：3
阿伏加德罗定律的推论二
依据：PV=n RT 或 PV= m RT M
2.同温同体积下，气体的压强之比等于物质
的量之比（已知T1=T2 ，V1=V2）
V
=
nRT P
=
1 8.314 298 1.106 105
=
22.4升
二、阿伏加德罗定律的几个推论
阿伏加德罗定律的推论一
依据：PV=n RT 或 PV= m RT M
1. 同温同压下，气体体积之比等于物质
的量之比 (已知P1=P2,T1=T2)
P1V1 P2V2
=
n1RT1 n2RT2
所以
V1 = n1
1. 同温同压下，体积相同的下列气体，
密度与其它三者不同的是（ ） D
（（AC））NCO2
（（BD））CH22HS4
2. 同温同压下，密度相同的气体组是
（A）
（（AC））CCO2H、4、NN2 O （（BD））NSOO、2、CCHl24
[练习4]
2. 同温同压下，将1体积的CO2和2体 积（1的）C分O进子行数比之较比，为则C1：O22与CO；的： （2）原子数之比为 3：4 ； （3）质量之比为 11：14 ； （4）物质的量之比为 1：2 ； （5）摩尔质量之比为 11：7 。
阿伏伽德罗定律及其推论
（1）同温同压下，V1/V2=n1/n2 （2）同温同体积时，P1/P2=n1/n2=N1/N2 （3）同温同压等质量时，V1/V2=M2/M1 （4）同温同压同体积时，M1/M2=ρ1/ρ2 分子间的平均距离又决定于外界的温度和压强，当温度、压强相同时，任何气体分子间的平均距离几乎相等(气体分子间的作用微弱，可忽略)，故定律成立。该定律在有气体参加的化学反应、推断未知气体的分子式等方面有广泛的应用。 阿伏加德罗定律认为：在同温同压下，相同体积的气体含有相同数目的分子。1811年由意大利化学了气体反应的体积关系，用以说明气体分子的组成，为气体密度法测定气态物质的分子量提供了依据。对于原子分子说的建立，也起了一定的积极作用。
克拉伯龙方程式
中学化学中，阿伏加德罗定律占有很重要的地位。它使用广泛，特别是在求算气态物质分子式、分子量时，如果使用得法，解决问题很方便。下面简介几个根据克拉伯龙方程式导出的关系式，以便更好地理解和使用阿佛加德罗定律。 克拉伯龙方程式通常用下式表示：PV=nRT……① P表示压强、V表示气体体积、n表示物质的量、T表示绝对温度、R表示气体常数。所有气体R值均相同。如果压强、温度和体积都采用国际单位（SI），R=8.31帕·米3/摩尔·开。如果压强为大气压，体积为升，则R=0.082大气压·升/摩尔·度。 因为n=m/M、ρ=m/v（n—物质的量，m—物质的质量，M—物质的摩尔质量，数值上等于物质的分子量，ρ—气态物质的密度），所以克拉伯龙方程式也可写成以下两种形式： Pv=m/MRT……②和PM=ρRT……③ 以A、B两种气体来进行讨论。 （1）在相同T、P、V时： 根据①式：nA=nB（即阿伏加德罗定律） 分子量一定 摩尔质量之比=密度之比=相对密度）。若mA=mB则MA=MB。 （2）在相同T·P时： 体积之比=摩尔质量的反比；两气体的物质的量之比=摩尔质量的反比） 物质的量之比=气体密度的反比；两气体的体积之比=气体密度的反比）。 （3）在相同T·V时： 摩尔质量的反比；两气体的压强之比=气体分子量的反比）。
初升高化学衔接课第六讲 阿伏伽德罗定律
第六讲阿伏伽德罗定律知识概要：一．阿伏加德罗定律及推论(1)阿伏加德罗定律的内容同温同压下相同体积的任何气体都含有相同数目的分子。
①适用范围：任何气体，可以是单一气体，也可以是混合气体。
②“四同”定律：同温、同压、同体积、同分子数中只要有“三同”则必有第“四同”。
即“三同定一同”。
(2)阿伏加德罗定律的推论：①同温、同压：气体的体积与物质的量成正比②同温、同压：气体的密度与摩尔质量成正比③同温、同压、同体积：气体的质量与摩尔质量成正比特别提醒①标准状况下的气体摩尔体积是22.4 L·mol-1，是阿伏加德罗定律的一个特例。
②以上推论只适用于气体(包括混合气体)，公式不能死记硬背，要在理解的基础上加以运用。
二．求气体摩尔质量的常用方法(1)根据标准状况下气体密度(ρ)M=ρ×22.4(2)根据气体的相对密度(D=ρ1/ρ2)M1/M2=D说明气体的相对密度是指在同温同压下两种气体的密度之比即。
m(3)根据物质的量(n)与物质的质量(m)M=n(4)根据一定质量(m)物质中的微粒数(N)和阿伏加德罗常数(N A)M= N A.m/N(5)根据化学方程式结合质量守恒定律m(6)混合气体平均摩尔质量M=n还可以用下式计算：M=M1×a%+M2×b%+M3×c%…M1、M2、M3……分别表示混合气体中各组成成分的摩尔质量，a%、b%、c%……分别表示各组成成分所占混合气体的体积分数(即物质的量分数)。
课堂练习一、选择题1、设NA代表阿伏加德罗常数，下列说法正确的是（）A 2.3g金属钠全部变成钠离子时失去的电子数目为0.2N AB 2g氢气所含原子数目为N AC 17gNH3所含的电子数为10N AD NA个氧分子和NA个氢分子的质量比等于16 ：12、设一个12C原子的质量为ag，一个R原子的质量为bg，阿伏加德罗常数为N A，则R的相对原子质量可以表示为（）A B C bN A D aN A3、判断下列叙述正确的是（）A.标准状况下，1mol任何物质的体积都约为22.4LB.1mol任何气体所含分子数都相同，体积也都约为22.4LC.在常温常压下金属从盐酸中置换出1molH2转移电子数为1.204×1024D.在同温同压下，相同体积的任何气体单质所含原子数目相同4、两个体积相同的密闭容器一个盛有氯化氢，另一个盛有H2和Cl2的混合气体，在同温同压下，两个容器内的气体一定具有相同的（）A.质量B.密度C.分子总数D.原子总数5、如果ag某气体中含有的分子数为b，则cg该气体在标准状况下的体积是（）A. B. C D.8．同温同压下，下列有关比较等质量的二氧化硫和二氧化碳气体的叙述正确的是（）A.体积比为1∶1B.体积比为11∶16C.密度比为16∶11D.密度比为11∶169．与8g SO3中氧原子数相同的是（）A．9.6g H2SO4 B．6.6g CO2C．6.4g SO4 D．6.72L CO(常温、常压) 10．3.6g碳在一定量的氧气中燃烧，反应后生成的气体质量为9.2g。
阿伏伽德罗定律
7、在相同体积的两个密闭容器中分别充满了O2 、O3 ， 当这两个容器内温度和气体密度都相等时，下列正确的是（ ） A、两个容器内气体的压强相等 B、O2 比O3的质量小 C、两个容器内气体的分子数相等 D、两个容器内氧原子数目相等
8、 NA表示阿伏加德罗常数的值，下列叙述中不正确的是 （ ） A、分子总数为NA的NO2和CO2的混合气体中含有的氧原子数为2NA
2、（双选）下列条件下，两瓶气体所含原子数一定相等的是（ ） A、同质量、不同密度的N2和CO B、同温度、同体积的H2和N2 C、同体积、同密度的C2H4和C3H6 D、同压强、同体积的N2O和CO2
3、 同温同压下，等质量的SO2和CO2相比较，下列叙述正确的是 （ ） A 、 密度比为16:11 B、 密度之比为11:16 C 、体积比为16：11 D 、体积比为11:16
4、在三个密闭容器中分别充入Ne、H2、O2三种气体，在以下 各种情况下排序正确的是（ ） A、当他们体积、温度、压强均相同时， 三种气体的密度ρ（H2）>ρ（Ne）>ρ（O2） B、当他们温度和密度都相同时， 三种气体的压强P（H2）> P（Ne）>P（O2） C、当他们质量、温度、压强均相同时， 三种气体的体积V（O2）>V（Ne）>V（H2） D、当他们体积、温度、压强均相同时， 三种气体的质量m（H2）> m（Ne）>m（O2）
5、代表阿伏加德常数，下列说法正确的是 （ ） A、在同温同压时，相同体积的任何气体单质所含的原子数目相同 B、2g氢气所含原子数目为NA C、在常温常压下，11.2L氮气所含的原子数目为NA D、17g氨气(NH )所含电子数目为10 NA 3
6、两个密闭容器中分别充有质量相同的甲、乙两种气体， 若两容器的压强和温度均相同，且甲的密度大于乙的密度， 则下列说法正确的是（ ） A、甲的分子数比乙的分子数多 B、甲的物质的量比乙的物质的量少 C、甲的摩尔体积比乙的摩尔体积小 D、甲的相对分子质量比乙的相对分子质量小
阿伏伽德罗定律
物质的量之比
P1 n1 N1 （T、V相同） P2 n2 N2
练习四
二、阿伏加德罗定律的推论：
➢依据：PV=nRT
或
PV=
m RT M
3.同温同压下，任何气体密度比
等于式量之比
1
M1
2
M2
（T、P相同）
练习二
二、阿伏加德罗定律的推论
➢依据：PV=nRT
或
PV=
m RT M
4.同温同压下，同体积任何气体的质量比
通过该公式可以理解阿伏伽德罗定律
二、阿伏加德罗定律的推论：
➢依据：PV=nRT
或
PV=
m RT M
1.同温同压下，气体体积之比
等于物质的量之比,等于粒子数之比
V1 n1 N1 （T、P相同） V2 n2 N2
练习三
二、阿伏加德罗定律的推论：
➢依据：PV=nRT
或
PV=
m RT M
2.同温同体积下，气体的压强之比等于
52chem化学网提供
2020/3/7
例题
1. 在空气中N2、O2、Ar的体积分数分别 为78%，21%，约1%，求空气的平均 式量
2. 相同条件下，氮气和氧气物质的量比为 1：3 ，求混合气体的平均式量。
阿伏加德罗定律及其 推论
阿伏伽德罗定律
1.内容：在相同的温度和压强下，相同体 积的任何气体含有相同数目的 粒子。
2.注意事项：①.适用于气体（单一或混合气体） ②.三同定一同 ③.粒子数相同则物质的量相同
一、介绍：理想气体状态方程：
PV=nRT
P-----压强 n-----物质的量 V-----体积 T=t+273K R=8.314 J·mol-1·K-1
阿伏加德罗定律推论
4.00g == 0.100olM(Ar)40g/mol
n(总)= n(Ar)+ n(O2)+ n(Ar)
= 0.0500mol + 0.0500mol + 0.100mol = 0.200mol
V（总）=n(总）· Vm=0.200molx22.4L/mol=4.48L
2021/3/26
9
2．利用气体摩尔体积，进行有关 式量的计算
【例题2】在标准状况时，0.2L的容器里所含一氧化碳
的质量为0.25g，计算一氧化碳的式量。
分析：M=m/n
n=V/Vm
【解】
2021/3/26
答：一氧化碳的式量是28。
10
气体的相对分子质量求算方法：
（1）标态密度法：Mr= 22.4×ρ
（2）摩尔质量法：M = m/n
（3）相对密度法：同T、P：
【例题1】8.5g氨在标准状况时体积是多少升？ 【解】氨的式量是17，氨的摩尔质量是17g／mol
n(NH3)=
m(NH3) M(NH3) =
8.5g 17g/mol = 0.5mol
V(NH3)=22.4L／mol×0.5mol=11.2L
答：8.5g氨在标准状况时的体积是11.2L。
2021/3/26
2021/3/26
13
练习：
在标准状况下，测得1.92g某气体的体积是672ml。 计算此物质的摩尔质量。
解： 672ml=0.672L n= 0.672L =0.03mol
22.4L/mol
1.92g
M=m/n=
=64g/mol 0.03mol
答：此物质的摩尔质量是64g/mol。
2021/3/26
阿伏加德律及其推论
诚西郊市崇武区沿街学校阿伏加德律及其推论1．理想气体状态方程我们设定：T ．温度；p ．气体夺强；n ．物质的量；V ．气体的体积；m .气体的质量；M ．气体的摩尔质量； .气体的密度N ．气体的分子数。
理想气体状态方程为：〔1〕111T V p ＝222T V p ；〔2〕pV ＝nRT ＝RT Mm 〔R 为常数〕。
对〔2〕假设p 的单位为大气压〔atm 〕，V 为升〔L 〕，T 为绝对温度时，R ＝0.082。
假设p 为帕斯卡〔Pa 〕，V 为立方米〔m3〕，T 为绝对温度时，R ＝1。
2．阿伏加德律在一样温度和压强下，一样体积的任何气体都含有一样数目的分子数。
这是意大利科学家阿伏加德罗最早提出的，因此称为“阿伏加德律〞。
理解时注意：在该定律中有“四同〞：同温、同压、同体积、同分子数目，有“三同〞就可定“一同〞。
如，同温同压下，同体积的两种气体必含有一样数目的分子；同温同压下，同分子数目的两种气体必然同体积；再如，在同温下，两种气体同体积又同分子数目，那么必然同压。
3．阿伏加德律的推论根据阿伏加德律及气态方程〔pV ＝nRT 〕限定不同的条件，便可得到阿伏加德律的多种形式，纯熟并掌握了它们，解答有关问题时，可到达事半功倍的效果。
条件结论语言表达T 、p 一样21N N ＝21V V 同温同压下，气体的分子数与其体积成正比 T 、V 一样21p p ＝21N N 温度、体积一样的气体，压强与其分子数成正比n 、p 一样21V V ＝21T T 分子数相等、压强一样的气体，体积与其温度成正比 n 、T 一样21p p ＝12V V 分子数相等、温度一样的气体，压强与其体积成反比 T 、p 、m 一样21M M ＝12V V 同温同压下，等质量的气体相对分子质量与其体积成反比。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
阿伏加德罗定律
•阿伏伽德罗定律：
同温同压下，相同体积的任何气体含有相同的分子数。
•
•阿伏伽德罗定律的使用范围：
阿伏伽德罗定律只对气体起作用，使用于任何气体，包括混合气体。
•方法与技巧：
1.“三同”定“一同”（温度、压强、气体体积、气体分子数）；“两同”
定“比例”。
2.阿伏伽德罗定律及其推论的数学表达式可由理想气体状态方程（PV=nRT）
或其变形形式(PM=ρRT)推出，不用死记硬背。
•理想气体状态方程:
理想气体状态方程的表达式：PV= nRT
P表示压强，V 表示体积，T表示温度，R是常数，n是气体的物质的量。
可根据此方程来推断阿伏伽德罗定律的相关推论：
一、阿伏伽德罗定律及推论
1、定律内容：同温同压下，相同体积的任何气体含有相同数目的分子。
注意：
(1)适应范围：任何气体。
(2)拓展：在定律中，可以“四同”中的任意“三同”为条件，均可导出“第四同”。
(3)与气体摩尔体积的关系：标准状况下的气体摩尔体积实际上是阿伏加德罗定律的一个特例。
2、重要推论：
根据理想气体状态方程推导：
(1)、同温同压下，任何气体的体积之比等于物质的量(或分子数)之比。
V1：V2=n1：n2=N1：N2。
(2)、同温同体积的任何气体的压强之比等于物质的量之比。
p1：p2=n1：n2。
(3)、同温同压下，气体密度之比等于相对分子质量之比。
ρ1：ρ2=M1：M2
(4)、同温同压下，同体积的气体的质量之比等于密度之比。
m1：m2=ρ1：ρ2
(5)、同温同压下，同质量的气体的体积之比等于相对分子质量的反比。
V1：V2=M2：M1
(6)、同温同体积同质量的任何气体的压强之比等于相对分子质量的反比。
p1：p2=M2：M1
【练习】
1.在体积相同的两个密闭容器中分别充满O2、O3气体，当这两个容器内气体的温度和密度相等时，下列说法正确的是( )
A.两种气体的压强相等
B.O2比O3质量小
C.两种气体的分子数目相等
D.两种气体的氧原子数目相等
参考答案：D
二、气体密度和气体相对分子质量的计算方法
1、气体密度的计算：
(1)密度定义法：任意情况下，ρ=m÷v
(2)摩尔质量法：在标准状况下，ρ=m÷v=M•n÷Vm•n=M÷22.4L.mol-1
(3)相对密度法：同温同压下，A气体对B气体的相对密度等于A气体的密度比B气体的密度，也等于A气体的相对分子质量比B 气体的相对分子质量。
D=ρA÷ρB=MA÷MB
2、气体相对分子质量的计算：
(1)标况密度法：M=22.4L•mol-1×ρ(g/l)
(2)相对密度法：MA=MB•D
(3)混合气体的平均式量(M)：
A、摩尔质量定义法：
M=m总÷n总=(M1n1+M2n2+…+Mini) ÷n总=(M1V1+M2V2+…+MiVi) ÷n总
B、物质的量或体积分数法：M=M1a1+M2a2+…+Miai
其中：M1、M2、…+Mi为各气体组分的摩尔质量，a1、a2、…、ai各气体组分的物质的量分数或体积分数。
【练习】
1.由CH4和O2组成的混合气体，标准状况下的密度为1g•L﹣1，则该混合气体中CH4和O2的体积比为( )
A. 2：1
B.3：2
C. 2：3
D.1：2
参考答案：B。