奔牛初中八下数学周周练试卷(2)
八年级下第三周周练数学试卷(有答案)

八年级下第三周周练数学试卷(有答案)一、选择(3*8=24)1.下列各式中,①,②,③,④﹣,⑤,⑥x+y,⑦=,⑧,分式个数为()A.3个 B.4个 C.5个 D.6个2.点M(﹣3,2)关于y轴对称的点的坐标为()A.(﹣3,﹣2)B.(3,﹣2)C.(3,2) D.(﹣3,2)3.下列可以判定两个直角三角形全等的条件是()A.斜边相等B.面积相等C.两对锐角对应相等D.两对直角边对应相等4.下列分式,,,,中,最简分式的个数是()A.1个 B.2个 C.3个 D.4个5.当x为任意实数时,下列分式一定有意义的是()A. B. C.D.6.下列式子计算正确的是()A. B.C. D.7.将中的a、b都扩大为原来的4倍,则分式的值()A.不变B.扩大原来的4倍C.扩大原来的8倍 D.扩大原来的16倍8.已知关于x的分式方程=1的解是非正数,则a的取值范围是()A.a≤﹣1 B.a≤1且a≠﹣2 C.a≤﹣1且a≠﹣2 D.a≤1二、填空(每空2分,20)9.要使分式无意义,则x的取值范围是.10.分式表示一个正整数时,整数m可取的值是.11.填写出未知的分子或分母:(1).(2).12.若,则m=,n=.13.若﹣=2,则的值是.14.已知==,则=.15.若关于x的方程有增根,则k的值为.16.若关于x的分式方程﹣2=无解,则m=.三、解答题17.计算:(1)﹣(2)•(3)÷(4)﹣a+b.18.解分式方程:(1)﹣=0(2)+1=.(3)5+=﹣.19.先化简÷(a+1)+,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.20.关于x的分式方程=﹣1的解为非负数,求k的取值范围.21.已知2x﹣3y+z=0,3x﹣2y﹣6z=0,且xyz≠0,求的值.22.已知:一次函数y=2x+b.(1)如果它的图象与一次函数y=﹣2x+1和y=x+4的图象交于同一点,求b的值;(2)如果它的图象与坐标轴所围成的图象的面积等于4,求b的值.23.观察下列各式:(1)由此可推测=;(2)试猜想此类式子的一般规律.用含字母m的等式表示出来.并说明理由(m表示整数);(3)请直接用(2)中的规律计算的值.24.如图1,已知一次函数y=﹣x+6分别与x、y轴交于A、B两点,过点B的直线BC交x 轴负半轴与点C,且OC=OB.(1)求直线BC的函数表达式;(2)如图2,若△ABC中,∠ACB的平分线CF与∠BAE的平分线AF相交于点F,求证:∠AFC=∠ABC;(3)在x轴上是否存在点P,使△ABP为等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.八年级(下)第三周周练数学试卷参考答案与试题解析一、选择(3*8=24)1.下列各式中,①,②,③,④﹣,⑤,⑥x+y,⑦=,⑧,分式个数为()A.3个 B.4个 C.5个 D.6个【考点】分式的定义.【分析】判断一个式子是否是分式,关键要看分母中是否含有字母,然后对分式的个数进行判断【解答】解:②,④﹣,⑤,⑧的分母中均含有字母,属于分式,其它不符合条件,故选:B.2.点M(﹣3,2)关于y轴对称的点的坐标为()A.(﹣3,﹣2)B.(3,﹣2)C.(3,2) D.(﹣3,2)【考点】关于x轴、y轴对称的点的坐标.【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y),可以直接得到答案.【解答】解:点M(﹣3,2)关于y轴对称的点的坐标为(3,2),故选:C.3.下列可以判定两个直角三角形全等的条件是()A.斜边相等B.面积相等C.两对锐角对应相等D.两对直角边对应相等【考点】直角三角形全等的判定.【分析】根据判定直角三角形全等的条件:SAS、ASA、AAS、HL进行分析即可.【解答】解:A、斜边相等,缺少一个条件,不能证明两个直角三角形全等,故此选项错误;B、面积相等,不能证明两个直角三角形全等,故此选项错误;C、两对锐角对应相等,缺少边相等的条件,不能证明两个直角三角形全等,故此选项错误;D、两对直角边对应相等,可利用SAS定理证明两个直角三角形全等,故此选项正确;故选:D.4.下列分式,,,,中,最简分式的个数是()A.1个 B.2个 C.3个 D.4个【考点】最简分式.【分析】根据分子和分母是否存在公因式进行判断,没有公因式的为最简分式.【解答】解:的分子与分母存在公因式x,此分式不是最简分式;的分母分解因式可得2(m+2),分子与分母存在公因式2,此分式不是最简分式;的分子与分母都没有公因式,这两个分式为最简分式;的分子分解因式可得(b﹣2)(b+2),分子与分母存在公因式(b+2),此分式不是最简分式;的分子可变形为﹣(b﹣a),分子与分母存在公因式(b﹣a),此分式不是最简分式.最简分式只有1个,故选A.5.当x为任意实数时,下列分式一定有意义的是()A. B. C.D.【考点】分式有意义的条件.【分析】根据分式有意义,分母不等于0对各选项分析判断即可得解.【解答】解:A、x=0时,分母等于0,分式无意义,故本选项错误;B、x=0时,分母等于0,分式无意义,故本选项错误;C、∵x2≥0,∴x2+1≥1,∴x为任意实数,分式一定有意义,故本选项正确;D、x=±2时,分母等于0,分式无意义,故本选项错误.故选C.6.下列式子计算正确的是()A. B.C. D.【考点】分式的乘除法;约分;分式的加减法.【分析】根据分式的乘除、加减运算法则,约分的知识点进行解答.【解答】解:A、,A错;B、,B正确;C、,C错;D、,D错.故选B.7.将中的a、b都扩大为原来的4倍,则分式的值()A.不变B.扩大原来的4倍C.扩大原来的8倍 D.扩大原来的16倍【考点】分式的基本性质.【分析】根据分式的分子分母都乘以(或除以)同一个不为零,分式的值不变,可得答案.【解答】解:中的a、b都扩大为原来的4倍,则分式的值扩大为原来的4倍,故选:B.8.已知关于x的分式方程=1的解是非正数,则a的取值范围是()A.a≤﹣1 B.a≤1且a≠﹣2 C.a≤﹣1且a≠﹣2 D.a≤1【考点】分式方程的解;解一元一次不等式.【分析】先解分式方程,再根据解为非正数,得出a的取值范围即可.【解答】解:a+2=x+1,解得x=a+1,∵解为非正数,∴a+1≤0,∴a≤﹣1,∵x+1≠0,∴x≠﹣1,∴a+1≠﹣1,∴a≠﹣2,∴a的取值范围是a≤﹣1且a≠﹣2故选C.二、填空(每空2分,20)9.要使分式无意义,则x的取值范围是x=﹣1.【考点】分式有意义的条件.【分析】根据分式无意义,分母等于0列方程求解即可.【解答】解:∵分式无意义,∴x+1=0,解得x=﹣1.故答案为:x=﹣1.10.分式表示一个正整数时,整数m可取的值是m=﹣2或﹣2或1或5.【考点】分式的值.【分析】根据题意把问题转化为方程即可解决问题.【解答】解:∵分式表示一个正整数,∴m+3=1或2或4或8,∴m=﹣2或﹣2或1或5.故答案为m=﹣2或﹣2或1或5.11.填写出未知的分子或分母:(1).(2).【考点】分式的基本性质.【分析】(1)分子、分母同时乘以(x﹣y);(2)分子、分母同时除以(y+1).【解答】解:(1)观察等式两边分式的分母知,原分式的分子、分母同时乘以(x﹣y),分式的值不变.故答案是:3x(x﹣y);(2)原式==.故答案是:y+1.12.若,则m=3,n=1.【考点】分式的加减法.【分析】已知等式右边通分并利用同分母分式的加法法则计算,列出关系式,求出m与n的值即可.【解答】解:∵=+=,∴4a﹣1=m(a﹣1)+n(a+2)=(m+n)a+2n﹣m,∴m+n=4,2n﹣m=﹣1,解得:m=3,n=1,故答案为:3;113.若﹣=2,则的值是.【考点】分式的加减法.【分析】先将﹣=2进行通分,然后化为x﹣y=2xy,然后将原式进行适当的变形后将x﹣y 代入即可求出答案.【解答】解:由题意可知:y﹣x=2xy即x﹣y=﹣2xy,∴原式===故答案为:14.已知==,则=4.【考点】比例的性质.【分析】根据等比性质,可得答案.【解答】解:设===k,得x=3k,y=4k,z=5k.==4,故答案为:4.15.若关于x的方程有增根,则k的值为﹣或3.【考点】分式方程的增根.【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x+3)(x﹣3)=0,得到x=﹣3或3,然后代入化为整式方程的方程算出k的值.【解答】解:方程两边都乘(x+3)(x﹣3),得x+3+k(x﹣3)=3+k∵原方程有增根,∴最简公分母(x+3)(x﹣3)=0,解得x=﹣3或3,当x=﹣3时,k=﹣,当x=3时,k=3,故a的值可能是﹣,3.故答案为﹣或3.16.若关于x的分式方程﹣2=无解,则m=.【考点】分式方程的解.【分析】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.【解答】解:去分母,得x﹣2(x﹣3)=m2,把x=3代入得3﹣2(3﹣3)=m2,解得:m=±.故答案是:.三、解答题17.计算:(1)﹣(2)•(3)÷(4)﹣a+b.【考点】分式的混合运算.【分析】(1)先找出最简公分母,然后通分化简即可.(2)根据分式的乘法法则即可求出答案(3)先将分子分母进行因式分解,然后根据分式的乘法法则即可求出答案(4)先通分,然后根据分式加减运算法则即可求出答案.【解答】解:(1)原式=﹣==(2)原式=(3)原式=•=(4)原式=﹣(a﹣b)==18.解分式方程:(1)﹣=0(2)+1=.(3)5+=﹣.【考点】解分式方程.【分析】解分式方程的步骤为:①去分母;②求出整式方程的解;③检验;④得出结论.【解答】解:(1)去分母,得(x﹣5)(x﹣1)﹣(x+1)(x﹣3)=0,即﹣4x+8=0,解得x=2,经检验:x=2是原方程的解,∴原方程的解为x=2;(2)原方程可化为+1=去分母,得15x﹣12+3x﹣6=4x+10,解得x=2,经检验:x=2是原方程的增根,∴原方程无解;(3)原方程可化为5+=+去分母,得5(x+4)(x﹣4)+96=(2x﹣1)(x﹣4)+(3x﹣1)(x+4),解得x=8,经检验:x=8是原方程的解,∴原方程的解为x=8.19.先化简÷(a+1)+,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.【考点】分式的化简求值.【分析】先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.【解答】解:原式=•+=+=,当a=2(a≠﹣1,a≠1)时,原式==5.20.关于x的分式方程=﹣1的解为非负数,求k的取值范围.【考点】分式方程的解;解一元一次不等式.【分析】首先解关于x的方程,利用方程的解是非负数,以及分式方程的分母不等于0列不等式求得k的范围.【解答】解:方程两边同时乘以(x﹣1)(x+2)得:(5﹣x)(x﹣1)=k﹣(x﹣1)(x+2),即6x﹣x2﹣5=k﹣x2﹣x+2,移项,得﹣x2+x2+6x+x=2+5﹣k,合并同类项,得7x=7﹣k,系数华为1得x=,根据题意得:≥0且≠﹣2,≠1,解得:k≤7且k≠0.21.已知2x﹣3y+z=0,3x﹣2y﹣6z=0,且xyz≠0,求的值.【考点】分式的值;解二元一次方程组.【分析】把z看成已知数,求出x、y,然后代入所求代数式进行化简即可.【解答】解:由题可得,解得,∴===.22.已知:一次函数y=2x+b.(1)如果它的图象与一次函数y=﹣2x+1和y=x+4的图象交于同一点,求b的值;(2)如果它的图象与坐标轴所围成的图象的面积等于4,求b的值.【考点】两条直线相交或平行问题.【分析】(1)由题意可知:三条直线交于一点,所以可先根据一次函数y=﹣2x+1与y=x+4求出该交点坐标.(2)分别求出一次函数y=2x+b与坐标轴的交点,然后根据它的图象与坐标轴所围成的图象的面积等于4列出方程即可求出b的值.【解答】解:(1)联立,∴解得:把(﹣1,3)代入y=2x+b,∴3=﹣2+b,∴b=5,(2)令x=0代入y=2x+b,∴y=b,令y=0代入y=2x+b,∴x=﹣,∵y=2x+b的图象与坐标轴所围成的图象的面积等于4∴×|b|×|﹣|=4,∴b2=16,∴b=±423.观察下列各式:(1)由此可推测=;(2)试猜想此类式子的一般规律.用含字母m的等式表示出来.并说明理由(m表示整数);(3)请直接用(2)中的规律计算的值.【考点】规律型:数字的变化类.【分析】(1)由已知各等式的规律可以总结得出=﹣;(2)由已知各等式的规律可以总结得出,再根据分式通分可以计算证明结论:=﹣;(3)由(2)总结规律可以容易求出各式运算结果得零.【解答】解:(1)==﹣∴=﹣(2)猜想:=﹣.理由如下:﹣=﹣==(3)原式=﹣﹣(﹣)+﹣=024.如图1,已知一次函数y=﹣x+6分别与x、y轴交于A、B两点,过点B的直线BC交x 轴负半轴与点C,且OC=OB.(1)求直线BC的函数表达式;(2)如图2,若△ABC中,∠ACB的平分线CF与∠BAE的平分线AF相交于点F,求证:∠AFC=∠ABC;(3)在x轴上是否存在点P,使△ABP为等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.【考点】一次函数综合题.【分析】(1)根据自变量与函数值的对应关系,可得A、B、C点的坐标,根据待定系数法,可得函数解析式;(2)根据角平分线的性质,可得∠FCA=∠BCA,∠FAE=∠BAE,根据三角形外角的关系,可得∠BAE=∠ABC+∠BCA,∠FAE=∠F+∠FCA,根据等式的性质,可得答案;(3)根据等腰三角形的定义,分类讨论:AB=AP=10,AB=BP=10,BP=AP,根据线段的和差,可得AB=AP=10时P点坐标,根据线段垂直平分线的性质,可得AB=BP=10时P点坐标;根据两点间的距离公式,可得BP=AP时P点坐标.【解答】解:(1)当x=0时,y=6,即B(0,6),当y=0时,﹣x+6=0,解得x﹣8,即A(8,0);由OC=OB,得OC=3,即C(﹣3,0);设BC的函数解析式为,y=kx+b,图象过点B、C,得,解得,直线BC的函数表达式y=2x+6;(2)证明:∵∠ACB的平分线CF与∠BAE的平分线AF相交于点F,∴∠FCA=∠BCA,∠FAE=∠BAE.∵∠BAE是△ABC的外角,∠FAE是△FAC的外角,∴∠BAE=∠ABC+∠BCA,∠FAE=∠F+∠FCA.∴∠ABC+∠BCA=∠F+∠BCA,∠ABC=∠F;(3)当AB=AP=10时,8﹣10=﹣2,P1(﹣2,0),8+10=18,P2(18,0);当AB=BP=10时,AO=PO=8,即P3(﹣8,0);设P(a,0),当BP=AP时,平方,得BP2=AP2,即(8﹣a)2=a2+62化简,得16a=28,解得a=,P4(,0),综上所述:P1(﹣2,0),P2(18,0),P3(﹣8,0);P4(,0).2017年4月18日。
八年级下数学第8周周末练习题

八年级下数学第8周周末练习题一、选择题(本大题共12小题,每小题4分,共48分)1.若x??3,则1?2迹ef的长为()a、 3.74b.3.75c.3.76d.3.7710。
你认识我吗?1.2,n?1.2,那么M2?氮气?3MN的值()1x等于()a、 9b、±3c、3d、5a.1b.-1c.3d.-32.若a?1,则二、填空题1是有意义的,那么M的值范围是。
M112.在下列命题中,逆命题成立(仅填写序列号)1a3化简后为()11.如果?MA.A.1.A.1b。
?1.A.1.交流电。
?A.1.1.公元1.A.A.一3.有五组数:①25,7,24;②16,20,12;③9,40,41;④4,6,8;⑤32,42,52,以各组数为边长,可以形成的直角三角形的数量是()a.1b。
2c。
3d。
四4.下列二次根式,不能与12合并的是().a、 48b.18c.1d。
?75① 同一侧的内角互补,两条直线平行;② 如果这两个角度是直角,那么它们是相等的;③如果两个实数相等,那么它们的平方相等;④ 如果三角形的三个边长a、B和C满足A2?b2?C2,那么这个三角形是直角三角形。
13.如图所示,这是一个三级步骤。
每个台阶的长度、宽度和高度分别为55cm、10cm和6cm。
A和B是这两个台阶的两端,所以蚂蚁从A点爬到B点的最短路线是14、如图,正方体abcd―a′b′c′d′的棱长为3,那么ac2=_______,a′c=________;15、一只蚂蚁从长、宽都是3,高是8的长方体纸箱的a点沿纸箱爬到b 点,那么它所行的最短路这条线的长度是_____;;16、如图,p为正方形abcd内一点,pa=1,pb=2,pc=3,则∠apb=_______.adbc?adbcpae第d公元题图b图CCB标题14的cba2135已知a,b,c为△abc三边,且满足(a-b)(a+b-c)=0,则它的形状为()a.rt△b、等腰三角形△ D.等腰三角形或rt△222226.众所周知,在RT中△ 美国广播公司,∠ C=90°,如果a+B=14cm,C=10cm,则RT的面积△ ABC是()a.24cm2b.36cm2c.48cm2d.60cm2227.如果直角三角形的三条边分别是a、B和C,a?144,b?25,那么C?()215a、169b、119c、169或119d、13或258.如图所示,在RT中△ 美国广播公司,∠ C=90°,D为AC上方的点,Da=DB=5,以及△ DAB为10,则DC的长度为();a、 4b、3c、5d、4.5aecda判定元件cbbcbafd图8问题10第9题图9.如图所示,对于一张直角三角形的纸,其两个右侧AC=6m,BC=8m。
八年级数学下学期第2周周练试题试题

后巷实验中学2021-2021学年八年级数学下学期第2周周练试题班级:_______________姓名:_______________一、选择题〔每一小题3分,一共24分〕1、以下说法中正确的选项是〔 〕A 、两个直角三角形全等B 、两个等腰三角形全等C 、两个等边三角形全等D 、两条直角边对应相等的直角三角形全等2、〔易错易混点〕如图,AB AD =,那么添加以下一个条件后,仍无法断定ABC ADC △≌△的是〔 〕A .CB CD = B .BAC DAC =∠∠C .BCA DCA =∠∠D .90B D ==︒∠∠3. 如下图, 将两根钢条AA ’、BB ’的中点O 连在一起, 使AA ’、BB ’可以绕着点O 自由旋转, 就做成了一个测量工件, 那么A ’B ’的长等于内槽宽AB, 那么断定△OAB ≌△OA ’B ’的理由是〔 〕A. 边角边B. 角边角C. 边边边D. 角角边4、如图,△ABC 中,∠C=90º,AD 平分∠CAB 交BC 于点D ,DE ⊥AB ,垂足为E ,且CD=6cm ,那么DE 的长为〔 〕A 、4cmB 、6cmC 、8cmD 、10cm5、〔易错易混点〕以下命题中:⑴形状一样的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有( )A 、3个B 、2个C 、1个D 、0个6、〔易错易混点〕如图,某同学把一块三角形的玻璃打破成了三块,如今他要到玻璃店去配一块完全一样形状的玻璃,那么最事的方法是带〔 〕去配。
A. ①B. ②C. ③D. ①和②7.以下说法中:①假如两个三角形可以根据“AAS 〞来断定全等,那么一定也可以根据“ASA 〞来断定它们全等;②假如两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等;③要判断两个三角形全等,给出的条件中至少要有一对边对应相等.正确的选项是〔 〕A .①和②B .②和③C .①和③D .①②③8、如图,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A ,B .以下结论中不一定成立的是〔 〕A .PA PB = B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP二、填空题〔每一小题3分,一共24分〕9、如图,假设111ABC A B C △≌△,且11040A B ∠=∠=°,°,那么1C ∠= .10、如图△ABD ≌△ACE ,且AB=8,BD=7,AD=6那么BC=________________.11、如图,AC=BD ,21∠=∠,那么△ABC ≌ , 其断定根据是_______。
八年级数学下学期第六周周练试题试题 (2)

人工智能在电子商务中的应用研究随着时代的发展,电子商务已经成为了现代的一项重要的商业形式。
越来越多的商家开始注重利用互联网这一平台进行商业交易。
而在电子商务的流程中,人工智能已经成为了一个非常关键的技术支持。
在此,本文就来深入研究人工智能在电子商务中的应用。
一、智能客服在传统的电商经营模式中,商家往往需要聘用一些客服人员,以便和顾客进行沟通和交流,及时解答顾客的疑问和提供帮助。
但是这种模式存在一个重要的局限性,即人类客服不可能在任何时刻都能够24小时全天候适应顾客不同的需求,因此会出现需要等待客服回复的时候,这不仅会影响顾客的体验,甚至会造成一定的挫败感。
而智能客服可以帮助商家完全解决这个难题。
智能客服是基于人工智能的智能聊天机器人,可以很好地替代人类客服的功能。
它能够根据顾客的提问与反馈,自动地配对相应的回答或解决方案。
当顾客有疑问或问题时,它可以随时随地和顾客进行较为自然和流畅的交流,解决各种问题,使得顾客的服务体验感到无比满意。
二、搜索引擎在购物过程中,搜索引擎是一个最为常见也最为重要的工具。
对于我们消费者而言,我们会根据不同的需求和欲望,在搜索输入框中输入自己需要的关键词,然后通过搜索引擎返回的结果,在海量的商品中筛选出特定的商品并选择购买。
人工智能在这一方面的应用是建立在深度学习模型之上的,在网络搜索引擎中可以为顾客提供极为出色的自然语言理解和语境感知技术,并通过将顾客的搜索历史和行为研究来实现精准的搜索排名。
三、个性化推荐根据顾客的购物和搜索习惯,人工智能可以对于顾客的反应和行为进行分析,进而在网站上进行个性化推荐,帮助顾客更加准确地寻找自己感兴趣的商品,并促进购物的顺利进行。
具体实现方法可以通过一些基于搜索行为的模型,通过计算模型来预测顾客可能感兴趣的商品,基本上正好是顾客最有可能买的商品,然后直接给顾客推荐这些商品。
这种基于搜索行为的推荐模型,不需要大量的训练,响应时间也可以很短,因此可以适用于很多不同的电商平台。
苏科版八年级数学下册周末练习2
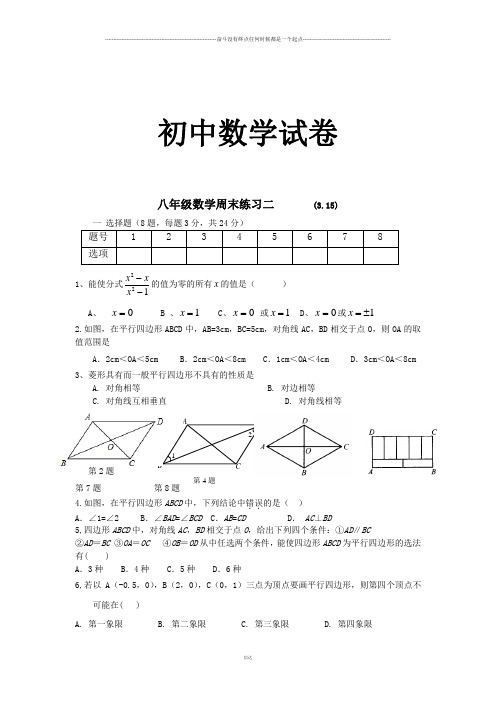
1 2 A B CD第4题初中数学试卷八年级数学周末练习二 (3.15)一 选择题(8题,每题3分,共24分)题号1 2 3 4 5 6 7 8 选项1、能使分式122--x x x 的值为零的所有x 的值是( ) A 、 0=x B 、1=x C 、0=x 或1=x D 、0=x 或1±=x2.如图,在平行四边形ABCD 中,AB=3cm ,BC=5cm ,对角线AC ,BD 相交于点O ,则OA 的取值范围是A .2cm <OA <5cmB .2cm <OA <8cmC .1cm <OA <4cmD .3cm <OA <8cm3、菱形具有而一般平行四边形不具有的性质是A. 对角相等B. 对边相等C. 对角线互相垂直D. 对角线相等第2题第7题 第8题 4.如图,在平行四边形ABCD 中,下列结论中错误..的是( ) A .∠1=∠2 B .∠BAD =∠BCD C .AB =CD D . AC ⊥BD5,四边形ABCD 中,对角线AC ,BD 相交于点O ,给出下列四个条件:①AD ∥BC②AD =BC ③OA =OC ④OB =OD 从中任选两个条件,能使四边形ABCD 为平行四边形的选法有( )A .3种B .4种C .5种D .6种6,若以A (-0.5,0),B (2,0),C (0,1)三点为顶点要画平行四边形,则第四个顶点不可能在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限7、如图,在菱形ABCD 中,∠ADC=120°,则BD :AC 等于( ).(A)3:2 (B )3: 3 (C )1:2 (D )3:18、如图,矩形ABCD 的周长为68,它被分成7个全等的矩形,则矩形ABCD•的面积为( )A .98B .196C .280D .284二 填空题(10题,每题2分,共20分)9、若关于x 的分式方程3232-=--x m x x 无解,则m 的值为________ 10、如图所示,把两个大小完全一样的矩形拼成“L ”形图案,则∠FAC=_______,∠FCA=_____11.平行四边形ABCD 的周长是18 cm ,对角线AC 、BD 相交于点O,若△AOD 与△AOB 的周长差是5 cm ,则边AB 的长是________ cm.12.平行四边形ABCD 中,E ,F 分别为AD ,BC 边上的一点.若再增加一个条件_________,就可得BE=DF 。
八年级数学下学期第2周周末作业试题 试题

卜人入州八九几市潮王学校大丰万盈二中二零二零—二零二壹八年级下学期第2周周末作业数学试题苏科班级__________一、选择题〔每一小题3分,一共24分〕1、在以下函数中表示y 关于x 的反比例函数的是--------------------―――--〔〕A 、x y 2=B 、x y 2=C 、12+=x yD 、22xy = 2、假设把分式2x x y+的x 和y 都扩大k 倍,那么分式的值应------------------〔〕A 、不变B 、扩大k 倍C 、缩小k 倍D 、无法确定 3、点〔2,5〕在反比例函数y=xk的图象上,那么以下各点在该函数图象上的是---〔〕 A 、〔2,—5〕B 、〔—5,—2〕C 、〔—3,4〕D 、〔4,—3〕 4、反比例函数xy 4=,那么当14-<<-x 时,y 的取值范围是--------――〔〕 A 、41<<y B 、24-<<-y C 、14-<<-y D 、42<<y5、如下列图,点B 是反比例函数y=kx 图象上一点,过点B 分别作x 轴、y•轴的垂线,假设构成的矩形面积是4,那么反比例函数的解析式是-()A 、y=-2xB 、y=2xC 、y=-4xD 、y=4xyxOCBA6、反比例函数xy 6=图象上有三个点)(11y x ,,)(22y x ,,)(33y x ,,其中3210x x x <<<,那么1y ,2y ,3y 的大小关系是------------------------------()A .321y y y <<B .312y y y <<C .213y y y <<D .123y y y <<7、函数1ky x-=的图象与直线y x =没有交点,那么k 的取值范围是--------〔〕 A .1k >B .1k <C .1k >-D .1k <-8、一次函数y=kx-k 与反比例函数y=kx在同一直角坐标系内的图象大致是---〔〕 二、填空题〔每一小题3分,一共30分〕9、函数124y x =-中,自变量x 的取值范围是. 10、如图,反比例函数xky =)0(<k 的图象与经过原点的直线l 相交于A 、B 两点,A 点坐标为)1,2(-,那么B 点的坐标为.11、y 是x 的反比例函数,且x =2时,y =7.那么y 与x 之间的函数关系式是. 12、双曲线xmy 21-=〔m 为常数〕当0<x 时,y 随x 的增大而增大,那么m 取值范围是 .13、假设双曲线y=(2m-1)22m x-的图象在第一、三象限,那么函数的解析式为.14、当m=________时,关于x 的分式方程213x mx +=--无解. 15、假设双曲线xk y 3-=的图象在一、三象限,直线x k y )92(-=过二、四象限,那么k 的整数值是. 16、假设直线y=2x+l 的图象与双曲线图象的一个交点横坐标为l ,那么双曲线解析式为. 17、如图,△OPQ 是边长为2的等边三角形,假设反比例函数的图象过点P,那么它的解析式是. 18、a 、b 为实数,且ab=1,设11a b Pa b =+++,1111Q a b =+++, 那么P______Q(填“>〞、“<〞或者“=〞)三、解答题〔第19、20每一小题6分,第21-24每一小题6分,25题10分,一共46分〕 19、化简.(1)4222a a a a ⎛⎫⎛⎫+-÷ ⎪ ⎪--⎝⎭⎝⎭(2)2222142442a a aa a a a a a+--⎛⎫-÷ ⎪--+-⎝⎭ 20、解以下分式方程.(1)132x x =-;(2)2133112133119x x x x x -++=+--. 21、假设关于x 的方程12-=--x ax 的解大于0,求a 的取值范围。
八年级下册数学第二周周清卷
初二数学第2周周末练习卷(内容:勾股定理,满分100分) 姓名: 总分:一、选择题(每小题3分,共12题,36分)1.下列各组数中以a ,b ,c 为边的三角形不是直角三角形的是( )A .2=a ,3=b , 4=cB .7=a ,24=b , 25=cC .6=a ,8=b , 10=cD .a=n 2﹣1,b=2n ,c=n 2+12.下列定理中,没有逆定理的是( )A.两直线平行,同旁内角互补B.直角三角形两锐角互余C.对顶角相等D.等腰三角形的两底角相等3.一直角三角形的斜边长比一直角边长大2,另一直角边长为6,则斜边长为()A.4B.8C.10D.124.如图所示:数轴上点A 所表示的数为a ,则a 的值是( )A .5+1B .-5+1C .5-1D .5 5.下列命题①如果a ,b ,c 为一组勾股数,那么a 4,b 4,c 4仍是勾股数;②如果直角三角形的两边是5、12,那么斜边必是13;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a ,b ,c (c b a =>),那么1:1:2::222=c b a 。
其中正确的是( ) A .①② B .①③ C .①④ D .②④6.如图所示,将一个有45°角的三角板的直角顶点放在一张宽为3cm 的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板的最大边的长为( )A.3 cmB.6cmC.23cmD.26cm7.如图,在△ABC 中,AB=AC=5,BC=6,点M 为BC 的中点,MN ⊥AC 于点N ,则MN 的长为( )A.56B.59C.512D.516 8..如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a ,较短直角边为b ,则ab 的值是( )A .4B .6C .8D .109.若△ABC 中,13,15AB AC ==,高AD=12,则BC 的长为( )30° 第6题图 AM C B N第7题图 12-3-210-13A 第4题图第8题图A .14B .4C .14或4D .以上都不对10.一座建筑物发生了火灾,消防陈到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最多能伸长13米,则云梯可以达到该建筑物的最大高度( )(消防车的高度忽略不计)A.12米B.13米C.14米D.15米11.如图,已知在直角三角形ABC 中,∠ACB=90°,AB=4,分别以AC,BC 长为直径作半圆,面积分别为21,S S ,则21S S +的值等于( )A.4B.8C.16D.2012.如图,在△ABC 中,∠BAC=90°,AB=3,AC=4,AD 平分∠BAC 交BC 于点D ,则BD 的长为( ) A.715 B.512 C.720 D.521 二、填空题(每小题3分,共6题,18分)13.利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为 ,该定理的结论其数学表达式是 。
初二数学周周练.docx
2 •下列运算错误的是c. -^1 x 1-1 4.平行四边形一边长为10, —条对角线长为6,则它的另一条对角线长a 的取值范围为A. 4<a<16B. 14<a<26C. 12<a<20D. 8<a<32 5•如图,将AABC 沿着它的中位线DE 折叠后,点A 落到点若ZC = 120°, ZA = 26°,则ZA'DB 的度数是().A. 120°B. 112°C. 110°D. 108°6. 如图,点D 、E 、F 分别是△ABC 三边的屮点,则下列判断错误的是() A.四边形AEDF —定是平行四边形B.若ZA = 90°,则四边形AEDF 是矩形C.若4D 平分ZA,则四边形AEDF 是正方形D.若AD 丄BC,则四边形AEDF 是菱形7. 如图,E 、F 、G 、H 分别是BD 、BC 、AC. AD 的中点,且AB=CD.下列结论:①EG 丄FH,②四边 形EFGH 是矩形,③平分ZEHG,④四边形EFGH 是菱形.其中正确的个数是( )A. 1B. 2C. 3D. 48. 如图,在 RtAABC 中,ZA=90°, AB=3, AC=4, P 为边 BC 上一动点,PE 丄 AB 于 E, PF 丄AC 于 F, 10. 已知y —2与x 成反比例,当x=3时,y=l,则y 与x 的函数关系式为 ___________________________ ____________ 211. 若实数a 、b 满足J2G +4 + Jb+4 =0,则仝= ;初二数学周周练4 一、选择题(每小题3分,共24分) 1.下列图形分别是桂林、湖南、甘肃、 佛山电视•台的台徵,为中心对称图形的是( )• A.B. D.C. -m - n A. ---------- tn + n B. U1 m - n m — n n — m C.二D. m-nY n-m)2 =13.下列分式中, 属于戢简分式的是 B 严 JT +1 则刃的取值范圉是 _________A ・£ 9.若匚石在实数范阖内有意义, 笫8题-k 2 -212. ------------------------- 在函数y = (k 为常数)的图象上有三个点(一2, Yl ), (-1,y 2),的大小为 ________________ 13・若一址二一=二一+亠一,则加二 (a + 2)(a —1) Q + 2 Q — \ 14. 某同学从家去学校上学的速度为d,放学回家吋的速度是b,则该同学上学、放学的平均速度为 ______________ •Y 4- 727 31T115. 若关于兀的方程—— + ^=3的解为正数,则加的取値范围是x-3 3-A16. 如图,在平行四边形ABCD 中,AD-2AB, F 是M )的中点,作CE 丄AB,垂足E 在线段AB 上,连接EFCF,则下列结论屮一定成立的是 ________________ .(把所有正确结论的序号都填在横线上)① 4CF 冷 ZBCD ② EF=CF ③④ZDFE=3/AEF.17. 如图,平面直角坐标系中,DOABC 的顶点A 坐标为(6, 0) , C 点坐标为(2, 2),若直线y 二mx+2平19. (本题8分)解下列方程.5x — 4 4x + 10 (1) -------- = --------- -1x-2 3兀一6 20. (本题10分)甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去 学校,乙同学骑自行车去学校.已知甲步行的速度是乙骑自行车速度的丄,公交车的速度是乙骑自行车速 2函数值yi, y2, y3n= ____________分[Z10ABC 的周长,则m 的值为 三、解答题:18・(木题8分)计算:t b a 2ab ⑴ ----- + ------- _ ---- 7 a-b a + b b~ _cr (2) 壬红—1+S) a 2b-alr 2abX+1 4 x 2-l度的2倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.(1)求乙骑自行车的速度;(2)当甲到达学校时,乙同学离学校还有多远?21.(本题8分)如图,直线y=kx+b与反比例函数y = —(xVO)的图象相交于点A、点B,与x轴交于点C,x其屮点A的坐标为(一2, 4),点B的横坐标为一4・(1)试确定反比例函数的关系式;(2)求ZiAOC的面积.22.(本题10分)如图,四边形ABCD中,ZA=ZABC=90° , AD=1, BC二3, E是边CD的中点,连接BE并延长与AD的延长线相交于点F. (1)求证:四边形BD FC是平行四边形;(2)若ABCD是等腰三角形,求四边形BDFC的面积.23.(本题12分)如图,矩形OABC的边0A在x轴正半轴上,边0C在y轴正半轴上,B点坐标为(1, 3).矩形O' A' BC'是矩形0ABC绕B点逆时针旋转得到的.(T点恰好在x轴的正半轴上,0/ C' 交AB于点D.①求点0,的坐标,并判断△()' DB的形状(要说明理由);②求边L (T所在直线的解析式;③延长BA到M使AM二1,在(2)屮求得的直线上是否存在点P,使得△P0M是以线段0M为直角边的直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.。
+2023-2024学年苏科版八年级下册数学第7周周练试卷
苏科版八年级下册数学第7周周练试卷班级: 姓名:一、选择题:1、已知四边形ABCD 是平行四边形,下列结论不正确的是 ( )A .当AB =BC 时,它是菱形 B .当AC ⊥BD 时,它是菱形C .当∠ABC =90°时,它是矩形D .当AC =BD 时,它是正方形2、直角三角形斜边上的中线与连结两直角边中点的线段的关系是 ( )A .相等且平分B .相等且垂直C .垂直平分D .垂直平分且相等3、如图,在平面直角坐标系中,菱形MNPO 的顶点P 坐标是(3,4),则顶点M 、N 的坐标分别是 ( )A .M (5,0),N (8,4)B .M (4,0),N (8,4)C .M (4,0),N (7,4)D .M (5,0),N (7,4)4、如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在C ′处,折痕为EF ,若AB =1,BC =2,则△ABE 和BC ′F 的周长之和为 ( )A . 8B . 6C . 4D . 35、如图,点A 是直线l 外一点,在l 上取两点B 、C ,分别以A 、C 为圆心,BC 、AB 长为半径画弧,两弧交于点D ,分别连接AB 、AD 、CD ,则四边形ABCD 一定是 ( )A .平行四边形B .矩形C .菱形D .梯形6、如图,在菱形ABCD 中,对角线AC 与BD 交于点O ,OE ⊥AB ,垂足为E ,若∠ADC =130°,则∠AOE 的大小为 ( )A .75°B .65°C .55°D .50°7、如图,在矩形ABCD 中,AB =4,BC =8,对角线AC 、BD 相交于点O ,过点O 作OE 垂直AC 交AD 于点E ,则AE 的长是 ( )A .3B .5C .2.4D .2.58、如图,在△ABC 中,点D 、E 分别是AB 、AC 的中点,∠C =105°,将△ABC 沿DE 折叠,点A 的对应点是点A ′,则∠AEA ′的度数为 ( )A .145°B .150°C .155°D .160°A B CDE F C ′ y x O M NP 第3题图 第6题图 第7题图 第8题图 第4题图第5题图二、填空题:9、菱形的两对角线长分别为10cm 和24cm ,则面积为 cm 2;一边上的高为 cm . 10、如图,在△ABC 中,点D 是BC 的中点,点E ,F 分别在线段AD 及其延长线上,且DE =DF .给出下列条件:①BE ⊥EC ;②BF ∥CE ;③AB =AC ;从中选择一个条件使四边形BECF 是菱形,你认为这个条件是__________(只填写序号).11、如图,菱形ABCD 中,∠DAB =60°,DF ⊥AB 于点E ,且DF =DC ,连接FC ,则∠ACF 的度数为 .12、如图,四边形ABCD 中,DC AD =, 90=∠=∠ABC ADC ,AB DE ⊥,若四边形ABCD 面积为16,则DE 的长为13、如图,平行四边形ABCD 的周长为36,对角线AC ,BD 相交于点O .点E 是CD 的中点,BD =12,则△DOE 的周长为 .14.如图,为估计池塘岸边A 、B 两点间的距离,在池塘的一侧选取点O ,分别取OA 、OB 的中点M 、N ,测得MN=4m ,则A 、B 两点间的距离是 m .15、如图,在四边形ABCD 中,P 是对角线BD 的中点,E 、F 分别是AB 、CD 的中点,AD =BC ,∠FPE =100°,则∠PFE 的度数是 .16、如图,□ABCD 的对角线AC ,BD 相交于点O ,点E ,F 分别是线段AO ,BO 的中点,若AC=10,BD=14,△OA B 的周长是18cm ,则EF = cm .三、解答题:17、如图,在菱形ABCD 中,AB =2,∠DAB =60°,点E 是AD 边的中点,点M 是AB 边上的一个动点(不与点A 重合),延长ME 交CD 的延长线于点N ,连接MD ,AN ,(1)求证:四边形AMDN 是平行四边形.(2)当AM 的值为何值时,四边形AMDN 是矩形?请说明理由.第10题 第11题 A B C DO E F A B C F D E 第12题图第13题图 A M B C DN E第14题 第15题 第16题18、如图,在正方形ABCD中,对角线AC、BD相交于点O,E是BC边上一点,连结AE交BD于点F,G是AC上一点,B、G关于直线AE对称.求证:四边形BEGF为菱形19、如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.(1)求证:∠AFD=∠EBC;(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.20、如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.(1)求证:四边形EGFH是平行四边形;(2)在(1)的条件下,若EF⊥BC,且EF=12BC,求证:平行四边形EGFH是正方形.21、在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.(1)如图1,当E是线段AC的中点时,求证:BE=EF.(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论:.(填“成立”或“不成立”)(3)如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.22、如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.(1)请写出CM和EM的数量关系和位置关系,并加以说理;(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD 上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.HMEFG BCD AHMEFGBCADHMEFGBCD A图1 图2 图3 图1 图2 图3。
苏科版八年级数学下册周末练习2.doc
E DC BA N M ∠︒E D CB A八年级周末练习(2)一、选择题1.矩形具有而一般平行四边形不具有的性质是 ( )A .对角线相等B .对边相等C .对角相等D .对角线互相平分2.下列图形中不一定是菱形的是 ( ) A .两条对角线互相垂直平分的四边形 B .一组邻边相等的四边形C .有一条对角线平分一个内角的平行四边形D .用两个全等的等边三角形拼成的图形 3.四边形ABCD 中,O 是对角线的交点,能判别此四边形是正方形的是 ( ) (1)AC=BD ,AB ∥CD ,AB=CD ; (2)AD ∥BC ,∠A=∠C ;(3)AO=CO ,BO=DO ,AB=BC ; (4)AO=BO=CO=DO ,AC ⊥BD A .1个 B .2个 C .3个 D .4个4.如图,将矩形ABCD 沿AE 折叠,若∠BAD'=30°,则∠AED'等于 ( ) A .30° B .45° C .60° D .75°5.如图,矩形ABCD 中,AB =3,BC =5.过对角线交点O 作OE ⊥AC 交AD 于E ,则AE 的长是 ( )A .1.6B .2.5C .3D .3.4 6.如图,正方形ABCD 中,CE=MN ,∠MCE=35°,那么∠ANM 是 ( ) A .45° B .55° C .65° D .75°7.已知矩形ABCD 的AB=2BC ,在CD 上取点E ,使AE=AB ,那么∠EBC 等于 ( ) A .10°; B .22.5°; C .30°; D .15°;(第7题) (第8题)8.平行四边形ABCD 中,点A 1,A 2,A 3,A 4和C 1,C 2,C 3,C 4分别是AB 和CD 五等分点,点B 1,B 2和D 1,D 2分别是BC 和DA 三等分点,若四边形A 4B 2C 4D 2面积为1.则平行四边形ABCD 面积为 ( ) A .2 B .35 C .53D .15 二、填空题1.在ABCD 中,若∠A -∠B=70°,∠A=________°,∠D=________°.2.在□ABCD中,一角的平分线把一条边分成3 cm和4 cm两部分,则□ABCD的周长为______.3.菱形的两条对角线长为6cm、8cm,其边长为cm,面积为cm²4.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F.连接CE,则CE的长是_______.5.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是_______厘米.6.如图所示,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=3,则PP′=_________7.如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奔牛初中八年级下学期周周练(2)
一、选择题:
1.下列图形中,既然是轴对称图形又是中心对称图形的是 ( )
A 、等腰三角形
B 、矩形
C 、平行四边形
D 、直角三角形
2.下列判断正确的个数是 ( ) ①平行四边形的对角线互相平分; ② 一组对角互补的平行四边形是矩形
③对角线互相平分的四边形是平行四边形; ④对角线相等的四边形是矩形。
A. 0个
B. 1个
C. 2个 D . 3个
3.下列关于矩形的说法中正确的是 ( )
A .对角线相等的四边形是矩形
B .对角线互相平分的四边形是矩形
C .矩形的对角线互相垂直且平分
D .矩形的对角线相等且互相平分
4.如图,在△ABC 中,CF ⊥AB 于F ,BE ⊥AC 于E ,M 为BC 的中点,EF=7,BC=10,
则△EFM 的周长是 ( )
A .17
B .21
C .24
D .27
第4题图 第5题图 第7题图 第8题图 5.如图,在菱形ABCD 中,AB=2,∠BAD=60°,E 是AB 的中点,P 是对角线AC 上的一
个动点,则PE+PB 的最小值为( )
A .1
B .
C .2
D .
二、填空题:
6.若一个平行四边形的一边长为8,一条对角线长为6,则另一条对角线x 的取值
范围
7.如图,矩形ABCD 中,AE ⊥BD ,垂足为E ,AB=2,BD=4,则∠BAE= ,BE=
8.如图,已知菱形ABCD 的周长为20cm ,∠A :∠ABC=2:1,则对角线BD 的长
度是 cm
9.平行四边形的一个角的平分线分平行四边形一边为3厘米和5厘米两部分,则这个四边
形的周长为 。
10.如图,矩形ABCD 中,AB=3,BC=4,点E 是BC 边上一点,把∠B 沿AE 折叠,使点
B 落在点B ′处,则:①AB ′= ;②当△CEB ′为直角三角形时,BE= .
三、解答题:
O E D C B A
11.如图,平行四边形ABCD的对角线相交于点,直线EF过点O分别交BC、AD于点E、
F,G、H分别为OB、OD的中点,四边形GEHF是平行四边形吗?为什么?
12.如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE
相交于点O.
(1)求证:四边形ADCE是矩形.
(2)若∠AOE=60°,AE=4,求矩形ADCE对角线的长.
13.如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,求∠COD和∠CFO的度数
14.如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由.
15.在平面直角坐标系xOy中,如图,已知Rt△DOE,∠DOE=90°,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5.∠ACB+∠ODE=180°,
∠ABC=∠OED,BC=DE.按下列要求画图(保留作图痕迹):
(1)将△ODE绕O点按逆时针方向旋转90°得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN;
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与(1)中的△OMN的边NM重合;
(3)求OE的长.
12.(1)证明:∵四边形ABDE是平行四边形,∴AB=DE,
又∵AB=AC,
∴DE=AC.
∵AB=AC,D为BC中点,
∴∠ADC=90°,
又∵D为BC中点,
∴CD=BD.
∴CD∥AE,CD=AE.
∴四边形AECD是平行四边形,
又∴∠ADC=90°,
∴四边形ADCE是矩形.
(2)解:∵四边形ADCE是矩形,
∴AO=EO,
∴△AOE为等边三角形,
∴AO=4,
故AC=8.
15.解:(1)△OMN如图所示;
(2)△A′B′C′如图所示;
(3)设OE=x,则ON=x,作MF⊥A′B′于点F,由作图可知:B′C′平分∠A′B′O,且C′O⊥O B′,所以,B′F=B′O=OE=x,F C′=O C′=OD=3,
∵A′C′=AC=5,
∴A′F==4,
∴A′B′=x+4,A′O=5+3=8,
在Rt△A′B′O中,x2+82=(4+x)2,
解得x=6,
即OE=6.。
