中考数学总复习考点系统复习第六节 二次函数的综合应用
中考数学考点,二次函数的应用,数的开方与二次根式,精品系列

第六节二次函数的应用,精品系列课标呈现指引方向会利用二次函数解决简单的实际问题考点梳理夯实基础1.二次函数的实际应用问题(1)利用顶点坐标来求最值(2)最值不在顶点处取得(3)分段函数求最值问题2.解决二次函数的实际应用问题的关键在于:(1)理解问题;(2)分析问题中变量之间的关系;(3)建立二次函数模型,得到解析式:(4)运用二次函数的有关性质求解;(4)将所得结果结合实际情况进行检验.考点精析专项突破考点一二次函数与几何问题【例1】(2016四川内江)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.(1)若苗圃园的面积为72平方米,求x;(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.解题点拨:二次函数常用来解决最优化问题,这类问题实际上就是求函数的最大(小)值.在此类实际问题中,最大(小)值有时会在顶点处取得,此时达到最大(小)值时的x即为顶点横坐标值,最大(小)值也就是顶点纵坐标值;有时会在端点取得.因此,对于实际问题中的最值问题要特别注意自变量的取值范围.解:(1)苗圃园与墙平行的一边长为(30-2x)米.依题意可列方程x( 30-2x)= 72,即x2-15x+36=0.解得x1 =3,x2 =12.∵当x=3时,30-2x =24>18,∴x=12.(2)依题意,得8≤30-2x≤18.解得6≤x≤11.面积S=x(30-2x)= -2(x-152)2+2252(6≤x≤11).①当x=152时,s有最大值,s最大=2252;②当x =11时,S有最小值,S最小=11x(30-22)=88.(3)令x(30-2x)= 100,得x2-15x+50=0.解得x1=5,x2=10.∴x的取值范围是5≤x≤10.考点二二次函数与利润问题【例2】(2016湖北随州)九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下:已知商品的进价为30元/件,设该商品的售价为y (单位:元/件),每天的销售量为p (单位:件),每天的销售利润为W (单位:元).(1)求出W 与x 的函数关系式;(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润.解题点拨:(1)此题主要考查了二次函数的应用以及配方法求二次函数最值等知识,建立函数并运用函数的性质是解题的关键;(2)分段函数的分类讨论是本题的考查重点,因此本题要分段考虑.解:(1)当o ≤x ≤50时,设商品的售价y 与时间x 的函数关系式为y =kx +b (k 、b 为常数且k ≠0), ∵y =kx +b 经过点(0,40)、(50,90),405090b k b =⎧⎨+=⎩,解得:140k b =⎧⎨=⎩, ∴售价y 与时间x 的函数关系式为y =x +40;当50<x ≤90时,y =90. ∴售价y 与时间x 的函数关系式为40050905090x x y x x x +≤⎧=≤<≤⎨⎩(,且为整数)(,且为整数) ’由题意可知每天的销售量p 与时间x 成一次函数关系,设每天的销售量p 与时间x 的函数关系式为P=mx +n (m 、n 为常数,且m ≠0),∵P=mx +n 过点(60,80)、(30,140), ∴608030140m n m n +=⎧⎨+=⎩,解得:2200m n =-⎧⎨=⎩,∴P =-2x +200(0≤x ≤90,且x 为整数),当0≤x ≤50时,W =(y -30)•p=(x +40-30)(-2x +200)=-2x 2+180x +2000;当50<x ≤90时,W =(90-30)(-2x +200)=-120x +12000.综上所示,每天的销售利润W 与时间x 的函数关系式是221802000050120120005090x x x x x x w x -++≤≤-+<≤⎧⎪=⎨⎪⎩(,且为整数)(,且为整数) (2)当0≤x ≤50时,W =-2x 2+180x +2000 =-2(x -45)2+6050, ∵a =-2<0且0≤x ≤50.∴当x =45时,W 取最大值,最大值为6050元. 当50<x ≤90时,W =-120x +12000, ∵k =-120<0,W 随x 增大而减小,∴当x = 50时,W 取最大值,最大值为6000元.∵6050>6000.∴当x=45时,W最大,最大值为6050元.即销售第45天时,当天获得的销售利润最大,最大利润是6050元.课堂训练当堂检测1.函数y=x2 +2x+3的最小值为( )A.-2 B.2 C.1 D.-1【答案】B2.已知0≤x≤1,那么函数y= -2x2+8x-6的最大值是( )2A.- 10.5 B.2 C.-2.5 D.-6【答案】C3.(2016四川成都)某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树,橙子的总产量为W.则W与x的关系式为.【答案】W=-5x2+100x+600004.(2016云南)草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y 与x的函教关系图象.(1)求y 与x 的函数解析式;(2)设该水果销售店试销草莓获得的利润为W 元,求W 的最大值, 解:(1)设y 与x 的函数关系式为y =kx +b . 根据题意,得:2030030280k b k b +=⎧⎨+=⎩,解得:2340k b =-⎧⎨=⎩,∴y 与x 的函数解析式为y =-2x +340,(20≤x ≤40). (2)由已知得:W =(x -20)(-2x +340) = -2x 2+380x -6800 = -2(x -95)2+11250, ∵-2<0.∴当x ≤95时,W 随x 的增大而增大, ∵20≤x ≤40.∴当x =40时,W 最大, W 最大值=-2(40-95)2+11250=5200(元) 中考达标 模拟自测A 组 基础训练一、选择题1.当x取( )时,二次函数y= -x2+1有最大值.B.0 C.1 D.2A.12【答案】B2.如果二次函数y= x2-2x+m的最小值为非负数,则m的取值范围是( ).A.m<1B.m>1C.m≤1D.m≥1【答案】D3.如图,教练对小明推铅球的录像进行技术分析,发现铅球行进高度y( m)与水平距离x(m)之间的关系为y=-1(x-4)2+3,由此可知铅12球推出的距离是()A.3mB.7mC.10mD.14m【答案】C4.如图,重庆某长江大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需()秒.A .12B .18C .24D .36 【答案】D 二、填空题5.已知二次函数y =-x 2+4x +5,其中-2≤x ≤1,则y 有最小值为,最大值为.【答案】-7 86.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数)出售,可卖出(40一x )件.若使利润最大,每件的售价应为元. 【答案】307.(2016浙江丽水改编)如图,地面BD 上两根等长立柱AB ,CD 之间悬挂一根近似成抛物线y =2143105x x -++3的绳子,则绳子最低点离地面的距离为m .【答案】1.4 三、解答题8.(2016山东潍坊)旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出:当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少l辆.已知所有观光车每天的管理费是1100元.(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入-管理费)(2)当每辆车的日租金为多少元时,每天的净收入最多?解:(1)由题意知,若观光车能全部租出,则0<x≤100,由50x-1100>0,解得x>22.又∵x是5的倍数,∴每辆车的日租金至少应为25元:(2)设每辆车的净收入为y元,当0<x≤100时,y1= 50x-1100,∵y随x的增大而增大,∴当x=100时,y1的最大值为50x100-1100= 3900;当x>100时.x ) x-1100y2=(50-1005=-1x2+70x-11005(x-175)x2+5025,=-15当x =175时,y 2的最大值为5025, 5025>3900.故当每辆车的日租金为175元时,每天的净收入最多是5025元. 9.课本中有一道作业题:有一块三角形余料,记作△ABC ,它的边BC = 120mm ,高AD = 80mm .要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB ,AC 上.问加工成的正方形零件的边长是多少mm ?小颖解得此题的答案为48mm .小颖善于反思,她又提出了如下的问题.(1)如果原题中要加T 的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm ?请你计算.(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.解:(1)设矩形的边长PN = 2ymm ,则P Q=ymm ,由条件可得△APN ∽△ABC . ∴PN AEBCAD =,即2120y =8080y -,解得y=2407,∴PN=2407×2=4807 ( mm),答:这个矩形零件的两条边长分别为2407mm ,4807mm ;(2)设PN =xmm ,由条件可得△APN ∽△ABC , ∴PN BC=AE AD,即120x=8080PQ -, 解得PQ= 8023x -.∴S=PN ·PQ=x(8023x -)=23x -2+80x=22(60)3x -- +2400,∴S 的最大值为2400mm 2,此时PN= 60mm ,PQ=802603-⨯ =40(mm).B 组 提高练习10.(2016山东青岛改编)如图,需在一面长度为l0m 的墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax 2+bx (a ≠0)表示.已知抛物线上B ,C 两点到地面的距离均为34m , 到墙边OA 的距离分别为12m ,32m .则最多可以连续绘制( )个这样的抛物线型图案? A .4 B .5 C .6 D .7第10题【答案】(提示:根据题意得:B(12,34),C(32,34),把B ,C 代入y =ax 2+bx 得311442393442a b a b ⎧=+⎪⎪⎨⎪=+⎪⎩,解得:12a b =-⎧⎨=⎩,∴抛物线的函数关系式为y=-x 2+2x ;令y=0,即-x 2+2x=0,∴x 1=0.x 2=2,∴l0÷2=5,∴最多可以连续绘制5个这样的抛物线型图案.选B )1 1.(2016浙江台州)竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t 秒时在空中与第二个小球的离地高度相同,则t= .【答案】(提示:设各自抛出后1.1秒时到达相同的最大离地高度为h ,则小球的高度y=a (t-l.l )2+h ,由题意a (t-l.l )2+h=a (t-l-l.l )2+h ,解得t=1.6.故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.)12.(2015年江苏南京)某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD 、线段CD 分别表示该产品每千克生产成本y 1(单元:元)、销售价 y 2(单位:元)与产量x (单位:kg )之间的函数关系.(1)请解释图中点D 的横坐标、纵坐标的实际意义. (2)求线段AB 所表示的y 1与x 之间的函数表达式.(3)当该产品产量为多少时,获得的利润最大?最大利润是多少? 【答案】解:(1)点D 的横坐标、纵坐标的实际意义:当产量为130kg 时,该产品每千克生产成本与销售价相等,都为42元. (2)设线段AB 所表示的y 1与x 之间的函数关系式为y=k 1x+b 1, ∵y 1=k 1x+b 1的图象过(0,60)与(90,42),∴111609042b k b =⎧⎨+=⎩,解得110.260k b =-⎧⎨=⎩∴线段AB 所表示的y 1与x 之间的函数表达式为y 1=- 0.2x+60(0≤x ≤90).(3)设y 2与x 之间的函数表达式为y 2 =k 2x+b 2, ∵y 2=k 2x+b 2的图象过(0,120)与(130,42),∴22212013042b k b =⎧⎨+=⎩,解得220.6120k b =-⎧⎨=⎩,第12题∴y 2与x 之间的函数表达式为y 2 =-0.6x+120(0≤x ≤130). 设产量为xkg 时,获得的利润为W 元, 当0≤x ≤90时.W=x[(-0.6x+120)-(-0.2x+60)]=-0.4(x-75)2+2250 ∴当x= 75时,W 的值最大,最大值为2250. 当90≤x ≤130时.W=x[(-0.6x+120)-42]= -0.6(x-65)2+2535,由-0.6<0知,当x>65时,W 随x 的增大而减小,因此当x= 90咐,W 的值最大,最大值为W=-0.6(90-65)2+2535= 2160. ∴90≤x ≤130时.W ≤2160.因此,当该产品产量为75kg 时获得的利润最大,最大利润是2250元.第四节数的开方与二次根式,精品系列了解二次根式、最简二次根式的概念,了解二次根式(根号下仅限于数)加、减、乘、除运算法则,会用它们进行有关的简单四则运算,1(a≥0)的式子叫做二次根式.其中a叫被开方数.2.二次根式的性质:(1) a≥0)具有双重非负性,一是a≥00.(2)2()0a a=≥(0)(0)a aaa a≥⎧==⎨-<⎩3.二次根式的有关概念(1)最简二次根式:满足下列两个“不含”条件的二次根式是最简二次根式.①被开方数中不含分母,分母中也不含二次根式:②被开方数中不含能开得尽方的因数或因式.(2)同类二次根式:几个二次根式化成最简二次根式后,如果被开方数相同,则把这几个二次根式叫做同类二次根式.4.二次根式的运算:(1)加减运算:在二次根式加减运算中,先把二次根式化为最简二次根式,再合并同类二次根式.二次根式的加减实质是合并同类二次根式.(2)0,0)0),b,=≥≥=≥>ab b a oa b a(3)运算顺序:先算乘方,再算乘除,最后算加减,如果有括号,就先算括号里的.实数中的运算律及乘法公式在二次根式中同样适用.考点一根式的性质【例1】(1)(2015x的取值范围在数轴上表示出来,正确的是( )【答案】C(2)已知2-+=,则x+y的值为()x y(3)0A.0 B.-1 C.1 D.5解题点拨:本题考查的知识点为:二次根式有意义则二次根式的被开方数是非负数.【答案】C考点二根式的运算【例2】(1)(2016龙岩)与()A B C D.【答案】C(2)(2016南充)下列计算正确的是 ( )A =B 2=C =D x = 【答案】A(3)下列运算中,错误的有 ( )个①5112=3=±2=1194520=+=. A .1 B .2 C .3 D .4 【答案】C(4)(2016解题点拨:先化简成最简根式,再合并,【答案】解:原式== 考点三 根式的化简【例3】(1)当l<x<4(2)a 、b 、c a b +解题点拨:利用二次根式的非负性这一性质去进行根式的化简时,注意符号运算.【答案】解:(1) ∵1<x<4,∴x-4<0,x-1>0,∴4125x x x =--+=-+.(2)由数轴可知,0<a<1,c<b<-1, ∴-a<0,a+b<0,c<0∴a a b c a b b c =--+=+-+.A 组 基础训练1.(2016白贡)若代数式x有意义,则x 的取值范围是 ( ) A .x ≥l B .x ≤1且x ≠0 C .x ≠1 D .x ≠0 【答案】A2.(2016巴中)下列二次根式中,是同类二次根式的是 ( )A.B. C D 【答案】B3.若2y =-则()yx y += .【答案】144.计算:(1)【答案】解:原式9=.(2) 2【答案】解:原式=0.(3) 2.【答案】解:原式= 30-(4)22(7(7-【答案】解:原式=2.一、选择题1.下列运算中错误的是 ( )AB C 2= D .2 (3= 【答案】A2.化简:341()(1)32a a a a -+---的结果等于 ( ) A .a-2 B .a+2 C .2 3a a -- D .32a a --【答案】B3.已知x y =,则22x xy y ++的值为( ) A .2 B .4 C .5 D .7 【答案】B4.(2015孝感)已知2x =2(7(2x x ++值是 ( )A .0B .石C .2+再D .2 -万 【答案】C 二、填空题 5.在函数y =x 的取值范围是 . 【答案】x>-26.(20153x =-,则x 的取值范围是【答案】3x ≤7.已知12x x =,则2212x x += .【答案】10 三、解答题8.计算:01-)603π°.【答案】解:原式= 412--= 4-1-3 =0.(2) 1). 【答案】解:原式=221)]1)3(21)321=-=--=-+=(3)0111)-+- 【答案】解:原式=11+=9.(2016桂林)已知任意三角形的三边长,如何求三角形面积?古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式一海伦公式s (其中a ,b ,c 是三角形的三边长,2a b cp ++=,s 为三角形的面积) 例如:在△ABC 中,a=3,b=4,c=5,那么它的面积可以这样计算: ∵a=3,b=4,c=5. ∴ 2a b cp ++==6 ∴6s ===. 如图,在△ABC 中,BC=5,AC=6,AB=9, (1)用海伦公式求△ABC 的面积; (2)求△ABC 的内切圆半径r .【答案】解:(1) ∵BC=5,AC=6,AB=9, ∴5691022BC AC AB p ++++===∴s =故△ABC 的面积:(2) ∵1()2s r AC BC AB =++,∴()15692r =++,解得:r =故△ABC 的内切圆半径r =B 组提高训练10.(2016乐山)在数轴上表示实数a 的点如图所示,2a -的结果为 ( )A .-7B .-3C .7D .3(提示:由圈可知2<a<5,原式=-(n-5)+a-2=3.) 【答案】D11.当a<1的结果是 .(提示:∵a<1, ∴a<0,原式==-)【答案】-12.观察下列运算1=-+==…,=利用上面的规律计算⋯++. 【答案】解∵1=-===∴原式(2--2-1=2013。
中考数学 考点系统复习 第三章 函数 第六节 二次函数的图象与性质及与a,b,c的关系

D.当x<2时,y随x的增大而增大
重难点 2:二次函数的图象与系数 a,b,c 的关系 如图,抛物线 y=ax2+bx+c 的对称轴为直线 x=1,与 x 轴交于点
A(-1,0),与 y 轴的交点在(0,-2),(0,-3)之间(包含端点),判断 下列结论的正误.
(1)abc<0 (2)2a+b=0 (3)2a-b>0 (4)b2-4ac<0 (5)a+c=b (6)3a+b<0 (7)3b+c>0 (8)3a+c=0
0),B(6,0),与y轴相交于点C,小红同学得出了以下结论:①b2-4ac
>0;② 4a+b=0;③当y>0时,-2<x<6;④a+b+c<0.其中正确
结论的个数为
(B)
A.4个
B.3个
C.2个
D.1个
x=1,则下列结论中,错误的是 A.ac<0
( C)
B.b2-4ac>0
C.2a-b=0
D.a-b+c=0
5.(2022·梧州第12题3分)如图,已知抛物线y=ax2+bx-2的对称轴是
x=-1,直线l∥x轴,且交抛物线于点P(x1,y1),Q(x2,y2),下列结论
中错误的是
(C )
A.b2>-8a
1.(2022·贺州第11题3分)已知二次函数y=2x2-4x-1在0≤x≤a时,y
取得的最大值为15,则a的值为
(D)
A.1
B.2
C.3
D.4
2.(2016·玉林、崇左、防城港第8题3分)抛物线y=
1 2
x2,y=x2,y=-
x2的共同性质是:①都是开口向上;②都以点(0,0)为顶点;③都以y轴
B.若实数m≠-1,则a-b<am2+bm
6.★(2019·贺州第17题3分)已知抛物线y=ax2+bx+c(a≠0)的对称轴 是直线x=1,其部分图象如图所示,下列说法中: ①abc<0;②a-b+c<0;③3a+c=0;④当-1<x<3时,y>0. 其中正确的是①①③③④④.(选填序号)
2020年中考数学复习专题之二次函数的综合应用问题
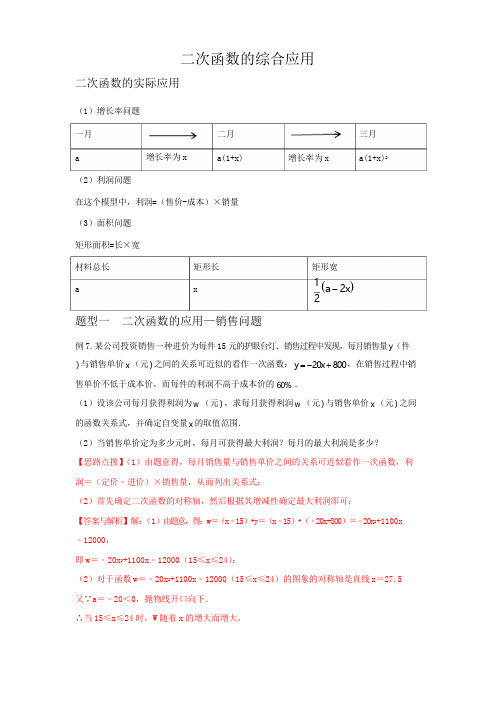
二次函数的综合应用二次函数的实际应用(1)增长率问题一月a增长率为x 二月a(1+x)增长率为x三月a(1+x)2(2)利润问题在这个模型中,利润=(售价-成本)×销量(3)面积问题矩形面积=长×宽材料总长a 矩形长x矩形宽1(a-2x)2题型一二次函数的应用—销售问题例7.某公司投资销售一种进价为每件15元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-20x+800,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)设该公司每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?【思路点拨】(1)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价﹣进价)×销售量,从而列出关系式;(2)首先确定二次函数的对称轴,然后根据其增减性确定最大利润即可;【答案与解析】解:(1)由题意,得:w=(x﹣15)•y=(x﹣15)•(﹣20x+800)=﹣20x2+1100x﹣12000,即w=﹣20x2+1100x﹣12000(15≤x≤24);(2)对于函数w=﹣20x2+1100x﹣12000(15≤x≤24)的图象的对称轴是直线x=27.5又∵a=﹣20<0,抛物线开口向下.∴当15≤x≤24时,W随着x的增大而增大,∴当x=24时,W=2880,答:当销售单价定为24元时,每月可获得最大利润,最大利润是2880元.变式训练1.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件,设衬衫的单价降x元,每天获利y元.(1)如果商场里这批衬衫的库存只有44件,那么衬衫的单价应降多少元,才能使得这批衬衫一天内售完,且获利最大,最大利润是多少?(2)如果商场销售这批衬衫要保证每天盈利不少于1200元,那么衬衫的单价应降多少元?【思路点拨】(1)列出y=44(40﹣x)=﹣44x+1760,根据一次函数的性质求解;(2)根据题意列出y=(20+2x)(40﹣x)=﹣2(x﹣15)2+1250,结合二次函数的性质求解;【答案与解析】解:(1)y=44(40﹣x)=﹣44x+1760,∵20+2x≥44,∴x≥12,∵y随x的增大而减小,∴当x=12时,获利最大值1232;答:如果商场里这批衬衫的库存只有44件,那么衬衫的单价应12元,才能使得这批衬衫一天内售完,且获利最大1232元;(2)y=(20+2x)(40﹣x)=﹣2(x﹣15)2+1250,当y=1200时,1200=﹣2(x﹣15)2+1250,∴x=10或x=20,∵当x<15时,y随x的增大而增大,当x>15时,y随x的增大而减小,当10≤x≤20时,y≥1200,答:如果商场销售这批衬衫要保证每天盈利不少于1200元,那么衬衫的单价应降不少于10元且不超过20元.变式训练2.为建设美丽家园,某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y(元)与x(m2)的函1数关系图象如图所示,栽花所需费用y(元)与x(m2)的函数关系式为2xy=-0.01x2-20x+30000(0剟1000).2(1)求 y (元 ) 与 x(m 2) 的函数关系式;1(2)设这块1000m 2 空地的绿化总费用为W (元 ) ,请利用W 与 x 的函数关系式,求绿化总 费用 W 的最大值.【思路点拨】(1)根据函数图象利用待定系数法即可求得y 1(元)与 x (m 2)的函数关系式 (2)总费用为 W =y 1+y 2,列出函数关系式即可求解 【答案与解析】解:(1)依题意当 0≤x≤600 时,y 1=k 1x ,将点(600,18000)代入得 18000=600k 1,解得 k 1=30∴y 1=30x当 600<x≤1000 时,y 1=k 2x+b ,将点(600,18000),(1000,26000)代入得,解得∴y 1=20x+600综上,y 1(元)与 x (m 2)的函数关系式为:(2)总费用为:W =y 1+y 2∴W=整理得故绿化总费用 W 的最大值为 32500 元.变式训练 3.某公司生产的某种商品每件成本为 20 元,经过市场调研发现,这种商品在未来 40 天内的日销售量 m (件 ) 与时间 t (天 ) 的关系如下表:时间 t (天 ) 1 3 5 10 36日销售量 m94 90 86 76 24(件 )未来 40 天内,前 20 天每天的价格 y 1(元/件)与时间 t (天)的函数关系式为 y 1= t +25(1≤t ≤20 且 t 为整数),后20 天每天的价格 y 2(元/件)与时间 t (天)的函数关系式为y 2=﹣ t +40(21≤t ≤40 且 t 为整数).下面我们就来研究销售这种商品的有关问题:(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的 m (件 ) 与 t (天 ) 之间的表达式;(2)请预测未来 40 天中哪一天的日销售利润最大,最大日销售利润是多少?【思路点拨】(1)从表格可看出每天比前一天少销售 2 件,所以判断为一次函数关系式;(2)日利润=日销售量×每件利润,据此分别表示前 20 天和后 20 天的日利润,根据函数性质求最大值后比较得结论.【答案与解析】解:(1)经分析知:m 与 t 成一次函数关系.设 m =kt+b (k≠0),将 t =1,m =94,t =3,m =90代入,解得,∴m=﹣2t+96;(2)前 20 天日销售利润为 P 1 元,后 20 天日销售利润为 P 2 元,则 P 1=(﹣2t+96)( t+25﹣20)=﹣ (t ﹣14)2+578,∴当 t =14 时,P 1 有最大值,为 578 元.P 2=(﹣2t+96)•( t+40﹣20)=﹣t 2+8t+1920=(t ﹣44)2﹣16,∵当 21≤t≤40 时,P 2 随 t 的增大而减小,∴t=21 时,P 2 有最大值,为 513 元. ∵513<578,∴第 14 天日销售利润最大,最大利润为 578 元.题型二 二次函数的应用—面积问题例 8.如图,用 30m 长的篱笆沿墙建造一边靠墙的矩形菜园,已知墙长18m ,设矩形的宽 AB为xm.(1)用含x的代数式表示矩形的长BC;(2)设矩形的面积为y,用含x的代数式表示矩形的面积y,并求出自变量的取值范围;(3)这个矩形菜园的长和宽各为多少时,菜园的面积y最大?最大面积是多少?【思路点拨】(1)设菜园的宽AB为xm,于是得到BC为(30﹣2x)m;(2)由面积公式写出y与x的函数关系式,进而求出x的取值范围;(3)利用二次函数求最值的知识可得出菜园的最大面积.【答案与解析】解:(1)∵AB=CD=xm,∴BC=(30﹣2x)m;(2)由题意得y=x(30﹣2x)=﹣2x2+30x(6≤x<15);(3)∵S=﹣2x2+30x=﹣2(x﹣7.5)2+112.5,∴当x=7.5时,S有最大值,S=112.5,最大此时这个矩形的长为15m、宽为7.5m.答:这个矩形的长、宽各为15m、7.5m时,菜园的面积最大,最大面积是112.5m2.变式训练1.为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.(1)求y与x之间的函数关系式,并注明自变量x的取值范围;(2)请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?【思路点拨】(1)三个矩形的面值相等,可知2FG=2GE=BC,可知:2BC+8FC=120,即FC=,即可求解;(2)y=﹣x2+45x=﹣(x﹣30)2+675即可求解.【答案与解析】解:(1)∵三个矩形的面值相等,可知2FG=2GE=BC,∴BC×DF=BC×FC,∴2FC=DC,2BC+8FC=120,∴FC=,∴y与x之间的函数关系式为y=3FC×BC=x(120﹣2x),即y=﹣x2+45x,(0<x<60);(2)y=﹣x2+45x=﹣(x﹣30)2+675可知:当BC为30米是,养殖区ABCD面积最大,最大面积为675平方米.变式训练 2.如图,ABCD是一块边长为8米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在A的延长线上,DG2BE,设BE的长为x米,改造后苗圃AEFG的面积为y平方米.(1)求y与x之间的函数关系式(不需写自变量的取值范围);(2)若改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,此时BE的长为米.(3)当x为何值时改造后的矩形苗圃AEFG的最大面积?并求出最大面积.【思路点拨】(1)根据题意可得DG=2x,再表示出AE和AG,然后利用面积可得y与x之间的函数关系式;(2)根据题意可得正方形苗圃ABCD的面积为64,进而可得矩形苗圃AEFG的面积为64,进而可得:﹣2x2+8x+64=64再解方程即可;(3)根据二次函数的性质即可得到结论.【答案与解析】解:(1)y=(8﹣x)(8+2x)=﹣2x2+8x+64,故答案为:y=﹣2x2+8x+64;(2)根据题意可得:﹣2x2+8x+64=64,解得:x1=4,x2=0(不合题意,舍去),答:BE的长为4米;故答案为:y=﹣2x2+8x+64(0<x<8);(3)解析式变形为:y=﹣2(x﹣2)2+72,所以当x=2时,y有最大值,∴当x为2时改造后的矩形苗圃AEFG的最大面积,最大面积为72平方米.变式训练3.如图,一面利用墙(墙的最大可用长度为10m),用长为24m的篱笆围成中间隔有一道篱笆的矩形花圃,设花圃的一边AB的长为x(m),面积为y(m2).(1)若y与x之间的函数表达式及自变量x的取值范围;(2)若要围成的花圃的面积为45m2,则AB的长应为多少?【思路点拨】(1)根据题意可以得到y与x的函数关系式以及x的取值范围;(2)令y=45代入(1)中的函数解析式,即可求得x的值,注意x的取值范围.【答案与解析】解:(1)由题意可得,y=x(24﹣3x)=﹣3x2+24x,∵24﹣3x≤10,3x<24,解得,x≥∴且x<8,,即y与x之间的函数表达式是y=﹣3x2+24x((2)当y=45时,45=﹣3x2+24x,解得,x1=3(舍去),x2=5,答:AB的长应为5m.题型三二次函数的应用—抛物线问题);例9.如图,已知排球场的长度O D为18米,位于球场中线处球网的高度AB为2.4米,一队员站在点O处发球,排球从点O的正上方1.6米的C点向正前方飞出,当排球运行至离点O的水平距离OE为6米时,到达最高点G建立如图所示的平面直角坐标系.(1)当球上升的最大高度为3.4米时,对方距离球网0.4m的点F处有一队员,他起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.(2)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)【思路点拨】(1)根据此时抛物线顶点坐标为(6,3.4),设解析式为y=a(x﹣6)2+3.4,再将点C坐标代入即可求得;由解析式求得x=9.4时y的值,与他起跳后的最大高度为3.1米比较即可得;(2)设抛物线解析式为y=a(x﹣6)2+h,将点C坐标代入得到用h表示a的式子,再根据球既要过球网,又不出边界即x=9时,y>2.4且x=18时,y≤0得出关于h的不等式组,解之即可得.【答案与解析】解:(1)根据题意知此时抛物线的顶点G的坐标为(6,3.4),设抛物线解析式为y=a(x﹣6)2+3.4,将点C(0,1.6)代入,得:36a+3.4=1.6,解得:a=﹣,∴排球飞行的高度y与水平距离x的函数关系式为y=﹣(x﹣6)2+;由题意当x=9.5时,y=﹣(9.4﹣6)2+≈2.8<3.1,故这次她可以拦网成功;(2)设抛物线解析式为y=a(x﹣6)2+h,将点C(0,1.6)代入,得:36a+h=1.6,即a=∴此时抛物线解析式为y=(x﹣6)2+h,,变式训练1.一位篮球运动员投篮,球沿抛物线y=-x2+运行,然后准确落入篮筐内,根据题意,得:,解得:h≥3.025,答:排球飞行的最大高度h的取值范围是h≥3.025.1752已知篮筐的中心距离底面的距离为3.05m.(1)求球在空中运行的最大高度为多少m?(2)如果该运动员跳投时,球出手离地面的高度为2.25m,要想投入篮筐,则问他距离蓝筐中心的水平距离是多少?【思路点拨】(1)由抛物线的顶点坐标即可得;(2)分别求出y=3.05和y=2.25时x的值即可得出答案.【答案与解析】解:(1)∵y=﹣x2+的顶点坐标为(0,),∴球在空中运行的最大高度为m;(2)当y=3.05时,﹣0.2x2+3.5=3.05,解得:x=±1.5,∵x>0,∴x=1.5;当y=2.25时,﹣0.2x2+3.5=2.25,解得:x=2.5或x=﹣2.5,由1.5+2.5=4(m),故他距离篮筐中心的水平距离是4米.变式训练2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.(1)当a=-124时,①求h的值;②通过计算判断此球能否过网.(2)若甲发球过网后,羽毛球飞行到与点的O水平距离为7m,离地面的高度为处时,乙扣球成功,求a的值.125m的Q【思路点拨】(1)①将点P(0,1)代入y=﹣(x﹣4)2+h即可求得h;②求出x=5时,y的值,与1.55比较即可得出判断;(2)将(0,1)、(7,)代入y=a(x﹣4)2+h代入即可求得a、h.【答案与解析】解:(1)①当a=﹣时,y=﹣(x﹣4)2+h,将点P(0,1)代入,得:﹣解得:h=;×16+h=1,②把x=5代入y=﹣∵1.625>1.55,∴此球能过网;(x﹣4)2+,得:y=﹣×(5﹣4)2+=1.625,(2)把(0,1)、(7,,)代入y=a(x﹣4)2+h,得:解得:,∴a=﹣.变式训练3.小明跳起投篮,球出手时离地面20m,球出手后在空中沿抛物线路径运动,并9在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.(1)求此抛物线对应的函数关系式;(2)此次投篮,球能否直接命中篮筐中心?若能,请说明理由;若不能,在出手的角度和力度都不变的情况下,球出手时距离地面多少米可使球直接命中篮筐中心?(3)在篮球比赛中,当进攻方球员要投篮时,防守方球员常借身高优势及较强的弹跳封杀对方,这就是平常说的盖帽.(注:盖帽应在球达到最高点前进行,否则就是“干扰球”,属犯规.)若此时,防守方球员乙前来盖帽,已知乙的最大摸球高度为3.19m,则乙在进攻方球员前多远才能盖帽成功?【思路点拨】(1)根据顶点坐标(4,4),设抛物线的解析式为:y=a(x﹣4)2+4,由球出手时离地面m,可知抛物线与y轴交点为(0,),代入可求出a的值,写出解析式;(2)先计算当x=8时,y的值是否等于3,把x=8代入得:y=,所以要想球经过(8,3),则抛物线得向上平移3﹣=个单位,即球出手时距离地面3米可使球直接命中篮筐中心;(3)将由y=3.19代入函数的解析式求得x值,进而得出答案.【答案与解析】(1)设抛物线为y=a(x﹣4)2+4,将(0,)代入,得a(0﹣4)2+4=,解得a=﹣,∴所求的解析式为y=﹣(x﹣4)2+4;(2)令x=8,得y=﹣(8﹣4)2+4=∴抛物线不过点(8,3),故不能正中篮筐中心;≠3,=∵抛物线过点(8,),∴要使抛物线过点(8,3),可将其向上平移 7/9 个单位长度,故小明需向上多跳 m 再投篮(即球出手时距离地面 3 米)方可使球正中篮筐中心.(3)由(1)求得的函数解析式,当 y =3.19 时,3.19=﹣19(x ﹣4)2+4解得:x 1=6.7(不符合实际,要想盖帽,必须在篮球下降前盖帽,否则无效),x 2=1.3∴球员乙距离甲球员距离小于 1.3 米时,即可盖帽成功.题型四 二次函数与图形面积的综合例 10.如图,抛物线 y = a(x + 1)2的顶点为 A ,与 y 轴的负半轴交于点 B ,且 OB = OA .(1)求抛物线的解析式;(2)若点 C (-3,b ) 在该抛物线上,求 S∆ABC 的值.【思路点拨】(1)由抛物线解析式确定出顶点 A 坐标,根据 OA =OB 确定出 B 坐标,将 B坐标代入解析式求出 a 的值,即可确定出解析式;(2)将 C 坐标代入抛物线解析式求出 b 的值,确定出 C 坐标,过 C 作 CD 垂直于 x 轴,三角形 ABC 面积=梯形 OBCD 面积﹣三角形 ACD 面积﹣三角形 AOB 面积,求出即可.【答案与解析】解:(1)由题意得:A (﹣1,0),B (0,﹣1),将 x =0,y =﹣1 代入抛物线解析式得:a =﹣1,则抛物线解析式为 y =﹣(x+1)2=﹣x 2﹣2x ﹣1;(2)过 C 作 CD⊥x 轴,将 C (﹣3,b )代入抛物线解析式得:b =﹣4,即 C (﹣3,﹣4),则 △S ABC =S 梯形 OBCD △﹣S ACD △﹣S A OB ×3×(4+1)﹣ ×4×2﹣ ×1×1=3.变式训练1.如图,已知二次函数图象的顶点为(1,-3),并经过点C(2,0).(1)求该二次函数的解析式;(2)直线y=3x与该二次函数的图象交于点B(非原点),求点B的坐标和∆AOB的面积;【思路点拨】(1)设抛物线的解析式为y=a(x﹣1)2﹣3,由待定系数法就可以求出结论;(2)由抛物线的解析式与一次函数的解析式构成方程组,求出其解即可求出B的坐标,进而可以求出直线AB的解析式,就可以求出AB与x轴的交点坐标,就可以求出△AOB的面积;【答案与解析】解:(1)抛物线的解析式为y=a(x﹣1)2﹣3,由题意,得0=a(2﹣1)2﹣3,解得:a=3,∴二次函数的解析式为:y=3(x﹣1)2﹣3;(2)由题意,得,解得:.∵交点不是原点,∴B(3,9).如图2,设直线AB的解析式为y=kx+b,由题意,得,△+S,△+S△+S解得:,∴y=6x﹣9.当y=0时,y=1.5.∴E(1.5,0),∴OE=1.5,△∴SAOB=SA OE BOE=+,=9.答:B(3,9),△AOB的面积为9;变式训练2.如图,抛物线y=x2+x-2与x轴交于A、B两点,与y轴交于点C.(1)求点A,点B和点C的坐标;(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;(3)若点M是直线AC下方抛物线上一动点,求四边形ABCM面积的最大值.【思路点拨】(1)利用待定系数法即可解决问题.(2)连接AC与对称轴的交点即为点P.求出直线AC的解析式即可解决问题.(3)过点M作MN⊥x轴与点N,设点M(x,x2+x﹣2),则AN=x+2,0N=﹣x,0B=1,0C=2,MN=﹣(x2+x﹣2)=﹣x2﹣x+2,根据S四边形ABCM△=SAOM OCM BOC构建二次函数,利用二次函数的性质即可解决问题.【答案与解析】解:(1)由y=0,得x2+x﹣2=0解得x=﹣2x=l,∴A(﹣2,0),B(l,0),由x=0,得y=﹣2,∴C(0,﹣2).(2)连接AC与对称轴的交点即为点P.△+S + =设直线 AC 为 y =kx+b ,则﹣2k+b =0,b =﹣2:得 k =﹣l ,y =﹣x ﹣2.对称轴为 x =﹣ ,当 x =﹣ 时,y =_(﹣ )﹣2=﹣ ,∴P(﹣ ,﹣ ).(3)过点 M 作 MN⊥x 轴与点 N ,设点 M (x ,x 2+x ﹣2),则 AN =x+2,0N =﹣x ,0B =1,0C =2,MN =﹣(x 2+x ﹣2)=﹣x 2﹣x+2,S四边形 ABCM△=S AOM OCM △S BOC (x+2)(﹣x 2﹣x+2)+ (2﹣x 2﹣x+2)(﹣x )+ ×1× 2=﹣x 2﹣2x+3=﹣(x+1)2+4.∵﹣1<0,∴当 x =_l 时,S 四边形 ABCM 的最大值为 4.变式训练 3.如图,二次函数 y = ax 2 + b x 的图象经过点 A(2,4) 与 B(6,0) .(1)求 a , b 的值;(2)点 C 是该二次函数图象上 A , B 两点之间的一动点,横坐标为 x (2 < x < 6) ,写出四边形 OACB 的面积 S 关于点 C 的横坐标 x 的函数表达式,并求 S 的最大值.△=△=△=△+S△+S【思路点拨】(1)把A与B坐标代入二次函数解析式求出a与b的值即可;(2)如图,过A作x轴的垂直,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,分别表示出三角形OAD,三角形ACD,以及三角形BCD的面积,之和即为S,确定出S关于x的函数解析式,并求出x的范围,利用二次函数性质即可确定出S的最大值,以及此时x的值.【答案与解析】解:(1)将A(2,4)与B(6,0)代入y=ax2+bx,得,解得:;(2)如图,过A作x轴的垂线,垂足为D(2,0),连接CD、CB,过C作CE⊥AD,CF⊥x 轴,垂足分别为E,F,SOADOD•AD=×2×4=4;SACDAD•CE=×4×(x﹣2)=2x﹣4;SBCDBD•CF=×4×(﹣x2+3x)=﹣x2+6x,则S=SOAD ACD BCD=4+2x﹣4﹣x2+6x=﹣x2+8x,∴S关于x的函数表达式为S=﹣x2+8x(2<x<6),∵S=﹣x2+8x=﹣(x﹣4)2+16,∴当x=4时,四边形OACB的面积S有最大值,最大值为16.。
中考数学专题复习之 二次函数的应用 课件

二次函数的应用
考点精讲·导析探究
B
( 1 )设 y = kx + b ,
把( 22 , 36 )与( 24 , 32 )代入得:
则 y =- 2x + 80 ;
( 2 )设当文具店每周销售这种纪念册获得 150元的利润时,每本纪念册的销售单价是
x 元,根据题意得:( x - 20 ) y = 150 ,
润是 192 元.
(1)∵ B ( 4 , m )在直线 y = x + 2 上
∴ m = 4 + 2 = ቤተ መጻሕፍቲ ባይዱ ,∴ B ( 4 , 6 )
∵抛物线 y =
ax2+
1 5
bx+ 6经过 A ( , ),B ( 4 , 6 )
2 2
∴抛物线的解析式为 y = 2x2 - 8x + 6 .
( 2 )设 P ( m , m + 2 ),则 D ( m , 2m2- 8m + 6 ).
整理得 w =-( x - 25 ) 2 + 225
∵- 1 < 0
∴当 x = 25 时, w 取得最大值,最大值为 225 元.
1
( 1 )根据题意得, y =- x + 50 ;
2
1
( 2 )根据题意得,( 40 + x )(- x + 50 )= 2 250 ,
2
解得: x 1 = 50 , x 2= 10 ,
=- 2 ( x - 30 ) 2 + 200 ,
此时当 x = 30 时, w 最大,
又∵售价不低于 20 元且不高于 28 元,
∴ x < 30 时, y 随 x 的增大而增大,即当 x = 28时, w 最大 =- 2 ( 28 - 30 ) 2 + 200 =
2024年中考数学总复习考点梳理第三章第六节二次函数的图象与性质

第六节 二次函数的图象与性质
返回目录
命题点2 二次函数图象与系数a,b,c的关系(2020.10) 课标要求 1.通过图象了解二次函数的性质,知道二次函数系数与图象形状和对称 轴的关系;(2022年版课标新增) 2.知道二次函数和一元二次方程之间的关系.(2022年版课标新增)
第六节 二次函数的图象与性质
考情及趋势分析
年份 2020
题号 10
题型 选择题
分值 3
考情分析 已知条件
函数图象、对称轴x=1
返回目录
考查设问 下列结论正确的是
第六节 二次函数的图象与性质
返回目录
命题点3 二次函数解析式的确定(6年4考,均在二次函数综合题考查)
考情及趋势分析
年份 题号 题型 分值 2022 23(1) 解答题(三) 5 2021 25(1) 解答题(三) 3
y=ax2+b
①C(0,-3),②y=x+m
【考情总结】考查特点:除2021年考查三个系数未知外,其余年份均考查两个系数未知.
第六节 二次函数的图象与性质
返回目录
命题点4 二次函数图象的平移(6年2考) 考情及趋势分析
考情分析
年份 题号 题型 分值 平移次数 平移方式 设问
溯源教材
教材改编维度
2021 12 填空题 4
第六节 二次函数的图象与性质
返回目录
3. [人教九上P47习题改编]如图,抛物线y=ax2+bx+c(a≠0)与x
轴的一个交点坐标为(-1,0),对称轴为直线x=1.下列结论正
确的有____②__③__⑥______.(填序号)
①bc<0;②2a+b=0;③9a+3b+c=0;
④4a+2b+c>0;⑤2c-3b<0;
中考数学 考点系统复习 第三章 函数 第六节 二次函数与几何综合题
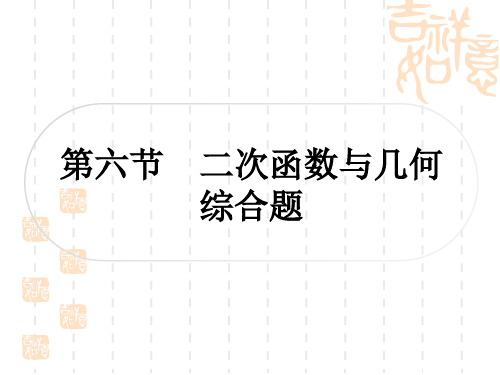
(2) 存在,取点 B 关于 y 轴的对称点 B′,则点 B′的坐标为(-1,0),
连接 B′D,直线 B′D 与 y 轴的交点 G,即为所求的点.
∵y=-12x2+52x-2=-12x-252+98, ∴顶点 D52,98,
99 故易求得直线 B′D 的解析式为 y=28x+28,
当
x=0
9 时,y=28,∴点
1
1
∴S△AOB= S△AOC+ S△ABC=2AC·xC+2AC·(xB-xC)=10.
方法二:补全法
解:过点 B 作平行于 y 轴的直线 DC,过点 A 作平行于 x 轴的直线 AD,两
直线相交于点 D,且直线 DC 交 x 轴于点 C.由题意得
D(6,4),C(6,0).
∴S = S - S - S △AOB
梯形 AOCD
△ADB
△BOC
=10.
4.如图,开口向下的抛物线与 x 轴交于点 A(-1,0),B(2,0),与 y 轴 交于点 C(0,4),点 P 是第一象限内抛物线上的一点.
(1)该抛物线所对应的函数解析式为 y=y-=2x-2+22x2+2x+x 4;
(2)若△PAB 的面积为 6,则点 P 的坐标+为(41(1,,44);
t+t+34 .
10.如图②,若点 P 是第四象限内抛物线上的一个动点,过点 P 作 PQ⊥y
轴交直线 BC 于点 Q,设点 P 的横坐标为 t,则 PQ 的长用 t 表示为 -t-2+t32t+(1 ≤t≤3).
3t(1≤t≤3)
(注:三阶 考向设问练;四阶 综合攻关练见本书“重难点突破九 ”)
类型三:二ห้องสมุดไป่ตู้函数与特殊三角形问题 考向 1:与等腰三角形有关的问题
2023年中考数学总复习第三章《函数》第六节 二次函数的实际应用
2023年中考数学总复习第三章《函数》第六节二次函数的实际应用一、选择题1.[2020·邢台模拟]把一个足球垂直于水平地面向上踢,该足球距离地面的高度h(米)与所经过的时间t (秒)之间的关系为h=10t-t 2(0≤t≤14).若存在两个不同的t 的值,使足球离地面的高度均为a (米),则a 的取值范围是()A.0≤a≤42B.0≤a<50C.42≤a<50D.42≤a≤502.[2020·长沙]“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”p 与加工煎炸时间(t 单位:分钟)近似满足的函数关系为:p=at 2+bt+c (a≠0,a,b,c 是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为()A. 3.50分钟B. 4.05分钟C. 3.75分钟D. 4.25分钟(第2题图)(第3题图)3.[2020·石家庄裕华区一模]从地面竖直向上抛出一小球,小球的高度h(单位:m )与小球运动时间t (单位:s )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是40m;②小球运动的时间为6s;③小球抛出3s 时,速度为0;④当t=1.5s 时,小球的高度h=30m.其中正确的是()A.①④B.①②C.②③④D.②④二、填空题4.[人九上课本P52,T8改编]某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为_______元.三、解答题5.[人九上课本P52,T5高仿]如图,西游乐园景区内有一块矩形油菜花田地(单位:m ),现在其中修建一条观花道(阴影所示),供游人赏花,设改造后观花道的面积为y m 2.(1)求y 与x 的函数关系式;(2)若改造后观花道的面积为13m 2,求x 的值;(3)若要求0.6≤x≤1,求改造后油菜花地所占面积的最大值.(第5题图)6.[2020·遵化二模]随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E 中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为x(单位:km ),乘坐地铁的时间y 1(单位:min )是关于x 的一次函数,其关系如下表:(1)求y1关于x 的函数解析式;(2)李华骑单车的时间y 2(单位:min)也受x 的影响,其关系可以用y 2=x 2-11x+78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最短时间.地铁站A B C D E x/km 79111213y 1/min1620242628。
中考数学总复习之 二次函数综合
连接 BC,如图①,∵B(5,0),C0,-52,∴设直线 BC 的解
析式为 y=kx+b(k≠0),∴5bk=+-b2= 5,0,
解得k=21, b=-52,
∴直线 BC 的解析式为 y=21x-52,当 x=2 时,y=1-52=-23, ∴P2,-32.
(3)存在,如图②. ①当点 N 在 x 轴下方时,∵抛物线的对称轴为直线 x=2, C0,-52,∴N14,-52. ②当点 N 在 x 轴上方时,如图②,过点 N2 作 N2D⊥x 轴于点 D,
解:(1)已知抛物线 y=21x2-32x-9,当 x=0 时,y=-9,则 C(0,-9),当 y=0 时,12x2-32x-9=0,得 x1=-3,x2=6, 则 A(-3,0),B(6,0),∴AB=9,OC=9.
(2)∵ED∥BC,∴△AED∽△ABC,
∴SS△△AAEBDC=AABE2,即12×S9×9=m9 2,得 S=21m2(0<m<9).
2.如图,抛物线 y=12x2-32x-9 与 x 轴交于 A ,B 两点,与 y 轴交于点 C ,连接 B C ,A C .
(1)求 AB 和 OC 的长; (2)点 E 从点 A 出发,沿 x 轴向点 B 运动(点 E 与点 A,B 不重 合),过点 E 作直线 l 平行于 BC,交 AC 于点 D.设 AE 的长为 m,△ADE 的面积为 S,求 S 关于 m 的函数关系式,并写出自 变量 m 的取值范围; (3)在(2)的条件下,连接 CE,求△CDE 面积的最大值;此时, 求出以点 E 为圆心,与 BC 相切的圆的面积(结果保留 π).
在 △AN2D
与 △M2CO
∠N2AD=∠CM2O, 中 , A∠NA2N=2CDM=2∠,M2CO,
初三数学复习《二次函数》(专题复习)PPT课件
面积问题
面积问题
在二次函数中,可以通过求函数与坐标轴的交点来计算图形的面积。例如,当函数与x轴交于两点时 ,可以计算这两点之间的面积;当函数与y轴交于一点时,可以计算这一点与原点之间的面积。这些 方法在解决实际问题时非常有用,例如在计算利润、产量等方面。
求解方法ቤተ መጻሕፍቲ ባይዱ
求出二次函数与x轴和y轴的交点坐标,然后根据这些坐标计算图形的面积。对于更复杂的问题,可能 需要使用积分或其他数学方法来求解。
05
综合练习与提高
基础练习题
巩固基础 覆盖全面 由浅入深
基础练习题主要针对二次函数的基本概念、性质和公 式进行设计,旨在帮助学生巩固基础知识,提高解题的 准确性和速度。
基础练习题应涵盖二次函数的各个方面,包括开口方 向、顶点坐标、对称轴、与坐标轴的交点等,确保学生 对二次函数有全面的了解。
题目难度应从易到难,逐步引导学生深入理解二次函 数,从简单的计算到复杂的综合题,逐步提高学生的解 题能力。
初三数学复习《二次函数》(专题复习)ppt课 件
目录 Contents
• 二次函数的基本概念 • 二次函数的解析式 • 二次函数的图像与性质 • 二次函数的实际应用 • 综合练习与提高
01
二次函数的基本概念
二次函数的定义
总结词
理解二次函数的定义是掌握其性 质和图像的基础。
详细描述
二次函数是形式为$f(x) = ax^2 + bx + c$的函数,其中$a, b, c$是 常数,且$a neq 0$。这个定义表 明二次函数具有两个变量$x$和 $y$,并且$x$的最高次数为2。
03
二次函数的图像与性质
开口方向
总结词:根据二次项系数a的正负判断开口方向 a>0时,开口向上
山东省滨州市2019中考数学 第三章 函数 第六节 二次函数的综合应用课件
(2)直线y=2x-1,当y=0时,x= . 如图,过点A作AF⊥CD于点F.设直线CD交x轴于点E, 则E( ,0).
(3)∵平移后抛物线的顶点P在直线y=2x-1上, ∴设P(t,2t-1), 则平移后抛物线的解析式为y=(x-t)2+2t-1. 联立
化简得x2-(2t+2)x+t2+2t=0, 解得x1=t,x2=t+2,即点P,Q的横坐标相差2,
易证Rt△PMG≌Rt△GNQ,
∴GN=PM,GM=QN.
在Rt△QNG中,由勾股定理得GN2+QN2=GQ2,
即PM2+QN2=10. ∵点P,Q横坐标相差2,∴NQ=PM+2, ∴PM2+(PM+2)2=10,解得PM=1, ∴NQ=3. 直线y=2x-1,当x=1时,y=1,
∴P(1,1),即OM=1, ∴OG=OM+GM=OM+NQ=1+3=4, ∴G(0,4). 综上所述,符合条件的点G有两个,其坐标为(0,4)或(0,9).
m的 对称点C′,过点C′作C′F⊥AB于F,交抛物线的对称轴 x=1于点E,此时CE+CF的值最小. 根据对称性,易知点C′(2,1). ∵点C′在抛物线上, ∴由(2)得,C′F= 即CE+EF的最小值为
1.如图,在平面直角坐标系中,抛物线与x轴交于点 A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C, 与抛物线交于点C,D.
②如果E在x轴的下方,则EF∥AB,EF=AB=6,点F的横坐标为-1, ∴E的横坐标为-1±6,即-7或5,
(3)抛物线的对称轴为x=-1,AC= ①如果MA=MC,则M为直线x=-1与AC的垂直平分线的 交点. 设AC的中点为H,连接OH,
则H的坐标是(1,1), ∴直线OH的解析式为y=x. ∵OA=OC,H为AC的中点, ∴OH为AC的垂直平分线, 又∵M为直线x=-1与y=x的交点, ∴M的坐标为(-1,-1).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当已知抛物线上任意三点时,通常设抛物线的表达式为 y=ax2+bx+c(a≠0)
二、二次函数与几何图形综合题
类型一 二次函数与特殊三角形判定
例1 已知抛物线y=ax2+bx+4(a≠0)与x轴交于A(4,0)、B(-2,0)两点,与y
轴交于点C.
(1)求该抛物线的表达式和对称轴;
(1)解:将A(4,0),B(-2,0)代入,
得
146aa-+24bb++44==00,解得
a=-12. b=1
∴该抛物线的表达式为y=- 1 x2+x+4,
2
对称轴为直线x=- 1 =1; -1×2 2
(2)将该抛物线平移后得到抛物线C1,且其正好经过A、O两点,求出平移后的抛物 线的表达式;
延长线于点K,过点R作RH⊥x轴于点H,
∵对称中心在x轴负半轴上,
∴2FG=EF=AB=6,
例1题解图③
∴FG=3,点F坐标为(x-3,0),点H坐标为(1,0),点K坐标为(x,9 ), 2
根据勾股定理得FR2=FH2+RH2=(x-4)2+( 9 )2=x2-8x+ 145 ,
FT2=FG2+GT2=32+( 9 )2= 117 ,
此类问题也可以利用数形结合,先找点,再计算: 1. 等腰三角形利用两圆一线找交点,即分①已知边为腰时,作圆找点;②已知 边为底时,作线段垂直平分线找点; 2. 直角三角形利用两线一圆找交点,即分①已知边为直角边,分别过边的两端 点作边的垂线找点;②已知边为斜边,作以斜边为直径的圆找点.
类型二 二次函数与特殊四边形判定 例2 已知抛物线L:y=ax2+bx+c(a≠0)经过A(3,0),B(-1,0),C(0,3)三点. (1)求抛物线L的表达式;
∴N(3,5 ). 2
综上所述,点N的坐标为(5,- 7 )或(3,5 );
2
2
(7)如图,设抛物线y=ax2+bx+4(a≠0)的顶点为R,点S是x轴负半轴上一点,抛物线y =ax2+bx+4与抛物线C2关于点S成中心对称,抛物线C2的顶点为T,与x轴相交于E、 F两点(点E在点F的右侧),当以点R、T、F为顶点的三角形是直角三角形时,求点S的 坐标.
2 ∴设抛物线的表达式为y=a(x-1)2+
9
,
把C(0,4)代入得a(0-1)2+
9
2 =4,解得a=-
1
,
∴抛物线的表达式为y=- 12(x-1)2+ 9 .
2
2
2
练习5题图
练习6 已知抛物线经过A(-1,0),B(1,-4),C(2,-3)三点,求该抛物线 的表达式.
解:设抛物线的表达式为y=ax2+bx+c,
,
∴该抛物线的表达式为y=-x2+2x+3.
形式二 表达式未给出 练习4 已知抛物线与x轴交于A(-2,0)、B(3,0)两点,且经过点C(-3,-4), 求该抛物线的表达式.
解:∵抛物线与x轴交于A(-2,0)、B(3,0)两点,
∴可设抛物线表达式为y=a(x+2)(x-3),
∵当x=0时,y=4,
【思维教练】要使△RTF为直角三角形,只需要三边满 足勾股定理即可.分三种情况:①当∠RFT=90°;② 当∠RTF=90°;③当FR⊥RT时,点T不可能在第三象 限,所以∠FRT≠90°,分别结合勾股定理讨论并求出点 S的坐标.
例1题图
解:由(1)可知抛物线y=ax2+bx+4=- 1 x2+x+4,
【思维教练】根据函数平移的规律,可知a不变,设出平移后的抛物线表达式,将 点A、O坐标代入表达式即可求解.
解:设平移后的抛物线表达式为y=- 1 x2+cx+d, 2
代入A(4,0),O(0,0),
得
4dc=-08+d=0,解得
c=2 d=0.
∴平移后的抛物线表达式为y=- 1 x2+2x; 2
(3)点P是坐标轴上的一点,连接CP,若CP=BP,求满足条件的点P坐标; 【思维教练】分两种情况讨论:①点P在x轴上,设P(m,0),②点P在y轴上,设P(0, m),分别用含有m的代数式表示出CP和BP,根据CP=BP,列方程求解即可.
将点A(-1,0)、B(1,-4)、C(2,-3)代入,
a-b+c=0
a=1
a+b+c=-4
b=-2
得 4a+2b+c=-3,解得 c=-3,
∴抛物线的表达式为y=x2-2x-3.
满分技法
待定系数法求表达式方法如下:
表达式已给出 找出抛物线上的两个点或三个点坐标代入即可
表达式 未给出
当已知抛物线与x轴的两个交点坐标或对称轴、抛物线与x轴的一个交 点时,通常设表达式为y=a(x-x1)(x-x2)(a≠0),其中抛物线与x轴交 点为(x1,0),(x2,0)
即 117+x2-2x+82=x2-8x+145,
4
解得x=-
25,
4
2
∴点S坐标为(-
23
,0);
4
③∵当FR⊥RT时,点T不可能在第三象限,
∴∠FRT≠90°.
综上所述,当点S的坐标为(- 7 ,0)或(- 23 ,0)时,以点R、T、F为顶点
8 的三角形是直角三角形.
4
满分技法
二次函数与等腰三角形或直角三角形判定结合的问题,解决的方法一般为: 1. 用点坐标表示三角形三边长的平方; 2. 根据等腰三角形的性质,分别令三边长中两两相等,得到三组方程;根据直角三角 形的性质,对直角顶点进行分类讨论,利用勾股定理分别列方程; 3. 分别解这几个方程,若方程有解,则这个解即为所求;若方程无解,则不存在这样 的三角形.
解:将A(3,0),B(-1,0),C(0,3)代入y=ax2+bx+c(a≠0),
得 9a+3b+c=0
a=-1
a-b+c=0 ,解得 b=2 ,
c=3
c=3
∴抛物线L的表达式为y=-x2+2x+3;
(2)求该抛物线的顶点坐标;
【思维教练】求抛物线顶点坐标有以下3种思路:①一般式化为顶点式;②顶点
例1题解图①
①当BQ=CQ时,32+n2=12+(n-4)2,
解得n=1,
∴Q1(1,1); ②当BQ=BC=2 5 时,32+n2=20, 解得n=± 11, ∴Q2(1,11),Q3(1,- 11); ③当CQ=BC=2 5 时,12+(n-4)2=20, 解得n=4± 19, ∴Q4(1,4+ 19),Q5(1,4- 19). 综上所述,点Q的坐标为Q1(1,1),Q2(1, 11),Q3(1,- 11),Q4(1,4+ 19 ), Q5(1,4- 19 );
将点A(4,0),C(0,4)代入, 得 4dk=+4d=0,解得 kd= =- 4 1, ∴线段AC的表达式为y=-x+4(0≤x≤4).
设M(m,-m+4)(m≠0),
例1题解图②
∵OA=OC,∴∠OCA=45°,
故只需满足∠OMC=90°或∠COM=90°即可使△COM为等腰直角三角形, 当OM1⊥AC时,易得∠COM1=45°, ∴m=-m+4,解得m=2, ∴M1(2,2); 当OC⊥OM2时,易得点M2与点A重合, ∴M2(4,0). 综上所述,点M的坐标为(2,2)或(4,0);
在Rt△BOP中,BP= OB2+OP2= 22+m2= 4+m2 ,
∵CP=BP,即(4-m)2=4+m2,
解得m= 3 ,
∴P(0,3
2 ).
综上所述2 ,满足条件的点P坐标为(3,0)、(0,3 );
2
(4)在抛物线的对称轴上,是否存在一点Q,使得△QBC为等腰三角形?若存在, 求出点Q的坐标;若不存在,请说明理由; 【思维教练】要使得△QBC为等腰三角形,则只需满足三边中有任意两边相等即 可.分BQ=CQ、BQ=BC和CQ=BC三种情况进行讨论. 解:存在点Q,使△QBC为等腰三角形. 如解图①,连接BC,设Q(1,n), BC= OB2+OC2= 22+42=2 5,BQ= 32+n2,CQ= 12+(n-4)2,
第六节 二次函数的综合应用
(每年第24题必考;10分)
重难点突破
一、二次函数表达式的确定 形式一 表达式已给出 练习1 已知抛物线y=ax2-4x+c,若抛物线的顶点坐标为(-2,4),求该抛物线 的表达式. 解:∵抛物线的顶点坐标为(-2,4), ∴抛物线对称轴为直线x=-2, ∴- -4 =-2,解得a=-1,
(6)点N是抛物线上一点,连接BC、BN、CN,若△BCN是以BC为直角边的直角三角形, 确定点N的坐标;
【思维教练】要使△BCN为直角三角形,且BC为直角边,则只需满足∠B=90°或∠C =90°即可.分BC⊥BN和BC⊥CN两种情况讨论,注意结果要符合题目条件“点N在 抛物线上”. 【知识拓展】此处可设出点N坐标,根据两垂直直线斜率之积等于-1计算.
∴-6a=4,解得a=- 2 ,
3 ∴该抛物线的表达式为y=-
2
(x+2)(x-3)=- 2
ቤተ መጻሕፍቲ ባይዱ
x2+ 2
x+4.
3
33
练习5 如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与 y轴交于点C(0,4),顶点坐标为(1,92 ),求该抛物线的表达式.
解:∵抛物线顶点坐标为(1,9 ),
如解图③,抛物线C2与抛物线y=-
1 2
2 x2+x+4关于点S成中心对称,
∴顶点R、T关于点S成中心对称,
∵点R是抛物线y=- 1 x2+x+4的顶点,
∴点R(1,9 ),
2
2 ∴点T的纵坐标为-
9
,设点T坐标为(x,-
9 ),则S(
x+1
,0),
2
