2023-2024学年八年级数学上册《第十三章 轴对称》单元测试卷含答案(人教版)
人教版 八年级数学上册 第十三章测试题含答案)

人教版八年级数学上册第十三章测试题含答案)13.1 轴对称一、选择题1. 点M(3,2)关于x轴对称的点的坐标为()A. (-3,2)B. (3,-2)C. (-3,-2)D. (3,2)2. 如图,线段AB与A′B′(AB=A′B′)不关于直线l成轴对称的是()3. 如果点(m-1,-1)与点(5,-1)关于y轴对称,那么m的值为()A.4 B.-4 C.5 D.-54. 将一张长与宽的比为2∶1的长方形纸片按图①②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④中的纸片展开铺平,所得到的图案是()5. 在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为()A.(4,-3) B.(-4,3)C.(-3,4) D.(-3,-4)6. [2018·河北] 图是由“○”和“□”组成的轴对称图形,则该图形的对称轴是直线()A.l1B.l2C.l3D.l47. 如图,以C为圆心,大于点C到AB的距离为半径作弧,交AB于点D,E,再以D,E为圆心,大于12DE的长为半径作弧,两弧交于点F,作射线CF,则()A.CF平分∠ACB B.CF⊥ABC.CF平分AB D.CF垂直平分AB8. 已知:在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a-m=4,b+n=0,则下列结论正确的是()A.把点A向左平移4个单位长度后,与点B关于x轴对称B.把点A向右平移4个单位长度后,与点B关于x轴对称C.把点A向左平移4个单位长度后,与点B关于y轴对称D.把点A向右平移4个单位长度后,与点B关于y轴对称9. 如图,分别以线段AB的两端点A,B为圆心,大于12AB的长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与点O重合),连接PA,PB,则下列结论不一定成立的是()A.PA=PB B.OA=OBC.OP=OF D.PO⊥AB10. 如图,在RtABC 中,90ACB ∠=︒,分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧相交于D E ,两点,作直线DE 交AB 于点F ,交BC 于点G ,连接CF .若3AC =,2CG =,则CF 的长为A .52B .3C .2D .72二、填空题11. 如图,在△ABC 中,AB =BC ,∠ABC =110°.AB 的垂直平分线DE 交AC 于点D ,连接BD ,则∠ABD =________度.12. 如图,△ABO 是关于y 轴对称的轴对称图形,点A 的坐标为(-2,3),则点B 的坐标为________.13. 如图所示,分别将标号为A ,B ,C ,D 的正方形沿图中的虚线剪开后,得到标号为E ,F ,G ,H 的四个图形,则剪前与剪后拼接的图形的对应关系是:A 与________对应,B 与________对应,C 与________对应,D 与________对应.14. 已知点P(x,y)的坐标满足等式(x-2)2+|y-1|=0,且点P与点P′关于y轴对称,则点P′的坐标为________.15. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.16. 数学活动课上,两名同学围绕作图问题:“如图①,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形,其中作法正确的为图(填“②”或“③”).三、解答题17. 如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.18. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D 和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.19. 如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.人教版八年级数学上册13.1 轴对称一、选择题1. 【答案】B2. 【答案】A3. 【答案】B[解析] ∵点(m-1,-1)与点(5,-1)关于y轴对称,∴m-1=-5,解得m=-4.4. 【答案】A5. 【答案】D[解析] 点A(3,4)关于x轴的对称点A′的坐标为(3,-4),将点A′向左平移6个单位长度,得到点B(-3,-4).6. 【答案】C[解析] 沿着直线l3折叠,直线两旁的部分能够互相重合,因此该图形的对称轴是直线l3.7. 【答案】B8. 【答案】A[解析] ∵a -m =4,∴a -4=m.又∵b +n =0(b≠0),∴b =-n.∴把点A 向左平移4个单位长度后,与点B 关于x 轴对称.9. 【答案】C[解析] 由作图可知,EF 垂直平分AB ,因此可得OA =OB ,PO ⊥AB ,由线段垂直平分线的性质可得PA =PB ,但不能得到OP =OF.10. 【答案】A【解析】由作法得GF 垂直平分BC , ∴FB FC =,2CG BG ==,FG BC ⊥, ∵90ACB ∠=︒,∴FG AC ∥,∴BF CF =, ∴CF 为斜边AB 上的中线,∵5AB ==, ∴1522CF AB ==.故选A .二、填空题11. 【答案】35 【解析】∵AB =BC ,∠ABC =110°,∴∠A =∠C =35°,∵DE 垂直平分AB ,∴DA =DB ,∴∠ABD =∠A =35°.12. 【答案】(2,3)[解析] ∵△ABO 是关于y 轴对称的轴对称图形,∴点A(-2,3)与点B 关于y 轴对称.∴点B 的坐标为(2,3).13. 【答案】GE F H [解析] A 剪开后是三个三角形,B 剪开后是两个直角梯形和一个三角形,C 剪开后是一个直角三角形和两个四边形,D 剪开后是两个三角形和一个四边形,因而,A 与G 对应,B 与E 对应,C 与F 对应,D 与H 对应.14. 【答案】(-2,1)[解析] ∵(x -2)2≥0,|y -1|≥0,又(x -2)2+|y -1|=0,∴x-2=0且y -1=0,即x =2,y =1.∴点P 的坐标为(2,1).那么点P 关于y 轴的对称点P′的坐标为(-2,1).15. 【答案】3[解析] ∵AD 平分∠BAC ,且DE ⊥AB ,∠C =90°,∴CD =DE=1.∵DE是AB的垂直平分线,∴AD=BD.∴∠B=∠DAB.∵∠DAB=∠CAD,∴∠CAD=∠DAB=∠B.∵∠C=90°,∴∠CAD+∠DAB+∠B=90°.∴∠B=30°.∴BD=2DE=2.∴BC=BD+CD=2+1=3.16. 【答案】③三、解答题17. 【答案】解:∵两个四边形关于直线l对称,∴四边形ABCD≌四边形FEHG,∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5 cm,b=4 cm. ∴∠G=360°-∠H-∠E-∠F=55°.18. 【答案】解:∵DE垂直平分线段AB,GF垂直平分线段BC,∴EB=EA,GB=GC.∵△BEG的周长为16,∴EB+GB+GE=16.∴EA+GC+GE=16.∴GA+GE+GE+GE+EC=16.∴AC+2GE=16.∵GE=3,∴AC=10.19. 【答案】证明:连接AC.∵点A在线段BC的垂直平分线MN上,∴AB=AC.∵AB=AD,∴AC=AD.∴点A在线段CD的垂直平分线上.13.2 画轴对称图形课时训练一.选择题1.点A(3,4)关于x轴的对称点的坐标为()A.(3,﹣4)B.(﹣3,﹣4)C.(﹣3,4)D.(﹣4,3)2.在平面直角坐标系中,点M(12,﹣17)关于x轴对称的点在()A.第一象限B.第二象限C.第三象限D.第四象限3.已知点P(3,﹣2),点Q(﹣3,2),点R(﹣3,﹣2),点H(3,2),下面选项中关于y轴对称的是()A.P和Q B.P和H C.Q和R D.P和R4.若点A(﹣4,m﹣3),B(2n,1)关于x轴对称,则()A.m=2,n=0B.m=2,n=﹣2C.m=4,n=2D.m=4,n=﹣2 5.蝴蝶标本可以近似地看做轴对称图形.如图,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为(5,3),则其关于y轴对称的点B的坐标为()A.(5,﹣3)B.(﹣5,3)C.(﹣5,﹣3)D.(3,5)6.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为()A.(1,7)B.(0,5)C.(3,4)D.(﹣3,2)7.在平面直角坐标系中,点A(﹣3,﹣4)平移后能与原来的位置关于y轴对称,则应把点A()A.向左平移6个单位B.向右平移6个单位C.向下平移8个单位D.向上平移8个单位8.已知点M(2,2),规定一次变换是:先作点M关于x轴对称,再将对称点向左平移1个单位长度,则连续经过2020次变换后,点M的坐标变为()A.(﹣2018,2)B.(﹣2018,﹣2)C.(﹣2017,2)D.(﹣2017,﹣2)二.填空题9.点A(5,﹣1)关于x轴对称的点A'的坐标是.10.若点(3+m,a﹣2)关于y轴对称点的坐标是(3,2),则m+a的值为.11.如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b=.12.已知点M(a,3),点N(2,b)关于y轴对称,则(a+b)2019的值是.三.解答题13.已知点M(﹣2,2b﹣1),N(3a﹣11,5).(1)若M,N关于y轴对称,试求a,b的值;(2)若M,N关于x轴对称,试求a+b的算术平方根.14.△ABC在平面直角坐标系中的位置如图.请画出△ABC关于y轴对称的△A1B1C1,并求出A1、B1、C1三点的坐标.15.如图,在长方形网格中有一个△ABC.(1)画出△ABC关于y轴对称的△A1B1C1.(2)若网格中的最小正方形边长为1,求△A1B1C1的面积.16.如图,△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.(1)写出△ABC三个顶点的坐标.(2)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标.17.如图,在平面直角坐标系中,A(1,0),B(3,3),C(5,1).(1)画出△ABC关于x轴的对称图形△AB1C1;(2)△ABC的面积为;(3)在x轴上求一点P,使得△APB的面积等于△ABC的面积.18.如图,在平面直角坐标系中.(1)作△ABC关于x轴对称的△A1B1C1;(2)求出△ABC的面积;(3)在x轴上是否存在一点P,使得△AA1P与△ABC面积相等?若存在,请求出点P 的坐标;若不存在,说明理由.参考答案一.选择题1.解:点A(3,4)关于x轴对称点的坐标为:(3,﹣4).故选:A.2.解:∵点(12,﹣17)关于x轴对称的坐标是(12,17),∴点M(12,﹣17)关于x轴对称的点在第一象限.故选:A.3.解:点P(3,﹣2),点Q(﹣3,2),点R(﹣3,﹣2),点H(3,2)中Q和H,P和R都关于y轴对称.故选:D.4.解:根据题意:m﹣3=﹣1,2n=﹣4,所以m=2,n=﹣2.故选:B.5.解:∵A,B关于y轴对称,A(5,3),∴B(﹣5,3),故选:B.6.解:由坐标系可得B(﹣3,1),将△ABC先沿y轴翻折得到B点对应点为(3,1),再向上平移3个单位长度,点B的对应点B'的坐标为(3,1+3),即(3,4),故选:C.7.解:∵点A(﹣3,﹣4)平移后能与原来的位置关于y轴轴对称,∴平移后的坐标为(3,﹣4),∵横坐标增大,∴点是向右平移得到,平移距离为|3﹣(﹣3)|=6.故选:B.8.解:由题可得,第2019次变换后的点M在x轴下方,∴点M的纵坐标为2,横坐标为2﹣2020×1=﹣2018,∴点M的坐标变为(﹣2018,﹣2),故选:B.二.填空题9.解:点A(5,﹣1)关于x轴对称的点A'的坐标是(5,1).故答案为:(5,1).10.解:∵点(3+m,a﹣2)关于y轴对称点的坐标是(3,2),∴3+m=﹣3,a﹣2=2,解得:m=﹣6,a=4,则m+a的值为:﹣6+4=﹣2.故答案为:﹣2.11.解:∵点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,∴a=﹣2,b=﹣3,∴a+b=﹣2﹣3=﹣5,故答案为﹣5.12.解:∵点M(a,3),点N(2,b)关于y轴对称,∴a=﹣2,b=3,∴(a+b)2019=(﹣2+3)2019=1.故答案为:1.三.解答题13.解:(1)依题意得3a﹣11=2,2b﹣1=5,∴a=,b=3.(2)依题意得3a﹣11=﹣2,2b﹣1=﹣5,∴a=3,b=﹣2,∴=1.14.解:A1(2,3)(1分)B1(3,2)(2分)C1(1,1)(3分)15.解:(1)△A1B1C1即为所求;(2)△A1B1C1的面积为:3×5﹣×2×3﹣×2×3﹣×1×5=15﹣3﹣3﹣2.5=6.5.16.解:(1)A、B、C三点的坐标分别为(2,4),(1,1),(3,2);(2)如图所示:△A1B1C1,点C1的坐标为:(﹣3,2).17.解:(1)如图所示,△AB1C1即为所求.(2)△ABC的面积为4×3﹣×2×3﹣×1×4﹣×2×2=5,故答案为:5;(3)设点P坐标为(m,0),根据题意,得:×|m﹣1|×3=5,解得m=或m=﹣,∴点P的坐标为(,0)或(﹣,0).18.解:(1)如图所示,△A1B1C1即为所求;(2)S△ABC=×(1+3)×5﹣×1×2﹣×3×3=;(3)存在,设点P坐标为(a,0),根据题意,得:×4×|a﹣1|=,解得a=或a=﹣,∴点P坐标为(,0)或(﹣,0).13.3 等腰三角形一、选择题1. 如图,等腰三角形的对称轴是()A.直线l1B.直线l2C.直线l3D.直线l42. 如图,AC=AD,BC=BD,则有()A.CD垂直平分ABB.AB垂直平分CDC.AB与CD互相垂直平分D.CD平分∠ACB3. 已知等腰三角形的一个角等于42°,则它的底角为() A.42°B.69°C.69°或84°D.42°或69°4. 已知实数x、y满足|x-4|+y-8=0,则以x、y的值为两边长的等腰三角形的周长是()A. 20或16B. 20C. 16D. 以上答案均不对5. 如图,AD是△ABC的中线,下列条件中不能推出△ABC是等腰三角形的是()A.∠BAD+∠B=∠CAD+∠C B.AB-BD=AC-CDC.AB+BD=AC+CD D.AD=BC6. 如图,∠AOB=50°,OM平分∠AOB,MA⊥OA于点A,MB⊥OB于点B,则∠MAB等于()A.50°B.40°C.25°7. 如图,△ABC是等边三角形,DE∥BC.若AB=10,BD=6,则△ADE的周长为()A.4 B.12 C.18 D.308. 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠BCD的度数为()A.150°B.160°C.130°D.60°9. 如图所示的正方形网格中,网格线的交点称为格点. 已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形.....,那么符合题意的点C的个数是()A. 6B. 7C. 8D. 910. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是()A.60°B.65°C.75°D.80°二、填空题11. 如图,在△ABC中,AB=AC,D是AC上一点,且BC=BD.若∠CBD=46°,则∠A=________°.12. 如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1=________.13. 一个等腰三角形的一边长是2,一个外角是120°,则它的周长是________.14. 如图所示,在△ABC中,DE是AC的垂直平分线,AE=5 cm,△ABD的周长为18 cm,则△ABC的周长为.15. 如图,BO平分∠CBA,CO平分∠ACB,MN过点O且MN∥BC,设AB=12,AC=18,则△AMN的周长为________.16. 如图,在△ABC中,若AB=AC=8,∠A=30°,则S△ABC=________.三、解答题17. 如图,在△ABC中,AB=BD,根据图中的数据,求∠BAC的度数.18. 如图,在△ABC中,O是边AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交△ABC的外角平分线于点F.探究线段OE与OF的数量关系,并说明理由.19. 如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠BAC的平分线分别交BC,CD于点E,F.求证:△CEF是等腰三角形.人教版八年级数学上册13.3 等腰三角形同步训练-答案一、选择题1. 【答案】A2. 【答案】B3. 【答案】D[解析] 在等腰三角形中,当一个锐角在未指明为顶角还是底角时,一定要分类讨论.①42°的角为等腰三角形的底角;②42°的角为等腰三角形的顶角,则底角为(180°-42°)÷2=69°.所以底角为42°或69°.4. 【答案】B【解析】∵|x -4|+y -8=0,∴x -4=0,y -8=0,解得x =4,y =8.分两种情况讨论:①当4为腰时,根据三角形三边关系知4+4=8,∴这样的等腰三角形不存在;②当8为腰时,则有4+8>8,这样能够组成等腰三角形,∴此三角形的周长是8+8+4=20.5. 【答案】D[解析] 由∠BAD +∠B =∠CAD +∠C 可得∠ADB =∠ADC ,又∠ADB +∠ADC =180°,所以∠ADB =∠ADC =90°,又BD =DC ,由垂直平分线的性质可得AB =AC.由等式的性质,根据AB -BD =AC -CD ,AB +BD =AC +CD ,又BD =CD ,均可得AB =AC.选项D 不能得到AB =AC.6. 【答案】C[解析] ∵OM 平分∠AOB ,MA ⊥OA 于点A ,MB ⊥OB 于点B ,∴∠AOM =∠BOM =25°,MA =MB.∴∠OMA =∠OMB =65°.∴∠AMB =130°.∴∠MAB =12×(180°-130°)=25°.故选C.7. 【答案】B[解析] ∵△ABC 为等边三角形,∴∠A =∠B =∠C =60°.∵DE ∥BC ,∴∠ADE =∠B =60°,∠AED =∠C =60°.∴△ADE 为等边三角形.∵AB =10,BD =6,∴AD =AB -BD =10-6=4.∴△ADE 的周长为4×3=12.8. 【答案】A[解析] ∵AB ∥ED ,∴∠E =180°-∠EAB =180°-120°=60°. 又∵AD =AE ,∴△ADE 是等边三角形.∴∠EAD =60°.∴∠BAD =∠EAB -∠EAD =120°-60°=60°.∵AB =AC =AD ,∴∠B =∠ACB ,∠ACD =∠ADC.在四边形ABCD 中,∠BCD =∠B +∠ADC =12(360°-∠BAD)=12×(360°-60°)=150°. 故选A. 9. 【答案】C10. 【答案】D[解析] ∵OC =CD =DE ,∴∠O =∠ODC ,∠DCE =∠DEC.∴∠DCE=∠O+∠ODC=2∠ODC.∵∠O+∠OED=3∠ODC=∠BDE=75°,∴∠ODC=25°.∵∠CDE+∠ODC=180°-∠BDE=105°,∴∠CDE=105°-∠ODC=80°.二、填空题11. 【答案】46[解析] ∵BC=BD,∠CBD=46°,∴∠C=∠BDC=12(180°-46°)=67°.∵AB=AC,∴∠ABC=∠C=67°.∴∠A=46°.12. 【答案】40°[解析] 如图.∵△BCD是等边三角形,∴∠BDC=60°.∵a∥b,∴∠2=∠BDC=60°.由三角形的外角性质和对顶角的性质可知,∠1=∠2-∠A=40°.13. 【答案】6[解析] 已知三角形的一外角为120°,则相邻内角度数为60°,那么含有60°角的等腰三角形是等边三角形.已知等边三角形的一边长为2,则其周长为6.14. 【答案】28 cm15. 【答案】30[解析] ∵MN∥BC,∴∠MOB=∠OBC.∵∠OBM=∠OBC,∴∠MOB=∠OBM.∴MO=MB.同理NO=NC.∴△AMN的周长=AM+MO+AN+NO=AM+MB+AN+NC=AB+AC=30.16. 【答案】16[解析] 如图,过点C作CD⊥AB,垂足为D,则△ADC是含30°角的直角三角形,那么DC=12AC=4,∴S△ABC=12AB·DC=12×8×4=16.三、解答题17. 【答案】解:∵∠ADB=30°+40°=70°,AB=BD,∴∠BAD=∠ADB=70°.∴∠BAC=∠BAD+∠CAD=100°.18. 【答案】解:OE=OF.理由:∵MN∥BC,∴∠OEC=∠BCE,∠OFC=∠DCF.∵CE平分∠ACB,CF平分∠ACD,∴∠OCE=∠BCE,∠OCF=∠DCF.∴∠OEC=∠OCE,∠OFC=∠OCF.∴OE=OC,OC=OF.∴OE=OF.19. 【答案】证明:∵∠ACB=90°,∴∠B+∠BAC=90°.∵CD⊥AB,∴∠CAD+∠ACD=90°.∴∠ACD=∠B.∵AE是∠BAC的平分线,∴∠CAE=∠EAB.∵∠EAB+∠B=∠CEF,∠CAE+∠ACD=∠CFE,∴∠CFE=∠CEF. ∴CF=CE.∴△CEF是等腰三角形.。
第13章 轴对称(压轴必刷30题10种题型专项训练)(原卷版)-2024-2025学年八年级数学上学

第13章轴对称(压轴必刷30题10种题型专项训练)一.全等三角形的判定与性质(共1小题)1.(2022秋•亭湖区期末)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC =∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.二.线段垂直平分线的性质(共4小题)2.(2023秋•广陵区校级月考)如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.(1)若△CMN的周长为15cm,求AB的长;(2)若∠MFN=70°,求∠MCN的度数.3.(2023秋•广陵区月考)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠C=40°,求∠BAD的度数;(2)若AC=5,DC=4,求△ABC的周长.4.(2022秋•兴化市月考)如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)求∠DAF的度数;(2)如果BC=10,求△DAF的周长.5.(2022秋•兴化市校级月考)如图:△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D,①若△BCD的周长为8,求BC的长;②若BC=4,求△BCD的周长.三.等腰三角形的性质(共2小题)6.(2022秋•宝应县月考)如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.(1)小棒能无限摆下去吗?答:.(填“能”或“不能”)(2)若已经摆放了3根小棒,则θ1=,θ2=,θ3=;(用含θ的式子表示)(3)若只能摆放4根小棒,求θ的范围.7.(2022秋•金湖县期中)如图,在△ABC中,AB=AC,D、E两点在BC边上,且AD=AE.求证:BD=CE.四.等腰三角形的判定(共2小题)8.(2022秋•淮安区期中)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)BP=(用t的代数式表示)(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?(3)当点Q在边CA上运动时,出发秒后,△BCQ是以BC或BQ为底边的等腰三角形?9.(2022秋•建邺区校级期中)在△ABC中,AB=8,BC=10,AC=6,动点P从点C出发,沿着CB运动,速度为每秒2个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:(1)求BC上的高;(2)当t为何值时,△ACP为等腰三角形?五.等腰三角形的判定与性质(共1小题)10.(2022秋•崇川区校级月考)如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD 交边AC于点D.(1)求证:△BCD为等腰三角形;(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.六.等边三角形的性质(共3小题)11.(2022秋•兴化市校级月考)在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.(1)如图1,当点M、N在边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时=;(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.12.(2022秋•鼓楼区期中)如图1,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM(点D与点A重合除外)上时,以CD为一边且在CD的下方作等边△CDE,连接BE.(1)判断AD与BE是否相等,请说明理由;(2)如图2,若AB=8,点P、Q两点在直线BE上且CP=CQ=5,试求PQ的长;(3)在第(2)小题的条件下,当点D在线段AM的延长线(或反向延长线)上时.判断PQ的长是否为定值,若是请直接写出PQ的长;若不是请简单说明理由.13.(2022秋•启东市校级期末)如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)何时△PBQ是直角三角形?(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ 变化吗?若变化,则说明理由,若不变,则求出它的度数.七.等边三角形的判定与性质(共1小题)14.(2022秋•铜山区校级月考)已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.求证:(1)AE=DB;(2)△CMN为等边三角形.八.含30度角的直角三角形(共1小题)15.(2023秋•高新区校级月考)如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.(1)求证:AE=2CE;(2)连接CD,请判断△BCD的形状,并说明理由.九.作图-轴对称变换(共13小题)16.(2022秋•亭湖区期末)如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.(1)格点△ABC(顶点均在格点上)的面积=;(2)画出格点△ABC关于直线DE对称△A1B1C1;(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.17.(2023秋•宝应县校级月考)如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;(2)三角形ABC的面积为;(3)以AC为边作与△ABC全等的三角形,则可作出个三角形与△ABC全等;(4)在直线l上找一点P,使PB+PC的长最短.18.(2022秋•通州区校级月考)如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)在DE上画出点P,使PB+PC最小.19.(2022秋•江阴市校级月考)如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).(1)在图中作出△ABC关于直线l对称的△A1B1C1(要求A与A1,B与B1,C与C1相对应);(2)求△ABC的面积;(3)在直线l上找一点P,使得△P AC的周长最小.20.(2022秋•沭阳县期末)如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;(2)在网格中画出△ABC关于直线m对称的△A2B2C2;(3)在直线m上画一点P,使得C1P+C2P的值最小.21.(2022秋•崇川区校级月考)在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.建立如图所示平面直角坐标系,点A的坐标为(﹣5,2).(1)画出与△ABC关于y轴对称的A1B1C1;(2)通过画图在x轴上确定点Q,使得QA与QB之和最小,画出QA与QB并直接写出点Q的坐标.Q 的坐标为.22.(2022秋•秦淮区月考)如图,△ABC的顶点A、B、C都在小正方形的顶点上,利用网格线按下列要求画图.(1)画△A1B1C1,使它与△ABC关于直线l成轴对称;(2)在直线l上找一点P,使点P到边AB、BC的距离相等.23.(2022秋•宜兴市月考)如图均为2×2的正方形网格,每个小正方形的边长均为1.请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形.24.(2022秋•锡山区校级月考)如图,在10×10的正方形中网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).(Ⅰ)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)(Ⅱ)若有一格点P到点A、B的距离相等(P A=PB),则网格中满足条件的点P共有个.25.(2022秋•姜堰区月考)如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.(1)在图中画出与△ABC关于直线l成轴对称的△A1B1C1;(2)在直线l上找出一点P,使得|P A﹣PC1|的值最大,该最大值为(保留作图痕迹并标上字母P)(3)在正方形网格中存在个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.26.(2022秋•云龙区校级月考)如图,方格纸上画有AB、CD两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法)(1)请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;(2)请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形,请画出所有情形.27.(2022秋•栖霞区校级月考)如图,在正方形ABCD中,点E是BC上一点,连接AE.请添加一条线段,使得图形是一个轴对称图形.(要求:画出示意图,并作出对称轴)28.(2022秋•仪征市校级期中)在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.一十.轴对称-最短路线问题(共2小题)29.(2023春•海门市期末)如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是()A.B.C.a+b D.a30.(2021秋•梁溪区校级期末)如图,点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=5,已知CD=4,P是直线MN上的一个动点,记P A+PB的最小值为a,|P A﹣PB|的最大值为b,则a2﹣b2的值为()A.160B.150C.140D.130。
人教版八年级数学上测第十三章《轴对称》检测题(含答案)

人教版八年级数学上测第十三章《轴对称》检测题(含答案)一、选择题(每小题3分,共30分)1. 现实世界中,对称现象无处不在,下列汉字是轴对称图形的是()A. 爱B. 我C. 中D. 华【答案】C.2.点M(1,2)关于x轴对称点的坐标为()A.(-1,2)B.(-1,-2)C.(1,-2)D.(2,-1)【答案】C.3. 如图,△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B度数为()A. 25°B. 30°C. 35°D. 40°【答案】B.4.下列每个网格中均有两个图形,其中一个图形可由另一个轴对称变换得到的是()A. B. C. D.【答案】B.5. 如图,∠MON内有一点P,点P关于OM、ON的对称点分别是G、H,连GH分别交OM、ON于A、B点,若GH=10cm,则△P AB的周长为()A. 5cmB.10cmC. 20cmD.15cm【答案】B. 提示:根据对称性,AG=AP,BH=GP,∴AP+AB+BP=AG+AB+BH=GH=10.6.等腰三角形的一个内角为70°,则另外两个内角的度数分别是()A. 55° ,55°B. 70°,40或70°,55°C.70°,40°D. 55°,55°或70°,40°【答案】D.7. 如图,在正方形ABCD的外侧,作等边△CDE,连接AE交CD于点F,则∠DF A的度数为()A. 45°B. 55°C. 60°D. 75°【答案】D. 提示:∠ADE=90°+60°=150°,∠DAF=∠DEA=15°,则∠DF A=75°.8. 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,BC=12cm,则DE的长度为()A. 5cmB. 5.4cmC. 2.4cmD. 3cm【答案】C. 提示:作DF⊥BC于F,∵BD平分∠ABC,故设DE=DF=h,由S△ABD+S△CBD=S△ABC,得:12(AB+BC)h=36,代入数值,解得h=2.4,故选C.9. 如图,在△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=()A.2ba+B.2ba-C. a-b D. b-a【答案】C. 提示:AD=BD=BC=b,CD=AC-AD=a-b.10. 如图OE是等边△AOB的中线,OB=4,C是直线OE上一动点,以AC为边在直线AC下方作等边△ACD,连接ED,下列说法正确的是()A. ED的最小值是2B. ED的最小值是1C. ED有最大值D. ED没有最大值也没有最小值【答案】B. 提示:连BD,则易得△AOC≌△ABD(SAS),∴∠ABD=∠AOC=30°,当∠BDE=90°时,ED最小,此时ED=12BE=1,故选B.二、填空题(每小题3分,共18分)11. 点P(m,n)和点Q(n-1,2m)关于x轴对称,则m+n的值为__________.【答案】13. 提示:m=n-1,2m+n=0,联立解得m=-13,n=23,∴m+n=13.12. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC,若DE=1,则BC的长是__________.【答案】3. 提示:由条件得AD=BD,∠CAD=∠BAD,∴∠CAD=∠BAD=∠B=30°,CD=DE=1,BD=2DE=2,∴BC=CD+BD=3.13. 如图,在△ABC中,DE垂直平分AC,若AE=3,△ABD周长为13,则△ABC周长为________.【答案】19. 提示:由题知AC=2AE=6,AD=CD,∴BC=BD+AD,∵AB+BD+AD=13,∴AB+BC=13,∴AB+BC+AC=13+6=19.14. 如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的力向被击出(球可以经过多次反射),那么该球最后将落入的球袋是________.【答案】1号袋. 提示:如图所示.15. 如图,在△ABC中,∠C=46°,将△ABC沿直线l折叠,点C落在点D的位置,则∠1-∠2的度数是___________ .【答案】92°. 提示:由飞镖模型,∠DNC=∠C+∠D+∠DMC,即:180°-∠2=46°+46°+(180°-∠1),∴∠1-∠2=92°.16 .已知A(1,2)、B(7,4),点M、N是x轴上的动点(M在N左边),MN=3,当AM+MN+NB最小时,直接写出点M的坐标为___________.【答案】(2,0). 提示:作点A关于x轴的对称点A′,将点B向左平移3个单位得点B′,连接A′B′,交x轴于点M.三、解答题(共8小题,共72分)17. (8分)如图,已知点M、N和∠AOB,用尺规作图作一点P,使P到点M、N的距离相等,且到∠AOB两边的距离相等.(保留作图痕迹,不写作法)【答案】1.作∠AOB的平分线OC;2.连MN,作MN的垂直平分线EF;则射线OC与直线EF的交点P即为所求.18. (8分)如图,在△ABC中,∠B=30°,∠C=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)直接写出∠BAC的度数;(2)求∠DAF的度数;(3)若△DAF的周长为20,求BC的长.【答案】(1)∠BAC=100°;(2)∵DE、FG分别垂直平分AB、AC,∴AD=BD,AF=CF,∴∠BAD=∠B=30°,∠CAF=∠C=50°,∴∠DAF=∠BAC-∠BAD-∠CAF=100°-30°-50°=20°;(3) ∵△DAF的周长为20,∴AD+DF+AF=20,∴BC=BD+DF+CF=AD+DF+AF=20.19. (8分)(1)如图,已知△ABC,请画出△ABC关于y轴对称的△A'B'C'(其中A'、B'、C'分别是A、B、C的对应点);(2)直接写出点A'、B'、C'点的坐标;(3)求△ABC的面积是多少?(4)用无刻度的直尺在y轴上找一点Q,使得QA+QB之和最小.(用虚线表示画图过程)【答案】(1) A'(2,3)、B'(3,1)、C'(-1,-2);(2)S△ABC=5×4-12×1×2-12×3×4-12×3×5=5.5;(3) 连接A′B(或AB′)交y轴于Q,即可.20. (8分)如图,在△ABC中,AB=AC,D是BC边上的一点,DE⊥AB于E,DF⊥AC于F,请添加一个条件,使DE=DF,并说明理由.【答案】添加的条件是:D为BC的中点. 理由如下:方法1:连接AD.∵AB=AC,D为BC中点,∴AD平分∠BAC.又∵DE⊥AB,DF⊥AC,∴DE=DF.方法2:∵AB=AC,∴∠B=∠C.∵D为BC中点,∴BD=CD.在△BDE与△CDF中,∵∠B=∠C,∠BED=∠CFD=90°,BD=CD,∴△BDE≌△CDF(AAS),∴DE=DF.21. (8分)如图,△ABC 是等边三角形,点D 在BC 延长线上,DE ⊥AB 于点E ,交AC 于G ,EF ⊥BC 于点F ,若CD =3AE ,CF =6,求AC 的长. 【答案】设AE =x ,则CD =3x .在等边△ABC 中,∠A =∠B =∠ACB =60°, 又DE ⊥AB ,∴∠D =∠AGE =∠CGD =30°. ∴AG =2AE =2x ,CG =CD =3x , ∴AB =BC =AC =2x +3x =5x . 则BE =5x -x =4x ,又∵EF ⊥BC ,∠B =60°,∴BF =12BE =2x ,∴BC =BF +CF =2x +6.∵BC =AC ,∴2x +6=5x ,∴x =2. ∴AC =5x =10.22. (10分)如图,在△ABC 中,∠ABC =∠ACB ,E 为BC 边上一点,以E 为顶点作∠AEF ,∠AEF 的边交AC 于点F ,使∠AEF =∠B . (1)如果∠ABC =40°,则∠BAC =________; (2)判断∠BAE 与∠CEF 的大小关系,并说明理由;(3)当△AEF 为直角三角形时,求∠AEF 与∠BAE 的数量关系.【答案】(1)100°; …………… 2分 (2)∠BAE =∠CEF ,理由如下: ∵∠AEC 是△ABE 的外角, ∴∠AEF +∠CEF =∠B +∠BAE . 又∵∠AEF =∠B ,∴∠CEF =∠BAE . …………… 5分(3)由(2),设∠CEF =∠BAE =α,设∠AEF =∠B =∠C =β.则∠AFE =∠CEF +∠C =α+β.∵∠AEF =∠B <90°,故分两种情况考虑:1°当∠EAF 为直角时,如图1,由∠AEF +∠AFE =90°,CBAFECBA备用图1CBA备用图2得β+(α+β)=90°,∴α+2β=90°,故有:∠BAE+2∠AEF=90°.2°当∠AFE为直角时,如图2,得α+β=90°,即:∠BAE+∠AEF=90°.综上,当△AEF为直角三角形时,∠BAE+2∠AEF=90°或∠BAE+∠AEF=90°. …………… 10分23. (10分)已知Rt△ABC中,AB=AC,∠ABC=∠ACB=45°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边在AD的右侧作Rt△ADE,AD=AE,∠ADE=∠AED =45°,连接CE.(1)〖发现问题〗如图1,当点D在边BC上时,①请写出BD和CE之间的数量关系为_____________,位置关系为____________;②求证:CE+CD=BC;(2)尝试探究:如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BC、CE、CD 之间存在的数量关系是否成立? 若成立,请证明;若不成立,请写出新的数量关系(不必证明);(3)拓展延伸:如图3,当点D在CB的延长线上且其他条件不变时,若BC=6,CE=2,求线段CD的长.【答案】(1)①BD=CE,BD⊥CE,…………… 2分②由条件得∠BAC=∠DAE=90°,∴∠BAD=∠CAE.又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=CE,∠ACE=∠ABD=45°,∴CE+CD=BD+CD=BC. …………… 5分(2) 不成立,此时关系式为BC+CD=CE. …………… 7分提示:同上,证明△BAD≌△CAE(SAS),得BD=CE,即BC+CD=CE.(3) 由条件得∠BAC=∠DAE=90°,∴∠BAD=∠CAE.又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=CE. ∵BD+BC=CD,∴CD =CE +BC =2+6=8. …………… 10分24. (12分)等腰Rt △ACB 中,∠ACB =90°,AC =BC ,点A 在x 轴正半轴上,C 在y 轴负半轴上.(1)如图1,求证:∠BCO =∠CAO ;(2)如图2,若OA =4,OC =2,M 是AB 与y 轴交点,求△AOM 的面积;(3)如图3,点C (0,2),点Q 、A 均在x 轴上,且S △ACQ =6a (a 为已知数). 分别以AC 、CQ 为腰在第一、第二象限作等腰Rt △CAN 、等腰Rt △QCM ,连接MN 交y 轴于P 点,间:S △MON 是否发生改变?若不变,求出S △MON 的值;若变化,求S △MON 的取值范围.【答案】(1) ∵∠ACB =90°,∴∠BCO +∠ACO =90°. 又∵∠AOC =90°,∴∠CAO +∠ACO =90°. ∴ ∠BCO =∠CAO . …………… 3分(2) 过B 作BD ⊥y 轴于D ,则△BCD ≌△CAO (AAS ), ∴BD =CO =2,CD =AO =4,OD =CD -OC =2,∴B (-2,2). 又∵A (4,0),C (0,-2),由割补法,得S △ABC =4×6-12×2×4-12×2×4-12×2×6=10, 又2142△△BCM ACM S BD S OA ===,∴S △ACM =23S △ABC =203. ∵S △AOC =12×2×4=4,∴S △AOM =S △ACM -S △AOC =203-4=83. (3) 过N 作NE ∥CM 交y 轴于E ,则∠CNE +∠MCN =180°,∵∠MCQ +∠ACN =90°+90°=180°, ∴∠ACQ +∠MCN =180°, ∴∠CNE =∠ACQ . 又∵∠ECN +∠ACO =90°,∠QAC +∠ACO =90°, ∴∠ECN =∠QAC . 在△ECN 和△QAC 中,∵∠CNE =∠ACQ ,CN =AC ,∠ECN =∠QAC , ∴△ECN ≌△QAC (ASA ),∴CE=AQ,EN=QC=MC.又NE∥CM,∴△PEN≌△PCM(ASA),∴PE=PC.∵点C(0,2),S△ACQ=6a,∴AQ=6a.∴CE=AQ=6a,∴CP=PE=3a.∴OP=OC+CP=2+3a.过M作MF⊥y轴于F,过N作NG⊥y轴于G,∵△MCQ为等腰直角三角形,∴△MCF≌△CQO(AAS),∴MF=CO=2,同理,NG=OC=2.则S△MON=S△MOP+S△NOP=12OP·MF+12OP·NG=2OP=6a+4.。
人教版八年级数学上册《第十三章轴对称》单元测试卷含答案
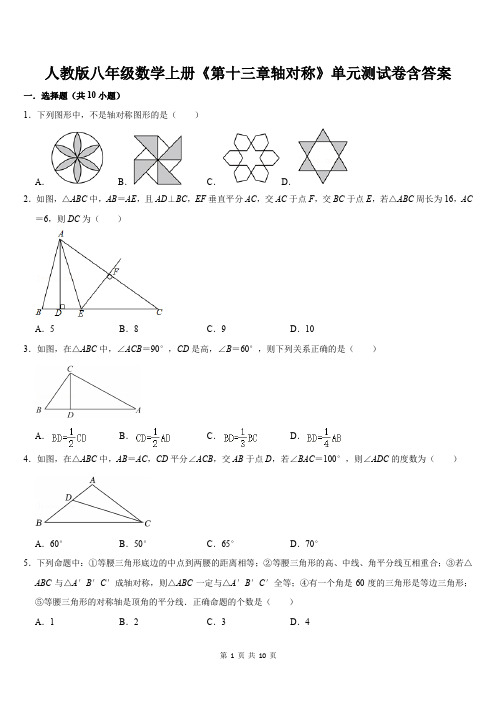
人教版八年级数学上册《第十三章轴对称》单元测试卷含答案一.选择题(共10小题)1.下列图形中,不是轴对称图形的是()A.B.C.D.2.如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC =6,则DC为()A.5B.8C.9D.103.如图,在△ABC中,∠ACB=90°,CD是高,∠B=60°,则下列关系正确的是()A.B.C.D.4.如图,在△ABC中,AB=AC,CD平分∠ACB,交AB于点D,若∠BAC=100°,则∠ADC的度数为()A.60°B.50°C.65°D.70°5.下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合;③若△ABC与△A′B′C′成轴对称,则△ABC一定与△A′B′C′全等;④有一个角是60度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是()A.1B.2C.3D.46.已知等腰三角形两边的长x、y满足|x2﹣9|+(y﹣4)2=0,则三角形周长为()A.10B.11C.12D.10或117.如图,在等边三角形ABC中,BC边上的中线AD=6,E是AD上的一个动点,F是边AB上的一个动点,在点E,F运动的过程中,EB+EF的最小值是()A.6B.4C.3D.28.如图,在正方形网格中,A,B两点都在小方格的顶点上,如果点C也是图中小方格的顶点,且△ABC是等腰三角形,那么点C的个数为()A.1B.2C.3D.49.如图,△ABC是等腰三角形,AB=AC,∠BAC是钝角.点D在底边BC上,连接AD,恰好把△ABC分割成两个等腰三角形,则∠B的度数是()A.30°B.36°C.45°D.60°10.若二元一次方程组的解x,y的值恰好是一个等腰三角形两边的长,且这个等腰三角形的周长为7,则m的值为()A.4B.1.5或2C.2D.4或2二.填空题(共8小题)11.等边三角形的两条中线所成的锐角的度数是度.12.已知点P(1﹣a,3+2a)关于x轴的对称点落在第三象限,则a的取值范围是.13.等腰三角形一腰上的高与另一腰的夹角为42°,则顶角为.14.如图,等腰三角形ABC中,CA=CB,∠C=40°,若沿图中虚线剪去∠A,则∠1+∠2的度数为度.15.如图,在△ABC中,DE是BC的垂直平分线,若AB=6,AC=9,则△ABD的周长是.16.如图,∠ABC和∠ACB的角平分线相交于点M,且过点M的直线DE∥BC,分别交AB、AC于D、E两点,若AB =12,AC=10,则△ADE的周长为.17.如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是秒.18.如图,在△ABC中,AB=AC,BC=4,△ABC的面积为20,AB的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则BM+DM的最小值为.三.解答题(共7小题)19.△ABC在直角坐标系内的位置如图所示:(1)分别写出点A,C的坐标:A的坐标:,C的坐标:;(2)请在这个坐标系内画出与△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标;(3)求△A1B1C1的面积.20.已知一个三角形的两条边长分别为4cm,8cm.设第三条边长为x cm.(1)求x的取值范围.(2)若此三角形为等腰三角形,求该等腰三角形的周长.21.如图所示,△ABC是等边三角形,AD为中线,AD=AE.(1)求∠EDC的度数;(2)若AD=2,求△AED的面积.22.如图,DC平分∠ACE,且AB∥CD,求证:△ABC为等腰三角形.23.如图,在等边三角形ABC中,D是BC边上一点,以AD为边作等腰三角形ADE,使AD=AE,∠DAE=80°,DE交AC于点F,∠BAD=15°.(Ⅰ)求∠CAE的度数;(Ⅱ)求∠FDC的度数.24.如图,在△ABC中,AB=AC,D是AB上的一点,过点D作DE⊥BC于点E,延长ED和CA,交于点F.(1)求证:△ADF是等腰三角形;(2)若∠F=30°,BD=4,EC=6,求AC的长.25.如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,CD的垂直平分线MF交AC 于F,交BC于M.(1)求∠BDE的度数;(2)证明△ADF是等边三角形;(3)若MF的长为2,求AB的边长.参考答案一.选择题(共10小题)1.B.2.A.3.:D.4.A.5.B.6.D.7.A.8.C.9.B.10.C.二.填空题(共8小题)11.60.12.a>1.13.48°或132°.14.250.15.15.16.22.17.4.18.10.三.解答题(共7小题)19.解:(1)A(0,3),C(﹣2,1);(2)如图所示,△A1B1C1即为所求;点B1(﹣4,﹣4);故答案为:(﹣4,﹣4);(3)△A1B1C1的面积=.20.解:(1)根据三角形三边关系得,8﹣4<x<8+4即4<x<12;(2)∵三角形是等腰三角形,等腰三角形两条边长分别为4cm,8cm,且4<x<12∴等腰三角形第三边只能是8cm∴等腰三角形周长为4+8+8=20cm.21.(1)解:∵△ABC是等边三角形∴∠BAC=60°AB=AC=BC∵AD为中线∴AD⊥CD∵AD=AE∴∴∠CDE=∠ADC﹣∠ADE=15°;(2)解:过D作DH⊥AC于H∴∠AHD=90°∵∠CAD=30°∴∵AD=AE=2∴.22.证明:∵AB∥CD∴∠A=∠ACD,∠B=∠DCE.∵DC平分∠ACE∴∠ACD=∠DCE∴∠B=∠A∴AC=BC∴△ABC为等腰三角形.23.解:(Ⅰ)∵三角形ABC为等边三角形∴∠BAE=60°∵∠BAD=15°∴∠DAC=60°﹣15°=45°∵∠DAE=80°∴∠CAE=80°﹣45°=35°;(Ⅱ)∵∠DAE=80°,AD=AE∴∠ADE=(180°﹣80°)=50°∠ADC=∠BAD+∠B=15°+60°=75°又∵∠ADE=50°∴∠FDC=∠ADC﹣∠ADE=75°﹣50°=25°.24.(1)证明:∵AB=AC∴∠B=∠C∵FE⊥BC∴∠F+∠C=90°,∠B+∠BDE=90°∴∠F=∠BDE∵∠BDE=∠FDA∴∠F=∠FDA∴AF=AD∴△ADF是等腰三角形;(2)解:∵DE⊥BC∴∠DEB=90°∵∠F=30°∴∠BDE=30°∵BD=4∴∵AB=AC∴△ABC是等边三角形∴AC=AB=BE+EC=825.(1)解:在△ABC中,AB=AC,∠BAC=120°∴∠B=∠C=×(180°﹣∠BAC)=30°在△BDE中,BD=BE∴∠BDE=∠BED=×(180°﹣∠B)=75°;(2)证明:∵CD的垂直平分线MF交AC于F,交BC于M ∴DF=CF,∠FMC=90°∴∠FDC=∠C=30°∴∠AFD=∠FDC+∠C=60°在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线∴∠BAD=∠CAD=∠BAC=60°∴∠CAD=∠AFD=60°∴△ADF是等边三角形;(3)在Rt△FMC中,∠C=30°,MF=2∴CF=2MF=4∴DF=CF=4由(2)可知:△ADF是等边三角形∴AF=DF=4∴AB=AC=AF+CF=4+4=8.。
八年级初二上册数学 人教版单元测试《轴对称》 练习试题 测试卷(含答案)(1)

人教版八年级数学上册 《第十三章 轴对称》单元测试卷一、选择题(共8小题,4*8=32)1.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )2.图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )A .l 1B .l 2C .l 3D .l 43.下列说法正确的是( )A .等腰三角形的高、中线、角平分线互相重合B .顶角相等的两个等腰三角形全等C .等腰三角形的两个底角相等D .等腰三角形一边不可以是另一边的2倍4.如图,在Rt △ABC 中,∠C =90°,∠B =15°,DE 垂直平分AB 交BC 于点E ,BE =4,则AC 的长为( )A .2B .3C .4D .以上都不对5.如图,在△ABC 中,AB =AC ,∠A =36°,BD ,CE 分别为∠ABC 与∠ACB 的角平分线,BD ,CE 相交于点F ,则图中的等腰三角形有( )A .6个B .7个C .8个D .9个6.如图,在已知的△ABC 中,按以下步骤作图:①分别以点B ,C 为圆心,以大于12 BC 的长为半径作弧,两弧相交于两点M ,N ;②作直线MN 交AB 于点D ,连接CD .若CD =AC ,∠A =50°,则∠ACB 的度数为( )A.90° B.95° C.100° D.105°7.如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )A.10 B.8 C.6 D.48.在平面直角坐标系xOy中,已知点A(2,-2),在y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有()A.1个B.2个C.3个D.4个二、填空题(共6小题,4*6=24)9.如图,△ABC沿着直线MN折叠后,与△DEF完全重合,AC,DF交于点P.△ABC与△DEF 关于直线_______对称,直线MN是_________;10.如图,A,B,C三点在同一条直线上,∠A=50°,BD垂直平分AE,垂足为点D,则∠EBC的度数为_____.11.如图,AD是△ABC的中线,∠ADC=60°,BC=6,把△ABC沿直线AD折叠,点C 落在C′处,连接BC′,则BC′的长为________.12.已知a>0,b<0,则点P(a+1,b-1)关于y轴的对称点一定在第__ __象限.13.如图,在三角形纸片ABC中,∠C=90°,∠A=30°,AC=6,折叠该纸片,使点C落在AB边上的点D处,折痕BE与AC交于点E,则折痕BE的长为__ __.14.如图,在四边形ABCD中,AB=BC=CD=AD,点D到AB的距离为3,∠BAD=60°,点F为AB的中点,点E为AC上的任意一点,则EF+EB的最小值为________.三、解答题(共5小题,44分)15.(6分) 如图,在△AOB中,点C在OA上,点E,D在OB上,且CD∥AB,CE∥AD,AB=AD,求证:△CDE是等腰三角形.16.(8分) 如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC +∠BCF=150°,求∠AFE+∠BCD的大小.17.(8分) 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.18.(10分) 如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.(1)求证△BCE≌△ACD;(2)求证CF=CH;(3)判断△CFH的形状并说明理由.19.(12分) (1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD 的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC 得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.因此,AB,AD,DC之间的等量关系是__ __;(2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.参考答案1-4DCCA 5-8CDCD9.MN,对称轴10.100°11.312.三13.414.315.解:∵CD∥AB,∴∠CDE=∠B.又∵CE∥AD,∴∠CED=∠ADB,又AB=AD,∴∠B=∠ADB,∴∠CDE=∠CED,∴△CDE是等腰三角形16.解:∵六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,∠AFC+∠BCF =150°,∴∠AFC=∠EFC,∠BCF=∠DCF,∴∠AFE+∠BCD=2(∠AFC+∠BCF)=300°17.解:(1)∵AB=AC,∴∠B=∠C=30°,∴∠BAC=120°,∠DAC=∠BAC-∠BAD=120°-45°=75°(2)∵∠ADC=∠B+∠DAB=75°,∴∠DAC=∠ADC,∴DC=AC,又∵AB=AC,∴DC=AB18.(1)证明:∵△ABC和△CDE都是等边三角形,∴BC=AC,CE=CD,∠ACB=∠ECD =60°.∴∠BCE=60°+∠ACE=∠ACD.∴△BCE≌△ACD(SAS).(2)证明:∵△BCE≌△ACD,∴∠FBC=∠HAC.∵∠ACB=60°,∠FCH=180°-∠ACB -∠ECD=60°,∴∠BCF=∠ACH.又∵BC=AC,∴△BCF≌△ACH(ASA).∴CF=CH.(3)解:△CFH是等边三角形.理由:∵CF=CH,∠FCH=60°,∴△CFH是等边三角形.19.解:(1)AD=AB+DC(2)AB=AF+CF.证明如下:如图,延长AE交DF的延长线于点G,∵AB∥DC,∴∠BAE =∠G,又∵BE=CE,∠AEB=∠GEC,∴△AEB≌△GEC(AAS),∴AB=GC.∵AE是∠BAF的平分线,∴∠BAG=∠FAG,∵∠BAG=∠G,∴∠FAG=∠G,∴AF=FG.∵CG=FG+CF,∴AB=AF+CF。
人教版初中八年级上册数学第十三章测试卷含答案解析和命题双向细目表-八上13

人教版数学八年级上册第13单元《轴对称》测试考生须知:●本试卷满分120分,考试时间100分钟。
●必须使用黑色字迹的钢笔或签字笔书写,字迹工整,笔迹清楚。
●请在试卷上各题目的答题区域内作答,选择题答案写在题中的括号内,填空题答案写在题中的横线上,解答题写在题后的空白处。
●保持清洁,不要折叠,不要弄破。
一.选择题:本大题有10个小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列图案中,是轴对称图形的是()A. B. C. D.2.在平面直角坐标系中,点(3, -2)关于y轴对称的点的坐标是()A.(3,2)B. (-3,2)C. (-3,-2)D. (3,-2)3.若等腰三角形的周长为25cm,一边为11cm,则腰长为()A.11cmB.7cm或11cmC.7cmD.3cm或11cm4.等腰三角形是轴对称图形,它的对称轴是()A.中线B.底边上的中线C.中线所在的直线D.底边上的中线所在的直线5.三个等边三角形的摆放位置如图所示,若∠1+∠2=125°,则∠3的度数为()A.85°B.55°C.45°D.25°6.如图,在△ABE 中,∠E=20°, AE 的垂直平分线MN 交BE 于点C ,且AB=CE ,则∠B 的度数是( )A.40°B.60°C.50°D.55°7.如图,已知直线m 是正五边形ABCDE 的对称轴,且直线m 过点A ,则∠1的度数为( )A.36°B.70°C.72°D.不确定8.如图,将边长为1的正方形OABC 沿x 轴正方向连续翻转2020次,点A 依次落在点A 1、A 2、 A 3、A 4....A 2020的位置上,则点A 2020的坐标为( )A.(2019,0)B.(2019,1)C.(2020,0)D.(2020,1)9.在△ABC 中,AB=BC ,点D 在AC 上,BD=6cm ,E ,F 分别是AB ,BC 边上的动点,△DEF 周长的最小值为6cm ,则∠ABC=( )A.20°B.25°C.30°D.35°10.如图,线段AB ,DE 的垂直平分线交于点C ,且∠ABC=∠EDC=72°,∠AEB=92°,则∠EBD 的度数为( )第5题 第6题第7题第9题 第8题 第10题A.168°B.158°C.128°D.118°二.填空题:本大题有6个小题,每小题4分,共24分。
人教版八年级(上册)数学 第13章 轴对称 单元测试及答案

八年级(上)数学第13章轴对称单元测试一、选择题(本大题共10题,每小题3分,共30分)1、下列说法正确的是().A.轴对称涉及两个图形,轴对称图形涉及一个图形B.如果两条线段互相垂直平分,那么这两条线段互为对称轴C.所有直角三角形都不是轴对称图形D.有两个内角相等的三角形不是轴对称图形2、点M(1,2)关于轴对称的点的坐标为().A.(-1,-2) B.(-1,2) C.(1,-2) D.(2,-1)3、下列图形中对称轴最多的是( ) .A.等腰三角形 B.正方形 C.圆 D.线段4、已知直角三角形中30°角所对的直角边为2,则斜边的长为().A.2 B.4 C.6 D.85、若等腰三角形的周长为26,一边为11,则腰长为().A.11 B.7.5 C.11或7.5 D.以上都不对6.在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于()(A)250(B)300(C)350(D)4007、如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为()厘米.A.16 B.18 C.26 D.28B 8、若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是 ( ).A .75°或15°B .75°C .15°D .75°和30°9、等腰三角形ABC 在直角坐标系中,底边的两端点坐标是(-2,0),(6,0),则其顶点的坐标,能确定的是( ).A .横坐标B .纵坐标C .横坐标及纵坐标D .横坐标或纵坐标10、下列图案是几种名车的标志,在这几个图案中不是轴对称图形的是( )A :B :C :D :二、填空题(每小题3分,共15分)11、已知点P 在线段AB 的垂直平分线上,PA=6,则PB= .12、等腰三角形一个底角是30°,则它的顶角是__________度.13、等腰三角形的一内角等于50°,则其它两个内角各为 .14、如图:点P 为∠AOB 内一点,分别作出P 点关于OA 、OB 的对称点P 1,P 2,连接P 1P 2交OA 于M ,交OB 于N ,P 1P 2=15,则△PMN 的周长为 .15.已知A (-1,-2)和B (1,3),将点A 向______平移________ 个单位长度后得到的点与点B 关于轴对称.三、解答题:16、如图,已知△ABC ,分别画出与△ABC 关于轴、轴对称的图形△A 1B 1C 1 和△A 2B 2C 2 ;(8分)17. (8分)在一次数学课上,王老师在黑板上画出下图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出△AED是等腰三角形.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)已知:求证:△AED是等腰三角形.证明:18.如图,点D、E在△ABC的边BC上,AD=AE,AB=AC,求证:BD=EC。
轴对称的性质—折叠问题(专项培优训练)2023-2024学年八年级数学上册(人教版)(解析版)

轴对称的性质—折叠问题(专项培优训练)试卷满分:100分 考试时间:120分钟 试卷难度:较难试卷说明:本套试卷结合人教版数学八年级上册同步章节知识点,精选易错,常考,压轴类问题进行专题汇编!题目经典,题型全面,解题模型主要选取热点难点类型!同步复习,考前强化必备!适合成绩中等及偏上的学生拔高冲刺。
一、选择题:本大题共10小题,每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(本题2分)(2022秋·天津津南·八年级校考期中)如图,把一张长方形纸片ABCD ,沿对角线AC 折叠,点B 的对应点为B ',AB '与DC 相交于点E ,则下列结论正确的有( )①ABC AB C ≅';②AE CE =;③ADE CB E ≅';④B CE EAB ∠'=∠.A .1个B .2个C .3个D .4个【答案】C 【分析】由折叠的性质可得ABC AB C ≅',,BAC CAB '∠=∠,AD BC B C =='由平行线的性质和等腰三角形的性质可得 ,ECA EAC AE CE ∠=∠=,由“HL ”可证()Rt ADE Rt CB E HL '≅,可得 ED EB =' ,即可进行判断;【详解】∵矩形纸片 ABCD 沿对角线 AC 折叠,点B 的对应点为 B '∴ABC AB C '≅,故①正确;,BAC CAB '∴∠=∠,AD BC B C =='∵AB CD ∥,BAC ACD ∴∠=∠,ACD CAB ∴∠=∠',ECA EAC ∴∠=∠∴AE CE =,故②正确;,,AE CE AD BC B C ==='在Rt ADE △ 和 Rt CB E '中,AE CE AD CB =⎧⎨=⎩∴()Rt ADE Rt CB E HL '≅故③正确;,DEA B CE '∴∠=∠,DEA EAB ∠≠∠,B CE EAB ∴∠'≠∠故④不正确;∴结论正确的有①②③共3个故选:C【点睛】本题考查了翻折变换,矩形的性质,全等三角形的性质,证明 AE EC = 是本题的关键.A .①②B .①②③C .①③④D .①②③④【答案】D 【分析】先求出点A ,点B 坐标,由勾股定理可求AB 的长,可判断①;由折叠的性质可得6OB BD ==,OC CD =,90BOC BDC ∠=∠=︒,由勾股定理可求OC 的长,可得点C 坐标,利用待定系数法可求BC 解析式,可判断②;由面积公式可求DH 的长,代入解析式可求点D 坐标,可判断③;分别讨论P 点在C 、B 点的情况,比较AP DP +值的情况,得出当P 点在C 点时,使得AP DP +的值最小可判断④,即可求解. 【详解】解:直线3=+64y x −分别与x 、y 轴交于点A 、B ,∴点()8,0A ,点()0,6B ,8OA ∴=,6OB =,10AB ∴=,故①正确;线段OB 沿BC 翻折,点O 落在AB 边上的点D 处,6OB BD ∴==,OC CD =,90BOC BDC ∠=∠=︒,4AD AB BD ∴=−=,222AC AD CD =+,()22816OC OC ∴−=+,3OC ∴=,∴点()3,0C ,设直线BC 解析式为:6y kx =+,036k ∴=+,2k ∴=−,∴直线BC 解析式为:26y x =−+,故②正确;如图,过点D 作DH AC ⊥于H ,3CD OC ==,5CA ∴=,1122ACD S AC DH CD AD =⋅=⋅△, 341255DH ⨯∴==,∴当125y =时,123654x =−+, 245x ∴=,∴点2412,55D ⎛⎫ ⎪⎝⎭,故③正确;直线BC 上存在一点P ,当P 点在C 点时,()OC DC P =,∴AP DP AC OC OA +=+=,当P 点在B 点时,AP DP AD DB AB +=+=,在Rt OAB 中,AB OA >∴当P 点在C 点时,使得AP DP +的值最小,则点P 的坐标是()3,0,故④正确;综上分析可知,正确的结论为①②③④,故D 正确.故选:D .【点睛】本题是一次函数综合题,考查了利用待定系数法求解析式,折叠的性质,面积法,勾股定理等知识,灵活运用这些性质解决问题是本题的关键. 3.(本题2分)(2023春·福建厦门·八年级厦门市湖滨中学校考期末)如图,在ABC 中,D 是AC 边上的中点,连接BD ,把BDC 沿BD 翻折,得到BDC ',DC '与AB 交于点E ,连接AC ',若2AD AC '==,3BD =,则C 到BD 的距离为( )【答案】B【分析】连接CC ',交BD 于点M ,由翻折知,BDC BDC '≌,BD 垂直平分CC ',证ADC '为等边三角形,利用含30度的直角三角形性质及勾股定理求出1DM =,CM =【详解】解:如图,连接CC ',交BD 于点M ,∵2AD AC ='=,D 是AC 边上的中点,∴2DC AD ==,由翻折知,BDC BDC '≌,BD 垂直平分CC ',∴2DC DC '==,BC BC '=,CM C M '=,∴2AD AC DC ''===,∴ADC '为等边三角形,∴60ADC AC D C AC ∠'=∠'=∠'=︒,∵DC DC =', ∴160302DCC DC C ∠'=∠'=⨯︒=︒,在Rt CDM △中,30DCC ∠'=︒,2DC =,∴1DM =,CM C M '∴=∴C 到BD故选B .【点睛】本题考查了等边三角形的判定及性质、含30度角的直角三角形的性质、勾股定理、折叠的性质、全等三角形的性质,熟练掌握性质定理是解题的关键. 4.(本题2分)(2020秋·广东广州·八年级校考期中)如图1,长方形ABCD 中,E 点在AD 上,且30ABE ∠︒=.分别以BE 、CE 为折线,将A 、D 向BC 的方向折过去,如图2,若图2中15AED ∠=︒,则BCE ∠度数为( )A .30︒B .32.5︒C .35︒D .37.5︒【答案】D 【分析】根据长方形的性质与三角形内角和定理,得到60AEB ∠=︒,再根据折叠的性质,得到A EB AEB '∠=,DEC D EC '∠=∠,由105AED '∠=︒,进而得到37.5DEC ∠=︒,最后根据平行线的性质,即可求出BCE ∠度数.【详解】解:四边形ABCD 是长方形,AD BC ∴∥,90A ∠=︒,30ABE ∠︒=,18060AEB A ABE ∴∠=︒−∠−∠=︒,由折叠的性质可知,60A EB AEB ∠=∠='︒,DEC D EC '∠=∠,15A ED ''∠=︒,606015105AED AEB A EB A ED ''''∴∠=∠+∠−∠=︒+︒−︒=︒,18075DED AED ''∴∠=︒−∠=︒,137.52DEC D EC DED ''∴∠=∠=∠=︒,AD BC ∥,37.5BCE DEC ∴∠=∠=︒,故选:D .【点睛】本题考查了折叠的性质,三角形内角和定理,平行线的性质,熟练掌握折叠的性质是解题关键.5.(本题2分)(2023春·陕西榆林·八年级校考期末)如图,在等腰ABC 中,AB AC =,50BAC ∠=︒,BAC ∠的平分线与AB 的垂直平分线交于点O ,点C 沿EF 折叠后与点O 重合,则CEF ∠的度数是( )A .55︒B .50︒C .45︒D .40︒【答案】B 【分析】连接OB ,OC ,先求出25BAO ∠=︒,进而求出40OBC ∠=︒,求出40COE OCB ∠=∠=︒,由三角形内角和定理和12CEF OEF CEO ∠=∠=∠即可求得答案. 【详解】解:如图,连接OB ,50BAC ∠=︒,AO 为BAC ∠的平分线,11502522BAO BAC ∴∠=∠=⨯︒=︒.又AB AC =,()1180652ABC ACB BAC ∴∠=∠=︒−∠=︒.DO 是AB 的垂直平分线,OA OB ∴=,25ABO BAO ∴∠=∠=︒,652540OBC ABC ABO ∴∠=∠−∠=︒−︒=︒.AO 为BAC ∠的平分线,AB AC =,∴直线AO 垂直平分BC ,OB OC ∴=,40OCB OBC ∴∠=∠=︒,点C 沿EF 折叠后与点O 重合,OE CE ∴=,12CEF OEF CEO ∠=∠=∠,40COE OCB ∴∠=∠=︒;在OCE △中,1801804040100CEO COE OCB ∠=︒−∠−∠=︒−︒−︒=︒,1502CEF CEO ∴∠=∠=︒.故选:B .【点睛】本题主要考查了等腰三角形的性质以及翻折变换及其应用,解题的关键是根据翻折变换的性质,找出图中隐含的等量关系,灵活运用有关知识来分析、判断. .将AFG 沿AG A .1B .32 【答案】C 【分析】由正方形的性质可得AD AB =,设BF CF a ==,则2CD a =,24DG CD CG a =−=−,由题意知,90ADE ABF ∠=∠=︒,由折叠的性质可得HG EF ⊥,AE AF =,GE GF =,证明()Rt Rt HL ADE ABF ≌,则DE BF a ==,2434GF GE a a a ==+−=−,由勾股定理得222GF CF DG −=,即()222344a a −−=,解得3a =,0a =(舍去),则3CF =,5EG =,9EC =,由勾股定理得EF ,根据1122CEF S EG CF EF HG =⨯=⨯,即115322HG ⨯⨯=⨯,计算求解即可.【详解】解:由正方形的性质可得AD AB =,设BF CF a ==,则2CD a =,24DG CD CG a =−=−, 由题意知,90ADE ABF ∠=∠=︒,由折叠的性质可得HG EF ⊥,AE AF =,GE GF =,∵AE AF =,AD AB =,∴()Rt Rt HL ADE ABF ≌,∴DE BF a ==,2434GF GE a a a ==+−=−,由勾股定理得222GF CF CG −=,即()222344a a −−=,解得3a =,0a =(舍去),∴3CF =,5EG =,9EC =,由勾股定理得EF ∵1122GEF S EG CF EF HG =⨯=⨯,∴115322HG ⨯⨯=⨯,解得HG =, 故选:C .【点睛】本题考查了正方形的性质,全等三角形的判定与性质,折叠的性质,勾股定理等知识.解题的关键在于对知识的熟练掌握与灵活运用.A .65︒B .62.5︒C .55︒D .52.5︒【答案】B 【分析】根据折叠得出90OB C B ''∠=∠=︒,求出55OB G '∠=︒,根据平行线的性质得出18055125B OB '∠=︒−︒=︒.根据折叠得出162.52BOG B OB '∠=∠=︒.【详解】解:根据折叠可知,90OB C B ''∠=∠=︒,∵35GB C ''∠=︒,∴55OB G '∠=︒,∵AB CD ∥,∴18055125B OB '∠=︒−︒=︒. 由折叠可知,162.52BOG B OB '∠=∠=︒,故B 正确. 故选:B .【点睛】本题主要考查了折叠的性质,平行线的性质,解题的关键是熟练掌握两直线平行,同旁内角互补. 8.(本题2分)(2023·浙江·八年级假期作业)如图,现有一块三角板ABC ,其中90ABC ︒∠=,60CAB ︒∠=,8AB =,将该三角板沿BC 边翻转得到A BC '△,再将A BC '△沿A C '边翻转得到A B C ''△,则A 与B '两点之间的距离为( )【答案】C 【分析】连接AB ',作B D AA ''⊥,交AA '延长线于点D ,在Rt A B D ''中求得B D '、A D '的长度,在Rt AB D '中,即可求得AB '.【详解】解:连接AB ',作B D AA ''⊥,交AA '延长线于点D ,如下图:由折叠的性质可得:8AB A B A B '''===,60CAB CA B CA B '''∠=∠=∠=︒∴60B A D ''∠=︒∵B D AA ''⊥,∴90D Ð=°,∴30A B D ''∠=︒, ∴142A D A B '''==,∴B D '==,20AD =,∴AB '=故选:C【点睛】此题考查了勾股定理,折叠的性质,含30︒直角三角形的性质,解题的关键是熟练利用相关性质进行求解.A .①②④B .①②③C .①③④D .①②③④【答案】D 【分析】作FM BC ⊥于M (见详解图),①根据翻折变换的性质和正方形的性质可证ABG AFG △△≌;②设BG GF x ==,在Rt EGC △中,根据勾股定理可证3BG GC ==;③通过tan 2AB AGB BG ∠==,tan 2FM FCM CM ∠==,证明AGB FCM ∠=∠,由平行线的判定定理可得AG CF ∥;④由②得到3GC =,由③得到125FM =,根据12FCG S GC FM =△即可计算面积.【详解】解:作FM BC ⊥于M ,四边形ABCD 是正方形,∴6AB BC CD DA ====,90B D BCD ∠=∠=∠=︒,AFE △是由ADE V 翻折,∴AD AF AB ==,90ADE AFE AFG ∠=∠=∠=︒,在Rt AGF 和Rt AGB 中,AG AG AF AB =⎧⎨=⎩,∴ABG AFG △△≌.故①正确.∴BG GF =,设BG GF x ==,在Rt EGC △中,90ECG ∠=︒,2DE =,6CD =,4EC =,2EG x =+,6GC x =−,∴()()222246x x +=+−,∴3x =,∴3BG GC ==,故②正确.FM BC ⊥,CD BC ⊥∴FM EC ∥ ∴GF FM GM GE ECGC ==,3GF =,5GE =,4EC =,3GC =∴125FM =,95GM =,65CM GC GM =−=, ∴6tan 23AGB ∠==, tan 2FM FCM CM ∠==,∴AGB FCM ∠=∠,∴AG CF ∥,故③正确. ∴112183255FCG S ==△,故④正确.综上,选项D 符合题意.故选:D .【点睛】本题考查了正方形的性质、全等三角形的判定和性质、翻折变换、勾股定理的应用等知识,熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键. 为对称轴将CDE 折叠得到CHE ,使得点 A .90CEF ∠=︒ B .CE 【答案】D 【分析】A.由折叠的性质可以知道EF 和CE 分别是AEG ∠和DEG ∠的平分线,同时AED ∠是平角,所以可知90CEF ∠=︒,故选项A 正确;B.由题意和折叠的性质可以知道EF AG ⊥、EF CE ⊥,就可以得到CE AG ∥,选项B 正确;C 和D.过点C 作C M A B ⊥于点M ,120CBA ∠=︒,可得2BM =,CM =BF a =,可以得到4FG AF a ==−,2FM BF BM a =+=+.根据折叠的性质可得4CG CD ==,根据勾股定理,求得2.4a =,即可得到 1.6FG =, 5.6CF =,所以5.6745CF AB ==.故选项C 正确,选项D 错误. 【详解】解:A.由折叠可知EF 和CE 分别是AEG ∠和DEG ∠的平分线. 又180AED ∠=︒,111809022CEF CEG FEG AED ∴∠=∠+∠=∠=⨯︒=︒, 故选项A 正确.B.又点A 与点G 关于EF 对称,∴EF AG ⊥, 又EF CE ⊥,∴CE AG ∥,故选项B 正确.C 和D.如答图,过点C 作C M A B ⊥于点M .120CBA ∠=︒,∴60CBM ∠=︒,4BC =,∴易知2BM =,CM =设BF a =,∴4FG AF a ==−,2FM BF BM a =+=+,点E 是AD 的中点,折叠后点H 落到EG 上,∴点G 与点H 重合,4CG CD ==.易知点C G F ,,共线,∴448CF FG CG a a =+=−+=−.222FM CM CF +=,()(()22228a a ∴+=−+,解得 2.4a =. ∴4 2.4 1.6FG =−=,88 2.4 5.6CF a =−=−=,5.6745CF AB ∴==,故选项C 正确,选项D 错误.综上,故选:D .【点睛】本题考查翻折变换(折叠问题)、菱形的性质、勾股定理,熟练掌握翻折的性质是解答本题的关键.二、填空题:本大题共10小题,每小题2分,共20分. 11.(本题2分)(2023春·河北承德·八年级统考期末)如图,小宇将一张平行四边形纸片折叠,使点A 落在长边CD 上的点1A 处,并得到折痕DE ,小宇测得长边6CD =,则四边形1A EBC 的周长为 .【答案】12【分析】根据折叠的性质,得到DA DA '=,EA EA '=,结合平行四边形的性质,得到DA DA BC '==,代入计算即可.【详解】根据折叠的性质,得到DA DA '=,EA EA '=,∵四边形ABCD 是平行四边形,∴DA DA BC '==,6AB CD ==,∴四边形1A EBC 的周长为1111212BC BE A E AC A D AC AE BE AB CD CD +++=+++=+==.故答案为:12.【点睛】本题考查了折叠的性质,平行四边形的性质,熟练掌握性质是解题的关键.12.(本题2分)(2023春·上海浦东新·八年级统考期末)如图,在ABC 中,90A ∠=︒,28BC AC ==,点M 在边BC 上,过点M 作MN BC ⊥,垂足为点M ,交边AB 于点N ,将ABC 沿直线MN 翻折,点A 、C 分别与点D 、E 对应,如果四边形ADBE 是平行四边形,那么CM 的长是 .【答案】3【分析】当点E 在线段BC 上时,连接DE 交AB 于点O ,过点O 作OH BC ⊥于点H ,则90BHO ∠=︒,求出AB =30ABC ∠=︒,由轴对称可得4DE AC ==,得OB =2OD OE ==,OH =,求出6CE =,由折叠可知,3CM =;假设点E 在线段CB 的延长线上,得到)4AN AF x ==−,与)2AN x =−矛盾,故点E 不可能在线段CB 的延长线上,即可确定CM 的长.【详解】解:当点E 在线段BC 上时,如图,连接DE 交AB 于点O ,过点O 作OH BC ⊥于点H ,则90BHO ∠=︒,∵90BAC ∠=︒,28BC AC ==,∴AB ==30ABC ∠=︒,∵将ABC 沿直线MN 翻折,点A 、C 分别与点D 、E 对应,∴4DE AC ==,∵四边形ADBE 是平行四边形,∴1122OB AB ==⨯=122OD OE DE ===,∴12OH OB ==∴3BH ==,∴1EH ==,∴312BE BH EH =−=−=,∴826CE BC BE =−=−=,由折叠可知,132CM EM CE ===,假设点E 在线段CB 的延长线上,延长MN 交AD 于点F ,则AD FM ⊥,12AF DF AD ==,∵90BAC ∠=︒,28BC AC ==,∴AB ==30ABC ∠=︒,设CM EM x ==,则8BM x =−,∴()828BE x x x AD=−−=−=, ∴142AF DF AD x ===−, 在Rt BMN △中,30ABC ∠=︒,90BMN ∠=︒, ∴1MN BN 2=,∴222BM MN BN +=,即22212BM BN BN ⎛⎫+= ⎪⎝⎭,则)8BN x ==−,))82AN BN x x ==−==−,在Rt ANF △中,142AF DF AD x ===−,30NAF ABC ∠=∠=︒,90AFN ∠=︒, ∴12FN AN =,∴222AF FN AN +=,即22212AF AN AN ⎛⎫+= ⎪⎝⎭,)4AN AF x ==−,与)2AN x =−矛盾,故点E 不可能在线段CB 的延长线上,综上可知,3CM =,故答案为:3【点睛】此题考查了勾股定理、平行四边形的性质、含30︒角的直角三角形的性质等知识, 分类讨论是解题的关键. 13.(本题2分)(2023春·北京丰台·八年级统考期末)如图,在Rt ABC △中,90B Ð=°,3AB =,4BC =,将ABC 折叠,使点B 恰好落在边AC 上,与点B '重合,AE 为折痕,则BE 的长等于 .【答案】1.5【分析】根据折叠得到BE EB '=,AB AB 3'==,设BE EB x '==,则4EC x =−,根据勾股定理求得AC 的值,再由勾股定理可列方程求解即可.【详解】解:根据折叠可得BE EB '=,AB AB 3'==,设BE EB x '==,则4EC x =−,在Rt ABC △中,90B Ð=°,3AB =,4BC =5AC ∴=532B C AC AB ''∴=−=−=在Rt B EC '△中,由勾股定理得,()222x 24x +=− 解得 1.5x =故答案为:1.5【点睛】本题考查的是翻折变换的性质,解题的关键是掌握折叠前后图形的形状和大小不变,对应边和对应角相等,能熟练运用勾股定理列方程解决问题.14.(本题2分)(2023春·四川达州·八年级统考期末)如图,在ABC 和DCB △中,90A D ∠=∠=︒,AC ,BD 相交于点E ,AE DE =.将CDE 沿CE 折叠,点D 落在点D ¢处,若40BED '∠=︒,则BCD '∠的大小为 .【答案】15︒/15度【分析】根据全等三角形的判定和性质得出BE CE =,再由等边对等角确定EBC ECB ∠∠=,利用折叠的性质及三角形内角和定理求解即可.【详解】解:在AEB 和DEC 中,90A D AE DE AEB DEC ∠∠∠∠==︒⎧⎪=⎨⎪=⎩,∴(ASA)AEB DEC ≌,∴BE CE =,∴EBC ECB ∠∠=,∵40BED '∠=︒,CDE 沿CE 折叠,点D 落在点D ¢处,∴70D EC DEC ︒'∠=∠=,∴180110BEC DEC ∠=︒−∠=︒,790200DCE ︒−︒=︒∠=,∴180110352EBC ECB ︒−∠︒=∠==︒,20DCE D CE ︒'∠=∠=,∴15BCD ECB D CE ''∠=∠−∠=︒,故答案为:15︒.【点睛】题目主要考查折叠的性质及全等三角形的判定和性质,三角形内角和定理及等腰三角形的判定和性质,理解题意,综合运用这些知识点是解题关键.15.(本题2分)(2023·浙江·八年级假期作业)折纸是一项有趣的活动,如图所示,一张长方形纸片()90ABCD A B C ∠=∠=∠=︒,先将纸片沿EF 折叠,再将折叠后的纸片沿GH 折叠,使得GD '与A B ''重合,展开纸片后若62BFE ∠=︒,则DGH ∠= ︒.【答案】17【分析】由平行线的性质得到62GEF BFE ∠=∠=︒,由平角定义得到180118AEF GEF ∠=︒−∠=︒,由轴对称的性质得到:90A A '∠=∠=︒,118A EF AEF '∠=∠=︒,DGH D GH '∠=∠,求出A EG '∠,由直角三角形的性质求出'∠A GE ,由对顶角的性质得到DGD A GE ''∠=∠,即可求出12DGH DGD '∠=.【详解】解:四边形ABCD 是矩形, AD BC ∴∥,90A ∠=︒,62GEF BFE ∴∠=∠=︒,180118AEF GEF ∴∠=︒−∠=︒,由题意得:90A A '∠=∠=︒,118A EF AEF '∠=∠=︒,DGH D GH '∠=∠,1186256A EG A EF GEF ''∴∠=∠−∠=︒−︒=︒,9034A GE A EG ''∴∠=︒−∠=︒,34DGD A GE ''∴∠=∠=︒,1172DGH DGD '∴∠==︒.故答案为:17.【点睛】本题考查轴对称的性质,平行线的性质,余角的计算,对顶角的性质,解题的关键是掌握轴对称的性质.16.(本题2分)(2023·浙江·八年级假期作业)如图,在△ABC 中,AB AC =,30C ∠=︒,将纸片沿DE 折叠,使点B 落到点A 处,若6BC =,则DE = .【答案】1【分析】利用等腰三角形的性质得到30B C ∠=∠=︒,则120BAC ∠=︒,再由折叠性质得BD AD =,30BAD B ∠=∠=︒,90AED ∠=︒,进而得到90DAC ∠=︒,再根据含30度角的直角三角形的性质求解即可.【详解】解:∵AB AC =,30C ∠=︒∴30B C ∠=∠=︒,则3018030120BAC ∠=−︒−︒=︒,由折叠性质得BD AD =,30BAD B ∠=∠=︒,90AED ∠=︒,∴1309020DAC ︒−︒=∠=︒,12DE AD =,∴2CD AD =,又6BC =,∴236BC BD CD AD AD AD =+=+==,∴2AD =, ∴112DE AD ==, 故答案为:1.【点睛】本题考查等腰三角形的性质、折叠性质、三角形的内角和定理、含30度角的直角三角形的性质,熟练掌握折叠性质和直角三角形的性质是解答的关键. 上一动点,把CDE 沿直线,若D BC '为等边三角形,【答案】1或4/4或1【分析】依据折叠的性质、菱形的性质以及等边三角形的性质,分两种情况得到DE 的长即可.【详解】解:由折叠及菱形的性质可得CD CD CB '==,故D BC '是以BD '底的等腰三角形,故当60D BC '∠=︒,D BC '为等边三角形,分以下两种情况讨论,1)如图(1),当点D ¢点A 重合时,60D BC '∠=︒,此时点E 为AD 的中点,故1DE =,2)如图(2),当点D ¢与点A 关于直线BC 对称时,D ¢,C ,D 三点共线,EC DC ⊥,故24DE DC ==, 综上所述,1DE =或4,故答案为:1或4.【点睛】本题考查了菱形的性质,折叠问题及等边三角形的性质等知识的综合运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等. 如图,ABC 中,【答案】108【分析】连接OB 、OC ,根据角平分线的定义求出BAO ∠,根据等腰三角形两底角相等求出ABC ∠,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA OB =,根据等边对等角可得ABO BAO ∠=∠,再求出OBC ∠,证明 OB OC =,再根据等边对等角求出OCB OBC ∠=∠,根据翻折的性质可得OE CE =,然后根据等边对等角求出COE ∠,再利用三角形的内角和定理列式计算即可.【详解】解:如图,连接OB 、OC ,54BAC ∠=︒Q ,AO 为BAC ∠的平分线,11542722BAO BAC ∴∠=∠=⨯︒=︒,又AB AC =,11(180)(18054)6322ABC BAC ∴∠=︒−∠=︒−︒=︒, DO 是AB 的垂直平分线,OA OB ∴=,27ABO BAO ∴∠=∠=︒,632736OBC ABC ABO ∴∠=∠−∠=︒−︒=︒, AO 为BAC ∠的平分线,AB AC =,∴点O 在BC 的垂直平分线上,∴OB OC =,36OCB OBC ∴∠=∠=︒,将C ∠沿(EF E 在BC 上,F 在AC 上)折叠,点C 与点O 恰好重合,OE CE ∴=,36COE OCB ∴∠=∠=︒,在OCE △中,1801803636108OEC COE OCB ∠=︒−∠−∠=︒−︒−︒=︒,故答案为:108.【点睛】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形三线合一的性质,等边对等角的性质,以及翻折变换的性质,三角形内角和定理等等,熟知相关知识是解题的关键.19.(本题2分)(2023春·辽宁沈阳·八年级统考期末)如图,在ABC ∆中,90A ∠=︒,30C ∠=︒,3AB =,点D 为AC 的中点,点E 是BC 边上一个动点,将CDE ∆沿着DE 翻折,使得点C 落在点F 处,当FE AC ⊥时,EF 的长为 .【答案】32或92【分析】根据题意,分两种情况:①当E 在D 的右侧时;②当E 在D 的左侧时,由翻折性质,结合含30︒的直角三角形边的关系列方程求解即可得到答案.【详解】解:在ABC 中,90A ∠=︒,30C ∠=︒,3AB =,点D 为AC 的中点,AC ∴=12CD AB =, 当E 在D 的右侧时,延长FE 交AC 于H ,如图所示:FE AC ⊥,90EHC ∴∠=︒,由翻折的性质知,CD DF ==,30C DFH∠=∠=︒, 设EF x =,则CE EF x ==,1122EH EC x ==, 32FH x ∴=,在直角三角形DFH 中,30DFH ∠=︒,则FH =,∴32x =,32x ∴=;当E 在D 的左侧时,如图所示:由翻折性质知,CD DF ==,30C EFD ∠=∠=︒,CE EF x ==,EF AC ⊥,90FHD ∴∠=︒,1122EH EC x ∴==,1122FH x x x =−=,在直角三角形FHD 中,HF =,∴12x =,解得92x =, 故答案为:32或92.【点睛】本题考查翻折性质,充分利用翻折性质及含30︒的直角三角形边的关系分情况讨论是解决问题的关键. 20.(本题2分)(2023春·重庆忠县·八年级统考期末)如图,在正方形ABCD 中,点E 是BC 上一点,连接DE ,将BDE 沿DE 翻折得到GDE ,连接CG .若CG BD ∥,则CEG ∠= .【答案】60︒/60度【分析】根据直角三角形斜边中线的性质得出CH DH HB ==,1=2CH DB ,由折叠的性质得DB DG =,∠=∠BDE GDE ,利用辅助线构造矩形并由其性质得出CH GK =,再由等量代换得出12GK DG =,最后由特殊直角三角形的性质得出30GDK ∠=︒,利用折叠的性质及正方形的性质即可求解. 【详解】解:如图,过点C 作直线CH DB ⊥于点H ,过点G 作直线GK DB ⊥于点K ,正方形ABCD 中,DC CB =,90452CDB ︒∠==︒,CH DH HB ∴==,1=2CH DB . GDE △由BDE 沿DE 翻折得到,GDE BDE ∴≌△△, DB DG ∴=,∠=∠BDE GDE ,CH DB ⊥,GK DB ⊥,CG BD ∥,CH GK ∴∥,90CHK ∠=︒,∴四边形CHKG 是矩形.CH GK ∴=, ∴11=22GK CH DB DG ==,90GKD ∠=︒,∴30GDK ∠=︒.11=30=1522BDE GDK ∴∠=∠⨯︒︒.∵正方形ABCD ,∴45DBE ∠=︒,∴1804515120BED ∠=︒−︒−︒=︒,60CED ∠=︒,∵BDE 沿DE 翻折得到GDE ,∴120BED DEG ∠=∠=︒,∴12060CEG DEC ∠=︒−∠=︒,故答案为:60︒.【点睛】本题考查正方形—翻折问题.具体考查正方形的性质,折叠的性质,全等三角形的性质,特殊直角三角形的性质,矩形的判定和性质等的综合运用能力.灵活添加辅助线是解本题的关键.三、解答题:本大题共7小题,21-25题每小题8分,26-27题每小题10分,共60分. 若将DAB 沿直线 (1)求点A B 、的坐标.(2)求三角形ACE 的面积.(3)求直线CD 的解析式.【答案】(1)()3,0A ,()0,4B(2)6(3)364y x =−【分析】(1)当0x =,4043y =−⨯+,解得4y =,则()0,4B ,当0y =,4043x =−+,解得3x =,则()3,0A ;(2)由折叠的性质可知AB AC =,OBA ECA ∠=∠,证明()AAS ABO ACE ≌,根据12ACE ABO S S OA OB ==⨯,计算求解即可;(3)由勾股定理得,5AB ,则8OC OA AC =+=,()80C ,,待定系数法求直线CD 的解析式即可.【详解】(1)解:当0x =,4043y =−⨯+,解得4y =,则()0,4B ,当0y =,4043x =−+,解得3x =,则()3,0A ,∴()3,0A ,()0,4B ;(2)解:由折叠的性质可知AB AC =,OBA ECA ∠=∠,∵OBA ECA ∠=∠,OAB EAC ∠=∠,AB AC =,∴()AAS ABO ACE ≌, ∴1134622ACE ABO S S OA OB ==⨯=⨯⨯=,∴三角形ACE 的面积为6;(3)解:由勾股定理得,5AB ==,由(2)可知5AC AB ==,8OC OA AC =+=,∴()80C ,,设直线CD 的解析式为y kx b =+,将()0,6D −,()80C ,,代入y kx b =+得,680b k b =−⎧⎨+=⎩,解得346k b ⎧=⎪⎨⎪=−⎩,∴直线CD 的解析式为364y x =−. 【点睛】本题考查了一次函数的解析式,勾股定理,折叠的性质,全等三角形的判定与性质,一次函数的图象坐标轴的交点.解题的关键在于对知识的熟练掌握与灵活运用. 22.(本题8分)(2023春·吉林长春·八年级统考期末)将边长为2的正方形纸片ABCD 按如下操作:【操作一】如图①,将正方形纸片ABCD 对折,使点A 与点B 重合,点D 与点C 重合,再将正方形纸片ABCD 展开,得到折痕EF .则点B 、点F 之间的距离为_____________.【操作二】如图②,G 为正方形ABCD 边BC 上一点,连接AG ,将图①的正方形纸片沿AG 翻折,使点B 的对称点H 落在折痕EF 上.连接BH .(1)求证:ABH 是等边三角形.(2)求四边形CFGH 的周长.(1)证明见解析;(2)5【分析】操作一:由题知,4BC =,122CF DF CD ===,利用勾股定理可得BF =操作二:(1)由翻折得EF 是AB 的垂直平分线,故BH AH =,又AB AH =,即AB BH AH ==,即得ABH 是等边三角形;(2)由ABH 是等边三角形,可得2AH AB ==,1AE =.HE ==可得2FH EF HE =−=即可得出四边形ABGH 的周长.【详解】解:操作一:如图,连接BF ,由题知2BC CD ==,由翻折,知112CF DF CD ===,由勾股定理,得BF操作二:(1)由翻折知EF 是AB 的垂直平分线,BH AH ∴=,又AB AH =,AB BH AH ∴==,ABH ∴是等边三角形;(2)∵ABH 是等边三角形.∴2AH AB ==,1AE =.∴HE =∴2FH EF HE =−=∴四边形CFHG 的周长CF HF HG CG CF HF CB +++=++122=+5=【点睛】本题主要考查四边形的综合题,涉及勾股定理,等边三角形的判定和性质,正方形的性质等知识点,熟练掌握轴对称的性质与勾股定理的应用是解题的关键. (1)试判断重叠部分BED 的形状,并证明你的结论;(2)若BE 平分ABD ∠,12BC =,求BED 的面积.【答案】(1)BED 是等腰三角形,证明见解析(2)BED 的面积【分析】(1)根据折叠性质得出EBD DBC ∠=∠,进而得出EDB EBD ∠=∠,可得EB ED =,根据等角对等边即可得证;(2)根据含30度角的直角三角形的性质,勾股定理得出DE ,进而根据三角形的面积公式即可求解.【详解】(1)BED 是等腰三角形,证明:四边形ABCD 是长方形,AD BC ∴∥,EDB DBC ∴∠=∠,由折叠可知:EBD DBC ∠=∠,EDB EBD ∴∠=∠,EB ED ∴=,BED ∴是等腰三角形;(2)四边形ABCD 是长方形,AB DC ∴=,12AD BC ==,90A ABC C ∠=∠=∠=︒, BE 平分ABD ∠,ABE EBD ∴∠=∠,30ABE EBD DBC ∴∠=∠=∠=︒,2,BC CD BC ∴==,DC BC ∴==AB ∴=EB ED =,12AE AD DE DE ∴=−=−,在Rt ABE △中,根据勾股定理,得222AE AB BE +=,222(12)DE DE ∴−+=,解得8DE =,BED ∴的面积11822DE AB =⨯⋅=⨯⨯=【点睛】本题考查了勾股定理,折叠问题,含30度角的直角三角形的性质,熟练掌握勾股定理与折叠的性质是解题的关键. 24.(本题8分)(2023春·山西阳泉·八年级统考期末)综合与实践问题情境:在综合实践活动课上,同学们以“平行四边形纸片的折叠”为主题开展数学活动.在平行四边形纸片ABCD 中,E 为CD 边上任意一点,将ADE V 沿AE 折叠,点D 的对应点为D ¢.分析探究:(1)如图1,当点D ¢恰好落在AB 边上时,四边形D BCE '的形状为 .问题解决:(2)如图2,当E ,F 为CD 边的三等分点时,连接FD '并延长,交AB 边于点G .试判断线段AG 与BG 的数量关系,并说明理由.(3)如图3,当60ABC ∠=︒,45DAE =︒∠时,连接DD '并延长,交BC 边于点H .若ABCD Y 的面积为24,4=AD ,请直接写出线段D H '的长.【答案】(1)平行四边形;(2)2BG AG =,理由见解析;(3)D H '=【分析】(1)利用平行四边形的性质及折叠的性质可得ABCD ,AD DE AD '==,可得四边形ADED '是菱形,可知DE AD =',继而可知BD CE '=,即可求解;(2)利用折叠的性质可得AED AED '∠=∠,ED ED ¢=,结合三等分点可知ED ED EF '==,进而可得ED F EFD ''∠=∠,利用三角形外角性质可得AED ED F ''∠=∠,进而可知AE FG ∥,可得四边形AEFG 是平行四边形,再结合平行四边形的性质即可得AG 与BG 的数量关系;(3)由折叠可知:45DAE D AE '∠=∠=︒,AD AD =',易知DAD '△为等腰直角三角形,延长AD '交BC 于M ,可知45MD H AD D ''∠=∠=︒,由平行四边形的性质可得,45BHM ADH MD H '∠=∠=︒=∠,AM AD ⊥,进而可知MD MH '=由ABCD Y 的面积为24,4=AD ,得24AD AM ⋅=,求得6AM =,可得2MD AM AD ''=−=,再利用勾股定理即可求解.【详解】解:(1)∵四边形ABCD 是平行四边形,∴AB CD ,AB CD =则D AE AED '∠=∠由折叠可知:AD AD =',DAE D AE '∠=∠,∴DAE AED ∠=∠,∴AD DE AD '==,∴四边形ADED '是平行四边形,又∵AD AD =',∴四边形ADED '是菱形,∴DE AD =',∴BD CE '=,∴四边形D BCE '是平行四边形,故答案为:平行四边形;(2)2BG AG =,理由如下:∵四边形ABCD 是平行四边形,∴AB CD ,AB CD =,又∵E ,F 为CD 边的三等分点, ∴13DE EF CF DC ===,由折叠可知:ED ED ¢=,AED AED '∠=∠,则ED ED EF '==,∴ED F EFD ''∠=∠,由三角形外角可知:DED ED F EFD AED AED ''''∠=∠+∠=∠+∠,∴AED ED F ''∠=∠,∴AE FG ∥,∴四边形AEFG 是平行四边形,∴EF AG =, ∵13EF DC =,AB CD =, ∴13AG AB =,则23BG AB =,∴2BG AG =;(3)由折叠可知:45DAE D AE '∠=∠=︒,AD AD =',∴90DAD '∠=︒,则DAD '△为等腰直角三角形,∴45ADH AD D '∠=∠=︒,延长AD '交BC 于M ,则45MD H AD D ''∠=∠=︒∵四边形ABCD 是平行四边形,∴AD BC ∥,∴45DHM ADH MD H ∠=∠=∠'︒=,90AMH DAD '∠=∠=︒,即AM AD ⊥,∴MD MH '=∵ABCD Y 的面积为24,4=AD ,即:24AD AM ⋅=,∴6AM =,则2MD AM AD AM AD ''=−=−=,∴D H '【点睛】本题考查平行四边形的判定及性质,菱形的判定,翻折的性质,等腰直角三角形的判定及性质,勾股定理等知识点,熟练掌握相关性质定理是解决问题的关键. 轴的负半轴上,若将DAB 沿直线(1)求线段AB 的长(2)求直线CD 的函数表达式;(3)点P 在直线CD 上,使得2PAC OAB SS =,求点【答案】(1)5AB =(2)364y x =− (3)7224,55⎛⎫ ⎪⎝⎭或824,55⎛⎫− ⎪⎝⎭【分析】(1)先根据点,A B 的坐标可得3,4OA OB ==,再利用勾股定理可得5AB =;(2)设点D 的坐标为()0,D m ,则4,BD m OD m =−=−,先根据折叠的性质可得4CD BD m ==−,再在Rt COD 中,利用勾股定理可得6m =−,从而可得()0,6D −,然后利用待定系数法即可得;(3)设点P 的坐标为3,64P n n ⎛⎫− ⎪⎝⎭,根据2PAC OAB S S =建立方程,解方程可得n 的值,由此即可得出答案.【详解】(1)解:()3,0A ,()0,4B , 3,4OA OB ∴==, x 轴y ⊥轴,5AB ∴=.(2)解:设点D 的坐标为()0,D m ,则4,BD m OD m =−=−,由折叠的性质得:4CD BD m ==−,5AC AB ==,8OC OA AC ∴=+=,∴点C 的坐标为()8,0,在Rt COD 中,222OD OC CD +=,即()()22284m m −+=−,解得:6m =−,()0,6D ∴−,设直线CD 的函数表达式为y kx b =+,将点()()8,0,0,6C D −代入得:806k b b +=⎧⎨=−⎩,解得346k b ⎧=⎪⎨⎪=−⎩,则直线CD 的函数表达式为364y x =−.(3)解:由题意,设点P 的坐标为3,64P n n ⎛⎫− ⎪⎝⎭, 3,4OA OB ==,162OAB S OA OB ∴=⋅=,2PAC OAB S S =,61562342n −∴⨯=⨯, 解得725n =或85n =, 当725n =时,732364424655n −=−=⨯,即此时7224,55P ⎛⎫ ⎪⎝⎭, 当85n =时,83246534564n =−=−−⨯,即此时824,55P ⎛⎫− ⎪⎝⎭, 综上,点P 的坐标为7224,55⎛⎫ ⎪⎝⎭或824,55⎛⎫− ⎪⎝⎭. 【点睛】本题考查了勾股定理、折叠的性质、求一次函数的解析式、一次函数的几何应用,熟练掌握折叠的性质和待定系数法是解题关键. 26.(本题10分)(2023春·江苏苏州·八年级星海实验中学校考期中)如图1,四边形ABCD 中,AD BC ∥,90ADC ∠=︒,8AD =,6BC =,点M 从点D 出发,以每秒2个单位长度的速度向点A 运动,同时,点N 从点B 出发,以每秒1个单位长度的速度向点C 运动.其中一个动点到达终点时,另一个动点也随之停止运动,过点N 作NP AD ⊥于点P ,连接AC 交NP 于点Q ,连接MQ .设运动时间为t 秒.(1)AM =______,AP =______.(用含t 的代数式表示)(2)当四边形ANCP 为平行四边形时,求t 的值;(3)如图2,将AQM 沿AD 翻折,得AKM ,是否存在某时刻t ,使四边形AQMK 为为菱形,若存在,求出t 的值;若不存在,请说明理由.【答案】(1)82t −,2t +(2)2t =(3)存在,1t =【分析】(1)由2DM t =,根据AM AD DM =−即可求出82AM t =−;先证明四边形CNPD 为矩形,得出6DP CN t ==−,则2AP AD DP t =−=+;(2)根据四边形ANCP 为平行四边形时,可得68(6)t t −=−−,解方程即可;(3)由NP AD ⊥,QP PK =,可得当PM PA =时有四边形AQMK 为菱形,列出方程628()6t t t −−=−−,求解即可.【详解】(1)解:如图1.2DM t =,82AM AD DM t ∴=−=−.在直角梯形ABCD 中,AD BC ∥,90ADC ∠=︒,NP AD ⊥于点P ,∴四边形CNPD 为矩形,6DP CN BC BN t ∴==−=−,8(6)2AP AD DP t t ∴=−=−−=+;故答案为:82t −,2t +.(2)四边形ANCP 为平行四边形时,CN AP =,68(6)t t ∴−=−−,解得:2t =;(3)存在时刻1t =,使四边形AQMK 为菱形.理由如下:NP AD ⊥,QP PK =,∴当PM PA =时有四边形AQMK 为菱形,628(6)t t t ∴−−=−−,解得1t =.【点睛】本题主要考查了四边形综合题,其中涉及到直角梯形的性质,矩形的判定与性质,等腰直角三角形的性质,轴对称的性质,等腰三角形的性质,正方形的性质等知识,综合性较强,难度适中.运用数形结合、方程思想是解题的关键.(1)BQ = ______ (含t 的代数式表示);(2)如图2,连接AD ,PF ,PQ ,当AD PQ ∥时,求PQF △的面积;(3)如图3,连接PF ,PQ ,D 点关于直线PF 的对称点为D '点,若'D 落在PQB △的内部则t 的取值范围为______.【答案】(1)4(02)t t −<≤(2)PQFS = (3)4453t <<【分析】(1)根据几何动点的速度和时间可得结论;(2)根据四边形BPDQ 是平行四边形,证明四边形APQD 是平行四边形,可得1t =,再证明EFD ≌△CFQ ,最后利用三角形的面积公式可解答;(3)先证明DF FQ =,再计算两个边界点时点t 的值;①如图3,点D '与Q 重合,②如图4,D '在斜边AB 上,由此可得结论.【详解】(1)解:在Rt ABC △中,90830C AB A ∠∠=︒==︒,,,142BC AB AC ∴===,由题意,CQ t =,()402BQ t t ∴=−<≤. 故答案为:()402t t −<≤; (2)如图2中,四边形BPDQ 是平行四边形,∴DQ AB ∥,BP DQ BQ PD ==,,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2023-2024学年八年级数学上册《第十三章轴对称》单元测试卷含答案(人教版)
学校:___________班级:___________姓名:___________考号:___________
一、选择题:(本题共8小题,每小题5分,共40分.)
1.等腰三角形的一个外角是100°,它的顶角的是()
A.80°B.20°C.20°或80°D.100°
2.等腰三角形的一边长为6cm,另一边长为12cm,则其周长为()
A.24cm B.30cm C.24cm或30cm D.18cm
3.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是()
A.AC=A′C′B.AB∥B′C′C.AA′⊥MN D.BO=B′O
4.如图,在中, AC=BC , AB=16 , CG=4 ,观察图中尺规作图的痕迹的面积为()
A.64 B.32 C.16 D.8
5.如图,梯形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于E,连接DE,则四边形ABED的周长等于( )
A.17 B.18 C.19 D.20
6.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是()
A.AD=BD B.BE=AC C.ED+EB=DB D.AE+CB=AB 7.如图,等边三角形ABC中,D、E分别为AB、BC边上的两个动点,且总使BD=CE,AE与CD交于点F,AG⊥CD于点G,则以下结论:(1)△ACE≌△CBD;(2)∠AFG=60°;(3)AF=2FG;(4)AC =2CE.其中正确的结论有()个
A.4 B.3 C.2 D.1
8.如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是()
A.B.C.a+ b D. a
二、填空题:(本题共5小题,每小题3分,共15分.)
9.知P1(a-1,4)和P2(2,b)关于x轴对称,则(a+b)2021的值为.
10.等腰三角形的一边长是2cm,另一边长是4cm,则底边长为cm.
11.如图,中,∠BAC=90°,AC=8cm,DE是BC边上的垂直平分线,的周长为14cm,
则的面积是.
12.如图,点是内的一点,OA=OB=OC,∠BAC=45°,则.
13.如图,是等边三角形,AD是BC边上的高,点E是AC边的中点,点P是AD上的一个动点,当PC+PE最小时,∠CPE的度数是.
三、解答题:(本题共5题,共45分)
14.在下面各图中画△A′B′C′,使△A′B′C′与△ABC关于l成轴对称图形.
15.如图,D为∠ACB平分线上一点,DE⊥CA于E,DF⊥CB于F.试探究CD与EF的位置关系,并证明你的结论.
16.如图,已知△ABC,AB=AC,AD是△ABC的角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,M,F.若∠CAD=20°,求∠MCD的度数.
17.如图,已知AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.
(1)求证:△OAB是等腰三角形;
(2)若∠CBA=60°,求证AC=3OC.
18.已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数;
(3)若BQ⊥AD于Q,PQ=6,PE=2,求AD的长.
参考答案:
1.C 2.B 3.B 4.C 5.A 6.D 7.B 8.B 9.
10.2
11.24
12.
13.60°
14.△A′B′C′如图所示.
15.解:CD垂直平分EF
证明:∵D为∠ACB平分线上一点
又∵
∴△CEF是等腰三角形.
根据等腰三角形三线合一的性质
CD垂直平分EF.
16.解:∵AB=AC,AD是△ABC的角平分线
∴AD⊥BC
∵∠CAD=20°
∴∠ACD=70°
∵EF垂直平分AC
∴AM=CM
∴∠ACM=∠CAD=20°
∴∠MCD=50°
17.(1)证明:∵AC⊥BC,BD⊥AD
∴∠ADB=∠ACB=90°
在Rt△ABC和Rt△BAD中
∴Rt△ABC≌Rt△BAD(HL)
∴∠CAB=∠DBA
∴AO=BO
即△OAB是等腰三角形;
(2)解:由(1)得:∠CAB=∠DBA ∴AO=BO
∵∠CBA=60°,∠ACB=90°
∴∠DBA=∠CAB=90°﹣∠ACB=30°∴∠OBC=∠CBA﹣∠DBA=30°
∴AO=BO=2OC
∵AC=AO+OC
∴AC=3OC.
18.(1)证明:∵△ABC是等边三角形∴∠BAC=∠C=60°,AB=CA
在△ABE和△CAD中
∴△ABE≌△CAD(SAS);
(2)解:∵△ABE≌△CAD
∴∠ABE=∠CAD
∴∠ABE+∠BAP=∠CAD+∠BAP
即∠BPQ=∠BAC=60°;
(3)解:∵BQ⊥AD
∴∠BQP=90°
∴∠PBQ=30°
∴BP=2PQ=12
∴BE=BP+PE=12+2=14
∵△ABE≌△CAD
∴BE=AD=14。
