相似三角形与全等三角形变式拓展题

合集下载

相似三角形拓展定理

相似三角形拓展定理（最新版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如幼儿教案、小学教案、中学教案、教学活动、评语、寄语、发言稿、工作计划、工作总结、心得体会、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of classic sample essays, such as preschool lesson plans, elementary school lesson plans, middle school lesson plans, teaching activities, comments, messages, speech drafts, work plans, work summary, experience, and other sample essays, etc. I want to know Please pay attention to the different format and writing styles of sample essays!相似三角形拓展定理这是相似三角形拓展定理，是优秀的数学教案文章，供老师家长们参考学习。

备战2021年九年级中考数学考点提升训练——专题：《三角形综合：全等与相似》(五)

备战2021年九年级中考数学考点提升训练——专题：《三角形综合：全等与相似》（五）1．在学习全等三角形知识时、数学兴趣小组发现这样一个模型：它是由两个共顶点且顶角相等的等腰三角形构成．在相对位置变化的同时，始终存在一对全等三角形．通过资料查询，他们得知这种模型称为“手拉手模型”，兴趣小组进行了如下操作：（1）如图1、两个等腰三角形△ABC和△ADE中，AB＝AC，AE＝AD，∠BAC＝∠DAE，连接BD、CE、如果把小等腰三角形的腰长看作小手，大等腰三角形的腰长看作大手，两个等腰三角形有公共顶点，类似大手拉着小手，这个就是“手拉手模型”，在这个模型中，和△ADB全等的三角形是，此时BD和CE的数量关系是；（2）如图2、两个等腰直角三角形△ABC和△ADE中，AB＝AC，AE＝AD，∠BAC ＝∠DAE＝90°，连接BD，CE，两线交于点P，请判断线段BD和CE的数量关系和位置关系，并说明理由；（3）如图3，已知△ABC，请完成作图：以AB、AC为边分别向△ABC外作等边△ABD 和等边△ACE（等边三角形三条边相等，三个角都等于60°），连接BE，CD，两线交于点P，并直接写出线段BE和CD的数量关系及∠PBC+∠PCB的度数．2．如图，△ABC为等边三角形，点D、E分别是边AB、BC所在直线上的动点，若点D、E以相同的速度，同时从点A、点B出发，分别延AB、BC方向运动，直线AE、CD交于点O．（1）如图1，求证：△ABE≌△CAD；（2）在点D、点E运动过程中，∠COE＝°；（3）如图2，点P为边AC中点，连接BO，PO，当点D、E分别在线段AB、BC上运动时，判断BO与PO的数量关系，并证明你的结论．3．如图，△ABC是等边三角形，△ADC与△ABC关于直线AC对称，AE与CD垂直交BC的延长线于点E，∠EAF＝45°，且AF与AB在AE的两侧，EF⊥AF．（1）依题意补全图形．（2）①在AE上找一点P，使点P到点B，点C的距离和最短；②求证：点D到AF，EF的距离相等．4．在△ABC中，AB＝AC，D是直线BC上一点，以AD为一条边在AD的右侧作△ADE，使AE＝AD，∠DAE＝∠BAC，连接CE．（1）如图，当点D在BC延长线上移动时，若∠BAC＝40°，则∠ACE＝，∠DCE＝，BC、DC、CE之间的数量关系为；（2）设∠BAC＝α，∠DCE＝β．①当点D在BC延长线上移动时，α与β之间有什么数量关系？请说明理由；②当点D在直线BC上（不与B，C两点重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．（3）当CE∥AB时，若△ABD中最小角为15°，试探究∠ACB的度数（直接写出结果，无需写出求解过程）．5．在学习了“等边对等角”定理后．某数学兴趣小组的同学继续探究了同一个三角形中边与角的数量关系，得到了一个正确的结论：“在同一个三角形中，较长的边所对的角较大”．简称：“在同一个三角形中，大边对大角”．即，如图：当AB＞AC时，∠C＞∠B．该兴趣小组的同学在此基础上对等腰三角形“三线合一”性质的一般情况，继续进行了深入的探究，请你补充完整：（1）在△ABC中，AD是BC边上的高线．①如图1，若AB＝AC，则∠BAD＝∠CAD；②如图2，若AB≠AC，当AB＞AC时，∠BAD∠CAD．（填“＞”，“＜”，“＝”）证明：∵AD是BC边上的高线，∴∠ADB＝∠ADC＝90°．∴∠BAD＝90°﹣∠B，∠CAD＝90°﹣∠C．∵AB＞AC，∴（在同一个三角形中，大边对大角）．∴∠BAD∠CAD．（2）在△ABC中，AD是BC边上的中线．①如图1，若AB＝AC，则∠BAD＝∠CAD；②如图3，若AB≠AC，当AB＞AC时，∠BAD∠CAD．（填“＞”，“＜”，“＝”）证明：6．如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，动点P从点A出发沿线段AB以每秒3个单位长的速度运动至点B，过点P作PQ⊥AB射线AC于点Q．设点P 的运动时间为t秒（t＞0）．（1）线段CQ的长为（用含t的代数式表示）（2）当△APQ与△ABC的周长的比为1：4时，求t的值．（3）设△APQ与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式．（4）当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时，直接写出t的值．7．已知△ABC与△A′B′C′关于直线l对称，其中CA＝CB，连接AB'，交直线l于点D（点D与点C不重合）．（1）如图1，若∠ACB＝40°，∠1＝30°，求∠2的度数；（2）若∠ACB＝40°，且0°＜∠BCD＜110°，求∠2的度数；（3）如图2，若∠ACB＝60°，0°＜∠BCD＜120°，求证：BD＝AD+CD．8．在△ABC与△ABD中，∠DBA＝∠CAB，AC与BD交于点F（1）如图1，若∠DAF＝∠CBF，求证：AD＝BC；（2）如图2，∠D＝135°，∠C＝45°，AD＝2，AC＝4，求BD的长．（3）如图3，若∠DBA＝18°，∠D＝108°，∠C＝72°，AD＝1，直接写出DB的长．9．思维启迪：（1）如图①，A，B两点分别位于一个池塘的两端，小亮想用绳子测量A，B间的距离，但绳子不够长，他出一个办法：先在地上取一个可以直接到达B点的点C，连接BC，取BC的中点P（点P可以直接到达A点），利用工具过点C作CD∥AB交AP的延长线于点D，此时测得CD＝200米，那么A，B间的距离是米．思维探索：（2）在△ABC和△ADE中，AC＝BC＝4，AE＝DE＝，∠ACB＝∠AED＝90°，将△ADE绕点A顺时针方向旋转，把点E在AC边上时△ADE的位置作为起始位置（此时点B和点D位于AC的两侧），设旋转角为α，连接BD，点P是线段BD的中点，连接PC，PE．①如图②，当△ADE在起始位置时，求证：PC⊥PE，PC＝PE．②如图③，当α＝90°时，点D落在AB边上，PC与PE的数量关系和位置关系分别为．③当α＝135°时，直接写出PC的值．10．如图1，在平面直角坐标系中，等边△ABC的边BC在x轴上，A（0，3），B（﹣，0），点M（m，0）为x轴上的一个动点，连接AM，将AM绕点A逆时针旋转60°得到AN．（1）当M点在B点的左方时，连接CN，求证：△BAM≌△CAN；（2）如图2，当M点在边BC上时，过点N作ND∥AC交x轴于点D，连接MN，若S＝S△MND，试求D点的坐标；四边形ACDN（3）如图3，是否存在点M，使得点N恰好在抛物线y＝﹣2x2+4x+3上，如果存在，请求出m的值，如果不存在，请说明理由．参考答案1．解：（1）因为∠DAE＝∠BAC，所以∠DAE+∠BAE＝∠BAC+∠BAE．所以∠DAB＝∠EAC，在△DAB和△EAC中，，所以△DAB≌△EAC（SAS），所以BD＝CE，故答案为：△AEC，BD＝CE；（2）BD＝CE且BD⊥CE；理由如下：因为∠DAE＝∠BAC＝90°，所以∠DAE+∠BAE＝∠BAC+∠BAE．所以∠DAB＝∠EAC．在△DAB和△EAC中，，所以△DAB≌△EAC（SAS），所以BD＝CE，∠DBA＝∠ECA，因为∠ECA+∠ECB+∠ABC＝90°，所以∠DBA+∠ECB+∠ABC＝90°，即∠DBC+∠ECB＝90°，所以∠BPC＝180°﹣（∠DBC+∠ECB）＝90°，所以BD⊥CE，综上所述：BD＝CE且BD⊥CE；（3）如图3所示，BE＝CD，∠PBC+∠PCB＝60°；因为△ABD和△ACE是等边三角形，所以AD＝AB，AC＝AE，∠ADB＝∠ABD＝∠BAD＝∠CAE＝60°，所以∠BAD+∠BAC＝∠CAE+∠BAC，所以∠CAD＝∠EAB，在△ACD和△AEB中，，所以△ACD≌△AEB（SAS），所以CD＝BE，∠ADC＝∠ABE，所以∠BPD＝180°﹣∠PBD﹣∠BDP＝180°﹣∠ABE﹣∠ABD﹣∠BDP＝180°﹣∠ABD﹣（∠ABE+∠BDP）＝180°﹣∠ABD﹣（∠ADC+∠BDP）＝180°﹣∠ABD﹣∠ADB＝60°，所以∠PBC+∠PCB＝∠BPD＝60°．2．（1）证明：∵△ABC为等边三角形，∴AB＝CA，∠ABE＝∠CAD＝60°，∵点D、E以相同的速度，同时从点A、点B出发，分别延AB、BC方向运动，∴BE＝AD，在△ABE和△CAD中，，∴△ABE≌△CAD（SAS）；（2）解：∵△ABC为等边三角形，∴∠BAC＝60°，∵△ABE≌△CAD，∴∠BAE＝∠ACD，∵∠COE是△ACO的外角，∴∠COE＝∠ACD+∠EAC＝∠BAE+∠EAC＝∠BAC＝60°，故答案为60；（3）解：BO与PO的数量关系为BO＝2PO，理由如下：延长OP到F，使PF＝OP，连接CF，以OC为边作等边△COG，连接BG，如图2所示：∵∠COE＝60°，∴O、E、G三点共线，∵点P为边AC中点，∴AP＝CP，在△APO和△CPF中，，∴△APO≌△CPF（SAS），∴AO＝CF，∠AOP＝∠F，∴CF∥AO，∴∠FCO＝∠COE＝60°，∵△COG是等边三角形，∴CO＝OG＝CG，∠COG＝∠GCO＝∠CGO＝60°，∴∠AOC＝180°﹣60°＝120°，∵∠ACB＝∠OCG＝60°，∴∠ACO＝∠BCG，在△ACO和△BCG中，，∴△ACO≌△BCG（SAS），∴∠BGC＝∠AOC＝120°，AO＝BG，∴CF＝BG，∠BGO＝∠BGC﹣∠CGO＝120°﹣60°＝60°，∴∠FCO＝∠BGO，在△FCO和△BGO中，，∴△FCO≌△BGO（SAS），∴BO＝OF，∵PF＝OP，∴BO＝2PO．3．（1）解：补全图形，如图1所示：（2）①解：如图2，连接BD，P为BD与AE的交点．点P即为所求；②证明：连接DE，DF．如图3所示：∵△ABC，△ADC是等边三角形，∴AC＝AD，∠ACB＝∠CAD＝60°．∵AE⊥CD，∴∠CAE＝∠CAD＝30°．∴∠CEA＝∠ACB﹣∠CAE＝30°．∴∠CAE＝∠CEA．∴CA＝CE．∴CD垂直平分AE．∴DA＝DE．∴∠DAE＝∠DEA，∵EF⊥AF，∠EAF＝45°，∴∠FEA＝45°．∴∠FEA＝∠EAF．∴FA＝FE，∠FAD＝∠FED，在△FAD和△FED中，，∴△FAD≌△FED（SAS）．∴∠AFD＝∠EFD．∴点D到AF，EF的距离相等．4．解：（1）如图1所示：∵∠DAE＝∠BAC，∴∠DAE+∠CAD＝∠BAC+∠CAD，∴∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴∠ACE＝∠B＝（180°﹣40°）＝70°，BD＝CE，∴BC+DC＝CE，∵∠ACD＝∠B+∠BAC＝∠ACE+∠DCE，∴∠BAC＝∠DCE，∵∠BAC＝40°，∴∠DCE＝40°，故答案为：70°；40°；BC+DC＝CE；（2）①当点D在线段BC的延长线上移动时，α与β之间的数量关系是α＝β，理由如下：∵∠DAE＝∠BAC，∴∠DAE+∠CAD＝∠BAC+∠CAD，∴∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴∠B＝∠ACE，∵∠ACD＝∠B+∠BAC＝∠ACE+∠DCE，∴∠BAC＝∠DCE，∵∠BAC＝α，∠DCE＝β，∴α＝β；②分三种情况：（Ⅰ）当D在线段BC上时，α+β＝180°，如图2所示，理由如下：同理可证明：△ABD≌△ACE（SAS），∴∠ADB＝∠AEC，∠ABC＝∠ACE，∵∠ADC+∠ADB＝180°，∴∠ADC+∠AEC＝180°，∴∠DAE+∠DCE＝180°，∵∠BAC＝∠DAE＝α，∠DCE＝β，（Ⅱ）当点D在线段BC反向延长线上时，α＝β，如图3所示，理由如下：同理可证明：△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵∠ACE＝∠ACD+∠DCE，∠ABD＝∠ACD+∠BAC，∴∠ACD+∠DCE＝∠ACD+∠BAC，∴∠BAC＝∠DCE，∵∠BAC＝α，∠DCE＝β，∴α＝β；（Ⅲ）当点D在线段BC的延长线上时，如图1所示，α＝β；综上所述，当点D在BC上移动时，α＝β或α+β＝180°；（3）∠ACB＝60°，理由如下：∵当点D在线段BC的延长线上或在线段BC反向延长线上移动时，α＝β，即∠BAC＝∠DCE，∵CE∥AB，∴∠ABC＝∠DCE，∴∠ABC＝∠BAC，∵AB＝AC，∴∠ABC＝∠ACB＝∠BAC，∴△ABC是等边三角形，∴∠ACB＝60°；∵当D在线段BC上时，α+β＝180°，即∠BAC+∠DCE＝180°，∵CE∥AB，∴∠ABC+∠DCE＝180°，∴∠ABC＝∠BAC，∵AB＝AC，∴∠ABC＝∠ACB＝∠BAC，∴△ABC是等边三角形，综上所述，当CE∥AB时，若△ABD中最小角为15°，∠ACB的度数为60°．5．（1）①证明：∵AD是BC边上的高线，∴∠ADB＝∠ADC＝90°．∴∠BAD＝90°﹣∠B，∠CAD＝90°﹣∠C．∵AB＝AC，∴∠C＝∠B，∴∠BAD＝∠CAD．②解：∵AD是BC边上的高线，∴∠ADB＝∠ADC＝90°．∴∠BAD＝90°﹣∠B，∠CAD＝90°﹣∠C．∵AB＞AC，∴∠C＞∠B（在同一个三角形中，大边对大角）．∴∠BAD＞∠CAD．故答案为：∠C＞∠B，＞；（2）①证明：延长AD至E，使ED＝AD，连接CE，如图1所示：∵AD是BC边上的中线，∴BD＝CD，又∵∠ADB＝∠EDC，∴△ABD≌△ECD（SAS），∴∠BAD＝∠E，AB＝EC，∵AB＝AC，∴EC＝AC，∴∠CAD＝∠E，∴∠BAD＝∠CAD；②解：延长AD至E，使ED＝AD，连接CE，如图3所示：同①得：△ABD≌△ECD（SAS），∴∠BAD＝∠E，AB＝EC，∵AB＞AC，∴EC＞AC，∴∠CAD＞∠E，∴∠BAD＜∠CAD，故答案为：＜．6．解：（1）在Rt△ABC中，tan A＝＝＝，由题意得，AP＝3t，在Rt△APQ中，tan A＝＝，∴PQ＝AP＝4t，根据勾股定理得，AQ＝＝＝5t．当0＜t≤时，如图1所示：CQ＝AC﹣AQ＝6﹣5t；当＜t≤时，如图2所示：CQ＝AQ﹣AC＝5t﹣6；故答案为：6﹣5t或5t﹣6；（2）∵PQ⊥AB，∴∠APQ＝90°＝∠ACB，∵∠A＝∠A，∴△APQ∽△ACB，∴＝＝，即＝，解得：t＝，即当△APQ与△ABC的周长的比为1：4时，t为秒．（3）分两种情况：①当0＜t≤时，如图1所示：△APQ与△ABC重叠部分图形的面积为S＝△APQ的面积＝×3t×4t＝6t2；即S＝6t2（0＜t≤）；②当＜t≤时，如图2所示：由（1）得：PQ＝3t，PQ＝4t，AQ＝5t，同（2）得：△CDQ∽△PAQ，∴＝＝，即＝＝，解得：CD＝（5t﹣6），∴△APQ与△ABC重叠部分图形的面积为S＝△APQ的面积﹣△CDQ的面积＝×3t ×4t﹣×（5t﹣6）×（5t﹣6）＝﹣t2+t﹣；即S＝﹣t2+t﹣（＜t≤）；（4）由（1）知，AQ＝5t，PQ＝4t，CQ＝6﹣5t或CQ＝5t﹣6，当CQ＝PQ时，四边形BCQP是轴对称图形，则4t＝6﹣5t，∴t＝；当＜t≤时，设PQ和BC相交于D，当AC＝AP时，四边形ACDP是轴对称图形，则6＝3t，∴t＝2．综上所述，当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时，t的值为秒或2秒．7．解：（1）∵△ABC与△A′B′C′关于直线l对称，其中CA＝CB，∴AC＝CB＝A'C＝B'C，∠BCD＝∠B'CD，∴∠1＝∠CB'D＝30°，∴∠ACB'＝120°，∵∠ACB＝40°，∴∠BCB'＝80°，∴∠BCD＝40°，∴∠2＝180°﹣∠1﹣∠ACD＝70°；（2）若点D在点C下方时，∵△ABC与△A′B′C′关于直线l对称，其中CA＝CB，∴AC＝CB＝A'C＝B'C，∠BCD＝∠B'CD，∴∠1＝∠CB'D＝＝70°﹣∠BCD，∴∠2＝∠CB'D+∠DCB'＝70°，若点D在点C上方时，同理可求∠2＝110°；（3）如图2，在BD上截取DH＝CD，连接CH，∵△ABC与△A′B′C′关于直线l对称，其中CA＝CB，∴AC＝CB＝A'C＝B'C，∠BCD＝∠B'CD，∴∠1＝∠CB'D＝＝60°﹣∠BCD，∴∠2＝∠CB'D+∠DCB'＝60°，又∵CD＝DH，∴△CDH是等边三角形，∴CH＝CD，∵∠BCA＝∠HCD＝60°，∴∠BCH＝∠ACD，在△BCH和△ACD中，，∴△BCH≌△ACD（SAS），∴AD＝BH，∴BD＝BH+DH＝AD+CD．8．（1）证明：∵∠DFA＝∠CFB，∠DAF＝∠CBF，∴∠D＝∠C，在△DAB和△CBA中，，∴△DAB≌△CBA（AAS），∴AD＝BC；（2）解：在FC上取一点E，使得∠FBE＝∠DAF，如图2所示：由（1）知，△DAB≌△EBA（AAS），∴BE＝AD＝2，DB＝EA，∠BDA＝∠AEB＝135°，∴∠BEC＝45°，∵∠C＝45°，∴∠BEC＝∠C，∴BC＝BE＝2，∠EBC＝90°，∴EC＝BE＝2，∵AC＝4，∴AE＝AC﹣EC＝4﹣2，∴BD＝AE＝4﹣2．（3）解：在FC上取一点E，使得∠FBE＝∠DAF，如图3所示：由（1）知△DAB≌△EBA（AAS），∴BE＝AD＝1，DB＝AE，∠BEA＝∠BDA＝108°，∠DBA＝∠EAB＝18°，∴∠BEC＝72°＝∠C，∠EFB＝∠DBA+∠EAB＝36°，∴BC＝BE＝1，∠EBC＝36°，∴∠C＝∠BEA﹣∠EBC＝72°，∴∠FBC＝72°，∴∠C＝∠FBC，∠EFB＝∠EBF＝36°，∴EF＝EB＝1，FB＝FC，∵∠DBA＝∠CAB，∴AF＝FB＝FC＝1+EC，∵∠EBC＝∠EFB，∠∠C＝∠C，∴△CBE～△CFB，∴，∴BC2＝CE•CF，∴CE•CF＝1，∴CE（CE+1）＝1，即CE2+CE﹣1＝0，解得：（负值已舍去），∴，∴，∴．9．（1）解：∵CD∥AB，∴∠ABP＝∠C，∵P是BC的中点，∴PB＝PC，在△ABP和△DCP中，，∴△ABP≌△DCP（ASA），∴AB＝CD＝200米；故答案为：200；（2）①证明：延长EP交BC于F，如图②所示：∵∠ACB＝∠AED＝90°，∴DE∥BC，∴∠EDP＝∠FBP，∠DEP＝∠BFP，∵点P是线段BD的中点，∴PB＝PD，在△FBP和△EDP中，，∴△FBP≌△EDP（AAS），∴PF＝PE，BF＝DE，∵AC＝BC，AE＝DE，∴FC＝EC，又∵∠ACB＝90°，∴△EFC是等腰直角三角形，∵PE＝PF，∴PC⊥EF，PC＝EF＝PE；②解：PC⊥PE，PC＝PE；理由如下：延长ED交BC于H，如图③所示：由旋转的性质得：∠CAE＝90°，∵∠AED＝∠ACB＝90°，∴四边形ACHE是矩形，∴∠BHE＝∠CHE＝90°，AE＝CH，∵AE＝DE，∴CH＝DE，∠ADE＝45°，∴∠EDP＝135°，∵∠ACB＝90°，AC＝BC，∴∠ABC＝45°，∵∠BHE＝90°，点P是线段BD的中点，∴PH⊥BD，PH＝BD＝PD，△BPH是等腰直角三角形，∴∠BHP＝45°，∴∠CHP＝135°＝∠EDP，在△CPH和△EPD中，，∴△CPH≌△EPD（SAS），∴PC＝PE，∠CPH＝∠EPD，∴∠CPE＝∠HPD＝90°，∴PC⊥PE；故答案为：PC⊥PE，PC＝PE；③解：当α＝135°时，AD⊥AC，延长CP，交AD延长线于点H，则AH∥BC，∴△BCP∽△DHP，∴＝＝，∵P是BD的中点，∴PD＝PB，∴DH＝BC＝4，PH＝PC，∵AD＝AE＝2，∴AH＝DH+AD＝6，∴CH＝＝＝2，∴PC＝CH＝．10．解：（1）证明：∵△ABC是等边三角形，∴∠BAC＝60°，AB＝AC，∵将AM绕点A逆时针旋转60°得到AN，∴AM＝AN，∠MAN＝60°＝∠BAC，即∠CAN+∠BAN＝∠MAB+∠BAN，∴∠CAN＝∠MAB，∴△BAM≌△CAN（SAS）；（2）如图1，连接CN，由（1）可知△BAM≌△CAN，∴∠B＝∠ACN＝60°，∵DN∥AC，∴∠NDC＝∠ACB＝60°，∴∠NCD＝60°，∴△CDN是等边三角形，∴CN＝DN，∠CND＝60°，∵AM＝AN，∠MAN＝60°，∴△AMN是等边三角形，∴AN＝MN，∠ANM＝60°，∴∠ANC＝∠MND，∴△ANC≌△MND（SAS），∴S△ACN＝S△MND，∵S四边形ACDN＝S△MND＝S△ACN+S△CDN，∴，∴CD＝AB，∵A（0，3），B（﹣，0），∴OA＝3，OB＝，∴AB＝＝2，∴CD＝，∴OD＝OC+CD＝＝，∴D（，0）；（3）如图2，过点C作CE∥AB交y轴于点E，由（1），（2）可知点N在直线CE 上，CE与抛物线交于点N1，N2，∴∠ABC＝∠OCE＝60°，OC＝OB＝，∴OE＝3，∴E（0，﹣3），设直线CE的解析式为y＝kx+b，∴，解得：，∴直线CE的解析式为y＝x﹣3，∴，解得：，，∴N1（2，3），N2（﹣，﹣），若AM绕点A逆时针旋转60°得到AN1时，M（m，0），∴AM＝AN1＝2，∵AB＝2，AN1∥x轴，∴点M与点C重合，即m＝，若AM绕点A逆时针旋转60°得到AN2时，M（m，0），∵C（0，），∴CN 2＝＝3，由（1）可知BM 2＝CN2＝3，∴OM2＝OB+BM2＝＝4，∴m＝﹣4．综合以上可得，m＝或﹣4．。

全等相似三角形证明经典题及相似三角形

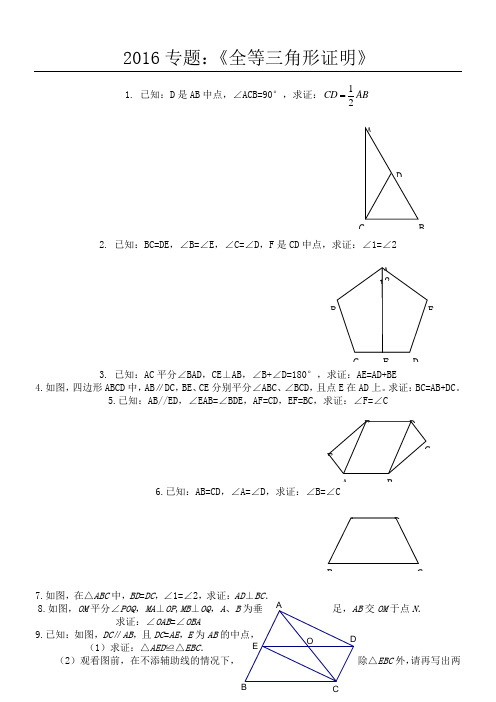
2016专题：《全等三角形证明》1. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB2. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE4.如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

5.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C6.已知：AB=CD ，∠A=∠D ，求证：∠B=∠C7.如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．8.如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA9.已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两C D F B CD C B AFEBC O ED CB AC A E 个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：10.如图：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

11.如图：在△ABC 中，BA=BC ，D 是AC 的中点。

求证：BD ⊥AC 。

12.AB=AC ，DB=DC ，F 是AD 的延长线上的一点。

求证：BF=CF13.如图：AB=CD ，AE=DF ，CE=FB 。

求证：AF=DE 。

14.已知：点A 、F 、E 、C 在同一条直线上，AF ＝CE ，BE∥DF ，BE ＝DF ．求证：△ABE≌△CDF．15.已知：如图所示，AB ＝AD ，BC ＝DC ，E 、F 分别是DC 、BC 的中点，求证：AE ＝AF 。

小学生数学习题练习相似和全等三角形计算

小学生数学习题练习相似和全等三角形计算相似和全等三角形是小学数学中的一个重要内容，它们在图形的形状判断和计算中起着重要的作用。

通过练习相似和全等三角形的计算，可以加深对这两种概念的理解，并且提高解决相关问题的能力。

下面是一些小学生数学习题练习，帮助大家巩固相似和全等三角形的计算方法。

1. 题目：已知直角三角形ABC，∠B为直角，AB=3cm，BC=4cm。

点D在BC上，且BD=2cm。

连接AD，求∠DAC的度数。

解析：首先要判断∆ABD和∆ACD是否相似或全等。

由于∠B是直角，所以∆ABD和∆ACD具有共边AB、AC和∠A相等，而且按照SAS相似判据，∆ABD和∆ACD是相似的。

根据相似三角形的性质，可得等式：AB/AC = BD/CD。

代入已知数据，得到3/AC = 2/CD。

解方程可得CD = 6cm。

由于∠DAC与直角∠B互补，所以∠DAC的度数为90-∠A，即90-∠DAC=∠B=90°。

因此，∠DAC的度数为90°。

2. 题目：已知∆ABC和∆DEF相似，且AB/DE = 2/3，BC/EF = 4/5。

若AC=15cm，求EF的长度。

解析：根据相似三角形的性质，相似三角形的对应边的比例相等。

已知AB/DE = 2/3，BC/EF = 4/5，可得出等式：AB/DE = BC/EF。

将已知数据代入，得到2/3 = 4/EF。

通过交叉相乘得到2EF = 12，解方程可得EF = 6。

因此，EF的长度为6cm。

3. 题目：已知∆ABC和∆DEF全等，且AC=12cm，BF=8cm，EF=6cm。

求BC的长度。

解析：由于∆ABC和∆DEF全等，所以它们的对应边相等。

已知AC=12cm，BF=8cm，EF=6cm，可得出等式：AC = DE，BC = EF，AB = DF。

将已知数据代入，得到BC = EF = 6。

因此，BC的长度为6cm。

4. 题目：已知任意一直角三角形的两条腰的长度分别为3cm和5cm，求斜边的长度。

备战2021年九年级中考数学考点提升训练——专题：《三角形综合：全等与相似》(一)

备战2021年九年级中考数学考点提升训练——专题：《三角形综合：全等与相似》（一）1．已知：等边△ABC中．（1）如图1，点M是BC的中点，点N在AB边上，满足∠AMN＝60°，求的值；（2）如图2，点M在AB边上（M为非中点，不与A、B重合），点N在CB的延长线上且∠MNB＝∠MCB，求证：AM＝BN．（3）如图3，点P为AC边的中点，点E在AB的延长线上，点F在BC的延长线上，满足∠AEP＝∠PFC，求的值．2．（1）发现如图1，△ABC和△ADE均为等边三角形，点D在BC边上，连接CE．填空：①∠DCE的度数是；②线段CA、CE、CD之间的数量关系是．（2）探究如图2，△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，点D在BC 边上，连接CE．请判断∠DCE的度数及线段CA、CE、CD之间的数量关系，并说明理由．（3）应用如图3，在Rt△ABC中，∠A＝90°，AC＝4，AB＝6．若点D满足DB＝DC，且∠BDC＝90°，请直接写出DA的长．3．（1）问题发现：如图1，△ABC和△ADE均为等边三角形，点D在BC的延长线上，连接CE，求证：△ABD≌△ACE．（2）类比探究：如图2，△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，D点在边BC的延长线上，连接CE．请判断：①∠ACE的度数为．②线段BC，CD，CE之间的数量关系是．（3）问题解决：在（2）中，如果AB＝AC＝，CD＝1，求线段DE的长．4．直角三角形ABC中，∠ACB＝90°，直线l过点C．（1）当AC＝BC时，如图①，分别过点A、B作AD⊥l于点D，BE⊥l于点E．求证：△ACD≌△CBE．（2）当AC＝8，BC＝6时，如图②，点B与点F关于直线l对称，连接BF，CF，动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动，同时动点N从点F出发，以每秒3个单位的速度沿F→C→B→C→F向终点F运动，点M、N到达相应的终点时停止运动，过点M作MD⊥l于点D，过点N作NE⊥l于点E，设运动时间为t秒．①CM＝，当N在F→C路径上时，CN＝．（用含t的代数式表示）②直接写出当△MDC与△CEN全等时t的值．5．已知在△ABC中，AB＝AC，过点B引一条射线BM，D是BM上一点．（1）如图1，∠ABC＝60°，射线BM在∠ABC内，∠ADB＝60°，求证：∠BDC ＝60°．请根据以下思维框图，写出证明过程．（2）如图2，已知∠ABC＝∠ADB＝30°．①当射线BM在∠ABC内，求∠BDC的度数．②当射线BM在BC下方，请问∠BDC的度数会变吗？若不变，请说明理由；若改变，请直接写出∠BDC的度数．（3）在第（2）题的条件下，作AF⊥BD于点F，连结CF，已知BD＝6，CD＝2，求△CDF的面积．6．（1）问题发现如图1，在Rt△ABC和Rt△DBE中，∠ABC＝∠DBE＝90°，∠ACB＝∠BED＝45°，点E是线段AC上一动点，连接DE．填空：①则的值为；②∠EAD的度数为．（2）类比探究如图2，在Rt△ABC和Rt△DBE中，∠ABC＝∠DBE＝90°，∠ACB＝∠BED＝60°，点E是线段AC上一动点，连接DE．请求出的值及∠EAD的度数；（3）拓展延伸如图3，在（2）的条件下，取线段DE的中点M，连接AM、BM，若BC＝4，则当△ABM是直角三角形时，求线段AD的长．7．如图，在△ABC中，AB＝AC，点D在△ABC内，BD＝BC，∠DBC＝60°，点E 在△ABC外，∠CBE＝150°，∠ACE＝60°．（1）求∠ADC的度数．（2）判断△ACE的形状并加以证明．（3）连接DE，若DE⊥CD，AD＝3，求DE的长．8．在等腰直角△ABC中，AB＝AC，∠BAC＝90°，以CA为边在∠ACB的另一侧作∠ACM＝∠ACB，点D为射线BC上任意一点，在射线CM上截取CE＝BD，连接AD、DE、AE．（1）如图1，当点D落在线段BC的延长线上时，直接写出∠ADE的度数；（2）如图2，当点D落在线段BC（不含边界）上时，AC与DE交于点F，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；（3）如图2，作AH⊥BC，垂足为H，作AG⊥EC，垂足为G，连接HG，判断△GHC 的形状，并说明理由．9．如图，已知在ABC中，AB＝AC＝5，BC＝6，点M在△ABC内，AM平分∠BAC．点E与点M在AC所在直线的两侧，AE⊥AB，AE＝BC，点N在AC边上，CN＝AM，连接ME、BN；（1）根据题意，补全图形；（2）ME与BN有何数量关系，判断并说明理由；（3）点M在何处时BM+BN取得最小值？请确定此时点M的位置，并求出此时BM+BN 的最小值．10．如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，以AB为一边向上作等边三角形ABD，点E在BC垂直平分线上，且EB⊥AB，连接CE，AE，CD．（1）判断△CBE的形状，并说明理由；（2）求证：AE＝DC；（3）填空：①若AE，CD相交于点F，则∠AFD的度数为．②在射线AB上有一动点P，若△PBC为等腰三角形，则∠ACP的度数为．参考答案1．解：（1）∵△ABC为等边三角形，∴∠B＝∠BAC＝60°，AB＝AC，∵点M是BC的中点，∴∠MAN＝30°，∠AMB＝90°，∵∠AMN＝60°，∴∠BMN＝30°，∴BM＝2BN，AB＝2BM，设BN＝x，则BM＝2x，AB＝4x，∴AN＝3x，∴；（2）证明：如图2，过点M作MG∥NC交AC于点G，∴∠A＝∠AMG＝∠AGM＝60°，∴△AMG为等边三角形，∴AM＝AG，∴BM＝CG，∵∠AGM＝∠ABC＝60°，∴∠MGC＝∠NBM＝120°，∵MG∥BC，∴∠GMC＝∠MCB，∵∠MNB＝∠MCB，∴∠GMC＝∠MNB，∴△MGC≌△NBM（AAS），∴MG＝BN，∵△AMG为等边三角形，∴AM＝MG，∴AM＝BN；（3）如图3，过点P作PM∥BC交AB于点M，∴△AMP为等边三角形，∴AP＝MP，∠AMP＝60°，∵P为AC的中点，∴AP＝PC，∴MP＝PC，∵∠ACB＝60°，∴∠EMP＝∠PCF＝120°，∵∠AEP＝∠PFC，∴△PCF≌△PME（AAS），∴CF＝ME，∴BF﹣BE＝BC+CF﹣ME+MB，又∵P为AC的中点，MP∥BC，∴MB＝，∴BF﹣BE＝BC+BC＝，∴．2．（1）发现解：①∵在△ABC中，AB＝AC，∠BAC＝60°，∴∠BAC＝∠DAE＝60°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴∠ACE＝∠B＝60°，∴∠DCE＝∠ACE+∠ACB＝60°+60°＝120°；故答案为：120°，②∵△BAD≌△CAE，∴BD＝CE，∴BC＝BD+CD＝EC+CD，∴CA＝BC＝CE+CD；故答案为：CA＝CE+CD．（2）探究∠DCE＝90°；CA＝CD+CE．理由：∵△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，∴AB＝AC，AD＝AE，∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE．∴△BAD≌△CAE（SAS）．∴BD＝CE，∠B＝∠ACE＝45°．∴∠DCE＝∠ACB+∠ACE＝90°．在等腰直角三角形ABC中，CB＝CA，∵CB＝CD+DB＝CD+CE，∴CA＝CD+CE．（3）应用DA＝5或．作DE⊥AB于E，连接AD，∵在Rt△ABC中，AB＝6，AC＝4，∠BAC＝90°，∴BC＝＝＝2，∵∠BDC＝90°，DB＝DC，∴DB＝DC＝，∠BCD＝∠CBD＝45°，∵∠BDC＝∠BAC＝90°，∴点B，C，A，D四点共圆，∴∠DAE＝45°，∴△ADE是等腰直角三角形，∴AE＝DE，∴BE＝6﹣DE，∵BE2+DE2＝BD2，∴DE2+（6﹣DE）2＝26，∴DE＝1，DE＝5，∴AD＝或AD＝5．3．（1）问题发现：证明：∵△ABC和△ADE是等边三角形∴AB＝AC，AD＝AE，且∠BAC＝∠DAE＝60°∴∠BAC+∠CAD＝∠DAE+∠CAD，即∠BAD＝∠CAE，在△ABD和△ACE中AB＝AC，∠BAD＝∠CAE，AD＝AE，∴△ABD≌△ACE（SAS）；（2）类比探究：①∵△ABC和△ADE均为等腰直角三角形，∴AB＝AC，∠BAD＝∠CAE，AD＝AE，在△ACE与△ABD中，，∴△ACE≌△ABD（SAS），∴∠ACE＝∠B＝45°，故答案为：45°；②∵△ACE≌△ABD，∴BD＝CE，∴BC+CD＝CE，故答案为：BC+CD＝CE；（3）问题解决：解：在（2）中，同（1）的方法可证：△ABD≌△ACE，∴∠ACE＝∠ABD＝45°，又∵∠ACB＝45°，∴∠BCE＝∠ACB+∠ACE＝90°，在Rt△BAC中，，∴，又∵CD＝1，由（2）得CE＝BC+CD＝3，在Rt△BAC中，，则线段DE的长是．4．解：（1）△ACD与△CBE全等．理由如下：∵AD⊥直线l，∴∠DAC+∠ACD＝90°，∵∠ACB＝90°，∴∠BCE+∠ACD＝90°，∴∠DAC＝∠ECB，在△ACD和△CBE中，，∴△ACD≌△CBE（AAS）；（2）①由题意得，AM＝t，FN＝3t，则CM＝8﹣t，由折叠的性质可知，CF＝CB＝6，∴CN＝6﹣3t．故答案为：8﹣t；6﹣3t．②由折叠的性质可知，∠BCE＝∠FCE，∵∠MCD+∠CMD＝90°，∠MCD+∠BCE＝90°，∴∠NCE＝∠CMD，∴当CM＝CN时，△MDC与△CEN全等，当点N沿F→C路径运动时，8﹣t＝6﹣3t，解得，t＝﹣1（不合题意），当点N沿C→B路径运动时，8﹣t═3t﹣6，解得，t＝3.5，当点N沿B→C路径运动时，由题意得，8﹣t＝18﹣3t，解得，t＝5，当点N沿C→F路径运动时，由题意得，8﹣t＝3t﹣18，解得，t＝6.5，综上所述，当t＝3.5秒或5秒或6.5秒时，△MDC与△CEN全等．5．（1）证明：在BM上取一点E，使AE＝AD．∵∠ADB＝60°，∴△ADE是等边三角形．∵AB＝AC，∠ABC＝60°，∴△ABC是正三角形，∴∠BAE＝60°﹣∠EAC＝∠CAD，∴△BAE≌△CAD（SAS），∴∠ADC＝∠AEB＝120°，∴∠BDC＝120°﹣60°＝60°．（2）①在BD上取一点E，AE＝AD，如图2，∵∠ABC＝∠ADB＝30°，且AB＝AC，∴∠ABC＝∠ACB＝30°，∠AED＝∠ADE＝30°，∴∠BAC＝∠EAD＝120°，∴∠BAE＝∠CAD，∴△BAE≌△CAD（SAS），∴∠ADC＝∠AEB＝180°﹣30°＝150°，∴∠BDC＝150°﹣30°＝120°．②会变．如图3．在DB延长线上取一点E，使得AE＝AD，同理可得：△BAE≌△CAD，∴∠ADC＝∠E＝30°，∴∠BDC＝∠ADE+∠ADC＝30°+30°＝60°．（3）如图，∵△BAE≌△CAD，∴BE＝CD，且AE＝AD，AF⊥DE，∴，作CH⊥BM，如图4，∵∠BDC＝120°，∴∠CDH＝60°，∴∠DCH＝30°，∴，∴，∴如图5，∵△BAE≌△CAD，∴BE＝CD，且AE＝AD，AF⊥DE，∴，，∴．6．解：（1）∵∠ABC＝∠DBE＝90°，∴∠ABC﹣∠ABE＝∠DBE﹣∠ABE即∠CBE＝∠ABD，∵∠ACB＝∠BED＝45°，∴∠ACB＝∠CAB＝45°，∠BED＝∠BDE＝45°，∴AB＝BC，DB＝BE，∴△ABD≌△CBE（SAS），∴AD＝CE，∠DAB＝∠ECB＝45°，∴＝1，∠EAD＝45°+45°＝90°．故答案为：1，90°．（2），∠EAD＝90°．理由如下：∵∠ABC＝∠DBE＝90°，∠ACB＝∠BED＝60°，∴∠ABD＝∠EBC，∠BAC＝∠BDE＝30°，∴在Rt△ABC中，tan∠ACB＝＝tan60°＝，在Rt△DBE中，tan∠BED＝＝tan60°＝，∴＝，又∵∠ABD＝∠EBC，∴△ABD∽△∠CBE，∴＝＝，∠BAD＝∠ACB＝60°．∵∠BAC＝30°，∴∠EAD＝∠BAD+∠BAC＝60°+30°＝90°．（3）如图，由（2）知：＝＝，∠EAD＝90°，∴AD＝CE，在Rt△ABC中，∠BAC＝30°，BC＝4，∴AC＝8，AB＝4，∵∠EAD＝∠EBD＝90°，且点M是DE的中点，∴AM＝BM＝DE，∵△ABM为直角三角形，∴AM2+BM2＝AB2＝（4）2＝48，∴AM＝BM＝2，∴DE＝4，设EC＝x，则AD＝x，AE＝8﹣x，Rt△ADE中，AE2+AD2＝DE2，∴（8﹣x）2+（x）2＝（4）2，解之得：x＝2+2（负值舍去）．∴EC＝2+2．∴AD＝CE＝2+6．∴线段AD的长为（2+6）．7．（1）解：∵BD＝BC，∠DBC＝60°，∴△DBC是等边三角形．∴DB＝DC，∠BDC＝∠DBC＝∠DCB＝60°．在△ADB和△ADC中，∵，∴△ADC≌△ADB（SSS）．∴∠ADC＝∠ADB．∴∠ADC＝（360°﹣60°）＝150°．（2）解：△ACE是等边三角形．理由如下：∵∠ACE＝∠DCB＝60°，∴∠ACD＝∠ECB．∵∠CBE＝150°，∠ADC═150°，∴∠ADC＝∠EBC．在△ACD和△ECB中，∵，∴△ACD≌△ECB（ASA）．∴AC＝CE．∵∠ACE＝60°，∴△ACE是等边三角形．（3）解：连接DE．∵DE⊥CD，∴∠EDC＝90°．∵∠BDC＝60°，∴∠EDB＝30°．∵∠CBE＝150°，∠DBC＝60°，∴∠DBE＝90°．∴EB＝DE．∵△ACD≌△ECB，AD＝3，∴EB＝AD＝3．∴DE＝2EB＝6．8．（1）解：∠ADE＝45°．∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∵∠ACM＝∠ACB，∴∠ACM＝∠ABC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴AD＝AE，∠CAE＝∠BAD，∴∠DAE＝∠BAC＝90°，∴∠ADE＝45°；（2）（1）中的结论成立证明：∵∠BAC＝90°，AB＝AC，∴∠B＝∠ACB＝45°．∵∠ACM＝∠ACB，∴∠B＝∠ACM＝45°．在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）．∴AD＝AE，∠BAD＝∠CAE．∴∠CAE+∠DAC＝∠BAD+∠DAC＝∠BAC＝90°．即∠DAE＝90°．∵AD＝AE，∴∠ADE＝∠AED＝45°．（3）△CGH为等腰直角三角形．理由如下：∵∠BCA＝∠ACE＝45°，∴∠GCH＝90°，又∵AH⊥BC，AG⊥CE，∴AG＝AH，∵∠ACG＝∠AGC＝45°，∴AG＝CG，∵AB＝AC，AH⊥BC，∴∠HCA＝∠HAC＝45°，∴AH＝HC，∴CH＝CG，∴△CGH为等腰直角三角形．9．解：（1）如图1所示：（2）ME＝BN．证明：延长AM交BC于点F，如图．∵AM平分∠BAC，∴∠BAM＝∠CAM．∵AE⊥AB，∴∠MAE+∠BAM＝90°．∴∠MAE+∠CAM＝90°∵AB＝AC，AM平分∠BAC，∴AF⊥BC．∴∠C+∠CAM＝90°．∴∠MAE＝∠C．又∵AM＝CN，AE＝BC，∴△AME≌△CNB（SAS）．∴ME＝BN．（3）由（2）知ME＝BN，则当B，M，E三点共线时，此时BM+BN取得最小值，点M的位置如图2，∵AB＝5，BC＝6，∴AE＝BC＝6，∴BE＝＝＝．∴BM+BN的最小值是．10．解：（1）△CBE是等边三角形．理由如下：∵点E在BC垂直平分线上，∴EC＝EB，∵EB⊥AB，∴∠ABE＝90°，∵∠ABC＝30°，∴∠CBE＝60°，∴△CBE是等边三角形．（2）∵△ABD是等边三角形，∴AB＝DB，∠ABD＝60°，∵∠ABC＝30°，∴∠DBC＝90°，∵EB⊥AB，∴∠ABE＝90°，∴∠ABE＝∠DBC，由（1）可知：△CBE是等边三角形，∴EB＝CB，∴△ABE≌△DBC（SAS）．∴AE＝DC；（3）①设AB与CD交于点G，∴∠EAB＝∠CDB，又∵∠AGC＝∠BGD，∴∠AFD＝∠ABD＝60°．故答案为：60°．②∵△BCP为等腰三角形，当BC＝BP时，如图2，∠ABC＝∠BCP+∠BPC＝30°，∴∠BCP＝15°，∴∠ACP＝90°+15°＝105°；当PC＝PB时，如图3，∴∠PCB＝30°，∵∠ACB＝90°，∴∠ACP＝60°；当BP＝BC时，如图4，∵∠ABC＝30°，∴∠PCB＝∠CPB＝（180°﹣30°）＝75°，∴∠ACP＝90°﹣75°＝15°．综合上述可得∠ACP的度数为15°或60°或105°．故答案为：15°或60°或105°．。

相似三角形与全等三角形

加油绽个性化辅导教案一、相似三角形知识点一：相似三角形的概念1．具有的图形称为相似性．2．对应角，对应边的三角形叫做相似三角形。

3．如果△ABC 和△A/B/C/相似，且k A C CAC B BC B A AB ===//////，那么这个比值k 就叫做这两个相似三角形的．例：三角尺在灯泡O 的照射下在墙上形成影子（如图1所示）.现测得20cm 50cm OA OA '==，，这个三角尺的周长与它在墙上形成的影子的周长的比是．解析：由于三角尺和它在灯泡O 的照射下在墙上形成影子相似，所以三角尺的周长与它在墙上形成的影子的周长的比等于相似比．因为20cm 50cm OA OA '==，，所以对应边的比为25．因此应填25．练习1．小明在一次军事夏令营活动中，进行打靶训练，在用枪瞄准目标点B 时，要使眼睛O 、准星A 、目标B 在同一条直线上，如图2所示，在射击时，小明有轻微的抖动，致使准星A 偏离到A ′，若OA ＝0.2米，OB ＝40米，AA ′＝0.0015米，则小明射击到的点B ′偏离目标点B 的长度BB ′为（） A ．3米 B ．0.3米 C ．0.03米D ．0.2米2．如图3，已知等边三角形ABC 的边长为2，DE 是它的中位线，则下面四个结论：教师:秦国荣学生:熊志林时间:2014年4月20日10:00-12:00 学科:数学年级:初三课题名称：相似三角形与全等三角形图1图3图2（1）DE ＝1，（2）△CDE ∽△CAB ，（3）△CDE 的面积与△CAB 的面积之比为1∶4．其中正确的有（） A ．0个B ．1个C ．2个D ．3个知识点二：相似三角形的条件1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形．2．对应相等，两三角形相似．3．两对应边且相等，两三角形相似． 4．三边，两三角形相似．5．如果一个直角三角形的一条斜边和一条直角边与另一个直角三角形的一条斜边和一条直角边，那么这两个直角三角形相似．例：如图4，D 、E 两点分别在△ABC 的边AB ，AC 上，DE 与BC 不平行，当满足条件（写出一个即可）时，△ADE ∽△ACB ．解析：．比如：∠ADE ＝∠ACB ，∠AED ＝∠ABC ，AD ∶AC ＝AE ∶AB ．任选其一均可满足题目要求练习1．如图8所示，给出下列条件：①B ACD ∠=∠；②ADC ACB ∠=∠； ③AC AB CD BC=； ④AB AD AC ∙=2．其中单独能够判定ABC ACD △∽△的个数为（） A ．1B ．2C ．3D ．42．如图9，小正方形的边长均为1，则下列图中的三角形（阴影部分）与ABC △相似的是（）知识点三：相似三角形的性质1．相似三角形的相等，对应边．图4图8A .图92．相似三角形对应高的比、对应中线的比、对应角平分线的比相似比． 3．相似三角形的周长比等于，面积比等于．例：将三角形纸片（△ABC ）按如图10所示的方式折叠，使点B 落在边AC 上，记为点B ′，折痕为EF ．已知AB ＝AC ＝3，BC ＝4，若以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是．解析：设BF 的长为x ，当B /F 平行于AB 时，我们有3x ＝44x -，解得x ＝712．当B /F 不平行于AB 时，我们有3x ＝34x -，解得x ＝2．所以BF 的长为712或2．练习1．在ABC △和DEF △中，22AB DE AC DF A D ==∠=∠，，，如果ABC △的周长是16，面积是12，那么DEF △的周长、面积依次为（） A ．8，3 B ．8，6 C ．4，3 D ．4，62．如图，Rt ABC △中，90ACB ∠=°，直线EF BD ∥，交AB 于点E ，交AC 于点G ，交AD 于点F ，若13AEG EBCGS S =△四边形，则CFAD= ．知识点四：相似三角形的应用例：如图12，路灯（P 点）距地面8米，身高1.6米的小明从距路灯的底部（O 点）20米的A 点，沿OA 所在的直线行走14米到B 点时，身影的长度是变长了还是变短了？变长或变短了多少米？解：∵ ∠MAC ＝∠MOP ＝90°，∠AMC ＝∠OMP ，∴ △MAC ∽△MOP ∴OP ACMO MA = 即 86.120=+MA MA ．解得MA ＝5．POBNAM图12图10图11同样由△NBD ∽△NOP 可求得NB ＝1.5．所以，小明的身影变短了3.5米．练习1．如图13，小东用长为3.2m 的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m 、与旗杆相距22m ，则旗杆的高为（） A ．12m B ．10mC ．8mD ．7m2．如图14是小明设计用手电来测量某古城墙高度的示意图,点P 处放一水平的平面镜,光线从点A 出发经平面镜反射后刚好射到古城墙CD 的顶端C 处，已知AB ⊥BD ，CD ⊥BD ，且测得AB ＝1.2米，BP ＝1.8米，PD ＝12米，那么该古城墙的高度是（） A ．6米 B ．8米二、全等三角形要善于灵活选择适当的方法判定两个三角形全等。

2021年九年级中考数学一轮复习专题《三角形综合：全等与相似》高频考点训练(三)

2021年中考数学一轮复习专题《三角形综合：全等与相似》高频考点训练（三）1．如图，△ABC是等边三角形，点D在AC上，点E在BC的延长线上，且BD＝DE．（1）如图1，若点D是AC的中点，求证：AD＝CE；（2）如图2，若点D不是AC的中点，AD＝CE是否成立？证明你的结论；（3）如图3，若点D在线段AC的延长线上，试判断AD与CE的大小关系，并说明理由．2．阅读材料：小明遇到这样一个问题：如图1，在△AC中，∠A＝2∠B，CD平分∠ACB，AD＝2.2，AC ＝3.6，求BC的长．小明的想法：因为CD平分∠ACB，所以可利用“翻折”来解决该问题．即在BC边上取点E，使EC＝AC，并连接DE（如图2）．（1）如图2，根据小明的想法，回答下面问题：①△DEC和△DAC的关系是，判断的依据是；②△BDE是三角形；③BC的长为．（2）参考小明的想法，解决下面问题：已知：如图3，在△ABC中，AB＝AC，∠A＝20°，BD平分∠ABC，BD＝2.3，BC＝2，求AD的长．3．如图，在△ABC中，AC＝BC，∠ACB＝90°，点D为△ABC内一点，且BD＝AD．（1）求证：CD⊥AB；（2）∠CAD＝15°，E为AD延长线上的一点，且CE＝CA．①若点M在DE上，连接MC且DC＝DM，请判断△MCD的形状，并给出证明；②若点N为直线AE上一点，且△CEN为等腰三角形，直接写出∠CNE的度数．4．在△ABC中，∠BAC＝90°，AB＝AC．点D在边BC上，DE⊥DA且DE＝DA，AE交边BC于点F，连接CE．（1）如图1，当AD＝AF时，求证：BD＝CF；（2）如图2，当AD≠AF时，请探究∠ACE的度数是否为定值，并说明理由；（3）如图3，在（2）的条件下，当时，过点D作AE的垂线，交AE于点P，交AC于点K，若CK＝，求DF的长．5．已知，△ABC中，∠BAC＝90°，AB＝AC，AE是过A的一条直线，且BD⊥AE于D，CE⊥AE于E．（1）如图1，当B、C在AE的异侧时，求证：BD＝DE+CE；（2）如图2，当B、C在AE的同侧时（BD＜CE），问BD与DE、CE的关系如何，请予证明；（3）如图3，当B、C在AE的同侧时（BD＞CE），其余条件不变，问BD与DE、CE的关系怎样？请直接写出结果，不需证明；（4）归纳（1）、（2）、（3），请用简洁的语言表述BD、DE、CE的关系．6．如图，以△ABC的两边AB，AC为边向外作等边△ABD和△ACE，DC，BE相交于点O．（1）求证：DC＝BE；（2）求∠BOC的度数；（3）∠BAC的度数发生变化时，∠BOC的度数是否变化？若不变化，请求出∠BOC的度数；若发生变化，请说明理由．7．在等腰△ABC中，AB＝BC，点D，E在射线BA上，BD＝DE，过点E作EF∥BC，交射线CA 于点F．请解答下列问题：（1）当点E在线段AB上，CD是△ACB的角平分线时，如图①，求证：AE+BC＝CF；（提示：延长CD，FE交于点M．）（2）当点E在线段BA的延长线上，CD是△ACB的角平分线时，如图②；当点E在线段BA的延长线上，CD是△ACB的外角平分线时，如图③，请直接写出线段AE，BC，CF之间的数量关系，不需要证明；（3）在（1）、（2）的条件下，若DE＝2AE＝6，则CF＝．8．问题引入：（1）如图①所示，△ABC中，点O是∠ABC和∠ACB的平分线的交点，若∠A＝α，则∠BOC＝（用α表示）：不用说明理由，直接填空．如图②所示，∠OBC＝∠ABC，∠OCB＝∠ACB，若∠A＝α，则∠BOC＝（用α表示），不用说明理由，直接填空．（2）如图③所示，∠OBC＝∠DBC，∠OCB＝∠ECB，若∠A＝α，则∠BOC＝（用α表示），填空并说明理由．9．如图，点O为直线AB上一点，将一个等腰直角三角尺（三个内角分别是90°、45°、45°）的直角顶点和另一个含30°角的直角三角尺的60°角顶点都放在O处．（1）如图①，∠AOM＝°；（2）如图②，将等腰直角三角尺绕点O旋转一定角度到图②的位置，OM恰好平分∠EOB 时，求出∠AOE和∠MOF的度数；（3）如图③，将等腰直角三角尺绕点O旋转一定角度到图③的位置，若∠AOE是∠MOF 的3倍，则等腰直角三角尺所旋转的角∠BOF＝°．10．探究：如图①，在△ABC中，∠ACB＝90°，CD⊥AB于点D，若∠B＝27°，则∠ACD的度数是．拓展：如图②，∠MCN＝90°，射线CP在∠MCN的内部，点A、B分别存CM、CN上，分别过点A、B作AD⊥CP、BE⊥CP于点D、E．若AC＝CB＝13，BE＝5，则DE＝．应用：如图③，点A、B分别在∠MCN的边CM、CN上，射线CP在∠MCN的内部，点D、E 在射线CP上，连结AD、BE、AE．且使∠MCN＝∠ADP＝∠BEP．当AC＝BC，CD＝2DE，且S＝8时，则△ACE的面积是．△CBE参考答案1．（1）证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，AB＝AC＝BC，∵D为AC中点，∴∠DBC＝30°，AD＝DC，∵BD＝DE，∴∠E＝∠DBC＝30°∵∠ACB＝∠E+∠CDE，∴∠CDE＝30°＝∠E，∴CD＝CE，∵AD＝DC，∴AD＝CE；（2）成立，如图2，过D作DF∥BC，交AB于F，则∠ADF＝∠ACB＝60°，∵∠A＝60°，∴△AFD是等边三角形，∴AD＝DF＝AF，∠AFD＝60°，∴∠BFD＝∠DCE＝180°﹣60°＝120°，∵DF∥BC，∴∠FDB＝∠DBE＝∠E，在△BFD和△DCE中，∴△BFD≌△DCE（AAS），∴CE＝DF＝AD，即AD＝CE．（3）AD＝CE．证明：如图3，过点D作DP∥BC，交AB的延长线于点P，∵△ABC是等边三角形，∴△APD也是等边三角形，∴AP＝PD＝AD，∠APD＝∠ABC＝∠ACB＝∠PDC＝60°，∵DB＝DE，∴∠DBC＝∠DEC，∵DP∥BC，∴∠PDB＝∠CBD，∴∠PDB＝∠DEC，在△BPD和△DCE中，，∴△BPD≌△DCE（AAS），∴PD＝CE，∴AD＝CE．2．解：（1）如答图1，①在△ACD与△ECD中，，∴△ACD≌△ECD（SAS）；②由①知，△ACD≌△ECD，∴AD＝DE，∠A＝∠DEC，∵∠A＝2∠B，∴∠DEC＝2∠B，∴∠B＝∠EDB，∴BE＝DE，∴△BDE是等腰三角形；③由①知，△ACD≌△ECD，则EC＝AC＝3.6，DE＝AD＝2.2．又∵BE＝DE，∴BE＝AD＝2.2．∴BC＝BE+EC＝2.2+3.6＝5.8．故答案是：①△ACD≌△ECD；SAS；②等腰；③5.8；（2）∵△ABC中，AB＝AC，∠A＝20°，∴∠ABC＝∠C＝80°，∵BD平分∠B，∴∠1＝∠2＝40°∠BDC＝60°，如答图2，在BA边上取点E，使BE＝BC＝2，连接DE，则△DEB≌△DBC，∴∠BED＝∠C＝80°，∴∠4＝60°，∴∠3＝60°，在DA边上取点F，使DF＝DB，连接FE，则△BDE≌△FDE，∴∠5＝∠1＝40°，BE＝EF＝2，∵∠A＝20°，∴∠6＝20°，∴AF＝EF＝2，∵BD＝DF＝2.3，∴AD＝BD+BC＝4.3．3．（1）证明：∵CB＝CA，DB＝DA，∴CD垂直平分线段AB，∴CD⊥AB．（2）①△MCD为等边三角形，理由如下：如图，连接MC，∵AC＝BC，∴∠CBA＝∠CAB，又∵∠ACB＝90°，∴∠CBA＝∠CAB＝45°，又∵∠CAD＝∠CBD＝15°，∴∠DBA＝∠DAB＝30°，∴∠BDE＝30°+30°＝60°，∵AC＝BC，∠CAD＝∠CBD＝15°，BD＝AD，在△ADC和△BDC中，，∴△ADC≌△BDC（SAS），∴∠ACD＝∠BCD＝45°，∴∠CDE＝60°，又∵DC＝DM，∴△MCD为等边三角形；②∵∠CAD＝15°，CE＝CA，∴∠E＝∠CAE＝15°．当EN＝EC时，∠ENC＝＝82.5°或∠ENC＝∠E＝∠7.5°；当CE＝CN时，点N与点A重合，此时∠ENC＝∠E＝15°；当EN＝CN时，∠ENC＝180°﹣2×15°＝150°；所以∠CNE的度数为7.5°、15°、82.5°、150°．4．（1）①证明：如图1中，∵AB＝AC，∴∠B＝∠ACF，∵AD＝AF，∴∠ADF＝∠AFD，∴∠ADB＝∠AFC，∴△ABD≌△ACF（AAS），∴BD＝CF．（2）结论：∠ACE＝90°．理由：如图2中，∵DA＝DE，∠ADE＝90°，AB＝AC，∠BAC＝90°，∴∠ACD＝∠AED＝45°，∴A，D，E，C四点共圆，∴∠ADE+∠ACE＝180°，∴∠ACE＝90°．（3）如图3中，连接EK．∵∠BAC+∠ACE＝180°，∴AB∥CE，∴＝＝，设EC＝a，则AB＝AC＝3a，AK＝3a﹣，∵DA＝DE，DK⊥AE，∴AP＝PE，∴AK＝KE＝3a﹣，∵EK2＝CK2+EC2，∴（3a﹣）2＝（）2+a2，解得a＝4或0（舍弃），∴EC＝4，AB＝AC＝12，∴AE＝＝＝4，∴DP＝PA＝PE＝AE＝2，EF＝AE＝，∴PF＝EF＝，∵∠DPF＝90°，∴DF＝＝＝5．5．证明：（1）∵∠BAC＝90°，∴∠BAD+∠EAC＝90°，又∵BD⊥AE，CE⊥AE，∴∠BDA＝∠AEC＝90°，∠BAD+∠ABD＝90°，∴∠ABD＝∠EAC，在△ABD与△CAE中，，∴△ABD≌△CAE（AAS），∴BD＝AE，AD＝CE，∵AE＝AD+DE＝CE+DE，∴BD＝DE+CE．（2）BD＝DE﹣CE．理由如下：同理可证：△ABD≌△CAE（AAS），∴BD＝AE，AD＝CE，∵DE＝AD+AE＝CE+DE，∴BD＝DE﹣CE．（3）BD＝DE+CE，理由如下：∵∠BAC＝90°，∴∠BAD+∠EAC＝90°，又∵BD⊥AE，CE⊥AE，∴∠BDA＝∠AEC＝90°，∠BAD+∠ABD＝90°，∴∠ABD＝∠EAC，在△ABD与△CAE中，，∴△ABD≌△CAE（AAS），∴BD＝AE，AD＝CE，∵DE＝AD+AE＝BD+CE，∴BD＝DE+CE．（4）归纳（1）、（2）、（3）可知：当B、C在AE的异侧时，BD＝DE+CE或CE＝BD+DE；当B、C在AE的同侧时，BD＝DE﹣CE．6．解：（1）∵△ADB和△AEC都是等边三角形，∴∠DAB＝∠EAC＝60°，AD＝AB，AE＝AC，∴∠DAC＝∠BAE，在△DAC和△BAE中，AD＝AB，∠DAC＝∠BAE，AC＝AE，∴△DAC≌△BAE（SAS）；∴DC＝BE；（2）∵△DAC≌△BAE，∴∠ADC＝∠ABE，∴∠ODB+∠OBD＝∠ADB﹣∠ADC+∠ABD+∠ABE＝∠ADB+∠ABD＝120°，∴∠BOC＝∠ODB+∠OBD＝120°；（3）不变化，为120°，理由：∵由（2）可得∠BOC＝∠ODB+∠OBD＝120°；∴∠BOC和∠BAC大小无关．7．解：（1）如图①，延长CD，FE交于点M．∵AB＝BC，EF∥BC，∴∠A＝∠BCA＝∠EFA，∴AE＝EF，∴MF∥BC，∴∠MED＝∠B，∠M＝∠BCD，又∵∠FCM＝∠BCM，∴∠M＝∠FCM，∴CF＝MF，又∵BD＝DE，∴△MED≌△CBD（AAS），∴ME＝BC，∴CF＝MF＝ME+EF＝BC+AE，即AE+BC＝CF；（2）当点E在线段BA的延长线上，CD是△ACB的角平分线时，BC＝AE+CF，如图②，延长CD，EF交于点M．由①同理可证△MED≌△CBD（AAS），∴ME＝BC，由①证明过程同理可得出MF＝CF，AE＝EF，∴BC＝ME＝EF+MF＝AE+CF；当点E在线段BA的延长线上，CD是△ACB的外角平分线时，AE＝CF+BC．如图③，延长CD交EF于点M，由上述证明过程易得△MED≌△CBD（AAS），BC＝EM，CF＝FM，又∵AB＝BC，∴∠ACB＝∠CAB＝∠FAE，∵EF∥BC，∴∠F＝∠FCB，∴EF＝AE，∴AE＝FE＝FM+ME＝CF+BC；（3）CF＝18或6，当DE＝2AE＝6时，图①中，由（1）得：AE＝3，BC＝AB＝BD+DE+AE＝15，∴CF＝AE+BC＝3+15＝18；图②中，由（2）得：AE＝AD＝3，BC＝AB＝BD+AD＝9，∴CF＝BC﹣AE＝9﹣3＝6；图③中，DE小于AE，故不存在．故答案为18或6．8．解：（1）在△ABC中，∠A＝α，∴∠ABC+∠ACB＝180°﹣∠A＝180°﹣α．如图①所示，∵OB平分∠ABC，OC平分∠ACB，∴∠OBC＝∠ABC，∠OCB＝∠ACB．∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣α）＝180°﹣90°+α＝90°+α；如图②所示，∵∠OBC＝∠ABC，∠OCB＝∠ACB，∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣α）＝180°﹣60°+α＝120°+α．故答案为：90°+α；120°+α．（2）∠BOC＝120°﹣α，理由如下：∵∠OBC＝∠DBC，∠OCB＝∠ECB，∠A＝α，∴∠BOC＝180°﹣（∠OBC+∠OCB），＝180°﹣（∠DBC+∠ECB），＝180°﹣（∠A+∠ACB+∠ABC+∠A），＝180°﹣（180°+∠A），＝180°﹣60°﹣α，＝120°﹣α．故答案为：120°﹣α．9．解：（1）∵∠MON＝60°，∴∠AOM＝180°﹣60°＝120°，故答案为120；（2）由题意得∠BOM＝∠EOM＝∠BOE，∵∠BOM＝60°，∴∠EOM＝60°，∠BOE＝120°∴∠AOE＝180°﹣∠BOE＝60°，∠MOF＝90°﹣∠EOM＝30°；（3）设等腰直角三角尺所旋转的角∠BOF＝α，∴∠AOE＝90°﹣α，∠MOF＝60°﹣α，∵∠AOE是∠MOF的3倍，∴90°﹣α＝3（60°﹣α），解得α＝45°，∴∠BOF＝45°，故答案为45．10．解：探究：∵CD⊥AB，∴∠CDB＝90°，∵∠B＝27°，∴∠BCD＝90°﹣∠B＝63°，∵∠ACB＝90°，∴∠ACD＝90°﹣∠BCD＝27°，故答案为：27°；拓展：∵∠MCN＝90°，∴∠ACD+∠BCE＝90°，∵AD⊥CP，BE⊥CP，∴∠ADC＝∠BEC＝90°，∴∠ACD+∠CAD＝90°，∴∠CAD＝∠BCE，在△ACD和△CBE中，，∴△ACD≌△CBE（AAS），∴CD＝BE，AD＝CE，∵AD⊥CP，∴∠ADC＝90°，∵AC＝13，BE＝CD＝5，∴AD＝＝＝12，∴DE＝CE﹣CD＝AD﹣BE＝12﹣5＝7，故答案为：7；应用：∵∠MCN＝∠ACD+∠BCD，∠MCN＝∠ADP，∴∠ADP＝∠ACD+∠BCD，∵∠ADP＝∠ACD+∠CAD，∴∠CAD＝∠BCE，∵∠ADP＝∠BEP，∴∠ADC＝∠CEB，在△ACD和△CBE中，，∴△ACD≌△CBE（AAS），∴S△ACD ＝S△CBE，∵S△CBE＝8，∴S△ACD＝8，∵CD＝2DE，∴S△ACD ＝2S△ADE，∴S△ADE ＝S△ACD＝4，∴S△ACE ＝S△ACD+S△ADE＝8+4＝12，故答案为：12．。

专题六二次函数综合题类型六全等、相似三角形问题

类型六全等、相似三角形问题例1 (2017·淄博)如图①，经过原点O 的抛物线y ＝ax 2＋bx(a ≠0)与x 轴交于另一点A(32，0)，在第一象限内与直线y ＝x 交于点B(2，t)．(1)求这条抛物线的表达式；(2)在第四象限内的抛物线上有一点C ，满足以B ，O ，C 为顶点的三角形的面积为2，求点C 的坐标；(3)如图②，若点M 在这条抛物线上，且∠MBO ＝∠ABO ，在(2)的条件下，是否存在点P ，使得△POC ∽MOB ？若存在，求出点P 的坐标；若不存在，请说明理由．图①图②例1题图【思路点拨】 (1)把(2，t)代入y ＝x 可求点B 坐标为(2，2)，然后把(2，2)、(32，0)代入y ＝ax 2＋bx 可得抛物线的表达式；(2)由点C 在抛物线y ＝2x 2－3x 可设点C 坐标为(x ，2x 2－3x)，然后过点C 作CQ ⊥y 轴，过点B 作BF ⊥y 轴，则由S △BOC ＝S 四边形CQFB －S △COQ －S △BOF 可得方程，解方程可得点C 的横坐标，从而求得点C 坐标；(3)由∠MBO ＝∠ABO ，可得△OBE ≌△OBA ，所以点E 坐标为(0，32)，从而可求直线MB 的解析式为y ＝14x ＋32，再由y＝14x ＋32和y ＝2x 2－3x 组成方程组，解方程组可得点M 坐标，再由△POC ∽△MOB 可得∠BOM ＝∠COP ，且OC OB ＝OP OM ＝12，从而可求点P 坐标．解：(1)把B(2，t)代入y ＝x 得t ＝2， ∴B(2，2)，把A(32，0)，B(2，2)代入y ＝ax 2＋bx 得⎩⎪⎨⎪⎧94a ＋32b ＝0，4a ＋2b ＝2，解得⎩⎨⎧a ＝2，b ＝－3. ∴抛物线的解析式为y ＝2x 2－3x ；例1题解图①(2)设点C 坐标为(x ，2x 2－3x)，如解图①，过点C 作CQ ⊥y 轴，过点B 作BF ⊥y 轴，则S △BOC ＝S 四边形CQFB －S △BOF －S △COQ ，即（2＋x ）[2－（2x 2－3x ）]2－2×2×12－12x(－2x 2＋3x)＝2，解得x ＝1.把x ＝1代入y ＝2x 2－3x 得y ＝2－3＝－1， ∴C(1，－1)；(3)存在．如解图②，连接AB ，OM ，设MB 交y 轴于点E ，由(1)得点B 坐标为(2，2)， ∴∠BOE ＝∠BOA ＝45°，在△BOE 和△BOA 中，⎩⎨⎧∠BOE ＝∠BOA ，OB ＝OB ，∠EBO ＝∠ABO ，∴△BOE ≌△BOA(ASA )，∴OA ＝OE ，∵A(32，0)，∴E(0，32)，设直线BE 的解析式为y ＝kx ＋b ，把(0，32)，(2，2)分别代入得⎩⎪⎨⎪⎧2x ＋b ＝2，b ＝32，解得⎩⎨⎧k ＝14，b ＝32.∴直线BM 的解析式为y ＝14x ＋32.由y ＝14x ＋32和y ＝2x 2－3x 组成方程组，得⎩⎪⎨⎪⎧y ＝14x ＋32，y ＝2x 2－3x ，解得⎩⎪⎨⎪⎧x 1＝2，y 1＝2(与B 点重合，舍去)，⎩⎨⎧x 2＝－38，y 2＝4532.∴点M 坐标为(－38，4532)．由点C 坐标为(1，－1)可得∠AOC ＝∠BOE ＝45°， ∴OB ＝22，OC ＝2， ∵△OPC ∽△OMB ， ∴OP OM ＝OC OB ＝12，且∠POC ＝∠BOM. 当点P 在第一象限时，如解图②所示，过点P 作PG ⊥x 轴，过点M 作MH ⊥y 轴， ∵∠BOM ＝∠COP ，∠COA ＝BOE ，例1题解图②∴∠POG ＝∠MOE ，又∵∠MHO ＝∠PGO ＝90°， ∴△POG ∽△MOH ， ∴OP OM ＝OG OH ＝PG MH ＝12， ∴OG ＝4564，PG ＝316，∴点P 坐标为(4564，316)；当点P 位于第三象限时，可求点P 坐标为(－316，－4564)．综上可得点P 坐标为(4564，316)或(－316，－4564)．【备考指导】相似三角形的存在性探究：1．探究三角形相似时，往往没有明确指出两个三角形的对应角(尤其是以文字形式出现让证明两个三角形相似)，或者涉及动点位置的不确定，此时应考虑不同的对应关系，分情况讨论；2．确定分类标准：找出一对对应相等的角，再根据对应边成比例进行分类讨论确定相似三角形成立的条件．【针对练习】 1．(2017·镇江)如图，在平面直角坐标系中，矩形OABC 的边OA 、OC 分别在x 轴、y 轴上，点B 坐标为(4，t)(t>0)，二次函数y ＝x 2＋bx(b<0)的图象经过点B ，顶点为点D.(1)当t ＝12时，顶点D 到x 轴的距离等于14；(2)点E 是二次函数y ＝x 2＋bx(b<0)的图象与x 轴的一个公共点(点E 与点O 不重合)，求OE·EA 的最大值及取得最大值时的二次函数表达式；第1题图(3)矩形OABC 的对角线OB 、AC 交于点F ，直线l 平行于x 轴，交二次函数y ＝x 2＋bx(b<0)的图象于点M 、N ，连接DM 、DN ，当△DMN ≌△FOC 时，求t 的值．解：(1)14；(2)将y ＝0代入抛物线的解析式得x 2＋bx ＝0，解得x ＝0或x ＝－b ，∵OA ＝4，∴AE ＝4－(－b)＝4＋b ，∴OE ·AE ＝－b(4＋b)＝－b 2－4b ＝－(b ＋2)2＋4， ∴OE ·AE 的最大值为4，此时b 的值为－2， ∴抛物线的表达式为y ＝x 2－2x ；第1题解图(3)过点D 作DG ⊥MN ，垂足为G ，过点F 作FH ⊥CO ，垂足为H ， ∵△DMN ≌△FOC ，∴MN ＝CO ＝t ，DG ＝FH ＝2.∵D(－b 2，－b 24)，∴N(－b 2＋t 2，－b 24＋2)，即N(t －b 2，8－b 24)．将点N 坐标代入抛物线的解析式得8－b 24＝(t －b 2)2＋b·(t －b2)，解得t ＝±2 2.∵t>0，∴t＝2 2.2．(2017·海南)抛物线y ＝ax 2＋bx ＋3经过点A(1，0)和点B(5，0)． (1)求该抛物线所对应的函数解析式；(2)该抛物线与直线y ＝35x ＋3相交于C 、D 两点，点P 是抛物线上的动点且位于x 轴下方，直线PM ∥y 轴，分别与x 轴和直线CD 交于点M 、N.①连接PC 、PD ，如图①，在点P 运动过程中，△PCD 的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；②连接PB ，过点C 作CQ ⊥PM ，垂足为点Q ，如图②，是否存在点P ，使得△CNQ 与△PBM 相似？若存在，求出满足条件的点P 的坐标，若不存在，说明理由．图①图②第2题图解：(1)抛物线对应的函数解析式为y ＝35x 2－185x ＋3；(2)①∵点P 是抛物线上的动点且位于x 轴下方，∴可设P(t ，35t 2－185t ＋3)(1<t<5)，∵直线PM ∥y 轴，分别与x 轴和直线CD 交于点M 、N ，∴M(t ，0)，N(t ，35t ＋3)，∴PN ＝35t ＋3－(35t 2－185t ＋3)＝－35(t －72)2＋14720.联立直线CD 与抛物线解析式可得⎩⎨⎧y ＝35x ＋3，y ＝35x 2－185x ＋3，解得⎩⎨⎧x 1＝0，y 1＝3，⎩⎪⎨⎪⎧x 2＝7，y 2＝365.∴C(0，3)，D(7，365)，第2题解图①分别过C 、D 作直线PN 的垂线，垂足分别为E 、F ，如解图①，则CE ＝t ，DF ＝7－t ，∴S △PCD ＝S △PCN ＋S △PDN ＝12PN·CE ＋12PN·DF ＝72PN ＝72[－35(t －72)2＋14720]＝－2110(t －72)2＋102940， ∴当t ＝72时，△PCD 的面积有最大值，最大值为102940；第2题解图②②存在．如解图②，∵∠CQN ＝∠PMB ＝90°，∴△CNQ 与△PBM 相似时，有NQ CQ ＝PM BM 或NQ CQ ＝BMPM两种情况，∵CQ ⊥PM ，垂足为Q ，∴Q(t ，3)，且C(0，3)，N(t ，35t ＋3)，∴CQ ＝t ，NQ ＝35t ＋3－3＝35t ，∴CQ NQ ＝53，∵P(t ，35t 2－185t ＋3)，M(t ，0)，B(5，0)，∴BM ＝5－t ，PM ＝0－(35t 2－185t ＋3)＝－35t 2＋185t －3. 当NQ CQ ＝PM BM 时，则PM ＝35BM ，即－35t 2＋185t －3＝35(5－t)，解得t ＝2或t ＝5(舍去)，此时P(2，－95)；当NQ CQ ＝BM PM 时，则BM ＝35PM ，即5－t ＝35(－35t 2＋185t －3)，解得t ＝349或t ＝5(舍去)，此时P(349，－5527)．综上可知，存在满足条件的点P ，其坐标为(2，－95)或(349，－5527)．3．(2017·常州)如图，在平面直角坐标系xOy ，已知二次函数y ＝－12x 2＋bx 的图象过点A(4，0)，顶点为B ，连接AB 、BO.第3题图(1)求二次函数的表达式； (2)若C 是BO 的中点，点Q 在线段AB 上，设点B 关于直线CQ 的对称点为B′；当△OCB′为等边三角形时，求BQ 的长度；(3)若点D 在线段BO 上，OD ＝2DB ，点E 、F 在△OAB 的边上，且满足△DOF 与△DEF 全等，求点E 的坐标．解：(1)∵二次函数的表达式为y ＝－12x 2＋2x ；第3题解图①(2)由抛的线y ＝－12x 2＋2x 得y ＝－12(x －2)2＋2，∴如解图①，点B 的坐标为(2，2)，OB ＝BA ＝22，易得△ABO 是等腰直角三角形，且∠OBA ＝90°. ∵△B ′OC 是等边三角形，∴∠OCB ′＝60°， ∴∠BCB ′＝120°，∵点B 与点B′关于CQ 对称， ∴∠BCQ ＝∠B′CQ ＝60°.∴在Rt △CBQ 中，BC ＝2，∠BCQ ＝60°，∴BQ ＝3BC ＝6； (3)∵OB ＝22，OD ＝2BD ，∴OD ＝423.如解图②，当点F ，点E 均在OA 上，且△DFO ≌△DFE ，则DF ⊥OA ，∴DF ＝43＝OF ＝EF ，此时点E 的坐标为(83，0)；其他情况不存在；如解图③，当点F 在OA 上，点E 在AB 上，当DE ∥OF ，即DE ∥x 轴，且OF ＝DE 时满足题意，此时点D 与点E 关于x ＝2对称，∵点D(43，43)，∴点E 的坐标为(83，43)；其他情况下不存在点E ；当点E 在BO 上，则不存在这样的点E ；当点F 在AB 上，无论点E 在何处，都不满足题意；当点E 与点O 重合时，△DOF 与△DEF 是同一个三角形，此时满足题意．综上，这样的点E 有3个，坐标分别为(0，0)，(83，0)，(83，43)．图②图③第3题解图4．(2017·鄂州)已知，抛物线y ＝ax 2＋bx ＋3(a<0)与x 轴交于A(3，0)、B 两点，与y 轴交于点C ，抛物线的对称轴是直线x ＝1，D 为抛物线的顶点，点E 在y 轴C 点的上方，且CE ＝12.(1)求抛物线的解析式及顶点D 的坐标； (2)求证：直线DE 是△ACD 外接圆的切线；第4题图(3)在直线AC 上方的抛物线上找一点P ，使S △ACP ＝12S △ACD ，求点P 的坐标；(4)在坐标轴上找一点M ，使以点B 、C 、M 为顶点的三角形与△ACD 相似，直接写出点M 的坐标．(1)解：抛物线的解析式为y ＝－x 2＋2x ＋3.顶点D 的坐标为(1，4)；(2)证明：∵点C 是抛物线y ＝－x 2＋2x ＋3与y 轴的交点，∴点C 的坐标为(0，3)，∴AC ＝32，CD ＝2，AD ＝25，∴AC 2＋CD 2＝AD 2， ∴△ACD 是直角三角形，且∠ACD ＝90°； ∴AD 是△ACD 外接圆的直径．如解图①，过点E 作EF ⊥CD 于点F ，易得EF ＝CF ＝22CE ＝24，∵CD ＝2，第4题解图①∴DF ＝2－24＝324，∴tan ∠EDF ＝EF DF ＝24324＝13，∵tan ∠CAD ＝CD AC ＝232＝13＝tan ∠CDE ，∴∠CAD ＝∠CDE ，∴∠CDE ＋∠CDA ＝∠CDA ＋∠CAD ＝90°， ∴DE 是△ADC 外接圆的切线；(3)解：∵S △ADC ＝12AC·DC ＝12·32·2＝3，∴S △APC ＝32.第4题解图②如解图②，过点P 作PL ∥y 轴，交AC 于点Q ，易得直线AC 的解析式为y ＝－x ＋3， ∴设点P 的坐标为(t ，－t 2＋2t ＋3)，则点Q 的坐标为(t ，－t ＋3)， ∴PQ ＝(－t 2＋2t ＋3)－(－t ＋3)＝－t 2＋3t ，∴S △APC ＝12PQ·|x A －x C |＝32(－t 2＋3t)， ∴32(－t 2＋3t)＝32，解得t 1＝3＋52，t 2＝3－52，当t ＝3＋52时，y ＝5－52；当t ＝3－52时，y ＝5＋52，∴所求点P 的坐标为(3＋52，5－52)或(3－52，5＋52)；(4)点M 的坐标为(0，0)或(9，0)或(0，－错误!).错误!。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题复习————类比、从特殊到一般的数学思想
相似三角形与全等三角形
类比：是对两个或几个相似的对象进行“联想”，把它们中某个较熟悉的性质转移到和它相似的对象上去，从而发现新规律，解决新问题
作用：通过类比推理和类比联想可以开阔思想，启迪思维，起到由此及彼，由表及里，举一反三，能类旁通的作用。

考点分析：三角形全等和相似是中考考查的重要知识点，而证明三角形全等和相似的过程中运作了类比这一思想方法，体现了从特殊到一般的数学思想。

一、例题：1.如图，△ABC ，△DBE 都是等边三角形，（1）△BCE 与△BAD 是否全等？请说明理由。

（2）AD 与BC 是否平行？请说明理由（3）若△ABC 和△DBE 是顶角相等的等腰三肴形，以上结论还成立吗？
二.、活动探究：
1.如图，等腰Rt △ABC ，AD=BD ，E 、F 分别是AC 、BC 边上的点，且∠EDF ＝90°，
（1）若DE ⊥AB ，探究DE ，DF 之间的数量关系。

（2)试探究DE ，DF 之间的数量关系。

2.如图，等腰Rt △ABC ，AD=kBD,E 、F 分别是AC 、BC 边上的点，且∠EDF ＝90°探究DE ，DF 之间的数量关系。

C
B
C
E
F A E B C D A
E
D
3、△ABC 中，AC=k·BC ，∠C=100°，O 为AB 上一点，且满足AO=mBO ， ∠MON=80°请你探索线段OM 、ON 的关系。

4
、如果D 是等腰直角三角形ABC 斜边BC 上的点，
作DE ∥AB ，D ∥BC ，将一块三角板45°角的顶点放
在D 处，其两边分别交直线EF 、AB 于G 、M 两点，
若CD ：BD=n
探究：DG ：DM 的值。

三．巩固练习：
如图2-1，正方形ABCD 和正方形QMNP ，
∠M =∠B ，M 是正方形ABCD 的对称中心,MN 交AB 于F ，QM 交AD 于E ． ⑴求证：ME = MF ．
⑵如图2－2，若将原题中的“正方形”改为“菱形”，其他条件不变，探索线段ME 与线段MF 的关系，并加以证明．
⑶如图2-3，若将原题中的“正方形”改为“矩形”，且AB = m BC ，其他条件不变，探索线段ME 与线段MF 的关系，并说明理由
⑷根据前面的探索和图2－4，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题；若不能，请说明理由．
B E _ _ _
P
_
四、连接中考：
1、（2010抚顺）如图所示，（1）正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=900, 连接
BE、DF.将Rt△AEF绕点A旋转,在旋转过程中，BE、DF具有怎样的数量关系和位置关系？结合图(1)给予证明；
(2)将（1）中的正方形ABCD变为矩形ABCD，等腰Rt△AEF变为Rt△AEF，且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化？结合图(2)说明理由；
(3)将（2）中的矩形ABCD变为平行四边形ABCD，将Rt△AEF变为△AEF，且∠BAD=∠EAF=α，其他条件不变.(2)中的结论是否发生变化？结合图(3)，如果不变，直接写出结论；如果变化，直接用k表示出线段BE、DF的数量关系，用α表示出直线BE、DF形成的锐角β.
2、（2009湖北省仙桃市）如图①，在△ABC 中，D 、E 分别是AB 、AC 上的点，且DE ∥BC ，将△ADE 绕A 点顺时针旋转一定角度，连结BD 、CE ，得到图②，然后将BD 、CE 分别延长至
M 、N ，使DM ＝21BD ，EN ＝2
1
CE ，连结AM 、AN 、MN ，得到图③，请解答下列问题：（1）若AB ＝AC ，请探究下列数量关系：
① 在图②中，BD 与CE 的数量关系是________________；
② 在图③中，猜想AM 与AN 的数量关系、∠MAN 与∠BAC 的数量关系，并证明你的猜想；
（2）若AB ＝k ·AC （k ＞1），按上述操作方法，得到图④，请继续探究：AM 与AN 的数量关系、
∠MAN 与∠BAC 的数量关系，直接写出你的猜想，不必证明．
D B C A E
图① D B C A 图②
E D B C A 图③
E M N D B C
A 图④
E
M N。