实验报告用EXCEL进行相关与回归分析
实验三Excel在相关回归分析中的应用
实验三 Excel在相关回归分析中的应用实验目的:掌握相关与回归分析的基本方法。
实验要求:计算相关系数,进行线性回归分析。
实验原理:普通最小二乘法(OLS)实验数据:教材第11章例11.1。
实验步骤:以教材第11章例11.1为例,利用Excel完成相关系数和回归分析的具体步骤。
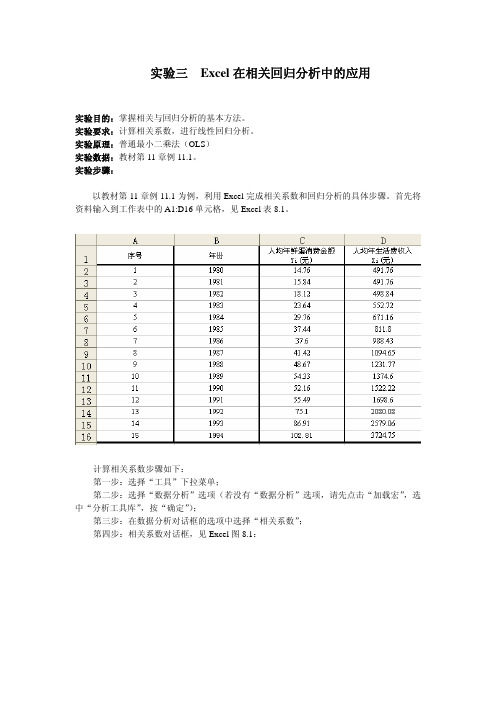
首先将资料输入到工作表中的A1:D16单元格,见Excel表8.1。
计算相关系数步骤如下:第一步:选择“工具”下拉菜单;第二步:选择“数据分析”选项(若没有“数据分析”选项,请先点击“加载宏”,选中“分析工具库”,按“确定”);第三步:在数据分析对话框的选项中选择“相关系数”;第四步:相关系数对话框,见Excel图8.1:图8.1 相关系数对话框在“输入区域”方框内键入C2:D16;在“分组方式”选项中,选择“逐列”;在“输出选项”中选择输出区域A19;选择“确定”。
根据上述步骤计算的相关系数矩阵见Excel表8.2。
Excel表8.3 人均年鲜蛋消费金额和人均年生活费收入的相关矩阵回归分析步骤如下:利用Excel可以很容易地进行回归分析,包括一元线性回归和多元线性回归。
操作步骤如下:第一步:选择“工具”下拉菜单;第二步:选择“数据分析”选项;第三步:在分析工具中选择“回归”;第四步:回归对话框见图8.2:图8.2 回归分析对话框在“输入Y 的区域”方框内键入C2:C16;在“输入X的区域”方框内键入D2:D16;在“输出选项”中选择输出区域键入F1;点击“确定”,上述步骤输出结果见Excel表8.4。
Excel表8.4 人均年鲜蛋消费金额和人均年生活费收入的回归分析结果表中回归统计部分给出了判定系数R2 、调整后的R2、估计标准误差等;方差分析表中给出的显著水平F值表明回归方程是显著的;最下面的一部分是β0=9.3255,β1=0.02797;pβ0和β1的置信以及β0和β1的标准差,t检验统计量值、下限95%和上限95%给出了−区间。
实验四 利用EXCEL软件进行回归与相关分析

实验四利用EXCEL软件进行回归与相关分析一、实验目的1.巩固和掌握相关与回归的概念、步骤、公式计算。
2.学会使用Excel进行相关与回归分析,掌握相关与回归的步骤。
二、实验器具计算机三、实验要求每位同学一台计算机独立完成操作,并结合习题按照操作情况写出。
四、原理及步骤:例1.某地一年级12名女大学生的体重与肺活量数据如下,试求肺活量(L)Y 对体重(kg)X的相关系数与直线回归方程。
体重(kg) X 42 42 46 46 46 50 50 50 52 52 58 58肺活量(L) Y 2.55 2.20 2.75 2.40 2.80 2.81 3.41 3.103.46 2.85 3.50 3.00分析提示:此为求肺活量(L)Y对体重(kg)X的直线回归方程,可用直线回归与相关分析。
(一)相关分析工具操作步骤:1)设置数据区域,并输入数据。
如本例A2:A13为体重(kg)X自变量数据区,B2:B13为肺活量(L)Y因变量数据区;2)选取“工具”栏中“数据分析”;3)选定“相关系数”;4)选择“确定”按钮;显示“相关系数”对话框。
;5)在“输入区域” 框输入J4:K16;6)在“分组方式”框选择“逐列”,即各变量数据按列分组;7)在“输出区域”框输入A14;8)再选择“确定”按钮;9)有关相关系数分析结果显示如下:检验结果:X相关系数r值(0.749482342)详细请见统计分析工具解释工作簿中相关与回归工作表。
(二)回归分析工具例1.同上操作步骤:1)设置数据区域,并输入数据。
如本例A2:A13为体重(kg)X自变量数据区,B2:B13为肺活量(L)Y因变量数据区;2)选取"工具"栏中"数据分析";3)选定"回归分析";4)选择"确定"按钮。
显示"回归分析"对话框;5)在"Y 值输入区域" 框输入B2:B13;6)在"X值输入区域" 框输入A2:A13;7)在"分组方式"框选择"逐列",即自变量和因变量数据按列分组;8)在"输出区域"框输入A14;9)再选择"确定"按钮;10)有关回归分析结果显示如下:检验结果:回归系数b值(0.058826087),截距 a值(0.000413043);直线回归方程(Y=0.000413+0.058826X)。
实验报告 用EXCEL进行相关与回归分析

实验三用EXCEL进行相关与回归分析
一、实验题目:用EXCEL进行相关与回归分析
二、实验教学目的
用EXCEL进行相关与回归分析,并能够解释实验结果。
三、实验教学要求:
掌握利用EXCEL数据分析中提供的样本等进行相关和回归分析,并能够解释实验结果。
四、实验内容:
1. 用Excel进行相关分析
2. 用Excel进行回归分析
五、实验步骤
1.用Excel进行相关分析
第一步:打开一张工作表,并输入相应的数据,如A2:C10
第二步:单击“工具”菜单→“数据分析”命令→选中“回归”功能,然后单击“确定”按钮,如图。
第三步:在弹出的对话框中输入相应的参数,然后再单击“确定”按钮,如图。
第四步:回归分析结果,
即。
2.用Excel进行回归分析
第一步打开工作表,输入数据,然后单击“工具”菜单→“数据分析”命令→“相关系数”功能,然后单击“确定”按钮,如图。
第二步:在方差分析对话框中,输入有关参数,再单击“确定”按钮,如图。
第三步:获得相关系数r值,但在此无法明确该相关系数的显著性程度。
第四步:显著性测验,由于,因此降水量与黏虫发生量之间有极显著的
相关性。
六、实验小结
0.01 r r。
用Excel进行相关性与回归分析分析

用Excel进行回归分析
Excel进行回归分析同样分函数和回归分析宏两种形 式,其提供了9个函数用于建立回归模型和预测,这 9个函数分别是:
1.INTERCEPT返回线性回归模型的截距 2.SLOPE返回线性回归模型的斜率 3.RSQ返回线性回归模型的判定系数 4.FORECAST返回一元线性回归模型的预测值 5.STEYX计算估计的标准误差 6.TREND计算线性回归线的趋势值 7.GROWTH返回指数曲线的趋势值 8.LINEST返回线性回归模型的参数 9.LOGEST返回指数曲线模型的参数
常用的统计量函数
由于公式执行后显示的是计算结果.按Ctrl+、键(位于键 盘左上角).可使公式在显示公式内容与显示公式结果之 间切换.
二、描述统计菜单项的使用
仍使用上面的例子 我们已经把数据输入到B2:B11单元格, 然后按以下步骤操作:
第一步:在工具菜单中选择数据分析选项,从其对话框中 选择描述统计,按确定后打开描述统计对话框。
用函数进行回归分析比较麻烦,这里介绍使用回归 分析宏进行回归分析。
用Excel进行回归分析
第一步:单击“工具”菜单,选择“数据分析”选项,出现 “数据分析”对话框,在分析工具中选择“回归”。
用Excel进行回归分析
第二步:单击“确定”按钮,弹出“回归”对话框,在“Y值输 入区域”输入$B$1:$B$11;在“X值输入区域”输入 $C$1:$C$11,在“输出选项”选择“$E$1”,如下图所示。
利用EXCEL计算相关系数
1.利用函数计算相关系数 2.用相关系数宏计算相关系数
1.利用函数计算相关系数
在Excel中,提供了两个计算两个变量之间相关系 数的方法,CORREL函数和PERSON函数,这两个 函数是等价的,这里我们介绍用CORREL函数计算 相关系数。
EXCEL——相关与回归分析

EXCEL——相关与回归分析回归分析是统计学中一种常用的分析方法,用于研究两个或多个变量之间的关系。
在Excel中,可以使用回归分析工具来进行回归分析。
回归分析可以帮助我们了解变量之间的相关性,预测一个变量的值,并探索影响一个变量的因素。
在Excel中,回归分析工具位于“数据”选项卡的“数据分析”功能中。
首先,我们需要确保已安装并加载了“数据分析”功能。
若没有,可以通过“文件”选项卡下的“选项”进入“Excel选项”窗口,然后选择“加载项”选项卡,点击“Excel加载项”下拉菜单中的“数据分析工具”复选框,最后点击确定。
完成加载后,我们可以通过“数据”选项卡中的“数据分析”按钮打开“数据分析”对话框,然后选择“回归”并点击确定。
在“回归”对话框中,我们需要将自变量和因变量的数据范围输入到“输入Y范围”和“输入X范围”中。
同时,我们还需要选择存储分析结果的输出范围。
除了使用回归分析工具进行回归分析外,Excel还提供了其他一些有用的函数和工具,可以辅助进行相关性和回归分析。
例如,可以使用CORREL函数计算相关系数,使用INTERCEPT函数和SLOPE函数计算回归方程的截距和斜率。
回归分析在各个领域都有广泛的应用。
在经济学中,回归分析可以用于研究经济变量的相互关系和预测经济趋势。
在市场营销中,回归分析可以帮助了解市场变量对销售额或利润的影响。
在医学研究中,回归分析可以用于探索患者生活方式和基因等因素对健康状况的影响。
总结来说,回归分析是一种重要的统计分析方法,在Excel中可以通过回归分析工具进行实施。
使用回归分析工具,我们可以了解变量之间的相关性,预测一个变量的值,并探索影响一个变量的因素。
同时,Excel 还提供了其他函数和工具,可以帮助进行相关性和回归分析。
回归分析在各个领域都有广泛的应用,为我们的研究和决策提供了有力的支持。
数据分析技巧Excel中的回归分析和相关性计算

数据分析技巧Excel中的回归分析和相关性计算在Excel中,回归分析和相关性计算是数据分析中常用的技巧。
通过这些分析方法,我们可以了解变量之间的关系,以及预测和解释数据的趋势。
本文将介绍Excel中回归分析和相关性计算的基本原理和操作方法。
一、回归分析回归分析是用于研究因变量和一个或多个自变量之间关系的方法。
在Excel中,我们可以使用“数据分析”功能来进行回归分析。
下面以一个示例来说明回归分析的具体步骤。
假设我们想研究一个人的身高与体重之间的关系。
首先,将收集到的身高和体重数据录入Excel表格中,如下所示:身高(cm)体重(kg)160 50165 55170 60175 65180 70接下来,在Excel的菜单栏中选择“数据”→“数据分析”→“回归”功能。
然后,选择“输入Y范围”为体重数据,选择“输入X范围”为身高数据。
点击“确定”,Excel会生成回归分析的结果。
回归分析的结果包括了斜率、截距、相关系数等信息。
通过这些信息,我们可以得出一个回归方程,用于预测体重。
例如,回归方程可能是:体重 = 0.5 ×身高 + 25。
通过回归分析,我们可以得到身高与体重之间的关系,并进行相关的预测和解释。
二、相关性计算相关性是用来描述两个变量之间关系的统计指标。
在Excel中,我们可以使用相关性函数来计算两个变量之间的相关系数。
下面以一个示例来说明相关性计算的具体操作。
假设我们有两列数据,分别是销售额和广告费用。
我们想知道这两个变量之间是否存在相关关系。
首先,在Excel表格中录入这两列数据,如下所示:销售额(万元)广告费用(万元)10 212 315 518 620 8然后,在Excel的一个空白单元格中输入“=CORREL(A2:A6, B2:B6)”并按下回车键,Excel会自动计算出这两个变量的相关系数。
相关系数的取值范围在-1到1之间。
相关系数为正值表示正相关,即当一个变量增加时,另一个变量也随之增加;相关系数为负值表示负相关,即当一个变量增加时,另一个变量会减少;相关系数为0表示没有线性关系。
实验二用EXCEL进行相关与回归分析

实验二用EXCEL进行相关与回归分析实验目的:用EXCEL进行相关与回归分析实验内容:1、相关分析2、回归分析实验步骤:采用下面的例子进行相关和回归分析。
学生身高(公分)体重(公斤)1 2 3 4 5 6 7 8 9 10 171167177154169175163152172160535664495566524758501. 用EXCEL进行相关分析首先把有关数据输入EXCEL的单元格中,如图1-20所示。
用EXCEL进行相关分析有散点图、计算相关系数,另一种是利用相关分析宏。
图1-20 EXCEL数据集(1)作散点图(2)利用函数计算相关系数在EXCEL中,提供了两个计算两个变量之间相关系数的方法,CORREL函数和PERSON函数,这两个函数是等价的,这里介绍用CORREL函数计算相关系数:第一步:单击任一个空白单元格,单击插入菜单,选择函数选项,打开粘贴函数对话框,在函数分类中选择统计,在函数名中选择CORREL,单击确定后,出现CORREL对话框。
第二步:在array1中输入B2:B11,在array2中输入C2:C11,即可在对话框下方显示出计算结果为,如图1-21所示。
图1-21 CORREL对话框及输入结果(3)用相关系数宏计算相关系数第一步:单击工具菜单,选择数据分析选项,在数据分析选项中选择相关系数,弹出相关系数对话框,如图1-22所示:图1-22 相关系数对话框第二步:在输入区域输入$B$1:$C$1,分组方式选择逐列,选择标志位于第一行,在输出区域中输入$E$1,单击确定,得输出结果如图1-23所示。
图1-23 相关分析输出结果在上面的输出结果中,身高和体重的自相关系数均为1,身高和体重的相关系数为,和用函数计算的结果完全相同。
2. 用EXCEL进行回归分析EXCEL进行回归分析同样分函数和回归分析宏两种形式,其提供了9个函数用于建立回归模型和预测。
这9个函数分别是:INTERCEPT 返回线性回归模型的截距SLOPE 返回线性回归模型的斜率RSQ 返回线性回归模型的判定系数FORECAST 返回一元线性回归模型的预测值STEYX 计算估计的标准误TREND 计算线性回归线的趋势值GROWTH 返回指数曲线的趋势值LINEST 返回线性回归模型的参数LOGEST 返回指数曲线模型的参数用函数进行回归分析比较麻烦,我们这里介绍使用回归分析宏进行回归分析。
EXCEL在描述统计相关系数与回归分析中的应用

EXCEL在描述统计相关系数与回归分析中的应用EXCEL是一款功能强大的电子表格软件,可用于各种数据分析和统计应用。
在描述统计相关系数和回归分析中,EXCEL提供了各种函数和工具,使其成为一种理想的分析工具。
在接下来的文章中,我们将讨论EXCEL在描述统计相关系数和回归分析中的应用。
一、描述统计相关系数相关系数是一种度量变量之间关系强度和方向的指标。
它用于确定两个变量是否相关以及相关性的程度。
EXCEL提供了一些函数来计算描述统计相关系数,包括PEARSON、CORREL和COVAR函数。
1. PEARSON函数:该函数用于计算两个变量之间的Pearson相关系数。
它采用多组数值作为输入,并返回-1到1之间的结果。
-1表示完全负相关,1表示完全正相关,0表示没有相关性。
PEARSON函数的语法如下:=PEARSON(array1,array2)array1和array2是包含数值数据的数组范围。
例如,要计算A列和B列之间的Pearson相关系数,可以使用以下公式:=PEARSON(A1:A10,B1:B10)2.CORREL函数:该函数也用于计算两个变量之间的相关系数,但它可以一次计算多个变量之间的相关系数。
CORREL函数的语法如下:=CORREL(array1,array2)array1和array2是包含数值数据的数组范围。
例如,要计算A列到C列之间的相关系数,可以使用以下公式:=CORREL(A1:A10,C1:C10)3.COVAR函数:该函数用于计算两个变量之间的协方差。
协方差衡量两个变量之间的总体相关性,不考虑它们的单位。
COVAR函数的语法如下:=COVAR(array1,array2)array1和array2是包含数值数据的数组范围。
例如,要计算A列和B列之间的协方差,可以使用以下公式:=COVAR(A1:A10,B1:B10)二、回归分析回归分析是一种统计技术,用于探索自变量(输入变量)和因变量(输出变量)之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告用EXCEL进行相关与回归分析
一、实验介绍
本实验通过用Excel进行相关和回归分析,以探讨两个变量之间的关系。
二、实验步骤
(1)首先,在Excel中收集数据,并将这些数据编入表格,表格中
的每一列分别表示变量,每一行表示一组观测数据;
(2)进行相关分析,首先,需要在Excel中计算出两个变量之间的
相关系数,然后判断相关系数的绝对值,确定变量之间的相关关系;
(3)接着,进行回归分析,在回归分析中,可以使用线性回归、非
线性回归等方法,用Excel中的函数计算出回归方程,以及回归系数r2,表示变量之间的回归关系;
(4)最后,根据实验结果,利用Excel拟合数据,画出变量之间的
拟合曲线,作出实验结果的图解;
三、实验结果
本次实验使用的数据集是一组实验观测数据,观测数据为抽样数据,
表示其中一种物品同时装入不同重量时的质量损失情况,两个变量分别为
物品的重量和质量损失。
在相关分析中,使用Excel函数计算出来的两个变量之间的相关系数为:0.837、根据结果可以判断,两个变量之间有较强的相关性。
而在回归分析中,使用Excel函数计算出来的线性回归方程为:
y=0.36x-1.27,回归系数r2为:0.701、由此可以看出,两个变量之间有较强的回归关系。
