地图投影及其坐标转换公式(OGP测量和定位指导书7-2坐标转换与变换公式第1部分)
地图投影和坐标转换

实验一地图投影和坐标转换实验目的:将扫描的地图从图形坐标转换到现实世界坐标(投影坐标)下,从而能够与GIS 数据库集成,可以用于矢量化,也可以作为矢量数据的背景。
实验准备:将实验数据拷贝到本地计算机上自己的工作文件夹中。
(路径和文件名字最好不要包括汉字、空格和特殊符号)阅读地图●启动ArcMap●将提供的扫描地图添加到地图上,注意查看系统的提示内容。
●放大地图浏览,查看经纬格网、标注的经纬度,检查地图的坐标。
●在地图上确定将采用的控制点。
处理控制点坐标●打开Excel,●记录下控制点的编号和经纬度坐标●可以利用公式将经纬度从度分秒转换为小数度数。
如假设b2单元格中存储的是117-20-20通过公式:=VALUE(LEFT(B2,3))+V ALUE(MID(B2,5,2))/60+V ALUE(RIGHT(B2,2))/3600计算出其为117.33889度。
●选择计算出的小数度数列,复制,然后在空列上进行选择性粘贴,指定只粘贴数值。
●除了最后粘贴的两列经纬度数和编号列外,删除其它的列。
●右键点击经度列,选择设置单元格格式。
将格式指定为数值,小数点5位。
同样设置纬度列的格式。
●将结果另存为dbase表格文件,保存到你的工作空间下。
●关闭Excel。
重新打开建立的DBF文件,查看数据是否正确(很多时候由于操作不当会导致另存为DBF文件丢失数据)。
将控制点添加到地图上●在ArcMap中,从Tools菜单下选择Add XY Data。
●在打开的对话框中指定使用你刚建立好的控制点坐标DBF文件。
●指定X字段为经度,Y字段为纬度。
●点下面的Edit按钮,打开空间参照属性对话窗口。
●点Select按钮选择坐标系统。
●浏览到地理坐标系统下的亚洲下的北京1954投影坐标。
Add添加坐标系统。
●在空间参照属性窗口中确定所选择的坐标系统,关闭对话窗口。
●在Add XY Data对话框中点OK确定添加数据。
可以看到,地图上添加了一个点事件(Event)图层。
地理坐标系转换公式

基(Molodenski)提出了相应三参数的直接转换方法。方法假定原坐标系与新坐标系的坐标 轴相互平行,正如前面已提到的,该假设不一定成立,由此得到的转换结果只能达到中等精 度,对范围大的区域尤其如此。 赫尔默特(Helmert)7 参数转换法提高了转换精度。由于三个旋转参数有两种相反的符 号协定,EPSG(欧洲石油勘探组织)将其分为两种不同的转换方法,其一称位置矢量法, 另一称坐标框架法,其中位置矢量法也称布尔莎-沃尔夫(Bursa-Wolf)转换法。赫尔默特方 法的关键在于转换参数的符号要与遵循的约定一致。 鉴于赫尔默特方法的平移和旋转参数之 间具有很强的相关性,有碍于实际应用,莫洛金斯基-巴德克斯(Molodenski-Badekas )提出 了改进的赫尔默特 7 参数转换法,避免了上述相关性问题。 根据研究区内一系列已知点的大地坐标或网格坐标改正量进行插值, 也是一种坐标系转 换方法。北美 1927 基准面(基于 Clarke 1966 椭球体)与北美 1983 基准面(基于 GRS 1980 椭球体)之间的坐标系转换就是其中一例。北美测量控制网是用传统大地测量方法建立的, 由于早期的仪器精度不足、网平差不完善等因素,基于 Clarke 1966 椭球体、并且只有一个 基准点(位于堪萨斯州 Meades Ranch)的老坐标网精度低、且误差分布不均匀;新坐标网 采用了卫星技术、 现代先进的测量仪器和电子计算机技术, 其精确度与可靠性完全能得到保 障。由此造成北美大陆网内,不同地区、甚至不同位置点的转换参数都有可能不一致,所以 如仅采用莫洛金斯基( Molodenski)和赫尔默特( Helmert)方法对付上述新、旧坐标系的 转换显然不合适,为此需要用到 EPSG(欧洲石油勘探组织)所谓的“双线性插值”转换技 术。到北美 NAD83 的坐标转换就是通过格网双线性插值实现的,其中采用了美国海岸带与 大地测绘局(US Coast & Geodetic Survey)的 NADCON 控制点网。注:美国以西经为正, 而 EPSG 文献中 NAD27 与 NAD83 坐标系的设定均以东经为正;加拿大的网格文件格式也 被澳大利亚与新西兰采用;英国采用北向与东向的双线性网格插值。 此外,经纬度多项式也可以用于坐标系转换,挪威在海岸带调查中,就采用这种方法进 行新(ED87— 欧洲 1987 基准面) 、旧(ED50— 欧洲 1950 基准面)坐标系之间的转换。挪 威地调局 Statens Kartwerk 发表的文献中列出了包含 15 个系数的经纬度 4 次多项式展开公 式。 上述格网插值及多项式拟合方法更适合于早期基准面与新建基准面之间的坐标值转换。 坐标系转换时,选择正确的转换参数符号非常重要,转换前应该明确转换的“从 (From) ”……“到(To) ” ……,避免符号混淆。
坐标转换公式说明
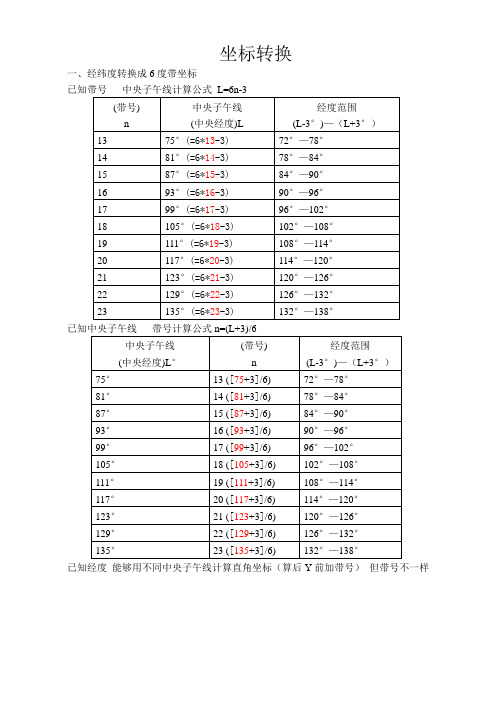
坐标转换一、经纬度转换成6度带坐标已知经度能够用不同中央子午线计算直角坐标(算后Y前加带号)但带号不一样二、经纬度转换3度带坐标已知经度能够用不同中央子午线计算直角坐标(算后Y前加带号)但带号不一样Mapgis坐标转换一、经纬度转换6度带坐标例:一、东经114°30′21″,北纬35°52′08″二、东经114°40′30″,北纬35°50′30″3、东经115°00′25″,北纬36°43′28″二、东经115°10′30″,北纬36°44′28″步骤:1从开始里找到程序,附件,打开“记事本”1143021,3552081144030,3550301150025,3643281151030,364428保留,保留文件为2打开Mapgis,有效效劳中的投影变换,按投影变换,查找用户文件投影转换,按“打开文件”,把文件1装入;3按“用户投影参数”,坐标系类型改成“地理坐标系”,椭球参数改成“北京54”,坐标单位设置“”,按“确信”;4按“结果投影参数”,坐标系类型改成“投影平面直角”,椭球参数改成“北京54”,坐标单位设置“米”,投影带类型设定为“6度带”,投影带序号设定为20((117+3)/6),(可通过坐标转换进行计算),按“确信”;5写到文件,保留文件为。
二、经纬度转换3度带坐标例:一、东经114°30′21″,北纬35°52′08″二、东经114°40′30″,北纬35°50′30″3、东经115°00′25″,北纬36°43′28″二、东经115°10′30″,北纬36°44′28″步骤:1从开始里找到程序,附件,打开“记事本”1143021,3552081144030,3550301150025,3643281151030,364428保留,保留文件为2打开Mapgis,有效效劳中的投影变换,按投影变换,查找用户文件投影转换,按“打开文件”,把文件A装入;3按“用户投影参数”,坐标系类型改成“地理坐标系”,椭球参数改成“北京54”,坐标单位设置“”,按“确信”;4按“结果投影参数”,坐标系类型改成“投影平面直角”,椭球参数改成“北京54”,坐标单位设置“米”,投影带类型设定为“3度带”,投影带序号设定为38,(可通过坐标转换进行计算)n=L/3,按“确信”;(也可投影带序号设定为39)5写到文件,保留文件为三、6度带坐标转换纬度例:一、Y=,X=3661532二、Y=,X=36618793、Y=,X=36618794、Y=,X=3661532步骤:1从开始里找到程序,附件,打开记事本(纯文本文件)输入260785,3661532270000,3661879260785,3661879270000,3661532保留,保留文件为1112打开Mapgis,有效效劳中的投影变换,按投影变换,查找用户文件投影转换,按“打开文件”,把文件111装入;3按“用户投影参数”,坐标系类型改成“投影平面直角坐标系”,椭球参数改成“北京54”,坐标单位设置“米”,投影带类型设定为“6度带”,投影带序号设定为20),(可通过坐标转换进行计算),4按“结果投影参数”,坐标系类型改成“地理坐标系”,椭球参数改成“北京54”,坐标单位设置“”;5写到文件,保留文件为;四、3度带坐标转换纬度例:一、Y=,X=3661532二、Y=,X=36618793、Y=,X=36618794、Y=,X=3661532步骤:1从开始里找到程序,附件,打开记事本(纯文本文件)输入260785,3661532270000,3661879260785,3661879270000,3661532保留,保留文件为aaa2打开Mapgis,有效效劳中的投影变换,按投影变换,查找用户文件投影转换,按“打开文件”,把文件aaa装入;3按“用户投影参数”,坐标系类型改成“投影平面直角坐标系”,椭球参数改成“北京54”,坐标单位设置“米”,投影带类型设定为“3度带”,投影带序号设定为38,(可通过坐标转换进行计算),4按“结果投影参数”,坐标系类型改成“地理坐标系”,椭球参数改成“北京54”,坐标单位设置“”;5写到文件,保留文件为;。
投影变换与坐标变换.

投影变换与坐标变换1 地理坐标系地理坐标系(GCS) 使用三维球面来定义地球上的位置。
GCS 往往被误称为基准面,而基准面仅是GCS 的一部分。
GCS 包括角度测量单位、本初子午线和基准面(基于旋转椭球体)。
可通过其经度和纬度值对点进行引用。
经度和纬度是从地心到地球表面上某点的测量角。
通常以度或百分度为单位来测量该角度。
下图将地球显示为具有经度和纬度值的地球。
在球面系统中,水平线(或东西线)是等纬度线或纬线。
垂直线(或南北线)是等经度线或经线。
这些线包络着地球,构成了一个称为经纬网的格网化网络。
位于两极点中间的纬线称为赤道。
它定义的是零纬度线。
零经度线称为本初子午线。
对于绝大多数地理坐标系,本初子午线是指通过英国格林尼治的经线。
其他国家/地区使用通过伯尔尼、波哥大和巴黎的经线作为本初子午线。
经纬网的原点(0,0) 定义在赤道和本初子午线的交点处。
这样,地球就被分为了四个地理象限,它们均基于与原点所成的罗盘方位角。
南和北分别位于赤道的下方和上方,而西和东分别位于本初子午线的左侧和右侧。
通常,经度和纬度值以十进制度为单位或以度、分和秒(DMS) 为单位进行测量。
维度值相对于赤道进行测量,其范围是-90°(南极点)到+90°(北极点)。
经度值相对于本初子午线进行测量。
其范围是-180°(向西行进时)到180°(向东行进时)。
如果本初子午线是格林尼治子午线,则对于位于赤道南部和格林尼治东部的澳大利亚,其经度为正值,纬度为负值。
用 X 表示经度值并用 Y 表示纬度值可能会有帮助。
这样,显示在地理坐标系上定义的数据就如同度是线性测量单位一样。
此方法与普通圆柱投影基本相同。
地理坐标系表面的形状和大小由球体或旋转椭球体定义。
尽管地球最适合用旋转椭球体表示,但有时将地球视作球体可使数学计算更为简便。
对于小比例尺地图(小于 1:5,000,000)来说,可以将地球假设为球体。
投影坐标转换

摘自武测毕业论文(赖增先)——我也是从网上弄来,转载时请务必保留此此信息。
第二节 平面坐标基准转换由于海上和陆地上在测量时,使用不同的坐标系和不同参考椭球,而且采用的投影也不同,使得我们获得的数据不统一,必须进行坐标转换。
§3·2·1 欧拉角设有两个空间直角坐标系,分别为O-XYZ 和O-X 'Y 'Z ',为了便于讨论其相应坐标轴间的变换,设其原点相同如图所示,选择εx 、y ε、z ε为欧拉角,又称旋转参数,经过三次旋转,使两个坐标系重合,既:(图见下页A )首先,绕O Z '轴,将O X '轴旋转到OX 0轴,所转的角为z ε;其次,绕OY 0轴,将O Z '轴旋转到OZ 0轴,所转的角为y ε;最后,绕OX 轴,将O Z 0轴旋转到OZ 轴,所转的角为εx ;ZZ 0 Z 'X ' OX 0X Y 0 YY '图A因此有X X 'Y = R 1(εx )R 2(y ε)R 3(z ε) Y 'Z Z '式中 R 1(εx )、R 2(y ε)、R 3(z ε)为旋转矩阵,其表达式在ε、y ε、z ε很小时可以最终表示为:X 1 z ε y ε X 'Y = -z ε 1 εx Y ' 公式1Z y ε - εx 1 Z '§3·2·2 不同三维空间直角坐标系的变换模型GPS 测量的WGS —84属地心坐标系,而1980年国家大地坐标系和1954年北京坐标系属参心坐标系,他们所对应得空间直角坐标系是不同的,这里将讨论不同空间直角坐标系的变换模型。
如图B 两个空间直角坐标系分别为O-XYZ 和O '-X 'Y 'Z ',其坐标系原点不同则存在三个平移参数∆X 0、∆Y 0、∆Z 0,他们表示O '- X 'Y 'Z '坐标系原点O '相对于O-XYZ 坐标系原点O 在三个坐标轴上的分量;又当各坐标轴相互不平行时,既存在三个旋转参数εx 、Y 'X X ' 1 z ε y ε X 'Y =(1+m ) Y ' -z ε 1 εx Y ' Z Z ' y ε - εx 1 Z '∆X 0+ ∆Y 0 公式一∆Z 0式中共有七个变换参数∆X 0、∆Y 0、∆Z 0、εx 、y ε、z ε、m,简称此公式为布尔莎七参数变换公式,是坐标变换中一个非常重要的公式。
常用地图投影转换公式

常用地图投影转换公式作者:青岛海洋地质研究所戴勤奋 投影计算公式往往表达方式不止一种,有时很难分辨谁对谁错,我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”(1:100万地形图规范中称作正轴等角圆锥投影,GB/T 14512-93)的正反转换公式列出,因为我基本能保证这些公式的正确性。
1.约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度,L -- 经度,单位弧度(RAD)-- 纵直角坐标,-- 横直角坐标,单位米(M)2.椭球体参数我国常用的3个椭球体参数如下(源自“全球定位系统测量规范 GB/T界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。
3.墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定, 假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
常用地图投影及转换公式
常用地图投影及转换公式中文名称:地图投影英文名称:Map Projection 定义1:按照一定的数学法则,把参考椭球面上的点、线投影到可展面上的方法。
所属学科:测绘学(一级学科);测绘学总类(二级学科) 定义2:根据一定的数学法则,将地球表面上的经纬线网相应地转绘成平面上经纬线网的方法。
所属学科:大气科学(一级学科);动力气象学(二级学科) 定义3:运用一定的数学法则,将地球椭球面的经纬线网相应地投影到平面上的方法。
即将椭球面上各点的地球坐标变换为平面相应点的直角坐标的方法。
所属学科:地理学(一级学科);地图学(二级学科)常用地图投影及转换公式1(约定椭球体参数a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e′ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度,L -- 经度,单位弧度(rad)-- 纵直角坐标, -- 横直角坐标,单位米(m)我国常用的3个椭球体参数如下(源自“全球定位系统测量规范 GB/T 18314-2001”):椭球体长半轴a(米) 短半轴b(米) Krassovsky(北京54采用) 6378245 6356863.0188 IAG 75(西安80采用) 6378140 6356755.2882WGS 84 6378137 6356752.31422(墨卡托(Mercator)投影2.1墨卡托投影简介墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512,1594)在1569年拟定, 假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
坐标系转换步骤以及公式
一、各坐标系下椭球参数WGS84大地参数北京54大地参数西安80大地参数参考椭球体:WGS 84 长半轴:6378137短半轴:6356752.3142 扁率:1/298.257224 参考椭球体:Krasovsky_1940长半轴:6378245短半轴:6356863.0188扁率:1/298.3参考椭球体:IAG 75长半轴:6378140短半轴:6356755.2882扁率:1/298.257000二、WGS84转北京54一般步骤(转80一样,只是椭球参数不同)前期工作:收集测区高等级控制点资料。
在应用手持GPS接收机观测的区域内找出三个以上分布均匀的等级点(精度越高越好)或GPS“B”级网网点,点位最好是周围无电磁波干扰,视野开阔,卫星信号强。
并到测绘管理部门抄取这些点的54北京坐标系的高斯平面直角坐标(x、y),大地经纬度(B、L),高程h ,高程异常值ξ和WGS-84坐标系的大地经纬度(B、L),大地高H。
如果没有收集到WGS-84下的大地坐标,则直接用手持GPS测定已知点B、L、H值。
转换步骤:1、把从GPS中接收到84坐标系下的大地坐标(经纬度高程B、L, H,其中B为纬度,L为经度,H为高程),使用84坐标系的椭球参数转换为84坐标系下的地心直角坐标(空间坐标):式中,N为法线长度,为椭球长半径,b为椭球短半径,为第一偏心率。
2、使用七参数转换为54坐标系下的地心直角坐标(x,y,z):x = △x + k*X- β*Z+ γ*Y+ Xy = △y + k*Y + α*Z - γ*X + Yz = △z + k*Z - α*Y + β*X + Z其中,△x,△y,△z为三个坐标方向的平移参数;α,β,γ为三个方向的旋转角参数;k为尺度参数。
(采用收集到的控制点计算转换参数,并需要验证参数)在小范围内可使用七参数的特殊形式即三参数,即k、α、β、γ都等于0,变成:x = △x+ Xy = △y+ Yz = △z + Z3、根据54下的椭球参数,将第二步得到的地心坐标转换为大地坐标(B54,L54,H54)计算B时要采用迭代,推荐迭代算法为:4、根据工程需要以及各种投影(如高斯克吕格)规则进行投影得到对应的投影坐标,即平面直角坐标。
测量坐标换算公式是什么
测量坐标换算公式是什么我们常常在测量工作中需要处理不同坐标系之间的换算。
当我们需要将一个点的坐标从一个坐标系转换到另一个坐标系时,我们需要使用坐标换算公式。
什么是坐标换算公式?坐标换算公式是一种用于在不同坐标系之间进行转换的数学表达式或方法。
它可以通过一系列的计算步骤将一个点的坐标从一个坐标系转换到另一个坐标系,使我们能够在不同的坐标系中进行准确的测量与定位。
常见的坐标系在测量工作中,常见的坐标系包括直角坐标系(笛卡尔坐标系)、极坐标系、大地坐标系等。
每种坐标系有自己特定的表示方法和坐标轴方向。
•直角坐标系(笛卡尔坐标系):通过横纵坐标轴来表示点的位置,如(x, y)。
•极坐标系:通过一个极径和一个极角来表示点的位置,如(r, θ)。
•大地坐标系:用于表示地球上的位置,通常使用经度和纬度来标定点的位置。
测量坐标换算的方法垂直坐标系之间的换算当我们需要将点的坐标从一种垂直坐标系转换到另一种垂直坐标系时,我们可以使用以下公式进行换算:H2 = H1 + ΔH其中:•H1 是点在第一个垂直坐标系下的高程值。
•ΔH 是两个垂直坐标系之间的高程差(可以是正值或负值)。
•H2 是点在第二个垂直坐标系下的高程值。
平面坐标系之间的换算当我们需要将点的坐标从一种平面坐标系转换到另一种平面坐标系时,我们可以使用以下公式进行换算:X2 = X1 + ΔXY2 = Y1 + ΔY其中:•X1 和 Y1 是点在第一个平面坐标系下的水平坐标值。
•ΔX 和ΔY 是两个平面坐标系之间的水平坐标差(可以是正值或负值)。
•X2 和 Y2 是点在第二个平面坐标系下的水平坐标值。
不同坐标系之间的换算当我们需要在不同的坐标系之间换算点的坐标时,需要先从垂直坐标系换算到平面坐标系,然后再进行平面坐标系之间的换算。
整体换算公式如下:X2 = X1 + ΔXY2 = Y1 + ΔYH2 = H1 + ΔH结论测量坐标换算公式是进行不同坐标系之间转换的重要工具。
(支撑2015.5.18)地图投影及其坐标转换公式
地图投影及其坐标转换公式
坐标转换与变换公式.
第1部分地图投影及其坐标转换公式
译文分两部分,郊l部分:地图投影及其坐标转抉公式,描述地图投影方法及计算公式;第2部分;非地图投影坐标运算公式,主要涉及大地基准面的变换,这里的基准面不单是水平坐标的基准面,还包括垂向的高程基准。
第2部分的2004年我曾在5年前译过,译文名为“坐标系转换公式”,现在再拿出来看发现里而有不少翻译不当的地方,因此这次基本上是重新译了一遍。
·定义坐标参照系(aiS),保正坐标瞄叫确表达其地理位置。
·定义坐标的转挟和变挟方法,使坐标能从一个cRs转换到另一个cRS,这里将坐标转
转换和坐标变换通称为坐标运算。
一个坐标系指定了坐标与点之间的数学关系,它包括对坐标轴、坐标单位以及坐标轴几何关系的定义.坐标系本来与地球无关,而坐标参照系(CRS)通过基准面建立了坐标系与地球之间的关联,习惯上所称谓的坐标系其实就是指坐标参照系。
利用坐标运算方法,坐标可以从一个参照系转换到另—个参照系。
坐标运算方妆可分为两类:
· 坐标转换:不涉及基准面变换,参数是既定定的,因此不受外部误差影响.
· 坐标变换:涉及基准面变换,变换参数由经验方法确定,因此受测量误差影响.投影坐标参照系是地理坐标参照系2的地图投影结果。
地图投影是一个坐标转换过程.每—种投影方法均有其特定的公式和参数。
2译者注:地理坐标参照系,是我们通常称谓的大地坐标系,球面坐标,坐标值用经纬度和大地高表示,当点在参考椭球面上时就成为常用时二维经纬度地理坐标了.
第1部分介到地图投影方法,其它的坐标转换和变换方法将在第二部分给出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
国际油气生产者协会测量和定位指导书7-2坐标转换与变换公式第1部分 地图投影及其坐标转换公式 2009年5月修订戴勤奋译2009年6月译者语本文译自国际油气生产者协会测量和定位指导书7-2的2009年5月 版(OGP Surveying and Positioning Guidance Note number 7, part 2 – May 2009),原文名“Coordinate Conversions and Transformations including Formulas”(坐标转换与变换公式)。
译文分两部分,第1部分:地图投影及其坐标转换公式(Map projections and their coordinate conversion formulas),描述地图投影方法及计算公式;第2部分:非地图投影坐标运算公式(Formulas for Coordinate Operations other than Map Projections),主要涉及大地基准面的变换,这里的基准面不单是水平坐标的基准面,还包括垂向的高程基准。
第2部分的2004年1月版我曾在5年前译过,译文名为“坐标系转换公式”,现在再拿出来看发现里面有不少翻译不当的地方,因此这次基本上是重新译了一遍。
接受以前的经验教训,这次译得比较认真,努力向信、达、雅靠拢,运算公式也反复校对,尽量避免错误,但是错误肯定在所难免,因此在正式场合采用文中的公式时请慎重核实它们的正确性。
本文献最初在1993年由国际石油技术软件开放公司(POSC)发布,1998年又由国际油气生产者协会(OGP)欧洲石油勘探组(EPSG)作为EPSG大地测量参数数据集(简称EPSG数据集)坐标运算方法的用户说明书发布。
文献中收录的坐标转换与变换方法都是目前常用的、或早期的方法现在仍可能遇到的。
文献中的公式主要源自斯奈德(John P. Snyder)编写、美国地质调查局(U.S.Geological Survey)1987年出版的《地图投影-工作手册》(Map Projection -A Working Manual),EPSG对其中的公式作了适当调整和更新,以适应全球范围的应用。
此外,EPSG也在文献中补充了其它的投影方法,以适应计算机及遥感技术的发展。
总之,原文献可以说是一本结合当前生产需要的、系统的坐标转换与变换实用手册。
原文献自发布以来一直处于不断的修订中,有些投影公式经多次修改才确定,有些仍处于修订状态,因此在使用本文档时请注意查看最新版本的相关内容。
前几年我曾经写过有关投影公式的文章,因此经常收到相关问题的Email,有的Email来自在国外承包测量工程的技术人员,但其实我在这方面的知识非常有限,我在工作中可能用到的坐标转换与变换方法也屈指可数,因此趁最近有空将本文献翻译出来,对我自己来说是一个很好的学习机会,同时也希望对大家有用。
戴勤奋2009年7月21日目 录 序 (1)修订记录 (3)1 地图投影及其坐标转换公式 (6)1.1 前言 (6)1.2 地图投影参数 (7)1.3 地图投影公式 (17)1.3.1 兰勃特等角圆锥投影 (18)1.3.1.1 兰勃特等角圆锥投影(双标准纬线) (18)1.3.1.2 兰勃特等角圆锥投影(单标准纬线) (20)1.3.1.3 兰勃特等角圆锥投影(西部专用) (21)1.3.1.4 兰勃特等角圆锥投影(比利时双标准纬线) (22)1.3.1.5 兰勃特似等角圆锥投影 (23)1.3.2 Krovak斜轴等角圆锥投影 (26)1.3.3 墨卡托投影 (29)1.3.3.1 墨卡托投影(球面) (32)1.3.3.2 公共可视化伪墨卡托投影 (33)1.3.4 卡西尼-索尔特奈投影 (35)1.3.4.1 双曲线卡西尼-索尔特奈投影 (37)1.3.5 横轴墨卡托投影 (39)1.3.5.1 常规横轴墨卡托投影 (39)1.3.5.2 横轴墨卡托分带网格坐标系 (42)1.3.5.3 横轴墨卡托投影(南部专用) (43)1.3.6 斜轴墨卡托投影和洪特尼斜轴墨卡托投影 (43)1.3.6.1 马达加斯加拉波德投影 (49)1.3.7 球面投影 (53)1.3.7.1 斜轴球面投影和赤道球面投影 (53)1.3.7.2 极地球面投影 (56)1.3.8 新西兰地图网格 (64)1.3.9 突尼斯采矿网格 (64)1.3.10 美国多圆锥投影 (65)1.3.11 兰勃特方位等面积投影 (67)1.3.11.1 兰勃特方位等面积投影(球面) (70)1.3.12 兰勃特圆柱等面积投影 (70)1.3.12.1 兰勃特圆柱等面积投影(球面) (70)1.3.13 阿尔勃斯等面积投影 (71)1.3.14 等距圆柱投影 (72)1.3.14.1 等距圆柱投影(球面) (75)1.3.14.2 伪平板卡尔瑞投影 (75)1.3.15 彭纳投影 (76)1.3.15.1 彭纳投影(南部专用) (77)1.3.16 方位等距投影 (77)1.3.16.1 改进的方位等距投影 (77)1.3.16.2 关岛投影 (79)1.3.17 透视投影 (82)1.3.17.1 引言 (82)1.3.17.2 垂直透视投影 (83)1.3.17.3 正射垂直透视投影 (84)1.3.18 正射投影 (86)序EPSG(欧洲石油勘探组)大地测量参数数据集(简称EPSG数据集)是一个参数库,用于:∙定义坐标参照系(CRS),保证坐标能明确表达其地理位置。
∙定义坐标的转换和变换方法,使坐标能从一个CRS转换到另一个CRS,这里将坐标转换和坐标变换通称为坐标运算。
EPSG数据集遵循ISO 19111标准(Spatial referencing by coordinates,基于坐标的空间参考),由OGP(国际油气生产者协会)测量和定位委员会大地测量分会维护。
数据集以三种途径分发:∙EPSG注册点,全称为EPSG大地测量参数注册点(EPSG Geodetic Parameter Registry), 一个基于web的分发平台,数据按ISO 19136中的CRS实体定义,用GML框架描述1。
∙EPSG数据库,全称为EPSG大地测量参数数据库(EPSG Geodetic Parameter Database), 一个关系数据库结构,其中的CRS模块实体和坐标运算实体分置在不同的表中,通过微软的Access数据库分发。
∙SQL脚本描述的关系数据库模型,用户可以利用该模型在Oracle、MySQL、PostgreSQL 等关系数据库中创建数据库,然后在数据库中装载EPSG数据集。
OGP测量与定位指导书7由多个EPSG数据集用户文档组成:∙文档7-0,快速入门(Quick Start Guide),是数据集及其用途的总览。
∙文档7-1,数据集使用(Using the Dataset),对数据集的内容、维护和使用方法作了 详尽的描述。
∙文档7-2,即本文档,公式(Formulas),针对EPSG数据集所支持的坐标运算方法, 提供了实现坐标转换和变换的计算公式,数据集中的大地测量参数是与这些公式相匹配的。
∙文档7-3,注册开发者指南(Registry Developer Guide),意在协助计算机应用开发人 员使用注册API,从数据集中查询并提取相关实体及属性。
∙文档7-4,数据库开发者指南(Database Developer Guide),意在协助计算机应用开发 人员使用数据库或关系数据库模型,从数据集中查询并提取相关实体及属性。
上述完整文档可在/guides/docs/G7.html上查找,数据集的使用条款可查看/CurrentDB.html。
除了上述文档外,注册点的用户注册界面挂接了在线帮助,数据库用户界面挂接了上下文关联敏感帮助信息,点击鼠标左键即可获取。
编写文档7-2是为了协助计算机应用开发人员有效地利用EPSG数据集所支持的坐标运算方法,也可供作其它参考。
1译者注:ISO 19136 标准名为地理标记语言(Geography Markup Language,简称GML),GML描述文件是按标准GML Schema框架描述的XML文件。
一个坐标系指定了坐标与点之间的数学关系,它包括对坐标轴、坐标单位以及坐标轴几何关系的定义。
坐标系本来与地球无关,而坐标参照系(CRS)通过基准面建立了坐标系与地球之间的关联,习惯上所称谓的坐标系其实就是指坐标参照系。
利用坐标运算方法,坐标可以从一个参照系转换到另一个参照系。
坐标运算方法可分为两类:∙坐标转换(conversion):不涉及基准面变换,参数是既定的,因此不受外部误差影响。
∙坐标变换(transformation):涉及基准面变换,变换参数由经验方法确定,因此受测量误差影响。
投影坐标参照系是地理坐标参照系2的地图投影结果。
地图投影是一个坐标转换过程,每一种投影方法均有其特定的公式和参数。
OGP测量和定位指导书7-2将在第1部分介绍地图投影方法,其它的坐标转换和变换方法将在第2部分给出。
2 译者注:地理坐标参照系即“geographic coordinate reference system”的直译,是我们通常称谓的大地坐标系,球面坐标,坐标值用经纬度和大地高表示,当点在参考椭球面上时就成为常用的二维经纬度地理坐标了。
修订记录版本日期修改内容1 1993-11第1 版,作为 POSC文献( POSC Epicentre 3)发布10 1998-05作为EPSG指导书另行发布11 1998-11添加西班牙多项式变换和突尼斯采矿网格投影方法12 1999-02修改简化莫洛金斯基公式13 1999-07添加兰勃特似等角圆锥投影和美国多圆锥投影方法14 1999-11修改球面投影公式和突尼斯采矿网格公式;添加Krovak投影方法15 2000-06添加一般多项式变换和仿射变换方法16 2000-11修改兰勃特等角圆锥投影(比利时)描述部分内容;补充斜轴墨卡托投影内容,添加斜轴墨卡托投影公式;修改相似变换可逆性部分内容17 2001-06修改兰勃特等角圆锥投影公式、墨卡托投影公式和赫尔默特变换公式18 2002-08纳入ISO 19111 术语;修订章节号;添加序;添加兰勃特等角(西部专用)、兰勃特方位等面积、阿尔勃斯、等距圆柱(平板卡尔瑞)、分带横轴墨卡托、彭纳投影,以及莫洛金斯基-巴德卡斯变换方法;修改横轴墨卡托(南部专用)公式19 2002-11修改多项式变换公式;修改等距圆柱投影的球半径计算公式;修改Krovak投影公式;添加degree representation4转换方法;改正上、下标编辑错误20 2003-05修改阿尔勃斯一节的希腊符号字体21 2003-10改正兰勃特等角圆锥投影(比利时)示例中的印刷错误;扩展极地球面投影公式用于正割模式;扩展一般多项式变换公式至13次项;添加简化莫洛金斯基变换示例、兰勃特方位等面积投影示例和可逆多项式公式22 2003-11改正兰勃特方位等面积投影示例中的FE与FN值23 2004-01修改极地球面投影方法的数据库编号;撤消degree representation转换方法3译者注:POSC Epicentre是石油行业的国际标准数据模型,由国际石油技术软件开放公司POSC(Petrotechnical Open Software Corporation)推出。
