第章几类常见的地图投影
几种常见地图投影各自的特点及其分带方法

高斯-克吕格(Gauss-Kruger)投影,是一种“等角横切圆柱投影”。
德国数学家、物理学家、天文学家高斯(Carl Friedrich Gauss,1777一 1855)于十九世纪二十年代拟定,后经德国大地测量学家克吕格(Johannes Kruger,1857~1928)于 1912年对投影公式加以补充,故名。
设想用一个圆柱横切于球面上投影带的中央经线,按照投影带中央经线投影为直线且长度不变和赤道投影为直线的条件,将中央经线两侧一定经差范围内的球面正形投影于圆柱面。
然后将圆柱面沿过南北极的母线剪开展平,即获高斯一克吕格投影平面。
一、只谈比较常用的几种:“墨卡托投影”、“高斯-克吕格投影”、“UTM 投影”、“兰勃特等角投影”1.墨卡托(Mercator)投影1.1 墨卡托投影简介墨卡托(Mercator)投影,是一种" 等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定,假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
“海底地形图编绘规范”(GB/T 17834-1999,海军航保部起草)中规定1:25万及更小比例尺的海图采用墨卡托投影,其中基本比例尺海底地形图(1:5万,1:25万,1:100万)采用统一基准纬线30°,非基本比例尺图以制图区域中纬为基准纬线。
3.2地图投影及其分类,3.3常用的地图投影解析PPT参考幻灯片
轴投影
5
§3 常用的地图投影
❖ 1.墨卡托投影(等角正圆柱投影) 投影原理:设想地球为一透明球体,球心置一点光
源,将圆柱投影面沿赤道与地球相切,地球上的经纬网格投 影到圆柱面上
6
墨卡托投影绘制的世界地图
§3 常用的地图投影
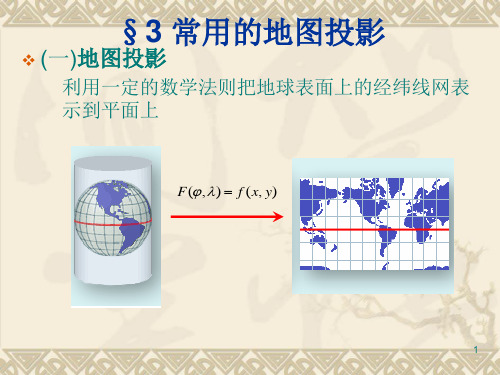
❖ (一)地图投影
利用一定的数学法则把地球表面上的经纬线网表 示到平面上
F(, ) f (x, y)
1
❖ 1. 地图投影的失真
由于地球椭球体表面是曲面,而地图通常是要绘制在平 面图纸上,因此制图时首先要把曲面展为平面,然而球 面是个不可展的曲面,即把它直接展为平面时,不可能 不发生破裂或褶皱。
为了保证地图的精度,采用分带投影方法,即将投 影范围的东西界加以限制,使其失真不超过一定的 限度,这样把许多带结合起来,可成为整个区域的 投影。
我国规定1:1 万、1:2.5 万、1:5 万、1:10万、 1:25 万、1:50 万比例尺地形图,均采用高斯克 -吕格投影。1:2.5 至1:50 万比例尺地形图采用 经差6 °分带,1:1 万比例尺地形图采用经差3° 分带。
绘制机场专用航图和涉及仪表飞行程序的基础用图; 国家大地测量和五十万分之一及更大比例尺的国家基本地形
图
13
❖ 高斯投影坐标网
经纬网(地理坐标网)
114°00 14
16
30° 202
40´
α
3396
94 -δ TH/TC
92
18 20 A( 20218 , 3394 )
90
TH/TC= α+(± δ)
第03章 地图投影
⑵ 不同变形性质投影的变形分布
⑶应用范围 • 根据圆柱投影的变形规律和经纬网的特点,在赤道附近沿 东西方向延伸地区的地图,最适宜采用各种变形性质的圆 柱投影; • 全球区域的地图可采用等角或等距圆柱投影,航海和航空 图上常常采用墨卡托投影; • 由于圆柱投影的经线为平行直线,便于显示时区的划分, 因此它也是世界时区图的主要投影。
⑵条件投影 • 根据某些条件,用数学解析法确定球面与平面之间点与点的 函数关系。 • 伪方位投影:在方位投影的基础上,根据某些条件改变经线 形状而成,除中央经线为直线外,其余均投影为对称中央经 线的曲线。 • 伪圆柱投影:在圆柱投影基础上,根据某些条件改变经线形 状而成,无等角投影。除中央经线为直线外,其余均投影为 对称中央经线的曲线。 • 伪圆锥投影:在圆锥投影基础上,根据某些条件改变经线形 状而成,无等角投影。除中央经线为直线外,其余均投影为 对称中央经线的曲线。 • 多圆锥投影:设想有更多的圆锥面与球面相切,投影后沿一 母线剪开展平。纬线投影为同轴圆弧,其圆心都在中央经线 的延长线上。中央经线为直线,其余经线投影为对称于中央 经线的曲线。
§3 地图投影
生命科学学院
§1. 常用的地图坐标系
• 1.1 平面直角坐标系
x,y
• 1.2 平面极坐标系
ρ,δ
• 1.3 平面直角坐标与极坐标的关系
x q cos y sin
§2. 地图投影的基本概念
• 2.1 地图投影的定义
为什么要进行地图投影?
2
ab ab
当投影后经纬线正交,即θ=90°时:
,b n ; P ab mn ;
a m
sin
2
几种常见地图投影各自的特点及其分带方法

几种常见地图投影各自的特点及其分带方法高斯-克吕格(Gauss-Kruger)投影,是一种“等角横切圆柱投影”。
德国数学家、物理学家、天文学家高斯(Carl Friedrich Gauss,1777一1855)于十九世纪二十年代拟定,后经德国大地测量学家克吕格(Johannes Kruger,1857~1928)于1912年对投影公式加以补充,故名。
设想用一个圆柱横切于球面上投影带的中央经线,按照投影带中央经线投影为直线且长度不变和赤道投影为直线的条件,将中央经线两侧一定经差范围内的球面正形投影于圆柱面。
然后将圆柱面沿过南北极的母线剪开展平,即获高斯一克吕格投影平面。
一、只谈比较常用的几种:“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”1.墨卡托(Mercator)投影1.1 墨卡托投影简介墨卡托(Mercator)投影,是一种" 等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定,假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
“海底地形图编绘规范”(GB/T 17834-1999,海军航保部起草)中规定1:25万及更小比例尺的海图采用墨卡托投影,其中基本比例尺海底地形图(1:5万,1:25万,1:100万)采用统一基准纬线30°,非基本比例尺图以制图区域中纬为基准纬线。
第三章方位投影

2
方 位 投 影
正射投影 透视投影 外心投影 球面投影 球心投影 纬线——一组同心圆 正轴 经线——交于投影中心的直 线束,夹角不变 非透视投影 横轴 等高圈——同心圆 斜轴 垂直圈——同心圆半径,夹 角不变
方位投影——又称平面投影
RZ C
式中C为积分常数。因Z = 0 时, = 0,故C = 0。 于是:
RZ
22
等距离方位投影的变形公式:
长度比为:
1 1 2
R sin Z Z sin Z
面积比为:
P 1 2 Z sin Z
a,b
最大角度变形为:
sin
2
投影中心: 平面和球面相切的一点 用圆球体代替椭球体:M=N=R B,L
投影中心
1. 方位投影分类
根据投影面和地球球体相切位置不同 当投影面切于地球极点时,为正轴投影。 当投影面切于赤道时,为横轴方位投影。 当投影面切于既不在极点也不在赤道时,斜轴方位投影。
2、正轴方位投影
投影中心为极点,纬线为同心 圆,经线为同心圆的半径,两 条经线间的夹角与实地相等。
由此得到直角坐标公式为:
x cos
LR sin Z cos D R cos Z
y sin
LR sin Z sin 4 D R cos Z
变形公式为:
d L( D cos Z R) RdZ ( D R cos Z )2 3 L 2 R sin Z D R cos Z
P 2
41
当Zk=0,即投影面切在投影中心,则有:
第二章下 常用地图投影

(2)变形规律
切点没变形,离切点越远,变形越 大。 等变形线是以切点为圆心的同心圆。 切点向任意一点的方位角没变形。
斜轴等积方位投影
(3)用途
主要用于绘制水、陆半球,除非洲、南极洲以外的各 大洲(例如亚洲、欧洲、大洋洲、北美洲、南美洲)。 适合中高纬地区呈圆形区域的国家或地区。(例如包 含南海诸岛的中国全国)
(2)经纬线形状
纬线投影成一组平行直 线,经线投影成与纬线垂 直的平行直线。 纬线间距,从赤道向两极 放大,经线间距相等。
(3)变形特点
角度没有变形。 赤道没有变形,离赤道越远,面积变形越大。 等变形线是平行于纬线的直线。
(4)用途
常用于绘制世界时区图、世界交通图。 适合绘制赤道附近沿东西延伸的国家或地区 由于等角航线投影为直线,所以广泛用来绘制 海图。
2、正轴割圆锥投影(南海诸岛作插图的中国全图)
正轴等角割圆锥投影(Lambert conformal projection兰勃特) 正轴等积割圆锥投影(Albers projection亚尔勃斯)
(1)投影的几何概念
以圆锥投影作为投影面,使圆锥面与球面相割 (两条割线为标准线),按等角或等积条件将球面 上的经纬线投影到圆锥面上,然后将圆锥面展为平 面而成。
纬线投影为同心圆弧,经线投影为放射状直线。纬 线间隔从标准纬线向南向北是逐渐缩小的。
(3)变形规律
①两条标准线没有变形,离标 准线越远变形越大。 ②等变形线是平行于纬线的圆 弧。 ③在两条标准线之间,长度比 小于 1 ,为负变形;而在两 条标准线之外,长度比大于 1,为正变形。
中国地图(南海诸岛作插图)的标准线: ϕ 1=25°,ϕ 2=45/47°
第五讲 常用地图投影

二)、墨卡托投影 )、墨卡托投影
墨卡托投影中,面积变形最大,在纬度 度地区 度地区, 墨卡托投影中,面积变形最大,在纬度60度地区,经纬线 比都扩大了2倍 面积比 比都扩大了 倍,面积比P=m*n=2*2=4,扩大了 倍,愈 ,扩大了4倍 接近两极,经纬线扩大的越多, 度时, 接近两极,经纬线扩大的越多,在φ=80度时,经纬线都 度时 扩大了近6倍 面积比扩大了 倍 所以墨卡托投影在 扩大了近 倍,面积比扩大了33倍,所以墨卡托投影在80 度以上高纬通常不绘。 度以上高纬通常不绘。 该投影被广泛应用于航海和航空方面,因为等角航线( 该投影被广泛应用于航海和航空方面,因为等角航线(或 等角航线 称斜航线),在此投影中表现为直线, 称斜航线),在此投影中表现为直线,等角航线是地球表 ),在此投影中表现为直线 面上与经线相交的相同角度的曲线, 面上与经线相交的相同角度的曲线,或者说地球上两点间 的一条等方位线,船只要按等角航线航行, 的一条等方位线,船只要按等角航线航行,不用改变方位 角就能从起点到达终点。 角就能从起点到达终点。
二)、墨卡托投影 )、墨卡托投影
等角正轴切圆柱投影是荷兰地图学家墨卡托于1569年所 等角正轴切圆柱投影是荷兰地图学家墨卡托于 年所 所以又称墨卡托投影。 创,所以又称墨卡托投影。
二)、墨卡托投影 )、墨卡托投影
• 赤道投影为正长,纬线投影成和赤道等 赤道投影为正长, 长的平行线段,即离赤道越远, 长的平行线段,即离赤道越远,纬线投 影的长度也越大,为了保持等角条件, 影的长度也越大,为了保持等角条件, 必须把地图上的每一点的经线方向上的 长度比和纬线方向上的长度比相等。所 长度比和纬线方向上的长度比相等。 以随着纬线长度比的增加, 以随着纬线长度比的增加,相应经线方 向上的长度比也得增加, 向上的长度比也得增加,并且增加的程 度相等。所以在墨卡托投影中, 度相等。所以在墨卡托投影中,从赤道 向两极,纬线间隔越来越大。 向两极,纬线间隔越来越大。
第二章投影及判断和选择

常用方位投影
5.2
正轴方位投影
5.2.3
正轴等距方位投影(波斯托投影)
特点: 由投影中心至任意一点 的距离均与实地相等。即该 投影后长度比 m=1。由于该 投影具有由投影中心至任意 点的距离和方位均保持与实 地的距离和方位不变,因此 在国际上应用的也比较广泛, 多用于两极地区图。
采用正轴等距方位投 影绘制的南极地图
常用方位投影
5.2
正轴方位投影
特点:投影中心为极点, 纬线为同心圆,经线为同 心圆的半径,两经线间的 夹角与实地相等。等变形 线都是以投影中心为圆心 的同心圆,包括等角、等 积、等距三种变形性质。 正轴方位投影主要用于制 作两极地区图。
三种方位投影纬线间隔变化示意图
常用方位投影
5.2
正轴方位投影
°等分,分别交线A于abc…,分别 以abc为圆心,以到C的长度为半径画 圆弧,即得各经线。 B C
①
②
常用方位投影
5.4
斜轴方位投影
5.4.2 斜轴等距方位投影
经纬线形式:
中央经线为直线,其
它经纬线均是曲线。在中 央经线上纬线间隔相等。
常用方位投影
5.4
斜轴方位投影
5.4.2 斜轴等距方位投影
非透视方位投影是借助于透视投影的方式,而附加上一定的 条件,如加上等积、等距等条件所构成的投影。在这类投影 中有等距方位投影和等积方位投影。
5.1.3
特点
在投影平面上,由投影中心(平面与球面相切的切点, 或平面与球面相割的割线的同心圆)向各个方向的方位角与 实地相等,其等变形线是以投影中心为圆心的同心圆,该投 影适合作区域轮廓大致为圆形的地图。
§4
地图投影的应用
高斯-克吕格投影(等角横切椭圆柱投影) 通用横轴墨卡托投影——UTM 投影 百万分一地形图投影 方位投影(正轴方位投影、正轴等角方位投影、正轴
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4.1 圆锥投影
1、单标准纬线等距离圆锥投影
设圆锥面切于地球0的一条纬线上,即 n0=1。则
A C r0 N 0 co s 0
AS 0 N 0 cot0
s0
0 Md
0
Q
n0
0
r0
1
r0 0
N0 cos0 N0 cot0
sin0
Q 0 c s0
c
0
s0
r0
s0
§4.1 圆锥投影
§4.1 圆锥投影
2、由投影性质决定的变形特点 (1)等角圆锥投影:经线长度比与纬线长度比相等(m=n ),角度没有变形,但面积变形较大(P=m2) 。 (2)等面积圆锥投影:经线长度比与纬线长度比互为倒数 (mn=1),面积没有变形,但角度变形较大。 (3)等距离圆锥投影: 变形介于等角投影与等 面积投影之间,经线长 度比保持为1(m=1), 纬线长度比与面积比相 等(n=P)。
2
Q nN nm 2
K
1 rN U
N
1 rm U
m
2
K
2
rm
rS U
m
U
S
( rmU
m
rS U
S
)
K
2
rm
rN U
m
U
N
( rmU
m
rN U
N
)
§4.1 圆锥投影
n N n m n S n m ( 1 )( 1 ) 1 2
对于纬差4°为一带的圆锥投影来说。υ2之值为9×10-8, 它对投影计算和实用精度,都没有什么影响,故可略去。
2、双标准纬线等距离圆锥投影
设圆锥面割于地球 1、 2 的两条纬线上,即n1=n2=1。
r1 N 1 c o s 1
r
2
s
1
N 2 cos 2 1 M d
0
s2
2 M d
0
( (
c c
s1 ) s2 )
r1 r2
r1
1
1
1 c s 1
r2
2
1
2 c s 2
双标准纬线规定如下:
1 S 40 2 N 40
投影常数按下式计算:
lg r1 lg r2 lg U 2 lg U 1
K
r1U
1
r2U
2
§4.1 圆锥投影
自1978年以后,我国1∶100万地图采用等角圆锥投影,分
幅与国际分幅一致,但标准纬线与国际上稍有差异,并规定根
据边纬与中纬长度变形绝对值相等的条件确定投影常数,即:
2
S0
§4.1 圆锥投影
2、双标准纬线等面积圆锥投影
设圆锥面割于地球1、 2的两条纬线上,即n1=n2=1。
r1 N 1 c o s 1
r2 S1
N2
1 0
co M
s2 N co
s
d
S 2
2 M N cos d
0
2 (c S1) r12
2
(c
S2
)
r22
1
r1
1
2 1
2
式: d
M d r
d M d
N cos
M
(1
a c (1
e
2 1
)
e
2 1
sin
2
3
)2
;
N
ac
(1
e
2 1
sin
2
1
)2
d
(1
e
2 1
)
d
(1
e
2 1
sin
2
)
cos
d
1
c
o
s
1
e
2 1
c
o
s
e
2 1
sin
2
d
§4.1 圆锥投影
d
d cos
e1 2
1
1 e1 sin
m
A'D AD
'
d Md
n
A'B' AB
d rd
r
在正轴圆锥投影中,经纬 线投影后仍保持互相垂直,所 以经纬线方向就是主方向,即
m=a,n=b,根据面积比
和角度变形定义有:
P ab mn
sin
2
ab ab
mn mn
§4.1 圆锥投影
现将圆锥投影的一般公式汇集如下:
f ( )
2、双标准纬线等角圆锥投影
设圆锥面割于地球1、 2的两条纬线上,即n1=n2=1。
s 2
e1
U
1
tan
45o
1 2
1
1
e1 e1
sin sin
1 1
2
e1
U
2
tan
45o
2 2
1
1
e1 e1
sin 2 sin 2
2
1 r1
应用该式推求标准纬线,基本符合 边纬与中纬长度变形绝对值相等的条件。
§4.2 方位投影
一、方位投影的一般公式及其分类 二、等角方位投影 三、等面积方位投影 四、等距离方位投影 五、透视方位投影 六、方位投影变形分析与应用
§4.2 方位投影
一、方位投影的一般公式及其分类 1、方位投影的定义
假设一个平面与地球面相切或相割,根据某种条件(如 等角、等面积、透视等)将地球上的经纬线投影到该平面上 ,即得到方位投影。
s为赤道到某纬度 的经线弧长。
§4.1 圆锥投影
现将等距离圆锥投影的一般公式汇集如下:
cs
s M d
x s cos y sin m 1 n
r P mnn
sin 1 n 2 1 n
在这组公式中,仍然有常数 α和 c 需要确定,但由于确定的 方法比较多,所以各种不同形式 的等距离圆锥投影也较多。
现将等面积圆锥投影的一般公式汇集如下:
2 2 (c S )
S M N cos d
x s cos y sin
n r
m1 n
P mn1
ta n
45
4
m
在这组公式中,仍然有常数 α和 c 需要确定,但由于确定的方 法比较多,所以各种不同形式的 等面积圆锥投影也较多。
切圆锥投影、割圆锥投影 (2)按圆锥面和地球面的位置关系分:
正轴圆锥投影、横轴圆锥投影、斜轴圆锥投影 (3)按投影的变形性质分:
等角圆锥投影、等积圆锥投影、任意圆锥投影
§4.1 圆锥投影
3、圆锥投影的一般公式
以正轴圆锥投影为例
纬线投影后为同心圆
圆弧,其半径ρ是纬度 的
函数,函数形式由投影性
质和投影条件决定。
根据等面积条件P=1,即mn=1,来确定ρ= f()的函数
形式:
d
1
M d r
d 1 M d N cos
d 1 M N cos d
d
1
M
N
cos
d
Q S M N cos d
2 2 (c S )
S为经差1弧度,纬差从
0°到纬度 的椭球面上的梯
形面积。
§4.1 圆锥投影
§4.1 圆锥投影
一、圆锥投影的一般公式及其分类 1、圆锥投影的定义 假设一个圆锥面与地球面相切或相割,根据某种条件(
等角、等面积、透视等)将地球上的经纬线投影到圆锥面上 ,然后沿圆锥面的一条母线(经线)切开展平,即得到圆锥 投影。
§4.1 圆锥投影
f ( )
§4.1 圆锥投影
2、圆锥投影的分类 (1)按圆锥面与地球面的切割关系分:
1 m 2 ( S N )
nS
K
rSU
S
1
nN
K
rN U
N
1
nm
K
rm U
m
1
Q nS nN
K
rSU
S
K
rN U
N
U
U
N S
rS rN
lg rS lg rN lg U N lg U S
Q nS nm 2
K
1 rSU
S
1 rm U
m
1
1
K
U
1
2 r2
2
1
K
U
2
K K
r1U
1
r2U
2
相减得 lgr1 lgr2
lgU2 lgU1
K r1U1 r2U2
§4.1 圆锥投影
3、应用举例:百万分一地图等角圆锥投影 1962年国际制图会议规定:1∶100万地图按国际标准分
幅,采用双标准纬线等角圆锥投影,自赤道起按纬差4°分 带,对每带单独进行投影。北纬84°以北和南纬80°以南的 地区,则采用等角方位投影。
以某一经线的投影为X轴,
经线投影后为相交于 以X轴和最南边纬线s的交点为
一点的直线束,且夹角δ与 原点,建立平面直角坐标系:
经差λ成正比。 f ( )
x
y
s cos sin
§4.1 圆锥投影
设平面梯形A`B`C`D`是地 球面上微分梯形ABCD的投影 ,根据经纬线长度比定义有:
设圆锥面切于地球0的一条纬线上,即 n0=1,则
AC r0 N0 cos0
AS 0 N0 cot0
e1
U0
tan
45o
0
2
1 1
e1 e1
sin0 sin0
2
n0
0
r0
1
r0
0
N0 cos0 N0 cot0
sin0
0 r 0
1
0
K
U
0
