电路原理清华PPT课件
合集下载
清华大学电路原理课件1
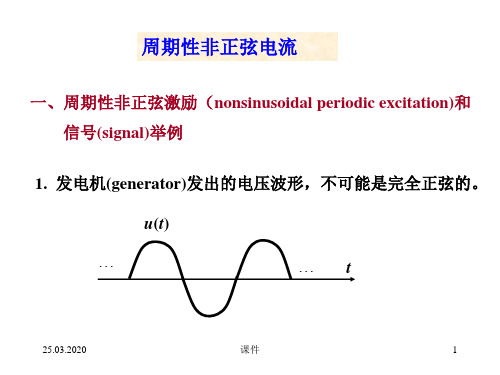
电路原理Principle of Electric Circuits于歆杰yuxj@Tel: 62771944西主楼1区308第一讲绪论，电压电流和功率第一部分：绪论Principles of Electric Circuits Lecture 1 Tsinghua University 2005什么是电路？a电路（electric circuits）就是由若干电气元件（electrical elements）相互连接构成的电流的通路。
a本课程中要接触的电气元件有`电阻、电容、电感、二极管、MOSFET、理想运算放大器（Operational Amplifier）、互感线圈、理想变压器等Principles of Electric Circuits Lecture 1 Tsinghua University 2005为什么要学习电路？a从学术的观点来看`电路是电气工程（Electrical Engineering）的基础。
`电路是计算机科学（Computer Science）的基础。
a从实际情况来看`电路原理是许多高级课程的先修课程。
`熟练掌握电路原理对现实生活有帮助。
Principles of Electric Circuits Lecture 1 Tsinghua University 2005t q t q t i t d d ∆∆lim )(0∆def ==→d d BABA Weq=AI110ΩU1U2t w p d d =uit qq w ==d dd d q wu d d =t qi d d =。
电路原理-清华-36共25页文档
u2u S
+
D
+
u
_
S
R
u
_
2
0
t
非线性电感(nonlinearity inductance)电路
i
+
us
uS i
0
t
25.03.2020
课件
2
3. 大量脉冲信号均为周期性非正弦信号
f(t)
…
f(t)
0
t0
t
f(t) 0
t
尖脉冲
方波
锯齿波
二、周期性非正弦电流电路的分析方法
—谐波(harmonic wave)分析法
（3） 2 I 0 I m k sik n tk ()(k 1 ,2 ,3 , )直次流谐分波量乘与积各
T 10 T2I0k 1Ikm sik nt(k)dt0
余弦函数是偶函数 coxscosx)(
…
-T
f(t)
…
t 0T
… -T
f(t)
T 0
…
t
此类函数的傅里叶级数展开式只包含余弦函数项，不 包含正弦函数项，可能有常数项。
25.03.2020
课件
13
2. 根据半波对称性质判断 (a) f(t)f(tT)
2
半波对称横轴
…
-T
f(t)
…
0T
t
f (t T ) 2
2E
k
(1
cos
k
)
4E
k
0
k为 奇 数 k为 偶 数
25.03.2020
课件
10
则
f(t)4Esi nt4 3Esin 3t4 5Esin 5t 4E(sint1 3sin 3t1 5sin 5t)
最新清华大学-电路原理教学讲义PPT课件
返回首页
def L
i
韦安（ ~i ）特性
0
i
二、线性电感电压、电流关系：
i
+–
ue –+
i , 右螺旋 e , 右螺旋
u , e 一致 u , i 关联
由电磁感应定律与楞次定律
e L di dt
u e Ldi dt
iL +u –
u L di dt
(1) 当 u，i 为关联方向时，u=L di / dt u，i 为非关联方向时，u= – L di / dt
一、 电功率：单位时间内电场力所做的功。
p d w dw dq ui d t dq dt
功率的单位名称：瓦（特） 符号（W） 能量的单位名称：焦（耳) 符号（J）
二、功率的计算 1. u, i 取关联参考方向
i 元件（支路）吸收功率
+
u
p=ui
或写为 p吸 = u i
–
2. u, i 取非关联参考方向
的参考方向。
UAB
A
B
三、电位
取恒定电场中的任意一点（O点），设该点的电位为零， 称O点为参考点。则电场中一点A到O点的电压UAO称为A
点的电位，记为A 。单位 V(伏)。
a
b
设c点为电位参考点，则 c= 0
a= Uac， b=Ubc， d= Udc
d
c
Uab = a- b
返回首页
电路元件的功率 (power)
短路
i = 0 , u由外电路决定
0
i
开路
电感 (inductor)元件
iL
变量: 电流 i , 磁链
+
u
–
清华大学电路原理于歆杰精品PPT课件
电路中某个支路（或元件）的电压（或电流）的控制。
电路符号
+– 受控电压源
受控电流源
清华大学电路原理教学组
一个受控电流源的例子（MOSFET）
IDS
MOSFET
＋ D
G
＋
S
UDS
IDS
UGS
－
－
电流源
电 阻
受控源与独立源的比较:
UDS
(1) 独立源电压(或电流)由电源本身决定，而受控源电压(或
电流)直接由控制量决定。
二、欧姆定律 (Ohm’s Law)
(1) 电压电流采用关联参考方向
i
R
+u
uRi
R 电阻 (resistance) 单位： (欧)
清华大学电路原理教学组
令G 1/R
G 电导 (conductance)
单位： S (西) (Siemens，西门子)
欧姆定律(关联参考方向下): i G u
u 关联参考方向下线性电阻器的u-i关系 :
清华大学电路原理教学组
（2） 伏安特性 i
+
iS
u
_
u
IS
0
i
（a）若iS= IS ，即直流电源，则其伏安特性为平行于电 压轴的直线，反映电流与端电压无关。
（b）若iS为变化的电源，则某一时刻的伏安关系也是 平行于电压轴的直线
（c）电流为零的电流源，伏安特性曲线与 u 轴重合，相 当于开路状态。
清华大学电路原理教学组
（3） 理想电流源的短路与开路
+
i
（1） 短路：R=0， i= iS ，u=0 ，
电流源被短路。
iS
u
R
_
电路符号
+– 受控电压源
受控电流源
清华大学电路原理教学组
一个受控电流源的例子（MOSFET）
IDS
MOSFET
＋ D
G
＋
S
UDS
IDS
UGS
－
－
电流源
电 阻
受控源与独立源的比较:
UDS
(1) 独立源电压(或电流)由电源本身决定，而受控源电压(或
电流)直接由控制量决定。
二、欧姆定律 (Ohm’s Law)
(1) 电压电流采用关联参考方向
i
R
+u
uRi
R 电阻 (resistance) 单位： (欧)
清华大学电路原理教学组
令G 1/R
G 电导 (conductance)
单位： S (西) (Siemens，西门子)
欧姆定律(关联参考方向下): i G u
u 关联参考方向下线性电阻器的u-i关系 :
清华大学电路原理教学组
（2） 伏安特性 i
+
iS
u
_
u
IS
0
i
（a）若iS= IS ，即直流电源，则其伏安特性为平行于电 压轴的直线，反映电流与端电压无关。
（b）若iS为变化的电源，则某一时刻的伏安关系也是 平行于电压轴的直线
（c）电流为零的电流源，伏安特性曲线与 u 轴重合，相 当于开路状态。
清华大学电路原理教学组
（3） 理想电流源的短路与开路
+
i
（1） 短路：R=0， i= iS ，u=0 ，
电流源被短路。
iS
u
R
_
电路原理-清华-33共21页
Uψ120o
3
计算电流：
•
•
•
IA
U an
UA
U
ψ φ
Z Z |Z|
•
•
•
IB
U bn
UB
U
ψ 120 o φ
Z Z |Z|
•
•
•
IC
U cn
UC
U
ψ 120 o φ
Z Z |Z|
流过每相负载的电流与流过相应火线的线电流是同
一电流，且三相电流也是对称的。
因N，n两点等电位，可将其短路，且其中电流为零。 这样便可将三相电路的计算化为一相电路的计算。当求 出相应的电压、电流后，再由对称性，可以直接写出其 它两相的结果。
3Uψ 90o
•
•
Uca UCA
3Uψ 150o
25.03.2020
课件
7
计算相电流：
•
•
I ab
U ab
Z
•
•
I bc
U bc
Z
3U ψ 30 o φ |Z | 3U ψ 90 o φ |Z |
A
+
•
U A_
•
UC
N
•
UB
C+
+B
•
•
I ca
U ca
3U ψ 150 o φ
25.03.2020
课件
4
A
+
•
• UA_ N
•
UC
UB
C+
+B
•
IA
c
•
IB
•
IC
a
Z
nZ
电路原理-清华-12
R 12 Δ
( u s3 )
R 12 Δ
u s3
5
us1 1
ia
us2 2 R11
R21
R12
R22 R12
R2 Δ
2
us1
1
R12 Δ
us22R Δ 22 u s1R 1Δ 2R 22 u s2R Δ 12 u s3
R22
u s 1 R 12
0 i a 1 R 11
把 usi 个系数合并为Gji
us1 usb
b
G uji si i 1
第i个电压源单独作用时在 第j 个回路中产生的回路电流
ij1ij2 iji ijb
支路电流是回路电流的线性组合，支路电流满足叠加定理。
同样可以证明：线性电阻电路中任意支路的电压
等于各电源（电压源、电流源）在此支路产生的电压
证明:
A ik
+
支
A
uk
路 k
A
–
B
A ik
+
+
A uk
uk
–
–
B
第k条支路也可用ik替代，留课后思考。
A ik
支+ 路 uk k–
–uk + C B – uk +
AC等电位
例
6
+ i1
i2 +
i3
20V
8 u
–
–
用节点法可求出
4 u=8V
+
i1=2A
-4V
i2=1A
i3=1A
用8V电压源替代8所在支路
i j Rl1
清华大学电路原理课件--电路原理_skja_09
i5 = i S
(5)
返回首页
回路电流法 (loop current method)
思路： 为减少未知量(方程)的个数，假想每个回路 中有一个回路电流。
a
i1 R1 uS1 + –
i2 R2 il1 + uS2 –
b
i3 il2 R3
设回路电流为 il1、 il2。 回路电流自动满足KCL 支路电流是回路电流的组合 i1= il1，i2= il2- il1， i3= il2。
1
3
i5 i6
4
R5
节点 1：i1 + i2 – i6 =0 节点 2：– i2 + i3 + i4 =0 节点 3：– i4 – i5 + i6 =0 节点 4：– i1 – i3 + i5 =0
这4个方程是不独立的
uS –
一般情况： 对有n个节点的电路，只有n-1个独立的KCL方程。任 意划去其中一个方程，剩余的就是独立方程。 独立节点：与独立KCL方程对应的节点。 被划去的节点通常被设为电路的参考节点。 由KVL所能列写的独立方程数为： l = b - (n-1) 上例 l = b - (n-1)=3
总有支路相互交叉 ∴是非平面电路
支路法列写方程的一般步骤： (1) 标定各支路电流参考方向； (2) 选定(n–1)个节点，列写其KCL方程；
(3) 选定b–(n–1)个独立回路，列写其KVL方程； (元件特性代入)
(4) 求解上述方程，得到b个支路电流。
例1
I1 R1 I2 R2 I1
a I3 R3
回路2中所有电压源电压升的代数和
一般情况，对于具有 l=b-(n-1) 个回路的电路，有 R11i1+R12i2+ …+R1l il=uSl1 R21i1+R22i2+ …+R2l il=uSl2 … Rl1i1+Rl2i2+ …+Rll il=uSll
电路原理-清华-44
t 1f(t)t2 e d 2 e (t 1 ) 2 e t t 1
课件
20
例3. e(t)2 [(t1)(t2)]h ,(t)et(t)
求 e1(t)*h (t)
解 由图解过程确定积分上下限：
e-(t-)
2
e-(-) 1
0
0
或
t1 f(t)0
1t 2 t
1t 2t t
1 t 2 f(t)t2 e (t )d 2 2 e (t 1 ) 1
解：先求该电路的冲激响应 h(t)
iS (t)mA
uC(0)C1
0
0 iSdt
1 C
0
(t)dt
103
100V0
0
C
uC()=0
R 5 C 0 13 0 0 1 60 0 .5 s
h(t)10e 0 2t(0t)V
09.02.2021
课件
17
再由卷积积分计算当 iS=2et (t) mA 时的响应 uC ( t ):
iC +
分二个时间段来考虑：
iS
R C uC
t
0 0
0
电容充电 电容放电
uC(0-)=0
1. t 从 0 0+
CduC uC (t)
dt R
uC 不可能是冲激函数 , 否则KCL不成立
0C d u Cdt0u Cdt0 (t)dt
0 d t
R 0
0
=0
=1
C [u C(0)u C(0) ]1
2
-1 0 1
f1(t-)
2
t’-1
-1 0 t 1 t’ f2() f1(t-)
2
1
-1 0 t 1
课件
20
例3. e(t)2 [(t1)(t2)]h ,(t)et(t)
求 e1(t)*h (t)
解 由图解过程确定积分上下限：
e-(t-)
2
e-(-) 1
0
0
或
t1 f(t)0
1t 2 t
1t 2t t
1 t 2 f(t)t2 e (t )d 2 2 e (t 1 ) 1
解：先求该电路的冲激响应 h(t)
iS (t)mA
uC(0)C1
0
0 iSdt
1 C
0
(t)dt
103
100V0
0
C
uC()=0
R 5 C 0 13 0 0 1 60 0 .5 s
h(t)10e 0 2t(0t)V
09.02.2021
课件
17
再由卷积积分计算当 iS=2et (t) mA 时的响应 uC ( t ):
iC +
分二个时间段来考虑：
iS
R C uC
t
0 0
0
电容充电 电容放电
uC(0-)=0
1. t 从 0 0+
CduC uC (t)
dt R
uC 不可能是冲激函数 , 否则KCL不成立
0C d u Cdt0u Cdt0 (t)dt
0 d t
R 0
0
=0
=1
C [u C(0)u C(0) ]1
2
-1 0 1
f1(t-)
2
t’-1
-1 0 t 1 t’ f2() f1(t-)
2
1
-1 0 t 1
清华考研_电路原理课件_第1章__电路元件和电路定律
Uab= ϕ a–ϕ b → ϕ b = ϕ a –Uab= –1.5 V
1.5 V Ubc= ϕ b–ϕ c → ϕ c = ϕ b –Ubc= –1.5–1.5 = –3 V
b
Uac= ϕ a–ϕ c = 0 –(–3)=3 V
1.5 V (2) 以b点为参考点，ϕ b=0
c
Uab= ϕ a–ϕ b → ϕ a = ϕ b +Uab= 1.5 V
2. 电压（voltage） 电场中某两点A、B间的电压（降）UAB 等于将点电荷q
从A点移至B点电场力所做的功WAB与该点电荷q的比值，即
uAB
=
dWAB dq
A
B
单位名称： 伏（特） 符号：V （Volt，伏特；1745 – 1827，Italian）
3. 电位（potential） 在分析电路问题时，常在电路中选一个点为参考点
• 用箭头表示：箭头的指向为电流的参考方向。 • 用双下标表示：如 iAB ，电流的参考方向由A指向B。
例
I 10V
A I1
10Ω
I2 B
电路中电流 I 的大小为1A, 其方向为从A流向B。 （此为电流的实际方向）
若参考方向如 I1 所示，则I1=1A
若参考方向如 I2 所示，则I2= -1A
因此，同一支路的电流可用两种方法表示。
电路模型
3. 集总参数电路 实际电路的尺寸必须远小于电路工作频率下的电磁波的波
长。
返回目录
1.2 电流、电压、电动势及其参考方向
一、电流、电压、电动势
1. 电流 带电质点有规律的运动形成电流。
电流的大小用电流强度表示。
电流强度：单位时间内通过导体横截面的电量。
清华大学电路原理课件-
实际方向 实际方向
参考方向：任意选定的一个方向即为电流的参考方向。
i
参考方向
A
B
电流的参考方向与实际方向的关系
i
参考方向
i
参考方向
实际方向
i> 0
实际方向
i< 0
电流参考方向的两种表示
• 用箭头表示：箭头的指向为电流的参考方向。 • 用双下标表示：如 iAB ，电流的参考方向由A指向B。
例
I 10V
Uac= a– c = 1.5 –(–1.5) = 3 V
结论：电路中电位参考点可任意选择；当选择不同的电 位参考点时，电路中各点电位将改变，但任意两点 间电压保持不变。
4. 电动势（electromotive force） 外力（非静电力）克服电场力把单位正电荷从负极经电
源内部移到正极所作的功称为电源的电动势。
_
_
模型（circuit model）不再存在）。
i
实际电压源
r
（physical source）
u
US
_
_
u
US
0
i
u=US – r i
二、理想电流源（ideal current source）
电路符号
iS
1. 特点：
（a） 电源电流由电源本身决定，与外电路无关； （b） 电源两端电压由外电路决定。
电容（ capacitor ）元件：表示各种电容器产生电场、 储存能量的作用。
电源（ source ）元件：表示各种将其它形式的能量转 变成电能的元件。
2. 电路模型
由理想电路元件组成的电路，其与实际电路具有基本相同 的电磁性质。
例
开关
10BASE-T wall plate
参考方向：任意选定的一个方向即为电流的参考方向。
i
参考方向
A
B
电流的参考方向与实际方向的关系
i
参考方向
i
参考方向
实际方向
i> 0
实际方向
i< 0
电流参考方向的两种表示
• 用箭头表示：箭头的指向为电流的参考方向。 • 用双下标表示：如 iAB ，电流的参考方向由A指向B。
例
I 10V
Uac= a– c = 1.5 –(–1.5) = 3 V
结论：电路中电位参考点可任意选择；当选择不同的电 位参考点时，电路中各点电位将改变，但任意两点 间电压保持不变。
4. 电动势（electromotive force） 外力（非静电力）克服电场力把单位正电荷从负极经电
源内部移到正极所作的功称为电源的电动势。
_
_
模型（circuit model）不再存在）。
i
实际电压源
r
（physical source）
u
US
_
_
u
US
0
i
u=US – r i
二、理想电流源（ideal current source）
电路符号
iS
1. 特点：
（a） 电源电流由电源本身决定，与外电路无关； （b） 电源两端电压由外电路决定。
电容（ capacitor ）元件：表示各种电容器产生电场、 储存能量的作用。
电源（ source ）元件：表示各种将其它形式的能量转 变成电能的元件。
2. 电路模型
由理想电路元件组成的电路，其与实际电路具有基本相同 的电磁性质。
例
开关
10BASE-T wall plate
清华大学电路原理电子课件
三相交流电路的分析方法
总结词
掌握三相交流电路的分析方法
详细描述
分析三相交流电路时，需要使用相量法、对称分量法等 数学工具，以便更好地理解电路的工作原理和特性。
三相交流电路的应用
总结词
了解三相交流电路的应用领域
详细描述
三相交流电在工业、电力、交通、通信等领域得到广泛应用，如电动机控制、输电线路、电力系统自动化等。
瞬态响应是指电路在输入信号的作用下， 电压和电流随时间从零开始变化至稳态的 过程。稳态响应是指电路达到稳定状态后 ，电压和电流不再随时间变化的状态。一 阶动态电路的响应可以通过求解一阶常微 分方程得到。
一阶动态电路的应用
总结词
一阶动态电路在电子工程、通信工程、自动 控制等领域有着广泛的应用。
详细描述
电路元件和电路模型
总结词
掌握电路元件和电路模型是分析电路的基本方法。
详细描述
电路元件包括电阻、电容、电感等，它们具有特定的电气特性。电路模型是用 图形符号表示电路元件及其连接关系的一种抽象表示方法。
电路的工作状态和电气参数
总结词
了解电路的工作状态和电气参数是评估电路性能的关键。
详细描述
电路的工作状态可以分为有载、空载和短路等，不同的工作状态对电路的性能产 生影响。电气参数包括电压、电流、功率等，它们是描述电路性能的重要指标。
二阶动态电路的应用
要点一
总结词
二阶动态电路在电子设备和系统中的应用
要点二
详细描述
二阶动态电路广泛应用于各种电子设备和系统中，如振荡 器、滤波器、放大器等，用于实现特定的信号处理和控制 系统功能。
06
三相交流电路分析
三相交流电的基本概念
总结词
清华大学电路原理课件-2
Ri
1 Gi
i
+
uS _
+
iu
Ri
_
i
iS
+
iS
GiiS
u _
注意：
（1） 变换关系
数值关系； 方向：电流源电流方向与电压源电压方向相反。
（2） 所谓的等效是对外部电路等效，对内部电路是不等效的。
例 开路的电压源中无电流流过 Ri； 开路的电流源可以有电流流过并联电导Gi 。 电压源短路时，电阻Ri中有电流； 电流源短路时, 并联电导Gi中无电流。
iS1
iS2
iSk
iS
串联:
i S i S k ,i S i S 1 i S 2 i S k
电流相同的理想电流源才能串联，并且每个电 流源的端电压不能确定。
三、 理想电源的串并联
例1
uS
iS
uS
例2
uS
iS
iS
例3
uS1
uS2 iS2
is1
iS
iS = iS2 – iS1
u
Rn + un _
_
uk
Rk Req
u
例 两个电阻分压（voltage division）， 如下图所示
i
+
+ u-1
R1
u-
u2 R2 _+
u1
R1 R1 R2
u
u2
R2 R1 R2
u
（注意方向 !）
4. 功率关系 p1 = R1i 2 ， p2 = R2i 2 ， ， pn = Rni 2 p1 : p2 : : pn= R1 : R2 : : Rn
清华大学电路原理课件--电路原理_skja_36
3 I ab 30 3 I bc 30 3 I ca 30
o
I ca
Uab
IB
o
I
B
30o
30o
UA
I C I ca I bc
2012-8-30
o
I bc
I ab
电路原理
IA
结论：
(1) 负载上相电压与线电压相等，且对称。 (2) 线电流与相电流也是对称的。线电流大小是相电 流的 3 倍，相位落后相应相电流30°。 故上述电路也可只计算一相，根据对称性即可得到其余 两相结果。 a A IA + IA a Z Z A UA _ I ca + N I ab n UC UB UA Z/3 c b – B Z IB C + I bc + n N
IA
IA
A
UCA
+ – N
A
UAB
IB
UA B UCA
UAN
UA B UCA
IB
–
B C
U BC
I C U BC
UCN
U BN
B C
将接电源用Y接电源替代，保证其线电压相等，再根 2012-8-30 电路原理 据上述Y–Y， Y– 接方法计算。
+
IC UBC
U
AN
1 3 1 3 1 3
U
AB
30 30 30
o
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电路定理
第一讲（总第十二讲）
叠加定理 替代定理
29.12.2020
.
1
叠加定理 (Superposition Theorem)
叠加定理
在线性电路中，任一支路电流(或电压)都是电路中 各个独立电源单独作用时，在该支路产生的电流(或电 压)的代数和。
单独作用：一个电源作用，其余电源不作用
不作用的
电压源（us=0) 短路 电流源 (is=0) 开路
u s 2 R 12
ia2
u s2 R 11
R 22 R 12
R 21 R 22
R 22 Δ
( us2 )
R 12 Δ
u s2
R 12
Δ
R 22
u s2
0
R 12
ia3
u s3 R 11
R 22 R 12
R 21 R 22
R 12 Δ
( u s3 )
R 12 Δ
u s3
证得 29.12.2020 ia = ia1 + ia2 + ia3 .即回路电流满足叠加定理 6
u s 1 R 12
0 i a 1 R 11
R 22 R 12
R 21 R 22
R 22 Δ
u s1
29.12.2020
i12
R1
R2
R3
ia2 + ib2
–us2
R11ia2+R12ib2=-us2
R21ia2+R22ib2=us2
u s 2 R 12
ia2
u s2 R 11
R 22 R 12
4A
–
u'=4V
u"= -42.4= -9.6V
共同作用：u=u'+u"= 4+(- 9.6)= - 5.6V
小结 :
i1 R1
+ us1
–
1. 叠加定理只适用于线性电路的电流、电压计算。
电压源为零—短路。 电流源为零—开路。 u，i 叠加时要注意各分量的方向。
2. 功率不能叠加(功率为电源的二次函数)。
推广到 l 个回路 , 第 j 个回路的回路电流：
第j列
R11 us11 R1l
R j1 u sjj R jl
i j Rl1
u sll Δ
R ll
Δ Δ 1 ju s1 1 Δ Δ 2 ju s2 2 Δ Δ jju sj j Δ Δ lju sll
29.12.2020
同样可以证明：线性电阻电路中任意支路的电压
等于各电源（电压源、电流源）在此支路产生的电压
的代数和。
29.12.2020
.
8
6
例1
求图中电压u。
+ 10V
–
解
(1) 10V电压源单独作用，
+
4 u
4A
–
(2) 4A电流源单独作用，
4A电流源开路 6
10V电压源短路 6
+ 10V
–
+
4 u' –
+
4 u''
其中
R11=R1+R2 R12= R21= -R2 R22=R2+R3 us11=us1-us2 us22=us2-us3
Δ R11 R12 R21 R22
R11 R22 R12 R21
i11
R1
R2
R3
+ ia1
ib1
–us1
R11ia1+R12ib1=us1
R21ia1+R22ib1=0
举例证明定理
i1
R1 + ia
–us1
R2 + ib
–us2
R3
+
–us3
i11
R1
R2
R3
+ ia1
ib1
–us1
证明
i1 = i11 + i12 + i13
i12
R1
R2
R3
ia2 + ib2
–us2
i13
R1 ia3
R2 ib3
R3
+
–us3
29.12.2020
.
3
i1
R1 + ia
–us1
Us"= -10I1"+U1”
I1' 6
+ 10 I1'–
+ 10V
–
+
+
4 U1' Us'
–
–
I1'' 6
+10 I1''–
+
+
4 U1" Us'' 4A
–
–
I1
10 64
1A
Us'= -10 I1'+U1’= -10 I1'+4I1' = -101+41= -6V
I14 4641.6A U1446649.6V
R 12 Δ
u s3
5
us1 1
ia
us2 2 R11
R21
R12
R22 R12
R2 Δ
2
us1
1
R12 Δ
us22R Δ 22 u s1R 1Δ 2R 22 u s2R Δ 12 u s3
R22
u s 1 R 12
0 i a 1 R 11
R 22 R 12
R 21 R 22
R 22 Δ
u s1
.
10
例2 求电压Us 。
I1 6
+ 10 I1 –
+
+
10V –
4
Us 4A
–
解:
(1) 10V电压源单独作用：
I1' 6
+ 10 I1'–
(2) 4A电流源单独作用：
I1'' 6
+10 I1''–
+
10V –
+
+
4 U1' Us'
–
–
+
+
4 U1" Us'' 4A
–
–
Us'= -10 I1'+U1'
p u ( u i u ) i i ( ) u i u i
3. 也可以把电源分组叠加(每个电源只能作用一次)
i1’
i1''
R2 +
us2 –
is R1
+
=
us1
–
R2 is R1 +
R2 +
us2 –
4. 含受控源电路亦可用叠加，但受控源应始终保留。
29.12.2020
R 21 R 22
R 22 Δ
( us2 )
R 12 Δ
u s2
R 12
Δ
R 22
.
u s2
i13
R1 ia3
R2 ib3
R3
+
–us3
R11ia3+R12ib3=0
R21ia3+R22ib3=-us3
0
R 12
ia3
u s3 R 11
R 22 R 12
R 21 R 22
R 12 Δ
( u s3 )
Us"= -10I1"+U1”
= -10 (-1.6)+9.6=25.6V 共同作用： Us= Us' +Us"= -6+25.6=19.6V
齐性原理（homogeneity property)
当电路中只有一个激励(独立源)时，则响应(电压或电流) 与激励成正比。
.
7
Δ Δ 1 ju s1 1 Δ Δ 2 ju s2 2 Δ Δ jju sj j Δ Δ lju sll
把 usi 个系数合并为Gji
us1 usb
b
G uji si i 1
第i个电压源单独作用时在 第j 个回路中产生的回路电流
ij1 ij2 iji ijb
支路电流是回路电流的线性组合，支路电流满足叠加定理。
R2 + ib
–us2
R3
+
–us3
由回路法
R11ia+R12ib=us11 R21ia+R22ib=us22
us1 1
ia
us2 2 R11
R21
R12
us1-us2
us2-us3
R22 R12
R2 Δ
2
us1
1
R12 Δ
us2
2
R22
R Δ 22 u s1R 1Δ 2R 22 u s2R Δ 12 u s3
第一讲（总第十二讲）
叠加定理 替代定理
29.12.2020
.
1
叠加定理 (Superposition Theorem)
叠加定理
在线性电路中，任一支路电流(或电压)都是电路中 各个独立电源单独作用时，在该支路产生的电流(或电 压)的代数和。
单独作用：一个电源作用，其余电源不作用
不作用的
电压源（us=0) 短路 电流源 (is=0) 开路
u s 2 R 12
ia2
u s2 R 11
R 22 R 12
R 21 R 22
R 22 Δ
( us2 )
R 12 Δ
u s2
R 12
Δ
R 22
u s2
0
R 12
ia3
u s3 R 11
R 22 R 12
R 21 R 22
R 12 Δ
( u s3 )
R 12 Δ
u s3
证得 29.12.2020 ia = ia1 + ia2 + ia3 .即回路电流满足叠加定理 6
u s 1 R 12
0 i a 1 R 11
R 22 R 12
R 21 R 22
R 22 Δ
u s1
29.12.2020
i12
R1
R2
R3
ia2 + ib2
–us2
R11ia2+R12ib2=-us2
R21ia2+R22ib2=us2
u s 2 R 12
ia2
u s2 R 11
R 22 R 12
4A
–
u'=4V
u"= -42.4= -9.6V
共同作用：u=u'+u"= 4+(- 9.6)= - 5.6V
小结 :
i1 R1
+ us1
–
1. 叠加定理只适用于线性电路的电流、电压计算。
电压源为零—短路。 电流源为零—开路。 u，i 叠加时要注意各分量的方向。
2. 功率不能叠加(功率为电源的二次函数)。
推广到 l 个回路 , 第 j 个回路的回路电流：
第j列
R11 us11 R1l
R j1 u sjj R jl
i j Rl1
u sll Δ
R ll
Δ Δ 1 ju s1 1 Δ Δ 2 ju s2 2 Δ Δ jju sj j Δ Δ lju sll
29.12.2020
同样可以证明：线性电阻电路中任意支路的电压
等于各电源（电压源、电流源）在此支路产生的电压
的代数和。
29.12.2020
.
8
6
例1
求图中电压u。
+ 10V
–
解
(1) 10V电压源单独作用，
+
4 u
4A
–
(2) 4A电流源单独作用，
4A电流源开路 6
10V电压源短路 6
+ 10V
–
+
4 u' –
+
4 u''
其中
R11=R1+R2 R12= R21= -R2 R22=R2+R3 us11=us1-us2 us22=us2-us3
Δ R11 R12 R21 R22
R11 R22 R12 R21
i11
R1
R2
R3
+ ia1
ib1
–us1
R11ia1+R12ib1=us1
R21ia1+R22ib1=0
举例证明定理
i1
R1 + ia
–us1
R2 + ib
–us2
R3
+
–us3
i11
R1
R2
R3
+ ia1
ib1
–us1
证明
i1 = i11 + i12 + i13
i12
R1
R2
R3
ia2 + ib2
–us2
i13
R1 ia3
R2 ib3
R3
+
–us3
29.12.2020
.
3
i1
R1 + ia
–us1
Us"= -10I1"+U1”
I1' 6
+ 10 I1'–
+ 10V
–
+
+
4 U1' Us'
–
–
I1'' 6
+10 I1''–
+
+
4 U1" Us'' 4A
–
–
I1
10 64
1A
Us'= -10 I1'+U1’= -10 I1'+4I1' = -101+41= -6V
I14 4641.6A U1446649.6V
R 12 Δ
u s3
5
us1 1
ia
us2 2 R11
R21
R12
R22 R12
R2 Δ
2
us1
1
R12 Δ
us22R Δ 22 u s1R 1Δ 2R 22 u s2R Δ 12 u s3
R22
u s 1 R 12
0 i a 1 R 11
R 22 R 12
R 21 R 22
R 22 Δ
u s1
.
10
例2 求电压Us 。
I1 6
+ 10 I1 –
+
+
10V –
4
Us 4A
–
解:
(1) 10V电压源单独作用：
I1' 6
+ 10 I1'–
(2) 4A电流源单独作用：
I1'' 6
+10 I1''–
+
10V –
+
+
4 U1' Us'
–
–
+
+
4 U1" Us'' 4A
–
–
Us'= -10 I1'+U1'
p u ( u i u ) i i ( ) u i u i
3. 也可以把电源分组叠加(每个电源只能作用一次)
i1’
i1''
R2 +
us2 –
is R1
+
=
us1
–
R2 is R1 +
R2 +
us2 –
4. 含受控源电路亦可用叠加，但受控源应始终保留。
29.12.2020
R 21 R 22
R 22 Δ
( us2 )
R 12 Δ
u s2
R 12
Δ
R 22
.
u s2
i13
R1 ia3
R2 ib3
R3
+
–us3
R11ia3+R12ib3=0
R21ia3+R22ib3=-us3
0
R 12
ia3
u s3 R 11
R 22 R 12
R 21 R 22
R 12 Δ
( u s3 )
Us"= -10I1"+U1”
= -10 (-1.6)+9.6=25.6V 共同作用： Us= Us' +Us"= -6+25.6=19.6V
齐性原理（homogeneity property)
当电路中只有一个激励(独立源)时，则响应(电压或电流) 与激励成正比。
.
7
Δ Δ 1 ju s1 1 Δ Δ 2 ju s2 2 Δ Δ jju sj j Δ Δ lju sll
把 usi 个系数合并为Gji
us1 usb
b
G uji si i 1
第i个电压源单独作用时在 第j 个回路中产生的回路电流
ij1 ij2 iji ijb
支路电流是回路电流的线性组合，支路电流满足叠加定理。
R2 + ib
–us2
R3
+
–us3
由回路法
R11ia+R12ib=us11 R21ia+R22ib=us22
us1 1
ia
us2 2 R11
R21
R12
us1-us2
us2-us3
R22 R12
R2 Δ
2
us1
1
R12 Δ
us2
2
R22
R Δ 22 u s1R 1Δ 2R 22 u s2R Δ 12 u s3