基于Matlab的发动机特性研究
基于MATLAB的货车动力性能的分析实验

基于MATLAB的货车动力性能的分析实验一、实验目的及要求1.1 实验目的1.了解MATLAB的基本知识,熟悉相关的操作;2.能够熟练运用其中的一些方法来解决和专业有关的基本问题。
1.2 实验要求1.掌握MATLAB数值计算、程序设计以及二维绘图的基本操作方法;2.以轻型货车为例,通过独立的编程实验确定汽车的动力性能;3.以4挡和5挡两种变速器的对比、2挡和4挡两种起步挡位的对比来分析变速器传动比和起步挡位的变化对汽车的动力性能的影响。
二、背景介绍数值计算指有效使用数字计算机求数学问题近似解的方法与过程,主要研究如何利用计算机更好的解决各种数学问题。
MATLAB软件具有出色的数值计算能力,在世界上同类软件中占据主导地位,它的数值计算功能主要包括:①变量和数值;②矩阵和数组;③多项式计算;④数据分析等四个方面的内容。
MATLAB语言简洁紧凑,使用方便灵活,其语法规则与人的思维和书写习惯相近,方面操作。
且程序书写形式自由,利用其丰富的库函数避开繁杂的子程序编程任务,压缩了很多不必要的编程工作。
另外,它的语法限制不严格,程序设计自由度大。
此外,MATLAB 还有着非常强大的绘图功能。
作为一个功能强大的工具软件,MATLAB 提供了大量的二维、三维图形函数。
由于系统采用面向对象的技术和丰富的矩阵运算,所以在图形处理方面既方便又高效。
在此背景下,像确定汽车动力性能这样不是很复杂的数值计算和二维图形处理问题,运用MATLAB来进行解决是绰绰有余的。
三、基本实验内容3.1 实验原理汽车的动力性系指汽车在良好路面上直线行驶时由汽车受到的纵向外力决定的、所能达到的平均行驶速度。
从获得尽可能高的平均行驶速度的观点出发,汽车的动力性主要由三方面的指标来评定,即:,指在水平良好的路面(混凝土或沥青)上汽车能达1)汽车的最高速度umax到的最高行驶速度;2)汽车的加速时间t,表示汽车的加速能力,常用原地起步加速时间与超车加速时间来表明汽车的加速能力;,指满载(或某一载质量)时汽车在良好路面上的3)汽车的最大爬坡度imax最大爬坡度,表征汽车的上坡能力。
基于MATLAB语言的发动机特性研究

) ?++ $"96; -D-")+)". ))?"? )E>") .+?H. .)+"F !"9@ ﹒
$AB ) C %,-
- )-? - .F- /+> - ?)+ ) ++D ) -?/ ) .F> ) D?? ) E?>
)>)H> ).+HD ))/H. )).HF ))+H/ ))+HE ))+HF ))DHF ).+H-
* 本文利用()*+),强大的数据处理和三
维曲线绘图功能 % 提出了一种绘制发动机特性的新
"% #
!
发动机特性数学模型
对发动机特性及其与车辆动力传动系匹配进行
式中 %) 和 , 分别表示任意 一 条 特 性 曲 线 的 纵 坐 标 与 横 坐 标 /* 为多项式的阶次 /’+为多项式各 项拟合系数 % 一般采用最小 二 乘法确定 *
根据以上原理 ! 用 !"#$%& 语言编制相应的程 序解出回归方程的系数向量 ! 即可得到试验数据的 回归方程 "
&+ & # $ &( ’ !"’ ! !$ ’ ( !#"!$"!#")!#"$"!$" *!#!$" % " * ’ $ &’,- ( %
- >++ $"96; !"9@ ﹒
$AB ) C%
()*+), 中 的 曲 线 拟 合 等 相 应 的 工 具 箱 或 ./01234%./01560 %./014//0%./017/82 等 函 数 可 以 非 常 好
MATLAB和Origin绘制发动机万有特性曲线程序及方法
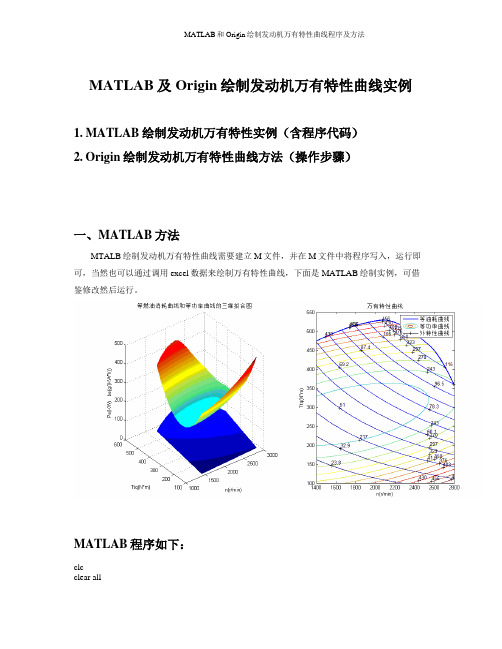
MATLAB及Origin绘制发动机万有特性曲线实例1.MATLAB绘制发动机万有特性实例(含程序代码)2.Origin绘制发动机万有特性曲线方法(操作步骤)一、MATLAB方法MTALB绘制发动机万有特性曲线需要建立M文件,并在M文件中将程序写入,运行即可,当然也可以通过调用excel数据来绘制万有特性曲线,下面是MATLAB绘制实例,可借鉴修改然后运行。
MATLAB程序如下:clcclear all%不同转速下的燃油消耗率与扭矩的曲线拟合be1=[222.8,220.4,232.4,228.5,227.8,232.6,248.5,245.9,272.4,329.7];Ttq1=[399.8,354.1,318.5,278.1,236.2,203.6,185.3,157.2,117.2,80.8];T1=80:320/9:400;%转换矩阵格式Be1=interp1(Ttq1,be1,T1,'spline');%n=1400r/min时燃油消耗率与扭矩的曲线拟合be2=[222.0,221.7,235.4,226.5,230.5,236.8,249.1,276.1,407.9,487.0];Ttq2=[409.1,365.7,328.3,284.1,243.7,203.2,164.3,123.9,83.5,39.7];T2=39:371/9:410;Be2=interp1(Ttq2,be2,T2,'spline');be3=[226.0,225.3,226.4,233.9,242.1,283.3,253.9,271.4,323.5,468.6];Ttq3=[408.3,368.3,328.3,289.0,244.4,208.8,167.7,132.1,89.5,46.1];T3=46:363/9:409;Be3=interp1(Ttq3,be3,T3,'spline');be4=[206.5,231.1,231.1,233.0,242.0,244.9,265.0,299.8,398.0,596.8];Ttq4=[425.6,380.3,332.7,290.9,244.4,205.1,160.2,114.5,68.8,30.7];T4=30:396/9:426;Be4=interp1(Ttq4,be4,T4,'spline');be5=[234.7,259.8,235.5,237.6,242.8,292.3,277.9,308.7,396.2,605.9];Ttq5=[420.7,379.6,334.6,291.6,244.4,202.8,157.5,116.0,74.1,37.8];T5=37:384/9:421;Be5=interp1(Ttq5,be5,T5,'spline');be6=[174.2,242.2,252.1,287.4,253.6,263.6,290.6,316.8,378.0,518.8];Ttq6=[404.6,360.5,322.7,283.0,243.3,205.5,162.1,124.7,86.8,52.4];T6=52:353/9:405;Be6=interp1(Ttq6,be6,T6,'spline');be7=[256.9,253.7,253.5,260.0,303.8,280.7,300.6,346.6,435.6,812.9];Ttq7=[378.0,344.7,310.3,264.3,226.1,186.8,154.2,115.3,76.3,34.1];T7=34:344/9:378;Be7=interp1(Ttq7,be7,T7,'spline');be8=[257.9,295.3,282.4,288.7,301.9,329.7,357.0,475.4,580.3,1080.1];Ttq8=[315.6,275.5,242.5,210.3,178.5,145.6,118.6,72.6,52.8,22.4];T8=22:294/9:316;Be8=interp1(Ttq8,be8,T8,'spline');B=[Be1';Be2';Be3';Be4';Be5';Be6';Be7';Be8'];N=[1400*ones(10,1);1600*ones(10,1);1800*ones(10,1);2000*ones(10,1);2200*ones(10,1);2400*ones (10,1);2600*ones(10,1);2800*ones(10,1)];Ttqn=[T1';T2';T3';T4';T5';T6';T7';T8'];G=[ones(80,1),N,Ttqn,N.^2,N.*Ttqn,Ttqn.^2];A=G\B;%A为6*1矩阵[n,Ttq]=meshgrid(1400:2800,100:600);%生成n-Ttq平面上的自变量“格点”矩阵be=A(1)+n.*A(2)++Ttq*A(3)+n.^2*A(4)+n.*Ttq*A(5)+Ttq.^2*A(6);Pe=Ttq.*n/9550;%外特性实验数据拟合Nw=[1403,1597,1797,1986,2102,2199,2303,2400,2507,2598,2700,2802]; Ttqw=[474,497,515,526,528.8,522.8,509.5,492.2,471.2,448.4,408.3,357.4]; n0=1400:2800;Ttqw_N=interp1(Nw,Ttqw,n0,'spline');h=repmat(Ttqw_N,501,1);ii=find(Ttq>h);%确定超出边界的“格点”下标be(ii)=NaN;%强制为非数Pe(ii)=NaN;%强制为非数%绘制等燃油消耗率曲线和等功率曲线三维拟合图subplot(1,2,1);mesh(n,Ttq,be);hold on;mesh(n,Ttq,Pe);axis([1000,3000,100,600,0,500]);hold on;xlabel('n(r/min)')ylabel('Ttq(N*m)')zlabel('Pe(KW) be(g/(KW*h))')title('等燃油消耗曲线和等功率曲线的三维拟合图')%绘制边界线(外特性曲线)subplot(1,2,2);plot(n0,Ttqw_N,'LineWidth',2);axis([1400,2800,100,550]);xlabel('n(r/min)');ylabel('Ttq(N*m)');title('万有特性曲线');hold on;%绘制等油耗率曲线的二维图B=contour(n,Ttq,be,11);%画等位线,并给出标识数据clabel(B);%把“等位值”沿等位线随机标识hold on;%绘制等功率曲线的二维图P=contour(n,Ttq,Pe,11);%画等位线,并给出标识数据clabel(P);%把“等位值”沿等位线随机标识legend('等油耗曲线','等功率曲线','外特性曲线')hold off二、Origin方法用origin软件绘制发动机万有特性曲线方法一、万有特性数据输入在excel中整理好发动机万有特性数据,主要包括发动机转速、扭矩、燃油消耗率及功率数据。
基于MATLAB的发动机特性实时处理和计算系统

即:
K
∑( yt - y′t ) 2
C=
1-
t =1 K
×100 % (2)
∑( yt - y) 2
t =1
其中
,y
=
1 Kt
K
∑yt
=1
为原始试验数据的总体均值 ;
K 为特性曲线的试验数据点数 。
MATLAB中 的 曲 线 拟 合 等 相 应 的 工 具 箱 或
Polyfit,Polyval,Polytool,Polyconf等函数可以非常好地
MATLABReal-TimeWorkshop 和相关的工具箱为平 台的开放软件包 ,各种新的测试和分析技术都能以 功能模块的形式加入到软件包 ,这样可以很方便地 进行软件的维护和二次开发以及应用的升级 ;整个 系统与 Windows有一致的用户界面 ;采用了面向对 象的程序设计方法 ,可以和其它 Windows环境下的 软件交换数据 。软件系统的功能框图见图 2 。
2
ingTherearemanyadvancedandscientificmethodsforprocessingtheengineperformancetestdataandengineperformancesimu
2
lationcomputing,anddatavisualizinginthissystem.ltprovidesareliableandefficienttooltoresearchintoengineperformanceand
式中 , ge 为 n = nj 时发动机万有特性函数 ,当 n 不等于 nj 时 ,利用插值计算 。ge ( nj , TPe ) 是建立的 发动机万有特性的神经网络模型 ,发动机的转速和
基于MATLAB基础上的发动机万有特性曲线的建立

基于MATLAB基础上的发动机万有特性曲线的建立杨丽娟;赵丹平【摘要】发动机性能的好坏直接影响着整车运行的平顺性、安全性、稳定性等,要全面评价发动机性能,万有特性曲线则是一个很好的工具.万有特性曲线是以发动机转速为横坐标,以扭矩或平均有效压力为纵坐标,在坐标系内画出等燃油消耗率曲线和等功率曲线[1].绘制万有特性曲线的方法有很多种,MATLAB语言是其中之一.本文利用强大的MATLAB绘图工具,绘制了发动机的万有特性曲线,经分析,该方法是一个有效的精确度较高的方法.【期刊名称】《交通节能与环保》【年(卷),期】2010(000)001【总页数】3页(P32-33,48)【关键词】MATLAB;发动机;万有特性【作者】杨丽娟;赵丹平【作者单位】内蒙古工业大学,内蒙古,赤峰,010051;内蒙古工业大学,内蒙古,赤峰,010051【正文语种】中文0 引言发动机是汽车的动力源,发动机性能的好坏直接影响着整车的动力性与经济性。
汽车的运行工况是个随机的过程,受到很多因素的影响,如道路条件、交通流量、气候条件以及汽车自身技术性能的变化等等。
在所有的运行工况下,发动机都应能够与传动系实现最佳匹配,以使整车动力性、经济性、排放性和噪声污染等方面均处于最佳状态。
然而,对发动机性能的分析与研究是保证整车性能达到最佳的重要前提。
MATLAB语言是一个功能强大的仿真软件,可以完成复杂的数学运算,实现对动态系统的建模仿真等,在工程计算中应用非常广泛。
本文利用MATLAB的强大的绘图功能,建立了发动机的输出转矩模型、油耗模型及万有特性曲线。
通过输出转矩模型,由当前发动机节气门开度及转速既可得到与之相对应的发动机的转出转矩,从而为分析发动机性能奠定基础;发动机油耗模型反应了其有效燃油消耗率与转速和转矩之间的关系,发动机在不同工况下运行时,由此模型既可得到不同工况下发动机的比油耗,从而为分析整车燃油经济性提供数据支持;万有特性曲线是在由发动机转速和转矩构成的坐标系内,绘制出等油耗曲线、等功率曲线、外特性曲线等,通过万有特性曲线既可较全面地了解发动机在不同工况下的性能指标。
基于MATLAB语言的发动机万有特性研究

第 25 卷 第 3 期 关志伟等 :基于 MATLAB 语言的发动机万有特性研究
341
图 1 发动机负荷特性曲线图 Fig111 Burden characteristic curve of engine
摘 要 : 在建立了发动机万有特性曲面拟合数学模型的基础上 ,利用 MATLAB 语言的矩阵运算 、三维曲线绘 图 、等值线法等方法 ,提出了一种计算并绘制发动机万有特性的新方法 。运用该方法 ,绘制了某发动机万有特 性的等油耗曲线 ,根据此曲线对某载货汽车等速行驶燃油经济性进行了模拟计算 ,并与试验结果进行对比 。 对比结果表明 ,该方法具有直观 、简便 、精度高 、实用性强等优点 。 关键词 : MATLAB ; 发动机 ; 万有特性 ; 三维曲面 中图分类号 : TP312 文献标识码 : A 文章编号 : 100025684 (2003) 0320339204
3 整车燃油经济性模拟计算及试验对比
利用上 述 发 动 机 万 有 特 性 数 学 模 型 及 基 于 MATLAB 语言的算法 ,并参考汽车理论中汽车燃 油经济性的计算方法 ,可对整车燃油经济性进行 模拟计算 。
已知某载货汽车整车有关参数 :汽车总质量 12 245 kg、汽 车 空 气 阻 力 系 数 0164 、迎 风 面 积 419 m2 、道 路 地 面 附 着 系 数 0178 、最 大 爬 坡 度 26 %、最高车速 120 km/ h 。以等速行驶燃油消耗 量为例 ,对该载货汽车燃油经济性进行模拟计算 。
表 1 模拟计算与试验结果对比
基于MATLAB的发动机特性实时处理和计算系统

詹 樟 松 , 兴 春 , 登 兴 , 晓进 刘 孙 何 ( 庆 长 安 汽 车 股 份 有 限公 司 技 术 中心 , 庆 402 ) 重 重 003
摘要: 应用 M T A A L B语 言开 发 的发 动机特 性 实时 处理 和 计算 系 统 , 一 个 数 据 实 时采 集 , 是 自动 化 程 度 高 、 率 高 和 效 精度 高 的测 试 、 理和 计算 系统 , 处 系统 采用 的 发动机 试 验数 据 处 理 和特 性 模 拟 计 算方 法 灵 活 多 样 , 学 先进 . 据 科 数 处 理 和 模 拟 计 算 的结 果 精 度 高 , 可 视 化 效 果 好 , 研 究 发 动 机 性 能 、 车 的 动 力 性 和 燃 油 经 济 性 等 提 供 了 一个 可 且 为 汽 靠 、 效 的 工具 : 有 关键 词 : 动机 特性 ; 据采 集 ; 学 模型 ; 合 ; 经 网络 ; T A 发 数 数 拟 神 MA L B 中图 分 类 号 : K 2 T 41 文 献标 识码 : A 文 章 编 号 :00—6 9 (0 2 0 10 44 20 )5一OO —0 09 4
并 以其 充 实 、 正 和 完 善 理论 , 到 内燃 机 设 计 的更 修 达
合 理 和 优 化 。 目前 大 部 分 单 位 在 进 行 发 动 机 试 验 及 试 验 数 据 处 理 过 程 中 仍 然 以 人 工 为 主 , 显 示 仪 表 即
型 的计 算 及 结 果 的可 视 化 , 可 根 据 需 要 做 进 一 步 并
Ab t a t E gn ef r n e r a —t r c s ig a d c mp t g s s m sd v lp d b f b l n u e I i a —t a s r c : n i e p r ma c e l i p o e sn n o u n y t i e e o e y Ma a a g  ̄ .t sa r l i d — o me i e l e me
基于MATLAB的发动机悬置系统振动烈度分析

则系统的六个自由度,用广义坐标描述为:
对于上述动力总成悬置系统力学模型,根据第二类拉格朗日方程式,振动微分方程为:
得出系统发动机悬置系统六自由度运动微分方程:
四、发动机悬置系统振动烈度的求解与仿真
为了求得方程 的解,可以将位移和速度都看作独立的变量,将原来的n个二阶微分方程作为2n个一阶常微分方程来处理,也就是对状态方程进行求解。
二、分析发动机悬置系统的振动
发动机作为汽车的主要振源,其振动经动力总成悬置系统传递到车架或车身上。因此动力总成悬置隔振系统的设计对于汽车减振降噪是非常重要的。发动机通过悬置元件安装在车架上,悬置元件既是弹性元件,又是减振装置,其特性直接关系到发动机振动向车体的传递,并影响整车的振动与噪声。合理的悬置不但可以减小振动、降低噪声以改善乘坐舒适性,还能提高零部件和整车寿命。因此,发动机的悬置设计越来越受到重视。
发动机振动对整车的影响有所提高,成为车辆的一个主要振源,其振动经悬置系统传递后引起车身的振动。所以建立合理的发动机动力总成悬置系统模型快速准确地获得动力总成悬置系统的动态特性显得尤为重要。通常采用悬置元件的静刚度建立悬置系统MATLAB力学模型,而在实际工况下,发动机悬置系统是在一定频率下振动的,建立系统实际工况下动力学模型时,用悬置元件动刚度代替静刚度,以发动机的一种工况为例,给出一种悬置系统实际工况条件下MATLAB建模的方法,具有较高的工程实用价值。
现对方程补充下列方程:
方程 和 可写为如下状态方程:
即:
其中 , ,
,
状态方程标准形式:
1)发动机不平衡激励
8V150发动机采取平衡措施后,只有倾覆力矩,图2为转速n=2200rpm时,在发动机一个工作循环倾覆力矩随曲轴转角的变化关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
=
arcsin(
Fi ma g
)
,从
图
1
可
知,
YC6J190-33 发动机时汽车最大车速是 87km/h,I 档最大爬
坡度 ilmax=57.9%,最大爬坡角 almax=30.08。;由图 2 可知,康
明斯 ISBE4+225 发动机时汽车最大车速是 90km/h,I 档最大
Polyval、Polytool、Polyconf 等函数均可对上述曲线拟合。 转 矩(332.156N•m)初 选 玉 柴 YC6J190-33 发 动 机、康 明 斯
ISBE4+225 发动机与德国曼 D0836LFL 发动机,通过其模拟曲
51
理论与算法
2019.08
线图,分别对发动机的转矩特性以及比油特性进行计算,借 助 Matlab 对多项式进行拟合,得出三种发动机的转矩和比油 特性拟合曲线。 2.1 动力性能计算
Research on Engine Characteristics Based on Matlab
Yuan Jian (BYD automobile industry co., LTD.,Shenzhen Guangdong,518118)
Abstract: In this paper, the engine’s external characteristic curve is drawn by using matlab, and the engine’s different torque characteristics and specific fuel consumption characteristics are obtained, and the quadratic polynomial fitting is carried out. The results show that the selected engine has better matching performance. Key words:matlab;engine;characteristics;comparative analysis
1.1 发动机外特性的数学模型
式中 :{a0...ak-1}——模型中待定系数 ; {e1...aN-1}——随机误差 ; N——实验数据点数 ; K——多项式项数(k=(l+1)(l+2)/2,l 为多项式最高 幂次)。 基于以上分析,可使用 Matleab 语言编制对应程序得出
关于发动机的外特性可以借助曲线拟合的方法来构建 回归方程系数向量,计算得出实验数据的回归方程如下 :
0 引言
利用 MATLAB 能够对汽车发动机的实验数据进行整理与 分析,获取相应的拟合曲线,实现动态系统的建模与仿真,因 此 MATLAB 被广泛应用于汽车工程计算中 [1]。
1.2 万有特性的数学模型 发动机的万有特性常使用多元回归方程拟合,将发动机
的有效燃油消耗率 ge 看成转速 ne 与有效转矩 Me 的函数,回 归模型如下 :
汽车在行驶的过程中需要克服滚动阻力(Ff)、空气阻力 (Fw)、坡度阻力(Fi),由此可得汽车行驶中驱动力和行驶过程
中阻力平衡方程为 :Ft=Ff+Fw+Fi,借助 Matlab 把各驱动力下 车速的变化以及不同坡度下 Ft 与车速的变化进行绘制,可得 到汽车行驶性能曲线,图 1、图 2、图 3 分别为三种发动机汽车 行驶性能和爬坡度曲线。
1 发动机特性的数学模型
目 前,使 用 实 验 数 据 对 发 动机性能进行描述的方法主要 有两种 :表格法与数学模型描 述法。其中,表格法的特点为计
ggee12
1 1
ne1 ne2
geN 1 neN
MMee12= nnee2122 nnee11MMee11 MMee1222nnee12l l nnee1l2−l1−M1Me1e2 MMe1el 2l × aa10
2 整车性能计算
P——多项式的阶次 ;
本次的研究对象为中型货车,总重为 6.75 吨,该车的
Ai——多项式拟合系数,一般通过最下二乘法确定。 Matlab 中 曲 线 拟 合 等 相 应 的 工 具 箱 或 Polyfit、
最 高 车 速 90km/h,其 中,发 动 机 的 额 定 转 速(np)为 2500r/ min,根 据 前 期 计 算 所 得 发 动 机 最 大 功 率(82.82kw)与 最 大
图 1 YC6J190-33 发动机时汽车的行驶性能曲线(左)与汽车爬坡 度图(右)
图 2 康明斯 ISBE4+225 发动机时汽车的行驶性能曲线(左)与汽 车爬坡度图(右)
图 3 德国曼 D0836LFL 发动机时汽车的行驶性能曲线(左)与汽车 爬坡度图(右)
由 Fi=magsina 可 得
M eN
neN 2
neN M eN
M eN 2 neN l
ne
l 2
−1M
e
2
M
e
l 2
ak
−1
ee10
eN
算简单、精度较高,但该法需要的实验数据测试量较大且测 量精度要求较高 ;数学模型描述法是通过构建发动机转速、 转矩以及油耗等参数间的数学模型对发动机的性能特性进 行描述,该方法的特点在于其模拟精度高低取决于建模的方 法,因此该方法的应用范围更广。
相关性能参数之间的关系,拟合形式多使用多项式,其中拟
合通式如下 :
p
∑ =y ai ⋅ xi i =1
= ge
ao
1,
ne
,
M
e
,
ne
2
,
ne
M
e
,
M
2 e
,,
M
l e
×
a1
ak −1
式中 :y——任意一条特征曲线的纵坐标 ; x——任意一条特征曲线的横坐标 ;
2019.08
理论与算法
基于 Matlab 的发动机特性研究
袁坚 (比亚迪汽车工业有限公司,广东深圳,518118)
摘要 :本文使用 Matlab 绘制出发动机的外特征曲线,获取发动机不同转矩特性与比油耗特性,并进行四次多项式拟合 , 结果表明所选取的发动机整车匹配性能较好。 关键词 :Matlab ;发动机 ;特性研究 ;对比分析
