弹道仿真
弹丸水下高速运动外弹道建模与仿真的开题报告

弹丸水下高速运动外弹道建模与仿真的开题报告一、研究背景和意义弹丸水下高速运动外弹道建模和仿真在军事、海洋工程、水下探测等领域都具有重要的应用价值。
在海洋探测与勘察领域,通过弹丸水下高速运动外弹道建模和仿真可以对海洋生态环境进行监测和保护,对自然灾害进行预警和防护。
在军事领域,水下武器的性能与弹道特性直接关系到其作战效果,因此弹丸水下高速运动外弹道建模和仿真对于提高水下武器的作战效能起到重要作用。
二、研究内容和方法1.研究内容(1)弹丸水下高速运动的力学特性研究;(2)计算流体力学仿真模型的建立;(3)弹道建模;(4)仿真算法设计。
2.研究方法(1)理论研究。
通过文献资料、实验数据等途径,对弹丸水下高速运动的力学特性进行理论研究。
(2)计算流体力学仿真模型的建立。
通过建立数值模型,对水流与弹丸之间的相互作用进行研究。
(3)弹道建模。
通过弹性力学、材料力学等理论建立弹丸外弹道的数值模型。
(4)仿真算法设计。
基于计算流体力学和弹道建模结果,设计仿真算法,对弹丸在水中的运动进行数值模拟。
三、研究进展和难点1.研究进展通过文献资料和实验数据的分析,已经对弹丸水下高速运动的力学特性进行了初步研究;通过计算流体力学领域的知识,已经建立了计算模型,掌握了模拟弹丸在水中运动的方法;通过弹性力学和材料力学的理论知识,已经对弹丸外弹道进行了初步建模,为后续的仿真算法设计提供了基础。
2.研究难点(1)对弹丸水下高速运动的力学特性进行深入研究;(2)建立精度更高的计算流体力学模型;(3)建立更为精确的弹道数值模型;(4)设计适用于弹丸水下高速运动仿真的算法。
四、预期目标和成果预期目标是通过建立计算流体力学和弹道建模的数值模型,并设计高效、精确的算法,实现对弹丸水下高速运动外弹道的仿真模拟,并得到精确的弹道参数。
此项研究的成果将为弹丸水下高速运动的实际应用提供有力的技术支撑。
水下高速运动体弹道仿真的开题报告

水下高速运动体弹道仿真的开题报告一、研究背景水下高速运动体弹道仿真是一项重要且具有挑战性的技术。
在水下高速运动体的弹道仿真中,需要考虑多种因素,如流动情况、水下环境、水下动力学、弹体结构和材料等。
目前,水下高速运动体的弹道仿真技术已经广泛应用于水下器材设计、潜艇设计、水下作业和海洋资源勘探等领域。
二、研究目的和意义目前国内外对水下高速运动体弹道仿真的研究还比较薄弱,单一的数值模拟方法往往难以满足实际生产需求。
因此,本文旨在探究一种新的水下高速运动体弹道仿真方法,采用实验测试和数值模拟相结合的方式,提高仿真精度和可靠性。
同时,对于深入研究水下高速运动体弹道仿真技术,将有利于推动航海领域的发展。
三、研究内容和方法1. 对水下高速运动体进行材料和结构设计,建立实验设备;2. 进行水下高速运动体弹道实验,并采集实验数据;3. 建立三维数值模型,并通过ANSYS等软件,模拟整个运动过程;4. 针对实验和模拟数据进行分析和比较,探究其规律性;5. 针对实验结果和模拟结果进行统计分析,得出较为准确的水下高速运动体弹道仿真结果。
四、主要研究内容1. 进行水下高速运动体弹道实验;2. 建立三维数值模型;3. 模拟水下高速运动体弹道运动;4. 对实验数据和仿真结果进行分析比较。
五、研究计划和预期结果1. 设计水下高速运动体模型,建立实验设备,进行实验研究;2. 建立三维数值模型,并进行仿真研究;3. 对实验和仿真结果进行比较分析,得出仿真结果的准确度;4. 完成相关论文和研究报告。
预期结果:论文发表,取得相应的研究成果,推动水下高速运动体弹道仿真技术在航海领域的应用与发展。
铅垂平面飞行弹道仿真及分析报告

.6933
1.5935
2.4706
3.3273
4.1790
5)推力数据
t(s)
.000
.15
.49
2.11
2.27
3.53
8.78
25.45
42.80
43.68
44.08
P(kgf)
331.2
614.3
505.4
607.8
48.65
43.97
42.01
41.00
40.80
40.79
2.22
-0.5791
0.7
-0.5366
-0.5502
-0.5649
-0.5790
-0.5927
-0.6058
0.8
-0.5738
-0.5871
-0.6014
-0.6153
-0.6287
-0.6415
0.9
-0.6272
-0.6407
-0.6553
-0.6694
-0.6830
-0.6960
当Xg=.8896时
%三个时间 b(1)为导弹离轨时间 b(2)为起飞发动机工作结束时间 b(3)为续航发动机工作结束时间
b=[0 2.1126 44.0832];
%系数表维数
n1=9;
n2=6;
%andm最小,最大值
andm(1)=0.1;
andm(2)=0.9;
%andaf最小,最大值
andaf(1)=0;
andaf(2)=10;
.0000 .6554 1.5007 2.3227 3.1197 3.9092;
.0000 .6617 1.5134 2.3409 3.1426 3.9401;
实验2-利用SIMULINK进行制导弹道仿真
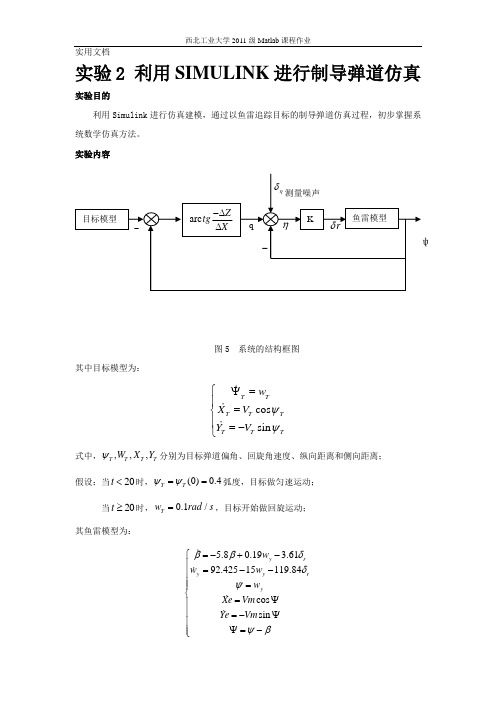
实验2 利用SIMULINK 进行制导弹道仿真 实验目的利用Simulink 进行仿真建模,通过以鱼雷追踪目标的制导弹道仿真过程,初步掌握系统数学仿真方法。
实验内容图5 系统的结构框图其中目标模型为:cos sin T T T T T T T T w X V Y V ψψ⎧ψ=⎪=⎨⎪=-⎩式中,,,,T T T T W X Y ψ分别为目标弹道偏角、回旋角速度、纵向距离和侧向距离;假设:当20t <时,(0)0.4T T ψψ==弧度,目标做匀速运动;当20t ≥时,0.1/T w rad s =,目标开始做回旋运动;其鱼雷模型为:5.80.19 3.6192.42515119.84cos sin y r y y ry w w w w Xe Vm Ye Vm ββδδψψβ⎧=-+-⎪=--⎪⎪=⎪⎨=ψ⎪⎪=-ψ⎪ψ=-⎪⎩式中,,,,,,,,y w r Vm Xe Ye βδψψ分别为鱼雷的侧滑角、回旋角速度、直舵角、航向角、弹道偏角、速度,地面坐标系中的X 轴和Z 轴坐标。
Vm=25m/s 。
鱼雷与目标的相对距离为,,T T X X Xe Y Z Ze ∆=-∆=-。
q 为地球视线角,q ηψ=-为雷体系中的提前角。
操舵规律,0.5,10r K K r δηδ=-=≤。
终端脱靶量定义为t f r =鱼雷模型仿真初值为:(0)(0)(0)(0)(0)(0)0.25/y w r Xe Ze Vm m s βδψ=======。
目标模型仿真初值为:(0)5/,(0)(0)1500,(0)0T T T T V m s X Z m w ====实验步骤由图5所示的系统控制结构图可知,该系统大致可以分为三个部分:目标模型,鱼雷模型以及观察模块。
1.根据目标模型和鱼雷模型的数学方程组,调用Simulink 工具箱模块库中的所需模块建立目标模型和鱼雷模型。
2.根据系统结构框图完成整个系统仿真模型的搭建,如图6 所示。
铅垂平面内有控导弹弹道仿真

铅垂平面内导弹弹道仿真及分析实验报告摘要本文以铅垂平面内有控飞行导弹的运动方程组为例,根据其数学模型,结合给定初值条件和导引方法,对有控飞行追踪目标的导弹进行数学仿真。
由于该运动方程组的数学模型很难得到它的解析解,所以工程上一般采用数值分析方法求取它的数值解。
本文采用四阶龙格库塔法、不等距单变元抛物线插值、不等距双变元抛物线线插值等数值分析方法结合C++编程语言来实现数值运算,得到了在给定初始条件和控制信号作用下的弹道飞行参数。
根据计算所得各项数据结合Matlab软件的绘图功能,可以得到在有控条件下导弹命中既定目标的弹道曲线和各项参数随时间变化的曲线。
关键词:铅垂平面内有控飞行运动方程组数值算法弹道仿真一、 绪论导弹运动方程是表征导弹运动规律的数学模型,也是分析、计算或者模拟导弹运动的基础。
完整描述导弹在空间运动和制导系统中各个元件工作过程的数学模型是相当复杂的、在不同的研究阶段,不同的设计要求,所需建立的导弹运动模型也不相同。
建立导弹运动方程组以经典力学为模型,涉及变质量学、空气动力学、推进和控制理论等方面。
一般来说、运动方程组的数目越多,描述导弹的运动越准确、越完整。
但是研究和解算也就相应的越复杂。
在工程上,特别是导弹和制导系统设计初级阶段,在解算精度允许的范围内,对方程组进行一定的简化,以便利用较简单的运动方程组来达到研究导弹运动的目的。
例如,在一定的假设条件下可以把导弹运动方程组分解为纵向运动和侧向运动,或简化为铅垂面内的运动方程组和水平面内的运动方程组等。
实践证明,这些简化和分解都具有一定的实用价值。
本文就是研究经过简化后的在铅垂面内飞行的导弹运动。
二、 铅垂平面内有控飞行导弹的运动方程组数值积分利用计算机编程求解运动方程组,首先要选定一个可靠的计算方案。
包括数学模型的建立、原始数据、计算方法、初值及初始条件、计算要求等。
本文计算的步骤如下。
1. 建立数学模型➢ 铅垂平面内有控飞行导弹运动方程组14cos sin sin cos cos sin 00zz zzC dV mP X mg dtd mV P Y mg dtd J M dtdxV dt dy V dtd dt dmm dt αθθαθωθθϑωαϑθφφ⎫=--⎪⎪⎪=+-⎪⎪⎪=⎪⎪⎪=⎪⎪⎬=⎪⎪⎪=⎪⎪=-⎪⎪⎪=-⎪=⎪⎪=⎭➢ 目标运动方程组cos cos sin cos sin t t t Vt t t t t t t Vt dx V dtdy V dt dz V dt θψθθψ⎫=⎪⎪⎪=⎬⎪⎪=-⎪⎭➢ 弹目相对运动方程组cos()cos()sin()sin()t y t y y t y t y dr V q V q dt dq r V q V q dt θθθθ⎫=---⎪⎪⎬⎪=--+-⎪⎭2. 原始数据求解导弹运动方程组,必须给定所需的初始数据,它们一般来源于总体初步设计、估算和实验结果。
基于高性能计算的弹道学建模与仿真技术研究

基于高性能计算的弹道学建模与仿真技术研究弹道学建模与仿真技术是军事领域中非常重要的一项技术,它可以有效地帮助军事指挥员进行战术决策和武器系统研发。
随着计算机技术的不断发展和高性能计算机的出现,基于高性能计算的弹道学建模与仿真技术也得到了快速的发展。
本文将就基于高性能计算的弹道学建模与仿真技术进行研究,从理论到应用进行全面的探讨。
弹道学建模与仿真技术是通过计算机模拟弹道运动过程,预测弹道轨迹和对弹道飞行特性进行分析的一种技术。
它主要包括弹道力学原理、材料力学、气动力学、航天动力学等多学科的综合应用,可以对导弹、火箭弹等武器系统的弹道特性进行研究。
基于高性能计算的弹道学建模与仿真技术的研究,主要是利用高性能计算机的强大计算能力,提高建模和仿真的精度和效率。
高性能计算机具备大规模并行计算和高速计算的特点,可以快速处理大量数据和复杂计算,实现高精度的弹道学建模和仿真。
首先,基于高性能计算的弹道学建模与仿真技术可以提高模拟精度。
高性能计算机可以处理更多的物理参数和复杂的数学模型,能够更准确地描述弹道运动过程中的各种因素。
通过精确的建模和仿真,可以更好地预测弹道轨迹、飞行速度、飞行高度等弹道特性,提供准确的数据支持军事指挥员的决策。
其次,基于高性能计算的弹道学建模与仿真技术可以提高计算效率。
高性能计算机的并行计算能力可以同时处理多个任务,大大加快建模和仿真的速度。
相比传统的计算方法,高性能计算可以减少计算时间,提高工作效率。
这对于军事指挥员在战时决策和武器系统研发中是非常重要的。
此外,基于高性能计算的弹道学建模与仿真技术还可以应用于武器系统的设计和优化。
通过建模和仿真,可以在计算机上对各种设计方案进行验证和优化,提前发现潜在问题并进行改进。
这样可以大大节省研发成本和时间,提高武器系统的性能和可靠性。
在基于高性能计算的弹道学建模与仿真技术的研究中,还需要充分考虑计算资源的利用和管理。
由于弹道学建模与仿真需要进行大规模复杂计算,需要合理规划计算资源,采用合适的算法和优化技术,以提高计算效率并确保结果的准确性。
弹道仿真

导弹无控弹道仿真蒋 洋(北京理工大学 宇航学院)摘 要:在进行导弹总体设计时,会进行无控和有控弹道仿真来验证导弹的设计是否合理,利用matlab 对导弹运动方程组进行求解可以得到导弹的无控弹道曲线等。
关键词:无控弹道;matlab ;导弹运动方程组Abstract : In the design of the missile, we will do uncontrolled and controlled ballistic trajectory simulation to verify whether the design is reasonable or not.With the help of matlab,we can easily solve the equations of motion of a missile to get uncontrolled trajectory curve. Key words : Uncontrolled trajectory;matlab; the equations of motion of a missile1、数学模型及公式由于四阶龙格-库塔法精度高且易于编写程序,所以在本次仿真实验中求解导弹运动方程组将使用龙格-库塔法,龙格-库塔法的运算公式如下:1*(,)k k t f t K x ∆=121*(,)22k k K K t t f t x ∆∆++= 231*(,)22k k K K t t f t x ∆∆++= 34*(,)k k t f t K t x K ∆+∆+=112341()6k k x x K K K K +=++++ 在实验中使用的数学模型如下方程所述sin mV cos cos s c i sin os n z z z z z zzc dVmP dt dxV dt dyV dt dmm X G d P Y G dt d J M M dt dtd d tωααθθαθωαωωαθθθϑϑ--==+-=+==-==-= 以上数学模型满足以下假设:1)侧向运动参数,,,,v x y βγγωω及舵偏角,x y δδ都比较小。
铅垂平面飞行弹道 仿真及分析 实验报告

铅垂平面飞行弹道仿真及分析实验报告姓名:Raigu学号:2005班级:0211CONTENT1. 实验内容与要求 (1)1.1. 实验名称: (1)1.2. 内容与要求: (1)2. 实验实现分析 (1)2.1. 数学模型 (1)2.2. 软件选择 (2)2.3. 原始数据: (2)2.4. 相关公式 (5)2.5. 弹道计算的相关算法 (5)3. 数据仿真 (6)3.1. 实验数据处理 (6)3.2. 程序运行 (6)3.3. 函数作用说明 (6)3.4. Matlab函数程序: (7)3.5. 相关数据的图象 (10)4. 仿真结果分析 (13)4.1. 导弹的受力变化 (13)4.2. 速度变化 (14)4.3. 弹道 (14)4.4. 攻角的变化 (15)4.5. 弹道倾角的变化 (15)4.6. 俯仰角的变化 (15)4.7. 俯仰角速度的变化 (15)4.8. 俯仰静稳定力矩和阻尼力矩 (16)1. 实验内容与要求1.1. 实验名称:铅垂平面飞行弹道仿真及分析1.2. 内容与要求:根据描述飞行器在铅垂平面内运动的数学模型,编制某导弹的铅垂平面无控飞行弹道仿真程序,利用计算机解算初始段无控飞行弹道,对初始段弹道参数的变化规律进行分析。
2. 实验实现分析2.1. 数学模型1、本实验所用的数学模型要描述在铅垂平面内飞行的导弹,于是数学模型如下面方程所述:cos sin sin cos cos sin z z z z z z z c dV P X G dtd mV P Y G dtd J M M dtd dt dx V dtdy V dtdm m dtωααϑθαθθαθωωϑωθθ=−=−−=+−=+====−以上数学模型需满足下述假设条件:侧向运动参数,,,,x y V βγγωω及舵偏角,x y δδ都比较小。
这样就可以令:cos cos cos 1V βγγ≈≈≈且略去小量的乘积sin sin ,sin ,,sin x y y V V z βγγωωωγ……以及参数βδδ对阻力X的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导弹无控弹道仿真蒋 洋(北京理工大学 宇航学院)摘 要:在进行导弹总体设计时,会进行无控和有控弹道仿真来验证导弹的设计是否合理,利用matlab 对导弹运动方程组进行求解可以得到导弹的无控弹道曲线等。
关键词:无控弹道;matlab ;导弹运动方程组Abstract : In the design of the missile, we will do uncontrolled and controlled ballistic trajectory simulation to verify whether the design is reasonable or not.With the help of matlab,we can easily solve the equations of motion of a missile to get uncontrolled trajectory curve. Key words : Uncontrolled trajectory;matlab; the equations of motion of a missile1、数学模型及公式由于四阶龙格-库塔法精度高且易于编写程序,所以在本次仿真实验中求解导弹运动方程组将使用龙格-库塔法,龙格-库塔法的运算公式如下:1*(,)k k t f t K x ∆=121*(,)22k k K K t t f t x ∆∆++= 231*(,)22k k K K t t f t x ∆∆++= 34*(,)k k t f t K t x K ∆+∆+=112341()6k k x x K K K K +=++++ 在实验中使用的数学模型如下方程所述sin mV cos cos s c i sin os n z z z z z zzc dVmP dt dxV dt dyV dt dmm X G d P Y G dt d J M M dt dtd d tωααθθαθωαωωαθθθϑϑ--==+-=+==-==-= 以上数学模型满足以下假设:1)侧向运动参数,,,,v x y βγγωω及舵偏角,x y δδ都比较小。
这样可以令:cos cos cos 1v βγγ≈≈≈且略去小量的乘积sin sin ,sin ,,sin v v x y y z βγγωωωγ ……以及参数,β,x y δδ对阻力X 的影响。
2)导弹基本上在铅垂面内飞行,即其弹道与铅垂面弹道差别不大。
3)俯仰操纵机构的偏转仅取决于纵向运动参数;而偏航、倾斜操纵机构的偏转仅取决于侧向运动参数。
其他相关公式: 空气动力 阻力212x X c V S ρ=升力212y Y c V S ρ=空气动力矩 21()2zzz z z z z z z M M M m m V Sωωααωαωρ=+=+其中,00()/z z y g g m m c X X L ααα=+- 2、原始数据 1) 初值X=0(m) y=20(m) ϑ=18︒ θ=18︒ v=20(m/s) ωz =0(rad/s) m=52.38(kg) 2) 攻角与马赫数范围攻角=0~10︒ 马赫数=0.1~0.9 3) 阻力系数表4)升力系数表5)推力6)发动机质量秒流量7) 转动惯量8) 导弹质心9) 静稳定力矩系数00z Xg Xg m α=10)阻尼力矩导数zmϖz 当X=0.9381时g当g X=0.8896时11)其他参数3、Matlab程序编写1)主程序mainfunction mainh=input('输入h =');t=input('输入t =');%输入步长h和时间tx=[20;0.314;0;0.314;0;20;52.38];%按照导弹运动方程顺序x=[v,θ,ωz,ϑ,x,y,m]n=fix(t/h);for i=1:nRES(:,i)=x;%将数据存入RESx=rk4(h*i,x,h);if RES(6,end)<0n=i;breakendendtime=num2str(i*h);disp(['飞行时间=',time,'s']);leng=num2str(RES(5,end));disp(['飞行距离 =',leng,'m']);%输出运算结果picture(RES,h,n)%画图2)画图程序picturefunction picture(RES,h,n)figure(1)plot(RES(5,:),RES(6,:),'Linewidth',1)title('弹道曲线 ','FontSize',15);ylim([0 160]);xlabel('x/m','FontSize',15),ylabel('y/m','FontSize',15)grid %利用 RES中的x,y的数据画出弹道曲线figure(2)plot(0:h:(n-1)*h,(RES(4,:)-RES(2,:))*57.3,'Linewidth',1);title('攻角时间曲线','FontSize',15);xlabel('t/s','FontSize',15),ylabel('{\alpha}/(\circ)','FontSize',15); grid %利用RES中的alpha数据画出以时间t为横轴的曲线figure(3)plot(0:h:(n-1)*h,RES(1,:),'Linewidth',1)title('速度时间曲线','FontSize',15);xlabel('t/s','FontSize',15),ylabel('V/(m*s^{-1})','FontSize',15)grid %利用 RES中速度V的数据画出速度时间曲线figure(4)plot(0:h:(n-1)*h,RES(2,:),'Linewidth',1)title('弹道倾角曲线 ','FontSize',15);xlabel('t/s','FontSize',15),ylabel('{\theta}/(rad)','FontSize',15) grid %利用 RES中的θ的数据画出弹道倾角曲线figure(5)plot(0:h:(n-1)*h,RES(4,:),'Linewidth',1)title('俯仰角曲线','FontSize',15);xlabel('t/s','FontSize',15),ylabel('{\vartheta}/(rad)','FontSize',15) grid %利用 RES中的ϑ数据画出俯仰角曲线figure(6)plot(0:h:(n-1)*h,RES(3,:),'Linewidth',1)title('俯仰角速度曲线','FontSize',15);xlabel('t/s','FontSize',15),ylabel('{\omega}_{z}/(rad*s^{-1})','FontSize',15)ω数据画出俯仰角速度曲线grid %利用RES中的z3)四阶龙格-库塔法程序rk4function xadd=rk4(t,x,h)K1=f(t,x);K2=f(t+h/2,x+h/2*K1);K3=f(t+h/2,x+h/2*K2);K4=f(t+h,x+h*K3);xadd=x+h/6*(K1+2*K2+2*K3+K4);4)插值以及运算程序ffunction dy=f(t,x)S=0.0227;L=1.8;SONIC=343.13;RHO=1.225;g=9.81;(以矩阵方式输入原始数据,由于数据太多,此处省略)P1=interp1(tP(1,:),tP(2,:),t,'linear');tmc=interp1(tMc(1,:),tMc(2,:),t,'linear');jy=interp1(tJy(1,:),tJy(2,:),t,'linear');XG1=interp1(tXG(1,:),tXG(2,:),t,'linear');%使用interp1函数对数据进行线性插值alpha=abs(180*(x(4)-x(2))/pi);Ma=x(1)/SONIC;Cx=interp2(0:2:10,0:0.1:0.9,aCx,alpha,Ma,'cubic');Cy=interp2(0:2:10,0:0.1:0.9,aCy,alpha,Ma,'cubic');%使用interp2函数对升力和阻力系数矩阵插值if x(4)-x(2)<0 %判断攻角是否为负来对升力系数和静稳定力矩进行变换正负处理Cy=-Cy;mza=-mza;endT=1/2*RHO*x(1)^2*S;X=Cx*T;Y=Cy*T;%计算空气动力P=P1;mc=tmc;Jz=jy;mza0=interp2(0:2:10,0:0.1:0.9,mza,alpha,Ma,'cubic');if alpha~=0mza=mza0+Cy*(XG1-0.9381)/(L);elsemza=mza0;endmzw1=interp2(0:2:10,0:0.1:0.9,mzw9381,alpha,Ma,'cubic'); mzw2=interp2(0:2:10,0:0.1:0.9,mzw8896,alpha,Ma,'cubic'); %使用interp2函数对阻尼力矩导数矩阵插值mzw=interp1([0.9381,0.8896],[mzw1,mzw2],XG1,'linear');dy=zeros(7,1);dy(1)=(P*g*cos(x(4)-x(2))-X-x(7)*g*sin(x(2)))/x(7);dy(2)=(P*g*sin(x(4)-x(2))+Y-x(7)*g*cos(x(2)))/(x(7)*x(1)); dy(3)=(mza/Jz+mzw/Jz*x(3)*L/x(1))*T*L;dy(4)=x(3);dy(5)=x(1)*cos(x(2));dy(6)=x(1)*sin(x(2));dy(7)=-mc;%导弹运动方程组4、运行结果1)数值结果输入h=0.005输入t=12飞行时间t=11.535s飞行距离L=2658.2788m2)图象。
