77-基于Simulink的鱼雷控制系统仿真
鱼雷控制系统计算机辅助分析设计与仿真课程设计

鱼雷控制系统计算机辅助分析设计与仿真课程设计简介鱼雷控制系统是一种用于海上军事作战的重要装备。
为了能够更好地研究和设计鱼雷控制系统,需要使用现代计算机技术来进行辅助分析和仿真。
本课程设计旨在提供计算机辅助分析设计与仿真的基础知识和技能,帮助学生更好地掌握鱼雷控制系统的设计与开发。
课程安排本课程设计将分为以下几个部分:第一部分:理论知识介绍(预计时间:2周)本部分将介绍课程设计所需要的理论知识。
具体内容包括: - 鱼雷控制系统的基本原理 - 现代计算机技术在鱼雷控制系统中的应用 - 计算机辅助分析设计与仿真的基本概念和方法第二部分:软件使用技能训练(预计时间:4周)本部分将介绍鱼雷控制系统的仿真软件,并通过实际操作,让学生掌握软件的使用技能。
具体内容包括: - 仿真软件的安装和配置 - 仿真软件的基本功能和操作方法 - 鱼雷控制系统仿真场景的设定和调整第三部分:鱼雷控制系统仿真设计(预计时间:4周)本部分将要求学生根据指定的仿真场景,使用仿真软件完成鱼雷控制系统的设计。
具体内容包括: - 仿真场景的设定和要求 - 鱼雷控制系统的设计和调整 - 仿真结果的分析和报告撰写第四部分:课程总结与展望(预计时间:1周)本部分将对本课程设计进行总结,并展望计算机辅助分析设计与仿真在鱼雷控制系统研究领域的未来发展方向。
学习方法学生可以通过以下方式获得本课程设计的学习资料和支持: - 在线课程:本课程设计的学习资料将以在线课程的形式提供,学生可以通过网络随时随地进行学习。
- 项目文档:本课程设计的项目文档将提供详细的指导和要求,学生可以根据文档进行实践和操作。
- 讨论区支持:本课程设计将设立讨论区,学生可以在讨论区与老师和同学进行交流和讨论,获得支持和帮助。
参考资料•蔡健祥.现代控制原理与应用[M].北京:高等教育出版社,2003.•杨永华. Matlab在控制系统设计中的应用[M]. 北京: 科学出版社, 2006.•任合忠, 江女.军事仿真及其应用[M]. 北京: 国防工业出版社, 2005.结语本课程设计将以计算机辅助分析设计与仿真为核心内容,通过理论介绍、实践操作和课程总结等环节,帮助学生更好地掌握鱼雷控制系统的设计和开发过程。
基于Simulink的鱼雷尺度靶收发干扰仿真

工具 箱对 干扰模型进行 了仿 真, 最后给 出了仿真结果 。结果表 明, 靶标 收发换 能器间的干扰会 导致转发信 号产 生畸
变, 但 其畸变对信号幅度的影响较小 , 不会对 目标模拟产 生影 响, 验证 了拖 曳靶进行 目标模拟的 可行 性 , 对鱼雷尺度 靶及其 它水声 目标模拟设备 的研制有 一定的参 考应 用价值 。
基于 S i m u l i n k的 鱼 雷 尺 度 靶 收 发 干 扰仿 真
邱 摘 政 ,张 维全 5 2 4 0 2 2 ) ( 解放军 9 1 3 8 8 部 队 ,广东 湛江
要: 在 分析尺度靶 多亮点 目标模 型的基础上 , 建 立了拖 曳线列阵靶 收发 干扰 和信 号处理模 型, 然后利 用 S i mu l i n k
关键词 : 尺度 靶 ;收发 干扰 ;多 亮 点 ; 目标 模 拟 中图 分 类 号 : E 9 2 5 . 4 ; E 9 1 1 文献标识码 : A DOI : 1 0 . 3 9 6 9 / j . i s s n . 1 6 7 3 — 3 8 1 9 . 2 0 1 4 . 0 2 . 0 2 1
第3 6卷 第 2期
2 0 1 4年 4月
文章编号 : 1 6 7 3 . 3 8 1 9 ( 2 0 1 4 ) 0 2 . 0 0 8 8 — 0 4
指挥控 制 与仿 真
C o mma n d Co n t r o l& S i mu l a t i o n
Vo l _ 3 6 NO . 2 Ap r . 2 01 4
T h e To r p e d o — s c a l e Ta r g e t Tr a n s c e i v e r I n t e r f e r e n c e S i mu l a t i o n Ba s e d o n S i mu l i n k
Simulink在系统仿真中的应用 ppt课件

封装方法
• Subsystem • Edit→Mask Subsystem
绘图命令
允许给该模块的 图标上绘制图形 plot/disp/image
图标边框
图标透明与否
图标是否旋转
增加变量
删除变量
提示栏变(量用(于用填于写关该联变量名) 变量的该提变示量信名息必)须与框图中的一致
• S函数就是系统函数的意思
• S函数有固定的程序格式,用MATLAB 语言可以编写,此外还可以用C语言、 C++、Fortran和Ada等语言来编写,用 这些语言编写需要用编译器生成动态链 接库DLL文件,可以在simulink中直接 调用
400
笨,没有学问无颜见爹娘 ……”
500
100
200
300
400
500
• “太阳当空照,花儿对我笑,小鸟说早早早……”
南京航空航天大学自动化学院应用电子教学中心 《MATLAB仿真技术与应用》研究生公共实验课电子讲义
主讲人:林雅洁(linyj@)
学习目标
• 熟悉simulink常用模块组及常用模块 • 使用simulink建立模型 • 非线性系统仿真分析 • Simulink高级建模仿真 • 子系统、模块封装 • S函数编写
• =sprintf(‘PID Control\n& Simulation\nBlockset’);
• blkStruct.OpenFcn=‘pidblock’;
• blkStruct.MaskDisplay=‘disp(“PID\ nBlockset”)’;
五.M函数、S函数编写及其应用
⑷离散系统模块组Discrete
• Zero-order Hold • First-order Hold • Discrete Transfer
实验2-利用SIMULINK进行制导弹道仿真
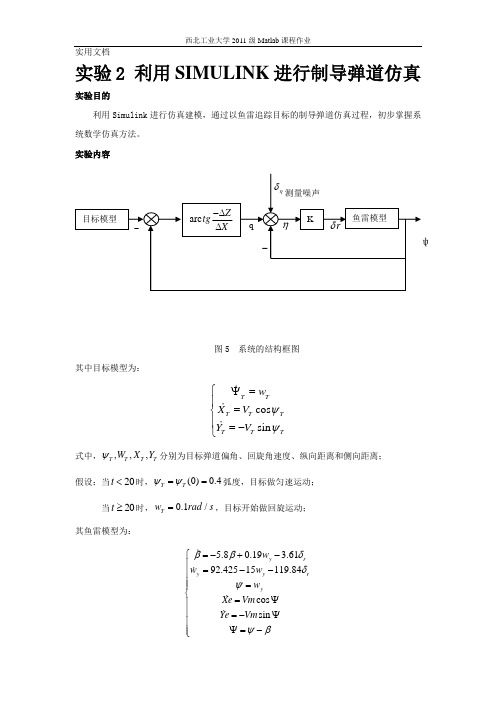
实验2 利用SIMULINK 进行制导弹道仿真 实验目的利用Simulink 进行仿真建模,通过以鱼雷追踪目标的制导弹道仿真过程,初步掌握系统数学仿真方法。
实验内容图5 系统的结构框图其中目标模型为:cos sin T T T T T T T T w X V Y V ψψ⎧ψ=⎪=⎨⎪=-⎩式中,,,,T T T T W X Y ψ分别为目标弹道偏角、回旋角速度、纵向距离和侧向距离;假设:当20t <时,(0)0.4T T ψψ==弧度,目标做匀速运动;当20t ≥时,0.1/T w rad s =,目标开始做回旋运动;其鱼雷模型为:5.80.19 3.6192.42515119.84cos sin y r y y ry w w w w Xe Vm Ye Vm ββδδψψβ⎧=-+-⎪=--⎪⎪=⎪⎨=ψ⎪⎪=-ψ⎪ψ=-⎪⎩式中,,,,,,,,y w r Vm Xe Ye βδψψ分别为鱼雷的侧滑角、回旋角速度、直舵角、航向角、弹道偏角、速度,地面坐标系中的X 轴和Z 轴坐标。
Vm=25m/s 。
鱼雷与目标的相对距离为,,T T X X Xe Y Z Ze ∆=-∆=-。
q 为地球视线角,q ηψ=-为雷体系中的提前角。
操舵规律,0.5,10r K K r δηδ=-=≤。
终端脱靶量定义为t f r =鱼雷模型仿真初值为:(0)(0)(0)(0)(0)(0)0.25/y w r Xe Ze Vm m s βδψ=======。
目标模型仿真初值为:(0)5/,(0)(0)1500,(0)0T T T T V m s X Z m w ====实验步骤由图5所示的系统控制结构图可知,该系统大致可以分为三个部分:目标模型,鱼雷模型以及观察模块。
1.根据目标模型和鱼雷模型的数学方程组,调用Simulink 工具箱模块库中的所需模块建立目标模型和鱼雷模型。
2.根据系统结构框图完成整个系统仿真模型的搭建,如图6 所示。
哈工大 计算机仿真技术实验报告 仿真实验四基于Simulink控制系统仿真与综合设计

基于Simulink 控制系统仿真与综合设计一、实验目的(1) 熟悉Simulink 的工作环境及其功能模块库; (2) 掌握Simulink 的系统建模和仿真方法;(3) 掌握Simulink 仿真数据的输出方法与数据处理;(4) 掌握利用Simulink 进行控制系统的时域仿真分析与综合设计方法; (5) 掌握利用 Simulink 对控制系统的时域与频域性能指标分析方法。
二、实验内容图2.1为单位负反馈系统。
分别求出当输入信号为阶跃函数信号)(1)(t t r =、斜坡函数信号t t r =)(和抛物线函数信号2/)(2t t r =时,系统输出响应)(t y 及误差信号)(t e 曲线。
若要求系统动态性能指标满足如下条件:a) 动态过程响应时间s t s 5.2≤;b) 动态过程响应上升时间s t p 1≤;c) 系统最大超调量%10≤p σ。
按图1.2所示系统设计PID 调节器参数。
图2.1 单位反馈控制系统框图图2.2 综合设计控制系统框图三、实验要求(1) 采用Simulink系统建模与系统仿真方法,完成仿真实验;(2) 利用Simulink中的Scope模块观察仿真结果,并从中分析系统时域性能指标(系统阶跃响应过渡过程时间,系统响应上升时间,系统响应振荡次数,系统最大超调量和系统稳态误差);(3) 利用Simulink中Signal Constraint模块对图2.2系统的PID参数进行综合设计,以确定其参数;(4) 对系统综合设计前后的主要性能指标进行对比分析,并给出PID参数的改变对闭环系统性能指标的影响。
四、实验步骤与方法4.1时域仿真分析实验步骤与方法在Simulink仿真环境中,打开simulink库,找出相应的单元部件模型,并拖至打开的模型窗口中,构造自己需要的仿真模型。
根据图2.1 所示的单位反馈控制系统框图建立其仿真模型,并对各个单元部件模型的参数进行设定。
所做出的仿真电路图如图4.1.1所示。
基于鱼雷武器的作训仿真系统设计与研究

基于鱼雷武器的作训仿真系统设计与研究鱼雷作为一种重要的水下武器系统,在海战中扮演着重要的角色。
为了提高鱼雷的实战能力和水面舰艇的水下作战能力,设计和研究基于鱼雷武器的作战仿真系统是非常必要的。
本文将从系统设计和研究两个方面进行阐述。
首先,基于鱼雷武器的作战仿真系统的设计是一个很重要的环节。
系统设计需要从整体上考虑作战仿真的目标和功能,并制定相应的系统体系结构。
鱼雷作战仿真系统需要包括以下几个主要模块:鱼雷系统模块、舰艇模块、海底地形模块、雷达与声纳模块、作战指挥模块等。
鱼雷系统模块是整个仿真系统的核心部分,包括鱼雷发射、导引、制导等关键技术,可以通过虚拟技术对鱼雷的性能进行模拟和评估。
舰艇模块是鱼雷作战仿真系统中的另一个重要组成部分,可以对水面舰艇的航行、指挥、战术等进行模拟和评估。
海底地形模块可以对水下地形进行三维建模,并与鱼雷系统模块和舰艇模块相结合,实现真实环境下的作战仿真。
雷达与声纳模块可以对水面舰艇和鱼雷进行探测和定位,为作战提供信息支持。
作战指挥模块可以对作战进行规划、指挥和评估,实现对整个作战过程的监控和控制。
其次,基于鱼雷武器的作战仿真系统的研究也是一个关键的方向。
研究需要重点考虑鱼雷系统的性能优化、舰艇与鱼雷的联合作战、作战规划与决策等问题。
首先,研究可以通过仿真来优化鱼雷的发射、导引和制导等技术参数,提高鱼雷的精确度和杀伤能力。
其次,研究可以建立鱼雷与舰艇的联合作战模型,探索鱼雷与舰艇之间的配合方式,提高作战效能。
最后,研究可以在作战仿真系统中加入作战规划与决策模块,通过优化作战方案和决策过程,提高作战指挥的能力。
总的来说,基于鱼雷武器的作战仿真系统的设计和研究对于提高鱼雷的实战能力和水面舰艇的水下作战能力具有重要意义。
通过合理的系统设计和深入的研究,可以提高鱼雷系统的性能和水下作战的效能,提高水下作战的实战能力。
这对于提高我国海军的整体战斗力,维护海上安全和国家利益具有重大影响。
控制系统Simulink仿真PPT课件(MATLAB学习资料)

积分环节的幅值与 成反比,相角恒为-
时,幅相特性从虚轴
处出发,
沿负虚轴逐渐趋于坐标原点,程序如下:
g=tf([0,1],[1,0]); nichols(g); grid on
运行程序输出如图6-14曲线②所示。
。当
在Simulink中积分环节的使用如如图6-15所示。 运行仿真输出图形如图6-10所示。
• 频域法是基于频率特性或频率响应对系统进行分析和设计的一种图解 方法,故又称为频率响应法,频率法的优点较多,具体如下:
• 首先,只要求出系统的开环频率特性,就可以判断闭环系统是否稳定。 • 其次,由系统的频率特性所确定的频域指标与系统的时域指标之间存
在着一定的对应关系,而系统的频率特性又很容易和它的结构、参数 联系起来。因而可以根据频率特性曲线的形状去选择系统的结构和参 数,使之满足时域指标的要求。 • 此外,频率特性不但可由微分方程或传递函数求得,而且还可以用实 验方法求得。这对于某些难以用机理分析方法建立微分方程或传递函 数的元件(或系统)来说,具有重要的意义。因此,频率法得到了广泛 的应用,它也是经典控制理论中的重点内容。
• 2)由于对数可将乘除运算变成加减运算。当绘制由多个环节串联而成的系统的对数坐标图 时,只要将各环节对数坐标图的纵坐标相加、减即可,从而简化了画图的过程。
• 3)在对数坐标图上,所有典型环节的对数幅频特性乃至系统的对数幅频特性均可用分段直 线近似表示。这种近似具有相当的精确度。若对分段直线进行修正,即可得到精确的特性曲 线。
其频率特性为:
一阶复合微分环节幅相特性的实部为常数1,虚部与 成正比,如图5-26曲线①所示。 不稳定一阶复合微分环节的传递函数为:
其频率特性为:
一阶复合微分环节的奈奎斯特曲线图编 程如下: clc,clear,close all g=tf([1,1],[0 1]);
Simulink与控制系统仿真第二版课程设计

MATLAB/Simulink与控制系统仿真第二版课程设计前言MATLAB/Simulink是一种常用的科学计算软件,在控制系统仿真中也有着广泛的应用。
本文将介绍MATLAB/Simulink与控制系统仿真第二版课程设计的相关内容,希望能够为初学者提供一些参考。
课程设计概述本次课程设计重点涵盖了以下内容:1.利用MATLAB/Simulink搭建控制系统仿真模型;2.设计控制器并进行参数调整;3.利用仿真结果进行系统性能分析。
软件准备在进行课程设计之前,我们需要准备以下软件:1.MATLAB/Simulink 软件,版本不低于 R2018a。
2.Control System Toolbox 软件。
可以通过MathWorks官网进行下载或安装。
实验进程实验一:建立控制系统模型1.利用模块库中的控制系统工具箱,选择Transfer Fcn模块,表示一般的传递函数。
2.建立一个常数块,作为控制输入变量。
3.利用Math Operation模块,实现控制输入变量和传递函数的乘积。
4.将Transfer Fcn模块的输出接入Scope模块,用于显示输出波形。
5.搭建完整的模型,并进行仿真,观察输出波形。
实验二:参数调整与PID控制1.在控制系统模型中,选择PID Controller模块。
2.设计PID控制器的参数,包括比例系数、积分时间和微分时间。
3.在仿真结果中,观察PID控制器的作用效果,并尝试进行参数调整,找到最优的控制器参数。
实验三:闭环控制系统1.利用模块库中的控制系统工具箱,搭建一个闭环控制系统模型。
2.包括控制器、对象以及反馈环节,模拟实际的控制系统。
3.在仿真结果中,观察闭环控制系统的工作效果,并进行性能分析。
实验结果与分析在完成以上三个实验后,我们得到了如下结果:•初步的控制系统仿真模型,可以实现基本的控制作用;•经过PID控制器的参数调整后,模型的控制精度得到了显著提高;•闭环控制系统的应用,进一步提升了系统的控制效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13
在编写 S 函 数时, 可 以使 用 MATLAB 提 供的 S 函 数 模 板, 根据用户的实际需求在相应的位置写入自 己的代码, S 函 数的基本格式如下:
# define S FUNCT ION NAME your sfunction name # define S FUNCT ION LEVEL 2 # include ∀ simstruc. h# static void mdlInitializeSizes( SimStruct * S) { } < additional S- function routines/ code> static void mdlT erminate( SimStruct * S) { } # ifdef MATLAB MEX FILE # include ∀ simulink. c# # else # include ∀ cg sfun. h# # endif mdlInitializeSizes( ) 是 Simulink 与 S 函数 交互 时调 用的 第 一个 子 程 序, S 函 数 中 还 有 一些 其 它 的 mdl* ( ) 子 程 序; Simulink 在调用 mdlInitializeSizes( ) 后, 再 与其它各个子程序 交 互; 最后调用 mdlTerminate 子程序, 所有 的 S 函数都 必须按 照 这样的格式进行。 根据 Simulink S 函 数 的 编 写 规 范, 我 们 分 别 编 写 了 Changalfabetav. c、Changede. c、Changedr . c、Changedd. c 和 F. c 五 个 S- 函数。下面以编写 F. c 函数为例 说明 S- 函 数的编 写 过程。 F. c 函数主要作用是 根据式( 1) 求解 鱼雷 动力学 方程 中 的线速度 Vx 、Vy、Vz 和角速 度 x 、 y 、 z 的导数, 然 后通过 积 分解算出鱼雷的线 速度和 角速 度。由于 作用 在鱼雷 上的 力 和力矩的表达式比较复杂, 用模块来实现比较 繁琐, 而采用 S - 函数来实 现这些 方程 就比 较方 便。模 型中, LU 模 块是 计 算质量逆矩阵[ A- 1] 为 6 ∃ 6 矩阵, 直 接可以利用 工具箱中 的 矩阵求逆的模块来实现。为了满足矩阵相 乘的要求, 必须 保 证 F. c 函数的输出维数是 6∃ 1, 所以在 F 函数的 初始化程 序 中要定义输入输出和状态变量的维数, 具体实 现方法如下: static void mdlInitializeSizes( SimStruct * S) {
x
= 0 sin!
cos !
y
( 3)
!
1 - tg cos! tg sin! z
式中 、 、! 分别为偏航角 、俯仰角 、横滚角 , x、 y、 z 分 别 为鱼雷角速度在雷体系X 、Y、Z 轴上 的投影。
3) 鱼雷重心 相对于地面坐标系的运动方程为:
X
V
Y
=
C
v 0
0
( 4)
Z
0
式中 Cv0 为速度坐标系到平 移坐标 系的变 换矩阵。据 此 可求解鱼雷空间运动坐标。
俯仰通道:
图 1 鱼雷控制系统的 Simulink 模型
∃e = k1( Y - YH ) + k2 + k3wz
( 6)
滚动通道:
∃d = k 3 !+ k 4 x
( 7)
航向通道:
∃r = k 5( - 0) + k 6 y
( 8)
式中 ∃e、∃d 、∃r 为鱼雷三通道控制 舵角; YH 为鱼 雷航行的设定 深度; 0 为设定的航向角; k 为控制系数。
Simulink 虽然提供了大量的线性、非线性 运算模 块, 但 仍 然不能满足鱼雷逻辑弹道等复杂系统的 建模需求, 这就需 要 采用 Simulink 和 C/ C+ + 混合 编程方 法实 现自 定义的 功能。 Simulink 提供的可自定义的外部接 口函数是 S 函数( S- func tion) , 用户 可 以 利 用 C/ C + + 编 写 自 定 义 S 函 数, 然 后 由 Simulink 调 用 S 函 数, 这 时 仿 真 程 序 的 主 框 架 是 建 立 在 Simulink 基础上的, 可以 充分利用 Matlab/ Simulink 提供的可 视 化编程能力, 完成模型的建立、修改、调试和分析 。
Simulation of Torpedo Control System Based on Simulink
GAO Li- e, KANG Feng- ju, ZHANG Jin- tao, CHE Yan- lin
( College of Marine Engineering, Northwestern Polytechnical University, Xi an Shanxi 710072, China)
Simulink 虽然 提 供 了 大 量 的 线 性 、非 线 性 运 算 模 块, 但仍 不能 适应 鱼 雷 逻 辑 弹 道 等 复 杂 系 统 的 建 模 需 求, 这 就需 要采 用 Simulink 和 C/ C+ + 混合 编 程 的方 法 , 实 现 鱼 雷控 制系 统 的 仿 真。 本 文 采 用 Simulink 的 方 法 完 成 了 鱼 雷控 制系 统 的设 计 与 仿 真, 与 传 统 上 采 用 的 C、FORTRAN 等语 言编 程相 比 大 大 减 少 了 编 程 工 作 量 , 缩 短 了 编 程 周 期, 且 可 以随 时修 改 参数 并立 即 看到 仿 真 结果 , 提 高 了 仿 真效 率。
鱼雷运 动学模型描 述了鱼 雷的空 间 运动 形式 和运 动规 律, 其运 动学 模型 如 下:
1) 鱼雷速度方程
V=
V2x +
V2y +
V
2 z
( 2)
式中 Vx、Vy 、Vz 为 鱼雷 速度 分别在 雷体 系 X 、Y、Z 轴 上的 投 影。
2) 鱼雷角速 度方程为:
0
cos! cos
- sin ! cos
2 鱼雷控制系统的数学模型
2. 1 动力学和运动学模型 根据流体动力学和航行动力学, 鱼雷在水 下空间运动 的
动力学方程为:
收稿日期: 2003- 07- 07
12
dVx / dt
Fsx + Fgx + Ftx
dVy / dt
Fsy + Fgy + Fty
dVz / dt = [ A- 1] ! Fsz + Fgz + Ftz
4) 运动学方 程和动力学方程中 ∀、# 用 下式计算:
∀=
arctg
-
Vy Vx
,
( 5)
# = arctg
Vz
V
2 x
+
V2y
2. 2 控制 系统模型 根据鱼雷类 型 的不 同, 鱼雷 控制 规 律主 要 包括 双 环 控
制、比例微分控制和 继电型 控制 等几种 典型 的控制 方式。某 型鱼雷的控制方程如下:
3 鱼雷控制系统的仿真模型
3. 1 鱼雷控制系统的 Simulink 建模 根据鱼雷的数学模型可以利用 Simulink 建立起模块化的
仿真模型, 鱼雷控制系统的仿真结构图 如图 1 所示。 模型中包 含 5 个自 定 义 S - Function 函 数, S- Function1
( Changealfabetav. c) 主 要根据式( 5) 解算鱼雷的攻角 ∀、侧滑 角 #; S- Function2( Changede. c) 、S- Function3( Changedr. c ) 、S Function4( Changedd. c) 分别根据式( 6) 、式( 7) 、式( 8) 完成鱼 雷 舵角 ∃e、∃r 、∃d 的计算; S- Function5( F. c) 主要根据式( 1) 求 解 鱼雷动力学方程中的线速度 Vx 、Vy、Vz 和角速 度 x 、 y 、 z 的 导数, 然后通过积分解算出鱼雷的线速 度和角速度。 3. 2 Simulink 和 C/ C+ + 混合编程
