电力拖动系统动力学 (2)
合集下载
第二章电力拖动系统的动力学基础解析

向都可能发生变化。因此运动方程式中的转矩都是带有正、负号的代数 量。因此须考虑转矩转速正负号,一般规定如下。 1.首先选定顺时针或逆时针中的某一个方向为规定正方向, 一般以电动机处于电动状态时的旋转方向为规定正方向。 2.转速的方向与规定正方向相同时为正,相反时为负。 3.电磁转矩方向与规定正方向相同时为正,相反时为负。 4.负载转矩与规定正方向相反时为正,相同时为负, 如图2-7所示。
动生产机械,我们称为电力拖动。 组成 电力拖动系统由电动机、生产机械的传动机构、工作机构、电动机的
控制设备以及电源等五部分组成,如图2-1所示。通常把生产机械的传动 机构及工作机构称为电动机的机械负载。
图2-1 电力拖动系统的组成
第2章 电力拖动系统的动力学基础
2.2 电力拖动系统的运动方程式
(2)电力拖动系统的优点 1.电能易于生产、传输、分配。 2.电动机类型多、规格全,具有各种特性,能满足各种生产机械的不同要
研究多轴电力拖动系统原则:不需要详细研究每根轴的问题,而只把电动 机的轴作为研究对象即可。为简单起见,采用折算的办法,即将实际的多轴 拖动系统等效为单轴拖动系统。
第2章 电力拖动系统的动力学基础
2.3 多轴电力拖动系统的简化
2.3.1多轴旋转系统的折算 (1)负载转矩的折算
Tem
TL
J
d
dt
图2-6 单轴电力拖动系统
第2章 电力拖动系统的动力学基础
2.2 电力拖动系统的运动方程式
转动惯量J可用下式表示
J m 2 G D 2 GD2
g 2 4g
工程实际计算中常用的运动方程式如下,这里 2n
60
Tem
TL
GD2 375
dn dt
式中 G为D2转动物体的飞轮矩(N·m2), GD2 ,4g它J 是电动机飞轮矩
动生产机械,我们称为电力拖动。 组成 电力拖动系统由电动机、生产机械的传动机构、工作机构、电动机的
控制设备以及电源等五部分组成,如图2-1所示。通常把生产机械的传动 机构及工作机构称为电动机的机械负载。
图2-1 电力拖动系统的组成
第2章 电力拖动系统的动力学基础
2.2 电力拖动系统的运动方程式
(2)电力拖动系统的优点 1.电能易于生产、传输、分配。 2.电动机类型多、规格全,具有各种特性,能满足各种生产机械的不同要
研究多轴电力拖动系统原则:不需要详细研究每根轴的问题,而只把电动 机的轴作为研究对象即可。为简单起见,采用折算的办法,即将实际的多轴 拖动系统等效为单轴拖动系统。
第2章 电力拖动系统的动力学基础
2.3 多轴电力拖动系统的简化
2.3.1多轴旋转系统的折算 (1)负载转矩的折算
Tem
TL
J
d
dt
图2-6 单轴电力拖动系统
第2章 电力拖动系统的动力学基础
2.2 电力拖动系统的运动方程式
转动惯量J可用下式表示
J m 2 G D 2 GD2
g 2 4g
工程实际计算中常用的运动方程式如下,这里 2n
60
Tem
TL
GD2 375
dn dt
式中 G为D2转动物体的飞轮矩(N·m2), GD2 ,4g它J 是电动机飞轮矩
第二章 电力拖动系统动力学PPT课件

m与G——旋转部分的质量(kg)和重量(N)
注意:运动方程式适用于单轴系统,因为速度量只有一个
将上式中的角速度Ω(Ω=2πn/60)化成为转速n,则有:
7
T
Tz
GD2 375
dn dt
(8-4)
GD2——飞轮惯量(N.m2),GD2=4gJ。电动机转子及其他转动 部件的飞轮惯量GD2 数值由产品目录中查出。
电动机拖动的生产机械的旋转部分会出现多种形状(圆柱体 和非圆柱体),需对常见形体的转动惯量作计算。
所有的旋转部分可分为两种情况:旋转轴线通过物体重心和 旋转轴线不通过重心。
(1) 旋转轴线通过该物体重心时,转动惯量公式为:
k
J ri2mi i 1
质量连续分布 J r2dm V
Δmi——该物体某个组成部分的质量 ri——该部分Δmi的重心到旋转轴的距离。对质量连续分布
20
传动图
'
等效折算图
21
四、工作机构直线运动质量的折算
系统中的重物作直线运动,需要把速度为vz(m/s)质量为mz (kg)的物体折算到电动机轴上, 用电动机轴上转动惯量JZ的 转动体来等效。
折算原则:转动惯量JZ中和质量mz中储存的动能相等,即:
JZ
2 2
GD2 = 4gJ = 4×9.8×16.933 N.m2 = 663.774 N.m2
14
第二节 工作机构转矩、力、飞轮惯量和质量的折算
◆实际拖动系统:轴往往有多根,不同的轴上有不同的转动 惯量和转速,以及不同的转矩和阻力距。
◆研究方法:列出每根轴的运动方程式,各轴间互相联系的 方程式,联系所有方程式。复杂
j = j1j2j3…
一般设备,电动机为高转速,工作机构轴为低速,则j>>1
电力拖动系统动力学(2)

(2)飞轮矩的折算
设做平移运动部分的物体重量为Gm,质量为m, 刨
折算前动能:
vm
刀
Fm
工件
折算后动能:
工作台
折算前后的动能不变。 ∴ ∴
传动机构中其他轴上的 GD2的折算,与前述相 同。
3.工作机构做提升和下放重物运动 时,转矩与飞轮矩的折算
(1)转矩的折算 1)提升重物时负载转矩的折算 重物对卷筒轴的负载转矩为GmR 不计传动机构的损耗,折算后的负载转矩为:
dt
系统处于稳定运转状态下。
2、当 T TL
dn 0 dt
电力拖动系统处于加速状态
3、当 T TL dn 0 dt
电力拖动系统处于减速状态
常把 GD 2
375
dn或
dt
(T TL )
称为动态转矩或加速转矩.
1.3.2多轴电力拖动系统转矩及飞轮矩的折算
1、折算前提:以电动机轴为研究对象。 2、折算原则:保持系统的功率传递关系及系统的贮 存动能不变。 3、负载转矩的折算:从已知的实际负载转矩求出等效 的负载转矩。 4、系统飞轮矩的折算:从已知的各转轴上的飞轮矩求
dn dn
数学表达式
文字表达式
n 2
n1
在交点处,在交点所对应的 转速之上应保证T<TL,而在 这转速之下则要求T>TL, nA
1 l'
A
0
TL
T
图1-21 拖动系统的不稳定运行
特点:大小恒定,方向总是与运
动的当方正向转相时反n为。正, TL与n方向
相反,应为正,即在第一象限
当反转时n为负, TL与n方向 相反,应为负,即在第三象限。
(2)位能性恒转矩负载 特点:绝对值大小恒定,方向固定不变,与n方向无关
电机与电力拖动第二章电力拖动系统的动力学基础

J
1
2
J
2 ...
2
Jz 2
Jd
J1
1 j2 1
J1
1 j2 j2 12
...
J
z
1 jz2
1
2
z
GD2 GDd2
GD2 1
j2 1
GD2 2
j2 j2 12
...GDz2 jz2
电机与电力拖动第二章电力拖动系 统的动力学基础
四、平移运动的转矩与飞轮矩的折算
1.转矩的折算
切削功率P Fv
4gmzv2
2n
60
2
365Gzv2 n2
其它轴上的飞轮矩的折算按旋转运动的方法 电机与电力拖动第二章电力拖动系 统的动力学基础
五、升降运动的转矩与飞轮矩的折算
GDd2
T
T GD2
电动机
GD12
z
电动机
等效负载 Tz
j1η1 1
滚筒
j2η2 GD22
mv 提升运动:电动机为电动状态
下降运动:电动电机机与电为力拖发动第电二章状电力态拖动系 统的动力学基础
刨刀
总质量mz
FV
折算前后功率不变T
z
Fv
c
T
zFcv
60Fv
c 2n
9.55 Fv
cn
T
电动机
n T 电动机
Jz 等效负载
Tz
电机与电力拖动第二章电力拖动系 统的动力学基础
四、平移运动的转矩与飞轮矩的折算
2.飞轮矩的折算
1 2
mzv2
1 2
J
z2
1 2
GDz2 4g
2n
60
2
《电机及拖动基础》第2章 电力拖动系统动力学

j j j
第二节 多轴电力拖动系统
2. 飞轮矩的折算
折算的原则是折算前后动能不变,旋转体的动能为:
E
1 2
J 2
1 2
GD2 4g
2 n
60
2
第二节 多轴电力拖动系统
电动机
T ,T0
n
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
上图所示的多轴电力拖动系统中,工作机构转轴 n f 的飞 轮矩为 GD2f ,折合到电动机轴上以后的飞轮矩为 GDF2 。
电动机
T ,T0
n
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
第一节 单轴电力拖动系统
通常把负载转矩与系统飞轮矩等效成单轴系统。
电动机 T , T0
n GD2
等效负载 TF
等效折算的原则是:保持系统的功率及系统贮存的动能 恒定。需进行负载转矩的折算和系统飞轮矩的折算。
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
同理,对于转轴 nb 和 nc 进行折算,可得:
GDB2
GDb2 j12
GDC2
GDc2 j1 j2 2
第二节 多轴电力拖动系统
n
电动机
T ,T0
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
如图所示的电力拖动系统,飞轮矩 GDa2 18.5N m2 ,GDb2 22N m2, GD2f 130N m,2 传动效率1 0.90 ,2 0.91,转矩Tf 85N m ,转 速n 2850r / min ,nb 950r / min ,nf 190r / min ,忽略电动机空 载转矩计算: (1) 折算到电动机轴上的负载转矩 TF ; (2) 折算到电动机轴上的系统总飞轮矩 GD2。
第二节 多轴电力拖动系统
2. 飞轮矩的折算
折算的原则是折算前后动能不变,旋转体的动能为:
E
1 2
J 2
1 2
GD2 4g
2 n
60
2
第二节 多轴电力拖动系统
电动机
T ,T0
n
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
上图所示的多轴电力拖动系统中,工作机构转轴 n f 的飞 轮矩为 GD2f ,折合到电动机轴上以后的飞轮矩为 GDF2 。
电动机
T ,T0
n
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
第一节 单轴电力拖动系统
通常把负载转矩与系统飞轮矩等效成单轴系统。
电动机 T , T0
n GD2
等效负载 TF
等效折算的原则是:保持系统的功率及系统贮存的动能 恒定。需进行负载转矩的折算和系统飞轮矩的折算。
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
同理,对于转轴 nb 和 nc 进行折算,可得:
GDB2
GDb2 j12
GDC2
GDc2 j1 j2 2
第二节 多轴电力拖动系统
n
电动机
T ,T0
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
如图所示的电力拖动系统,飞轮矩 GDa2 18.5N m2 ,GDb2 22N m2, GD2f 130N m,2 传动效率1 0.90 ,2 0.91,转矩Tf 85N m ,转 速n 2850r / min ,nb 950r / min ,nf 190r / min ,忽略电动机空 载转矩计算: (1) 折算到电动机轴上的负载转矩 TF ; (2) 折算到电动机轴上的系统总飞轮矩 GD2。
电力拖动课件(2)电力拖动系统动力学

0
TLfz M
T M
反抗性负载转矩特性
2.位能性恒转矩负载特性
• 特点: Mfz的方向与n 的方向无关。 Mfz具 有固定不变的方向。 • 例如:起重机的提升 机构,不论是提升重 物还是下放重物,重 力的作用总是方向朝 下的,即重力产生的 负载转矩方向固定。
n n=ff(( TLM ) fz) n=
反抗性恒转矩负载
当转速n=0时,外加 转矩不足以使系统运动。 根据作用力与 反作用力原 理,这时反抗性负载转矩 大小和方向取决于外加转 矩的大小和方向。即与外 加转矩大小相等,方向相 反。负载转矩特性应与横 轴重合。例如轧机,机床 刀架平移机构等。
n
n= M n=ff( (T L) fz)
-Tfz L -M
单轴电力拖动系统运动方程式
负载
电动机
d ΩD 运动方程式:MD – Mfz = JD d t
这里, JD 是电动机轴上所有转动体的转动惯量,单位N.m.s2 ΩD 是电动机轴上的角速度,单位rad/s
GDD2 d n 实用公式: MD – Mfz = 375 d t
GDD2 这里, GDD2是旋转体的飞轮矩,单位N.m2, JD= 4g
0
TL M fz
T M
位能性负载转矩特性
恒功率负载转矩特性
• 特点:当转速n变化时,负载功率基 本不变。 • 根据 P 2 M fz 常数
n
P2 60 M fz P2 2n
1 M fz n
n= M n=f( (TL ) fz)
• 如车床的主轴机构和轧钢机的主传 动。 • 适用于金属切削车床。
返回总目录 本章目录 上一节 下一节 下一章
生产实践中多为多轴电力拖动系统
第2章 电力拖动系统动力学

在T=TL处:
dT dn
dTL dn
或
dT dn
dTL dn
0
▲ 交点转速之上:T< TL时系统稳定 ▲或交点转速之下:T> TL时系统稳定
怎样判断稳定?
n 例3. 试判断下例系统是否稳定?
TL T (a) T (d) TL (e) (b) T
TL
TL T (c)
T TL
(f)
TL
T
T
(a)表示电动机机械特性T的硬度为负值,而负载转矩TL硬度为正值; (b)表示电动机机械特性T和负载转矩TL硬度都为正值; (c)表示电动机机械特性T和负载转矩TL硬度都为负值;
又称摩擦转矩、反作用转矩
-TL +TL
T T n
特点:
①转矩的方向总是阻碍运动方向, n 当运动方向改变时,反抗性转矩的方向随之改变; ②但大小(绝对值)不随转速变化; ③当n=0时,反抗性转矩的大小、方向是不确定的; ④机械特性位于Ⅰ、 Ⅲ象限,且与纵轴平行的直线。
2-3负载的转矩特性
⑵位能性负载特性 特点:
n
K TL = ----n
即:P = TΩ≈ 常数 n
T
3. 风机类负载
鼓风机、水泵、输油泵等。其转矩与转速的 二次方成正比。即 TL∝ n2 写为:TL=K n2
实际负载可能是几种典型的综合,如实际风机。
T
电力拖动系统稳定运行的条件
电动机机械特性与负载转矩特性在 T-n 平面上有相交点,是电力拖动系统可能稳 定的必要条件;(但不够充分) 稳定运行充分条件:若电力拖动系统原在 交点处稳定运行,由于某种干扰使转速变 化,可达到新的平衡。干扰消除后,可回 到原来的平衡点位置,则称此系统是稳定 的。
2.电力拖动系统动力学ppt课件
.
2、性质 : 动转矩等于零时,系统处于恒转速运行的稳态; 动转矩大于零时,系统处于加速运动的过渡过
程中; 动转矩小于零时,系统处于减速运动的过渡过
程中。
.
2.2 负载的转矩特性
• 机械的工作机构的负载转矩与转速之间的 关系,称之为负载的转矩特性。一般用n=f (TL)曲线表示。
• 1 恒转矩负载的转矩特性 • (1) 反抗性恒转矩负载 • (2)位能性恒转矩负载 • 2 泵类负载的转矩特性 • 3 恒功率负载的转矩特性
.
.
2.3 电力拖动系统稳定运行的条件
• P20 充分必要条件:电动机机械特性与负载 转矩特性必须相交,在交点处T=TL,实现 转矩平衡,在工作点要满足dT / dn < dTL / dn
.
.
• 1、恒转矩负载特性 • 指负载转矩与其转速n无关的特性,即当转速变化时,
负载转矩保持常数。 • (1)反抗来自恒转矩负载特性 • 是由摩擦力产生的,绝对值大小不变,方向总是和运
动方向相反。是阻碍运动的制动性转矩。 • 属于这一类的生产机械有提升机的走行机构,皮带运
输机,轧钢机以及某些金属切削机床的平移机构等。 • 其特性曲线是位于平面坐标系的第一与第三象限内,
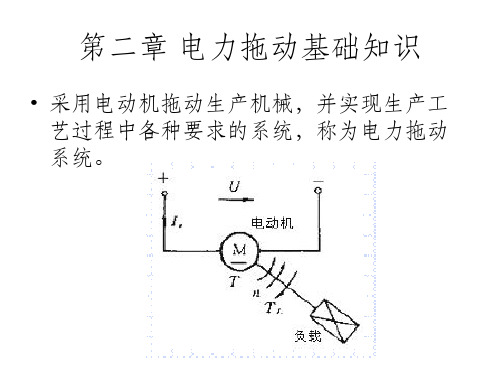
第二章 电力拖动基础知识
• 采用电动机拖动生产机械,并实现生产工 艺过程中各种要求的系统,称为电力拖动 系统。
.
2.1 电力拖动系统的运动方程
• 1、单轴电机拖动系统-包含一根轴的系统
.
• 当电动机的转矩作用于这一系统时,根据动 力学定律可知,电动机的转矩除了克服运动 系统的静阻转矩外,还使整个系统沿着电动 机转矩的作用方向,产生角加速度。角加速 度的大小与旋转体的转动惯量J成反比。
2、性质 : 动转矩等于零时,系统处于恒转速运行的稳态; 动转矩大于零时,系统处于加速运动的过渡过
程中; 动转矩小于零时,系统处于减速运动的过渡过
程中。
.
2.2 负载的转矩特性
• 机械的工作机构的负载转矩与转速之间的 关系,称之为负载的转矩特性。一般用n=f (TL)曲线表示。
• 1 恒转矩负载的转矩特性 • (1) 反抗性恒转矩负载 • (2)位能性恒转矩负载 • 2 泵类负载的转矩特性 • 3 恒功率负载的转矩特性
.
.
2.3 电力拖动系统稳定运行的条件
• P20 充分必要条件:电动机机械特性与负载 转矩特性必须相交,在交点处T=TL,实现 转矩平衡,在工作点要满足dT / dn < dTL / dn
.
.
• 1、恒转矩负载特性 • 指负载转矩与其转速n无关的特性,即当转速变化时,
负载转矩保持常数。 • (1)反抗来自恒转矩负载特性 • 是由摩擦力产生的,绝对值大小不变,方向总是和运
动方向相反。是阻碍运动的制动性转矩。 • 属于这一类的生产机械有提升机的走行机构,皮带运
输机,轧钢机以及某些金属切削机床的平移机构等。 • 其特性曲线是位于平面坐标系的第一与第三象限内,
第二章 电力拖动基础知识
• 采用电动机拖动生产机械,并实现生产工 艺过程中各种要求的系统,称为电力拖动 系统。
.
2.1 电力拖动系统的运动方程
• 1、单轴电机拖动系统-包含一根轴的系统
.
• 当电动机的转矩作用于这一系统时,根据动 力学定律可知,电动机的转矩除了克服运动 系统的静阻转矩外,还使整个系统沿着电动 机转矩的作用方向,产生角加速度。角加速 度的大小与旋转体的转动惯量J成反比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 磁滞性
磁滞性:磁性材料中磁感应强度B的变化总是滞后于
外磁场变化的性质。
磁性材料在交变磁场中反复磁化,其B-H关系曲
线是一条回形闭合曲线,称为磁滞回线。 B
剩磁感应强度Br (剩磁) :
当线圈中电流减小到零
Br •
(H=0)时,铁心中的磁感应强度。
矫顽磁力Hc: 使 B = 0 所需的 H 值。
线(常取磁通作为闭合回线)的线积分;
I 是穿过闭合回线所围面积的电流的代数和。
安培环路定律电流正负的规定:
任意选定一个闭合回线的围绕方向,凡是 电流方向与闭合回线围绕方向之间符合右螺 旋定则的电流作为正、反之为负。
安培环路定律将电流与磁场强度联系起来。
在均匀磁场中 Hl = IN
N匝 x
或 H IN l
却随铁心的饱
和程度有关。
4)对电路,当为线性电路时可以应用叠加原理。但对铁心磁路(非线性)不 可应用叠加原理。
3. 磁路与电路的比
较
磁路
磁通势F
磁通
磁感应强度B
磁阻 R m l
S
I
N
F NI
Rm
l
S
电路
电动势 E
电流 I 电流密度 J 电阻 R l
S
I
+
E
R
_
I E R
E l
S
4. 磁路分析的特点 (1)在处理电路时不涉及电场问题,在处理磁路时离 不开磁场的概念;
葛洲坝水利枢纽工程
三峡电站
三峡水力发电机组
• 三峡电站的水轮发电机-全球最大的水轮发电机
火力发电厂
火力发电机组
丹麦Vesta公司生产的风力发电机组
电能的传输、变换
• 电能的传输和变化离不开电机。要传 输一定的电能,为了减小传输线上的 损耗,希望电压越高越好,而用户用 电则为低压电。因此在电能的传输中 必须使用变压器。
(3) 计算各段磁路的磁压降 (Hi li )
(4) 根据下式求出磁通势( NI )
n
NI Hili i 1
注意
①磁化曲线与温度有关,磁导率 一
般随温度的升高而下降,高于某一 温度时(居里点)可能完全失去磁 性材料的磁性。
②磁导率 随H
变化,B与H为
非线性关系。
返回 上页 下页
按磁性物质的磁性能,磁性材料分为三种类型:
B=0H
即 B与 H 成正比,呈线性关系。
Φ
由于 B ,
H NI
O
H( I )
S
l
所以磁通 与产生此磁通的电流 I
成正比,呈线性关系。
(2) 磁性物质 磁性物质内部形成许多小区域,其分子间存在 的一种特殊的作用力使每一区域内的分子磁场排列 整齐,显示磁性,称这些小区域为磁畴。
在没有外磁场作用的普通磁性物质中,各个磁畴排 列杂乱无章,磁场互相抵消,整体对外不显磁性。
的总磁通恒等于零,即磁通连续性
定律。 0
(2)磁路的基尔霍夫第二定律沿任 何闭合磁路的总磁动势恒等于各段磁位 降的代数和。
物质的磁性
(1)非磁性物质
非磁性物质分子电流的磁场方向杂乱无章,几乎
不受外磁场的影响而互相抵消,不具有磁化特性。
非磁性材料的磁导率都是常数,有:
0 , r 当1磁场媒质是非磁性材料时,有: B( )
• 4、交流电力拖动系统逐步取代 直流电力拖动系统
• 5、自动化电力拖动迈向计算机 控制的生产过程自动化。
• 6、自动化电力拖动系统成为低 成本自动化系统的重要组成部分。
二、本课程的性质
电子信息类学科自动化专业 和非电机学专业、电气工程等电 气类专业及以电为主的机电一体 化类专业的一门重要技术基础课
是电气控制与PLC、 自动控 制原理、伺服系统、数控机床等 课程的基础。
三、本课程的任务与内容
• 1、本课程的任务:使学生掌握常用交直流电机、控制电机及变压器等 的基本结构与工作原理以及电力拖动系统的运行性能、分析计算、电机 选择与实验方法。为后续课程准备必要的基础知识。
• 2、本课程的内容:主要研究电机与电力拖动系统的基本理论问题,具 有“电机学”和“电力拖动基础”的基本内容。
磁
外
畴
磁
场
磁化:在外磁场作用下,磁畴方向发生变化,使之 与外磁场方向趋于一致,物质整体显示出磁性来, 称为。即磁性物质能被磁化。
磁性材料的磁性能
磁性材料主要指铁、镍、钴及其合金等。
1. 高导磁性
磁性材料的磁导率通常都很高,即 r 1 (如坡莫合金,其 r 可达 2105 ) 。
磁性材料能被强烈的磁化,有很高的导磁性 能。
5. 磁路的分析计算
主要任务: 预先选定磁性材料中的磁通 (或磁感 应强度),按照所定的磁通、磁路各段的尺寸和材
料,求产生预定的磁通所需要的磁通势F=NI , 确
定线圈匝数和励磁电流。 基本公式:
设磁路由不同材料或不同长度和截面积的 n
段组成,则基本公式为:
NI H 1l 1 H 2 l 2 H n l n
10kV/380V
连接发电机与电网的升压变压器
连接发电机的封 闭母线
与电网相连的 高压出线端
大型电力变压器(保定天威生产)
配电变压器
电路板上所使用的低压高频变压器
电能的利用
• 电能的利用主要是指将电能转换为所需的能量形式,其中最为主要的就是将电能转 换为机械能。要求在转换过程中(1)、转换效率高;(2)、可靠性高。
磁性物质的高导磁性被广泛地应用于电工设 备中,如电机、变压器及各种铁磁元件的线圈中 都放有铁心。在这种具有铁心的线圈中通入不太 大的励磁电流,便可以产生较大的磁通和磁感应 强度。
2. 磁饱和性
磁性物质因磁化所产生的磁化磁场不会随着外
磁场的增强而无限的增强。当外磁场增大到一定程
度时,磁性物质的全部磁畴的磁场方向都转向与外
电气与信息工程学院电气工程系
绪言
• 一、电机及电力拖动技术的发展概况 • (一)电机的发展概况
1、电能的应用非常广泛,其优点有: 生产和变换经济 传输和分配比较容易 使用和控制方便
• 2、电机在电能的应用与生产上起着关 键作用:
电力工业中:发电机与变压器
工业企业:电动机作为原动机大量 使用
自动控制技术:控制电动机被广泛 使用
(1)软磁材料 具有较小的矫顽磁力,磁滞回线较窄。一般用
来制造电机、电器及变压器等的铁心。常用的有铸 铁、硅钢、坡莫合金即铁氧体等。 (2)硬磁材料
具有较大的矫顽磁力,磁滞回线较宽。一般用 来制造永久磁铁。常用的有碳钢及铁镍铝钴合金等。
(3)矩磁材料 具有较小的矫顽磁力和较大的剩磁,磁滞回线
接近矩形,稳定性良好。在计算机和控制系统中用 作记忆元件、开关元件和逻辑元件。常用的有镁锰 铁氧体等。
磁感应强度B的方向:
与电流的方向之间符合右手螺 旋定则。
磁感应强度B的大小:
B F Il
磁感应强度B的单位: 特斯拉(T),
1T = 1Wb/m2
均匀磁场: 各点磁感应强度大小相 等,方向相同的磁场,也称匀强磁 场。
2. 磁通
穿过垂直于B方向的面积S中的磁力线总数。
在均匀磁场中 = B S 或 B= /S
表示磁场媒质磁性的物理量,衡量物质的导磁能力。
单位:亨/米(H/m)
真空的磁导率为常数,用 0表示,有:
相对磁导率 r: 0 4π 107 H/m
任一种物质的磁导率 和真空的磁导率0的比值。
r
0
H 0 H
B B0
安培环路定律(全电流定律)
I
H
Hdl I
式中: H d l 是磁场强度矢量沿任意闭合
n
即
NI Hili
i 1
基本步骤: (由磁通 求磁通势F=NI )
(1) 求各段磁感应强度 Bi
各段磁路截面积不同,通过同一磁通 ,故
有:
B1 S1 , B2 S2 , ... , Bn Sn
(2) 求各段磁场强度 Hi
根据各段磁路材料的磁化曲线 Bi=f ( Hi) ,求B1,
B2 ,……相对应的 H1, H2 ,……。
磁性物质不同,其磁滞回
• O •Hc H •
线和磁化曲线也不同。
磁滞回线
磁路与电路的性质:
I R 1)电路中有电流I时,就有功率损耗
;而在直流磁路中,维2持一定量
的磁通量
时,铁心中没用功率损耗。
2)电路中可以认为导线外无电流,但磁路中铁心外却有漏磁通。即没有绝对
的磁绝缘体。
3)电路中的电阻率 在一定温度下时不变的,磁导率
I
Hx S
线圈匝数与电流的乘积NI ,称为磁通势,
用字母 F 表示,则有 F = NI
磁通由磁通势产生,磁通势的单位是安
[培]。
2、磁路的欧姆定律
F Rm /
F-磁路的磁通势,F=Ni,即为作用在
铁心上的安匝数,单位为A
Rm
l
S
为磁路的磁阻,单位为A/Wb
3、磁路的基尔霍夫定律 (1)磁路的基尔霍夫第一定律 穿出或进入任何一闭合面
• 往往在能量转换的同时也能对运动进行控制,这就引入了一个新的研究分支-电力 传动。
• 相对而言,电机这一概念往往是指电动机。
哈尔滨电机厂生产的1MW电机
手机震动电机
电动自行车所用的无刷直流电机
电机图
返回
第一章磁路 §1-1 磁路的基本物理量
1. 磁感应强度B
表示磁场内某点磁场强弱和
方向的物理量。
当励磁电流为交流时,磁路为交流 磁路,其磁通随时间变化而变化。如: 变压器、感应电动机、交流接触器、交 流继电器等。
• 3、铁心损耗:
