实验四三次样条插值Word版

实验四三次样条插值的应用

一、问题描述

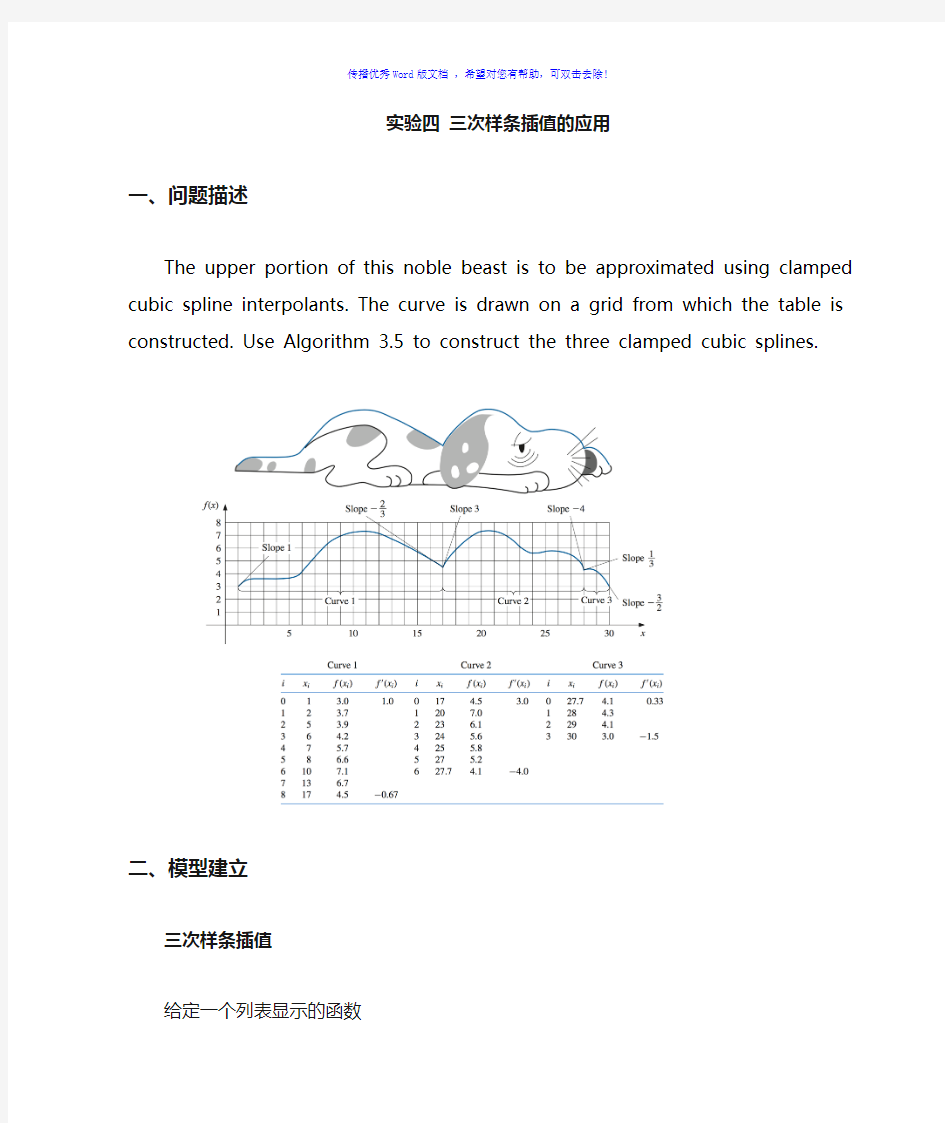
The upper portion of this noble beast is to be approximated using clamped cubic spline interpolants. The curve is drawn on a grid from which the table is constructed. Use Algorithm 3.5 to construct the three clamped cubic splines.

二、模型建立

三次样条插值

给定一个列表显示的函数

yi=y(xi),i=0,1,2,...,N-1。特别注意在xj和xj+1之间的一个特殊的区间。该区间的线性插值公式为：

(3.3.1)式和(3.3.2)式是拉格朗日插值公式(3.1.1)的特殊情况。

因为它是(分段)线性的，(3.3.1)式在每一区间内的二阶导数为零，在横坐标为xj处的二阶导数不定义或无限。三次样条插值的目的就是要得到一个内插公式，不论在区间内亦或其边界上，其一阶导数平滑，二阶导数连续。

做一个与事实相反的个假设，除yi的列表值之外，我们还有函数二阶导数y"的列表值，即一系列的yi"值，则在每个区间内，可以在(3.3.1)式的右边加上一个三次多项式，其二阶导数从左边的yj"值线性变化到右边的yj+1"值，这么做便得到了所需的连续二阶导数。如果还将三次多项式构造在xj和xj+1处为零，则不会破坏在终点xj和xj+1处与列表函数值yj和yj+1的一致性。

进行一些辅助计算便可知，仅有一种办法才能进行这种构造，即用

注意,(3.3.3)式和(3.3.4)式对自变量x的依赖，是完全通过A和B对x的线性依赖，以及C和D(通过A和B)对x的三次依赖而实现。可以很容易地验证，y"事实上是该插值多项式的二阶导数。使用ABCD的定义对x求(3.3.3)式的导数，计算dA/dx dB/dx dC/dx dD/dx,结果为一阶导数

因为x=xj是A=1，x=x(i+1)时A=0，而B正相反，则(3.3.6)式表明y"恰为列表函数的二阶导数。而且该二阶导数在两个区间(xj-1, xj)和(xj, xj+1)上是连续的。

现在唯一的问题是，假设yj"是已知的。而实际上并不知道。然而，仍不要求从(3.3.5)式算出的一阶导数在两个区间的边界处是连续的。三次样条的关键思想就在于要求这种连续性，并用它求得等式的二阶导数yi"。

设(3.3.5)式在区间(xj-1, xj)上对x=xj求得的值，等于同一等式在区间(xj,x[j+1])上对x=xj求得的值，便可得到所求方程，是新整理得到(对j=1,......,N-2)

这意味着有N-2个线性方程，但却有N个未知数yi",i=0,......,N-1。因此，存在一个具有两个参数的可能解集。为求得唯一解，需要给出两个进一步的条件，

一般取x0和x[n-1]处的边界条件。最常见的做法有：

[1]设y[0"]和y[n-1]"之一或两个都为零，得到所谓的自然三次样条函数，其一个或两个边界的二次导数为零。

[2]设y[n]"和y[n-1]"为(3.3.5)式计算得到的值，使得该插值函数的一阶导数一个或两个边界处有特定的值。

三次样条插值特别实用的原因之一在于，有两个附加边界条件的方程组(3.3.7)，它不仅是线性的，而且是三对角的。每个yj"仅与其最邻近的j+-1的值有关。因此，方程可以用三对角算法在O(N)次运算内求解。该算法非常简明，很容易正确地构造出样条计算的程序。但是这使得程序不像(3.3.7)式的实现那样完全透明。

三、模型求解

借助Matlab软件进行编程求解，Matlab代码如下

最终生成的插值函数图像为

四、实验感悟

三次样条插值优点是计算简单，稳定性好，收敛性有保证且易在计算机上实现。缺点是它只能保证各小段曲线在连接点的连续性，却无法保证整条曲线的光滑性，这就不能满足某些工程技术的要求。但它依旧很强大，我们要好好掌握其精髓。