微电子器件课后答案(第三版)
微电子器件基础第六章习题解答课件

垒 区
电 子 扩
N 中
散性
区区
反向小注入下,P区接电源负极,N区接电源正 极,势垒区电场强度增加,空间电荷增加,势垒 区边界向中性区推进。
势垒区与N区交界处空穴被势垒区强电场驱向P 区,漂移通过势垒区后,与P区中漂移过来的空 穴复合。中性N区平衡空穴浓度与势垒区与N区 交界处空穴浓度形成浓度梯度,不断补充被抽取 的空穴,对PN结反向电流有贡献。
注入空穴在N区与势垒区交界处堆积,浓 度比N区平衡电子浓度高,形成浓度梯度, 产生流向中性N区的空穴扩散流,扩散过 程中不断与中性N区漂移过来的电子复合, 经过若干扩散长度后,全部复合。
3、 解、
VR
P
N
IR
n p0 np
pn0
pn
xp 0 x n
x
JR(JpJn)
Jp
Jn
P空
中穴 势
性 区
扩 散 区
k0T q
2 i
np
2
npp1Ln
1
nLp
kq0Tnpi212
n p
1
pLn
1
nLp
kq0Tbb1i22
5、 解、 硅突变PN结,
n 5 c ,p m 1 1 6 s ;0 p 0 . 1 c ,n m 5 1 6 s 0
N区、P区多子浓度, nn0nq 1n51.611 0 1913 59.0 31104 cm 3 pp0pq 1p0.11.61 1 0 19501 0.31107 cm 3
正向小注入下,忽略势垒区复合和表面复合,空穴电流密度等于势垒区 与空穴扩散区交界处的空穴扩散电流密度,电子电流密度等于势垒区与电 子扩散区交界处电子扩散电流密度,
Jp qDp ddpn xx xxn qDp pLnp0ekq0TV1 Jn qD n ddnp xx xxp qD n nLpn0ekq0TV1
微电子器件课后答案(第三版)

Hale Waihona Puke 得:VBE 0.55V WB2 1 WB 已知: 1 1 , 将 n 106 s 及 WB 、DB 2 LB 2 DB n
q
s
N D xn , 由此得:xn
q
s
N A xp , 由此得:xp
s Emax
qN A
(2) 对于无 I 型区的 PN 结: q xi1 0, xi2 0, E1 N D ( x xn ), s
在 x 0 处,电场达到最大, Emax q
E3 N D xn
0
AE q 2 DE ni2 1 QEO
1
再根据注入效率的定义,可得:
J pE QBO DE J nE J nE 1 1 J E J nE J pE J nE QBE DB
9、
I C AE J nC AE J nE
1 2
39、
qV I F I 0 exp kT dI F qI F gD dV kT kT 当 T 300K 时, 0.026 V, 对于 I F 10 mA 0.01 A, q 10 1 gD 0.385s, rD 2.6 26 gD kT 373 在 100C 时, 0.026 0.0323V, q 300 10 1 gD 0.309s, rD 3.23 32.3 gD
微电子器件_电子科技大学中国大学mooc课后章节答案期末考试题库2023年

微电子器件_电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.线性缓变结的耗尽层宽度正比于【图片】。
参考答案:正确2.反向偏置饱和电流可看成是由中性区内少数载流子的产生而导致的。
参考答案:正确3.减薄p+n突变结的轻掺杂区厚度,不但能减少存储电荷,还能降低反向抽取电流。
参考答案:错误4.在异质结双极型晶体管中,通常用()。
参考答案:宽禁带材料制作发射区,用窄禁带材料制作基区5.( )的集电结反向电压VCB称为共基极集电结雪崩击穿电压,记为BVCBO。
参考答案:发射极开路时,使6.【图片】对高频小信号注入效率的影响的物理意义是,【图片】的存在意味着【图片】必须先付出对势垒区充放电的多子电流【图片】后,才能建立起一定的【图片】。
这一过程需要的时间是()。
参考答案:发射结势垒电容充放电时间常数7.某长方形扩散区的方块电阻为200Ω,长度和宽度分别为100μm和20μm,则其长度方向的电阻为()。
参考答案:1KW8.要提高均匀基区晶体管的电流放大系数的方法()。
参考答案:减小基区掺杂浓度_减小基区宽度9.防止基区穿通的措施是提高()。
参考答案:增大基区宽度_增大基区掺杂浓度10.从发射结注入基区的少子,由于渡越基区需要时间tb ,将对输运过程产生三方面的影响( )。
参考答案:时间延迟使相位滞后_渡越时间的分散使减小_复合损失使小于111.晶体管的共发射极输出特性是指以输入端电流【图片】作参量,输出端电流【图片】与输出端电压【图片】之间的关系。
参考答案:正确12.电流放大系数与频率成反比,频率每提高一倍,电流放大系数下降一半,功率增益降为四分之一。
参考答案:正确13.特征频率【图片】代表的是共发射极接法的晶体管有电流放大能力的频率极限,而最高振荡频率【图片】则代表晶体管有功率放大能力的频率极限。
参考答案:正确14.模拟电路中的晶体管主要工作在()区。
参考答案:放大15.共发射极电路中,基极电流IB是输入电流,集电极电流IC是输出电流。
电子电工技术第三版课后答案
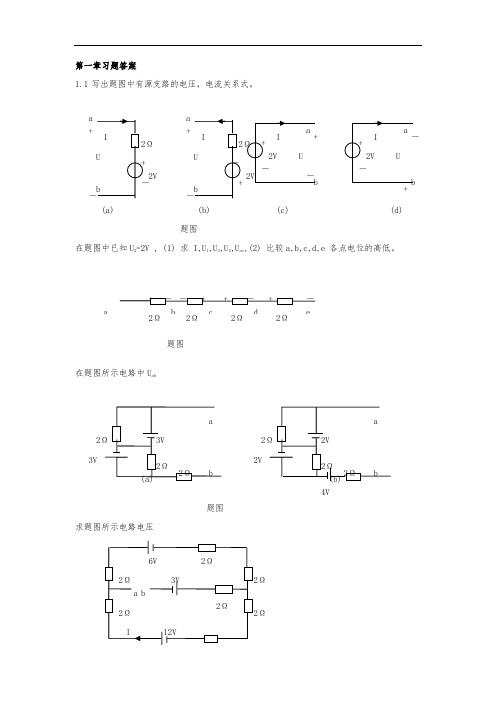
第一章习题答案1.1 写出题图中有源支路的电压,电流关系式。
(a) (b) (c) (d) 题图在题图中已知U 2=2V , (1) 求 I,U 1,U 3,U 4,U ac ,(2) 比较a,b,c,d,e 各点电位的高低。
题图在题图所示电路中U ab题图 求题图所示电路电压+a2V Ω + a+ 2Ω 2Ω 2Ω 2Ωa b c d e3V 22V24VΩΩ题多量程直流电流表如题图所示,计算0-1,0-2及0-3各端点的等效电阻,即各挡的电流表内阻,已知表头等效电阻R A =15k Ω,各分流电阻R 1=100Ω,R 2=400Ω,R 3=500Ω。
题图 两个额定值是110V,40W 的灯泡能否串联后接到220V 的电源上使用如果两个灯泡的额定电压相同,都是110V ,而额定功率一个是40W ,另一个是100W,问能否把这两个灯泡串联后接在200V 电源上使用,为什么电路如题图所示.试问ab 支路是否有电压和电流题图题图中若(1)U=10V, I=2A, (2)U=10V,I=-2A 。
试问哪个元件是吸收功率哪个元件是输出功率为什么题图1. 计算题图所示各电路的等效电阻.1 23U UUU +++ + - -- -(c)(a) (b) (d)1. 电路如题图所示,试求以下电路的电压U 和电流I 。
(c) (d)在指定的电压u 和电流i 参考方向下,写出图所示各元件u 和i 的约束方程.(a) (b) (c)(d) (e)1A 20Ω+ 30V U-U 30V + -u - + - u 10μF u -+U5V +-U + -求题图所示电路中的U 1和U 2.题图求题图中所示电路化成等值电流源电路。
(a) (b) (c) 题图求题图中所示电路化成等值电压源电路。
(a(b)题图求题图所示电路的电流I 和电压U 。
4V1A2V 1A6V6V3A( a) (b) 题图求题图所示各电流源输出的功率。
题图求题图所示各电路源输出的功率。
微电子器件(3-2)

均匀基区pnp晶体管能带图 放大状态:EFn − EFp = qV饱和状态:截止状态:倒向放大状态: 平衡态均匀基区pnp晶体管的各边界上少子浓度⎛ qVEB ⎞ nE = nE0 exp ⎜ ⎟ kT ⎝ ⎠E Emitter P⎛ qVEB ⎞ pB = pB0 exp ⎜ ⎟ ⎝ kT ⎠Base N Collector P CnE = nE0BnC = nC0⎛ qVCB ⎞ pB = pB0 exp ⎜ ⎟ ⎝ kT ⎠⎛ qVCB ⎞ nC = nC0 exp ⎜ ⎟ ⎝ kT ⎠均匀基区pnp晶体管的少子分布图: 放大状态:饱和状态:截止状态:倒向放大状态:忽略势垒区产生复合电流, 处于放大状态的晶体管内部的 各电流成分如下图所示:I pEI pCI prI nEI nrI ncI E = I pE + I nE , I B = I nE + I nr − I nc ≈ I nE + I nr , I C = I pc + I nc ≈ I pC = I pE − I pr = I E − I nE − I nrI pEI pCI prI nEI nr从 IE 到 IC ,发生了两部分亏损(PNP): InE 与 In r 。
要减小 InE ,就应使NE >> NB ; 要减小In r ,就应使WB << LB 。
§ 3-2 均匀基区晶体管的放大系数均匀基区晶体管:基区掺杂为均匀分布。
少子在基区中主 要作扩散运动,又称为 扩散晶体管。
(本节以pnp为例)均匀基区晶体管(理想晶体管)• 发射区、基区、集电区均匀非简并掺杂,发射结与集 电结为突变结; • 晶体管在一维稳态条件下工作; • 中性区满足小注入水平; • 发射结与集电结的耗尽区内复合-产生可以忽略不 计; • 发射区与集电区的中性区宽度远大于少子扩散长度, 而基区的中性区宽度则远小于少子扩散长度。
微电子器件期末复习题含答案

(复合损失使小于 1β0*
小于 1)、
(时间延迟使相位滞后)和(渡越时间的分散使|βω*|减小)
。
53、基区渡越时间 b 是指(从发射结渡越到集电结所需要的平均时间)
。当基区宽度加
倍时,基区渡越时间增大到原来的(2)倍。
54、晶体管的共基极电流放大系数 随频率的(增加)而下降。当晶体管的 下
比例增大,使注入效率下降。
微电子器件(第三版)陈星弼
电子科技大学中山学院/——4
陈卉/题目 王嘉达/答案
答案为个人整理,如有错误请 仔细甄别 ! 厚德 博学 求是 创新
34、发射区重掺杂效应是指当发射区掺杂浓度太高时,不但不能提高(注入效率)
,反
而会使其(下降)
。造成发射区重掺杂效应的原因是(发射区禁带变窄)和(俄歇
(提高)基区掺
杂浓度。[P90]
47、比较各击穿电压的大小时可知,BVCBO(大于)BVCEO ,BVCBO(远大于)BVEBO。
48、要降低基极电阻 rbb ,应当(提高)基区掺杂浓度,
(提高)基区宽度。
49、无源基区重掺杂的目的是(为了降低体电阻)
。
微电子器件(第三版)陈星弼
电子科技大学中山学院/——5
降到(
0
)时的频率,称为 的截止频率,记为(
2
f
)。
55、晶体管的共发射极电流放大系数 随频率的(增加)而下降。当晶体管的 下
降到
1
0 时的频率,称为 的(截止频率),记为( f )。
2
56、当 f f 时,频率每加倍,晶体管的 降到原来的(½)
微电子器件(3-3)

均匀基区相关知识点I pEI pCI prI nEI nr相关公式β∗W B2 τb =1− =1− 2 2 LB τBD EW B N B WBρE γ = 1− D W N = 1− W ρ B E E E B⎛ W B2 α =⎜ ⎜1 − 2 L2 B ⎝2 B 2 BR口E = 1− R口B1⎞⎛ R口E ⎞ W B2 R口E ⎟ ⎟⎜ ⎟ ≈ 1 − 2 L2 − R ⎜1 − R ⎟ 口 B1 ⎠ B 口 B1 ⎠⎝⎛W R口E ⎜ β ≈⎜ + R口B1 ⎝ 2L⎞ ⎟ ⎟ ⎠−1§3-3 缓变基区晶体管的放大系数以NPN 管为例,结电压为 VBE 与 VBC 。
现代晶体管,如双扩散外延平面管 属缓变基区晶体管,由于载流子在 基区主要是以漂移运动在传输,故 它又称为 漂移晶体管。
N+0PN杂质浓度分布图:x jE x jCWB = x jC − x jEN E ( x) N B ( x)NC0x jE x jCx1、基区内建电场的形成与求解 形成的物理机理(以P型基区的Xmb-Xjc段为例)xjE 和xjC为发射结 和集电结结深, xmB为杂质补偿后 基区净杂质浓度 的极值位置杂质浓度高的地方留下不 可移动的电离杂质电荷 (NA-),杂质浓度低的地 方积累多子(空穴)杂质(NA) 浓度梯度杂质电离多子(空 穴) 浓度梯度多子(空 穴) 扩散正负电荷 分离内建电场内建电场的作用 漂移晶体管电场方向:指向发射结 加速场 电场作用: 基区的少子(电子) 向集电结方向漂移运 动,对少子有加速作用 向发射结方向漂移运动, 抵消多子扩散运动 多子电流等于零基区的多子(空穴)xjE到xmB段,将产生一个与EB方向相反的自建电场EB’,它将阻止 基区中少子(电子)流向集电结,称阻滞电场,该部分基区称阻 滞区。
一般情况下,相对与整个基区而言,阻滞区很窄,一般可以忽略。
请从以下几方面总结半导体器件中的内建电场① 掺杂不均匀产生的内建电场 ~ 产生机理? 对多数载流子运动的影响? 对少数载流子运动的影响? ② 大注入产生的内建电场 ~ 产生机理? 对多数载流子运动的影响? 对少数载流子运动的影响 ? ③ p-n结中的内建电场 ~ 产生机理? 势垒区(阻挡层)→阻挡多数载流子还是阻挡少数载流子? 耗尽层近似?→ 耗尽什么种类的载流子?三个内建电场形成机理的比较内建电场种类形成原因 P区与N区刚接触 时冶金结两边存 在自由载流子浓 度差 大注入时中性区 多子具有浓度梯 度分布电荷分离的表现形式 冶金结两边自由载流子扩散,留下不 可移动的电离施主和受主杂质电荷在 空间上分离 多子与少子同时扩散,但由于多子扩 散得不到补充,最终使得靠近耗尽区 少子浓度高于多子浓度,远离耗尽区 边界少子浓度低于多子浓度,最终多 子与少子电荷在空间上分离 多子浓度扩散,使得靠近发射结耗尽 区的电离杂质电荷高于多子,靠近集 电结耗尽区的电离杂质电荷低于多 子,造成电离杂质电荷与多子电荷在 空间上分离作用 载流子的扩散运 动等于漂移运动PN结空间电 荷区内建电 场 大注入PN结 中性区中的 内建电场 (自建场) 缓变基区BJT 中基区内建 电场多子的扩散运动 与漂移运动抵 消,加强少子扩 散运动 多子的扩散运动与 漂移运动抵消,少 子在基区以漂移运 动为主掺杂原子具有浓 度梯度,多子具 有相同的浓度梯 度分布基区内建电场表达式的推导 设基区杂质浓度分布为:NB (0)NB (x)⎛ ηx ⎞ N B ( x ) = N B ( 0 ) exp ⎜ ⎜− W ⎟ ⎟ B ⎠ ⎝ 式中 η 是表征基区内杂质变化程度的一个参数:NB (WB )0WBxN B (W B ) = N B ( 0 ) exp (− η )N B (0) η = ln N B (W B )当 η = 0 时为均匀基区。
EDA技术使用教程课后答案(第三版)潘松版

第一章1-1 EDA技术与ASIC设计和FPGA开发有什么关系? P3~4 答:利用EDA技术进行电子系统设计的最后目标是完成专用集成电路ASIC的设计和实现;FPGA和CPLD是实现这一途径的主流器件。
FPGA和CPLD 通常也被称为可编程专用IC,或可编程ASIC。
FPGA和CPLD的应用是EDA 技术有机融合软硬件电子设计技术、SoC(片上系统)和ASIC设计,以及对自动设计与自动实现最典型的诠释。
1-2与软件描述语言相比,VHDL有什么特点? P6答:编译器将软件程序翻译成基于某种特定CPU的机器代码,这种代码仅限于这种CPU而不能移植,并且机器代码不代表硬件结构,更不能改变CPU的硬件结构,只能被动地为其特定的硬件电路结构所利用。
综合器将VHDL程序转化的目标是底层的电路结构网表文件,这种满足VHDL设计程序功能描述的电路结构,不依赖于任何特定硬件环境;具有相对独立性。
综合器在将VHDL(硬件描述语言)表达的电路功能转化成具体的电路结构网表过程中,具有明显的能动性和创造性,它不是机械的一一对应式的“翻译”,而是根据设计库、工艺库以及预先设置的各类约束条件,选择最优的方式完成电路结构的设计。
l-3什么是综合?有哪些类型?综合在电子设计自动化中的地位是什么? P5 什么是综合? 答:在电子设计领域中综合的概念可以表示为:将用行为和功能层次表达的电子系统转换为低层次的便于具体实现的模块组合装配的过程。
有哪些类型?答:(1)从自然语言转换到VHDL语言算法表示,即自然语言综合。
(2)从算法表示转换到寄存器传输级(RegisterTransport Level,RTL),即从行为域到结构域的综合,即行为综合。
(3)从RTL级表示转换到逻辑门(包括触发器)的表示,即逻辑综合。
(4)从逻辑门表示转换到版图表示(ASIC设计),或转换到FPGA的配置网表文件,可称为版图综合或结构综合。
综合在电子设计自动化中的地位是什么?答:是核心地位(见图1-3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
exp
qVBE kT
1
1
ro
IC VCE
VBE
AE qDB ni 2
exp
qVBE kT
1
NB
(WB
)
dWB dVCE
WB 0
NBdx
2
IC
NB (WB )
WB
dWB dVCE
0 NBdx
IC VA
WB
VA 0 NBdx
N
B
(WB
)
dWB dVCE
对均匀基区,VA
qV kT
1
Jdp Ln Dp NA Ln p NA 1 Jdn Lp Dn ND Lp n ND
24、 PN 结的正向扩散电流为
I
I0
exp
qV kT
式中的 I0 因含 ni2 而与温度关系密切,因此正向扩散电流可表为
I
C1ni2
exp
qV kT
C2
exp
EG kT
qV
于是 PN 结正向扩散电流的温度系数与相对温度系数分别为
ni2 NB
exp
qVBE kT
,
得:VBE
kT q
ln nB (0)NB , ni2
将
kT q
、nB
(0)、NB
及 ni
之值代入,
得:VBE 0.55V
已知:
1
1 2
WB LB
2
1 WB2
2DB n
,
将n
106 s 及 WB 、DB
之值代入,得: 0.9987。
7、
b
WB2 2DB
WB2 2L2B
2
1
1
β0 与 β 也有类似的关系 。
将
N
(x)
N0
exp(
x
)
代入,得:E
kT
q
再将 kT 0.026 V, 0.4 μm 代入,得:E 650 V cm
q
1
突变结的最大电场强度表达式为:|
Emax
|
2qN0Vbi
s
2
式中:N0
NDNA ND NA
ND
1015 cm3,
Vbi
kT q
ln
NDNA ni2
0.757 V,
100
6、
由
J nE
qDBnB (0) , WB
可得:nB (0)
J nEWB qDB
,
将
JnE 0.1Acm2 , WB 2 104 cm, q 1.6 1019 C, DB 15cm2 s1
之值代入,得: nB (0) 8.331012 cm3
又由
nB (0)
np0
exp
qVBE kT
0,由此得:E1
q
s
ND (x
xi1
xn )
在 I 型区, dE2 0, dx
E2 常数 Emax
在 P型区,
dE3 dx
q
s
NA
,
E3
q
s
NA x
C3
边界条件:在
x
xi2
xp
处,E3
0,由此得:E3
q
s
NA (x
xi2
xp )
N
I
P
xi1 xn xi1 0 xi2
xi2 xp
E2 Emax E
1
xdB W xdB
2
144
1
9
3 9
2
80V
34、
已知对于单边突变结,
1
CT
A
s qN
2(Vbi
0
V
)
2
Vbi
K V
1
2
当 Vbi 0.6 V,
V 3V 时, CT
K 10 pF , 由此可得 3.6
K 10 3.6, 因此当 V 0.2 V时,
E1
E3
xi1 xn xi1 0 xi2
x
xi2 xp
在
x
xi1 处,E1
Emax
q
s
ND xn ,
由此得:xn
s Emax
qND
在
x
xi2 处,E3
Emax
q
s
NA xp
,
由此得:xp
s Emax
qNA
(2) 对于无 I 型区的PN结:
xi1 0,
xi2 0,
E1
q
s
ND (x
xn ),
dI dT
C2
exp
EG kT
qV
EG kT
qV
2
I
EG kT
qV
2
1 dI I dT
EG qV kT 2
31、 当 N- 区足够长时,开始发生雪崩击穿的耗尽区宽度为:
xdB
2VB EC
2 144 32
9μm
当 N- 区缩短到 W = 3m 时,雪崩击穿电压成为:
VB
'
VB
qVBE kT
1
AEq2 DEni2 QEO
exp
qVBE kT
1
再根据注入效率的定义,可得:
J nE JE
J nE JnE JpE
1
J pE J nE
1
1
QBO QBE
DE DB
1
9、
IC
AE J nC
AE J nE
AE
qDBni2 WB NB
exp
qVBE kT
Vbi
1 2
Emax xn
Emax xi
1 2
Emax xp
kT q
ln
NDNA ni2
Emax
xn
2Vbi 2xi
xp
式中,xi xi1 xi2
将
xn
s Emax
qND
,
xp
s Emax
qNA
代入,解出 Emax ,得:
1
Emax
qN0 xi
s
1
2 sVbi
qN0 xi2
2
1
1
对于PN结,可令
WB dWB dVCE
式中,dWB dxdB , VCE VCB VBE
因
VBE
保持不变,所以 dVCE
dVCB ,
于是:VA
WB dxdB dVCB
1
xdB
2s N
qNB
C
(
(Vbi VCB ) NC NB)
2
1
dxdB dVCB
2qNB
(NC
s NC
NB )(Vbi
2
VCB
式中,
1
1 2
WB LB
2
1
WB2
2DB B
0.9986
将 AE 104 μm2 , 0.9986, q 1.6 1019 C,
DB 18cm2 s1, ni 1.51010 cm3, WB 0.7 104 cm,
NB 1017 cm3,
VBE 0.7 V,
kT 0.026 V 之值代入, q
DE 2cm2s1, DB 18cm2s1, 代入 中,得: 0.9972
(2) 1 WB2 0.9999 2DB B
(3) 0.9971, 344 1
(4) 当由基区输运造成的亏损非常小时,可假设 1,这时
可用 ' QEODB 来代替 。
QBO DE
' QEODB 360, 误差为: | e | | ' | 4.7%
2
1
1
1.1251011(s)
8、以 NPN 管为例,当基区与发射区都是非均匀掺杂时, 由式(3-33a)和式(3-33b),
JnE
qDBni2
WB 0
NBdx
exp
qVBE kT
1
AE q 2 DBni2 QBO
exp
qVBE kT
1
JpE
qDE ni2
WE 0
NEdx
exp
得:IC 4.55 (mA)
0.9936,
1
155,
IB
IC
0.029 (mA)
10、
(1)
1
DEWB NB
DB
WE 0
NEdx
1
DE ABqWB NB
DB ABq
WE 0
NEdx
1 QBO DE QEO DB
式中,QBO ABqWB NB 3.2 1011C, QEO 1.28109 C,
48、
IC IE ICBO
0
dIC dIE
d( IE )
dIE
IE
d
dIE
在 IE 很小或很大时,α 都会有所下降。
当
IE
很小时,d
dI E
0,
这时 α0 >α ;
当
IE
很大时,d
dI E
0,
这时 α0
< α;
在正常的
IE
范围内,α
几乎不随
IE
变化,
d
dI E
0,
这时
0
1
R口E R口B1
Emax
Ex
q
s
NDx
当 x = xn 时,E(x) = 0,因此
Emax
q
s
ND xn ,于是得:
E
x
q
s
x
xn
ND
0 x xn
(2-5a)
