连杆机构运动分析
高等机构学第8章-空间单链连杆机构的运动分析

第八章 空间单链连杆机构的运动分析
8.1、RCCC机构运动分析 8.2、串联机器人机构的位置分析 8.3、串联机器人的雅可比矩阵
8.1、RCCC机构运动分析
8.1、RCCC机构运动分析
8.1.1、位置分析 8.1.2、速度分析 8.1.3、加速度分析 8.1.4、构件上任意点的运动分析
8.1、RCCC机构运动分析
或
cos3
cos1
sin 30 sin 01 cos30 sin 12 sin 23
cos01
cot 12
cot 23
(8-9)
8.1.1、位置分析
仿上将该式(8-9)中符号下标数字的排列由0-1-2-3轮换成3-0-1-2,可得由0求2的 关系式为
cos2
cos0
(8-3)
由此可得各输入输出角位置方程式
sin0 sin1 sin23 sin01 cos1 sin01(cos0 sin23 cos30 cos23 sin30 ) cos01( cos0 sin23 sin30 cos23 cos30 ) cos12
8.1.1、位置分析
如图8-1所示为RCCC空间机构。机构 的已知结构参数为S0、h1、h2、h3、h0、 α01、α12、α23、α30,设杆1为原动件而1 为输入转角,要求分析运动参数0、2、 3、S3、S2、S1。
平面连杆机构运动分析及设计

3选不同的构件为机架
3
1
4
A
2
B
C
直动滑杆机构
手摇唧筒
这种通过选择不同构件作为机架以获得不同机构的方法称为:
机构的倒置
B
C
3
2
1
4
A
导杆机构
3
1
4
A
2
B
C
曲柄滑块机构
3
1
4
A
2
B
C
摇块机构
3
1
4
A
2
B
C
A
B
C
3
2
1
4
天津工业大学专用 作者: 潘存云教授
摆转副——只能作有限角度摆动的运动副;
曲柄
连杆
摇杆
§3-2 平面四杆机构的类型和应用
1 平面四杆机构的基本型式
天津工业大学专用 作者: 潘存云教授
第三章 平面连杆机构运动分析与设计
§3-1 连杆机构及其传动特点
§3-2 平面四杆机构的类型和应用
§3-3 平面四杆机构的基本知识
§3-6 平面四杆机构的设计
§3-4 运动分析——速度瞬心法
§3-5 运动分析——矢量方程图解法
天津工业大学专用 作者: 潘存云教授
作者:潘存云教授
1 改变构件的形状和运动尺寸
偏心曲柄滑块机构
对心曲柄滑块机构
曲柄摇杆机构
曲柄滑块机构
双滑块机构
正弦机构
s
=l sin φ
↓ ∞
→∞
φ
l
2 平面四杆机构的演化型式
天津工业大学专用 作者: 潘存云教授
第5章 平面连杆机构的运动分析
( xBi x A ) 2 ( y Bi y A ) 2 ( xB1 x A ) 2 ( y B1 y A ) 2 ( xCi xD ) 2 ( yCi y D ) 2 ( xC1 xD ) 2 ( yC1 y D ) 2 i 2,3
(a12 cos12 b12 sin 12 x A cos12 y A sin 12 x A ) x B1 (b12 cos12 a12 sin 12 x A sin 12 y A cos12 y A ) y B1 1 2 2 a12 x A b12 y A (a12 b12 ) 2 (a13 cos13 b13 sin 13 x A cos13 y A sin 13 x A ) x B1 (b13 cos13 a13 sin 13 x A sin 13 y A cos13 y A ) y B1 1 2 2 a13 x A b13 y A (a13 b13 ) 2
cos 1i D1i sin 1i 0
xBi xB1 y D y 1i B1 Bi 1 1
xCi xC1 y D y 1i C1 Ci 1 1
Qi Pi Bi
Q1
i P1
B1
1
Ci
C1
A
D
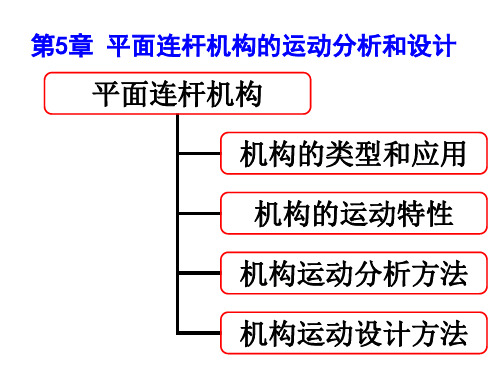
铰链四杆机构实现连杆的三个精确位置P1Q1,,
P2Q2,P3Q3 的设计图解方法
实现三个位置
机构不能可靠到位
曲柄摇杆机构
机构不能顺序到位
5.6.2 平面连杆机构运动设计的位移矩阵法
1.刚体运动位移矩阵 刚体运动→矢量运动
曲柄连杆机构的运动与受力分析讲解学习

定义“曲拐当量质量”为:
则: Prqmqdr2
mqdmqx2mqbrb
如果曲拐的某一曲柄臂上设有平衡重,其质量为 m p ,而其质心
距曲轴轴线的距离为 p ,则平衡重的旋转惯性力为:
Prpmpp2r2mprp
定义“平衡重当量质量”为:
mpd
mp
p
r
(1-32)
则: Prpmpdr2 (1-33)
(2)活塞速度:在0 ºCA~90 ºCA之间和 270 ºCA~360 ºCA之间,活塞速度各出现 一个正极值和负极值。 (3)活塞加速度:在上止点前后活塞加 速度是正值,方向是活塞下行的方向,往 复惯性力朝上;在下止点前后活塞加速度 是负值,方向是活塞上行的方向,往复惯 性力朝下。根据极值方法求解,可得:
1.2.2.2 单个曲拐的旋转惯性力
曲轴上曲柄不平衡部 分的质量分为两部分:
(1)曲柄销部分:
图1-10 单曲拐的旋转惯性力
Prxmqxr2 (1-28)
(r为曲柄半径)
(2)曲柄臂部分: Prbmqbb2 (1-29)
( b 为曲柄臂质心至曲轴轴线的垂直距离)
整个曲拐的旋转惯性力就是:
P rq P rx 2 P rb r2 m q x2 m qbrb
由式(1-3)知:
arc s i(n1-12)
极值: e arcsin角速度: l Nhomakorabead
dt
cos cos
cos 1 2 sin 2
1 (1-13)
2
角速度极值:le
角加速度:l d d l t c s i o n d d s tc o c s s2 o i n s d d t
1.2.2.3 连杆的惯性力
第九章-曲柄连杆机构动力学分析
Pj m j a m j R 2 cos m j R 2 cos2 PjI PjII
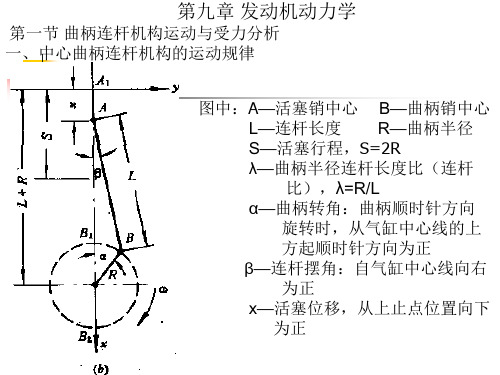
(2)、旋转惯性力Fr=mrRω2 2、沿气缸中心线的总作用力F 总作用力F是缸内气体作用力Fg与往复惯性力的代数和 F=Fg+Fj 气体作用力 D 2 Fg p g - p? g 4
1、活塞位移x:
x ( L R) ( L cos R cos )
2 2
R(1 cos ) L(1 1 sin )
(精确式)
R x R(1 cos ) (1 cos 2 ) x I x II (近似式) 4
近似式与精确式相比误差很小,如当λ =1/3.5时,曲柄转角为 90度时误差为最大,在0.003R左右,此精度在工程上已足够。
பைடு நூலகம்
(精确式)
1 2 L sin 1 1 3 cos2 (近似式) 2
2
在α =90º 或270º 时达到极值:
Le
2 (1 2 )1 / 2
(精确式)
1 (近似式) 2 摆动角速度和角加速度精确式中分母均近似等于 1 ,因此两者均 随α 近似按简谐规律变化。
L L 1 m j m p m 1 m p m l L 作旋转运动的不平衡质量mr,包括曲柄换算质量mk和连杆换算
L1 mr mk m 2 mk1 2mk 2 mL R L
到大头中心的质量m2,集中作用于曲柄销中心,即
三、曲柄连杆机构作用力和力矩 1、惯性力 、 (1)旋转惯性力 (1)、 往复惯性力
2、活塞速度:
sin( ) v R cos
5连杆机构运动分析

机械原理(苗老师)
结论:当已知一构件上两点的速度时,则该构件上的其他 任一点的速度便可利用速度影像与构件图形相似的原理求 出。
注意点: 相对速度方向垂直于机构位置图上与之对应的两点连
线, 这是就同一构件上两点而言的,不能用于机构不同构 件上的各点。
ω
C
α
A
VBA
B aA
VA
ω2
B
2
1
ω1
α1
C
E 3 ω3
机械原理(苗老师)
2.速度瞬心分类 (1) 绝对瞬心
若两构件之一是静止的,称瞬心其为绝对瞬心 因此绝对瞬心是构件上瞬时绝对速度为零的的一点 (2) 相对瞬心 如果两构件都是运动的称其瞬心为相对瞬心 相对瞬心是两构件上具有同一瞬时绝对速度的重合点 3.表示法:构件i和构件j的瞬心一般用符号Pij或Pji 4.机构瞬心的数目
ω1/ω3为该机构的原动件1与从动件3的瞬时角速度之比
ω1/ω3=LP34P13 / LP14P13
VP13
机械原理(苗老师) P24
P14 A
P23 C B
2
1 P12
3
4 P34
D
上式表明两构件的角速度与其绝对速度瞬心至相对速度瞬 心的距离成反比。两个角速度的方向相同。应用该方法,也 可以求得该机构其他任意两构件得角速度比的大小和角速度 的方向
K
其瞬心位于过接触点的共法线n-n上
n1
n 2
VK1K2
机械原理(苗老师)
3、由“三心定理”确定机构的瞬心
(1)适用范围:当机构中不互相直接联接的各构件之间的瞬心
,用前面的方法往往不易确定。在这种情况下,均可应用“三 心定理”
(2)定理的叙述“作平面运动的三个构件有三个瞬心,它们
平面连杆机构及其分析与设计

平面连杆机构及其分析与设计平面连杆机构是由连杆和连接点组成的机械结构,广泛应用于各种机械设备中。
它的功能是将输入的旋转运动转化为输出的直线运动或者将输入的直线运动转化为输出的旋转运动。
本文将对平面连杆机构的分析与设计进行介绍。
首先,对平面连杆机构进行分析。
平面连杆机构的主要组成部分是连杆和连接点。
连杆是连接点之间的刚性杆件,可以是直杆、曲杆或者具有其他特殊形状的杆件。
连接点是连杆的两个端点或者连杆与其他机构的连接点,可以是支点、铰链等。
平面连杆机构的运动可以分为三种基本类型:平动、转动和复动。
平动是指连杆的一端保持固定,另一端进行直线运动;转动是指连杆的一端保持固定,另一端进行旋转运动;复动是指连杆的一端进行直线运动,另一端同时进行旋转运动。
进行平面连杆机构的设计时,需要考虑以下几个要点。
首先,确定机构的类型和功能。
根据机构的动作要求和功能要求,选择适合的连杆类型和连接点类型。
其次,进行机构的运动分析。
根据机构的运动要求,确定连杆的长度和连接点的位置,使连杆能够实现所需的运动。
然后,进行机构的力学分析。
根据机构的受力情况,确定连杆的截面尺寸和材料,保证机构的刚度和强度。
最后,进行机构的优化设计。
考虑机构的性能要求和制造要求,对机构进行优化设计,提高机构的工作效率和使用寿命。
在平面连杆机构的设计中,还需要考虑机构的动力学问题。
机构的动力学分析包括静力学分析和动力学分析两个方面。
静力学分析是指在机构静止或静力平衡状态下,对机构受力和力矩进行分析。
动力学分析是指在机构进行运动时,对机构的加速度、速度和位移进行分析。
通过对机构的动力学分析,可以确定机构的惯性力和惯性矩,从而确定机构的动态特性和振动特性。
总之,平面连杆机构的分析与设计是一项复杂而重要的工作。
在进行分析与设计时,需要考虑机构的类型和功能,进行运动分析和力学分析,优化设计和动力学分析。
通过合理的分析与设计,可以使机构具有较好的工作性能和使用寿命,满足各种工程应用的要求。
四连杆机构运动分析
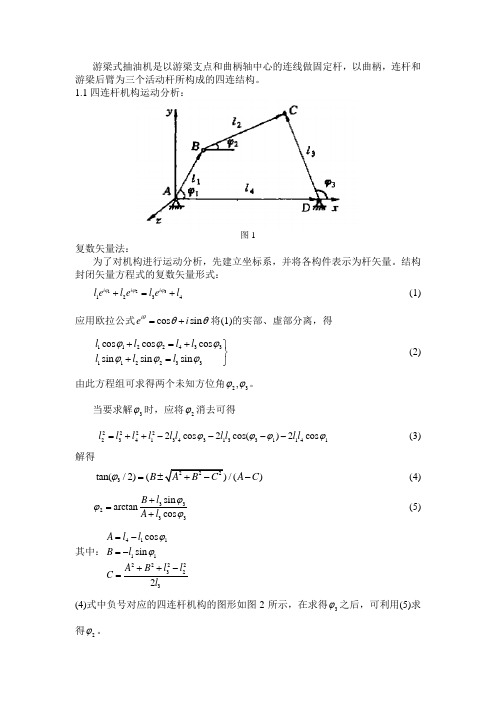
游梁式抽油机是以游梁支点和曲柄轴中心的连线做固定杆,以曲柄,连杆和游梁后臂为三个活动杆所构成的四连结构。
1.1四连杆机构运动分析:图1复数矢量法: 为了对机构进行运动分析,先建立坐标系,并将各构件表示为杆矢量。
结构封闭矢量方程式的复数矢量形式:3121234i i i l e l e l e l ϕϕϕ+=+ (1)应用欧拉公式cos sin i e i θθθ=+将(1)的实部、虚部分离,得1122433112233cos cos cos sin sin sin l l l l l l l ϕϕϕϕϕϕ+=+⎫⎬+=⎭(2)由此方程组可求得两个未知方位角23,ϕϕ。
当要求解3ϕ时,应将2ϕ消去可得2222234134313311412cos 2cos()2cos l l l l l l l l l l ϕϕϕϕ=++---- (3)解得2223tan(/2)()/()B A B C A C ϕ=+-- (4)33233sin arctancos B l A l ϕϕϕ+=+ (5)其中:411112222323cos sin 2A l l B l A B l l C l ϕϕ=-=-++-=(4)式中负号对应的四连杆机构的图形如图2所示,在求得3ϕ之后,可利用(5)求得2ϕ。
图2由于初始状态1ϕ有个初始角度,定义为01ϕ,因此,我们可以得到关于011t ϕϕω=+,ω是曲柄的角速度。
而通过图形3分析,我们得到OA 的角度0312πθϕϕ=--。
因此悬点E 的位移公式为||s OA θ=⨯,速度||ds d v OA dt dtθ==,加速度2222||dv d s d a OA dt dt dtθ===。
图3已知附录4给出四连杆各段尺寸,前臂AO=4315mm ,后臂BO=2495mm ,连杆BD=3675mm ,曲柄半径O ’D=R=950mm ,根据已知条件我们推出''||||||||OO O D OB BD +>+违背了抽油系统的四连结构基本原则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理大作业一课程名称:机械原理设计题目:连杆机构运动分析1 、题目如图所示机构,一只机构各构件的尺寸为AB=100mm,BC=4.28AB,CE=4.86AB,BE=8.4AB,CD=2.14AB,AD=4.55AB,AF=7AB,DF=3.32AB,∠BCE=139˚。
构件1的角速度为ω1=10rad/s,试求构件2上点E的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
ABCDEF123452、机构结构分析该机构由6个构件组成,4和5之间通过移动副连接,其他各构件之间通过转动副连接,主动件为杆1,杆2、3、4、5为从动件,2和3组成Ⅱ级RRR基本杆组,4和5组成Ⅱ级RPR基本杆组。
如图建立坐标系ABCD EF12345YX3、各基本杆组的运动分析数学模型1) 位置分析⎩⎨⎧+=+=i AB A B iAB A B l y y l x x ϕϕsin cos 2) 速度和加速度分析将上式对时间t 求导,可得速度方程:sin cos BAB B A i iB AB B A i i dx x x l dtdy y y l dtϕϕϕϕ⎧==-⎪⎪⎨⎪==+⎪⎩ 将上式对时间t 求导,可得加速度方程:222222cos sin cos cos BAB AB B A i i i i B AB AB B A i i i id x x x l l dtd y y y l l dt ϕϕϕϕϕϕϕϕ⎧==--⎪⎪⎨⎪==-+⎪⎩RRR Ⅱ级杆组的运动分析如下图所示 当已知RRR 杆组中两杆长L BC 、L CD 和两外副B 、D 的位置和运动时,求内副C 的位置、两杆的角位置、角运动以及E 点的运动。
CXY1) 位置方程cos cos sin sin BC CD C B i D jBC CD C B i D jx x l x l y y l y l ϕϕϕϕ=+=+⎧⎪⎨=+=+⎪⎩ 由移项消去j ϕ后可求得i ϕ:002arctan i ϕ=⎝⎭式中,()()00222022BC D B BC D B BC BD CDBDA l x xB l y yC l l l l ⎧=-⎪=-⎪⎪⎨=+-⎪⎪=⎪⎩可求得j ϕ:2arctan C D j C D y y x x ϕ⎛⎫-=⎪-⎝⎭E 点坐标方程:()()cos sin BE E B i BE E B i x x l y y l ϕθϕθ=+-⎧⎪⎨=+-⎪⎩ 其中222cos 2i k ji k l l l l l θ⎛⎫+-= ⎪ ⎪⎝⎭2) 速度方程两杆角速度方程为()()()()11//i i j D B j D B j j i D B i D B C x x S y y G C x x S y y G ωϕωϕ⎧⎡⎤==-+-⎪⎣⎦⎨==-+-⎡⎤⎪⎣⎦⎩ 式中,1cos cos sin sin i j j i BC i i CD j j BC i i CD j jG C S C S C l C l S l S l ϕϕϕϕ=-====点E 速度方程为()()()()sin sin cos cos Ex B i BE i Bx i BE i EyB i BE i By i BE i v x l v l v y l v l ϕϕθωϕθϕϕθωϕθ=--=--⎧⎪⎨=+-=+-⎪⎩ 3) 加速度方程两杆角加速度为()()231231//i i j j j j i i G C G S G G C G S G αϕαϕ⎧==+⎪⎨==+⎪⎩ 式中,222223D B i i j j D B i i j j G x x C C G y y S S ϕϕϕϕ⎧=-+-⎪⎨=-+-⎪⎩点E 加速度方程为()()()()()()()()2222sin cos sin cos cos sin cos sin ex B i BE i i BE i Bx i BE i i BE i ey B i BE i i BE i By i BE i i BE i a x l l a l l a y l l a l l ϕϕθϕϕθαϕθωϕθϕϕθϕϕθαϕθωϕθ⎧=----=----⎪⎨=+---=+---⎪⎩RPR Ⅱ级杆组的运动分析(1) 位移方程arctanE FiE Fx x y y ϕ-=-(2)速度方程()sin cos /i Ex i Ey i iv v l ωϕϕ=-+其中i l =(3)加速度方程()sin cos /i Ex i Ey i i a a l αϕϕ=-+4、 计算编程利用MATLAB 软件进行编程,程序如下:% 点B 和AB 杆运动状态分析 >>r=pi/180; w 1=10; e 1=0; l 1=100; Xa=0; Ya=0; Vax=0; Vay=0; aax=0; aay=0;f1=0:1: 360; % B 点位置Xb=Xa+l1*cos(r*f1); Yb=Ya+l1*sin(r*f1); % B 点速度Vbx=V ax-w1*l1*sin(r*f1);Vby=Vay+w1*l1*cos(r*f1);% B点加速度abx=aax-l1*w1.^2.*cos(r*f1);aby=aay-l1*w1.^2.*sin(r*f1);% RRR2级杆组运动分析% 输入D点参数l2=428;l3=214;Xd=455;Yd=0;Vdx=0;Vdy=0;adx=0;ady=0;% 计算E点、2杆、3杆运动参数lbe=840;lce=486;a0=2*l2*(Xd-Xb);b0=2*l2*(Yd-Yb);c0=l2^2+(Xb-Xd).^2+(Yb-Yd).^2-l3^2;f2=2*atan((b0+sqrt(a0.^2+b0.^2-c0.^2))./(a0+c0)); % C点位置Xc=Xb+l2*cos(f2);Yc=Yb+l2*sin(f2);% 2杆、3杆运动参数计算dX=Xc-Xd;dY=Yc-Yd;for n=1:length(dX)if dX(n)>0&dY(n)>=0f3(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f3(n)=pi/2;elseif dX(n)<0&dY(n)>=0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f3(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f3(n)=2*pi+atan(dY(n)/dX(n));endendC2=l2*cos(f2);C3=l3*cos(f3);S2=l2*sin(f2);S3=l3*sin(f3);G1=C2.*S3-C3.*S2;w2=(C3.*(Vdx-Vbx)+S3.*(Vdy-Vby))./G1;w3=(C2.*(Vdx-Vbx)+S2.*(Vdy-Vby))./G1;G2=adx-abx+(w2.^2).*C2-(w3.^2).*C3;G3=ady-aby+(w2.^2).*S2-(w3.^2).*S3;e2=(G2.*C3+G3.*S3)./G1;% E点位置w=acos((l2^2+lbe^2-lce^2)/(2*l2*lbe));Xe=Xb+lbe*cos(f2-w);Ye=Yb+lbe*sin(f2-w);Vex=Vbx-lbe*w2.*sin(f2-w);Vey=Vby+lbe*w2.*cos(f2-w);aex=abx-lbe*(e2.*sin(f2-w)+w2.^2.*cos(f2-w));aey=aby+lbe*(e2.*cos(f2-w)-w2.^2.*sin(f2-w));% 计算杆5运动参数Xf=646.2912088;Yf=-268.9008617;l5=sqrt((Xe-Xf).^2+(Ye-Yf).^2);dX=Xe-Xf;dY=Ye-Yf;for n=1:length(dX)if dX(n)>0&dY(n)>=0f5(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f5(n)=pi/2;elseif dX(n)<0&dY(n)>=0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f5(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f5(n)=2*pi+atan(dY(n)/dX(n));endendw5=(-Vex.*sin(f5)+Vey.*cos(f5))./l5;a5=(-aex.*sin(f5)+aey.*cos(f5))./l5;% 画出各参数曲线figure(1);plot(Xe,Ye,'k');xlabel('Xe/\mm');ylabel('Ye/mm');grid on;title('E点位置'); figure(2);plot(f1,f5,'k');xlabel('f/\circ');ylabel('f5/\circ');grid on;title('5杆角位移'); figure(3);plot(f1,w5,'k');xlabel('f/\circ');ylabel('w5/rad/s');grid on;title('5杆角速度'); figure(4);plot(f1,a5,'k');xlabel('f/\circ');ylabel('a5/rad/s2');grid on;title('5杆角加速度'); Warning: Unable to interpret TeX string "Xe/\mm"5、计算结果图一:E点的运动轨迹图二:5杆角位移图三:5杆角速度图四:5杆角加速度6、计算结果分析由E点位置图像可看出,构件4做周期往复运动,由图二、三、四可看出,构件5的角位移、角速度、角加速度均成周期性变化。
