同济大学游泳馆张弦钢屋盖施工技术
钢屋盖张弦梁结构监理质量控制要点——以某游泳馆工程为例

钢屋盖张弦梁结构监理质量控制要点——以某游泳馆工程为
例
周建青
【期刊名称】《建设监理》
【年(卷),期】2024()5
【摘要】某游泳馆屋盖采用张弦梁钢结构,钢屋盖施工前下部混凝土结构已施工完成,根据现场施工条件和钢结构设计特点,按照先支设支撑胎架、再跨外布置履带吊吊装上弦钢梁、然后进行钢索安装和张拉、最后完成金属屋面维护结构的流程进行施工。
基于此游泳馆工程,通过对张弦梁结构施工监理实践的总结,介绍了张弦梁结构监理质量控制要点。
【总页数】6页(P95-99)
【作者】周建青
【作者单位】上海建科工程咨询有限公司
【正文语种】中文
【中图分类】TU712
【相关文献】
1.74m大跨度张弦梁钢结构屋盖施工关键技术及质量控制
2.监利游泳馆张弦梁屋盖结构设计
3.论钢结构屋盖工程施工监理质量控制的工作要点
4.某体育馆钢屋盖双向张弦梁结构分析与设计
5.大跨度张弦梁结构屋盖安装质量控制及施工技术优化
因版权原因,仅展示原文概要,查看原文内容请购买。
大跨度张弦梁钢结构屋盖分块吊装施工关键技术研究

定性,该文将初始吊点设置在支座处,其他吊点以被吊装的
钢桁架段重心为中心,均匀地分布在重心的两侧,使被吊单
元中部与两端的力矩保持平衡。吊点的数量为偶数,能确保
分段单元被平稳起吊。另外,吊点位置受力均匀,吊点与钢
丝绳间的夹角在 45° ~60°,可以保障钢桁架的吊装安全性。
该文将钢桁架的吊装区域分为 3 个部分:1~7 轴、8~21 轴和
如图 2 所示,黑色框内的钢柱截面为 ø1200mm×50mm, 其余钢柱截面均为 ø1200mm×42mm。在 ø1200mm×50mm 钢 柱抬吊的过程中,选用主臂长为 32.25m、吊装半径为 8m, 分段吊重为 11.8t+2.5t、吊装能力为 21.2t、起吊高度为 31.2m 的机械。最先吊装 ø1200mm×50mm 的钢柱,用 50t 汽车吊就 近吊装浅灰色的钢柱,并完成焊接拼装。在 4 根钢柱安装完 成后,采用 350t 履带吊分段吊装分段柱节 ø1200mm×50mm 的钢柱。当吊装第一节钢柱时,吊装半径控制在 12m 内,50t 汽车吊 30.92m,主臂半径为 12m,在此工况下,能够吊起 10.1t 的钢柱。该工程第一节钢柱最大质量为 7.5t,可以满足 吊装的质量需求。该工程用到履带吊的钢柱最大分段质量为 51.6t,最高为 48m,同样可以满足钢柱分段吊装需求。
体育馆张弦梁无盖钢结构施工技术分析

体育馆张弦梁无盖钢结构施工技术分析摘要:本文采取案例分析的方式,以xxx体育馆张弦梁无盖钢结构作为主要的研究对象,从多个角度展开分析与讨论,分析其施工管关键技术,为他人带来理论基础。
关键词:体育馆;张弦梁无盖钢;施工技术1、工程概述xxx体育馆的主体结构属于钢筋混凝土框架结构,其建筑面积为3567m2,体育馆的屋盖为倾斜9.6%的平面屋面,采取张弦梁无盖钢结构,其中在该工程中张弦梁钢结构材质为Q345B,其结构模型见图1.图1 xxx体育馆屋盖张弦梁结构模型2、本工程的重点从整体角度分析,在本工程的施工过程中受到主客观因素的影响,导致各类问题层出不穷,其中主要包括四点:第一是张弦梁跨度比较大,并且吊装质量大;第二是张弦梁组装精度以及焊接质量要求比较高;第三是屋盖形状是倾斜平板,虽然跨度相同,但是张弦梁拉锁张力却不尽相同;第四是因为多方面的限制,其施工工期比较紧张,现场拼装以及吊装的构建比较多,交叉施工十分严重。
3、张弦梁无盖钢结构的流程与安装技术3.1 安装工艺从整体角度分析,屋盖钢结构安装工艺流程涉及到的内容比较多,包括了施工准备、组装场地整理、放线、焊接、防火涂料涂装、面漆涂装、张弦梁组合件吊装、金属屋面板的安装、竣工。
3.2 施工准备积极做好施工准备意义重大,其中张弦梁钢结构的吊装主要采取了工厂加工、分段运输、现场组装等各方式,其中需要在体育馆的操场上整理出一块拼装场地,保证场地的平整性,并且在拼装的时候需要严格按照实际的发展情况将钢板箱进行铺设,保证其平整性与稳固性。
3.3 吊机的选择与吊装顺序在选择吊机的时候需要严格按照屋盖张弦梁无盖钢结构的形式以及相关的数据,并且在经过论证之后采取跨外机械吊装的方式,简而言之便是需要将屋盖钢结构划分为多个吊装单位,在地面拼装之后应用吊机进行吊装到位,并且在空中安装各个单元件的杆件。
其中需要注意的一点是张弦梁组合单元最大的吊装质量是35t,并且吊机需要选择LTM1500型5000kN全液压汽车式起重机进行吊装,此外还需要配备一台汽车式起重机,将其应用在现场构件卸车以及构件组装,还有是在吊装的时候,构件吊离胎架50cm的时候则需要停止提升,要对张弦梁的挠度进行检查,这样在没有问题之后才可以继续进行起吊,等到张弦梁组合件安装完成之后,需要做好杆件等的安装,并且要实现其稳定性,保证其安全。
大学体育馆弦支穹顶钢结构屋盖的分析与设计

3.3 荷载态的弹性设计计算
✓考虑了14个大类的荷载组合 。当恒荷载起有利作用时,其分项系数取为1.0;温度的分项系数1.0, 组合系数0.7。各个组合中均已包括了1.0倍的预应力作用: (1) 1.0结构自重(即预应力初始态) (2) 1.2恒+1.4雪 (3) 1.2恒+1.4风 (4) 1.2恒+1.0温 (5) 1.2恒+1.4雪+1.4×0.6风 (6) 1.2恒+1.4风+1.4×0.7雪 (7) 1.2恒+1.4雪+0.7温(升温时取活) (8) 1.2恒+1.0温+1.4×0.7雪(升温时取活) (9) 1.2恒+1.4风+0.7温 (10) 1.2恒+1.0温+1.4×0.6风 (11) 1.2恒+1.4雪+1.4×0.6风+0.7降温 (12) 1.2恒+1.4风+1.4×0.7雪+0.7降温 (13) 1.2恒+1.0降温+1.4×0.6风+1.4×0.7雪 (14) 1.2(恒+0.5雪)+1.3水平地震
某大学体育馆弦支穹顶 屋盖的分析与设计
主要内容
1. 工程概况 2. 结构体系与结构布置 3. 结构静力与动力计算分析 4. 静力弹塑性极限承载力计算分析 5. 节点设计 6. 施工张拉过程的仿真计算 7. 结语
2
1. 工程概况
钻石形建筑造型; 正六边形柱网外接圆直径87.757m,最 大挑檐长度6m,屋盖总高度11.55m; 矢跨比1/8.6; 屋面坡度12度,局部凸屋面15度; 屋盖中央设置正六边形的采光玻璃天窗, 外接圆直径24m。
第8振型表现为整体环向振动,周期为T8=0.77s
某游泳馆屋盖张弦梁设计
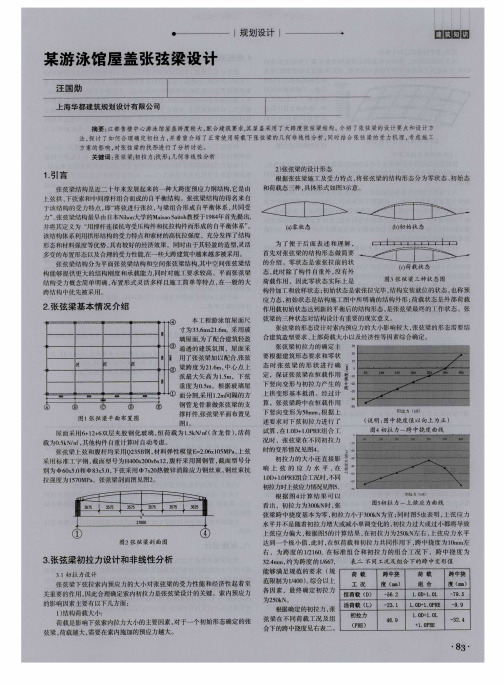
合建 筑造 型 要求 、 上部 荷 载 大小 以及 经济 性 等因 素综 合 确定 。 张 弦 梁初 拉 力 的 确 定 主 要根 据 建 筑 形态 要 求 和 零 状
态 时 张 弦 梁 的 形 状 进 行 确 目
力” 张弦梁 结 构最 早 由 日本 N i h o n 大学 的Ma i s a o S a i t o h 教授 于 1 9 8 4 年首 先提 出,
2 ) 张 弦梁 特 点 , 将 张 弦 梁 的结 构 形 态分 为零 状 态 、 初 始态 和荷载 态 三种 , 具体 形 式如 图 3 示意。
( a ) 零 状 态
( b ) 初始 状 态
为 了便 于 后 面 表 述 和 理 解 ,
首 先 对 张弦 梁 的 结 构 形 态做 简 要 的介 绍 。零 状 态 是索 张托 前 的 状 态, 此时 除 了构 件 自重 外 , 没 有 外 荷载 作用 ,因 此 零状 态 实际 上 是
用 了张 弦梁 加 以配 合, 张 弦
酷
● _
梁跨 度 为 2 1 . 6 m, 中 心 点 上 弦最大矢高为 1 . 5 m,下弦
垂度为0 . 5 m。 根据 玻 璃屋
定 ,保 证 张弦 梁 在 恒 载 作用
岳 下 竖 向 变 形 与初 拉 力产 生 的 斑
-
面 分 割, 采用1 . 2 m间隔 的方 钢 管 龙 骨兼 做张 弦 梁 的 支
:
啪
别为中6 0 x 5 . 0 和 中8 3 x 5 . 0 , 下弦采用 q b 7 x 2 0 热镀锌消除应力钢丝束 , 钢丝束抗
张弦梁技术在体育场馆建设中的突破与应用

张弦梁技术在体育场馆建设中的突破与应用体育场馆作为体育赛事和娱乐活动的重要场所,对于场馆建设和设施的要求越来越高。
作为专业的体育场地建设和维护服务提供商,张弦梁技术在体育场馆建设中展现出了突破性的应用和优势。
本文将重点介绍张弦梁技术在体育场馆建设中的突破与应用。
一、张弦梁技术概述张弦梁技术是一种基于结构力学和材料力学原理的创新技术,通过合理的设计和选择材料的张弦力使结构物达到强度和稳定性的最优化。
该技术在体育场馆建设中得到了广泛应用,有效解决了传统结构在大跨度、大载荷和大挠度等方面的困难,使体育场馆的建设更加灵活高效。
二、张弦梁技术在体育场馆建设中的突破1. 大跨度设计突破:传统的体育场馆在大跨度设计上存在困难,通常需要采用大量的柱子和横梁来支撑结构,影响观众的视野和活动空间。
而张弦梁技术通过合理的受力分配和材料的选择,能够有效减少柱子和横梁的使用,实现更大的活动空间和更佳的视野体验。
2. 强度与稳定性的提升:体育场馆建设中,结构的强度和稳定性是非常重要的考虑因素。
张弦梁技术通过合理的材料选择和力学设计,使结构更加坚固和稳定,能够承受不同类型的载荷,如人流、风载和雪载等,并保持结构的整体稳定性。
3. 节约成本和施工时间:传统的体育场馆建设需要大量的材料和较长的施工时间。
而张弦梁技术可以通过合理的设计和快速建造技术大大节约材料和施工时间。
这不仅可以降低建设成本,还能够更快地完成体育场馆的建设,提供更好的服务。
三、张弦梁技术在体育场馆建设中的应用1. 巨大屋盖结构:张弦梁技术可以应用于巨大屋盖结构的设计和建设,如体育场馆、体育中心和体育馆等。
通过合理的张弦梁力学设计,可以实现大跨度、大面积的屋盖结构,为观众提供更大的活动空间和更好的视野。
2. 观众席和看台设计:张弦梁技术在观众席和看台设计中也有广泛的应用。
通过合理的设计和力学计算,可以实现观众席和看台的合理分布和受力均衡,提高观众的观赛体验和安全性。
74m大跨度张弦梁钢结构屋盖施工关键技术
【 摘要 】 南京 国际博 览 中心 二期工 程 中1 、2 展 馆采 用张弦梁 钢结构 屋盖 。由于其 跨度大 、单榀 自重大 ,决 定采用 “ 分段 吊装 、高 空对接 、一次张拉 ”的施 工方 案。通过仿 真计算 ,并在施工 中强化 对拉索张拉的位移及 索力监控 ,确 保 了拉索下料 、张弦 梁体 系拼装 、张拉 的精度和可靠度 ,保 证了张弦梁体 系的空 间形 态 ,使 建筑符合结构受 力及观感
s e g me n t a l h o i s t i n g , h i g h - a l t i t u d e d o c k i n g, a n d o n e - t i me t e n s i o n i n g . Th e s i mu l a t i o n c a l c u l a t i o n c o mb i n e d wi t h s t r e n g t h e n i n g di s p l a c e me n t a n d mo n i t o r i n g of c a b l e t e n s i on f or c e i n t h e c o n s t r u c t i o n e n s u r e t h e p r e c i s i on a n d r e l i a b i l i t y o f c a b l e
bl a n k i n g 。 s t r i n g b e a m s t r u c t u r e a s s e mb l i n g a n d t en s i on , a s we l l a s g u a r a n t e e t h e s p a c e f 0 r m o f s t r i n g b e a m s t r u c t u r e s y s t e m. wh i c h ma k e t h e b u i l d i n g me e t t h e r e q u i r e me n t s o f t h e s t r u c t u r e s t r e s s a n d a p p e a r a n c e i mp r e s s i o n s .
游泳馆屋面弦支木结构的技术要求和安全措施
游泳馆屋面弦支木结构的技术要求和安全措施作者:尹卫东来源:《中国房地产业·中旬》2021年第10期【摘要】游泳馆屋面弦支木的结构设计分析中,需要结合工程概述的基本要求分析。
以苏州市第二工人文化宫项目为例,分析施工平面的整体布置要求,施工标准和技术条件。
明确游泳馆屋面弦支木结构,确定施工方案和可行性编制依据,按照施工技术要求建立BIM建筑模型,分析确定屋面整体的安装总体思路方式。
搭建临时支撑体系和施工标准,确定支撑架相关高度内的平台处理方式。
弦支木结构加工需要做好深入化的设计,确定金属构件操作加工的标准要求,对节点的连接方式进行分析,做好加工委托验收操作。
按照弦支木结构的技术要求,根据施工进度和技术工艺,提出符合施工作业要求的安全措施方案,优化游泳馆屋面弦支木结构的应用水平。
【关键词】游泳馆;屋面弦支木结构;技术要求和安全措施【DOI】10.12334/j.issn.1002-8536.2021.游泳馆屋面弦支木结构施工中,需要从整体确定木结构的加工工艺,分析木材料加工的基本概述要求。
从相关的施工技术规范入手,分析确定施工工艺的技术标准和进度计划方式。
综合安全计划组织保障思维方式,实施应急保障体系建设,确定建立完善的安全措施评估方案,注意临时用电、消防安全措施的管理,提升施工结构设计的合理性,最后完成工程验收工作,拓展施工技术操作支撑体系的合理建设,注意施工脚手架搭接的操作,满足游泳馆屋面使用的技术规范。
1、工程概况苏州市第二工人文化宫项目为例,依据施工平面布置规范要求和技术指标条件,结合项目整体进行分析。
本项目位于江苏省苏州市,总建筑面积为80748.33m2,其中包含游泳池、戏水池,可以容纳将近200多人使用。
其中屋面采用坡屋面操作形式,屋盖采用弦支木结构方式,框架结构方式。
游泳馆建筑面积5100m2,主要包含内装、屋面、外立面、主体结构。
其中重点是屋盖结构。
屋盖结构纵向的实际跨度为67.2m,横向跨度为36.3m,房檐的高度为15m,屋脊的高度为19m。
某体育文化中心大跨屋盖结构设计
!"#$%& '()*+,-
1)标准柱跨区域,采用钢框架结构,与大跨连接处的钢梁采 用铰接,释放大跨桁架变形引起的弯矩,见图 3。 2)主场馆大跨区域:建筑要求结构主要构件沿场馆的 45°斜 向正交布置,以契 合 建 筑 效 果,综 合 考 虑 跨 度、经 济 性 等 因 素,大 跨区域采 用 双 向 正 交 布 置 的 张 弦 桁 架 结 构。张 弦 桁 架 总 高 度 5m。上弦采用双向 正 交 布 置 的 桁 架 结 构,桁 架 采 用 钢 管 焊 接 而 成,总高度 1.8m。下弦采用双向正交布置的索系,索系下凸形成 一个凸透镜面,在索系和上部桁架构件的节点位置布置竖向撑杆
所示。初始状态下,主 桁 架 压 弯 构 件 上 下 弦 的 内 力 都 较 小,拉 索
内力较为均匀。
!"#$%&' %'!$(') %'*+,%%.,+/&! %!%+*', %%.+'%* %%0+.&% %)(+%'& %(!+)). %(*+(&(
12
! "#$%&'()*
在 竖 向 荷 载 作 用 下 ,主 桁 架 压 弯 构 件 的 上 弦 和 下 弦 以 承 受
摘 要:根据建筑效果的需求,上海某体育文化活动中心屋盖选用双向正交布置的张弦桁架结构,通过建立屋盖与下部混凝土结
构的整体模型,分析了各工况的结构内力和变形,并利用 ANSYS有限元软件对屋盖结构进行了极限承载力分析,结果表明屋盖结
构具有良好的受力性能。
关键词:正交布置,张弦桁架,静力分析,极限承载力
张弦梁结构在体育场馆建设中的优势和实践案例
张弦梁结构在体育场馆建设中的优势和实践案例体育场馆作为大型公共建筑,其设计和结构具有特殊的要求。
张弦梁结构作为一种常用的结构形式,在体育场馆建设中具有许多优势。
本文将对张弦梁结构在体育场馆建设中的优势和一些实际案例进行详细探讨。
首先,张弦梁结构具有良好的承载性能。
张弦梁结构通过张拉钢缆形成的张力,能够有效分担结构的荷载,使结构的承载能力得到提升。
这一特点在体育场馆中尤为重要,体育场馆通常需要承载大量观众和设备的重量,张弦梁结构能够满足这一需求,并保证场馆的安全稳定运行。
其次,张弦梁结构具有灵活性。
张弦梁结构的设计和施工相对简单,可以根据具体的需要进行灵活调整,适应不同体育项目的需求。
体育场馆作为多功能场所,需要满足各种比赛项目的要求,张弦梁结构的灵活性使之成为一个理想的选择。
同时,张弦梁结构还具有较大的跨度能力,能够提供更多的可用空间,提升观众的视野和体验。
此外,张弦梁结构具有良好的抗震性能。
体育场馆建设在地震带上时,抗震设计是必不可少的。
张弦梁结构通过设计合理的张拉力和刚度,能够有效抵抗地震荷载产生的水平力和竖向力,保障场馆的安全。
这一优势在实际的抗震实践中得到了充分验证,多个体育场馆采用张弦梁结构在大地震中表现出色,保障了观众和运动员的安全。
接下来,我们将通过一些实际的案例来进一步说明张弦梁结构在体育场馆建设中的应用。
首先是中国国家游泳中心,俗称“水立方”。
作为2008年北京奥运会的标志性场馆之一,水立方的张弦梁结构充分展示了其优势。
它采用了由逾10000根张力钢缆组成的外包结构,不仅具有出色的承载性能和抗震性能,还给人们带来了独特的视觉享受。
另一个例子是日本国立竞技场。
该场馆作为2020年东京奥运会的主场馆,采用的是由高强度钢缆和金属桁架构成的张弦梁结构。
这个设计能够满足场馆举办各种大型赛事的需求,同时提供了良好的观赏视角和舒适的观众体验。
最后,中国广州奥体中心是一个典型的张弦梁结构案例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第35卷第2期2007年4月福州大学学报(自然科学版)Journal of Fuzhou University(Natural Science)Vol.35No.2Ap r.2007文章编号:1000-2243(2007)02-0266-04预应力空间张弦梁结构找形分析周瑞钦,房贞政(福州大学土木工程学院,福建福州 350002)摘要:介绍应用有限元软件ANSYS对预应力张弦梁结构进行找形的方法.通过ANSYS软件的AP DL功能实现此类结构的找形,克服了找形过程中人工调节结构参数的困难,指出应用有限元法对结构找形时应该注意结构的受力和变形特性,建议对计算模型施加相应的约束以防止计算发散.关键词:预应力;张弦梁;找形;AP DL中图分类号:T U394文献标识码:AAna lysis of form-f i n d i n g of spa ti a l beam str i n g structureZHOU Rui-qin,F ANG Zhen-zheng(College of Civil Engineering,Fuzhou University,Fuzhou,Fujian350002,China) Abstract:Presents a method of for m-finding of beam string structure(BSS)app lying the s oft w areANSYS.W ith AP DL,a functi on of ANSYS,the f or m-finding of BSS can overcome difficulties of ad2justing the structure’s para meters in the p r ocess of f or m-finding.Besides,the mechanical characterand def or mati on of the structure should be noted when f or m-finding is carried out with finite ele mentmethod,and t o p revent divergence of the computati on,the according restrains should be app lied t o thestructure.Keywords:p restress;bea m string structure;for m-finding;AP DL为了使张弦梁结构在施加了预应力和重力荷载产生变形后其形状为设计的形状,需要进行找形分析算出结构的原始形状,作为杆件的下料依据.找形分析也称为初始平衡问题,进行找形分析的方法有:①物理模型实验方法;②非线性有限元法;③支座位移法;④力密度法;⑤动力松弛法等[1-3].非线性有限元法可以同时对结构进行受力分析和找形分析,对张弦梁结构进行找形比较适宜.有限元法的难点在于在找形时对结构的平衡形状和预应力分布难于确定,需要不断调整、试算,所以比较费时[4].本文应用ANSYS的AP DL二次开发语言分别对单榀桁架、多榀单向桁架、双向张弦梁进行找形计算,取消了人为调整的过程,大大简化计算过程,节省计算的时间.AP DL(ANSYS Para metric Design Language)即ANSYS参数化设计语言.应用该种语言可以编写出参数化的用户程序,实现全过程的有限元分析.1 非线性有限元法的应用和找形注意问题根据张弦梁结构不同的荷载状态,结构形态可以分3种.①零状态(又称放样态):预应力索尚未张拉时结构的状态.此时杆件中应力为零,故称为零状态;②初始态(又称预应力态):预应力索张拉完毕时结构的状态;③荷载态:预应力索张拉完毕并且外荷载也施加完毕时结构的状态.对于索中预应力的大小,可以根据预应力度和相应的索力设计准则来确定,因此张弦梁的找形分析就属于第二种找形分析:在给定预应力分布状态的情况下,寻找零状态几何形状.文献[5]提出了逆迭代法进行张弦梁的找形.逆迭代法需要多次的非线性迭代、试算,要求有一定的计算经验,才能减少试算次数.同时在这种方法中以固定的力来代替结构中的索,结构的刚度并未考虑索的贡献.找形结束后,模型不能直接应用于结构的后续荷载态分析.文献[6]应用ANSYS基于逆迭代法的收稿日期:2006-06-29作者简介:周瑞钦(1980-),男,硕士研究生;通讯联系人:房贞政,教授.第2期周瑞钦,等:预应力空间张弦梁结构找形分析原理对一榀单向张弦梁进行找形.该方法适用于上部为型钢梁的平面张弦梁结构,要求结构具有对称性.实际上,上弦梁的形式通常是立体桁架.在桁架中由于斜腹杆的存在使结构产生不对称的位移.当应用ANSYS 中的UPGE OM 命令时,将使变形误差得到累积,而给下一次的计算增加了结构初始变形缺陷,在非线性计算时结构将由于失稳而停止;计算过程中仍然需要重新建立模型;计算中依然以力代索,没有考虑索的刚度,模型不能直接应用于后续分析.逆迭代法的步骤简述如下:第一次迭代时零状态{x y z}0k (k =1)就是初始状态{x y z},即{x y z}0k ={x y z};循环体:在{x y z}0k 的形状下计算得到位移{u}k ;{x y z}k ={x y z}0k +{u}k ;Δ={x y z}-{x y z}k ;满足精度要求则结束计算,否则往下算.{x y z}0,k +1={x y z}0k +Δ;k =k +1,循环体结束.计算结束后,{x y z}0k 为零状态坐标.对于结构的找形,无论是采用有限元法或是物理模型实验方法等其他方法,都必须在计算之前对结构的性能有足够的了解才能使分析正确地进行.2 张弦梁的找形计算单榀单向张弦桁架模型中桁架和索的形状曲线采用抛物线,上弦中心线和下弦索的曲线方程是:Y 1=f 1(1-4X 2/L 2),Y 2=-f 2(1-4X 2/L 2),其中:f 1为垂度,f 2为矢高,X 为横坐标,Y 为纵坐标,L 为跨度.取:f 1=3m ,f 2=10.2m ,L =132m .撑杆的间距为6m ,上弦宽度为3m ,桁架高度2.2m ,桁架中心线过截面的三角形中心.桁架中的索力设计值取1500k N ,荷载仅考虑结构的自重.单向九榀张弦桁架的杆件采用与单榀张弦桁架一致的杆件和拉索,桁架间的斜支撑采用同腹杆一致的杆件,具体的杆件型号见表1.,截面型号为:3200×3200×80×80,其余杆件同单向张弦梁模型.模型双向对称,对于中间榀张弦梁L =72m ,f 1=6m ,f 2=2m ;在边榀张弦梁中,f 1=415m ,f 2=1.5m .上弦的外形采用同单向张弦梁上弦一致的抛物线.为了使软件能够通过读取生成的节点坐标文件来建立模型,可以采用直接建模的方法.因为张弦梁结构中的杆件可以用梁单元、杆单元和索单元来模拟,所以直接建模的方法是可行的.对于单向张弦桁架模型,上弦杆件、下弦杆件、腹杆和撑杆均采用L ink8单元,下弦索采用只能受拉不能受压的L ink10单元.计算模型如图1所示.表1 计算模型中的构件型号Tab .1 Co m ponen t types i n the co m put a ti ona l m odel杆件类别杆件型号S /m2d 壁厚/mm d 外径/mm E /Pa上弦杆件热轧无缝钢管0.01429410.04652.06×1011下弦杆件热轧无缝钢管0.02256916.04652.06×1011撑杆热轧无缝钢管0.0079678.03252.06×1011腹杆热轧无缝钢管0.0030546.01682.06×1011下弦索Φ7×4090.01574——1.80×1010图1 模型示意图Fig .1 Model sche matic diagra m・762・福州大学学报(自然科学版)第35卷 如上所述,UPGEOM 命令将撑杆在每一次计算后的侧向偏移量累加到零状态的节点坐标,使撑杆在非线性计算时产生失稳而使计算不收敛.解决这个问题有2种方法:①在找形时,保持撑杆的平面外坐标(Z 轴向)不变,只改变平面内(X 、Y 轴向)的坐标值;②在找形时,对撑杆的上下节点在侧向(Z 轴向)上施加单向位移约束.对一榀单向张弦梁按以上两种方法进行找形,两种方法所得出来的结点坐标是一致的.对于双向张弦梁,由于横向索和纵向索的相互影响,采用L ink8杆单元无法收敛,可以用梁单元bea m 44来代替杆单元.计算结果表明,应用梁单元来模拟撑杆,可以保证非线性计算收敛.在实际的结构中,撑杆的上弦同上部梁是铰接的,采用梁单元计算将加大结构的刚度.对一榀张弦桁架分别用梁单元和杆单元来模拟撑杆.计算结果表明,模型中采用梁单元模拟撑杆进行计算时,上弦构件、撑杆和索的各项内力小于杆单元模型,但是两者的差别非常小.因此可以采用梁单元来模拟双向张弦梁中的撑杆.在找形时,可以先采用杆单元来模拟撑杆,对撑杆的上下两端施加双向位移约束,使撑杆在竖向自由.找形结束后,去掉撑杆两端的约束,并换用梁单元模拟撑杆进行计算;也可以直接用梁单元模拟撑杆计算,此时可不在撑杆两端施加约束.找形过程中索力的确定需要采用一定的方法来保证其达到设计值.为了考虑索的刚度对总刚的贡献,采用对索两端施加初应变的方法在结构中引入预应力.对索单元施加初应变后,结构的变形使索内的预应力产生很大的损失.因此必须采取超张拉的办法施加预应力.计算的结果表明,预应力损失大小在每次计算中并不一致,但是损失率([(施加索力-当前索力)/施加索力]×100%)的差别很小.假定m 为计算次数,目标预应力为F,每次计算时预应力损失率均为α,则:当m =1时,施加的索力为F,索力损失值为αF,索内的最终索力为(1-α)F;当m =2时,施加的超张拉索力为(1+α)F,索力损失值为α(1+α)F,索内的最终索力为(1-α)(1+α)F;照此计算,每次需施加的超张拉初始索力为(1+α)m -1F .经过m 次计算后结构中的索力为(1-α)(1+α)m -1F .当第一次试算完成后,即可求出α.若要结构中的最终索力为F,则需(1-α)(1+α)m -1=1,由该式可计算出m 的值和超张拉估计索力(1-α)(1+α)m -1F .根据估计索力即可换算出估计的初应变.所估算出的初应变值不是精确的结果,还应进行迭代计算提高精度.由于在每次的计算中均要考虑几何非线性的影响,索力值和初应变值并不是成正比例关系,而需要考虑两者的非线性关系.索力和初应变所要满足的非线性函数为未知函数,此时可以应用弦截法或抛物线法进行线性迭代求解.弦截法是对牛顿迭代法的简化,计算中以差商代替函数的导函数值.弦截法的迭代公式为:εk +1=εk +εk -εk -1f k -f k -1(f 0-f k ),其中:εk 为第k 次的初应变,f 0为目标索力,f k 为第k次索力.在上式中,每次的初应变修正需要两个索力值.在第一次计算中,只有一个计算索力值,故无法进行上述运算.这时可以假设初应变和索力成正比关系,即ΔεEA =ΔF 来获得第二个索力值;在第二次的计算中即可根据前两次的计算结果采用弦截法进行初应变的修正.计算流程图如图2所示.部分单向张弦桁架的节点坐标和索力的计算结果列于表2.表2 单向张弦桁架节点坐标的计算结果Tab .2 Results of noda l coord i n a tes i n un i d i recti ona l truss str i n g structure节点编号设计态坐标X /mY /mZ /m计算坐标X /mY /mZ /m坐标误差X /mY /mZ /m1-66.00000.7333-1.5000-65.99980.7339-1.49910.00020.00060.00092-64.50001.1917-1.5000-64.50001.1918-1.49920.00000.00010.00083-61.50002.0768-1.5000-61.50002.0769-1.49920.00000.00010.00084-58.50002.9198-1.5000-58.50002.9199-1.49920.00000.00010.00085-55.50003.7206-1.5000-55.50003.7207-1.49920.00000.00010.0008F /k N15001500.8880.888 从结果中可以看出,节点坐标的精度在1mm 以内,索力的误差不超过0.1t,满足施工时的精度控制要求.对于双向张弦梁,误差随上弦梁的刚度变化而变化,上弦梁柔性越大,则误差越大.在双向张弦梁模型的找形分析中,节点坐标的误差最大不超过7.7c m.・862・第2期周瑞钦,等:预应力空间张弦梁结构找形分析图2 ANSYS 参数化语言找形程序流程图Fig .2 AP DL p r ogra m fl owchart3 结语张弦梁结构是一种半刚性的结构,结构的找形可以应用ANSYS 有限元软件进行计算,减少了编写专门程序进行找形的工作.一般应用非线性有限元进行计算时,需要多次的试算,费时费力,对经验的依赖性比较强.应用软件的AP DL 功能,可以使软件自动反复试算,输出正确的节点坐标文件,减少人工参与,提高了计算效率.参考文献:[1]陆赐麟,尹思明,刘锡良.现代预应力钢结构[M ].北京:人民交通出版社,2003.[2]刘锡良.现代空间结构[M ].天津:天津大学出版社,2003.[3]张毅刚,薛素铎,杨庆山,等.大跨空间结构[M ].北京:机械工业出版社,2005.[4]马美玲.张弦梁结构找形和受力性能研究[D ].杭州:浙江大学,2004.[5]张其林,张莉,罗晓群.预应力梁-索屋盖结构形状确定[C ]//第九届空间结构学术会议论文集.北京:中国建筑科学研究院建筑结构研究所,2000:387-394.[6]齐永胜,周泓,苏康.用AP DL 语言解决张弦梁结构找形问题的方法[J ].山西建筑,2004,30(3):20-21.(责任编辑:杨青)・962・。
