matlab simulink例子
matlab simulink案例

matlab simulink案例1. 电机传动系统模拟在这个案例中,我们将使用Simulink来模拟一个简单的电机传动系统。
我们将建立一个由电机、负载和控制器组成的系统,并使用Simulink来模拟系统的动态行为。
通过调整输入信号和控制器参数,我们可以观察系统的响应,并优化控制器的性能。
2. PID控制器设计在这个案例中,我们将使用Simulink来设计一个PID控制器,并将其应用于一个简单的控制系统。
我们将建立一个由传感器、控制器和执行器组成的系统,并使用Simulink来模拟系统的动态行为。
通过调整PID控制器的参数,我们可以观察系统的响应,并优化控制器的性能。
3. 机器人路径规划在这个案例中,我们将使用Simulink来进行机器人的路径规划。
我们将建立一个由传感器、路径规划器和执行器组成的系统,并使用Simulink来模拟机器人在不同环境中的路径规划行为。
通过调整路径规划器的算法和参数,我们可以优化机器人的路径规划性能。
4. 电力系统稳定性分析在这个案例中,我们将使用Simulink来进行电力系统的稳定性分析。
我们将建立一个由发电机、负载和传输线路组成的电力系统,并使用Simulink来模拟系统的动态行为。
通过调整系统的参数和控制策略,我们可以评估系统的稳定性,并优化系统的运行性能。
5. 汽车动力学模拟在这个案例中,我们将使用Simulink来进行汽车的动力学模拟。
我们将建立一个由车辆、发动机和传动系统组成的模型,并使用Simulink来模拟车辆在不同驾驶条件下的动力学行为。
通过调整车辆参数和控制策略,我们可以评估车辆的性能,并优化驾驶体验。
6. 无人机飞行控制在这个案例中,我们将使用Simulink来进行无人机的飞行控制。
我们将建立一个由无人机、传感器和控制器组成的系统,并使用Simulink来模拟无人机在不同飞行任务下的控制行为。
通过调整控制器的参数和飞行任务的要求,我们可以优化无人机的飞行性能。
matlab simulink求解微分方程组例题

matlab simulink求解微分方程组例题以下是一个使用MATLAB Simulink求解微分方程组的例子:假设有一个简单的二阶线性微分方程组:dx1/dt = a11*x1 + a12*x2dx2/dt = a21*x1 + a22*x2其中,a11、a12、a21和a22是给定的常数。
1. 创建一个新的Simulink模型。
2. 在模型中添加两个积分器(Integrator)模块,分别表示x1和x2的积分变量。
3. 添加两个乘法器(Gain)模块,分别表示a11和a12,将常数a11和a12连接到相应的乘法器输入。
4. 将积分器和乘法器的输出连接到一个加法器(Sum)模块,表示a11*x1 + a12*x2。
5. 重复步骤3和4,添加两个乘法器和一个加法器,表示a21*x1 + a22*x2。
6. 将两个加法器的输出连接到相应的积分器的输入,表示dx1/dt和dx2/dt。
7. 添加一个作用于积分器输出的数据记录器(To Workspace)模块,用于记录x1和x2的值。
通过上述步骤,我们建立了一个包含两个积分器和四个乘法器的模型,表示二阶线性微分方程组。
我们可以通过设置初始条件和常数a11、a12、a21和a22的值,使用Simulink模型求解微分方程组并观察结果。
例如,假设初始条件为x1(0) = 1,x2(0) = 0,a11 = 2,a12 = -1,a21 = 1,a22 = -2。
设置初始条件后,运行Simulink模型,模型将在仿真时间内求解微分方程组,并将x1和x2的值保存在工作空间中。
通过查看工作空间中的数据记录,我们可以获得仿真时间内x1和x2的值,并观察它们的变化情况。
matlab simulink 里的矩阵运算

matlab simulink 里的矩阵运算Matlab Simulink 中的矩阵运算矩阵运算是Matlab Simulink 中常用到的一种操作,通过矩阵运算,我们可以进行高效且方便的线性代数计算。
本文将详细介绍Matlab Simulink 中的矩阵运算,并逐步回答与之相关的问题。
一、Matlab Simulink 中的矩阵在Matlab Simulink 中,矩阵是一种经常用到的数据结构。
矩阵是由行和列组成的二维数组,用于存储和处理多个相关数据。
1.1 矩阵的定义和表示在Matlab Simulink 中,可以通过使用方括号"[]" 表示矩阵。
下面是一个简单的例子:A = [1, 2, 3; 4, 5, 6; 7, 8, 9]这个例子定义了一个3x3 的矩阵A,其中包含了9 个元素。
1.2 矩阵的运算Matlab Simulink 提供了一系列矩阵运算函数,用于执行各种矩阵操作。
下面我们将逐步回答与矩阵运算相关的问题。
问题1:如何计算两个矩阵的加法和减法?答:在Matlab Simulink 中,可以使用"+" 运算符执行矩阵的加法操作,使用"-" 运算符执行矩阵的减法操作。
下面是一个示例代码:A = [1, 2; 3, 4];B = [5, 6; 7, 8];C = A + B 矩阵加法D = A - B 矩阵减法在这个示例中,我们定义了两个2x2 的矩阵A 和B,并计算了它们的加法和减法。
结果存储在矩阵C 和D 中。
问题2:如何计算矩阵的乘法?答:在Matlab Simulink 中,可以使用"*" 运算符执行矩阵的乘法操作。
下面是一个示例代码:A = [1, 2; 3, 4];B = [5, 6; 7, 8];E = A * B 矩阵乘法在这个示例中,我们定义了两个2x2 的矩阵A 和B,并计算了它们的乘法。
simulink实例(有好多实例)

Simulink仿真实例
--精品--/SIMULINK的系统建模与仿真
Simulink仿真实例
--精品--/SIMULINK的系统建模与仿真
--精品--/SIMULINK的系统建模与仿真
Simulink仿真实例
--精品--/SIMULINK的系统建模与仿真
Simulink仿真实例
例题8,建立一个积分器,输入为1,初始 条件为-50,如果输出超过20,则重置为-100。
--精品--/SIMULINK的系统建模与仿真
Simulink仿真实例
--精品--/SIMULINK的系统建模与仿真
Simulink仿真实例
仿真曲线为
--精品--/SIMULINK的系统建模与仿真
Simulink仿真实例
假设未伸长时绳索的端部距地面为50m, 为了得到更真实的曲线,将50减去输出位置
--精品--/SIMULINK的系统建模与仿真
Simulink仿真实例
南京航空航天大学
基于MATLAB/SIMULINK的系 统建模与仿真
任课教师:刘燕斌 二○一零年三月
--精品--
Simulink仿真实例
例题1,使用Simulink创建系统,求解非 线性微分方程 (3x2x2)x 4x4x.其初始 值为 x (0)0,x(0)2,绘制函数的波形.
创建仿真系统为
--精品--/SIMULINK的系统建模与仿真
例题4,下图所示简单的单摆系统,假 设杆的长度为L,且质量不计,钢球的质量为 m.单摆的运动可以以线性的微分方程式来 近似,但事实上系统的行为是非线性的,而 且存在粘滞阻尼,假设粘滞阻尼系数为 bkg/ms-1.
matlAB,SIMULINK联合仿真经典例子
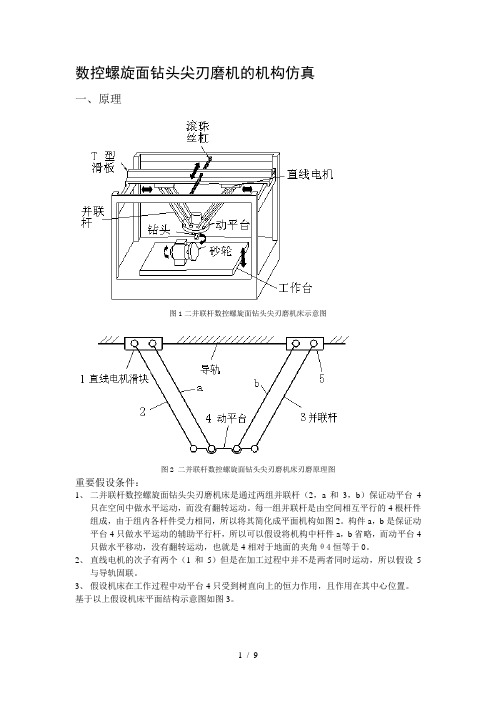
数控螺旋面钻头尖刃磨机的机构仿真一、原理图1二并联杆数控螺旋面钻头尖刃磨机床示意图图2 二并联杆数控螺旋面钻头尖刃磨机床刃磨原理图重要假设条件:1、二并联杆数控螺旋面钻头尖刃磨机床是通过两组并联杆(2,a和3,b)保证动平台4只在空间中做水平运动,而没有翻转运动。
每一组并联杆是由空间相互平行的4根杆件组成,由于组内各杆件受力相同,所以将其简化成平面机构如图2。
构件a,b是保证动平台4只做水平运动的辅助平行杆,所以可以假设将机构中杆件a,b省略,而动平台4只做水平移动,没有翻转运动,也就是4相对于地面的夹角θ4恒等于0。
2、直线电机的次子有两个(1和5)但是在加工过程中并不是两者同时运动,所以假设5与导轨固联。
3、假设机床在工作过程中动平台4只受到树直向上的恒力作用,且作用在其中心位置。
基于以上假设机床平面结构示意图如图3。
图3二并联杆数控螺旋面钻头尖刃磨机床简化机构平面结构示意图二、建立仿真方程C2=cos(θ2) S2=sin(θ2) C3=cos(θ3) S3=sin(θ3)一)力方程(分别对各个杆件进行受力分析) 对动平台4:受力分析如图4图4动平台4的受力分析对并联杆2:受力分析如图5图5并联杆2的受力分析 对直线电机滑块1:受力分析如图6图6直线电机滑块1的受力分析对并联杆3:受力分析如图7图7并联杆3的受力分析 二)闭环矢量运动方程(矢量图如图8)图8 闭环矢量图矢量方程为:R1+R2=R3+R4将上述矢量方程分解为x 和y 方向,并分别对方程两边对时间t 求两次导数得: r1_dot_dot+r2*α2*S2+r2*w2^2*C2=r3*α3*S3+r3*w3^2*C3 (12) r2*α2*C2-r2*w2^2*S2=r3*α3*C3-r3*w3^2*S3 (13) 三)质心加速度的矢量方程矢量关系:Ac3=Rc3_dot_dotAc4=R3_dot_dot+ Rc4_dot_dotAc2=R3_dot_dot+ R4_dot_dot+ Rc2_dot_dot (_dot_dot 表示对时间求两次导数)将上述三个矢量方程分别分解为x 和y 方向,则它们等效为以下六个方程;Ac3x=-rc3*w3^2*C3-rc3*α3*S3 (14) Ac3y=-rc3*w3^2*S3+rc3*α3*C3 (15) Ac4x=-r3*w3^2*C3-r3*α3*S3 (16) Ac4y=-r3*w3^2*S3+r3*α3*C3 (17) Ac2x=-r3*w3^2*C3-r3*α3*S3-rc2*w2^2*C2-rc2*α2*S2 (18) Ac2y=-r3*w3^2*S3+r3*α3*C3-rc2*w2^2*S2+rc2*α2*C2 (19) 力未知量为:F12x,F12y,F24x,F24y,F43x,F43y,F13x,F13y,Fy,Fm 引入的加速度有:α2,α3,r1_dot_dot ,Ac3x ,Ac3y ,Ac4x ,Ac4y ,Ac2x ,Ac2y三、系统方程的组装将所有19个方程组装成矩阵形式101000000000020001010000000000200002222222200000020000000000101000000000000400001010000000000004000101000000000000010000000010010000000100000010000000000000010100000000m m rc S rc C rc S rc C I m m m ⋅⋅-⋅-⋅-----3000000001010000000030000003333000003000000000000000002233100000000000000002233000000000000000002233010000000000000002233001000000000000000330001000000000000m m r C r S I r S r S r C r C rc S r S rc C r C rc S ⋅⋅-⋅-⋅⋅-⋅⋅⋅⋅⋅-⋅0033000010000000000000330000010000000000003300001rc C r S r C ⎛⎫⎪⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪⎪⋅-⎪⋅ ⎪⎪ ⎪⋅-⎝⎭120120240240434301301300020333^2322^2222^2233^2322^222233441F x F y F x F y F x p F y F x F y Fy Fm r w C r w C r w S r w S rc w C Ac x Ac y Ac x Ac y Ac x Ac y r αα∙∙⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⨯= ⎪ ⎪ ⎪⋅⋅-⋅⋅ ⎪ ⎪⋅⋅-⋅⋅ ⎪-⋅⋅ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭33^2322^2233^2333^2333^2333^2333^23r w S rc w S r w S rc w C rc w S r w C r w S ⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪-⋅⋅ ⎪⋅⋅+⋅⋅ ⎪ ⎪-⋅⋅ ⎪ ⎪⋅⋅ ⎪-⋅⋅ ⎪⎪ ⎪⋅⋅⎝⎭ 四、初始条件的设定假设图3位置就是初始位置。
simulink实例(matlab)

Simulink 仿真培训之实例
——厚积薄发
微分方程:
注意两点:
一:结合着各个线上标的注释看,这样就会理解其原理; 二:看图的时候可以放倍数。
题目:
⎩⎨
⎧−=−+=2122221124x x x x x x
对应model :
偏微分方程:
对方程实行拉普拉斯变换可以转化成常微分方程,而且初始条件也一并考虑到,解出
常微分方程后进行反演就可以了。
这个过程很容易实现的,只要增加一个Laplace 变换模块和反Laplace 变换模块。
差分方程组:
说明:(这个例子是我转载的一个例子。
)对于里面的一些难理解的地方,我在下面做了补充: 1、下面的图和等式的对应关系是:仿真所得到的model 中红色的部分和差分等式组对应,这点大家在看的时候要注意;
2、
对于这个模块,他表示的含义是:一个采样周期的延迟模块,当输入x (k+1),它会输出:x (k ) 题目:
⎩⎨
⎧++−=++=+)()(094.0)(sin 05.0)1()(1.0)()1(212211k u k x k x k x k x k x k x
对应model :。
基于MATLABSimulink的动态仿真的事例

2 3
4
MATLAB/Simulink应用实例 MATLAB/Simulink应用实例
1、背景知识 、 什么是系统仿真 什么是系统仿真? 是系统仿真
LOGO
系统仿真是建立在控制理论、相似理论、信 息处理技术和计算技术等理论基础之上的,以计 算机和其它专用物理效应设备为工具,利用系统 模型对真实或假想的系统进行试验,并借助于专 家经验知识、统计数据和信息资料对试验结果进 行分析研究,进而做出决策的一门综合性的和试 验性的学科。 在工程技术界,系统仿真是指通过对系统模 型的试验,间接地获取原形的规律性认识
LOGO
LOGO
例:已知系统模型G(s)= 期为5s的方波信号作用下的响应。
M文件代码 文件代码
,计算系统在周
响应曲线
Thank you
MATLAB的语言特点
编程效率高 使用方便 高效方便的科学计算 先进的可视化工具 开放性,可扩展性强 运行时动态连接外部C或FORTRAN C FORTRAN应用函数 MATLAB及其他标准格式的数据文件 输入输出各种MATLAB 特殊应用工具箱 高效仿真工具Simulink Simulink
MATLAB的模块构成
LOGO
SIMULINK是一个进行动态系统建模、仿真和综合分析的集 是一个进行动态系统建模、 是一个进行动态系统建模 成软件包。它可以处理的系统包括:线性、非线性系统; 成软件包。它可以处理的系统包括:线性、非线性系统;离 连续及混合系统;单任务、 散、连续及混合系统;单任务、多任务离散事件系统 SIMULINK 提供的图形用户界面 提供的图形用户界面GUI上,只要进行鼠标的简 上 单拖拉操作就可构造出复杂的仿真模型。 单拖拉操作就可构造出复杂的仿真模型。它外表以方块图形 式呈现,且采用分层结构。 式呈现,且采用分层结构。 从建模角度讲,这既适于自上而下( 从建模角度讲,这既适于自上而下(Top-down)的设计流 ) 概念、功能、系统、子系统、直至器件), ),又适于自下 程(概念、功能、系统、子系统、直至器件),又适于自下 而上( 而上(Bottum-up) 逆程设计。 ) 逆程设计。 从分析研究角度讲, 从分析研究角度讲,这种 SIMULINK 模型不仅能让用户知 道具体环节的动态细节,而且能让用户清晰地了解各器件、 道具体环节的动态细节,而且能让用户清晰地了解各器件、 各子系统、各系统间的信息交换, 各子系统、各系统间的信息交换,掌握各部分之间的交互影 响。 SIMULINK 环境中,用户将观察到现实世界中非线性因素 环境中, 和各种随机因素对系统行为的影响。 和各种随机因素对系统行为的影响。 SIMULINK 环境中,用户可以在仿真进程中改变感兴趣的 环境中, 参数,实时地观察系统行为的变化。 参数,实时地观察系统行为的变化。
Matlab课程Simulink基础实例

实验二 Simulink 基 础一·实验目的1.熟练运用simulink 为函数建模2.完成simulink 搭建模型的仿真过程二.实验内容【例1-2-1】对书上第35页图1-2-21所示系统,取fixed-step(固定步长)模式进行系统的单位阶跃响应过程仿真。
解:(1)步长类型选fixed-step,解法器算法odel(Euler),仿真步长取0.05;仿真曲线如图(a )所示。
由图(a )可见,其阶跃响应曲线是发散的。
因为系统本身是稳定的,不应该发散,所以此仿真曲线与实际不符。
原因是所取仿真步长偏大,致使仿真误差过大。
(2)步长类型选fixed-step,解法器算法odel(Euler),仿真步长取0.01;仿真曲线如图(b )所示。
由图(b )可见,仿真步长取下后的阶跃响应曲线就正确了。
图(a ) 图(b )【例1-2-2】对系统44)(2++=s s s G ,试求单位阶跃仿真响应,用varible-step 模式。
解 首先在Simulink 下搭建系统的仿真模型,结构如图所示。
然后设置步长类型为varible-step ,解法器算法为ode45,仿真得到的响应曲线如图(a )所示。
由(a )可见,其响应曲线不够光滑,在最大峰值点处出现折线响应,这是仿真误差偏大的表现。
为此,应当减小solver 选项中relative tolerance (相对误差)的值,默认值为1e-3(即310-)修改为1e-6,运算所得的阶跃响应曲线如图(b )所示。
图(a ) 图(b )课内练习【1.2.1】已知一单位反馈系统的开环传递函数为)4(16)(0+=s s s G ,试搭建Simulink 模型并进行该闭环系统的阶跃响应和斜坡响应实验。
解:分别选用信号源后,按照如下图所示构建模型,选择合适参数后,运行结果如下。
【1.2.2】已知系统的闭环传递函数为)2)(3(16)(++=s s s G ,试分别用定步长和变步长的方法求其单位阶跃响应,并讨论不同解法器的选用区别。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab simulink例子
以下是一个简单的 MATLAB Simulink 的例子:
1. 首先,在 MATLAB 命令窗口中输入 `simulink` 打开Simulink 编辑器。
2. 在 Simulink 编辑器中,选择 File -> New -> Model,创建一个新的模型。
3. 在模型中添加一个 Constant 模块,这个模块将输出一个常数。
4. 添加一个 Scope 模块,用于显示模拟结果。
5. 连接 Constant 模块的输出到 Scope 模块的输入。
6. 在右上角的模型名称旁边的按钮上点击 Run 按钮,开始模拟。
7. 在模拟过程中,Scope 窗口将显示 Constant 模块输出的常数值。
这是一个非常简单的例子,但它演示了如何在 Simulink 中创建一个简单的模型,如何添加模块以及如何查看模拟结果。
你可以根据你的需求添加更多模块和功能来创建更复杂的模型。
