第3章分类与决策树
第3章_决策树学习

表3-2 目标概念PlayTennis的训练样例
Day Outlook Temperature Humidity
D1
Sunny
Hot
High
D2
Sunny
Hot
High
D3 Overcast
Hot
High
D4
Rainy
Mild
High
D5
Rainy
Cool
Normal
D6
Rainy
Cool
Normal
• S的正反样例数量不等, 熵介于0,1之间
• 抛一枚均匀硬币的信息熵是多少? 解:出现正面与反面的概率均为0. 5,信息熵 是
q
E x p xi log p xi i1
(0.5log 0.5 0.5log 0.5)
1
• 用信息增益度量期望的熵降低
– 属性的信息增益,由于使用这个属性分割样例 而导致的期望熵降低
• 返回root
最佳分类属性
• 信息增益(Information Gain)
– 用来衡量给定的属性区分训练样例的能力 – ID3算法在增长树的每一步使用信息增益从候选属性中
选择属性
• 用熵度量样例的均一性
– 给定包含关于某个目标概念的正反样例的样例集S,那 么S相对这个布尔型分类的熵为
E n tr o p y (S ) p lo g 2 p plo g 2 p
ID3算法的核心问题是选取在树的每个节点要测试的属性。
表3-1 用于学习布尔函数的ID3算法
• ID3(Examples, Target_attribute, Attributes)
• 创建树的root节点
• 如果Examples都为正,返回label=+的单节点树root
习题3(第三章 分类技术)

习题3(第三章 分类技术)1. 在决策树归纳中,选项有:(a)将决策树转化为规则,然后对结果规则剪枝,或(b)对决策树剪枝,然后将剪枝后的树转化为规则。
相对于(b),(a)的优点是什么? 解答:如果剪掉子树,我们可以用(b)将全部子树移除掉,但是用方法(a)的话,我们可以将子树的任何前提都移除掉。
方法(a)约束更少。
2. 在决策树归纳中,为什么树剪枝是有用的?使用分离的元组集评估剪枝有什么缺点?解答:决策树的建立可能过度拟合训练数据,这样就会产生过多分支,有些分支就是因为训练数据中的噪声或者离群点造成的。
剪枝通过移除最不可能的分支(通过统计学方法),来排除这些过度拟合的数据。
这样得到的决策树就会变得更加简单跟可靠,用它来对未知数据分类时也会变得更快、更精确。
使用分离的元组集评估剪枝的缺点是,它可能不能代表那些构建原始决策树的训练元组。
如果分离的元组集不能很好地代表,用它们来评估剪枝树的分类精确度将不是一个很好的指示器。
而且,用分离的元组集来评估剪枝意味着将使用更少的元组来构建和测试树。
3. 画出包含4个布尔属性A,B,C,D 的奇偶函数的决策树。
该树有可能被简化吗?解答:决策树如下,该树不可能被简化。
4. X 是一个具有期望Np 、方差Np(1-p)的二项随机变量,证明X/N 同样具有二项分布且期望为p 方差为p(1-p)/N 。
解答:令r=X/N ,因为X是二项分布,r同样具有二项分布。
期望,E[r] = E[X/N] = E[X]/N = (Np)/N = p; 方差,E[错误!未找到引用源。
] = E[错误!未找到引用源。
] = E[错误!未找到引用源。
]/错误!未找到引用源。
= Np(1-p)/错误!未找到引用源。
= p(1-p)/N5. 当一个数据对象同时属于多个类时,很难评估分类的准确率。
评述在这种情况下,你将A B C D Class T T T T T T T T F F T T F T F T T F F T T F T T F T F T F T T F F T T T F F F F F T T T F FTTFTF T F T TF T F F FF F T T TF F T F F F F F T F F F F F T使用何种标准比较对相同数据建立的不同分类器。
分类与回归树 决策树
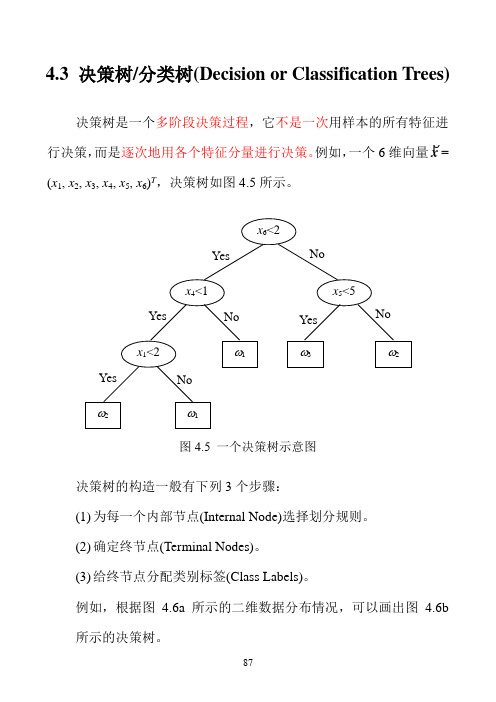
4.3 决策树/分类树(Decision or Classification Trees)
决策树是一个多阶段决策过程,它不是一次用样本的所有特征进
行决策,而是逐次地用各个特征分量进行决策。
例如,一个6维向量x
=
(x 1, x 2, x 3, x 4, x 5, x 6)T ,决策树如图4.5所示。
决策树的构造一般有下列3个步骤:
(1) 为每一个内部节点(Internal Node)选择划分规则。
(2) 确定终节点(Terminal Nodes)。
(3) 给终节点分配类别标签(Class Labels)。
例如,根据图 4.6a 所示的二维数据分布情况,可以画出图 4.6b 所示的决策树。
x 6<2
x 5<5
x 4<1 x 1<2
ω1 ω2
ω1
ω3 ω2 Yes No
Yes Yes
Yes No
No
No
图4.5 一个决策树示意图
我们可以利用决策树的原理来解决多类别问题,例如,用一个线性分类器(例如Fisher 分类器)解决多类别问题。
图4.6a 一个二维空间样本分布示例
图4.6b 对应的决策树
x k >b 2
x k <b 1
x i <a 2 x k >b 3 ω8
ω9 ω6
ω4
Yes No
Yes Yes
Yes
No
No No x i >a 1
ω10
ω1 Yes
No。
数据挖掘作业

第3章分类与回归3.1简述决策树分类的主要步骤。
3.2给定决策树,选项有:(1)将决策树转换成规则,然后对结果规则剪枝,或(2)对决策树剪枝,然后将剪枝后的树转换成规则。
相对于(2),(1)的优点是什么?3.3计算决策树算法在最坏情况下的时间复杂度是重要的。
给定数据集D,具有m个属性和|D|个训练记录,证明决策树生长的计算时间最多为)⨯。
m⨯Dlog(D3.4考虑表3-23所示二元分类问题的数据集。
(1)计算按照属性A和B划分时的信息增益。
决策树归纳算法将会选择那个属性?(2)计算按照属性A和B划分时Gini系数。
决策树归纳算法将会选择那个属性?3.5证明:将结点划分为更小的后续结点之后,结点熵不会增加。
3.6为什么朴素贝叶斯称为“朴素”?简述朴素贝叶斯分类的主要思想。
3.7考虑表3-24数据集,请完成以下问题:(1)估计条件概率)|-C。
P)A(+|(2)根据(1)中的条件概率,使用朴素贝叶斯方法预测测试样本(A=0,B=1,C=0)的类标号;(3)使用Laplace估计方法,其中p=1/2,l=4,估计条件概率)P,)C(+|(-P,A||(+P,)P,)A(+B|(-P。
|C(-P,)|)B(4)同(2),使用(3)中的条件概率(5)比较估计概率的两种方法,哪一种更好,为什么?3.8考虑表3-25中的一维数据集。
表3-25 习题3.8数据集根据1-最近邻、3-最近邻、5-最近邻、9-最近邻,对数据点x=5.0分类,使用多数表决。
3.9 表3-26的数据集包含两个属性X 与Y ,两个类标号“+”和“-”。
每个属性取三个不同值策略:0,1或2。
“+”类的概念是Y=1,“-”类的概念是X=0 and X=2。
(1) 建立该数据集的决策树。
该决策树能捕捉到“+”和“-”的概念吗?(2) 决策树的准确率、精度、召回率和F1各是多少?(注意,精度、召回率和F1量均是对“+”类定义)(3) 使用下面的代价函数建立新的决策树,新决策树能捕捉到“+”的概念么?⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-=+--=+===j i j i j i j i C ,,10),(如果实例个数实例个数如果如果(提示:只需改变原决策树的结点。
数据挖掘作业

证明决策树生长的计算时间最多为 m D log( D ) 。
3.4 考虑表 3-23 所示二元分类问题的数据集。 表 3-23 习题 3.4 数据集
A
B
类标号
T
F
+
T
T
+
T
T
+
T
F
-
T
T
+
F
F
-
F
F
-
F
F
-
T
T
-
T
F
-
(1) 计算按照属性 A 和 B 划分时的信息增益。决策树归纳算法将会选择那个属性?
y ax 转换成可以用最小二乘法求解的线性回归方程。
表 3-25 习题 3.8 数据集
X 0.5 3.0 4.5 4.6 4.9 5.2 5.3 5.5 7.0 9.5
Y-
-
+++-
-
+-
-
根据 1-最近邻、 3-最近邻、 5-最近邻、 9-最近邻,对数据点 x=5.0 分类,使用多数表决。
3.9 表 3-26 的数据集包含两个属性 X 与 Y ,两个类标号“ +”和“ -”。每个属性取三个不同值策略: 0,1 或
记录号
A
B
C
类
1
0
0
0
+
2
0
0
1
-
3
0
1
1
-
4
0
1
1
-
5
0
0
1
+
6
1
0
1
+
7
1
数据挖掘PPT-第3章分类

应用市场:医疗诊断、人脸检测、故障诊断和故障预警 ······
2 of 56
More
高级大数据人才培养丛书之一,大数据挖掘技术与应用
第三章 分类
3.1 基本概念 3.2 决策树 3.3 贝叶斯分类 3.4 支持向量机 3.5 实战:决策树算法在Weka中的实现 习题
3 of 56
*** 基本概念
6 of 56
高级大数据人才培养丛书之一,大数据挖掘技术与应用
第三章 分类
3.1 基本概念 3.2 决策树 3.3 贝叶斯分类 3.4 支持向量机 3.5 实战:决策树算法在Weka中的实现 习题
7 of 56 7
*** 决策树
第三章 分类
决策树是数据挖掘的有力工具之一,决策树学习算法是从一组样本数据集(一个样 本数据也可以称为实例)为基础的一种归纳学习算法,它着眼于从一组无次序、无规则 的样本数据(概念)中推理出决策树表示形式的分类规则。
E
X ,a
g X,a H X,a
第三章 分类
*** 分类的基本概念
分类(Classification)是一种重要的数据分析形式,它提取刻画重要数据类的模型。 这种模型称为分类器,预测分类的(离散的、无序的)类标号。这些类别可以用离散值 表示,其中值之间的次序没有意义。
分类也可定义为: 分类的任务就是通过学习得到一个目标函数(Target Function)ƒ ,把每个属性集x映 射到一个预先定义的类标号y 。
11
No Small 55K ?
12 Yes Medium 80K ?
13 Yes Large 110K ?
14
No Small 95K ?
15
No Large 67K ?
决策树(完整)

无缺失值样本中在属性 上取值 的样本所占比例
ቤተ መጻሕፍቲ ባይዱ
谢谢大家!
举例:求解划分根结点的最优划分属性
根结点的信息熵:
用“色泽”将根结点划分后获得3个分支结点的信息熵分别为:
属性“色泽”的信息增益为:
若把“编号”也作为一个候选划分属性,则属性“编号”的信息增益为:
根结点的信息熵仍为:
用“编号”将根结点划分后获得17个分支结点的信息熵均为:
则“编号”的信息增益为:
三种度量结点“纯度”的指标:信息增益增益率基尼指数
1. 信息增益
香农提出了“信息熵”的概念,解决了对信息的量化度量问题。香农用“信息熵”的概念来描述信源的不确定性。
信息熵
信息增益
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大。决策树算法第8行选择属性
著名的ID3决策树算法
远大于其他候选属性信息增益准则对可取值数目较多的属性有所偏好
2. 增益率
增益率准则对可取值数目较少的属性有所偏好著名的C4.5决策树算法综合了信息增益准则和信息率准则的特点:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
3. 基尼指数
基尼值
基尼指数
著名的CART决策树算法
过拟合:学习器学习能力过于强大,把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,导致泛化性能下降。欠拟合:学习器学习能力低下,对训练样本的一般性质尚未学好。
过拟合无法彻底避免,只能做到“缓解”。
不足:基于“贪心”本质禁止某些分支展开,带来了欠拟合的风险
预剪枝使得决策树的很多分支都没有“展开”优点:降低过拟合的风险减少了训练时间开销和测试时间开销
管理学第三章计划课后练习题带答案
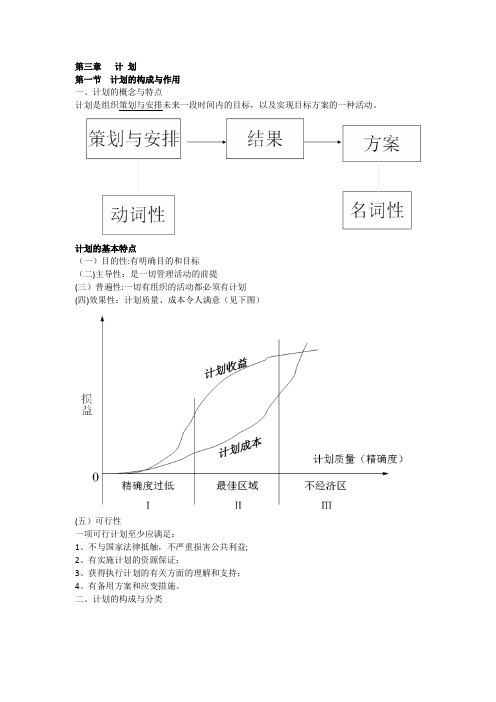
第三章计划第一节计划的构成与作用一、计划的概念与特点计划是组织策划与安排未来一段时间内的目标,以及实现目标方案的一种活动。
计划的基本特点(一)目的性:有明确目的和目标(二)主导性:是一切管理活动的前提(三)普遍性:一切有组织的活动都必须有计划(四)效果性:计划质量、成本令人满意(见下图)(五)可行性一项可行计划至少应满足:1、不与国家法律抵触,不严重损害公共利益;2、有实施计划的资源保证;3、获得执行计划的有关方面的理解和支持;4、有备用方案和应变措施。
二、计划的构成与分类三、计划的作用计划是管理者进行指挥与协调的依据计划是管理者实施控制的标准计划是降低未来不确定性的手段计划也是激励士气的手段计划同样是资源有效配置的手段第二节计划的程序一、环境分析(一)组织与环境管理是一切组织活动必备的功能,其目标、方式、对象都是由组织内部因素决定的.任何一个组织的行为都不是孤立的,都要受自然条件、文化传统、政治制度、经济制度和科学技术等外部环境的影响和制约。
组织环境是对组织各种活动具有直接或间接作用的各种条件和因素的总和。
斯蒂芬·罗宾斯认为:环境是对组织绩效具有潜在影响的外部机构或力量。
(二)组织环境及环境因素的层次性分解1、环境的分类(1)一般环境(宏观环境)自然环境自然环境主要包括气候条件、时间、自然资源、地理条件等。
社会环境社会环境是指与组织活动相联系的各种社会条件和因素关系的总和。
主要是:文化环境经济环境政治环境技术环境。
文化环境文化环境是指由决定人们生活、生产方式的观念形态构成的影响组织活动的条件和因素总和。
通常学术界把下列内容视为文化环境的组成部分:①人们的生活方式;②个人从其所在群体中继承的社会遗产;③思想、感情、宗教和信仰的活动方式;④积累起来的知识学习;⑤社会组织、政治制度及经济关系;⑥教育水平和方式;⑦伦理道德与价值标准;⑧行为方式;⑨历史的积淀。
经济环境经济环境主要是由经济结构、经济发展水平、经济体制和宏观经济政策等四个要素的总和构成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二步——用模型进行分类
•分类规则
•测试集
•未知数据 •(Jeff, Professor, 4)
•Tenured?
第3章分类与决策树
监督学习 VS. 无监督学习
v 监督学习(用于分类)
™ 模型的学习在被告知每个训练样本属于哪个类的 “指导”下进行
™ 新数据使用训练数据集中得到的规则进行分类
算法步骤
1. 树以代表训练样本的单个节点(N)开始 2. 如果样本都在同一个类,则该节点成为树叶,并用该类标记 3. 否则,算法调用Attribute_selection_method,选择能够最
好的将样本分类的属性;确定“分裂准则”,指出“分裂点” 或“分裂子集”。
第3章分类与决策树
决策树归纳策略 (2)
v 预测器可以看作一个映射或函数y=f(X) ™ 其中X是输入;y是输出,是一个连续或有序的值 ™ 与分类类似,准确率的预测,也要使用单独的测试集
第3章分类与决策树
3.1 决策树概述
❖ 决策树(Decision Tree) 一种描述概念空间的有效的归纳推理办
法。基于决策树的学习方法可以进行不相 关的多概念学习,具有简单快捷的优势, 已经在各个领域取得广泛应用。 ❖ 决策树是一种树型结构,其中每个内部结 点表示在一个属性上的测试,每个分支代 表一个测试输出,每个叶结点代表一种类 别。
v 典型应用 ™ 欺诈检测、市场定位、性能预测、医疗诊断
❖ 分类是一种应用非常广泛的数据挖掘技术 ❖ 分类与预测的区别:
当估计的属性值是离散值时,这就是分类; 当估计的属性值是连续值时,这就是预测。
第3章分类与决策树
分类和预测---示例
v 分类
™ 银行贷款员需要分析数据,来弄清哪些贷款申请 者是安全的,哪些是有风险的(将贷款申请者分 为“安全”和“有风险”两类)
v 判定结构可以机械的转变成产生式规则。可以通过对结构进行 广度优先搜索,并在每个节点生成“IF…THEN”规则来实现。 如图6-13的决策树可以转换成下规则:
IF “个子大” THEN
根结点
IF “脖子短” THEN IF “鼻子长” THEN 可能是大象
形式化表示成
个 子 小
个 子大
不 会 吱 吱叫
可能是松鼠 可能是老鼠
鼻子短
鼻子长 可能是长颈鹿
在陆地上
可能是大象 在水里
可能是犀牛
可能是河马
第3章分类与决策树
v 可以看到,一个决策树的内部结点包含学习的实例,每层分枝 代表了实例的一个属性的可能取值,叶节点是最终划分成的类。 如果判定是二元的,那么构造的将是一棵二叉树,在树中每回 答 一 个 问 题 就 降 到 树 的 下 一 层 , 这 类 树 一 般 称 为 CART (Classification And Regression Tree)。
v 无监督学习(用于聚类)
™ 每个训练样本的类编号是未知的,要学习的类集 合或数量也可能是事先未知的
™ 通过一系列的度量、观察来建立数据中的类编号 或进行聚类
第3章分类与决策树
数据预测的两步过程
v 数据预测也是一个两步的过程,类似于前面描述的数据分类 ™ 对于预测,没有“类标号属性” ™ 要预测的属性是连续值,而不是离散值,该属性可简称 “预测属性” v E.g. 银行贷款员需要预测贷给某个顾客多少钱是安全 的
v 通用的决策树分裂目标是整棵树的熵总量最小,每一步分裂时,选择使熵减小 最大的准则,这种方案使最具有分类潜力的准则最先被提取出来
第3章分类与决策树
•记录 •样本
•决策树的基本原理
•预测变量
•目标变量 •类标号属性
•类别集合:Class={“优”,“良”,“差”}
第3章分类与决策树
•根节点 •分裂谓词
4. 对测试属性每个已知的值,创建一个分支, 并以此划分元组
5. 算法使用同样的过程,递归的形成每个划分 上的元组决策树。一旦一个属性出现在一个 节点上,就不在该节点的任何子节点上出现
6. 递归划分步骤停止的条件
划分D(在N节点提供)的所有元组属于同一类 没有剩余属性可以用来进一步划分元组——使用多数表决 没有剩余的样本 给定分支没有元组,则以D中多数类创建一个树叶
第3章分类与决策树
v 树是由节点和分枝组成的层
次数据结构。节点用于存贮
信息或知识,分枝用于连接
各个节点。树是图的一个特
例,图是更一般的数学结构,
如贝叶斯Байду номын сангаас络。
不会吱吱叫
根结点 个子小
会吱吱叫
个子大 脖子短
脖子长
v
决策树是描述分类过程的一 种数据结构,从上端的根节 点开始,各种分类原则被引 用进来,并依这些分类原则 将根节点的数据集划分为子 集,这一划分过程直到某种 约束条件满足而结束。
第3章分类与决策树
v 决策树学习是以实例为基础的归纳学习。
v 从一类无序、无规则的事物(概念)中推理出决策树表示的分类规 则。
v 概念分类学习算法:来源于
™ Hunt,Marin和Stone 于1966年研制的CLS学习系统,用于学习 单个概念。
™ 1979年, J.R. Quinlan 给出ID3算法,并在1983年和1986年对 ID3 进行了总结和简化,使其成为决策树学习算法的典型。
分类的实例在每一节点处与该节点相关的属性值进行比较, 根据不同的比较结果向相应的子节点扩展,这一过程在到 达决策树的叶节点时结束,此时得到结论。 v 从根节点到叶节点的每一条路经都对应着一条合理的规则, 规则间各个部分(各个层的条件)的关系是合取关系。整 个决策树就对应着一组析取的规则。 v 决策树学习算法的最大优点是,它可以自学习。在学习的 过程中,不需要使用者了解过多背景知识,只需要对训练 例子进行较好的标注,就能够进行学习。如果在应用中发 现不符合规则的实例,程序会询问用户该实例的正确分类, 从而生成新的分枝和叶子,并添加到树中。
•分裂属 性
•叶子节点
•每一个叶子节点都被确定一个类标号第3章分类与决策树
v 每一个节点都代表了一个数据集。
™ 根节点1代表了初始数据集D ™ 其它节点都是数据集D的子集。
v 例如,节点2代表数据集D中年龄小于40岁的那部分样本组成 的数据集。
v 子节点是父节点的子集。
v If (年龄<40) and (职业=“学生” or职业=“教师”) Then 信用等级 =“优”
第3章分类与决策树
2020/11/26
第3章分类与决策树
主要内容
v 分类与决策树概述 v ID3、C4.5与C5.0 v CART
第3章分类与决策树
分类 VS. 预测
v 分类和预测是两种数据分析形式,用于提取描述重要数据类或预测未来 的数据趋势 的模型 ™ 分类: v 预测类对象的分类标号(或离散值) v 根据训练数据集和类标号属性,构建模型来分类现有数据,并用 来分类新数据 ™ 预测: v 建立连续函数值模型 v 比如预测空缺值,或者预测顾客在计算机设备上的花费
™ Schlimmer 和Fisher 于1986年对ID3进行改造,在每个可能的 决策树节点创建缓冲区,使决策树可以递增式生成,得到ID4算 法。
™ 1988年,Utgoff 在ID4基础上提出了ID5学习算法,进一步提高 了效率。
™ 1993年,Quinlan 进一步发展了ID3算法,改进成C4.5算法。 ™ 另一类决策树算法为CART,与C4.5不同的是,CART的决策树
第3章分类与决策树
3.2 ID3、C4.5与C5.0
v 熵,是数据集中的不确定性、突发性或随机性的 程度的度量。
v 当一个数据集中的记录全部都属于同一类的时候, 则没有不确定性,这种情况下的熵就为0。
v 决策树分裂的基本原则是,数据集被分裂为若干 个子集后,要使每个子集中的数据尽可能的 “纯”,也就是说子集中的记录要尽可能属于同 一个类别。如果套用熵的概念,即要使分裂后各 子集的熵尽可能的小。
v If (年龄<40) and (职业!=“学生”and职业!=“教师”) Then 信用等 级=“良”
v If (年龄≥40) and (月薪<1000) Then 信用等级=“差” v If (年龄≥40) and (月薪≥1000 and月薪≤3000) Then 信用等级=“良” v If (年龄≥40) and (月薪>3000) Then 信用等级=“优”
第3章分类与决策树
v 数据集D被按照分裂属性“年龄”分裂为两 个子集D1 和D2
•信息增益: •Gain(D,年龄)= H(D)–[P(D1)×H(D1)+ P(D2)×H(D2)]
第3章分类与决策树
v 显 然 , 如 果 D1 和 D2 中 的 数 据 越 “纯”,H(D1)和H(D2)就越小,信 息增益就越大,或者说熵下降得越 多。
可 能 是 松鼠
会吱吱 叫
脖 子短
脖 子长
可 能 是 鼻子
老鼠
短
鼻 子长
可 能 是 长 颈鹿
在 陆 地上
可 能 是 在 大象 水里
可 能 是 犀牛
可 能 是 河马
第3章分类与决策树
v 构造一棵决策树要解决四个问题: ™ 收集待分类的数据,这些数据的所有属性应该是完全标注的。 ™ 设计分类原则,即数据的哪些属性可以被用来分类,以及如何将该属性量 化。 ™ 分类原则的选择,即在众多分类准则中,每一步选择哪一准则使最终的树 更令人满意。 ™ 设计分类停止条件,实际应用中数据的属性很多,真正有分类意义的属性 往往是有限几个,因此在必要的时候应该停止数据集分裂: v 该节点包含的数据太少不足以分裂, v 继续分裂数据集对树生成的目标(例如ID3中的熵下降准则)没有贡献, v 树的深度过大不宜再分。
