流体力学蔡增基
流体力学龙天渝蔡增基版课后答案第五章孔口管嘴管路流动

第五章孔口管嘴管路流动1.图中穿孔板上各孔眼的大小形状相同,问每个孔口的出流量是否相同? 解:由02gH AQ μ=与深度无关,所以每个孔口的出流量相同2.有一水箱水面保持恒定(5m ),箱壁上开一孔口,孔口直径10。
(1)如果箱壁厚度δ=3,求通过孔口的流速和流量。
(2)如果箱壁厚度δ=40,求通过孔口的流速和流量。
解:(1)视作薄壁小孔口,97.0=ϕ,62.0=μs m gh v /6.92==ϕ 得:s m vA Q /1082.434-⨯==μ(2)视作管嘴,82.0==μϕs m gh v /12.82==ϕ 得:s m vA Q /1038.634-⨯==μ3.一隔板将水箱分为A 、B 两格,隔板上有直径为d 1=40的薄壁孔口,如题5-3 图,B 箱底部有一直径为d 2=30的圆柱形管嘴,管嘴长0.1m ,A 箱水深H 1=3m 恒定不变。
(1)分析出流恒定性条件(H 2不变的条件)。
(2)在恒定出流时,B 箱中水深H 2等于多少? (3)水箱流量Q 1为何值? 解:(1)当Q 12时 出流恒定 (2)因为Q 12,=-)(22111H H g A μ)1.0(2222+H g A μ查表得6.01=μ,82.02=μ,解得:m H 85.12= (3)解得=1Q 3.58×10-3m 34.证明容器壁上装一段短管(如图所示),经过短管出流时的流量系数μ与流速系数为∑++==11ζλμϕdl证:∵∑++=gv d l g v g v H 2222220λζ∴02gH v ϕ= 其中=ϕ∑++11ζλdl5.某诱导器的静压箱上装有圆柱形管嘴,管径为4,长度l =100,λ=0.02,从管嘴入口到出口的局部阻力系数5.0=ζ∑,求管嘴的流速系数和流量系数(见上题图)。
解:由题得707.011=++==∑ζλμϕdl6.如上题,当管嘴外空气压强为当地大气压强时,要求管嘴出流流速为30。
流体力学第二版蔡增基2

测压管
M点旳相对压强为
p p' pa gh
于是,用测得旳液柱高度h,可得到容器中液体旳计示 压强及绝对压强。
测压管只合用于测量较小旳压强,假如被测压强较高, 则需加长测压管旳长度,使用就很不以便。
二、U形管测压计
1.构造
这种测压计是一种装在刻度板上两端开口旳U形玻璃管
。测量时,管旳一端与被测容器相接,另一端与大气相通,
dz
dy dx
y
x
z px
作用在ACD面上 旳流体静压强 py
x
dz
dy dx
pz
作用在BCD面
pn
上旳静压强
y
作用在ABD 和上旳静 压强
图2-2 微元四面体受力分析
设作用在ACD、 ABD、ABC和BCD四个面上旳流体静压
强分别为px、py、pz和pn,pn与x、y、z轴旳夹角分别为α、β
所以 p2dA p1dA gldAcos 0 整顿得 p2 p1 gh 0 或p gh
或 p2 p1 gh
静止液体中任两点旳压强差等于两点间旳深度差与密 度、重力加速度旳乘积。
二、流体静压强旳基本方程式
p0
对于静止液体密度为ρ旳液体, 设液面旳压强为p0 ,如图示。
深度为h处旳压强为: h
点旳位置一定,不论那个方向,压强大小相同。
§ 2-2流体静压强旳分布规律
在实际工程中,经常遇到并要研究旳流体是质量力只 有重力旳液体。
一、压强关系式
P3 P4
在静止液体中任意取出一 微小圆柱体,如图所示。
微元流体在图示力旳作用 下处于平衡状态。 轴向方向满足:
其中 P2 p2dA
P2 P1 Gcos 0 P1 p1dA G gldA
流体力学第一章

蔡增基《流体力学》考点精讲及复习思路第一章 绪论1 本章考情分析本章主要介绍了流体力学中的最基本概念和流体的主要力学性质,考试中主要在名词解释、简答以及小计算题涉及,相对来说属于基础题,但切不可掉以轻心,本章是理解全书的基础。
在试卷后五道计算大题中,本章的内容虽不会直接予以考察,但对于理解题目、分析和计算中占有举足轻重的地位,所以这一章显得尤为关键。
2.本章框架结构本章首先介绍了流体的概念,然后介绍了流体的主要力学性质,继而按照流体上力的作用方式分析了作用在流体上的力。
最后阐述了力学模型及三大假设。
3.[考点精讲]考点一 流体的概念(1)流体流体指可以流动的物质,包括气体和液体。
特点(与固体比较):流体分子间引力较小,分子运动剧烈,分子排列松散,流体不能保持一定的形状,具有较大的流动性。
(2)气体和液体差别:一是气体具有很大的压缩性,液体压缩性非常小;二是气体将充满整个容器,而液体则有可能存在自由液面。
(3)流体的分类:一、按流体作用力的角度分类:流体静力学、流体运动学、流体动力学二、按力学模型分类:理想流体动力学、粘性流体动力学、非牛顿流体力学、可压缩流体动力学、不可压缩流体动力学(4)牛顿流体与非牛顿流体符合牛顿内摩擦定律的流体称为牛顿流体,牛顿流体受力后极易变形,是切应力与变形率成正比的低粘性流体。
凡不同于牛顿流体的流体都称为非牛顿流体。
常见的牛顿流体:空气,水,酒精,特定温度下的石油等;常见的非牛顿流体:聚合物溶液,原油,血液等。
(5)实际流体和理想流体实际流体:粘度不为0的流体称为实际流体或粘性流体。
理想流体:粘性为0的流体称为理想流体或无粘流体。
(6)不可压缩流体:不可压缩流体是指每个质点在运动全过程中密度不变的流体,对于均值的不可压缩流体,密度是是处处都不变化,即ρ=常数。
液体分子距很难缩小,而可以认为液体具有一定的体积,因此通常称为不可压缩流体考点二 连续介质假设(1)连续介质假设定义这一假设认为流体质点(微观上充分大,宏观上充分小的分子团)连续的充满了流体所在的整个空间,流体所具有的的宏观物理量(如质量、速度、压力、温度等)满足一切应该遵循的物理定律及物理性质,例如质量守恒定律,牛顿运动定律、能量守恒定律、热力学定律以及扩散、粘性及热传导等输运性质。
流体力学蔡增基_课后习题解析

绪论1. 流体的容重及密度有何区别及联系?解: © = 〉 g 〉是流体的本身属性。
© 还与g 有关。
2.已知水的密度 〉 = 1000kg/m 3 ,求其容重。
若有这样的水1L,它的质量和重力各是多少?解: © = 〉 g=1000×9.807=9807N/m 3m= 〉 v=1000×0.001=1kg G=mg=1×9.807=9.807N3.什么是流体的粘滞性?它对流体流动有什么作用?动力粘滞系数 ∝和运动粘滞系数⎠有何区别及联系?答:流体内部质点间或流层间因为相对运动的性质叫粘滞性,它使流动的能量减少。
∝表征单位速度梯度作用下的切应力,反映粘滞性的动力性质。
⎠是单位速度梯度作用下的切应力对单位体积质量作用产生的阻力加速度。
⎠ = ∝ / 〉4.水的容重 © =9.17kN/ m 3 , ∝ =0.599×10 3 pa.s 求它的运动粘滞系数⎠解:⎠ = ∝= ∝ g/ © =6.046×10 5 m 2 /s〉5.空气容重 © =11.5N/ m 3,⎠ =0.157cm 2 /s,求它的动力粘滞系数 ∝。
解: ∝ = 〉⎠ = ©⎠= 11.5 ⋅ 0.157 ⋅10 4 / 9.807 = 1.841⋅10 5 pa.sg6.当空气从0℃增加到20℃时, ⎠增加15%,容重减少110%,问此时 ∝增加多少?解: ∝ = 〉⎠ = ©⎠g = (1 10%)(1 + 15%)© 0⎠ 0g© ⎠= 1.035 0 0g所以 ∝增加了3.5%7.水平方向运动的木板,其速度为1m/s,平板浮在油面上,™ = 10mm ,油的 ∝ =0.09807pa.s。
求作用于平板单位面积上的阻力。
解:⎜ = ∝ du = 0.09807 ⋅1/ 0.01 = 9.807 N / m 2dy8.温度为20℃的空气,在直径为2.5cm 管中流动,距管壁上1mm 处的空气速度为3cm/s。
流体力学泵与风机 蔡增基 第五版 下 答案讲解学习

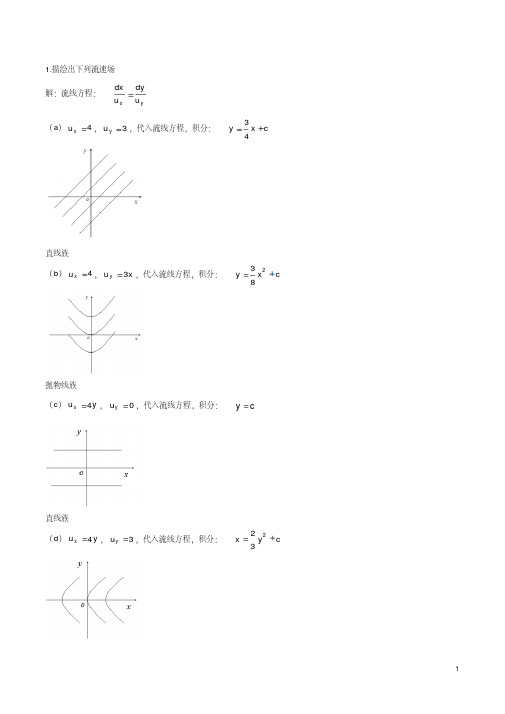
流体力学泵与风机蔡增基第五版下答案1.描绘出下列流速场解:流线方程: yx u dy u dx = (a )4=x u ,3=y u ,代入流线方程,积分:c x y +=43直线族(b )4=x u ,x u y 3=,代入流线方程,积分:c x y +=283抛物线族(c )y u x 4=,0=y u ,代入流线方程,积分:c y =直线族(d )y u x 4=,3=y u ,代入流线方程,积分:c y x +=232抛物线族(e )y u x 4=,x u y 3-=,代入流线方程,积分:c y x =+2243椭圆族(f )y u x 4=,x u y 4=,代入流线方程,积分:c y x =-22双曲线族(g )y u x 4=,x u y 4-=,代入流线方程,积分:c y x =+22同心圆(h )4=x u ,0=y u ,代入流线方程,积分:c y =直线族(i )4=x u ,x u y 4-=,代入流线方程,积分:c x y +-=22抛物线族(j )x u x 4=,0=y u ,代入流线方程,积分:c y =直线族(k )xy u x 4=,0=y u ,代入流线方程,积分:c y =直线族(l )rc u r =,0=θu ,由换算公式:θθθsin cos u u u r x -=,θθθcos sin u u u r y +=220y x cx r xr c u x +=-=,220y x cyr y r c u y +=+=代入流线方程积分:c y x=直线族 (m )0=r u ,r c u =θ,220y x cy r yr c u x +-=-=,220y x cxr x r c u y +=+=代入流线方程积分:c y x =+22同心圆2.在上题流速场中,哪些流动是无旋流动,哪些流动是有旋流动。
如果是有旋流动,它的旋转角速度的表达式是什么?解:无旋流有:x uy u yx ∂∂=∂∂(或r ru u r∂∂=∂∂θθ)(a ),(f ),(h ),(j ),(l ),(m )为无旋流动,其余的为有旋流动对有旋流动,旋转角速度:)(21y ux u xy ∂∂-∂∂=ω(b )23=ω (c )2-=ω (d )2-=ω (e )27-=ω(g )4-=ω (i )2-=ω (k )x 2-=ω3.在上题流速场中,求出各有势流动的流函数和势函数。
流体力学第三章

vx =(a+1)et-1=x+t
vy =(b+1)et-1=y+t
可进一步求得欧拉变数下的加速度为:
ax =vtx +vxvxx +vyvyx +vzvzx =x+t+1
ay =vty +vxvxy +vyvyy +vzvzy =y+t+1
(4)有效断面、流量和平局流速等
流管
流管———在流场中作一条不与流线重合的任意封闭曲线,则通过此曲线上任一点的所有流线将 — 5—
如上图,一条迹线表示一个流体质点在一段时间内描述的路径。 特点:迹线上各点的切线方向表示的是同一流体质点在不同时刻的速度方向。 (2)流线 流线:流线是用来描述流场中各点流动方向的曲线,即矢量场的矢量线。在某一时刻该曲线上任 意处质点的速度矢量与此曲线相切。 注:矢量线———线上任一点的切线方向与该点的矢量方向重合,称为矢量线。
— 3—
2)二元流动:流体的运动参数只有两个坐标的函数。平面流动是二元流动。实际流体由于具有 黏性,故其流动至少是二元的,例如实际流体在圆管内的流动。由于水的黏性影响,靠近管壁的流速 低于中部的流速,即管道中的流速随管道的半径和流动方向的位移而变化,所以是二元流动。
3)三元流动:流体在空间流动一般说都是三元流动,运动参数是空间三坐标的函数。 考点四 流体运动学的基本概念和相关计算 (1)迹线 迹线:流体质点在不同时刻的运动轨迹。
构成一个管状曲面,这个管状曲面称为流管。
流束———充满在流管内部的流体。微小流束:断面无穷小的流束。 总流———管道内流动的流体的集合。 流管特点: ①流管表面不可能有流体穿过;②稳定流动时流管的形状和位置都不随时间变化,就像固体管道 的管壁;非稳定流动时,流管的形状及位置有可能随时间变化;③流管不可能在流场内部中断。 有效断面 有效断面———流束或总流上垂直于流线的断面。(有效断面可能是平面,也可能是曲面)
流体力学泵与风机 蔡增基 第五版 下 答案

1.描绘出下列流速场 解:流线方程: y x u dy u dx = (a )4=x u ,3=y u ,代入流线方程,积分:c x y +=43直线族(b )4=x u ,x u y 3=,代入流线方程,积分:c x y +=283抛物线族(c )y u x 4=,0=y u ,代入流线方程,积分:c y =直线族(d )y u x 4=,3=y u ,代入流线方程,积分:c y x +=232抛物线族(e )y u x 4=,x u y 3-=,代入流线方程,积分:c y x =+2243椭圆族(f )y u x 4=,x u y 4=,代入流线方程,积分:c y x =-22双曲线族(g )y u x 4=,x u y 4-=,代入流线方程,积分:c y x =+22同心圆(h )4=x u ,0=y u ,代入流线方程,积分:c y =直线族(i )4=x u ,x u y 4-=,代入流线方程,积分:c x y +-=22抛物线族(j )x u x 4=,0=y u ,代入流线方程,积分:c y =直线族(k )xy u x 4=,0=y u ,代入流线方程,积分:c y =直线族(l )r c u r =,0=θu ,由换算公式:θθθsin cos u u u r x -=,θθθcos sin u u u r y += 220y x cx r x r c u x +=-=,220y x cy r y r c u y +=+= 代入流线方程积分:c y x =直线族(m )0=r u ,r c u =θ,220y x cy r y r c u x +-=-=,220y x cx r x r c u y +=+= 代入流线方程积分:c y x =+22同心圆2.在上题流速场中,哪些流动是无旋流动,哪些流动是有旋流动。
如果是有旋流动,它的旋转角速度的表达式是什么?解:无旋流有:x u y u y x ∂∂=∂∂(或rr u u r ∂∂=∂∂θθ) (a ),(f ),(h ),(j ),(l ),(m )为无旋流动,其余的为有旋流动对有旋流动,旋转角速度:)(21yu x u x y ∂∂-∂∂=ω (b )23=ω (c )2-=ω (d )2-=ω (e )27-=ω (g )4-=ω (i )2-=ω (k )x 2-=ω3.在上题流速场中,求出各有势流动的流函数和势函数。
新版流体力学泵与风机蔡增基第五版下答案-新版.pdf
xa
ux
y 2 ( y2 ( x a) 2 y 2 ( x a) 2 )
Q
y
y
uy
ห้องสมุดไป่ตู้
x 2 ( y 2 (x a)2 y 2 ( x a) 2 )
4 ydy
3xdx 2 y2 3 x2 2
(g)积分路径可以选
0,0 x,0 : dy 0, y 0
x,0 x, y : dx 0, x x
4ydy ( 4x)dx 2 y 2 2x 2
(L )积分路径可以选 0,0 x,0 : dy 0, y 0
x,0 x, y : dx 0, x x
ux ur cos u sin
1.描绘出下列流速场 解:流线方程: dx dy
ux uy
(a) u x 4 , u y 3 ,代入流线方程,积分:
3 y xc
4
直线族 (b) u x 4 , u y 3x ,代入流线方程,积分:
y 3 x2 c 8
抛物线族
(c) u x 4y , uy 0 ,代入流线方程,积分: y c
直线族 (d) u x 4 y , uy 3 ,代入流线方程,积分:
xa
6
驻点在 y 0, x
l 处,由 l 2
2,b
0.5 得椭圆轮廓方程:
x2 1
y2 (0.25) 2
1
即: x2 16 y2 1
8. 确定绕圆柱流场的轮廓线,主要取决于哪些量?已知
R 2 m ,求流函数和势函数。
解:需要流速 v0 ,柱体半径 R
v0 (r ∵R 2
R2 ) sin
r ∴ v0(r
4) sin r
R2
v0 (r
) cos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体力学蔡增基
引言
流体力学是研究流体运动的学科,是物理学的重要分支之一。
在流体力学中,蔡增基是中国著名的学者之一,他在这一领域做出了杰出的贡献。
本文将介绍流体力学的基本概念,并重点介绍蔡增基的研究成果和影响。
流体力学概述
流体力学是研究流体运动和相互作用的科学。
它涉及到液体和气体的力学性质、流动规律和应用。
流体力学分为两个主要分支:流体静力学和流体动力学。
流体静力学研究静止流体中的力学性质,主要研究压力、密度等静态参数的分布和变化规律。
而流体动力学研究流体在运动状态下的力学性质,主要研究流速、流量、压力损失等动态参数的变化规律。
蔡增基个人简介
蔡增基(1934年-2019年)是中国力学学会和中国工程院的院士,被称为“流体力学之父”。
他是中国流体力学研究的奠基人之一,对流体力学的研究和发展做出了重要贡献。
蔡增基在1960年代开始研究流体力学,并在70年代提出了一种新的流体力学理论——相对运动理论,在国际上产生了重大影响。
他的研究成果使得传统流体力学的理论得以扩展和完善,为进一步研究和应用流体力学提供了新的思路和方法。
蔡增基的研究成果
1.相对运动理论
蔡增基在70年代提出的相对运动理论是他最重要的研究成果之一。
相对运动理论引入了微分运动变量,将流体运动的描述从欧拉描述转变为拉格朗日描述。
这一理论充分考虑了流体粒子间的相互作用,对于高速流动和复杂流动问题的研究具有重要意义。
2.流动控制技术
蔡增基还在流体力学的应用领域做出了突出贡献。
他提出并研究了多孔介质流动控制技术,该技术可用于控
制流体的流动行为,对于提高流体传递效率、减小流体阻
力等方面具有重要作用。
这一技术在航空航天、能源、化
工等领域得到了广泛应用。
3.教育与推广工作
蔡增基不仅在科研方面取得了杰出成就,还致力于流体力学的教育与推广工作。
他培养了一大批优秀的学生,并在学术交流和学术会议上积极推广流体力学的发展。
蔡增基的影响和荣誉
蔡增基的研究成果对于国内外学术界产生了重要影响,他
的相对运动理论为流体力学的发展提供了新的视角和方法。
他曾获得过中国科学院大奖、国家自然科学二等奖等荣誉,是中国流体力学研究的重要奠基人和领军人物。
结论
蔡增基是中国著名的流体力学学者,他的研究成果对流体
力学的发展产生了重要影响。
他在相对运动理论、流动控制技术等方面做出了杰出贡献,成为中国流体力学研究的重要奠基人和领军人物。
蔡增基的研究成果不仅对学术界产生了影响,也为工程领域的应用提供了新的思路和方法。
他的精神和学术成就将继续影响和激励着后人在流体力学领域的研究和发展。
