SPSS统计分析—差异分析(1)
SPSS第四章基本统计分析

中 0 500 0
高 0 0 600
一致
1 - 29
青 中 老
低 0 0 400
中 0 600 0
高 500 0 0
应用举例
受教育程度越高通信支出越高吗? 受教育程度越高通信支出比例越高吗?
1 - 30
多选项分析
什么是多选项问题?
(1)即:在回答某些问题时,答案在两个以上 例如:请问您平时主要的休闲娱乐方式是: a.看电视、听广播 b.玩游戏 c.体育运动 d.逛街购物e.经常去港澳游玩 f.看书学习 g.喝酒聊天 h.工作太忙,没时间休闲娱乐 又如:您经常浏览的网站?在下列品牌中您信任哪些 品牌? (2)多选项问题不能直接处理。因为SPSS中的一个变 量对每一个答案只能取一个值。
2 2
2
C
2
1 - 27
分析列联表中变量间的关系
Ordinal(定序变量)
反映定序变量一致性指标 行变量等级越高,列变量等级也越高或越低 ——一致性高 行变量等级越高,列变量等级不定——不一 致 指标绝对值越大越相关,越接近0越无关
1 - 28
定序变量一致性检验
年龄与工资收入交叉列联表 低 青 400 一致 中 0 老 0
n 3
3
计算描述统计量
描述陡峭程度的统计量
峰度(kurtosis):描述某变量所有变量值 分布形态陡缓程度的统计量。
峭度为0表示与正态分布峭度相同。 大于0表示比正态分布陡,尖峰。 小于0表示比正态分布缓;平峰。
Kurtosis
1 - 12
1 n -1
i 1 ( xi x) / SD 3
n 4 4
计算描述统计量
《精品》SPSS统计分析—差异分析

《精品》SPSS统计分析—差异分析差异分析是一种用于比较两个或多个组之间差异的统计方法。
在实际研究中,我们常常需要比较不同组别或条件下的测量变量之间的差异,如不同性别间的身高差异、不同年龄组别间的成绩差异等。
利用SPSS进行差异分析可以快速准确地得出结论,并辅助我们做出决策。
SPSS统计软件是一款常用的数据分析工具,它提供了丰富的统计分析功能。
下面将介绍如何使用SPSS进行差异分析。
首先,打开SPSS软件,并导入要进行差异分析的数据。
选择“文件”菜单中的“打开”选项,找到数据文件,并点击“打开”。
在数据文件打开后,我们可以进行数据的预处理工作,如数据清洗和缺失值处理。
选择“数据”菜单中的“数据清理”选项,对数据进行相应的清洗操作。
接下来,选择“分析”菜单中的“描述性统计”选项。
在弹出的对话框中,选择需要进行差异分析的变量,并点击“确定”。
在得到了描述性统计结果后,我们可以对不同组别之间的差异进行进一步的分析。
选择“分析”菜单中的“方差分析”选项。
在弹出的对话框中,将需要进行差异分析的自变量和因变量添加进去,并点击“确定”。
SPSS会自动计算出方差分析的结果,并给出显著性水平。
如果显著性水平小于设定的阈值(通常为0.05),则可以认为不同组别之间存在显著差异。
除了方差分析,SPSS还提供了其他多种差异分析方法,如t检验、卡方检验等。
根据实际情况选择合适的方法进行分析。
最后,我们可以将结果导出为文档、图片或报告,以便于展示和分享。
选择“文件”菜单中的“导出”选项,选择需要导出的格式,填写相应的内容,并点击“确定”。
综上所述,差异分析是一种重要的统计方法,在研究中具有广泛的应用价值。
通过SPSS统计软件进行差异分析,可以快速准确地得出结论,并帮助我们做出科学决策。
希望以上介绍能够对您有所帮助。
利用SPSS对五点式量表进行差异性分析

v1.0可编辑可修改利用SPSS寸五点式量表进行差异性分析(两个变项)町* E 粧山』'L 峠:氐間护P) JJ 各日g.tL 居和出:'田口 TM 習第」•:」雋即I 删程式 1:U 1 鯉 biK+4J5r.*'^> »| 中卑擞世0ftl *沾-岷疋址事玛JU *116 317 *11 «19 ui24曲:g渤3laR 丁任疋山1J 12 i 51flsnxaj戍为搏*:極生0.J id 4巧、J■1 J •1 414 2 2o ] 】L 21d护陨评件(2)■1& 55(3色2?2J 4 $ J IO 1 5 L 1d» »■1 325 $ 22\ x:3iJ2 2S J J4 njt ] II 1 11 ■ 2121L*>XA qd 4』 g22*5 如 J 11 1r 1Brtfipt 列 G» 44 4斗<it \、: aA 4 d i d 36 do & ] 山 1 j 2t443 221 5%ua444 4 2i10? 1144<.1Ad71 2 51齿咽址廿034 4 4- 415 i £ ]L« ] 11] 2 JI 23233543 5 i 5i 卜卜检苹+ 勺魏沖45» 曲 1 1.2 :J2 53 J343 & 5&1 i4&110jL 2£5 5土i J£11(* 1 11 175力中\/化匕/k 临缶 11 111 1 11 1 rJ j13 22 3i J< JJ J%-j4i11 L :] 11 . i1 1 32 5444J2 1 L:厂a茁J44B iu ] 1 1 j 1 11 35LL 4扌4 4ii Q 4a aAJ 4 4 4<14 叮& ] B 1i 11L 2242443334 扌44d4 』 i 151151 1J232 112 342 43& i ii 圍 43J 4 <百4 41611*1 |l)13: 912 74 j 443 41i片44a4444 4i171171 112 j2j 132 ■1 4 4 4; 32 2 t !4打 3 nJ4 百 4 百 5~~1? l]t ] II41 J424 3 J # 4224 14 3 黄4 4 4 4 4卡1» 1191 11 1 1 1 1 L2 j2 54 i S&4£ S4r■1 ■1iS 4J201 9 a J斗 1JJ iJ 2 4 3J 、JJ J 讥4 4贯2 JJ3 :-*21 血 2 & iLa J2 L2二4 J1 12I Q :电 J i2125 4 i22 w? 27 1J 11. 13 3L1 4 55 3 2 ii35 j 1 ■1 4 3 5 522 12L12 1333 2 J53 14J5 5©4J.145J4 ■A丄.| 菊逗册晦.-£离 ww SEPUMimi ITffh* 11』曲M 竺;'0召・』£ 15下平网「-r Grt* 1瀰訂丁丁甘児 lg: I. Q 二 H >■ -5I «1d粘團目| • | | 口和处4 |亡|口工||\|锚划]2dnlH曲皿心砧羿個泗泌*.•F咸**■Jr--r-rf£•■*.畑1 ]»]do& jwF「]Lt320鈔琥I鼻.12如吳飙M曲邀商辽•・m\ iji20212245&71112D£_!_ J__i 1 1/选择公私立学校‘为分组变数米用T检疋只能考验两个变项2>25C3212J1213325534J5\50 可43■1 | 45---1 L J 67」亘工站応的I邪44冲0召■連上HifiCB-lll 顧二宜I・1. Levene 检定用于考验两组变异数是否同质,F= P=>,未达显著差异,故两 组变异数可视为相等,因此须看「假设变异数相等」这一列;否则即须看「不 假设变异数相等」这一列。
SPSS统计分析—差异分析

点击“确定”,运值等统计量,判断两组 数据是否存在显著性差异
撰写结论:根据P值判断结果, 解释两组数据之间的差异是否 具有统计学意义
05
SPSS差异分析的实例
单因素方差分析实例
目的:比较不同 组别的数据差异
步骤:选择数据→ 定义变量→选择分 析方法→设置参数 →分析结果
选择控制变量:考虑可能影响结果的其他因 素
确定样本量:根据研究目的和预期结果确定 合适的样本量
检查数据质量:确保数据完整、准确、可靠
选择合适的差异分析方法:根据研究目的和 变量类型选择合适的差异分析方法
设置差异分析选项
在弹出的窗口中,选择“独立样 本t检验”或“配对样本t检验”
选择“分析”菜单,点击“比 较平均值”选项
SPSS操作:在SPSS中输入数据,选择双因素方差分析, 得到结果
结果解读:分析不同产品类型和不同销售渠道对销售额 的影响程度和显著性水平
结论:根据分析结果,提出改进建议和策略
T检验实例
目的:比较两组数据的平均值是否存在显著性差
01 异
单击此处输入你的项正文,文字是您思想的提炼,请
尽量言简意赅的阐述观点
大数据环境下的SPSS差异分析: 利用大数据技术提高分析效率和 准确性
SPSS差异分析与人工智能技术的结 合:利用人工智能技术进行自动分 析和预测,提高分析效果和效率
添加标题
添加标题
添加标题
添加标题
云计算环境下的SPSS差异分析: 利用云计算技术实现分布式计算 和存储,提高分析速度和灵活性
SPSS差异分析在跨学科研究中的应用: 与其他领域的研究相结合,拓展SPSS 差异分析的应用范围和深度
b. 样本量的大小
c. 假设检验的设置
SPSS——单因素方差分析报告详解

SPSS——单因素方差分析来源:李大伟的日志单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。
还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-Way ANOVA过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几个因变量之间彼此不独立,应该用Repeated Measure 过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表1-1所示。
表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中,变量格式如图1-1。
图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量“幼虫”和因素水平变量“品种”,然后输入对应的数值,如图1-1所示。
或者打开已存在的数据文件“data1.sav”。
2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“Compare Means”项,在右拉式菜单中点击“0ne-Way ANOVA”项,系统打开单因素方差分析设置窗口如图1-2。
图1-2 单因素方差分析窗口3)设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量:选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图1-3所示的对话框。
该对话框用于设置均值的多项式比较。
图1-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设H0:第一组均值的1.1倍与第二组的均值相等。
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章).doc
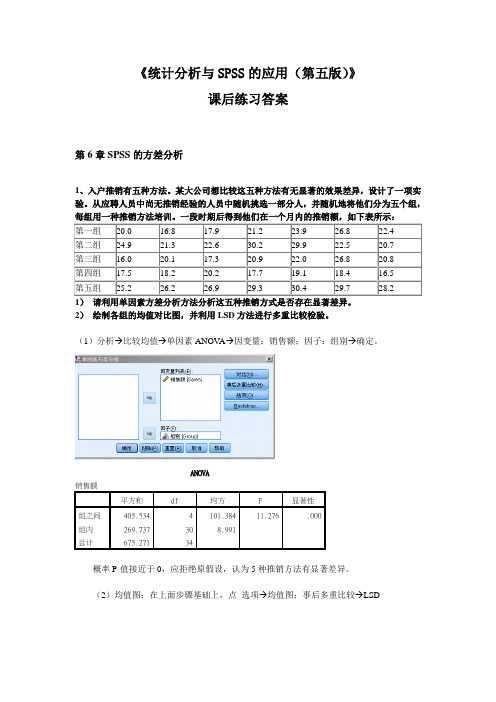
《统计分析与SPSS的应用(第五版)》课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,第一组20.0 16.8 17.9 21.2 23.9 26.8 22.4第二组24.9 21.3 22.6 30.2 29.9 22.5 20.7第三组16.0 20.1 17.3 20.9 22.0 26.8 20.8第四组17.5 18.2 20.2 17.7 19.1 18.4 16.5第五组25.2 26.2 26.9 29.3 30.4 29.7 28.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项→均值图;事后多重比较→LSD多重比较因变量: 销售额LSD(L)(I) 组别(J) 组别平均差(I-J) 标准错误显著性95% 置信区间下限值上限第一组第二组-3.30000* 1.60279 .048 -6.5733 -.0267 第三组.72857 1.60279 .653 -2.5448 4.0019第四组 3.05714 1.60279 .066 -.2162 6.3305第五组-6.70000* 1.60279 .000 -9.9733 -3.4267 第二组第一组 3.30000* 1.60279 .048 .0267 6.5733 第三组 4.02857* 1.60279 .018 .7552 7.3019第四组 6.35714* 1.60279 .000 3.0838 9.6305第五组-3.40000* 1.60279 .042 -6.6733 -.1267 第三组第一组-.72857 1.60279 .653 -4.0019 2.5448 第二组-4.02857* 1.60279 .018 -7.3019 -.7552第四组 2.32857 1.60279 .157 -.9448 5.6019第五组-7.42857* 1.60279 .000 -10.7019 -4.1552 第四组第一组-3.05714 1.60279 .066 -6.3305 .2162第二组-6.35714* 1.60279 .000 -9.6305 -3.0838第三组-2.32857 1.60279 .157 -5.6019 .9448第五组-9.75714* 1.60279 .000 -13.0305 -6.4838第五组第一组 6.70000* 1.60279 .000 3.4267 9.9733 第二组 3.40000* 1.60279 .042 .1267 6.6733第三组7.42857* 1.60279 .000 4.1552 10.7019第四组9.75714* 1.60279 .000 6.4838 13.0305*. 均值差的显著性水平为 0.05。
SPSS中的方差分析法(1)

方差分析(多因素,协方差)一、方法名称单因素二、定义(方法及结果)三、用途四、实现过程1、格式数据整理2、提交显示3、分析变量处理:自变量、因变量ANOVA检验:显示表,是否齐次1 方差分析法方差分析是一种是一种假设检验,它把观测总变异的平方和自由度分解为对应不同变异来源的平方和自由度,将某种控制性因素所导致的系统性误差和其他随机性误差进行对比,从而判断各组样本之间是否存在显著性差异,以分析该因素是否对总体存在显著性影响。
2 样本数据要求方差分析法采用离差平法和对变差进行度量,从总离差平方分解出可追溯到指定来源的部分离差平方和。
方差分析要求样本满足以下条件:2.1 可比性样本数据各组均数本身必须具有可比性,这是方差分析的前提。
2.2 正态性方差分析要求样本来源于正态分布总体,偏态分布资料不适用方差分析。
对偏态分布的资源要考虑先进行对数变换、平方根变换、倒数变换、平方根反正弦变换等变量变换方法变换为正态或接近正态后再进行方差分析。
2.3 方差齐性。
方差分析要求各组间具有相同的方差,满足方差齐性。
3 单因素分析法实验操作单因素分析用于分析单一控制变量影响下的多组样本的均值是否存在显著性差异。
单因素分析法的原理,单因素方差分析也称为一维方差分析,用于分析单个控制因素取不同水平时因变量的均值是否存在显著差异。
单因素方差分析基于各观测量来自于相互独立的正态样本和控制变量不同水平的分组之间的方差相等的假设。
单因素方差分析将所有的方差划分为可以由该因素解释的系统性偏差部分和无法由该因素解释的随机性偏差,如果系统性偏差明显超过随机性偏差,则认为该控制因素取不同水平时因变量的均值存在显著差异。
3.1 实验数据描述某农业大学对使用不同肥料的实验数据对比。
产量(千克/亩产)施肥类型864 普通钾肥875 普通钾肥891 普通钾肥873 普通钾肥883 普通钾肥859 普通钾肥921 控释肥944 控释肥986 控释肥929 控释肥973 控释肥963 控释肥962 复合肥941 复合肥985 复合肥974 复合肥977 复合肥在SPSS的变量视图中建立变量“产量”和“施肥类型”,分别表示实验田产量和实验田的施肥类型。
SPSS数据统计与分析标准教程差异性均值分析

“ H0 为 x x0 ,而 H1 为 x x0 ,该情形中的备选假设的总均值大于确定的 x0 ,拒 绝原假设的拒绝域应安排在左侧,使用单侧检验中的右侧检验。
4.2 均值比较
均值过程是计算一个或多个自变量类别中因变量的子组均值和相关的单变量统计, 通过均值还可以获得单因素方差分析、eta 和线性相关检验。另外均值可以对数据进行分 组,并将各组的统计检验变量放在一起进行直接比较。 均值比较过程中的因变量为定量变量,自变量为分类变量,其分类变量的值可以为 iwei 数值,也可以为字符串。另外,一些可选的子组统计量是基于正态理论的,适用于 具有对称分布的定量变量。而稳健统计量(如中位数)则适用于可能符合或可能不符合 正态假设的定量变量。
4
章 差异性均值分析
4.1.2
两种类型的错误
假设检验是通过比较检验量的样本数量来做出统计决策的,一般情况下根据分析统 计量会出现正确的判断、弃真错误、取伪错误等决策类型,其具体情况如表 4-1 所示。
表 4-1
统计决策表 类型 接受原假设(H0) 正确的判断 取伪错误(β) 拒绝原假设(H0) 弃真错误(α) 正确的判断
4.1 假设检验概述
假设检验为显著性检验,是用来判断样本与样本、样本与总体的差异造成原因的一 种统计推断方法,也是数理统计学中根据一定假设条件由样本推断总体的一种方法。在 本小节中,主要介绍假设检验的基本原理、两种类型的错误、单侧与双侧检验等假设检 验基础内容。
4.1.1
假设检验基本原理
第
假设检验首先需要提出一个假设,然后通过检验样本统计量的差异来推断总体参数 之间是否存在差异。假设检验是以最小概率为标准,对总体的状况所做出的假设进行判 断。而最小概率是指一个发生概率接近 0 的事件,是一种不可能出现的事件。 在统计学内,假设检验被划分为原假设与备选假设。在检验之前需要先确定原假设 与备选假设。其中: “ 原假设 原假设又称为零假设,通常用 H0 表示。 “ 备选假设 备选假设是与原假设对立的一种假设,通常用 H1 表示。备选假设是 在原假设被否认时可能成立的另外一种结论。在实际分析中,一般情况是需要将 期望出现的结论作为备选假设。 确定原假设与备选假设之后,还需要一个统计量来决定接受/拒绝原假设或备选假 设。其后,需要利用统计的分布及显著水平来确定检验统计量的杜绝域。在给定的显著 水平 α 下,检验统计量的可能取值范围被分为小概率与大概率区域。其中: “ 小概率区域 小概率区域是原假设的拒绝区域,其概率不超过显著水平 α 的 区域。 “ 大概率区域 大概率区域是原假设的接受区域,其概述为 1–α 的区域。 当样本统计量位于拒绝域内,则拒绝原假设而接受备选假设;当样本统计量位于接 受区域内,则接受原假设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学成绩表
性别
数学
Male
99
79
59
89
79
89
99
Female
88
54
56
23
t检验就是检验统计量为t的假设检验。
用于检验两个变量之间的差异。
假设检验的一般步骤: 根据实际问题提出原假设H0与备择假设 H1。 选择统计量t作为检验统计量,并在H0成立的条件下确定t的
分布。 选择显著性水平 ,并根据统计量t的分布查表确定临界值及
SPSS中实现过程
分析——比较均值——独立样本T检验
SPSS中实现过程
研究问题 分析A、B两所高校大一学生的高考数学成
绩之间是否存在显著性差异。
两所学校学生的高考数学成绩表
学校 清华 北大
数学 99 88 79 59 54 89 79 56 89 99 23 89 70 50 67 78 89 56
◆注意 单样本t检验和独立两样本t检验样本内部数据的顺序是可以任意调换。而配 对样本t检验的样本必须是一一对应的。样本内数据的顺序不能随意交换顺序。
SPSS将自动计算T值,由于该统计量服从
n−1个自由度的T分布,SPSS将根据T分布表给 出t值对应的相伴概率值。
如果相伴概率值小于或等于用户设想的显著性
在具体的计算中需要通过两步来完成: 第一,利用F检验判断两总体的方差是否 相同; 第二,根据第一步的结果,决定T统计量 和自由度计算公式,进而对T检验的结论作出 判断。
P<=.05 异质 T值显著否? P>.05
F值
P>.05(接受虚无假设)
是否显著? 同质
P<=.05 结果显著 结果不显著
T值显著否?
两配对样本T检验的前提要求如下: • 两个样本应是配对的。在应用领域中,主要的配对资料包 括:具有年龄、性别、体重、病况等非处理因素相同或相似者。首 先两个样本的观察数目相同,其次两样本的观察值顺序不能随意改 变。 • 样本来自的两个总体应服从正态分布。
• 原理 1、配对样本t检验是配对设计的样本差数的均值同总体均值0比较的t
H0的拒绝域。 根据样本值计算统计量的值,并将其与临界值作比较。 下结论:若统计量的值落入拒绝域内,就拒绝H0;否则,不
拒绝H0。
显著性水平: 0.05——显著 0.001——非常显著 0.0001——极其显著
t检验的类型
单样本t检验——样本均值与总体均值的比较 独立两样本t检验——独立两样本均值比较 配对样本t检验——配对设计的差数均值与总体均
于研究者较为有利。但是,采用单尾检验必须提出支持证据,除非理论文献支持单
侧的概念,或是变量间的关系具有明确的线索显示必需使用单侧检验,否则需采用
双侧检验来检验平均数的特性。
(邱 P169)
独立两样本t检验
定义:所谓独立样本是指两个样本之间彼此独立没有任 何关联,两个独立样本各自接受相同的测量,研究者的主要 目的是了解两个样本之间是否有显著差异存在。这个检验的 前提如下:
水平,则拒绝H0,认为两总体均值之间存在 显著差异。
相反,相伴概率大于显著性水平,则不拒绝 H0,可以认为两总体均值之间不存在显著差异。
SPSS中实现过程
分析——比较均值——配对样本T检验
方差分析
多个独立样本的差异显著性检验,通常可以使用方 差分析方法。
• 油菜品种差异性分析
P164
不同教学方式是否给学生成绩造成了显著影响; 不同地区的考生成绩是否有显著的差异等。
数学 99.00 88.00 99.00 89.00 94.00 90.00 79.00 56.00 89.00 99.00 70.00 89.00 55.00 50.00 67.00 67.00 56.00 56.00
组别 0 0 0 0 0 0 2 2 2 2 2 2 1 1 1 1 1 1
实现步骤
(1)首先是单因素方差分析的前提检验 结果,也就是Homogeneity of variance test——方差齐次性检验
(2)输出的结果文件中第2个表格如下所示。
(3)输出的结果文件中第3个表格如下所示。
(4)输出的结果文件中第4个表格察变 量均值的折线图,如图5-6所示。
值0的比较
单样本t检验
统计学上的定义和计算公式
定义:SPSS单样本T检验是检验某个变量 的总体均值和某指定值之间是否存在显著差异。 统计的前提是样本总体服从正态分布。也就是 说单样本本身无法比较,进行的是其均数与已 知总体均数间的比较。
单样本T检验的零假设为H0总 体均值和指定检验值之间不存在 显著差异。采用T检验方法,按照 下面公式计算T统计量:
SPSS中实现过程
分析——比较均值——单样本T检验
SPSS中实现过程
研究问题 分析某班级学生的高考数学成绩和全国的
平均成绩70之间是否存在显著性差异。数据如 表所示。
数学成绩表
性别
数学
Male
99
79
59
89
79
89
99
Female
88
54
56
23
单尾检验与双尾检验
在平均数的检验中,研究者的兴趣往往在于比较不同平均数的差距,而提出两 个平均数大于、小于与不等于几种不同形式的研究假设,形成有特定方向的检验或 无方向性的检验两种不同模式。当研究者只关心单一一个方向的比较关系时(例如男 生的数学成绩X1优于女生X2),平均数的检验仅有一个拒绝区,需使用单尾检验 (one-tailed test),范例如下:
图4-6 “Independent-Samples T Test”对话框
图4-7 “Define Groups”对话框
结果和讨论
两配对样本T检验
统计学上的定义和计算公式
定义:两配对样本T检验是根据样本数据对样本来自的两配对 总体的均值是否有显著性差异进行推断。一般用于同一研究对象 (或两配对对象)分别给予两种不同处理的效果比较,以及同一研 究对象(或两配对对象)处理前后的效果比较。前者推断两种效果 有无差别,后者推断某种处理是否有效。
检验。
2、配对样本t检验是针对配对数据的t检验。其检验方法是首先求出 每对样本的差值,然后比较样本差值的均值和总体均值0之间的关 系。
如果两组数据没有差别,那么其样本差值的均值应该在0附近波动。 否则为两组数据是有差别的。这种方法的本质就是在对配对样本的 差值同总体均值0做单样本t检验。
两配对样本T检验的零假设H0为两总体均 值之间不存在显著差异。
总变异 = 随机变异 + 处理因素导致的变 异
总变异 = 组内变异 + 组间变异
这样,我们可采用一定的方法来比较组内变异和组间变 异的大小,如果后者远远大于前者,则说明处理因素的影响 确实存在,如果两者相差无几,则说明影响不存在,这就是 方差分析的基本思想。
计算公式
SST=SSW+SSB
其中,k为水平数;ni为第i个水平 下的样本容量。可见,组间样本离 差平方和是各水平组均值和总体均 值离差的平方和,反映了控制变量 的影响。
在方差分析中,代表变异大小,并用来进行变异分解的 指标是离均差平方和。总的变异平方和记为SST,被分解为两 项:第一项是各组的离均差平方和之和,代表组内变异(即 随机变量引起的变异),称为组内平方和SSW(Within Groups);第二项是按样本含量大小加权的各组均数与总均 数的差值平方之和,代表组间变异(由控制变量引起的变 异),称为组间平方和或者处理平方和SSB(Between Groups)。
P>.05(接受 虚无假设)
1.判断两个总体的方差是否相同
SPSS采用Levene F方法检验两总体方差 是否相同。
如果“F值”检验不显著(Sig.的值大于.05),表示两个组别群体变异 数相等,此时看“方差齐性相等”所列之t值,看其是否显著。 如果“F值”检验显著(Sig.的值小于.05),表示两个组别群体变异数 不相等,此时看“方差齐性不相等”所列之t值,看其是否显著。
在菜单中选择“One-Way ANOVA”命令
“One-Way ANOVA”对话框
“One-Way ANOVA:Contrasts”对话框
“One-Way ANOVA:Options”对话框
“One-Way ANOVA:Post Hoc Multiple Comparisons”
对话框
结果和讨论
◆注意:方差分析的适用条件 1、样本来自的总体服从正态分布。 2、样本方差必须是齐次的。 3、各样本之间相互独立。
方差分析的类型
单因素方差分析
单因素方差分析是指只单独考虑一个因素A对指标X的影响。 此时其他因素都不变或者控制在一定的范围之内。考虑因素A 有k个水平,在每次水平下做ni次试验。
SPSS中实现过程
分析——比较均值——单因素ANOVA
SPSS中实现过程
研究问题
三组学生的数学成绩
人名 hxh yaju yu shizg hah s watet jess wish
2_new1 2_new2 2_new3 2_new4 2_new5 2_new6 2_new7 2_new8 2_new9
方差分析基本概念
方差分析是R.A.Fister发明的,用于两个及两个以上样 本均数差别的显著性检验。方差分析方法在不同领域的各个 分析研究中都得到了广泛的应用。从方差入手的研究方法有 助于找到事物的内在规律性。
由于各种因素的影响,研究所得的数据呈现波动状而有 所不同。造成波动的原因可分成两类:
一类是不可控的随机因素的影响,这是人为很难控制的 一类影响因素,称为随机变量;
差异分析
1、均值描述—Means过程 2、t检验 3、方差分析
均值描述——Means过程
