高考数学总复习第8章立体几何初步第5课时空间几何体的表面积和体积课时训练(含解析)

合集下载

2020秋新人教版高中数学必修二第八章立体几何初步复习课题型课知识框架思维导图

第八章立体几何初步复习课要点训练一空间几何体的结构特征1.紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.2.通过举反例对结构特征进行辨析,即要说明一个命题是错误的,只要举出一个反例即可.1.设有四个命题:①底面是矩形的平行六面体是长方体;②棱长都相等的直四棱柱是正方体;③侧棱垂直于底面两条边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.其中真命题的个数是()A.1B.2C.3D.4解析:底面是矩形的直平行六面体是长方体,①错误;棱长都相等的直四棱柱是正方体,②正确;侧棱垂直于底面两条相邻边的平行六面体是直平行六面体,③错误;任意侧面上两条对角线相等的平行六面体是直平行六面体,④错误.故命题正确的个数是1.答案:A2.在四棱锥的四个侧面中,直角三角形最多可有()A.1个B.2个C.3个D.4个解析:如图所示,在长方体ABCD-A1B1C1D1中,取四棱锥A1-ABCD,则此四棱锥的四个侧面都是直角三角形.答案:D要点训练二空间几何体的表面积与体积1.空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积问题注意衔接部分的处理.(3)旋转体的表面积问题,应注意其侧面展开图的应用.2.空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体问题是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等进行求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,再根据条件求解.1.已知一个六棱锥的体积为2√3 ,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为12.解析:由题意可知,该六棱锥是正六棱锥.设该六棱锥的高为h ,则13×6×√34×22×h =2√3,解得h =1.由题意,得底面正六边形的中心到其边的距离为√3,所以侧面等腰三角形底边上的高为√(√3)2+1=2,所以该六棱锥的侧面积为6×12×2×2=12. 2.如图所示,三棱锥O -ABC 为长方体的一角,其中OA ,OB ,OC 两两垂直,三个侧面OAB ,OAC ,OBC 的面积分别为1.5 cm 2,1 cm 2,3 cm 2,求三棱锥O -ABC 的体积.解:设OA ,OB ,OC 的长依次为x cm,y cm,z cm,由已知可得12xy =1.5,12xz =1,12yz =3,解得x =1,y =3,z =2. 将三棱锥O -ABC 看成以C 为顶点,以OAB 为底面,易知OC 为三棱锥C -OAB 的高.故V 三棱锥O -ABC =V C -OAB =13S △OAB ·OC =13×1.5×2=1(cm 3). 3.如图所示,已知三棱柱ABC -A'B'C',侧面B'BCC'的面积是S ,点A'到侧面B'BCC'的距离是a ,求三棱柱ABC -A'B'C'的体积.解:连接A'B ,A'C ,如图所示,这样就把三棱柱ABC -A'B'C'分割成了两个棱锥,即三棱锥A'-ABC 和四棱锥A'-BCC'B'.设所求体积为V ,显然三棱锥A'-ABC 的体积是13V. 而四棱锥A'-BCC'B'的体积为13Sa , 故有13V +13Sa =V ,所以V =12Sa. 要点训练三与球有关的切、接问题与球相关问题的解题策略(1)作适当的截面(如轴截面等)时,对于球内接长方体、正方体,则截面一要过球心, 二要过长方体或正方体的两条体对角线,才有利于解题.(2)对于“内切”和“外接”等问题,首先要弄清几何体之间的相互关系,主要是指特殊的点、线、面之间的关系,然后把相关的元素放到这些关系中来解决.1.正四棱锥的顶点都在同一球面上,若该棱锥的高为6,底面边长为4,则该球的表面积为( )A.443πB.4849πC.814πD.16π 解析:如图所示,设PE 为正四棱锥P -ABCD 的高,则正四棱锥P -ABCD 的外接球的球心O 必在其高PE 所在的直线上,延长PE 交球面于一点F ,连接AE ,AF.由球的性质可知△PAF 为直角三角形,且AE ⊥PF.因为该棱锥的高为6,底面边长为4,所以AE =2√2,PE =6,所以侧棱长PA =√PE 2+AE 2=√62+(2√2)2=√44=2√. 设球的半径为R ,则PF =2R. 由△PAE ∽△PFA ,得PA 2=PF ·PE ,即44=2R ×6,解得R =113,所以S =4πR 2=4π×(113)2=484π9.答案:B2.一个球与一个正三棱柱的三个侧面和两个底面都相切,如果这个球的体积是323π,那么这个正三棱柱的体积是( ) A.96√3 B.16√3 C.24√3 D.48√3解析:由球的体积公式可求得球的半径R =2. 设球的外切正三棱柱的底面边长为a ,高即侧棱长,为h ,则h =2R =4. 在底面正三角形中,由正三棱柱的内切球特征,得a 2×√33=R =2,解得a =4√3. 故这个正三棱柱的体积V =12×√32×(4√3)2×4=48√3.答案:D要点训练四空间中的平行关系1.平行问题的转化关系2.直线与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)面与面平行的性质.3.平面与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)推论;(4)a ⊥α,a ⊥β⇒α∥β.1.如图所示,三棱柱ABC -A'B'C'中,M ,N 分别为BB',A'C'的中点.求证:MN ∥平面ABC'.证明:取B'C'的中点P ,连接MP ,NP (图略),则MP ∥BC',NP ∥A'B'. 因为A'B'∥AB ,所以NP ∥AB.因为AB ⊂平面ABC',NP ⊄平面ABC',所以NP ∥平面ABC'.同理MP∥平面ABC'.因为NP∩MP=P,所以平面MNP∥平面ABC'.因为MN⊂平面MNP,所以MN∥平面ABC'.2.两个全等的正方形ABCD和ABEF所在平面相交于AB, M∈AC,N∈FB,且AM=FN,过点M作MH⊥AB于点H.求证:平面MNH∥平面BCE.证明:因为正方形ABCD中,MH⊥AB,BC⊥AB,所以MH∥BC.因为BF=AC,AM=FN,所以FNBF =AM AC.因为MH∥BC,所以AMAC =AH AB,所以FNBF =AH AB,所以NH∥AF∥BE.因为MH⊂平面MNH,NH⊂平面MNH,MH∩NH=H, BC⊂平面BCE,BE⊂平面BCE,BC∩BE=B,所以平面MNH∥平面BCE.要点训练五空间中的垂直关系1.空间中垂直关系的相互转化2.判定线线垂直的方法(1)平面几何中证明线线垂直的方法.(2)线面垂直的性质:a⊥α,b⊂α⇒a⊥b;a⊥α,b∥α⇒a⊥b.3.判定线面垂直的常用方法(1)利用线面垂直的判定定理.(2)利用“两平行线中的一条与平面垂直,则另一条也与这个平面垂直”.(3)利用“一条直线垂直于两平行平面中的一个,则与另一个平面也垂直”.(4)利用面面垂直的性质.4.判定面面垂直的方法(1)利用定义:两个垂直平面相交,所成的二面角是直二面角.(2)判定定理:a⊂α,a⊥β⇒α⊥β.1.如图所示,Rt△AOC可以通过Rt△AOB以直角边AO所在直线为轴旋转得到,且二面角B-AO-C是直二面角,D是AB上任意一点.求证:平面COD⊥平面AOB.证明:由题意,得CO⊥AO,BO⊥AO,所以∠BOC是二面角B-AO-C 的平面角.因为二面角B-AO-C是直二面角,所以∠BOC=90°,所以CO⊥BO.因为AO∩BO=O,所以CO⊥平面AOB.因为CO⊂平面COD,所以平面COD⊥平面AOB.2.如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2, AD=CD=√7,PA=√3,∠ABC=120°,G为线段PC上的点,O为AC,BD交点.(1)证明:BD⊥平面APC;(2)若G满足PC⊥平面BGD,求PG的值.GC(1)证明:由AB=BC,AD=CD,得BD垂直平分线段AC.所以O为AC的中点,BD⊥AC.因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD.因为AC∩PA=A,AC⊂平面APC,PA⊂平面APC,所以BD⊥平面APC.(2)解:连接OG,如图所示.因为PC⊥平面BGD,OG⊂平面BGD,所以PC⊥OG.在△ABC中,由余弦定理,得AC=√22+22-2×2×2×cos120°=2√3.在Rt△PAC中,得PC=√AC2+PA2=√12+3=√所以由△GOC∽△APC可得GC=AC·OCPC =2√155.从而PG=3√155,所以PGGC=32.要点训练六空间角的求解方法1.找异面直线所成角的三种方法(1)利用图中已有的平行线平移.(2)利用特殊点(线段的端点或中点)作平行线平移.(3)补形平移.2.线面角求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足.通常是解由斜线段、垂线段、斜线在平面内的射影所组成的直角三角形.3.求二面角的两种常用方法(1)定义法:在二面角的棱上找一个特殊点,在两个半平面内分别过该点作垂直于棱的射线.(2)垂面法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.1.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°, AB≠AC,D,E分别是BC,AB的中点,AC>AD,设PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是α<β<γ.解析:因为D,E分别是BC,AB的中点,所以DE∥AC,所以PC与DE所成的角为∠PCA,即α.因为PA⊥平面ABC,所以PD与平面ABC所成的角为∠PDA,即β.如图所示,过点A作AH⊥BC,垂足为H,连接PH,易证BC⊥平面PAH,所以∠PHA是二面角P-BC-A的平面角,即γ.因为AB≠AC,所以AD>AH.因为AC >AD,所以AC >AD >AH,所以PAAC <PAAD<PAAH,所以tan α<tan β<tan γ,所以α<β<γ.2.如图所示,AB是☉O的一条直径,PA垂直于☉O所在的平面,C 是圆周上不同于A, B的一动点.(1)证明:△P BC是直角三角形;(2)若PA=AB=2,且当直线PC与平面ABC所成角的正切值为√2时,求直线AB与平面PBC所成角的正弦值.(1)证明:因为AB是☉O的一条直径, C是圆周上不同于A,B的一动点,所以BC⊥AC.因为PA⊥平面ABC,所以BC⊥PA.因为PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC,所以BC⊥PC,所以△BPC是直角三角形.(2)解:如图所示,过点A作AH⊥PC于点H,连接BH.因为BC⊥平面PAC,所以BC⊥AH.因为PC∩BC=C,PC⊂平面PBC,BC⊂平面PBC,所以AH⊥平面PBC,所以∠ABH是直线AB与平面PBC所成的角.因为PA⊥平面ABC,所以∠PCA即是PC与平面ABC所成的角.因为tan∠PCA=PAAC=√2,PA=2, 所以AC=√2.在Rt△PAC中,AH=√PA2+AC2=23√3,在Rt△ABH中,sin∠ABH=23√32=√33,即AB与平面PBC所成角的正弦值为√33.要点训练七转化思想转化思想是指在解决数学问题时,一个数学对象在一定条件下转化为另一种数学对象的思想.它包括从未知到已知的转化,从一般到特殊的转化等,折叠问题中体现了转化思想.解决折叠问题的关键在于认真分析折叠前后元素的位置变化情况,看看哪些元素的位置变了,哪些元素的位置没有变,基本思路是利用“不变求变”,一般步骤如下:(1)平面→空间:根据平面图形折出满足条件的空间图形,想象出空间图形,完成平面图形与空间图形在认识上的转化.(2)空间→平面:为解决空间图形问题,要回到平面上来,重点分析元素的变与不变.1.如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.若将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列结论正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析:因为在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°, ∠BAD=90°,所以BD⊥CD.因为平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,所以CD⊥平面ABD,所以CD⊥AB.因为AD⊥AB,AD∩CD=D,AD⊂平面ADC,CD⊂平面ADC,故AB⊥平面ADC.因为AB⊂平面ABC,所以平面ABC⊥平面ADC.答案:D2.如图所示,在矩形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,垂足为K.设AK=t,则t的取值范围是(1,1).2→解析:如图所示,过点K作KM⊥AF于M点,连接DM,易得DM⊥AF,与折前的图形对比,可知在折前的图形中D,M,K三点共线,且DK⊥AF, 于是△DAK∽△FDA,所以AKAD =ADDF.所以t1=1DF.所以t=1DF.因为DF∈(1,2),所以t∈( 12,1).3.如图①所示,在等腰梯形CDEF中,DE=CD=√2,EF=2+√2,将它沿着两条高AD,CB折叠成四棱锥E-ABCD(E,F两点重合),如图②所示.①②(1)求证:BE⊥DE;(2)设M为线段AB的中点,试在线段CE上确定一点N,使得MN∥平面DAE.(1)证明:因为AD⊥EF,所以AD⊥AE,AD⊥AB.因为AB∩AE=A,AB⊂平面ABE,AE⊂平面ABE,所以AD⊥平面ABE,所以AD⊥BE.由题图①和题中所给条件知,AE=BE=1,AB=CD=√2,所以AE2+BE2=AB2,即AE⊥BE.因为AE∩AD=A,AE⊂平面ADE,AD⊂平面ADE,所以BE⊥平面ADE,所以BE⊥DE.(2)解:如图所示,取EC的中点G,BE的中点P,连接PM,PG,MG, 则MP∥AE,GP∥CB∥DA,所以MP∥平面DAE,GP∥平面DAE.因为MP∩GP=P,所以平面MPG∥平面DAE.因为MG⊂平面MPG,所以MG∥平面DAE,即存在点N与G重合满足条件,使得MN∥平面DAE.。

2015届高考数学总复习第八章立体几何初步第5课时空间几何体的表面积和体积教学案(含最新模拟、试题改编)

第八章立体几何初步第5课时空间几何体的表面积和体积⎝ ⎛⎭⎪⎫对应学生用书（文）108～110页（理）110～112页考情分析考点新知了解柱、锥、台、球的表面积和体积计算公式，会求一些简单几何体的表面积和体积，体会积分思想在计算表面积、体积中的运用． ① 了解柱、锥、台、球的表面积和体积计算公式(不要求记忆公式). ② 会求直棱柱、正棱锥、正棱台、圆柱、圆锥、圆台和球的表面积和体积.1. (必修2P 69习题10改编)用长、宽分别是3π与π的矩形硬纸卷成圆柱的侧面，则圆柱的底面面积为________．答案：94π或14π解析：有两种情况：以3π为圆柱的高时，圆柱底面积为14π，以π为圆柱的高时，圆柱底面积为94π.2. (原创)若等腰直角三角形的直角边长为2，则以一直角边所在的直线为轴旋转一周所成的几何体体积是__________.答案：83π解析：几何体为圆锥，圆锥的底面半径为2，高也为2，体积V ＝13×π×4×2＝83π.3. (2013·南京二模)已知圆锥的侧面展开图是一个半径为3 cm ，圆心角为2π3的扇形，则此圆锥的高为________cm.答案：22解析：设圆锥的底面半径为r ，则2πr ＝2π3×3，所以r ＝1，此圆锥的高为32－12＝2 2.4. (必修2P 55练习4改编)已知正方形ABCD 的边长为2，E 、F 分别为BC 、DC 的中点，沿AE 、EF 、AF 折成一个四面体，使B 、C 、D 三点重合，则这个四面体的体积为________．答案：13解析：折成的四面体为三棱锥AECF ，S △ECF ＝12×1×1＝12，高为AB ＝2，所以这个四面体的体积为V ＝13S △ECF ·AB ＝13×12×2＝13.5. (必修2P 69复习题5改编)若长方体三个面的面积分别为2，3，6，则此长方体的外接球的表面积是________．答案：6π解析：设长方体的过同一顶点的三条棱长分别为a 、b 、c ，则⎩⎨⎧ab ＝2，ac ＝3，bc ＝ 6.解得⎩⎨⎧a ＝1，b ＝2，c ＝ 3.长方体外接球半径为R ＝1212＋（2）2＋（3）2＝62，外接球的表面积为S ＝4π⎝⎛⎭⎫622＝6π.1. 侧棱与底面垂直的棱柱叫做直棱柱，直棱柱的侧面积公式是S 直棱柱侧＝ch ，底面是正多边形的直棱柱叫做正棱柱．柱体的体积公式是V 柱体＝Sh ．2. 如果一个棱锥的底面是正多边形，并且顶点在底面的正投影是底面的中心，该棱锥为正棱锥．正棱锥的侧面积公式是S 正棱锥侧＝12ch ′；锥体的体积为V 锥体＝13Sh ．3. 正棱锥被平行于底面的平面所截，截面和底之间的部分叫做正棱台，其侧面积公式是S 正棱台侧＝12(c ＋c′)·h′；台体的体积公式是34. 圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环；圆柱的侧面积公式是S 圆柱侧＝cl ＝2πr ，圆锥的侧面积公式为S 圆锥侧＝12cl ＝πrl ，圆台的侧面积公式为S 圆台侧＝12(c ＋c′)l ＝π(r ＋r′)l ．5. 球体的体积公式是V 球＝43πR 3，其中R 为球的半径．[备课札记]题型1 与几何体的表面积有关的问题例1如图所示，正方体ABCDA 1B 1C 1D 1的棱长为6，则以正方体ABCDA 1B 1C 1D 1的中心为顶点，以平面AB 1D 1截正方体外接球所得的圆为底面的圆锥的全面积为________．答案：(182＋24)π解析：设O 为正方体外接球的球心，则O 也是正方体的中心，O 到平面AB 1D 1的距离是体对角线长的16，即为 3.又球的半径是正方体对角线长的一半，即为33，由勾股定理可知，截面圆的半径为（33）2－（3）2＝26，圆锥底面面积为S 1＝π·(26)2＝24π，圆锥的母线即为球的半径33，圆锥的侧面积为S 2＝π×26×33＝182π.因此圆锥的全面积为S ＝S 2＋S 1＝182π＋24π＝(182＋24)π.备选变式（教师专享）如图，在球面上有四个点P 、A 、B 、C ，如果PA 、PB 、PC 两两互相垂直，且PA ＝PB ＝PC ＝a ，求这个球的表面积．解：如题图，设过A 、B 、C 三点的球的截面圆半径为r ，圆心为O′，球心到该圆面的距离为d ，在三棱锥PABC 中，∵PA 、PB 、PC 两两垂直，PA ＝PB ＝PC ＝a ， ∴AB ＝AC ＝BC ＝2a ，且点P 在△ABC 内的射影是△ABC 的中心O′，由正弦定理，得2a sin60° ＝2r ，∴r ＝63a.又根据球的截面圆性质，有OO′⊥平面ABC ，而PO′⊥平面ABC ，∴P 、O 、O′三点共线，球的半径R ＝r 2＋d 2.又PO′＝PA 2－r 2＝a 2－23a 2＝33a ，∴OO ′＝R －33a ＝d ＝R 2－r 2，∴⎝⎛⎭⎫R －33a 2＝R 2－⎝⎛⎭⎫63a 2，解得R ＝32a.∴S 球＝4πR 2＝3πa 2.题型2 与几何体体积有关的问题例2 如图①所示，在Rt △ABC 中，AC ＝6，BC ＝3，∠ABC ＝90°，CD 为∠ACB 的平分线，点E 在线段AC 上，CE ＝4.如图②所示，将△BCD 沿CD 折起，使得平面BCD ⊥平面ACD ，连结AB ，设点F 是AB 的中点．(1) 求证：DE ⊥平面BCD ；(2) 若EF ∥平面BDG ，其中G 为直线AC 与平面BDG 的交点，求三棱锥B-DEG 的体积．图①图②(1) 证明：在题图①中，∵ AC ＝6，BC ＝3，∠ABC ＝90°，∴ ∠ACB ＝60°. ∵ CD 为∠ACB 的平分线，∴ ∠BCD ＝∠ACD ＝30°.∴ CD ＝2 3. ∵ CE ＝4，∠DCE ＝30°，∴ DE ＝2.则CD 2＋DE 2＝EC 2.∴ ∠CDE ＝90°.DE ⊥DC. 在题图②中，∵ 平面BCD ⊥平面ACD ，平面BCD ∩平面ACD ＝CD ，DE 平面ACD ，∴ DE ⊥平面BCD.(2) 解：在题图②中，∵ EF ∥平面BDG ，EF Ì平面ABC ，平面ABC ∩平面BDG＝BG ，∴ EF ∥BG .∵ 点E 在线段AC 上，CE ＝4，点F 是AB 的中点， ∴ AE ＝EG ＝CG ＝2.作BH ⊥CD 交于H.∵ 平面BCD ⊥平面ACD ，∴ BH ⊥平面ACD.由条件得BH ＝32.S △DEG ＝13S △ACD ＝13×12AC ·CD ·sin30°＝ 3.三棱锥B-DEG 的体积V ＝13S △DEG ·BH ＝13×3×32＝32.变式训练在△ABC 中，∠BAC ＝90°，∠B ＝60°，AB ＝1，D 为线段BC 的中点，E 、F 为线段AC 的三等分点(如图①)．将△ABD 沿着AD 折起到△AB′D 的位置，连结B′C (如图②)．(1) 若平面AB′D ⊥平面ADC ，求三棱锥B′-ADC 的体积；(2) 记线段B′C 的中点为H ，平面B′ED 与平面HFD 的交线为l ，求证：HF ∥l ； (3) 求证：AD ⊥B′E.图①图②(1) 解：在直角△ABC 中，D 为BC 的中点，所以AD ＝BD ＝CD.又∠B ＝60°，所以△ABD 是等边三角形．取AD 中点O ，连结B′O ，所以B′O ⊥AD.因为平面AB′D ⊥平面ADC ，平面AB′D ∩平面ADC ＝AD ，B′O 平面AB′D ，所以B′O ⊥平面ADC.在△ABC 中，∠BAC＝90°，∠B ＝60°，AB ＝1，D 为BC 的中点，所以AC ＝3，B ′O ＝32.所以S △ADC ＝12×12×1×3＝34.所以三棱锥B′ADC 的体积为V ＝13×S △ADC ×B ′O ＝18. (2) 证明：因为H 为B′C 的中点，F 为CE 的中点，所以HF ∥B′E.又HF 平面B′ED ，B ′E 平面B ′ED ，所以HF ∥平面B′ED.因为HF Ì平面HFD ，平面B′ED ∩平面HFD ＝l ，所以HF ∥l.(3) 证明：连结EO ，由(1)知，B ′O ⊥AD.因为AE ＝33，AO ＝12，∠DAC ＝30°，所以EO ＝AE 2＋AO 2－2AE·AOcos30°＝36.所以AO 2＋EO 2＝AE 2.所以AD ⊥EO.又B′O Ì平面B′EO ，EO Ì平面B′EO ，B ′O ∩EO ＝O ，所以AD ⊥平面B′EO.又B′E Ì平面B′EO ，所以AD ⊥B′E. 题型3 简单几何体的综合应用例3 (2013·徐州调研)在边长为a 的正三角形铁皮的三个角切去三个全等的四边形，再把它的边沿虚线折起(如图)，做成一个无盖的正三角形底铁皮箱，当箱底边长为多少时，箱子容积最大？最大容积是多少？解：设箱底边长为x ，则箱高为h ＝33×a －x 2(0<x<a)，箱子的容积为V(x)＝12x 2×sin60°×h ＝18ax 2－18x 3(0<x<a)．由V′(x)＝14ax －38x 2＝0，解得x 1＝0(舍)，x 2＝23a ，且当x ∈⎝⎛⎭⎫0，23a 时，V ′(x)>0；当x ∈⎝⎛⎭⎫23a ，a 时，V ′(x)<0，所以函数V(x)在x ＝23a 处取得极大值，这个极大值就是函数V(x)的最大值： V ⎝⎛⎭⎫23a ＝18a ×⎝⎛⎭⎫23a 2－18×⎝⎛⎭⎫23a 3＝154a 3.答：当箱子底边长为23a 时，箱子容积最大，最大值为154a 3.备选变式（教师专享）四面体的六条棱中，有五条棱长都等于a. (1) 求该四面体的体积的最大值；(2) 当四面体的体积最大时，求其表面积．解： (1) 如图，在四面体ABCD 中，设AB ＝BC ＝CD ＝AC ＝BD ＝a ，AD ＝x ，取AD 的中点为P ，BC 的中点为E ，连结BP 、EP 、CP.得到AD ⊥平面BPC ，∴ V A －BCD ＝V A －BPC ＋V D －BPC ＝13·S △BPC ·AP ＋13S △BPC ·PD ＝13·S △BPC ·AD ＝13·12·aa 2－x 24－a24·x＝a 12（3a 2－x 2）x 2≤a 12·3a 22＝18a 3(当且仅当x ＝62a 时取等号)． ∴ 该四面体的体积的最大值为18a 3.(2) 由(1)知，△ABC 和△BCD 都是边长为a 的正三角形，△ABD 和△ACD 是全等的等腰三角形，其腰长为a ，底边长为62a ，∴ S 表＝2×34a 2＋2×12×62a ×a 2－⎝⎛⎭⎫64a 2＝32a 2＋62a ×10a 4＝32a 2＋15a 24＝23＋154a 2.【示例】 (本题模拟高考评分标准，满分14分)如图，底面边长为a ，高为h 的正三棱柱ABC-A 1B 1C 1，其中D 是AB 的中点，E 是BC 的三等分点．求几何体BDEA 1B 1C 1的体积．学生错解：解 ∵ BD ＝a 2，BE ＝a3，∠DBE ＝60°，∴ S △DBE ＝12BD ·BEsin ∠DBE ＝324a 2，S △A 1B 1C 1＝12·A 1B 1·B 1C 1sin60°＝34a 2.由棱台体积公式得VBDEA 1B 1C 1＝13h(S △BDE ＋S △A 1B 1C 1＋S △BDE ·S △A 1B 1C 1)＝13h ⎝ ⎛⎭⎪⎫324a 2＋34a 2＋324a 2·34a 2 ＝73＋3272a 2h.审题引导： (1) 弄清组合体的结构，这里几何体DBEA 1B 1C 1不是棱台，也可补上一个三棱锥使之成为一个三棱台；(2) 运用体积公式进行计算．规范解答：解：如图，取BC 中点F ，连结DF 、C 1D 、C 1E 、C 1F ，得正三棱台DBFA 1B 1C 1及三棱锥C 1DEF.∵S △A 1B 1C 1＝34a 2，S △DBF ＝14S △ABC ＝316a 2，(4分)∴VDBFA 1B 1C 1＝13h(S △DBF ＋S △A 1B 1C 1＋S △DBF ·S △A 1B 1C 1)＝13h(34a 2＋316a 2＋34a 2·316a 2)＝7348a 2h.(8分) ∴ VC 1DEF ＝13h ·112·34a 2＝3144a 2h ，(10分)∴ VBDEA 1B 1C 1＝VDBFA 1B 1C 1VC 1DEF ＝7348a 2h －3144a 2h ＝5338a 2h.(14分)错因分析：没有弄清所给几何体的结构，几何体DBEA 1B 1C 1不是棱台．1. (2013·南京调研)如图，已知正三棱柱ABCA 1B 1C 1的底面边长为2 cm ，高为5 cm ，则一质点自点A 出发，沿着三棱柱的侧面绕行两周到达点A 1的最短路线的长为________cm.答案：13解析：根据题意，利用分割法将原三棱柱分割为两个相同的三棱柱，然后将其展开为如图所示的实线部分，则可知所求最短路线的长为52＋122＝13(cm)．2. 一个圆锥的侧面展开图是圆心角为43π，半径为18 cm 的扇形，则圆锥母线与底面所成角的余弦值为________．答案：23解析：设母线长为l ，底面半径为r ，则依题意易知l ＝18 cm ，由αl ＝2πr ，代入数据即可得43π×18＝2πr ，解得r ＝12 cm ，因此所求角的余弦值即为r l ＝1218＝23.3. (2013·济南模拟改)如图所示，在正三棱锥S-ABC 中，M 、N 分别是SC 、BC 的中点，且MN ⊥AM ，若侧棱SA ＝23，则正三棱锥SABC 外接球的表面积是________．答案：36π解析：在正三棱锥S-ABC 中，易证SB ⊥AC ，又MN ∥12BS ，∴ MN ⊥AC.∵ MN ⊥AM ，∴ MN ⊥平面ACM.∴ MN ⊥SC ，∴ ∠CSB ＝∠CMN ＝90°，即侧面为直角三角形，底面边长为2 6.此棱锥的高为2，设外接球半径为R ，则(2－R)2＋⎝⎛⎭⎫26×32×232＝R 2，∴ R ＝3，∴ 外接球的表面积是36π.4. 我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水．天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸．若盆中积水深九寸，则平地降雨量是________寸．(注：① 平地降雨量等于盆中积水体积除以盆口面积；② 一尺等于十寸)答案：3解析：本题考查圆台的体积公式．做出圆台的轴截面如图，由题意知，BF ＝14(单位寸，下同)，OC ＝6，OF ＝18，OG ＝9，即G 是OF 中点，所以GE 为梯形的中位线，所以GE ＝14＋62＝10，即积水的上底面半径为10.所以盆中积水的体积为13(100π＋36π＋100π×36π)＝588π.盆口的面积为142π＝196π，所以588π196π＝3，即平地降雨量是3寸．5. 如图，四棱锥P-ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，点E 在线段AD 上，且CE ∥AB. (1) 求证：CE ⊥平面PAD ；(2) 若PA ＝AB ＝1，AD ＝3，CD ＝2，∠CDA ＝45°，求四棱锥P-ABCD 的体积． (1) 证明：因为PA ⊥平面ABCD ，CE 平面ABCD ，所以PA ⊥CE. 因为AB ⊥AD ，CE ∥AB ，所以CE ⊥AD. 又PA ∩AD ＝A ，所以CE ⊥平面PAD.(2) 解：由(1)可知CE ⊥AD.在Rt △ECD 中，DE ＝CD·cos45°＝1，CE ＝CD·sin45°＝1.因为AB ＝CE ＝1，AB ∥CE ，所以四边形ABCE 为矩形．所以S ABCD ＝S ABCE ＋S △ECD ＝AB·AE ＋12CE ·DE ＝1×2＋12×1×1＝52.又PA ⊥平面ABCD ，PA ＝1，所以V P-ABCD ＝13S ABCD ·PA ＝13×52×1＝56.1. (2013·福州模拟)如图所示，已知三棱柱ABC －A 1B 1C 1的所有棱长均为1，且AA 1⊥底面ABC ，则三棱锥B 1－ABC 1的体积为________．答案：312解析：三棱锥B 1－ABC 1的体积等于三棱锥A －B 1BC 1的体积，三棱锥A －B 1BC 1的高为32，底面积为12，故其体积为13×12×32＝312. 2. 一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积是323π，那么这个三棱柱的体积是________．答案：483解析：因为球的体积为323π，柱体的高为2r ＝4，又正三棱柱的底面三角形内切圆半径与球半径相等，r ＝2，所以底面边长a ＝43，所以V 柱＝34×(43)2×4＝48 3.3. (2013·杭州模拟)如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积．解：由已知得CE ＝2，DE ＝2，CB ＝5，S 表面＝S 圆台侧＋S 圆台下底＋S 圆锥侧＝π(2＋5)×5＋π×25＋π×2×22＝(60＋42)π，V＝V 圆台－V 圆锥＝13(π·22＋π·52＋22·52π2)×4－13π×22×2＝1483π.4. 如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，再用S 平方米塑料片制成圆柱的侧面和下底面(不安装上底面)．当圆柱底面半径r 取何值时，S 取得最大值？并求出该最大值(结果精确到0.01平方米)．解：由题意可知矩形的高即圆柱的母线长为9.6－8×2r8＝1.2－2r ，∴ 塑料片面积S ＝πr 2＋2πr(1.2－2r)＝πr 2＋2.4πr －4πr 2＝－3πr 2＋2.4πr ＝－3π(r 2－0.8r)＝－3π(r －0.4)2＋0.48π.∴ 当r ＝0.4时，S 有最大值0.48π，约为1.51平方米．1. 几何体体积的求法：(1) 若所给几何体为柱、锥、台、球等简单几何体，可直接套用公式计算求解；(2) 若所给几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．熟练掌握柱、锥、台、球等各种简单几何体的结构特征，弄清组合体的结构十分必要．2. 求几何体表面上两点间的最短距离的常用方法：选择恰当的棱或母线将几何体展开，转化为求平面上两点间的最短距离．请使用课时训练(B)第5课时(见活页)．[备课札记]。

二、空间几何体的表面积与体积复习课件

考点探究 • 挑战高考
答案： 3
考向瞭望 • 把脉高考
第8章立体几何
双基研习 • 面对高考
5．(2009年高考上海卷)若等腰直角三角形的直角边长为2，则以一直角边所在的直线为轴旋转一周所成的几何体体积是________．
8π 答案： 3
考点探究 • 挑战高考
考点探究 • 挑战高考
考向瞭望 • 把脉高考
第8章立体几何
双基研习 • 面对高考
2 ∴AP＝AB＝ 2，EG＝ . 2 1 ∴S△ABC＝ AB· BC 2 1 ＝ × 2×2＝ 2， 2 1 ∴VEABC＝ S△ ABC· EG 3 1 2 1 ＝ × 2× ＝ . 3 2 3
考向瞭望 • 把脉高考
第8章立体几何
双基研习 • 面对高考
解：如图所示，只有当圆柱的底面圆为直三棱柱的底面三角形的内切圆时，圆柱的体积最大，削去部分体积才能最小，设此时圆柱的底面半径为R，圆柱的高即为直三棱柱的高．
考点探究 • 挑战高考
考向瞭望 • 把脉高考
考向瞭望 • 把脉高考
第8章立体几何
考点探究•挑战高考
考点突破几何体的表面积求解有关多面体表面积的问题，关键是找到其特征几何图形，如棱柱中的矩形，棱台中的直角梯形，棱锥中的直角三角形，它们是联系高与斜高、边长等几何元素间的桥梁，从而架起求侧面积公式中的未知量与条件中已知几何元素间的联系；求球的表面积关键是求其半径；旋转体的侧面积就是它们侧面展开图的面积．
双基研习 • 面对高考
考点探究 • 挑战高考

第8章+立体几何初步知识点汇总

《人教A版必修二知识点汇总》第8章《立体几何初步》知识点汇总8.1 基本立体图形1.空间几何体、多面体、旋转体的定义（1）空间几何体的定义空间中的物体都占据着空间的一部分，如果只考虑这些物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体.（2）多面体的概念像纸箱、金字塔这样，由若干个平面多边形围成的几何体叫做多面体.①面：围成多面体的各个多边形叫做多面体的面.如图，有面ABE, 面BCE，面ABF等.②棱：两个面的公共边叫做多面体的棱；如图，有棱BE，棱CE，棱DE等.③顶点：棱与棱的公共点叫做多面体的顶点.如图，有顶点A,顶点B,顶点C等.（3）旋转体的概念像奶粉罐、篮球和足球这样，一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面，封闭的旋转面围成的几何体叫做旋转体，这条定直线叫做旋转体的轴 .如图：圆柱体就是由矩形OAA1O1绕轴OO1旋转而成.（4）小结2.特殊的多面体（1）棱柱①棱柱的概念与结构特征如图，一般地，有两个面互相平行，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱.Ⅰ.底面(底)：两个互相平行的面叫做棱柱的底面，它们是全等的多边形.Ⅱ.侧面：其余各面叫做棱柱的侧面，它们都是平行四边形.Ⅲ.侧棱：相邻侧面的公共边叫做棱柱的侧棱，它们都是相互平行且相等的线段.Ⅳ.顶点：侧面与底面的公共顶点叫做棱柱的顶点.温馨提示A.两个底面与平行于底面的截面是全等的多边形，如图（a）所示;B.过不相邻的两条侧棱的截面是平行四边形，如图(b)所示;C.有两个面平行，其余各面都是平行四边形的几何体不一定是棱柱，如图(c)所示.②棱柱的表示与分类棱柱用表示底面各顶点的字母来表示，棱柱的底面可以是三角形、四边形、五边形……，我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……例如，右图中的棱柱分别表示为三棱柱ABC−A1B1C1,四棱柱ABCD−A1B1C1D1,五棱柱ABCDE−A1B1C1D1E1.③几种特殊的棱柱Ⅰ.直棱柱：一般地，我们把侧棱垂直于底面的棱柱叫做直棱柱.如右图中直四棱柱ABCD−A1B1C1D1.Ⅱ.斜棱柱：侧棱不垂直于底面的棱柱叫做斜棱柱.如右图中斜三棱柱ABC−A1B1C1.Ⅲ.正棱柱：底面是正多边形的直棱柱叫做正棱柱.如右图中五棱柱ABCDE−A1B1C1D1E1.Ⅳ.平行六面体：底面是平行四边形的四棱柱也叫做平行六面体.如右图中平行六面体ABCD−A1B1C1D1.（2）棱锥①棱锥的概念与结构特征有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥.Ⅰ.底面：这个多边形面叫做棱锥的底面；Ⅱ.侧面：有公共顶点的各个三角形面叫做棱锥的侧面；Ⅲ.侧棱：相邻侧面的公共边叫做棱锥的侧棱；Ⅳ.顶点：各侧面的公共顶点叫做棱锥的顶点.温馨提示：对于棱锥要注意，有一个面是多边形，其余各面都是三角形的几何体不一定是棱锥，如图所示，必须强调其余各面是具有公共顶点的三角形.②棱锥的表示与分类棱锥用表示顶点和底面各顶点的字母来表示，棱锥的底面可以是三角形、四边形、五边形……，我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱锥……注：其中三棱锥又叫四面体.例如，右图中的棱锥分别表示为三棱锥(四面体)O−ABC,四棱锥O−ABCD,五棱锥O−ABCDE.③特殊的棱锥——正棱锥底面是正多边形，并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.（3）棱台①棱台的概念与结构特征用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的那部分多面体叫做棱台.Ⅰ.上（下）底面：在棱台中，原棱锥的底面和截面分别叫做棱台的下底面和上底面，且上下底面是相似图形.Ⅱ.侧面：其余各个梯形面叫做棱台的侧面；Ⅲ.侧棱：相邻侧面的公共边叫做棱台的侧棱；Ⅳ.顶点：侧面与底面的公共顶点叫做棱台的顶点.温馨提示：棱台中各侧棱延长后必相交于一点，否则不是棱台.②棱台的表示与分类棱台用表示底面各顶点的字母来表示，由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……例如，右图中的棱台分别表示为三棱台ABC−A1B1C1,四棱台ABCD−A1B1C1D1,五棱锥ABCDE−A1B1C1D1E1.3.特殊的旋转体（1）圆柱以矩形的一边所在直线为旋转轴，其余三边旋转一周形成的面所围成的旋转体叫做圆柱.①轴：旋转轴叫做圆柱的轴；②底面：垂直于轴的边旋转而成的圆面叫做圆柱的底面；③侧面：平行于轴的边旋转而成的曲面叫做圆柱的侧面；④母线：无论旋转到什么位置，平行于轴的边都叫做圆柱的母线.注：圆柱用表示它的轴的字母表示，如图中的圆柱记作圆柱O1O.（2）圆锥以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体叫做圆锥.①轴：旋转轴叫做圆锥的轴；②底面：垂直于轴的边旋转而成的圆面叫做圆锥的底面；③侧面：直角三角形的斜边旋转而成的曲面叫做圆锥的侧面；④母线：无论旋转到什么位置，不垂直于轴的边都叫做圆锥的母线.注：圆锥用表示它的轴的字母表示，如图中的圆锥记作圆锥SO.（3）圆台用平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做圆台.①轴：旋转轴叫做圆台的轴；②底面：垂直于轴的边旋转而成的圆面叫做圆台的底面；③侧面：不垂直于轴的边旋转一周所形成的曲面叫做圆台的侧面；④母线：无论旋转到什么位置，不垂直于轴的边都叫做圆台的母线.注：圆台用表示它的轴的字母表示，如图中的圆台记作圆台O1O.（4）球半圆以它的直径所在直线为旋转轴，旋转一周形成的曲面叫做球面，球面所围成的旋转体叫做球体，简称球 .①球心：半圆的圆心叫做球的球心；②半径：连接球心和球面上任意一点的线段叫做球的半径；③直径：连接球面上两点并经过球心的线段叫做球的直径；注：球常用表示球心的字母表示，如图中的球记作球O.4.简单组合体（1）定义：由简单几何体组合而成的几何体叫做简单组合体.（2）构成形式①一种是由简单几何体拼接而成的，如图1；②另一种是由简单几何体截去或挖去一部分而成的，如图2.8.2 立体图形的直观图二.知识清单（导学、自学）1.直观图的概念像上面这样，把空间图形(平面图形和立体图形的统称)画在平面内，使其既富有立体感，又能表达出主要部分的位置关系和度量关系的图形叫做直观图.2.用斜二测画法画水平放置平面图形的直观图（1）建系在已知图形中取互相垂直的 x 轴和 y 轴，两轴相交于点O.画直观图时，把它们画成对应的x′轴与y′轴，两轴相交于点 O′ ，且使∠x′O′ y′=45°或135°，它们确定的平面表示水平面.（2）划线（平行不变）已知图形中平行于 x 轴和 y 轴的线段，在直观图中分别画成平行于x′轴与y′轴的线段.3.取长度(与 x 轴平行长度不变，与y轴平行长度取半)已知图形中平行于 x 轴的线段，在直观图中保持原长度不变；平行于 y轴的线段，在直观图中长度为原来的一半.温馨提示画平面图形的直观图时，除多边形外，还经常会遇到画圆的直观图的问题，生活的经验告诉我们，水平放置的圆看起来非常像椭圆，因此我们一般用椭圆作为圆的直观图.2.用斜二测画法画空间几何体的直观图（1）探究用斜二测画法画长、宽、高分别为4 cm，2 cm，2 cm的长方体ABCD－A′ B′ C′ D′的直观图.解画法步骤如下①画轴：如图（1）画 x 轴，y 轴， z 轴，三轴相交于点O，使∠xOy=45°，∠xOz=90°.②画底面:如图（2），在 x 轴正半轴上取线段AB，使AB=4cm；在y 轴正半轴上取线段AD，使AD=1cm；过点B作y轴的平行线，过点D作x轴的平行线，设它们的交点为C，则平行四边形ABCD就是长方体的底面ABCD的直观图.③画侧棱:在z轴正半轴上取线段AA′，使AA=2cm，过B，C，D各点分别作的z轴的平行线，在这些平行线上分别截取2 cm长的线段 BB′，CC′，DD′.④连线成图：顺次连接A′ ，B′ ，C′ ，D′，并加以整理(去掉辅助线，将被遮挡的部分改为虚线)，就得到长方体的直观图.（2）用斜二测画法画空间几何体的直观图的步骤①画轴：画 x 轴，y 轴， z 轴，三轴相交于点O，使∠xOy=45°或135°，∠xOz＝90°.②画底面：按照平面图形的画法，，在平面xOy画底面的直观图.③画侧棱：已知图形中平行于z轴(或在z轴上)的线段，在其直观图中平行性和长度都不变.④连线成图：去掉辅助线，将被遮挡的部分改为虚线.温馨提示画空间几何体的直观图时，需特别注意实虚线的应用，被遮住的线必须用虚线，体现层次性和立体感.4.用斜二测画法画圆锥、球的直观图（1）圆锥体的直观图对于圆锥的直观图，一般先画圆锥的底面，再借助于圆锥的轴确定圆锥的顶点，最后画出两侧的两条母线，如图所示.（2）球的直观图画球的直观图，一般需要画出球的轮廓线，它是一个圆，同时还经常画出经过球心的截面圆，它们的直观图是椭圆，用以衬托球的立体性，如图所示.8.3.1 棱柱、棱锥、棱台的表面积和体积1.复习导入——正方体、长方体的体积公式及其表面积公式（1）正方体体积公式及其表面积公式设正方体ABCD－A′B′C′D′的棱长为a(a>0),那么S正方体=6×一个面的面积=6a2.V正方体=底面积×高=棱长×棱长×棱长=a3.（2）长方体体积公式及其表面积公式设长方体ABCD－A′B′C′D′的长、宽、高分别为 a,b ,c(a,b,c>0),那么S长方体=(S底+S正+S右)×2=2(ab+ac+bc).V长方体=底面积×高=长×宽×高=abc.2.多面体的表面积由刷漆原理可知：(1)多面体的表面积就是围成多面体各个面的面积的和.(2)棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.3.棱柱、棱锥、棱台的体积（1）棱柱的体积由堆积原理可知：一般地，如果棱柱的底面积是S，高是ℎ，那么这个棱柱的体积为V棱柱=底面积×高=Sh简述为：“棱柱的体积等于它底面积与高的乘积 . ”注：棱柱的高是指两底面之间的距离，即从一底面上任意一点向另一个底面作垂线，这点与垂足(垂线与底面的交点)之间的距离.（2）棱锥的体积由灌注原理可知：一般地，如果棱锥的底面积是S，高是ℎ，那么这个棱锥的体积为V棱锥=13V棱柱=13Sh简述为：“棱锥的体积等于与它等底等高棱柱体积的13”注：棱锥的高是指从顶点向底面作垂线，顶点与垂足之间的距离. （4）棱台的体积由截去原理可知：一般地，棱台的体积公式为V棱台=13h(S+√SS′+S′)其中S′与S分别为棱台的棱台的上、下底面面积，ℎ为棱台的高.简述为：“棱台的体积等于上下底面的面积与它们的几何平均数之和，再乘以棱台高的乘积的13.”注：棱台的高是指两底面之间的距离，即从上底面上任意一点向下底面作垂线，这点与垂足之间的距离.（4）棱柱、棱锥、棱台的体积之间的关系①当S′=S时，棱台变为棱柱，棱台的体积公式也就是棱柱的体积公式;②当 S′=0时，棱台变为棱锥，棱台的体积公式也就是棱锥的体积公式.4.实例运用例1 如图，四面体P－ABC的各棱长均为a，求它的表面积．解：由题意可知四面体P－ABC是由4个边长为a的正三角形面围成∵S正三角形PBC =12a2sin60°=12×√32∙a2=√34∙a2∴S四面体P－ABC =4S正三角形PBC=4×√34∙a2=√3a2答：四面体P－ABC的表面积为√3a2.例2 如图，一个漏斗的上面部分是一个长方体，下面部分是一个四棱锥，两部分的高都是0.5m，公共面ABCD是边长为1m的正方形，那么这个漏斗的容积是多少立方米(精确到0.01m)解：由题意可得V长方体ABCD－A′B′C′D′=Sℎ=12×0.5=0.5(m3)V棱锥P−ABCD =13Sℎ=13×12×0.5=16(m3)∴V漏斗=V长方体ABCD－A′B′C′D′+ V棱锥P−ABCD=0.5+ 16=23≈0.67(m3)答：这个漏斗的容积约是0.67m3.8.3.2 圆柱、圆锥、圆台的体积1.圆柱、圆锥、圆台的体积（互学）（1）圆柱的体积由堆积原理可知：一般地，如果圆柱的底面圆半径是r，高是ℎ，那么这个圆柱的体积为V圆柱=底面圆面积×高= Sh =π r2∙h.简述为：“圆柱的体积等于它底面圆面积与高的乘积”例如已知一圆柱的底面圆半径为2cm，高为3cm，则这个圆柱的体积为V圆柱=π r2∙ℎ=π× 22×3=12π(cm3)（2）圆锥的体积由灌注原理可知：一般地，如果圆锥的底面圆半径是r，高是ℎ，那么这个圆锥的体积为V圆锥=13V圆柱=13Sh=13π r2∙h简述为：“圆锥的体积等于与它等底等高圆柱体积的13”(3)例如已知一圆锥的底面圆半径为2m，高为3m，则这个圆柱的体积为V圆锥=13Sℎ=13π r2∙ℎ=13π×22×3=4π(m3)3.圆台的体积由截去原理可知：一般地，圆台的体积公式为V圆台=13h(S＇+√S＇S+S)=13h(πr＇2+√πr＇2πr2+πr2)=13πh(r＇2+r＇r+r2) .其中S′与S分别为圆台的上、下底面圆面积，ℎ为圆台的高，r′与r分别为上、下底面圆半径.简述为：“圆台的体积等于上下底面圆的面积与它们的几何平均数之和，再乘以圆台高的乘积的13”(3)例如已知一圆台的上下底面圆半径分别为1dm、2dm, 高为3dm，则这个圆台的体积为V圆台=13πℎ(r＇2+r＇r+r2)=13π×3×(12+1×2+22)=7πdm3.（4）圆柱、圆锥、圆台的体积之间的关系①当 r′=r时，圆台变为圆柱，圆台的体积公式也就是圆柱的体积公式;②当 r′=0 时，圆台变为圆锥，圆台的体积公式也就是圆锥的体积公式.2.实例运用例1 已知某圆柱高为10，底面周长为8π，求圆柱的体积.解：设圆柱的底面圆半径为 r (r>0)∵已知C底=8π∴满足2πr=8π ,解得r=4又∵已知 ℎ=10∴V圆柱=π r2∙ℎ=π× 42×10=160π答：这个圆柱的体积为160π例2 已知圆锥的轴截面是等腰直角三角形，侧面积是16√2π，求圆锥的体积.解：作圆锥的轴截面，如图所示∵已知轴截面是等腰直角三角形∴在∆SAB中，∠ASB=90°, 且SA=SB设圆锥的底面圆半径是r，高是 ℎ则 ℎ=r, SB=√2r又∵已知S侧=16√2π∴12×2πr∙SB=16√2π , 即πr×√2r=16√2π解得r=4，∴ℎ=r=4∴V圆锥=13Sℎ=13π r2∙ℎ=13π×42×4=64π3例3已知圆台的上、下底面半径分别为2和 3 ，它的高为 6 ，求圆台的体积. 解：设圆台的高为ℎ，上、下底面圆半径分别为r′与r，则V圆台=13ℎ(S＇+√S＇S+S)=13πℎ(r＇2+r＇r+r2)=13π×6×(22+2×3+32)=38π答：这个圆台的体积为38π8.4.1 平面1.平面的概念、画法及表示（1）面的概念几何里所说的“平面”，就是从生活中的平静的湖面、课桌面、美丽的草原抽象出来的.类似于直线向两端无限延伸，平面是向四周无限延展的，没有厚薄、没有大小、没有形状.（2）平面的画法与表示①画法在立体几何中，平面通常画成一个含45°角的平行四边形.Ⅰ.当平面水平放置时，通常把平行四边形一组对边画成横向，如图（1）；Ⅱ.当平面竖直放置时，通常将平行四边形的一组对边画成竖向，如图Ⅲ.如果一个平面被另一个平面遮挡住，为了增强它的立体感，把被遮挡部分用虚线画出来或者不画.②表示Ⅰ.我们常用希腊字母α，β，γ等表示平面，如平面α、平面β、平面γ等，并将它写在代表平面的平行四边形的一个角内;Ⅱ.也可以用代表平面的平行四边形的四个顶点，或者相对的两个顶点的大写英文字母作为这个平面的名称.如图（1）中的平面α，也可以表示为平面ABCD、平面 AC 或者平面 BD.2.点、线、面之间的关系及符号表示∵直线上有无数个点，平面内有无数个点，∴直线、平面都可以看作以点为元素组成的集合，于是可将点、线、面之间的关系用符号表示如下所示：位置关系符号表示位置关系符号表示点P在直线l上P∈l点Q在直线l外Q∉l点P在平面α内P∈α点H在平面α外H∉α直线l在平面α内l⊂α直线m在平面α外m⊄α3.平面的基本事实及其推论（1）基本事实1过不在一条直线上的三个点，有且只有一个平面.简述为：“不共线的三点确定一个平面.”基本事实1用数学符号语言表示为：A，B，C三点不共线⇒存在唯一的平面α，使 A，B，C∈α（2）基本事实2如果一条直线上的两个点在一个平面内，那么这条直线在这个平面内.注1(作用)：利用基本事实2，可以判断直线是否在平面内.基本事实2用数学符号语言表示为：A∈l，B∈l，且 A∈α，B∈α ⇒l⊂α（3）基本事实3如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.注：如无特殊说明，本章中的两个平面均指两个不重合的平面.基本事实3用数学符号语言表示为：P∈α，P∈β⇒α∩β＝l，且P∈l （4）平面基本事实的三个推论利用基本事实1和基本事实2，再结合“两点确定一条直线”，可以得到下面三个推论:推论1 经过一条直线和这条直线外一点，有且只有一个平面.推论2 经过两条相交直线，有且只有一个平面.推论3 经过两条平行直线，有且只有一个平面.平面基本事实的三个推论用数学符号语言表示为：推论1：点 A∉l⇒l与A共面于平面α，且平面唯一；推论2：a∩b＝P⇒a与b共面于平面α，且平面唯一；推论3：直线a∥b⇒直线a，b共面于平面α，且平面唯一.3.实例运用例1下列命题正确的是( )A. 三点确定一个平面B. 一条直线和一个点确定一个平面C. 圆心和圆上两点可确定一个平面D. 梯形可确定一个平面解：对于A，空间不共线的三点可以确定一个平面，∴A错;对于B，在空间中，如果这个点在直线上，就不能确定一个平面，∴B错；对于C，圆心和圆上的两点如果在一条直线上，就不能确定一个平面，∴C错;对于D，梯形只有一组对边平行，所以梯形可以确定一个平面，∴D正确.故选D.例2用符号表示下列语句，并画出相应的图形；(1)点A在平面α内，点B在平面α外；(2)直线a既在平面α内，又在平面β内．解：（1）“点A在平面α内，点B在平面α外”表示为：A∈α，B∉α，如图（1）所示.例4解（2）“直线a既在平面α内，又在平面β内”表示为：a⊂α，a⊂β,且 α⋂β=a，如图（2）所示.8.4.2 空间点、直线、平面之间的位置关系1.空间中两条直线的位置关系由图可知，（1）平行直线：直线AB与DC在同一个平面ABCD内，它们没有公共点，它们是平行直线;（2）相交直线：直线AB与BC在同一个平面ABCD内，它们只有一个公共点B，它们是相交直线;（3）异面直线①定义：如图（1），像直线AB与CC′这样，空间中不同在任何一个平面内的两条直线叫做异面直线.②画法：如图（2），如果直线a，b为异面直线，为了表示它们不共面的特点，作图时，通常用一个或两个平面衬托.③判定方法：由异面直线的定义及画法可得如下异面直线的判定方法Ⅰ.定义法：不同在任何一个平面内的两条直线是异面直线；Ⅱ.反证法：既不平行，也不相交的两条直线是异面直线；Ⅲ.定理法：与一个平面相交的直线和这个平面内不经过交点的直线是异面直线.(如右图一)定理法数学语言表示为：“AB∩α=B,A∉α,a⊂α,B∉a⇒直线AB与a是异面直线”（4）实例运用例1选择题(1)如果两条直线a与b没有公共点，那么a与b( )A.共面B.平行C.是异面直线D.可能平行，也可能是异面直线(2)设直线a,b分别是长方体的相邻两个面的对角线所在的直线,则a与b( )A.平行B.相交C.是异面直线D.可能相交，也可能是异面直线解：（1）选D（2）选D例2 如图，在长方体ABCD−A′B′C′D′中，判定直线AB与AC，直线AC与A′C′，直线A′B与AC，直线A′B与C′D的位置关系．解:如图，在长方体ABCD−A′B′C′D′中直线AB与AC为相交直线，直线AC与A′C′为平行直线，直线A′B与AC为异面直线，直线A′B与C′D为异面直线2.空间中直线与平面的位置关系由探究可知，直线与平面的位置关系有且只有如下三种：（1）关系1：直线a在平面α内——有无数个公共点，记作 a⊂α.（2）关系2：直线a与平面α相交——只有1个公共点，记作 a∩α=A.（3）关系3：直线a与平面α平行——没有公共点，记作 a∥α.温馨提示：直线a在平面α外包括两种情形——a∥α与a∩α＝A.3.空间中平面与平面的位置关系（1）空间中平面与平面的位置关系由探究可知，平面与平面的位置关系有且只有如下两种：①关系1：平面a与平面β平行——没有公共点，记作α∥β.②关系2：平面a与平面β相交——有一条公共直线，记作 α∩β=l.温馨提示：画两个互相平行的平面时，要注意使表示平面的两个平行四边形的对应边平行.（2）实例运用例3如图，用符号表示下列图形中直线、平面之间的位置关系．解：在图（1）中，α∩β=l,a∩α=A,a∩β=B.在图（2）中，α∩β=l,a⊂α, b⊂β a∩l=P,b∩l=P,a∩b=P.8.5.1 直线与直线平行1.基本事实4（平行线的传递性）（1）基本事实4（平行线的传递性）空间中平行于同一条直线的两条直线平行.基本事实4用数学符号表示为： a∥b,b∥c⇒a∥c温馨提示:基本事实4表明了平行的传递性，它可以作为判断两直线平行的依据，同时也给出了空间两直线平行的一种证明方法.（2）实例运用例1如图，空间四边形ABCD中，E,F,G,H分别是边AB,BC,CD,DA的中点求证：四边形EFGH是平行四边形．证明：如图，连接BD,∵已知E,H分别是边AB，DA的中点∴EH为∆ABD的中位线∴ EH∥BD,且EH=12BD同理可得FG∥BD,且FG=12BD∴EH ∥= FG∴四边形EFGH是平行四边形．2.等角互补定理（互学）（1）等角互补定理如果空间中两个角的两条边分别对应平行，那么这两个角相等或互补.等角互补定理用数学符号表示为：已知空间中两个角∠BAC与∠B′A′C′,且AB∥A′B′ ,AC∥A′C′⇒∠BAC=∠B′A′C′,或∠BAC+∠B′A′C′=180°（2）实例运用例2如图，在四面体A−BCD中，E,F,G分别为AB,AC,AD上的点，若EF∥BC,FG∥CD，则∆EFG和∆BCD有什么关系？为什么？解:∵EF∥BC，∴AEAB =AFAC=EFBC又∵FG∥CD，∴AFAC =AGAD=FGCD，∴AEAB =AGAD,∴EG∥BD∴由等角定理可知∠EFG=∠BCD，∠FGE=∠CDB,∠GEF=∠DBC∴△EFG∽△BCD(三角定理)8.5.2 直线与平面平行1.直线与平面平行的判定定理（1）直线与平面平行的判定定理如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行.直线与平面平行的判定定理用数学符号表示为：a⊄α,b⊂α,且a∥b⇒a∥α温馨提示:(1)定理中的三个条件“a⊄α，b⊂α，a∥b”缺一不可;(2)判定定理实质是——“ 线线平行⇒线面平行”.（2）实例运用例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边的平面.（四）成果展示1(迁移变通、检测实践)例1 解：第1步：作图第2步：数学语言翻译已知：如图，空间四边形ABCD中，E,F分别是AB,AD的中点.求证：EF∥平面BCD.第3步：证明证明：如图，连接BD,∵已知E,F分别是AB,AD的中点∴EF为∆ABD的中位线∴EF∥BD又∵ EF⊄平面BCD,BD⊂平面BCD,∴EF∥平面BCD故原命题成立2.直线与平面平行的性质定理（1）直线与平面平行的性质定理一条直线与一个平面平行，如果过该直线的平面与此平面相交，那么该直线与交线平行.直线与平面平行的性质定理用数学符号表示为：a∥α,a⊂β,且α⋂β=b⇒a∥b温馨提示(1)定理中的三个条件“a∥α,a⊂β,且α⋂β=b”缺一不可.(2)性质定理实质是——“线面平行⇒线线平行”.（2）实例运用例2 已知α⋂β=a,b⊂α,c⊂β,b∥c求证：a∥b∥c解：∵已知 b∥c，b⊄α,且c⊂β∴ b∥β又∵已知 b⊂α，α⋂β=a,∴ b∥a∴a∥b∥c8.5.3平面与平面平行1.平面与平面平行的定义如图，空间中没有公共点的两个平面叫做平行平面.记作：α∥β .温馨提示:两个平面平行的充要条件为（1）如果两个平面平行，那么这个平面内的任意一条直线都与另一个平面没有公共点.（2）如果一个平面内的任意一条直线都与另一个平面平行，那么这两个平面平行.2.平面与平面平行的判定定理（1）平面与平面平行的判定定理如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行.平面与平面平行的判定定理用数学符号表示为：a⊂β，b⊂β，a∩b＝P，a∥α，b∥α⇒β∥α温馨提示:(1)平面与平面平行的判定定理中的平行于一个平面内的“两条相交直线”是必不可少的条件.(2)平面与平面判定定理实质是——“线面平行⇒面面平行”.（2）实例运用例1 如图，已知正方体ABCD−A1B1C1D1,求证平面AB1D1∥平面BC1D.证明：∵已知ABCD−A1B1C1D1为正方体∴D1C1∥=A1B1, AB∥=A1B1∴D1C1∥= AB∴四边形D1C1BA为平行四边形∴D1A∥C1B又∵D1A⊄平面BC1D,C1B⊂平面B C1D,∴D1A∥平面B C1D, 同理可得D1B1∥平面B C1D又∵D1A⋂D1B1=D1且D1A，D1B1⊂平面AB1D1∴平面AB1D1∥平面BC1D.3.直线与平面平行的性质定理（1）平面与平面平行的性质定理两个平面平行，如果另一个平面与这两个平面相交，那么两条交线平行.平面与平面平行的性质定理用数学符号表示为：α∥β，α∩γ＝a，β∩γ＝b⇒a∥b温馨提示(1)定理中的三个条件“ α∥β，α∩γ＝a，β∩γ＝b”缺一不可.(2)性质定理实质是——“面面平行⇒线线平行”.（2）实例运用例2求证：夹在两个平行平面间的平行线段相等.第一步：作图；第二步：数学语言翻译；如图，已知α∥β，AB∥CD,且A∈α,C∈α,B∈β,C∈β求证：AB=CD.第三步：证明；证明：如图，过平行线AB，CD作平面γ，与平面α和β分别交于AC和BD∵已知 α∥β,α∩γ＝AC，β∩γ＝BD∴AC∥BD又∵已知AB∥CD∴四边形ABCD为平行四边形∴AB=CD8.6.1 直线与直线垂直1.异面直线所成的角（1）平面内相交直线所成的角规定：平面内两条直线相交形成4个角，其中不大于90°的角称为这两条直线所成的角(或夹角)，它刻画了一条直线相对于另一条直线倾斜的程度.特别地，当两条相交直线a与b所成角为90°时，就称这两条相交直线互相垂直, 记作a⊥b .提示：类似地，我们也可以用“异面直线所成的角”来刻画两条异面直线的位置关系.。

高考数学知识点：空间几何体的表面积和体积

高考数学知识点：空间几何体的表面积和体积第1篇：高考数学知识点之空间几何体的表面积和体积在我们周围存在着各种各样的物体，它们都占据着空间的一部分。

下面小编给大家介绍高考数学知识点之空间几何体的表面积和体积，赶紧来看看吧!1、圆柱体:表面积:2πRr+2πRh体积:πRh(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR+πR[(h+R)的平方根]体积:πRh/3(r为圆锥体低圆半径,h为其高,3、正方体a-边长,S=6a,V=a4、长方体a-长,b-宽,c-高S=2(ab+ac+bc)V=abc5、棱柱S-底面积h-高V=Sh6、棱锥S-底面积h-高V=Sh/37、棱台S1和S2-上、下底面积h-高V=h[S1+S2+(S1S2)^1/2]/38、拟柱体S1-上底面积,S2-下底面积,S0-中截面积h-高,V=h(S1+S2+4S0)/69、圆柱r-底半径,h-高,C—底面周长S底—底面积,S侧—侧面积,S表—表面积C=2πrS底=πr,S侧=Ch,S表=Ch+2S底,V=S底h=πrh10、空心圆柱R-外圆半径,r-内圆半径h-高V=πh(R^2-r^2)11、直圆锥r-底半径h-高V=πr^2h/312、圆台r-上底半径,R-下底半径,h-高V=πh(R+Rr+r)/313、球r-半径d-直径V=4/3πr^3=πd^3/614、球缺h-球缺高,r-球半径,a-球缺底半径V=πh(3a+h)/6=πh(3r-h)/315、球台r1和r2-球台上、下底半径h-高V=πh[3(r1+r2)+h]/616、圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr=π2Dd/417、桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D+d)/12,(母线是圆弧形,圆心是桶的中心)V=πh(2D+Dd+3d/4)/15(母线是抛物线形)第2篇：高考数学知识点：空间几何体的表面积和体积数学是研究数量、结构、变化、空间以及信息等概念的一门学科，下面是小编整理的高考数学知识点：空间几何体的表面积和体积，希望对大家有帮助!1、圆柱体:表面积:2πRr+2πRh体积:πRh(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR+πR[(h+R)的平方根]体积:πRh/3(r为圆锥体低圆半径,h为其高,3、正方体a-边长,S=6a,V=aa-长,b-宽,c-高S=2(ab+ac+bc)V=abc5、棱柱S-底面积h-高V=Sh6、棱锥S-底面积h-高V=Sh/37、棱台S1和S2-上、下底面积h-高V=h[S1+S2+(S1S2)^1/2]/3 8、拟柱体S1-上底面积,S2-下底面积,S0-中截面积h-高,V=h(S1+S2+4S0)/69、圆柱r-底半径,h-高,C—底面周长S底—底面积,S侧—侧面积,S表—表面积C=2πrS底=πr,S侧=Ch,S表=Ch+2S底,V=S底h=πrh10、空心圆柱R-外圆半径,r-内圆半径h-高V=πh(R^2-r^2)11、直圆锥r-底半径h-高V=πr^2h/312、圆台r-上底半径,R-下底半径,h-高V=πh(R+Rr+r)/313、球r-半径d-直径V=4/3πr^3=πd^3/614、球缺h-球缺高,r-球半径,a-球缺底半径V=πh(3a+h)/6=πh(3r-h)/3 15、球台r1和r2-球台上、下底半径h-高V=πh[3(r1+r2)+h]/616、圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr=π2Dd/4D-桶腹直径d-桶底直径h-桶高V=πh(2D+d)/12,(母线是圆弧形,圆心是桶的中心)V=πh(2D+Dd+3d/4)/15(母线是抛物线形)第3篇：高考数学知识点:空间几何体的表面积和体积知识解析一、柱、锥、台和球的侧面积和体积典型例题1：1、几何体的侧面积和全面积：几何体侧面积是指(各个)侧面面积之和，而全面积是侧面积与所有底面积之和.对侧面积公式的记忆，最好结合几何体的侧面展开图来进行.2、求体积时应注意的几点：(1)、求一些不规则几何体的体积常用割补的方法转化成已知体积公式的几何体进行解决.(2)、与三视图有关的体积问题注意几何体还原的准确*及数据的准确*.3、求组合体的表面积时注意几何体的衔接部分的处理.典型例题2：1、以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量.2、多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.3、旋转体的表面积问题注意其侧面展开图的应用.典型例题3：1、计算柱、锥、台体的体积，关键是根据条件找出相应的底面面积和高，应注意充分利用多面体的截面和旋转体的轴截面，将空间问题转化为平面问题求解.2、注意求体积的一些特殊方法：分割法、补体法、转化法等，它们是解决一些不规则几何体体积计算常用的方法，应熟练掌握.3、等积变换法：利用三棱锥的任一个面可作为三棱锥的底面.①求体积时，可选择容易计算的方式来计算;②利用“等积法”可求“点到面的距离”.第4篇：空间几何体的表面积与体积的数学知识点一、课标要求：了解一些简单的几何体的表面积的计算方法，了解棱柱、棱锥、台的表面积计算公式(不要求记忆公式)二、教学目标：(1)了解平面展开图的概念及柱、锥、台的表面积公式;(2)会求一些简单几何体的表面积公式;(3)让学生经历空间几何体的侧面展开过程，感知几何体的形状;(4)让学生通过对照比较，理顺柱体、锥体、台体侧面积之间的转换关系，体会数和形的完美结合.(5)通过学习使学生感受到空间几何体侧面积的求解过程，对自己空间思维能力的影响，从而增强学习数学的信心.三、教学重点、难点：重点;空间几何体侧面积的计算难点;空间几何体侧面展开四、设计思路：借助多媒体，通过动态演示一些多面体的平面展开图的过程，让学生在直观感知的基础上了解平面展开图的概念，进而结合前面已研究的柱、锥、台这三类几何体的概念，介绍正棱柱、正棱锥、正棱台的概念，结合模型组织学生感知探索侧面展开图的形成过程及侧面展开图的构成，得出它们侧面积的计算公式。

高考数学一轮复习第八章立体几何第5讲简单几何体的再认识(表面积与体积)教学案理

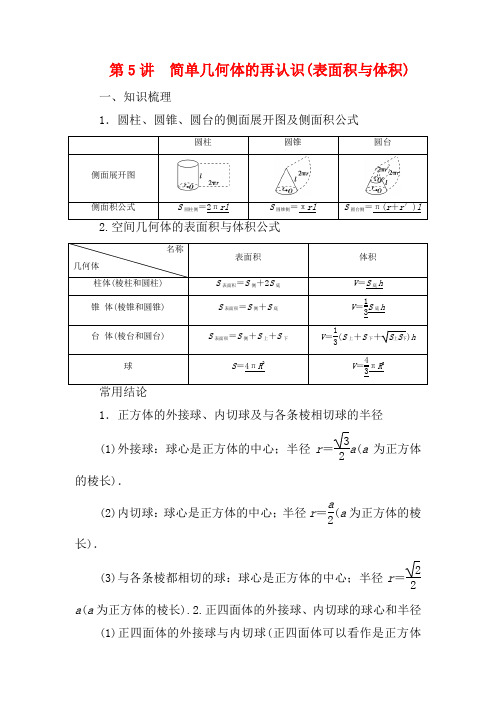
第5讲简单几何体的再认识(表面积与体积)一、知识梳理1．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrl S 圆锥侧＝πrlS 圆台侧＝π(r ＋r ′)l名称几何体表面积体积柱体(棱柱和圆柱) S 表面积＝S 侧＋2S 底 V ＝S 底h 锥体(棱锥和圆锥) S 表面积＝S 侧＋S 底 V ＝13S 底h台体(棱台和圆台)S 表面积＝S 侧＋S 上＋S 下V ＝13(S 上＋S 下＋S 上S 下)h球S ＝4πR 2V ＝43πR 31．正方体的外接球、内切球及与各条棱相切球的半径 (1)外接球：球心是正方体的中心；半径r ＝32a (a 为正方体的棱长)．(2)内切球：球心是正方体的中心；半径r ＝a2(a 为正方体的棱长)．(3)与各条棱都相切的球：球心是正方体的中心；半径r ＝22a (a 为正方体的棱长).2.正四面体的外接球、内切球的球心和半径(1)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分)．(2)外接球：球心是正四面体的中心；半径r ＝64a (a 为正四面体的棱长)．(3)内切球：球心是正四面体的中心；半径r ＝612a (a 为正四面体的棱长)．二、教材衍化1．已知圆锥的表面积等于12π cm 2，其侧面展开图是一个半圆，则底面圆的半径为________．解析：S 表＝πr 2＋πrl ＝πr 2＋πr ·2r ＝3πr 2＝12π，所以r 2＝4，所以r ＝2. 答案：2 cm 2．如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为________．解析：设长方体的相邻三条棱长分别为a ，b ，c ，它截出棱锥的体积V 1＝13×12×12a ×12b ×12c ＝148abc ，剩下的几何体的体积V 2＝abc －148abc ＝4748abc ，所以V 1∶V 2＝1∶47.答案：1∶47 一、思考辨析判断正误(正确的打“√”，错误的打“×”) (1)多面体的表面积等于各个面的面积之和．( ) (2)锥体的体积等于底面积与高之积．( )(3)球的体积之比等于半径比的平方．( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差．( )(5)长方体既有外接球又有内切球．( )答案：(1)√(2)×(3)×(4)√(5)×二、易错纠偏常见误区|Ｋ(1)不能把三视图正确还原为几何体而错解表面积或体积；(2)考虑不周忽视分类讨论；(3)几何体的截面性质理解有误；(4)混淆球的表面积公式和体积公式．1．已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图所示(单位：m)，则该四棱锥的体积为________m3.解析：根据三视图可知该四棱锥的底面是底边长为2 m，高为1 m的平行四边形，四棱锥的高为 3 m．故该四棱锥的体积V＝1 3×2×1×3＝2(m3)．答案：22．将一个相邻边长分别为4π，8π的矩形卷成一个圆柱，则这个圆柱的表面积是________．解析：当底面周长为4π时，底面圆的半径为2，两个底面的面积之和是8π；当底面周长为8π时，底面圆的半径为4，两个底面的面积之和为32π.无论哪种方式，侧面积都是矩形的面积32π2，故所求的表面积是32π2＋8π或32π2＋32π.答案：32π2＋8π或32π2＋32π3．已知圆柱的上、下底面的中心分别为O 1，O 2，过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为________．解析：因为过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为22，底面圆的直径为22，所以该圆柱的表面积为2×π×(2)2＋22π×22＝12π.答案：12π4．一个球的表面积是16π，那么这个球的体积为________．解析：设球的半径为R ，则由4πR 2＝16π，解得R ＝2，所以这个球的体积为43πR 3＝323π.答案：323π空间几何体的表面积(师生共研)(1)(2020·河南周口模拟)如图，在三棱柱ABC A 1B 1C 1中，AA 1⊥底面ABC ，AB ⊥BC ，AA 1＝AC ＝2，直线A 1C 与侧面AA 1B 1B 所成的角为30°，则该三棱柱的侧面积为( )A ．4＋4 2B ．4＋43C ．12D ．8＋42(2)(2020·四川泸州一诊)在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )A ．(5＋2)πB ．(4＋2)πC ．(5＋22)πD ．(3＋2)π【解析】 (1)连接A 1B .因为AA 1⊥底面ABC ，则AA 1⊥BC ，又AB ⊥BC ，AA 1∩AB ＝A ，所以BC ⊥平面AA 1B 1B ，所以直线A 1C 与侧面AA 1B 1B 所成的角为∠CA 1B＝30°.又AA 1＝AC ＝2，所以A 1C ＝22，BC ＝ 2.又AB ⊥BC ，则AB ＝2，则该三棱柱的侧面积为22×2＋2×2＝4＋42，故选A.(2)因为在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2，所以将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB ＝1，高为BC －AD ＝2－1＝1的圆锥，所以该几何体的表面积S ＝π×12＋2π×1×2＋π×1×12＋12＝(5＋2)π.故选A.【答案】 (1)A (2)A空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量．(2)多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理．(3)旋转体的表面积问题注意其侧面展开图的应用． 1．在如图所示的斜截圆柱中，已知圆柱底面的直径为40 cm ，母线长最短50 cm ，最长80 cm ，则斜截圆柱的侧面面积S ＝________cm 2.解析：将题图所示的相同的两个几何体对接为圆柱，则圆柱的侧面展开图为矩形．由题意得所求侧面展开图的面积S＝12×(50＋80)×(π×40)＝2 600π(cm2)．答案：2 600π2．已知一几何体的三视图如图所示，它的主视图与左视图相同，则该几何体的表面积为________．解析：由三视图知，该几何体是一个正四棱柱与半球的组合体，且正四棱柱的高为2，底面对角线长为4，球的半径为2，所以该正四棱柱的底面正方形的边长为22，该几何体的表面积S＝1 2×4π×22＋π×22＋22×2×4＝12π＋16.答案：12π＋16空间几何体的体积(多维探究)角度一直接利用公式求体积(2020·山东省实验中学模拟)我国古代《九章算术》里，记载了一个“商功”的例子：今有刍童，下广二丈，袤三丈，上广三丈，袤四丈，高三丈．问积几何？其意思是：今有上下底面皆为长方形的草垛(如图所示)，下底宽2丈，长3丈，上底宽3丈，长4丈，高3丈．问它的体积是多少？该书提供的算法是：上底长的2倍与下底长的和与上底宽相乘，同样下底长的2倍与上底长的和与下底宽相乘，将两次运算结果相加，再乘以高，最后除以6.则这个问题中的刍童的体积为( )A．13.25立方丈B．26.5立方丈C．53立方丈D．106立方丈【解析】由题意知，刍童的体积为[(4×2＋3)×3＋(3×2＋4)×2]×3÷6＝26.5(立方丈)，故选B.【答案】 B角度二割补法求体积《九章算术》卷五商功中有如下问题：今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何？刍甍：底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图，设网格纸上每个小正方形的边长为1)，那么该刍甍的体积为( )A ．4B ．5C ．6D ．12【解析】如图所示，由三视图可还原得到几何体ABCDEF ，过E ，F 分别作垂直于底面的截面EGH 和FMN ，可将原几何体切割成三棱柱EHG FNM ，四棱锥E ADHG 和四棱锥F MBCN ，易知三棱柱的体积为12×3×1×2＝3，两个四棱锥的体积相同，都为13×1×3×1＝1，则原几何体的体积为3＋1＋1＝5.故选B.【答案】 B角度三等体积法求体积(2020·贵州部分重点中学联考)如图，在直四棱柱ABCD A 1B 1C 1D 1中，底面ABCD 是平行四边形，点E 是棱BB 1的中点，点F 是棱CC 1上靠近C 1的三等分点，且三棱锥A 1AEF 的体积为2，则四棱柱ABCD A 1B 1C 1D 1的体积为( )A ．12B ．8C ．20D ．18【解析】设点F 到平面ABB 1A 1的距离为h ，由题意得V A 1AEF＝V F A 1AE .又V F A 1AE ＝13S △A 1AE ·h ＝13×⎝ ⎛⎭⎪⎫12AA 1·AB ·h ＝16(AA 1·AB )·h ＝16S 四边形ABB 1A 1·h ＝16V ABCD A 1B 1C 1D 1，所以V ABCD A 1B 1C 1D 1＝6V A 1AEF ＝6×2＝12.所以四棱柱ABCD A 1B 1C 1D 1的体积为12.故选A.【答案】 A(1)处理体积问题的思路①“转”：指的是转换底面与高，将原来不易求面积的底面转换为易求面积的底面，或将原来不易看出的高转换为易看出并易求解长度的高；②“拆”：指的是将一个不规则的几何体拆成几个简单的几何体，便于计算；③“拼”：指的是将小几何体嵌入一个大几何体中，如将一个三棱锥复原成一个三棱柱，将一个三棱柱复原成一个四棱柱，这些都是拼补的方法．(2)求空间几何体的体积的常用方法①公式法：对于规则几何体的体积问题，可以直接利用公式进行求解；②割补法：把不规则的图形分割成规则的图形，然后进行体积计算；或者把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算其体积；③等体积法：一个几何体无论怎样转化，其体积总是不变的．如果一个几何体的底面面积和高较难求解时，我们可以采用等体积法进行求解．等体积法也称等积转化或等积变形，它是通过选择合适的底面来求几何体体积的一种方法，多用来解决有关锥体的体积，特别是三棱锥的体积．1．(2020·江西上饶二模)已知下图为某几何体的三视图，则其体积为( )A ．π＋23B ．π＋13C ．π＋43D ．π＋34解析：选C.几何体为半圆柱与四棱锥的组合体(如图)，半圆柱的底面半径为1，高为2，四棱锥的底面为边长为2的正方形，高为1，故几何体的体积V ＝12×π×12×2＋13×22×1＝π＋43.故选C.2．(2019·高考全国卷Ⅲ)学生到工厂劳动实践，利用3D 打印技术制作模型．如图，该模型为长方体ABCD A 1B 1C 1D 1挖去四棱锥O EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，AB ＝BC ＝6 cm ，AA 1＝4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗，制作该模型所需原料的质量为________g.解析：由题易得长方体ABCD A 1B 1C 1D 1的体积为6×6×4＝144(cm 3)，四边形EFGH 为平行四边形，如图所示，连接GE ，HF ，易知四边形EFGH 的面积为矩形BCC 1B 1面积的一半，即12×6×4＝12(cm 2)，所以V四棱锥O EFGH ＝13×3×12＝12(cm 3)，所以该模型的体积为144－12＝132(cm 3)，所以制作该模型所需原料的质量为132×0.9＝118.8(g)．答案：118.8球与空间几何体的接、切问题(多维探究) 角度一外接球(1)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A ．πB ．3π4C.π2D ．π4(2)已知三棱锥S ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥S ABC的体积为9，则球O 的表面积为________．【解析】 (1)设圆柱的底面圆半径为r ，则r 2＝12－⎝ ⎛⎭⎪⎫122＝34，所以，圆柱的体积V ＝34π×1＝3π4，故选B.(2)设球O 的半径为R ，因为SC 为球O 的直径，所以点O 为SC 的中点，连接AO ，OB ，因为SA ＝AC ，SB ＝BC ，所以AO ⊥SC ，BO ⊥SC ，因为平面SCA ⊥平面SCB ，平面SCA ∩平面SCB ＝SC ，所以AO ⊥平面SCB ，所以V S ABC ＝V A SBC ＝13×S △SBC ×AO ＝13×(12×SC ×OB )×AO ，即9＝13×(12×2R ×R )×R ，解得R ＝3，所以球O 的表面积为S ＝4πR2＝4π×32＝36π.【答案】 (1)B (2)36π角度二内切球(1)如图，在圆柱O 1O 2内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱O 1O 2的体积为V 1，表面积为S 1，球O 的体积为V 2，表面积为S 2，则V 1V 2的值是__________，S 1S 2＝________. (2)已知棱长为a 的正四面体，则此正四面体的表面积S 1与其内切球的表面积S 2的比值为________．【解析】 (1)设圆柱内切球的半径为R ，则由题设可得圆柱O 1O 2的底面圆的半径为R ，高为2R ，所以V 1V 2＝πR 2·2R 43πR 3＝32.S 1S 2＝2πR ·2R ＋2πR 24πR 2＝32. (2)正四面体的表面积为S 1＝4×34×a 2＝3a 2，其内切球半径r 为正四面体高的14，即r ＝14×63a ＝612a ，因此内切球表面积为S 2＝4πr 2＝πa 26，则S 1S 2＝3a 2πa 26＝63π. 【答案】 (1)32 32 (2)63π解决与球有关的切、接问题，其通法是作截面，将空间几何问题转化为平面几何问题求解，其解题的思维流程是：1.(2020·四川成都一诊)如图，在矩形ABCD 中，EF ∥AD ，GH ∥BC ，BC ＝2，AF ＝FG ＝BG ＝1.现分别沿EF ，GH 将矩形折叠使得AD 与BC 重合，则折叠后的几何体的外接球的表面积为( )A ．24πB ．6π C.163π D ．83π 解析：选C.由题意可知，折叠后的几何体是底面为等边三角形的三棱柱，底面等边三角形外接圆的半径为23× 12－⎝ ⎛⎭⎪⎫122＝33.因为三棱柱的高为BC ＝2，所以其外接球的球心与底面外接圆圆心的距离为1，则三棱柱外接球的半径为R ＝⎝ ⎛⎭⎪⎪⎫332＋12＝233，所以三棱柱外接球的表面积S ＝4πR 2＝16π3.故选C.2．(2020·黑龙江哈尔滨师范大学附属中学模拟)在底面是边长为2的正方形的四棱锥P ABCD 中，点P 在底面的射影H 为正方形ABCD 的中心，异面直线PB 与AD 所成角的正切值为2.若四棱锥P ABCD 的内切球半径为r ，外接球的半径为R ，则r R＝( ) A.23B ．25 C.12D ．13解析：选B.如图，取E ，F 分别为AB ，CD 的中点，连接EF ，PE ，PF .由题意知，P ABCD 为正四棱锥，底面边长为2.因为BC ∥AD ，所以∠PBC 即为异面直线PB 与AD 所成的角．因为∠PBC 的正切值为2，所以四棱锥的斜高为2，所以△PEF 为等边三角形，则正四棱锥P ABCD 的内切球的半径r 即为△PEF 的内切圆的半径，为33. 设O 为正四棱锥外接球的球心，连接OA ，AH .由题可得AH ＝2，PH ＝ 3.在Rt △OHA 中，R 2＝(2)2＋(3－R )2，解得R ＝536，所以r R ＝25. 确定球心位置的三种方法决定球的几何要素是球心的位置和球的半径，在球与其他几何体的结合问题中，通过位置关系的分析，找出球心所在的位置是解题的关键，不妨称这个方法为球心位置分析法．方法一由球的定义确定球心若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球．也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体外接球的球心．(1)长方体或正方体的外接球的球心是其体对角线的中点；(2)正三棱柱的外接球的球心是上、下底面中心连线的中点；(3)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点；(4)正棱锥的外接球球心在其高上，具体位置可通过建立直角三角形运用勾股定理计算得到；(5)若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心．已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是( )A．16π B．20πC．24πD．32π【解析】已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，可求得底面边长为2，故球的直径为22＋22＋42＝26，则半径为6，故球的表面积为24π，故选C.【答案】C方法二构造长方体或正方体确定球心(1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补形成长方体或正方体；(2)同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补形成长方体或正方体；(3)若已知棱锥含有线面垂直关系，则可将棱锥补形成长方体或正方体；(4)若三棱锥的三个侧面两两垂直，则可将三棱锥补形成长方体或正方体．如图，边长为2的正方形ABCD中，点E，F分别是边AB，BC的中点，将△AED，△EBF，△FCD分别沿DE，EF，FD折起，使A，B，C三点重合于点A′，若四面体A′EFD的四个顶点在同一个球面上，则该球的半径为( )A. 2 B．6 2C.112D．52【解析】易知四面体A′EFD的三条侧棱A′E，A′F，A′D 两两垂直，且A′E＝1，A′F＝1，A′D＝2，把四面体A′EFD补成从顶点A′出发的三条棱长分别为1，1，2的一个长方体，则长方体的外接球即为四面体A′EFD的外接球，球的半径为r＝1 212＋12＋22＝62.故选B.【答案】B方法三由性质确定球心利用球心O与截面圆圆心O′的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质，确定球心．正三棱锥ABCD内接于球O，且底面边长为3，侧棱长为2，则球O的表面积为________．【解析】如图，M为底面△BCD的中心，易知AM⊥MD，DM＝1，AM＝ 3.在Rt△DOM中，OD2＝OM2＋MD2，即OD2＝(3－OD)2＋1，解得OD＝23 3，故球O的表面积为4π×⎝⎛⎭⎪⎪⎫2332＝163π.【答案】163π[基础题组练]1．圆柱的底面积为S ，侧面展开图是一个正方形，那么圆柱的侧面积是( )A ．4πSB ．2πSC ．πSD ．233πS 解析：选A.由πr 2＝S 得圆柱的底面半径是S π，故侧面展开图的边长为2π·S π＝2πS ，所以圆柱的侧面积是4πS ，故选A. 2．已知圆锥的高为3，底面半径长为4，若一球的表面积与此圆锥的侧面积相等，则该球的半径长为( ) A ．5B ．5C ．9D ．3解析：选B.因为圆锥的底面半径R ＝4，高h ＝3，所以圆锥的母线l ＝5，所以圆锥的侧面积S ＝πRl ＝20π.设球的半径为r ，则4πr 2＝20π，所以r ＝5，故选B.3．(2020·安徽黄山一模)如图所示为某几何体的三视图，则几何体的体积为( )A.12B ．1 C.32D ．3 解析：选B.由主视图可得如图的四棱锥P ABCD ，其中平面ABCD ⊥平面PCD .由主视图和俯视图可知AD ＝1，CD ＝2，P 到平面ABCD 的距离为32. 所以四棱锥P ABCD 的体积为V ＝13×S 长方形ABCD ×h ＝13×1×2×32＝1.故选B.4．(2020·河南郑州三模)某几何体的三视图如图所示，则该几何体的体积为( )A.5π3B ．4π3 C.π3D ．2π3 解析：选D.几何体是半个圆柱挖去半个圆锥所形成的，如图，由题意可知几何体的体积为：12×12·π×2－13×12×12·π×2＝2π3.故选D. 5．(2020·广东茂名一模)在长方体ABCD A 1B 1C 1D 1中，四边形ABCD 是边长为2的正方形，D 1B 与DC 所成的角是60°，则长方体的外接球的表面积是( )A ．16πB ．8πC ．4πD ．42π解析：选A.如图，在长方体ABCD A 1B 1C 1D 1中，因为DC ∥AB ，所以相交直线D 1B 与AB 所成的角是异面直线D 1B 与DC 所成的角．连接AD 1，由AB ⊥平面ADD 1A 1，得AB ⊥AD 1，所以在Rt △ABD 1中，∠ABD 1就是D 1B 与DC 所成的角，即∠ABD 1＝60°，又AB ＝2，AB ＝BD 1cos 60°，所以BD 1＝AB cos 60°＝4，设长方体ABCD A 1B 1C 1D 1外接球的半径为R ，则由长方体的体对角线就是长方体外接球的直径得4R 2＝D 1B 2＝16，则R ＝2，所以长方体外接球的表面积是4πR 2＝16π.故选A.6．一个四棱锥的侧棱长都相等，底面是正方形，其主视图如图所示，则该四棱锥的侧面积是________．解析：因为四棱锥的侧棱长都相等，底面是正方形，所以该四棱锥为正四棱锥，如图，由题意知底面正方形的边长为2，正四棱锥的高为2，取正方形的中心O ，AD 的中点E ，连接PO ，OE ，PE ，可知PO 为正四棱锥的高，△PEO 为直角三角形，则正四棱锥的斜高PE ＝22＋12＝ 5.所以该四棱锥的侧面积S ＝4×12×2×5＝4 5. 答案：457.已知圆锥SO ，过SO 的中点P 作平行于圆锥底面的截面，以截面为上底面作圆柱PO ，圆柱的下底面落在圆锥的底面上(如图)，则圆柱PO 的体积与圆锥SO 的体积的比值为________．解析：设圆锥SO 的底面半径为r ，高为h ，则圆柱PO 的底面半径是r 2，高为h 2，所以V 圆锥SO ＝13πr 2h ，V 圆柱PO ＝π⎝ ⎛⎭⎪⎫r 22·h 2＝πr 2h 8，所以V 圆柱PO V 圆锥SO ＝38. 答案：388．已知正三棱锥的高为1，底面边长为23，内有一个球与四个面都相切，则棱锥的内切球的半径为________．解析：如图，过点P 作PD ⊥平面ABC 于点D ，连接AD 并延长交BC 于点E ，连接PE ，因为△ABC 是正三角形，所以AE 是BC 边上的高和中线，D 为△ABC 的中心．因为AB ＝BC ＝23，所以S △ABC ＝33，DE ＝1，PE ＝ 2.所以S 表＝3×12×23×2＋33＝36＋3 3. 因为PD ＝1，所以三棱锥的体积V ＝13×33×1＝ 3. 设球的半径为r ，以球心O 为顶点，三棱锥的四个面为底面，把正三棱锥分割为四个小棱锥，则r ＝3336＋33＝2－1. 答案：2－19．已知一个几何体的三视图如图所示．(1)求此几何体的表面积；(2)如果点P ，Q 在正视图中所示位置，P 为所在线段的中点，Q 为顶点，求在几何体表面上，从P 点到Q 点的最短路径的长．解：(1)由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体，其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和．S 圆锥侧＝12(2πa )·(2a )＝2πa 2， S 圆柱侧＝(2πa )·(2a )＝4πa 2，S 圆柱底＝πa 2，所以S 表＝2πa 2＋4πa 2＋πa 2＝(2＋5)πa 2.(2)沿P 点与Q 点所在母线剪开圆柱侧面，如图．则PQ ＝AP 2＋AQ 2＝a 2＋（πa ）2＝a 1＋π2，所以从P 点到Q 点在侧面上的最短路径的长为a 1＋π2.10.如图，四边形ABCD 为菱形，G 为AC 与BD 的交点，BE ⊥平面ABCD .(1)证明：平面AEC ⊥平面BED ；(2)若∠ABC ＝120°，AE ⊥EC ，三棱锥E ACD 的体积为63，求该三棱锥的侧面积．解：(1)证明：因为四边形ABCD 为菱形，所以AC ⊥BD . 因为BE ⊥平面ABCD ，所以AC ⊥BE .故AC ⊥平面BED .又AC 平面AEC ，所以平面AEC ⊥平面BED .(2)设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得AG ＝GC＝32x ，GB ＝GD ＝x 2.因为AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝32x .由BE ⊥平面ABCD ，知△EBG 为直角三角形，可得BE ＝22x .由已知得，三棱锥E ACD 的体积V 三棱锥E ACD ＝13×12·AC ·GD ·BE＝624x 3＝63，故x ＝2.从而可得AE ＝EC ＝ED ＝ 6.所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为 5. 故三棱锥E ACD 的侧面积为3＋2 5.[综合题组练])1.如图，以棱长为1的正方体的顶点A 为球心，以2为半径作一个球面，则该正方体的表面被球面所截得的所有弧长之和为( )A.3π4 B ．2π C.3π2D ．9π4解析：选C.正方体的表面被该球面所截得的弧长是相等的三部分，如图，上底面被球面截得的弧长是以A 1为圆心，1为半径的圆周长的14，所以所有弧长之和为3×2π4＝3π2.故选C.2．(2020·江西萍乡一模)如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为( )A.236 B ．72C.76D ．4解析：选A.由三视图可得，该几何体是如图所示的三棱柱ABB 1DCC 1，挖去一个三棱锥E FCG 所形成的，故所求几何体的体积为12×(2×2)×2－13×⎝ ⎛⎭⎪⎫12×1×1×1＝236. 故选A.3．(2020·福建厦门外国语学校模拟)已知等腰直角三角形ABC 中，∠ACB ＝90°，斜边AB ＝2，点D 是斜边AB 上一点(不同于点A ，B )．沿线段CD 折起形成一个三棱锥A CDB ，则三棱锥A CDB 体积的最大值是( )A ．1B ．12C.13D ．16解析：选D.设AD ＝x ，将△ACD 折起使得平面ACD ⊥平面BCD .在△ACD 中，由面积公式得12CD ·h 1＝12AD ·1(h 1为点A 到直线CD 的距离)，则h 1＝x1＋（x －1）2.由题易知h 1为点A 到平面BCD 的距离，故三棱锥A CDB 体积为V ＝13S △BCD ·h 1＝13×⎝ ⎛⎭⎪⎫12BD ·1·h 1＝16·2x －x 2x 2－2x ＋2，x ∈(0，2)．令t ＝x 2－2x ＋2，则t ∈[1，2)，故V ＝16·2－t 2t ＝16·⎝ ⎛⎭⎪⎫2t －t .由于2t －t 是减函数，故当t ＝1时，V取得最大值为16×(2－1)＝16.故选D.4．设A ，B ，C ，D 是同一个半径为4的球的球面上的四点，△ABC 为等边三角形且其面积为93，则三棱锥D ABC 体积的最大值为( )A ．12 3B ．183C ．24 3D ．543解析：选B.如图，E 是AC 的中点，M 是△ABC 的重心，O 为球心，连接BE ，OM ，OD ，BO .因为S △ABC ＝34AB 2＝93，所以AB ＝6，BM ＝23BE＝23AB 2－AE 2＝2 3.易知OM ⊥平面ABC ，所以在Rt △OBM 中，OM ＝OB 2－BM 2＝2，所以当D ，O ，M 三点共线且DM ＝OD ＋OM 时，三棱锥D ABC 的体积取得最大值，且最大值V max ＝13S △ABC ×(4＋OM )＝13×93×6＝18 3.故选B. 5.如图所示，已知三棱柱ABC A 1B 1C 1的所有棱长均为1，且AA 1⊥底面ABC ，则三棱锥B 1ABC 1的体积为________．解析：三棱锥B 1ABC 1的体积等于三棱锥A B 1BC 1的体积，三棱锥A B 1BC 1的高为32，底面积为12，故其体积为13×12×32＝312.答案：3126．已知半球O 的半径r ＝2，正三棱柱ABC A 1B 1C 1内接于半球O ，其中底面ABC 在半球O 的大圆面内，点A 1，B 1，C 1在半球O 的球面上．若正三棱柱ABC A 1B 1C 1的侧面积为63，则其侧棱的长是________．解析：依题意O 是正三角形ABC 的中心，设AB ＝a ，分析计算易得0<a <23，AO ＝33a ，在Rt △AOA 1中，A ′O ＝r ＝2，则AA 1＝r 2－AO 2＝4－a 23，所以正三棱柱ABC A 1B 1C 1的侧面积S ＝3a ·AA 1＝3a4－a 23＝3－a 43＋4a 2＝63，整理得a 4－12a 2＋36＝0，解得a 2＝6，即a ＝6，此时侧棱AA 1＝ 2.答案：27.如图，正方体ABCD A 1B 1C 1D 1的棱长为1，P 为BC 边的中点，Q 为线段CC 1上的动点，过点A ，P ，Q 的平面截正方体所得的截面为S ，当CQ ＝1时，S 的面积为________．解析：当CQ ＝1时，Q 与C 1重合．如图，取A 1D 1，AD 的中点分别为F ，G .连接AF ，AP ，PC 1，C 1F ，PG ，D 1G ，AC 1，PF .因为F 为A 1D 1的中点，P 为BC 的中点，G 为AD 的中点，所以AF ＝FC 1＝AP ＝PC 1＝52，PG 綊CD ，AF 綊D 1G .由题意易知CD 綊C 1D 1，所以PG 綊C 1D 1，所以四边形C 1D 1GP 为平行四边形，所以PC 1綊D 1G ，所以PC 1綊AF ，所以A ，P ，C 1，F 四点共面，所以四边形APC 1F 为菱形．因为AC 1＝3，PF ＝2，过点A ，P ，Q 的平面截正方体所得的截面S 为菱形APC 1F ，所以其面积为12AC 1·PF ＝12×3×2＝62.答案：628．已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45°.若△SAB 的面积为515，则该圆锥的侧面积为________．解析：如图所示，设S 在底面的射影为S ′，连接AS ′，SS ′.△SAB 的面积为12·SA ·SB ·sin ∠ASB ＝12·SA 2·1－cos 2∠ASB ＝1516·SA 2＝515，所以SA 2＝80，SA ＝4 5.因为SA 与底面所成的角为45°，所以∠SAS ′＝45°，AS ′＝SA ·cos 45°＝45×22＝210.所以底面周长l ＝2π·AS ′＝410π，所以圆锥的侧面积为12×45×410π＝402π.答案：402π。

8-5简单几何体的面积与体积

北师大版
第8章第五节
高考数学总复习
[点评] 空间几何体表面上的距离最小问题是立体几何的基本问题，其解题思路是将空间几何体侧面展开，把立体几何问题转化为平面几何问题，然后利用平面几何知识去解决．
北师大版
第8章第五节
高考数学总复习
有一根长为 3πcm，底面半径为 2cm 的圆柱形铁管，用
力、计算能力．
北
2．多与三视图、简单组合体相联系，在知识交汇点处命
师大
版
题．
3．多以选择题、填空题的形式考查，偶尔在解答题中出
现，属容易题．
第8章第五节
高考数学总复习
北师大版
第8章第五节
高考数学总复习
知识梳理 1．圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、
扇环；它们的表面积等于侧面积与底面积之和 .
△PB1C1
和△PBC
中，PB1＝B1C1＝4＝1， PB BC 8 2
∴PB1＝B1B＝8，B1 为 PB 的中点，E1 为 PE 的中点．
在 Rt△PEB 中，
北师
大
PE＝ PB2－BE2＝ 162－42＝4 15(cm)，
版
E1E＝12PE＝2 15(cm)．在 Rt△POE 中，
PO＝ PE2－OE2＝ 4 152－42＝4 14(cm)，
台体的体积 V 台＝31(S 上＋ S上·S下＋S 下)·h. 4．球的表面积 S＝ 4πR2；体积 V＝43πR3.
北师大版
第8章第五节
高考数学总复习
基础自测
北师
大
版
第8章第五节
高考数学总复习
1.(2011·湖北文，7)设球的体积为 V1，它的内接正方体的体

第8章立体几何初步(复习课件)高一数学(人教A版2019必修第二册)

81 C. 4 π
D．16π
(1)如图，设 PE 为正四棱锥 P-ABCD 的高，则正四棱锥 P-ABCD 的外接球的球心 O 必在其高 PE 所在的直线上，延长 PE 交球面于一点 F，连接 AE，AF.
由球的性质可知△PAF为直角三角形且AE⊥PF，
又底面边长为4, 所以AE＝2 2 ， PE＝6, 所以侧棱长PA＝
3
在Rt△CDE中,
故二面角B-AP-C的正切值为2.
tanCED CD 2 3 2， DE 3
归纳总结
(1)求异面直线所成的角常用平移转化法(转化为相交直线的夹角). (2)求直线与平面所成的角常用射影转化法(即作垂线、找射影). (3)二面角的平面角的作法常有三种：①定义法；②三垂线法； ③垂面法.
的表面积为 16π，则 O 到平面 ABC 的距离为
A. 3
3 B.2
√C.1
3 D. 2
解析如图所示，过球心O作OO1⊥平面ABC，则O1为等边三角形ABC的外心. 设△ABC的边长为a，则 43a2＝943，解得 a＝3， ∴O1A＝23× 23×3＝ 3. 设球O的半径为r，则由4πr2＝16π，得r＝2，即OA＝2. 在 Rt△OO1A 中，OO1＝ OA2－O1A2＝1，
五、直线、平面平行的判定与性质
1．直线与平面平行
(1)判定定理：平面外一条直线与这个平面内的一条直线平行，则该直线与此平面平行(线线平行⇒线面平行).
(2)性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”).
2．平面与平面平行
则直线 PB 与 AD1 所成的角为( )
A．
2

人教A版(新教材)高中数学第二册(必修2)课件：第八章立体几何初步章末复习课

6πS 9π2 .
要点二空间中的平行关系在本章中，空间中的平行关系主要是指空间中线与线、线与面及面与面的平行，其中三种关系相互渗透.在解决线面、面面平行问题时，一般遵循从“低维”到“高维” 的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而利用性质定理时，其顺序相反，且“高维”的性质定理就是“低维”的判定定理.特别注意，转化的方法总是由具体题目的条件决定，不能过于呆板僵化，要遵循规律而不局限于规律.如下图所示是平行关系相互转化的示意图.
证明 (1)因为平面PAD⊥底面ABCD，PA在平面PAD内且垂直于这两个平面的交线AD，所以PA⊥底面ABCD. (2)因为AB∥CD，CD＝2AB，E为CD的中点，所以AB∥DE，且AB＝DE. 所以四边形ABED为平行四边形. 所以BE∥AD. 又因为BE⊄平面PAD，AD⊂平面PAD，所以BE∥平面PAD.
V 圆锥＝13πr2h (r 是底面半径， h 是高)
用平行于圆锥底面
圆的平面去截圆锥，
台底面与截面之间的
旋
部分
转
体
半圆以它的直径所
圆
在直线为旋转轴，
球旋转一周形成的曲
面叫做球面，球面
所围成的旋转体
S圆台＝π(r′2＋r2＋ r′l＋rl)(r′，r分别是上、下底面半径，l是母线长)
V 圆台＝13πh(r′2＋ r′r＋r2)(r′，r 分别是上、下底面半径，h 是高)
以矩形的一边所在
圆直线为旋转轴，其
柱余三边旋转形成的
旋
面所围成的旋转体
转
体
以直角三角形的一
圆圆条直角边所在直线为旋转轴，其余两
锥边旋转一周形成的
面所围成的旋转体

第八章-立体几何初步复习课图文课件

简单说，斜二测画法的规则是：横竖不变，纵减半，平行
性不变．
复习回顾结合正八棱柱的直观图，说出用斜二测画法画空间几何体的直观图的基本步骤．
横竖不变，纵减半，平行性不变
复习回顾
问题3 对于空间几何体，可以有不同的分类，你能选择不同的分类标准对柱、锥、台、球等空间几何体进行分类吗？如何计算柱、锥、台、球的表面积和体积？你能说出柱、锥、台、球的体积公式之间的联系吗？
，得 α ∩ γ ＝a；又γ ∩ β ＝直线b，故a与b
重合，
α ， β ， γ相交于同一条直线．
复习回顾
探究3 已知三个不同的平面 α， β， γ两两相交，设 α ∩ β＝直线 c，
β ∩ γ ＝直线a， γ ∩ α ＝直线b，试问a，b，c有怎样的位置关系？
说明理由并画出相应图形． ②当a与c相交时，设a∩c＝点O，由 α ∩ β ＝直线c， β ∩ γ
复习回顾探究4 怎样求图中的四个四面体的外接球与内切球的半径？
四个四面体的外接球与正方体的
类比
外接球相同，其一条直径为正方
体的体对角线，半径
．
复习回顾
问题4 刻画平面的三个基本事实是立体几何公理体系的基石，是研究空间图形、进行逻辑推理的基础．实际上，三个基本事实刻画了平面的“平”、平面的“无限延展”，你能归纳一下刻画的方法
探究1 说明作出点H的过程．点H在线段DB1的什么位置？
设B1D1 ∩A1C1＝P，点P为线段B1D1的中点，且平面
A1BC1 ∩平面BB1D1D＝BP．
在矩形BB1D1D中， BP∩B1D＝H．
由△B1HP∽△DHB，且．
，知
复习回顾
探究1 说明作出点H的过程．点H在线段DB1的什么位置？

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第八章立体几何初步第5课时空间几何体的表面积和体积
1. 棱长为1的正三棱锥的全面积是________．
答案： 3
解析：因为四个面是全等的正三角形，则S表面积＝4S底面积＝4×
3
4
＝ 3.
2. 圆柱的底面半径为3cm，体积为18πcm3，则其侧面积为________cm2.
答案：12π
解析：V＝πr2l＝9πl＝18π，所以l＝2，
故S侧面积＝2πrl＝12π.
3. 如图所示，已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成，则该多面体的体积是________．
答案：
2 6
解析：由题知该多面体为正四棱锥，底面边长为1，侧棱长为1，斜高为
3
2
，连结顶点和
底面中心即为高，可求高为
2
2
，所以体积为V＝
1
3
×1×1×
2
2
＝
2
6
.
4. (2013·苏州调研)如图，在长方体ABCD-A1B1C1D1中，AB＝AD＝3 cm，AA1＝2 cm，则三
棱锥AB 1D 1D 的体积为________cm 3
.
答案：3
解析：VAB 1D 1D ＝VB 1AD 1D ＝VB 1AA 1D ＝13·S △AA 1D ·B 1A 1＝13×1
2
×2×3×3＝3.
5. 等边圆柱(底面直径和高相等的圆柱)的底面半径与球的半径相等，则等边圆柱的表面积与球的表面积之比为________.
答案：32
解析：等边圆柱的表面积为S 1＝2πR ·2R ＋2·πR 2＝6πR 2，球的表面积S 2＝4πR 2
，∴
S 1S 2
＝6πR 2
4πR 2＝32. 6. (2013·课标Ⅱ)已知正四棱锥O-ABCD 的体积为32
2
，底面边长为3，则以O 为球心，
OA 为半径的球的表面积为________．
答案：24π
解析：设正四棱锥的高为h ，则13×(3)2
h ＝322
，
解得高h ＝32
2
.
则底面正方形的对角线长为2×3＝6，
所以OA ＝⎝ ⎛⎭⎪⎫3222＋⎝ ⎛⎭⎪⎫622
＝6，
所以球的表面积为4π(6)2
＝24π.
7. (2013·江苏)如图，在三棱柱A1B1C1-ABC中，D、E、F分别是AB、AC、AA1的中点，设三棱锥FADE的体积为V1，三棱柱A1B1C1ABC的体积为V2，则V1∶V2＝________．
答案：1∶24
解析：三棱锥FADE与三棱锥A1ABC的相似比为1∶2，故体积之比为1∶8.又因三棱锥A1ABC 与三棱柱A1B1C1ABC的体积之比为1∶3.所以，三棱锥FADE与三棱柱A1B1C1ABC的体积之比为1∶24.
8. 圆锥母线长为6cm，底面直径为3cm，在母线OA上有一点B，AB＝2cm，那么由A点绕圆锥侧面一周到B点的最短矩离为__________cm.
答案：213
解析：设侧面展开扇形圆心角为n，底面周长＝3π，则6nπ
180°
＝3π，解得n＝90°，在展开扇形中，∠O＝90°，OB＝6－2＝4.Rt△AOB中，AB＝AO2＋BO2＝62＋42＝213.
9. 如图(a)，在直角梯形ABCD 中，∠ADC ＝90°，CD ∥AB ，AB ＝4，AD ＝CD ＝2，将△ADC 沿AC 折起，使平面ADC ⊥平面ABC ，得到几何体DABC ，如图(b)所示．
(1) 求证：BC⊥平面ACD ； (2) 求几何体DABC 的体积．
(1) 证明：在图中，可得AC ＝BC ＝22，从而AC 2
＋BC 2
＝AB 2
，故AC⊥BC.又平面ADC⊥平面ABC ，平面ADC∩平面ABC ＝AC ，BC Ì平面ABC ，∴ BC ⊥平面ACD.
(2) 解：由(1)可知，BC 为三棱锥BACD 的高，BC ＝22，S △ACD ＝2，
∴ V BACD ＝13S △ACD ·BC ＝13×2×22＝423，由等体积性可知，几何体DABC 的体积为42
3
.
10. 正三棱锥的高为1，底面边长为26，内有一个球与它的四个面都相切(如图)．求：
(1) 这个正三棱锥的表面积；
(2) 这个正三棱锥内切球的表面积与体积．
解：(1) 底面正三角形中心到一边的距离为13×3
2×26＝2，则正棱锥侧面的斜高为
12
＋（2）2
＝ 3.
∴ S 侧＝3×1
2
×26×3＝9 2.
∴ S 表＝S 侧＋S 底＝92＋12×32
×(26)2
＝92＋6 3.
(2) 设正三棱锥PABC 的内切球球心为O ，连结OP 、OA 、OB 、OC ，而O 点到三棱锥的四个面的距离都为球的半径r.
∴ V PABC ＝V OPAB ＋V OPBC ＋V OPAC ＋V OABC ＝13S 侧·r ＋13·S △ABC ·r ＝1
3S 表·r ＝(32＋23)r.
又V PABC ＝13×12×32×(26)2
×1＝23，∴ (32＋23)r ＝23，得r ＝2332＋23＝
23（32－23）
18－12
＝6－2.
∴ S 内切球＝4π(6－2)2
＝(40－166)π.
V 内切球＝43π(6－2)3
＝83
(96－22)π.
11. 如图，已知四棱锥PABCD 中，底面ABCD 是直角梯形，AB ∥CD ，∠ABC ＝45°，DC ＝1，AB ＝2，PA ⊥平面ABCD ，PA ＝1.
(1) 求证：AB∥平面PCD ； (2) 求证：BC⊥平面PAC ；
(3) 若M 是PC 的中点，求三棱锥MACD 的体积.
(1) 证明：已知底面ABCD 是直角梯形，
∴ AB ∥DC.又AB Ë平面PCD ，CD Ì平面PCD ， ∴ AB ∥平面PCD.
(2) 证明：在直角梯形ABCD 中，过C 作CE⊥AB 于点E ，则四边形ADCE 为矩形， ∴ AE ＝DC ＝1.又AB ＝2，
∴ BE ＝1.在Rt △BEC 中，∠ABC ＝45°，
∴ CE ＝BE ＝1，CB ＝2，则AC ＝AD 2＋CD 2
＝2，
∴ AC 2＋BC 2＝AB 2
，
∴ BC ⊥AC.又PA⊥平面ABCD ，
∴ PA ⊥BC.又PA∩AC＝A ，∴ BC ⊥平面PAC. (3) 解：∵ M 是PC 的中点，
∴ M 到平面ADC 的距离是P 到平面ADC 距离的一半．
∴ V MACD ＝13S △ACD ·⎝ ⎛⎭⎪⎫12PA ＝13×⎝ ⎛⎭⎪⎫12×1×1×12＝1
12.。