化工热力学剩余性质推导

合集下载

化工热力学公式

热力学是以热力学第一、第二定律及其他一些基本概念理论为基础，研究能量、能量转换以及与转换有关的物质性质相互之间关系的科学。

有工程热力学、化学热力学、化工热力学等重要分支。

化工热力学是将热力学原理应用于化学工程技术领域。

化工热力学主要任务是以热力学第一、第二定律为基础，研究化工过程中各种能量的相互转化及其有效利用，研究各种物理和化学变化过程达到平衡的理论极限、条件和状态。

热力学的研究方法，原则上可采用宏观研究方法和微观研究方法。

以宏观方法研究平衡态体系的热力学称为经典热力学。

体系与环境：隔离体系，封闭体系，敞开体系流体的P-V-T关系在临界点C ：临界点是汽液两相共存的最高温度和最高压力，即临界温度Tc，临界压力Pc。

纯流体的状态方程(EOS) 是描述流体P-V-T性质的关系式。

由相律可知，对纯流体有：f( P, T, V ) = 0混合物的状态方程中还包括混合物的组成（通常是摩尔分数）。

状态方程的应用（1）用一个状态方程即可精确地代表相当广泛范围内的P、V、T实验数据，借此可精确地计算所需的P、V、T数据。

（2）用状态方程可计算不能直接从实验测定的其它热力学性质。

（3）用状态方程可进行相平衡和化学反应平衡计算。

压缩因子（Z）即:在一定P，T下真实气体的比容与相同P，T下理想气体的比容的比值.理想气体方程的应用（1 ）在较低压力和较高温度下可用理想气体方程进行计算。

（2 ）为真实气体状态方程计算提供初始值。

（3 ）判断真实气体状态方程的极限情况的正确程度，当或者时，任何的状态方程都还原为理想气体方程。

维里方程式Virial系数的获取( 1 ) 由统计力学进行理论计算目前应用很少( 2 ) 由实验测定或者由文献查得精度较高( 3 ) 用普遍化关联式计算方便，但精度不如实验测定的数据两项维里方程维里方程式Z=PV/RT=1+ B/P （1）用于气相PVT性质计算，对液相不能使用；（2）T<Tc, P<1.5MPa, , 用两项维里方程计算，满足工程需要；温度更高时，压力的范围可以更大些。

化工热力学-第3章(自学考试参考)

把压缩因子的普遍化式子代入到剩余焓和剩余熵普遍化后的式子，就可得到：
H RfTr， P r， SRfTr， P r，
44
（2）计算方法
两种方法——普维法和普压法
1) 普维法是以两项维里方程为基础计算在恒压下对T求导：
Z 1 BP RT
Z TP
PTB
R T
P
RPT1TBP
TB2
B
f(T)
25
dH cpdT
H dH
=
H
0
T T0
C
p
dT
H
*
H
* 0
C
* p
dT
同理:
S* S0
T CpdTRln p
T T0
p0
H * , S * — 所求状态(T，p)的H和S，理想气体；
H0*, S0* — 任意选择的基准态(T0，P0)所对应H和S。
26
⒊ H R 和 S R 的计算式
1 V V T p
∴ V V
T p
19
有了H，S的基本计算式就可以解决热力学其它函数的计算问题。
如:
U=H-PV A=U-TdS=H-PV-TS G=H-TS
20
计算原理及方法(Clculative Pinciple and Method of Thermodynamic Properties)
HR0pVRdpT0PVTRPdP (恒T)
SR
P 0
VR T
dP P
(恒T)
35
▪做图
VR
p
V R dp
0
P求
P
36
VR P1 P2 P3
V R T

化工热力学考试重点终极版整理

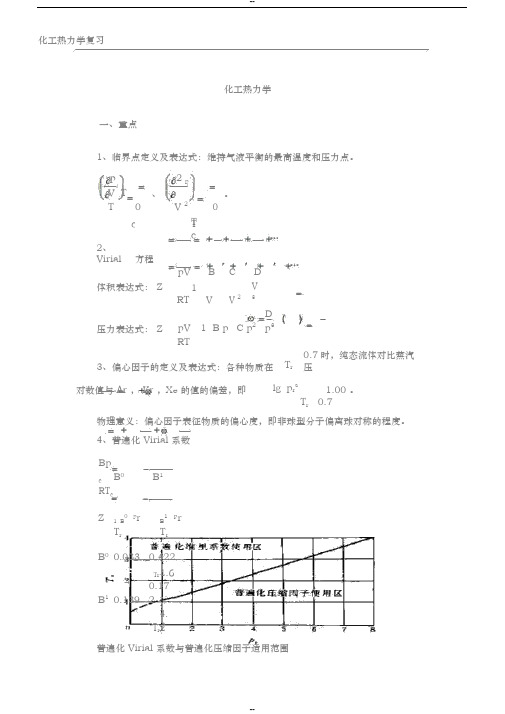
化工热力学复习化工热力学一、重点1、临界点定义及表达式：维持气液平衡的最高温度和压力点。

p 0 、 2 p 0 。

V T T V 2c T Tc2、Virial 方程体积表达式： Z pV B CD RT 1V 2 V 3V 压力表达式： Z pV 1 B p C p 2 Dp 3RT3、偏心因子的定义及表达式：各种物质在 T r 0.7时，纯态流体对比蒸汽压对数值与 Ar ， Kr ，Xe 的值的偏差，即lg p r s 1.00 。

T r 0.7物理意义：偏心因子表征物质的偏心度，即非球型分子偏离球对称的程度。

4、普遍化 Virial 系数BpcB 0B 1 RT cZ 1 B 0 p r B 1 p r T r T r B 0 0.083 0.422 Tr 1.6B 1 0.139 0.172T r 4.2普遍化 Virial 系数与普遍化压缩因子适用范围1化工热力学复习5、Prausnitz 混合规则Tcij T ci T cj0.5 1 k ij1 1 3 V ci 3 V cj 3 Vcij2ZcijZci Z zj 2p cij Zcij RT cij Vcij ciji j 26、熵的表达式的推导第一 dS 方程当 S S T ,V 时，则有dS SdT S dV T VVT因C V Q T d SS T T V TV T V得 S C VT V TS又V T p T V所以 dS dT pd VC V T TV积分得到S S 0 TVS C V d ln T T 0 V 0p dV T V第二 dS 方程当S S T , p 时，则有SdT SdSdp T p p T2化工热力学复习因S C p S VT p T p T T p所以 dS C p dT Vdp T T p积分得到TpS S0S C p d ln T T0p0第三 dS 方程V dp T p当S S p,V 时，则有dS S SdpdV p V V p因为SpS V VpTpTVVpSTSTT C VV p V TT C pp VpTC V T C p TdSp dp d VT V T V p 积分得到S S0p C V T V C p T dV T p VdpT VpV0p7、焓的表达式推导利用刚刚导出的三个dS 方程来得到三个 dH 方程。

化工热力学3-1Chapter3纯流体的热力学性质计算(1-2)

热力学的四个基本公式
对热力学四个基本公式的说明： (1) 虽然在四个基本公式的推导过程中采用了可逆过程，
如 d Qr = TdS 和 d W膨胀 = pdV ，但这些公式适用于包括可逆过
程和不可逆过程在内的任何过程。这是因为公式中的物理量皆为状态函数，其变化值仅取决于始态和终态。
注意：只有在可逆过程中，上述公式中的 TdS 才代表热效应，pdV 才代表膨胀功。若是不可逆过程，则根据热力学第二
y
(3 6)
02:12
11
§3.1 热力学性质间的关系 Chapter3.纯流体的热力学性质计算
3.1.2 点函数间的数学关系式
(1)全微分关系式与偏微分原理——Green定律
式（3-5）、（3-6）即为Green定律,其意义:
①若x、y、Z都是点函数，热力学即为状态函数或称系统性质，且Z是自变量x、y的连续函数，则Z必有全微分式且存在式（3-6）；
dU=TdS－pdV (3-1) dH=TdS+Vdp (3-2) dA=SdTpdV (3-3) dG=SdT+Vdp (3-4)
注意基本微分方程的应用条件及其含义：
定量、定组成、单相、无非体积功的体系！
定量——封闭体系或稳流体系；
只有
定组成——无化学反应；
状态
单相——无相变
变化
02:12
无需可逆条件
dH=T·dS+V ·dp 等温时两边除dp (H/p)T=V+T (S/p)T
S p
T
V T
p
H p
T
V
T V T
p
H
T2 T1
cpdT
p2 p1
V

化工热力学讲义-3-第三章-纯流体的热力学性质

第三章纯流体的热力学性质3.1热力学性质间的关系3.1.1单相流体系统基本方程根据热力学第一、二定律，对单位质量定组成均匀流体体系，在非流动条件下，其热力学性质之间存在如下关系： pdV TdS dU -=；Vdp TdS dH +=pdV SdT dA --=；Vdp SdT dG +-=上述方程组是最基本的关系式，所有其他的函数关系式均由此导出。

上述基本方程给我们的启示是：p-V-T 关系数据可以通过实验测定，关键是要知道S 的变化规律，若知道S 的变化规律，则U 、H 、A 、G 也就全部知道了。

下面所讲主要是针对S 的计算。

3.1.2点函数间的数学关系式对于函数：()y x f z ,=，微分得：dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂=如果x 、y 、z 都是点函数，且z 是自变量x 、y 的连续函数，Ndy Mdx +是z （x ，y ）的全微分，则M 、N 之间有：该式有两种意义：①在进行热力学研究时，如遇到（1）式，则可以根据（2）式来判断dz 是否全微分，进而可判定z 是否为系统的状态函数；②如已知z 是状态函数，则可根据（2）式求得x 与y 之间的数学关系。

以下循环关系式也经常遇到：3.1.3Maxwell 关系式由于U 、H 、A 和G 都是状态函数，将（2）式应用于热力学基本方程，则可获得著名的Maxwell 方程：V S S p V T ⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂；p S S V p T ⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ T V V S T p ⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂；Tp p S T V ⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫⎝⎛∂∂能量方程的导数式：T S H S U pV =⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂；p V A V U T S -=⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂V p G p H TS =⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂；S T A T G V p -=⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂ 在实际工程应用中，Maxwell 方程应用之一是用易于实测的某些数据来代替或计算那些难于实测的物理量。

化工热力学重点难点考点剖析

第一章绪论（1）明确化工热力学的主要任务是应用经典热力学原理，推算物质的平衡性质，从而解决实际问题，所以物性计算是化工热力学的主要任务。

（2）掌握热力学性质计算的一般方法（3）热力学性质计算与系统有关。

大家必须明确不同系统的热力学性质计算与其热力学原理的对应关系，这一点对于理解本课程的框架结构十分重要。

第二章流体的P-V-T关系（4）应该理解状态方程不仅可以计算流体的p-V-T性质，而且在推算热力学性质中状态方程是系统特征的重要模型。

（5）熟悉纯物质的P-V-T相图及其相图上的重要概念，如三相点、临界点、汽化线、熔化线、升华线、等温线、等压线等容线、单相区、两相共存区、超临界流体区等。

能在p-v图和p-T图中定性表达出有关热力学过程和热力学循环。

（6）掌握由纯物质的临界点的数学特征约束状态方程常数的方法。

（7）理解以p为显函数和以V为显函数的状态方程的形式，以及它们在性质计算中的区别。

（8）能借助于软件用PR和SRK方程进行p-V-T性质计算，清楚计算时所需要输入的物性常数及其来源。

对于均相混合物性质的计算，需要应用混合法则，了解相互作用参数的含义和取值。

（9）理解对应态原理的概念，掌握用图表和三参数对应态原理计算物性的方法，了解偏心因子对应态原理。

（10）能够通过查寻有关手册，估算蒸汽压、饱和气液相摩尔体积、汽化焓等物性，清楚它们之间的关系。

第三章纯流体热力学性质的计算（11）均相封闭系统的热力学原理给出了热力学性质之间的普遍化依赖关系，结合表达系统特征的模型就能获得不同热力学性质之间的具体表达式。

在物性推算中应该明确需要给定的独立变量，需要计算的从属变量，以及从属变量与独立变量之间的关系式。

另外，还必须输入有关模型参数，结合一定的数学方法，才能完成物性推算。

（12）清楚剩余性质的含义，能用剩余性质和理性气体热容表达状态函数的变化。

能够用给定的状态方程推导出剩余性质表达式。

化工热力学纯流体的热力学性质

习
题
Байду номын сангаас
2.解：始态1→终态2的焓变为ΔHT H2=H1+ΔHT 或者采用剩余焓HR计算
H1
状态1 T1，p1 理想气体
ΔHT
状态2 T1，p2 真实气体
H2
因为p1较低，故可以视为id.g
ΔH
id
HR
＝0
ΔH T = ΔH id + H R = H R
理想气体 T1，p2
H2=H1+ΔHT＝H1+HR
Chemical Engineering Thermodynamics
第三章纯流体的热力学性质
通过本章的学习，可以实现：由一个状态方程 EOS和Cpid 的信息推算任意状态下的热力学性质（有些性质是基于参考态的相对值）。真实气体热力学性质的计算方法一般有两种偏离函数法（偏差函数法）剩余性质法（残余函数法）依据：H， U和S均为状态函数，与路程无关
ΔH = ∫ C dT = ∫ (0.571 + 0.0009T )dT
' 12 T2 T1 l p 9.4 88
ΔH’12＝-48.33 kcal/kg≠0
与ΔH=0不符，说明必然有汽化发生假设节流后为饱和蒸汽，则焓变为 ΔH”12= ΔH’12+ ΔHV ΔHV可根据克-克方程求出
ΔH V dp S = dT T (V V − V L )
⎛ dB 0 dB1 ⎞ SR = − pr ⎜ ⎟ ⎜ dT + ω dT ⎟ R r ⎠ ⎝ r
(3 - 62)
得到：
H1R = -2690.6 J/mol S1R = -4.668 J/mol.K
●过程二：理想气体变化过程

化工热力学复习总结

第2章流体的P-V-T 关系1.掌握状态方程式和用三参数对应态原理计算PVT 性质的方法。

2.了解偏心因子的概念，掌握有关图表及计算方法。

1. 状态方程：在题意要求时使用该法。

① 范德华方程：常用于公式证明和推导中。

② R —K 方程： ③ 维里方程：2. 普遍化法：使用条件：在不清楚用何种状态方程的情况下使用。

三参数法：① 普遍化压缩因子法② 普遍化第二维里系数法3、Redlich-Kwong （RK ）方程3、Soave （SRK ）方程4、Peng-Robinson （PR ）方程()22a 0.45724c r cR T T P α=0.0778c cRT b P =§2-5高次型状态方程5、virial 方程 virial 方程分为密度型：和压力型：第3章纯物质的热力学性质1、热力学性质间的关系dU TdS pdV =-H=U+PV d H T d S V d =+A=U-TS d A S d Tp d V =--G=H-TS d G S d TV d =-+ Maxwell 关系式S V T P V S ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭ S P T V P S ∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭ V T P S T V ∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭ P TV S T P ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭ 转换公式： 1Z X YX Y Z Y Z X ∂∂∂⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭3.2计算H ∆和S ∆的方法1.状态方程法： P P V d H C d T V T d PT ⎡⎤∂⎛⎫=+- ⎪⎢⎥∂⎝⎭⎣⎦ P PC V d S d T d PT T ∂⎛⎫=- ⎪∂⎝⎭ 2.剩余性质法：①普遍化压缩因子图()()1R R RTC C CH H HRT RT RT ω=+ ()()01R R RTS S S R RRω=+②普遍化的第二维里系数方法0101R T r r r C r r H dB dB P B T B T RT dT dT ω⎡⎤⎛⎫=-+-⎢⎥ ⎪⎝⎭⎣⎦ 01R T r r r S dB dB P R dT dT ω⎛⎫=-+ ⎪⎝⎭0 1.60.4220.083r B T =-14.20.1720.139r B T =-导出： 0 2.60.675r r dB dT T = 15.20.772r rdB dT T = 第6章化工过程能量分析热力学第一定律一、功 Wp dVδ=-外不可逆过程: 2112W P dV =-⎰外体可逆过程： 21V rev V W p dV =-⎰体体规定：体系吸热为正，放热为负；对外做功为负，接受功为正。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ｗｉｍｐｒｔｒｎｏｕｓｉｄｐｎｅｔａｉｂｅｔｔｈｅｅａｕｅａｄｖｌｍｅａｅｅｄｎｒｌｎｖａ
Ｋｅｗｏｄ：ｈｍｉａｈｒｏｙｎｍｉｓｒｓｄａｐｏｅｔ；ｉｄｐｎｅｔａｉｂｅｙｒｓｃｅｃｌｅｍｄａｃ；ｅｉｕｌｒｐｒｙｎｅｅｄｎｒｌｔｖａ
２１年第５期０１
２４５ｗｗｗ．ｄｈｍ．ｏｇｃｅｃｍ
第３卷总第２７８１期
化工热力学剩余性质推导
胡光辉，潘湛昌，魏志钢
（广东工业大学轻工化工学院，广东广州５００）０６１
【要】绍了剩余性质的概念及其数学表达，在以压力、温度为独立变量的剩余性质公式的基础上，推导了以温度、体积为独立变量的剩摘介余性质公式。由于多数热力学状态方程以压力为显函数，即ｐｐＴ）＝（，Ｖ，因此推导以温度、体积为独立变量的剩余性质公式具有应用意义。【词】工热力学；剩余性质；独立变量关键化［图分类号］４中Ｇ［献标识码】文Ｂ［章编￣］７１６（０１５０５—１文－ｍ０—８５２１）。２４０ｏ
：
［］］：导＋。筹ｒ
‘ ６ ’
ｌ —筹ｆ］筹ｌ筹一：］
Ｐ）一
在恒定温度条件下，公式（）以如下变化：３可
１以压力和温度为独立变量的剩余性质
根据热力学性质基本关系：
ｄ＝ＶｐＳＧｄｄＴ・Ｇ＝Ｈ —ＴＳ
Ｇ：
ｆ（ｊ（ＤｆｆｖＰｗ：ｖ一ｖ
ｌＰｎｎ一＿ Ⅳ ｆ
Ｇ＝而ｆ）ＲｆＲ（ｄＶ＝ｖ
‘
吉布斯函数Ｇ是温度的函数，故：
【）Ｔ熹而（—ｒ熹ｄ导ＲｒＲＶＳ）ＴＲ＝Ｔ＝ｄＲＲ丁１ｄＴｐＴ旦ｄ，苦咖熹
＝
式中Ｖ为理想气体的摩尔体积。压力看成是温度与体把积的函数，则公式（）８进一步推导如下：
ＤｅｄｕｃｉｎｏｓｄｕａｏｒｙｏｈｍｉａｔｏｆＲｅｉｌＰｒｐｅｔｆＣｅｃｌＴｈｅｍｏｙｎａｉｓｒｄｍｃ
ＨｕＧｕｎｈｉＰｎＺａｃａｇＷｅｈｇｎａｇｕ，ａｈｎｈｎ，ｉｉａｇＺ
ＡｂｔａｔｔｗａｎｒｄｃｄｔａｏｃｐｆｒｓｄａｐｏｅｔｎｔｍａｈｍａｉｘｒｓｉｎＢａｅｎｅｕｔｏｓｏｅｉｕｌｐｏｅｔｉｒｓｕｅａｄｓｒｃ：ＩｓｉｔｏｕｅｈｔｃｎｅｔｏｅｉｕｌｒｐｒｙａｄｉｔｅｔｅｐｅｓｏｓｃｓｄｏｑａｉｎｆｒｓｄａｒｐｒｙｗｔｐｅｓｒｎｈｔｍｐｒｔｒｓｉｄｐｎｅｔａｉｂｅｗｅｄｄｃｄｔｅｅｐｅｓｏｆｅｉｕｌｒｐｒｔｅｅａｕｅａｄｖｌｍｅａｎｅｅｄｎａｉｂｅＢｅａｓｆｒｓｕｅａｅｅａｕｅａｎｅｅｄｎｒａｌ，ｅｕｅｘｒｓｉｎｏｓｄａｐｏｅｔｗｉｔｍｐｒｔｒｎｏｕｓｉｄｐｎｅｔｒａｌ．ｃｕｅｏｅｓｒｓａｖｈｒｙｈｖｐ
化工热力学性质ｕ，Ｈ，Ａ，Ｇ，Ｓ函数的绝对值是多少，在实际应用ｔ我们并不关心，ｔｔ只要能得到它们随状态的变化值就够了。计算热力学函数变化时，常用到剩余性质或者偏离函数的概念＿ＪＩ。剩余性质是指在相同温度、压力下，真实气体与理想气体的热力学性质的差值；偏离函数与剩余性质的差异主要是作参考态的理想气体压力不同。文章主要讨论用状态方程法计算热力学性质时，剩余性质的计算公式推导。
ｅｐｉｔｕｃｏｆｅｐｒｔｒｎｏｍｅｉｍｏｔｈｒｄｎｍｉｓｔｅｕｔｎ，ｈｔａ＝（，）ｉｗｓａｉｇｕｅｕቤተ መጻሕፍቲ ባይዱｅｆｒｌｏｓｕｌｒｐｒｘｌｉｆｎｔｎｏｍｅａｅａｄｖｌｓｔｅｍｏｙａｃｔｅｑａｉｓｔａｗｓｐＴＶ，ｔａｎｎｆｌｏｄｄｃｏｍｕａｆｅｉａｐｏｅｔｃｉｔｕｕｎａｏｐｍｅｔｒｄｙ
（ａｕｔｆｈｍｉａＥｇｎｅｉｇａｄＬｇｔｎｕｔ，ｕｎｄｎｉｒｉｆｅｈｏｏｙＦｃｌｏｅｃｌｎｉｅｒｎｉｈｄｓｙＧａｇｏｇｙＣｎＩｒＵｎｖｓｙｏｃｎｌｇ，ｅｔＴ
Ｇａｇｈｕ５０６Ｃｉａｕｎｚｏ１０，ｈｎ）０