反常积分与无穷级数的对数审敛法
对数审敛法

对数审敛法一、概述对数审敛法是一种用于求解无穷级数的方法,它利用了对数函数的特殊性质,能够快速地判断级数的收敛性。
该方法具有简单易行、适用范围广等优点,在实际应用中得到了广泛的应用。
二、基本思路对数审敛法的基本思路是将原级数化为一个形式相似但更易判断收敛性的级数,然后利用对数函数的单调性或者极限值来判断原级数的收敛性。
具体来说,可以分为以下几个步骤:1. 对原级数进行变形,使其形式与某个已知收敛或发散的级数相似。
2. 利用对数函数的单调性或者极限值来判断新级数的收敛性。
3. 根据新级数和原级数之间的关系,得出原级数是否收敛。
三、具体方法比较审敛法是对数审敛法中最常用的一种方法。
它将原级数与一个已知收敛或发散的级数进行比较,从而得出原级数是否收敛。
具体来说,可以分为以下两种情况:(1)若存在正整数 N 使得a_n ≤ b_n (n ≥ N),且级数∑b_n 收敛,则级数∑a_n 也收敛。
(2)若存在正整数 N 使得a_n ≥ b_n (n ≥ N),且级数∑b_n 发散,则级数∑a_n 也发散。
2. 极限审敛法极限审敛法是对数审敛法中另一种常用的方法。
它利用对数函数的极限值来判断原级数的收敛性。
具体来说,可以分为以下两种情况:(1)若存在正整数 N 使得lim(n→∞) n·ln(a_n) = L,其中 L 是一个有限的实数,则级数∑a_n 收敛。
(2)若存在正整数 N 使得lim(n→∞) n·ln(a_n) = +∞,则级数∑a_n 发散。
积分审敛法是对于一类特殊的无穷级数而言的。
它是将原级数转化为一个函数的积分形式,然后利用积分的性质来判断原级数的收敛性。
具体来说,可以分为以下两种情况:(1)若函数 f(x) 在[1, +∞) 上单调递减且非负,则原级数收敛当且仅当积分∫[1, +∞) f(x)dx 收敛。
(2)若函数 f(x) 在[1, +∞) 上单调递减且非负,则原级数发散当且仅当积分∫[1, +∞) f(x)dx 发散。
反常积分的审敛法

例1 判别反常积分 ∫ 1
+∞
dx
3
x4 + 1
的收敛性 .
解 ∵当 x ∈ [1,+∞ ) 时 ,
0<
1
3
<
+∞ 1
1
3
x +1
3
4
4 = , p = > 1, 4 3 x4 / 3 x
1
收敛.
∴ 反常积分 ∫
dx x4 + 1
(比较审敛法1)
定理 4 ( 极限审敛法1) 设函数 f ( x ) 在区间 [a ,+∞ ) (a > 0) 上连续,且 f ( x ) ≥ 0. 如果存在常数 p > 1,使得 lim x p f ( x ) 存在,
判别反常积分
∫
3
1
dx 的收敛性 . ln x
1 ∵ lim = + ∞ ∴ x = 1是瑕点 x →1+ lnx
1 x −1 lim ( x − 1) = lim + x →1 x →1+ ln x ln x
0 ( )型 0
= lim +
x →1
= 1 > 0, 3 dx ∴ 反常积分 ∫ 发散 . (极限审敛法2) 1 ln x
1.递推公式 Γ( s + 1) = sΓ( s ) ( s > 0).
证明 Γ( s + 1) =
+∞ −x s 0
∫
+∞
0
e x
+∞ 0 +∞
−x
( s + 1 ) −1
dx
−x
= ∫ e x dx = ∫ = [ x ( −e )]
反常积分与无穷级数收敛关系的讨论

(1) 无界区域上广义二重积分的柯西判别法.
设 为无界区域,如果 ,当 时,有
.
其中 为常数,则广义二重积分 收敛;
(2)含瑕点的广义二重积分的柯西判别法
设在 内 有瑕点 ,若对于 充分接近的点 ,有
.
其中 则
收敛.
那么对于广义二重积分 而言, 收敛与 绝对收敛(即 收敛)之间有何关系?
对于无穷区域上的广义二重积分和含瑕点的广义二重积分而言,收敛和绝对收敛之间的关系[]如下:
Key words:improperintegral, mathematicalanalysis, method ofsubstitution,
improper double integral, infinite series
第
1.1
Riemann积分要求积分区间 有限且被积函数 在该区间上有界.但在实际的应用(特别是物理应用)中,上述条件不满足,仍需要某种形式的积分.因此,积分的概念需要推广,保证我们也可以讨论区间无限或无界函数的类似的积分问题,这就是本章所介绍的反常积分或广义积分.
以下假设 ,若对任何 , , ;若 .
Cauchy判敛法的极限形式 :设 是在任何有限区间 可积的正值函数. 且 . 则
1)
2) .
(二) 阿贝尔判别法与狄利克雷判别法:
1) 阿贝尔判别法:若 在区间 上可积 , 单调有界 , 则积分 收敛.
2) 狄利克雷判别法:设 在区间 上有界 , 在 上单调,且当 时, .则积分 收敛.
关键词:反常积分;数学分析;换元法;反常二重积分;无穷级数
Abstract
From the background of the improper integral, this paper introduces the definition, properties and convergence criterion. In addition ,itdiscussessome simply questions of improper doubleintegral, as well as a simple application in the realof improper integral.Finally, the paper also describes the ties and differences between infinite integral and infinite series.
《高等数学》第6章2 反常积分判敛法
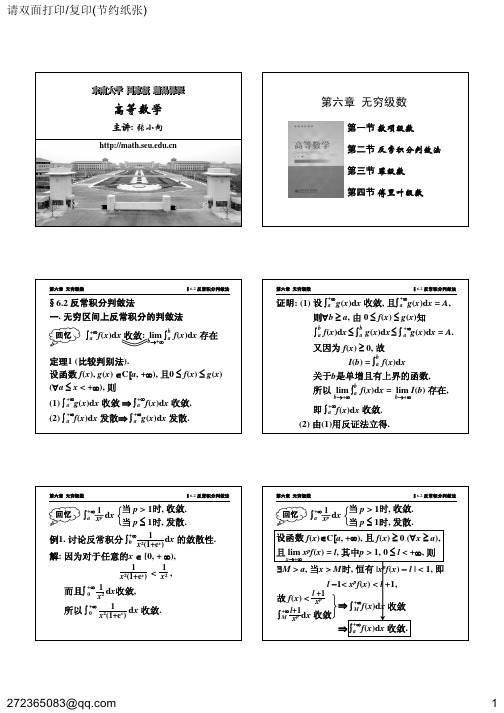
§6.2 反常积分判敛法
例3. 判别下列瑕积分的敛散性.
(1)
∫
1 0
lnx √x
dx.
分析: 令 f(x) = lnx , 则
lim (x − a)pf(x) = l
x→a+
p<1, 0≤l<+∞: 收敛
√x
p≥1, 0<l≤+∞: 发散
① f(x) ∈ C(0, 1],
k = p − 1/2
② f(x) ≤ 0 (∀0 < x ≤ 1),
第六章 无穷级数
§6.2 反常积分判敛法
证明:
(1)
设
∫
+∞ a
g(x)dx
收敛,
且∫
+a∞g(x)dx
=
A,
则∀b ≥ a, 由 0 ≤ f(x) ≤ g(x)知
∫
b a
f(x)dx
≤
∫
b a
g(x)dx ≤
∫
+a∞g(x)dx
=
A.
又因为 f(x) ≥ 0, 故
I(b)
=
∫
b a
f(x)dx
关于b是单增且有上界的函数,
∃M > a, 当x > M时, 恒有 |xpf(x) − l | < l/2, 即
l/2 < xpf(x) < 3l/2,
故 f(x) >
l/2 xp
∫
+∞ M
l/2 xp
dx
发散
⇒
∫
+∞ M
f(x)dx
发散
⇒
∫
+∞ a
f(x)dx
反常积分审敛万能公式

反常积分审敛万能公式在咱们学习数学的过程中,有个叫反常积分审敛的东西,这玩意儿可不简单,不过别担心,今天咱就来聊聊所谓的反常积分审敛万能公式。
先给大家举个例子哈。
有一次我去超市买零食,看到巧克力在打折,那种巧克力平时卖得挺贵,这次居然降价了。
我就想,这降价是不是有个“极限”呢?就像反常积分,积分区间无限延伸,那这个巧克力价格的变化是不是也能找到一个类似的规律?说回反常积分审敛万能公式。
这个公式就像是一把神奇的钥匙,能帮我们打开判断反常积分收敛还是发散的大门。
比如说,对于形如∫[a,+∞) f(x)dx 的反常积分,我们通过一些特定的计算和判断,就能知道它到底是收敛还是发散。
那这个万能公式具体是啥样呢?其实它涉及到一些复杂的数学运算和条件判断。
比如说,我们得看看被积函数的形式,是多项式啊,还是指数函数啊,或者是其他更复杂的形式。
然后根据不同的形式,运用不同的方法和定理来判断。
我还记得有个学生,他在做反常积分审敛的题目时,总是搞不清楚那些条件和公式的运用。
我就跟他说,你别把这当成特别难的东西,就像你玩游戏,每个关卡都有规则,咱们只要熟悉了规则,就能通关。
后来他慢慢地掌握了,那高兴劲儿,就像终于在游戏里打败了大 boss 一样。
在实际应用中,反常积分审敛万能公式能帮我们解决很多问题。
比如说在物理中,计算一些无限过程的能量或者功的时候,就能用这个公式来判断结果是否合理。
而且,大家别觉得这个公式只是为了考试才学的。
其实在很多实际的科学研究和工程计算中,都能用到它。
就像建筑师在设计高楼的时候,需要考虑各种力的作用,这里面可能就涉及到反常积分的计算和审敛。
总之,反常积分审敛万能公式虽然看起来有点复杂,但只要我们耐心去理解、多做练习,就一定能掌握它。
就像我当初学会挑选巧克力一样,只要掌握了方法,就能买到最实惠的美味。
希望大家在学习反常积分审敛万能公式的时候,都能充满信心,加油!。
反常积分审敛法-精品文档

则
a
f ( x)dx 收 敛 ;
x
如 果limxf ( x) d 0 (或 limxf ( x) ), 则
x
af ( x)dx 发Fra bibliotek散 .
证明
dx 的收敛性 . 例2 判别反常积分 2 1 x1 x 1 2 解 lim x 1 , p21 2 x x1 x
F (x )在 [a , )上是单调增加的 .
F (x ) 在 [ a , ) 上有上界
lim F (x ) 存在 (极限的存在准则)
x x
即 lim 存在 f(t)dt
x a
收敛 f(x)dx
a
程序设计 网络课件 教学设计 多媒 体课件 PPT文档
f(x ) dx 发散 a 1 特别地,取 g( x ) p ,即得下面的 x
网络课件 教学设计 多媒 比较审敛法. 程序设计体课件 PPT文档
定理 3 (比较审敛法1 ) 设函数 f ( x) 在区间 [a, ) (a 0) 上连续,且 f ( x) 0. 如果存在常数 M 0 及 p 1 ,使得
arctan x 例4 判 别 反 常积 dx 分 的收 . 敛性 1 x arctan x x lim arctan x 解 lim 0 x x x 2
定理 2 ( 比较审敛原 ) 理 设函数 f (x)、 g(x) 在 区 间 [a, )上 连 续 、 非 , 负
如果 f (x) g(x),(a x ),并 且 a g(x)dx收 敛 , 则a f (x)dx也 收 敛 ; 如 f( 果 x) g(x),(a x ), 并且 则 f (x)dx也 发 散 . a g(x)dx发 散 , a
反常积分极限审敛法

反常积分极限审敛法反常积分极限审敛法(IntegralLimitComparisonTest)是一种常用的数学分析方法,可以用来判断一个无穷级数的收敛性质以及它的收敛情况如何。
它是一种非常重要的定理,有助于我们解决无穷级数的问题。
反常积分极限审敛法(Integral Limit Comparison Test)是一种在数学分析中有着重要应用的定理,它可以根据一般情况下的某个无穷级数的收敛性质,对比另一个无穷级数,从而实现对两个无穷级数的收敛性质的比较。
其基本原理是,如果一个无穷级数的某项分母大于另一无穷级数的某项分母,且比值的反常积分不等于零,则该级数收敛。
反常积分极限审敛法的具体步骤是使用经典反常积分技术,先将待证明的无穷级数和另一个已知收敛的无穷级数,比如收敛正项级数,列出来,然后将它们做出比较,比较的结果若为恒等式,则证明无穷级数收敛;若为大于等于式,则证明无穷级数收敛;若为小于等于式,则证明无穷级数可能收敛,但不一定收敛;最后,通过对比反常积分的值,可以得出有关无穷级数收敛性质的最终结论。
反常积分极限审敛法具有很多优势,其中最主要的优势就是可以用来判断一个无穷级数的收敛性质及其如何收敛,只要满足其在无穷级数上的充要条件,就可以得出有关的结论。
另外,由于反常积分的某一项收敛性质被推广到一般情况,因此可以比较一般情况下的无穷级数的收敛性质,而不是只比较其特殊情况下的收敛情况。
最后,通过反常积分极限审敛法,可以有效解决无穷级数的问题,从而提高研究的效率。
综上所述,反常积分极限审敛法是一种非常重要的定理,在数学分析中有着十分重要的应用,它可以用来判断一个无穷级数的收敛性质以及它的收敛情况如何,并可以有效的解决无穷级数的问题,提高研究的效率。
然而,同时也要根据实际情况,审慎选择反常积分极限审敛法,以期获得比较准确的研究结果。
无穷限反常积分敛散性及审敛法则(教案)

无穷限反常积分敛散性及审敛法则一、教学目标分析在开始本节课程学习之前,学生已经对定积分有所了解,并初步掌握定积分的基本知识,本节通过介绍反常积分,加深学生对积分的了解,使同学对积分的了解更加系统化,并通过讲解让同学们减轻对积分的迷惑。
让学生反常积分在一些实际问题中的应运。
二、学情/学习者特征分析学生通过对前面课程的学习,对积分已经有了初步的了解。
但对于一些特殊积分或者有关实际问题的积分还是存在着一定的迷惑。
由于本节内容有点枯燥,所以要积极调动学生的兴趣,培养好课堂气氛,使学生充分掌握本节课的内容。
三、学习内容分析1.本节的作用和地位通过对本节的学习来解决一些不属于定积分的问题,这些问题通常是一些实际问题。
例如:常会遇到积分区间为无穷区间,或者被积函数为无界函数的积分等问题。
2.本节主要内容1. 无穷限反常积分的定义与计算方法2. 无穷限反常积分的性质3. 无穷限反常积分的比较审敛法则4. 条件收敛与绝对收敛 3.重点难点分析教学重点:无穷限反常积分计算,无穷限反常积分的比较审敛法则; 教学难点:无穷限反常积分的比较审敛法则。
4.课时要求:2课时四、教学理念学生在之前就已经掌握了一定的知识,通过本节对学生的教学使学生进一步了解反常积分,尤其是其在一些实际问题中的应运。
五、教学策略在教学中主要讲清反常积分的定义及其性质,并适时举例讲解,引导学生互动,相互讨论解决问题。
六.教学环境网络环境下的多媒体教室与课堂互动。
七、教学过程一、无穷限反常积分的定义定义1 设函数/定义在无穷区间[+∞,a )上,且在任何有限区间[u a ,]上可积.如果存在极限 则称此极限J 为函数f 在[+∞,a )上的无穷限反常积分(简称无穷积分),记作dx x f J a⎰+∞=)(,并称dxx f a ⎰+∞)(收敛.如果极限J dx x f uau =⎰+∞→)(lim不存在,亦称dx x f a ⎰+∞)(发散.类似地,可定义f 在(b ,∞-]上的无穷积分:.)(lim )(dx x f dx x f buu b⎰⎰-∞→∞-=对于f 在(+∞∞-,)上的无穷积分,它用前面两种无穷积分来定义:,)()()(dx x f dx x f dx x f a a ⎰⎰⎰+∞∞-∞-+∞+=其中a 为任一实数,当且仅当右边两个无穷积分都收敛时它才是收敛的.注: dx x f a⎰+∞)(收敛的几何意义是:若f 在],[+∞a 上为非负连续函数,则介于曲线)(x f y =,直线ax =以及x 轴之间那一块向右无限延伸的阴影区域有面积J .例1 讨论无穷积分.1)102⎰+∞+x dx ,.1)22⎰∞+∞-+xdx ,.)302⎰+∞-dx xe x 的收敛性. 例2 讨论下列无穷积分的收敛性:⎰+∞1)1p xdx, ;)(ln )22⎰+∞p x x dx 二、无穷积分的性质由定义知道,无穷积分⎰+∞adx x f )(收敛与否,取决于积分上限函数=)(u F ⎰uadx x f )(在+∞→u 时是否存在极限.因此可由函数极限的柯西准则导出无穷积分收敛的柯西准则. 定理11.1 无穷积分⎰+∞adx x f )(收敛的充要条件是:任给ε>0,存在G ≥a ,只要G u u >21,,便有ε<=-⎰⎰⎰2121)()()(u u u au adx x f dx x f dx x f .此外,还可根据函数极限的性质与定积分的性质,导出无穷积分的一些相应性质.性质1 若dx x f a)(1⎰+∞与dx x f a)(2⎰+∞都收敛,1k ,2k 为任意常数,则[]dx x f k x f k a⎰+∞+)()(2211也收敛,且[]dx x f k dx x f k dx x f k x f k aaa )()()()(22112211⎰⎰⎰+∞+∞+∞+=+.性 质 2 若f 在任何有限区间[u a ,)上可积,且有⎰+∞adx x f )(收敛,则⎰+∞adx x f )(亦必收敛,并有⎰⎰+∞+∞≤aadx x f dx x f )()(.证:⎰+∞adx x f )( 由收敛,根据柯西准则(必要性),任给0>ε,存在G ≥a ,当G u u >>12时,总有⎰⎰≤2121)()(u u u u dx x f dx x f . 利用定积分的绝对值不等式,又有⎰21)(u u dx x f ≤ε<⎰21)(u u dx x f .再由柯西准则(充分性),证得⎰+∞adx x f )(收敛又因⎰uadx x f )(≤⎰uadx x f )(,令+∞→u 取极限,立刻得到不等式.当⎰+∞adx x f )(收敛时,称⎰+∞adx x f )(为绝对收敛.性质3指出:绝对收敛的无穷积分,它自身也一定收敛.但是它的逆命题不成立,称收敛而不绝对收敛的无穷积分为条件收敛.性质3 若f 在任何有限区间[u a ,]上可积,b a <,则⎰+∞adx x f )(与⎰+∞bdx x f )(同敛态(即同时收敛或同时发散),且有⎰+∞adx x f )(=⎰b adx x f )(+⎰+∞bdx x f )(,性质2相当于定积分的积分区间可加性,由它又可导出⎰+∞adx x f )(收敛的另一充要条件:任给ε>0,存在0≥G ,当u >G 时,总有.)(ε<⎰+∞adx x f .事实上,这可由⎰⎰⎰+∞+∞+=uaudx x f dx x f dx x f )()()(结合无穷积分的收敛定义而得.三、比较判别法首先给出无穷积分的绝对收敛判别法.由于⎰uadx x f )(关于上限u 是单调递增的,因此⎰+∞adx x f )(收敛的充要条件是⎰uadx x f )(存在上界.根据这一分析,便立即导出下述比较判别法:定理11.2 (比较法则) 设定义在[+∞,a )上的两个函数f 和g 都在任何有限区间[u a ,]上可积,且满足 则当⎰+∞adx x g )(收敛时dx x f a⎰+∞)(必收敛(或当dx x f a⎰+∞)(发散时,⎰+∞adx x g )(必发散).例3 讨论dx x x⎰+∞+021sin 的收敛性. 解:由于],0[,111sin 22+∞∈+≤+x x x x ,而2102π=+⎰+∞x dx 为收敛,故dx xx ⎰+∞+021sin 为绝对收敛. 当选用⎰+∞1p xdx作为比较对象⎰+∞a dx x g )(时,比较判别法有如下两个推论(称为柯西判别法). 推论1 设f 定义于[+∞,a ] (0>a ),且在任何有限区间[u a ,]上可积,则有:(i)当 ),[,1)(+∞∈≤a x xx f p ,且1>p 时, dx x f a ⎰+∞)(收敛; (ii)当),[,1)(+∞∈≥a x xx f p 且1≥p 时, dx x f a ⎰+∞)(发散.推论2 设定义于[+∞,a ),在任何有限区间[u a ,.]上可积,且λ=+∞→)(lim x f xpx .则有:(i)当 +∞<≤>λ0,1p 时, dx x f a⎰+∞)(收敛; (ii)当 +∞≤<≤λ0,1p 时,dx x f a⎰+∞)(发散.推论3 若f 和g 都在任何[u a ,)上可积,0)(>x g ,且,)()(lim c x g x f x =+∞→则有(i)当+∞<≤c 0时,由⎰+∞adx x g )(收敛可推知dx x f a ⎰+∞)(也收敛; (ii)当+∞≤<c 0时,由⎰+∞adx x g )(发散可推知dx x f a⎰+∞)(也发散.四、狄利克雷判别法与阿贝尔判别法这里来介绍两个判别一般无穷积分收敛的判别法. 定理11.3 (狄利克雷判别法) 若⎰=uadx x f u F )()(在[+∞,a )上有界,)(x g 在[+∞,a )上当+∞→x 时单调趋于0,则无穷积分⎰+∞adx x g x f )()(收敛.定理11.4 (阿贝尔(Abel)判别法) 若⎰+∞adx x f )(收敛,)(x g 在[+∞,a )上单调有界,则无穷积分⎰+∞adx x g x f )()(收敛.用积分第二中值定理来证明狄利克雷判别法与阿贝尔判别法. 例5 讨论dx x xp ⎰+∞1sin 与)0(cos 1>⎰+∞p dx xx p 的收敛性. 解:这里只讨论前一个无穷积分,后者有完全相同的结论.下面分两种情形来讨论: (i)当p >1时dx x xp ⎰+∞1sin 绝对收敛.这是因为),,[,1sin +∞∈≤a x x x x p p 而⎰+∞1p xdx 当p >1时收敛,故由比较法则推知dx x xp⎰∞+1sin 收敛. (ii)当10≤<p 时dx x x p ⎰+∞1sin 条件收敛.这是因为对任意u ≥1,有2co s 1co s si n 1≤-=⎰u x d x u ,而p x 1当0>p 时单调趋于)(0+∞→x ,故由狄利克雷判别法推知dx x xp ⎰+∞1sin 工当0>p 时总是收敛的. 另一方面,由于),1[,22cos 21sin sin 2+∞∈-=≥x x x x x x x x p ,其中dt ttdx x x ⎰⎰+∞+∞=21cos 2122cos 是收敛的,而⎰+∞12xdx是发散的,因此当10≤<p 时该无穷积分不是绝对收敛的.所以它是条件收敛的. 例6 证明下列无穷积分都是条件收敛的.,sin 12⎰+∞dx x ,cos 12⎰+∞dx xdx x x ⎰+∞14sin证:前两个无穷积分经换元2x t =得到,2sin sin 112dt tt dx x ⎰⎰+∞+∞=.2cos cos 112dt tt dx x ⎰⎰+∞+∞=由例5知它们是条件收敛的.对于第三个无穷积分,经换元2x t =而得⎰⎰+∞+∞=1214sin 21sin dt t dx x x ,它也是条件收敛的.从例6中三个无穷积分的收敛性可以看到,当+∞→x 时被积函数即使不趋于零,甚至是无界的,无穷积分仍有可能收敛.八、学习评价本节成功向学生讲解了两种定积分的推广即反常积分,尤其对无穷反常积分进行介绍,并对其敛散性及审敛性附带介绍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
!" #$%&’"’()*" +*, ’ -)./"01,.(’"0)"2 )" 31(()"2 (41 5)6)( *+ 7/’&)(8 9/":()*"
) 0123 45$ 6 7$89&,
( & ! "#$%! &’ ()%*#+)%,-. / 0&+$1%#2 3-,#4-#, 0*&456,45 74,8#2.,%9 &’ :2%. )4; 3-,#4-#. , <&45-*1)4 0*&456,45 /,)&:, ,0*,4); ) ! =&.%52);1)%# 3-*&&>, 3&1%*?#.% 74,8#2;&! , 0*,4))
*J
-
!!
"
" $# 收敛, 故 ##
-
!!
"
( $ #) $# 收敛% & &)( $ #) " &! ’ ! 知, 对" ’ ( *, 存在 " ( " , 使得对任意的 # ( " , 有 &)# #
当 ! % " 时, 由 &’(
#& ! !
& &)( $ #) " " % !!", 即有 ( $ # ) ( ! ! " ’ ! !" ; 而无穷积分 &)# # ## 散% 由比较原则知反常积分 #+ 瑕积分的对数审敛法
当 ! ’ # K 时, 对) ’ ", 存在 % $ * , 使得对任意的 " $ % , 有
! [ 收稿日期] "##) H ** H *M
[ 作者简介] 毛一波( *J$* H ) ,男,四川广安人,讲师,硕士,主要从事基础数学研究E [ 基金项目] 重庆文理学院科研项目资助( N"##M?+D" ) E
-
!!
"
" $# 当 ) % " 时发散, 从而 #)
-
!!
" #
! !" #
"
$# 发
-
!!
"
( $ #) $# 发散, 也即
-
!!
"
( $ #) $# 发散%
$ #)为定义在区间 ( *, +]上的正值函数, 在点 * 的任一右邻域 ( *, * ! #)( ( *, 定理 #+ 设函数 ( +]上无界, 且在任何区间 [ $, +]( ( *, +]上可积, &’( ( " )* % ! % " 时, 瑕积分 ( $ #) $# 收敛;
!
定理 ,+ 设无穷级数 * - , 的通项 - , ( * , 且 &’(
, ’" ,& ! !
& &) ( -, ) ’ !, 则: &),
(") 当 " % ! % ! ! 时, 无穷级数 * - , 收敛;
, ’" !
当 * % ! % " 时, 无穷级数 * - , 发散% (#)
, ’"
( 上接第 ), 页) [ 参考文献]
[&] 华东师范大学数学系* 数学分析 ( 第 ’ 版) [ +] * 北京: 高等教育出版社, ),,&* [)] 孙本旺, 汪浩* 数学分析中的典型例题和解题方法 [ +] * 长沙: 湖南科学技术出版社, &-.&* [’] 裴礼文* 数学分析中的典型问题与方法 [ +] * 北京: 高等教育出版社, &--’* [/] 吴良森, 毛羽辉, 等* 数学分析习题精解 [ +] * 北京: 科学出版社, ),,)*
5*2’,)(461(): >,)(1,)’ +*, !;"*,6’& ?"(12,’& ’"0 ?"+)")(1 @1,)1. +1N O$ 6 FD
( "#$%! &’ ()%*#+)%,-. )4; 0&+$1%#2 3-,#4-#,0*&456,45 74,8#2.,%9 &’ :2%. )4; 3-,#4-#.,<&45-*1)4 0*&456,45 /,)&:, , 0*,4))
)/
反常积分与无穷级数的对数审敛法
作者: 作者单位: 刊名: 英文刊名: 年,卷(期): 被引用次数: 毛一波, MAO Yi-bo 重庆文理学院,数学与计算机科学系,重庆,永川,402160 重庆文理学院学报(自然科学版) JOURNAL OF CHONGQING UNIVERSITY OF ARTS AND SCIENCES(NATURAL SCIENCE EDITION) 2007,26(1) 0次
* #& !* !
& &)( $ #) ’ !, 则: &) ( # & *)
-
+
瑕积分 ( $ #) $# 发散% ( # )" % ! % ! ! 时,
*
-
+
证明+ 当 * % ! % " 时, 对" ’
" &! ( *, 存在 # ( * ( # % " ), 使得当 # $( *, * ! #)时, #
!;.(,’:(: <=$> 5?@$A#B B#$%$85@BC 5 CDEF@ G=B8 58 $%7D?@58@ HE8A@$D8 #$%$@ $> E>BC $8 9B@@$89 @=B #$%$@ DH CE5#$@I HE8A@$D8* <=$> 757B? 95JB 5 7D>$@$JB 58>GB? 58C 5#>D 95JB 58 BK7#585@$D8 HD? 5 %$>E8CB?>@58C$89 $8 9B@@$89 @=B #$%$@ DH CE5#$@I HE8A@$D8* L@58C$89 D8 @=B J$BG7D$8@ DH @=B 757B?, @=B 5E@=D? BK758CBC @=B %B@=DC DH 9B@@$89 @=B #$%$@ DH CE5#$@I HE8A@$D8 $8 9B@@$89 @=B #$%$@ DH $??5@$D85# BK7?B>>$D8* <18 =*,0.: CD%5$8 DH CBH$8$@$D8;$%7D?@58@ HE8A@$D8 #$%$@; $CB8@$A5# BME5@$D8
定理 , 可借助 ) 级数的敛散性进行证明% 例+ 对任意的实数 % , 无穷积分 事实上,
#& ! !
-
!!
"
# % . &# $# 收敛%
&’(
& &) ( # % . &# ) # ’ &’( ( & %) ’ ! ! , #& ! ! &) # &)# ( 下转第 #- 页)
由定理 " 的极限形式知结论成立% #*
* # * + +
当瑕点为右端点时也有类似情形% 此外, 定理 # 也有类似于定理 " 的一般形式% ,+ 无穷级数的对数审敛法 无穷级数的敛散性与无穷积分的敛散性密切相关, 最能体现二者之间关系的当数无穷级数的积 分审敛法% 因此, 对比无穷级数和无穷积分的关系, 关于无穷级数也有类似的对数审敛法%
+ + " " " ( ! &", 即( $ #) ( ’ ; 而 $ # 发散, 所以瑕积分 ( $ #) $# 发散% ! !" ! !" ! &" * * ( # & *) ( # & *)# ( # & *)#
-
-
& &)( $ #) " 当 ! ’ ! ! 时, 存在 # ( * ( # % " ), 使得当 # $ ( *, * ! #)时, (#, 即( $ #)% # &) ( # & *) ( # & *) ; 而 所以瑕积分 - ( $ #) $# 收敛% - ( # &" *)$# 收敛,
-
#K
*
( ! ") >" 收敛; 反之, 若存在 % $ * , 使得对任意的
-
#K
*
( ! ") >" 发散E
定理 * 有如下极限形式: 设函数 ( ! ")为定义在区间 [ * ,# K )上的正值函数, 且 17L (*) 当 * ( ! % # K 时, 无穷积分 (") 当 ! ( * 时, 无穷积分 下面就极限形式给出证明E & 1/( ! ") ! &* ’ ! 知, 对" ’ $#, 存在 % $ * , 使得对任意 1/" " #K #K & 1/( ! ") * * * 的 " $%, 有 $ !&", 即( ! ")( ! & " ’ ! #* ; 而无穷积分 从而 ) > " 当 ) $ * 时收敛, % % 1/" " " "" 证明! 当 * ( ! ( # K 时, 由 17L
